2014, Vol. 29
2. 中国科学院地质与地球物理研究所, 岩石圈演化国家重点实验室 100029;
3. 中国科学院大学, 北京 100039
2. State Key Laboratory of Lithospheric Evolution, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 10029, China;
3. University of Chinese Academy of Sciences, Beijing 100039, China
0 引 言
地球物理中的层析成像是一种基于Radon变换原理，采用地表观测集来获得地下介质物性参数二维和三维图像的技术，已被广泛应用于地球内部结构探测、地球动力学、工程和灾害地质、矿产等资源研究等领域(滕吉文等，2003;Nolet，2008; Shearer，2009; Rowlinson et al., 2010; 田有等，2011; Liu and Gu， 2012).
Aki和Lee(1976)首先将层析成像方法应用于地震深部探测中，提出地震走时层析成像方法，并成功获得美国加利福尼亚地区的地壳结构.20世纪80年代，金安蜀等(1980)将地震走时层析成像应用到北京地区壳幔速度结构的研究中，从此拉开了中国地球物理学领域应用地震层析成像技术探测地球内部结构的序幕.经过了三十多年的发展，地震层析成像技术已经成为了透视深部地球的利器，在造山带深部构造、火山活动、地幔柱、板块动力学等研究中取得了许多重要成果(Van der Hilst et al., 1997; 王辉和黄鼎成，2000; 胥颐等，2001; 雷建设等，2002; 滕吉文等，2003; Montelli et al., 2004; 胥颐等，2006; 李志伟等，2006; Zhao et al., 2007; 田有等， 2007，2009; Nolet，2008; 江国明等，2008;雷建设等，2009; Zhao et al., 2009，2012; Rawlinson et al., 2010; 郑洪伟等，2011; Liang et al., 2012).
随着计算机技术的不断发展，通过直接求解声波方程或弹性波方程来模拟实际地球模型中地震波的传播过程已经成为了现实(Komatitsch et al., 2004).数值求解全波方程来模拟地震波的传播能够提供更加完整、准确的合成地震数据，有利于地震层析成像方法获得高精度、高分辨率的地球内部结构信息(Tromp et al., 2008).波形反演可以利用直达波、反射波、折射波、散射波、转换波、多次波等全波场的波形信息，这是地震层析成像方法的最终目标之一.但是，基于数值求解声波或弹性波方程的成像方法计算量很大，对运行速度和内存等计算硬件有很高的要求，将波形反演广泛应用于精细壳幔结构的探测，尤其是三维情况，还存在较大的距离.尽管频率域波形反演，能用少数几个频率的波形反演，结果与全时间域的波形反演结果相当，效果提高一到二个数量级(Pratt，1999; 武振波等，2014)，但对于全球尺度范围，由于计算平台的限制，目前依然很难实现基于精细网格、较高频率范围的大尺度反演.因此，地震波走时层析成像仍然是目前高精度壳幔速度结构探测的最常用手段.
根据研究范围的大小，地震层析成像可分为全球层析成像、区域层析成像和局部层析成像；根据所利用的地震波类型不同，可分为体波层析成像和面波层析成像等.面波能量沿着二维扩散，在水平方向上的衰减较体波小得多，但是面波在深度方向上能量衰减很快(指数规律衰减)，反演时对 1 3 波长的深度敏感.相对于地表近似大圆弧路径传播的面波，在地球内部传播的地震体波在纵向衰减相对比较慢，适用于局部、区域以及全球等多尺度结构的研究.
在固体地球物理研究中，我们往往假设地球是一个弹性体，在地球介质中传播的地震波满足弹性波方程(Dahlen and Tromp， 1998; Cerveny，2001; Nolet，2008; 滕吉文等，2003).由于大尺度地球内部介质反演精度的要求及计算机技术的限制，早期地震体波层析成像方法主要是以射线理论层析成像方法为主.地震射线的理论基础是在高频近似条件下，地震波场的主要能量沿着射线轨迹附近传播至接收器(Cerveny，2001; 徐涛等，2004; Xu et al., 2006，2010，2014; 李飞等，2013).基于射线理论的走时层析成像，首先由射线追踪方法获得介质内传播的地震射线，并由计算的理论到时和观测到时差来反演介质属性.该方法计算量相对较小，计算效率高，是体波走时层析成像的常规方法(Zhao et al., 1992，1994; 丁志峰等，1999; Nolet，2008).利用远震震相相对走时差可以反演介质的相对速度扰动场(Zhao et al., 1992)，利用近震震相的绝对走时差可以反演介质的绝对速度场(Zhao et al., 1994).陈立华和宋仲和(1990)获得华北地区的速度场，显示该区具有强烈的横向不均匀性.滕吉文等(1994)重建了西北塔里木盆地及其邻区的地壳地幔三维速度图，表明该区地壳、地幔结构在纵向和横向上都是不均匀的.吕庆田等(1996)获得青藏高原的速度场，显示青藏高原上地幔速度较正常大陆上地幔速度要低，羌塘地块上地幔速度更低.田有等(2007)反演了兰德斯地震区三维P波和S波速度结构和泊松比分布，显示了地震的发生和分布与地壳结构的横向不均匀性有密切的关系，且大地震的发生与其周围的构造环境密切相关，并非发生在任何地方，而兰德斯地震可能是由于流体存在使地壳岩石弱化才引发的.由于地壳内速度的横向不均匀性会导致远震射线在地壳内的交叉较差，如果不能利用近震到时数据或人工爆破数据对地壳内的速度结构进行约束，深部成像的质量会受到影响.针对在无法获取某地区的近震数据或人工爆破数据的情况下，如何消除地壳速度结构对远震层析成像结构的影响的问题，江国明(2009)采用地壳校正的方法加以限制消除，得到的成像结构能更好地解释深部构造特征.
由程函方程的数值解可以直接获得地球介质的初至走时场，根据走时场的梯度方向反向追踪射线路径，并由此进行速度结构成像.该方法能够保证射线走时的最小值，特别适合初至波成像，且能适应剧烈变化的横向非均匀速度场.程函方程的数值解，常用的是有限差分法(Vidale， 1988，1990; Qin et al., 1992; 段永红等，2002; Lan and Zhang， 2013a，2013b).快速推进法(FMM)利用迎风有限差分格式求解局部程函方程(Sethian，1996)，该方法无条件稳定，计算速度快，且能保证得到的是初至波到时.Rawlinson等(2004，2006)基于FMM发展了初至波及反射波层析成像方法，现已被普遍应用到地震层析成像中(郭飚等，2009; 张风雪等， 2011，2013).由于该方法能处理反射波，因此，同样可以应用在人工源宽角地震数据，反演地壳尺度的速度结构.由于射线理论通过速度网格节点来插值获得连续介质，而基于程函方程数值解方法，模型参数则为离散介质；因此获得同样分辨率的反演结果，需要更密集的速度网格分布，但这将导致计算量显著增多(李飞等，2013).
射线理论假设地震波是无限高频的，且只考虑传播路径上的速度结构对地震波走时的影响.实际上，地震产生的波是有频率范围的.地震波从震源出发，经地下介质传播到达地表的地震台站，其能量在震源和台站间一定宽度空间范围内传播，即第一菲涅尔体，相应的射线称为第一菲涅尔体射线(Cerveny and Soares， 1992).杨国辉(2009)分别利用精确法和傍轴近似方法计算了初至波菲涅尔体射线，而Bai等(2013)将之应用于层析成像研究中.
Dahlen等(2000)针对地震波频率的有限性，提出了有限频层析成像(Finite-Frequency Tomography)理论，并利用射线求和及傍轴近似两种方法分别获得三维灵敏度算核(Dahlen et al., 2000; Hung et al., 2000).Zhao等(2000)用简正振型方法获得球对称介质中弹性波的三维有限频走时灵敏度算核.有限频理论基于波动方程，对于任意有限频率的波都成立，因此比无限高频近似的射线理论更接近真实的正演理论.相对于射线理论，有限频理论计算量大，且成像效果是否有显著的改进，还是处于争论中的问题，有待更深入的研究(Maarten et al., 2005; van der Hilst et al., 2005; Li and van der Hilst，2010; 江燕等，2011).
3 0多年来，随着全球性和区域性的综合地震台网的建立，计算机技术的不断发展及地球物理学家的不断努力，体波层析成像方法无论是在理论还是在方法上都得到了很大的推动，并取得了卓有成效的成果.根据成像方法的不同，本文主要将介绍目前普遍使用的三种代表性体波走时层析成像方法，即基于高频近似射线理论的成像方法(Zhao et al., 1992，1994)，基于程函方程数值解的初至波成像方法(Rawlinson and Sambridge， 2004; Rawlinson et al., 2006)及有限频成像方法(Dahlen et al., 2000; Hung et al., 2000). 1 基于高频近似射线理论的成像方法
基于高频近似射线理论的成像方法，其地震波运动满足光学传播的几何特征，即在一定的数学模型基础上计算射线路径及相应的走时信息.不同的成像方法主要区别在于其模型参数化和射线追踪的不同.
射线理论主要基于层状模型(Zhao et al., 1992，1994; Zelt and Smith， 1992)和块状模型(Xu et al., 2006，2010，2014)；在层内或块内，介质通过函数表达式(Xu et al., 2006，2010)或网格插值(Thurber 1983; Zhao et al., 1992; Xu et al., 2014)获得连续介质分布.
传统的射线追踪方法包括试射法(Langan et al., 1985; Virieux and Farra， 1991; 徐涛等，2004)和弯曲法(Julian and Gubbins， 1977; Thurber and Ellsworth， 1980; Um and Thurber， 1987; Pereyra，1992; Xu et al., 2006，2010，2014).其中，Um和Thurber(1987)提出的伪弯曲法(Pseudo-bending)，能够准确、快速地获得连续速度场中的射线路径和走时，但是该方法不适用于存在速度间断面的介质.
我们以Zhao等(1992)方法为例介绍基于高频近似射线理论的走时层析成像方法.Zhao等(1992，1994)对地球模型进行分层划分，以一组离散的二维网格节点来描述速度间断面，如Moho面等.在每层介质内通过网格节点速度的线性插值获得连续分布的速度场，即任意一点的速度可以由该点周围相邻的八个网格节点的速度值进行线性插值得到，即：
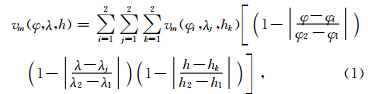
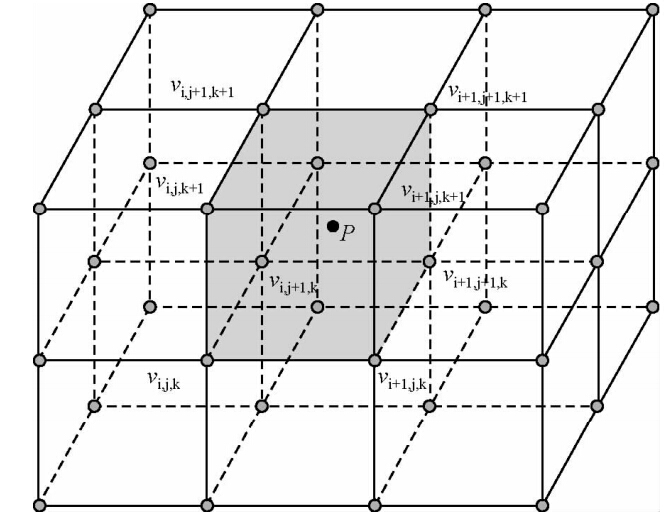 | 图 1 对三维速度网格节点，通过某种插值方式获得任意点(如P点)速度分布(Xu et al., 2014) Fig. 1 Velocity distribution of an arbitrary point (e.g. P point)obtained by an interpolation way to the three-dimensional velocity grid nodes(Xu et al., 2014) |
Zhao等(1992)采用弯曲法来进行正演射线追踪.结合伪弯曲法(Um and Thurber， 1987)和二分法(Bisection method)分别扰动修正落在层状介质内部和界面上的路径点.二分法为多次迭代修正的方法，Xu等(2014)将该方法改进为一阶显式增量修正的方式，由于该修正过程在射线追踪过程中存在成千上万次的重复计算，因此能够显著提高射线追踪的效率.
在反演过程中，采用的是对震源参数与速度参数的联合反演.在球坐标系下其走时方程形式为
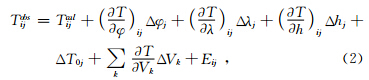
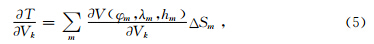
利用高频近似的射线理论进行射线追踪，并计算走时残差，然后通过理论走时对参数的偏导数建立反演方程组.采用反复迭代计算参数的扰动值，并对原模型进行修正，最终得到与真实值接近的模型参数.在该层析成像反演过程中，初至 P波和S波以及后至相都可以被利用.Zhao等人利用该方法，采用初至P波和S波数据及俯冲板块边缘和Moho面处的转换波，研究了日本东北部地区俯冲带的三维P波速度结构(Zhao et al., 1992).郑洪伟等(2007)利用远震P波相对走时残差对青藏高原及其周缘地区进行成像，发现印度岩石圈地幔在不同的位置向北俯冲的形态不同，但俯冲前缘都到达羌塘地体之下.雷建设等(2009)利用大量的P波到时资料，反演得到了龙门山断裂带及其周边地区的地壳精细三维P波速度结构，揭示了龙门山断裂带地壳上地幔存在显著的横向不均匀性.除此之外，该方法也被应用到了阿拉斯加(Zhao et al., 1995)、印度(Kayal and Zhao， 1998)、加利福尼亚(Zhao et al., 1996)等一系列俯冲带和大陆碰撞区.这些三维地壳和地幔模型为这些区域的地震大地构造、岩浆活动和地球动力学等方面的研究提供了地震学框架.图 2是通过该成像方法得到的日本东北部整个日本弧的三维P波、S波速度及泊松比的成像图(Zhao et al., 2007).图中红色和蓝色分别表示低速和高速.白色圆点表示沿着剖面15公里宽的范围内发生的地震.红色三角表示活火山，黑色倒三角表示日本沟的位置.剖面顶部的粗水平线表示地震台所在的陆上区域.三条粗曲线分别表示Conrad间断面、Moho间断面及俯冲太平洋板片的上边界，虚线表示板片的下边界.成像结果图清晰地显示了俯冲的太平洋板块形态，该板块呈现出了明显的高速异常，比正常地幔速度高出5%~6%.
 | 图 2 日本东北部日本弧体波成像剖面结果(Zhao et al., 2007)(a)P波速度;(b)S波速度;(c)泊松比. Fig. 2 Vertical cross-sections of(a)P-wave velocity，(b)S-wave velocity，and (c)Poisson’s ratio images along Japan Arc(Zhao et al., 2007). |
基于射线成像方法虽然计算量小、速度快，但是当非均匀速度场剧烈变化的时候，由于正演射线追踪存在多路径的原因，反演迭代过程中有可能会不收敛.因此利用程函方程有限差分数值解，获得初至波走时，并反演速度结构也是重要的途径.有限差分走时算法最初由Vidale(1988)提出，并将其推广到三维空间中(Vidale，1990).Hole(1992)利用有限差分走时场(Vidale， 1988，1990)，根据走时场的梯度方向，反向追踪射线路径，并通过反投影方法获得上地壳速度场.段永红等(1992)利用Hole(1992)的算法采用Pg波的初至到时得到了华北地区上部地壳的三维速度结构，结果显示了华北地区具有复杂的地质构造和发生强震的深部背景.由于该走时场相当于利用了直达波(回折波)、折射波等初至波走时信息，没有利用到续至波中的反射波等信息，因此主要应用在浅层速度结构的反演中.Rawlinson等(2004，2006)则利用快速推进法(FMM)，不仅可以获得绝对最小走时场，而且还可以考虑反射波信息.下面将介绍基于FMM的初至波成像方法.
由于传统的有限差分方法存在稳定性问题，即获得的不一定是绝对最小走时场(Vidale 1988，1990; Qin et al., 1992)，Sethian等(1996，1999)提出了一种基于网格的有限差分数值算法，即快速推进法(FMM).FMM利用迎风差分格式求解局部程函方程，采用窄带延拓重建旅行时波前，利用堆排序技术保存旅行时，将最小旅行时放在堆的顶部(Sethian and Popovici， 1999).该方法显著缩短了寻找极小值的时间，计算量由波前扩展法的O(N3)减少到O(N·logN)，其中N是计算区域网格节点总数.该方法能获得绝对最小走时场，具有无条件稳定性，适用于强烈的非均匀速度场.Rawlinson等(2004，2006)将FMM应用到地震层析成像方法中，可以同时考虑反射波震相信息；该方法由于在初至波成像及其稳定性等方面的优势而得到了广泛应用(Rawlinson et al., 2006; 郭飚等，2009; 张风雪等， 2011，2013).
FMM通过求解程函方程来计算走时.程函方程给出了波前任意一点的走时梯度的大小与慢度(速度的倒数)之间的关系，即：
在进行程函方程求解时，有限差分方法的一个明显的缺陷是地震波波前的梯度可能是不连续的.解决方法之一是获得方程的弱解(Rawlinson et al.， 2004)，即当ε→0(粘性限制)时，令：
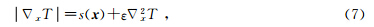
将模型进行参数化，划分为立体网格，在网格中通过迎风差分格式对方程进行离散，在球坐标系下程函方程的差分数值解为
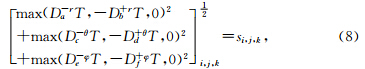
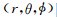下每个节点所处的位置，a，b，c，d，e，f定义了六个差分算子的精度的阶数.算子
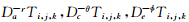的一阶形式为
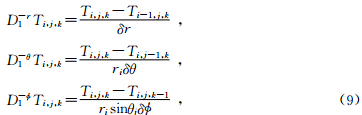
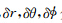分别表示在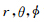
方向的差分步长，ri，θj分别代表节点 (i，j，k)所在位置的半径和余纬.算子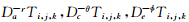的二阶形式为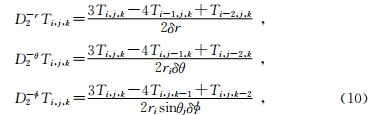
FMM算法的实现需要节点走时的更新的顺序与信息流的方向(即从较小的T到较大T方向)一致.为实现走时计算，在FMM中采用满足波前传播过程中 “熵守恒”的窄带技术实现波前扩展(图 3).窄带技术将计算区域分为上风(Upwind)(图 3a中黑色点所在区域)、窄带(Narrow b and )(图 3a中灰色点所在区域)、下风(Downwind)(图 3a中空心点所在区域)三种区域，而区域内的所有网格节点分为活动点(黑色点)、窄带点(灰色点)和远离点(空心点).上风区域中的节点全为活动点，窄带中的节点全部为窄带点，下风区全部为远离点.算法在初始化时，震源点为唯一的活动点，与震源点最邻近的八个网格节点为窄带点，它们构成初始窄带，即初始波前，其余的所有网格节点为远离点.图(3b)中展示了窄带是如何从一个震源点进行更新的.
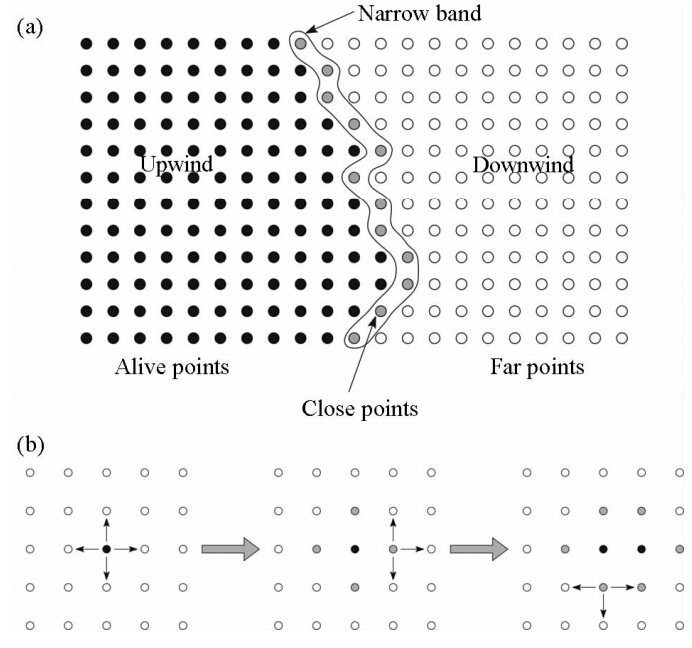 | 图 3 (a)窄带技术原理图(b)窄带从一个震源点进行更新的示意图(Rawlinson and Sambridge， 2004). Fig. 3 (a)The principle of the narrow-b and method; (b)Example of how the narrow b and evolves from a source point.(Rawlinson and Sambridge， 2004). |
窄带技术的具体实现步骤为：
(1)从窄带内选取走时最小的窄带点作为波前上的子震源点，并将其属性改为活动点；
(2)对子震源邻近的几个网格节点作判断，若为远离点则将其纳入窄带，同时其属性变为窄带点，然后通过迎风差分格式计算其走时(若为窄带点，采用迎风差分格式更新其走时，如果新计算的走时小于原先走时则更新其走时，否则保持原来走时值不变；若为活动点，其走时值不变)；
(3)若窄带为空，则结束计算，否则跳回到第一步继续循环计算.
计算炮点到模型空间网格节点的走时场后，从接收器出发，可以根据走时场的梯度方向反向追踪射线路径.由于反射波为入射初至波和反射初至波走时之和最小，即反射点可以理解为，反射界面上所有的散射点中分别到炮点和接收器初至走时之和最小的点.图 4为单层起伏界面上初至波走时场及反射路径(Rawlinson and Sambridge， 2004).
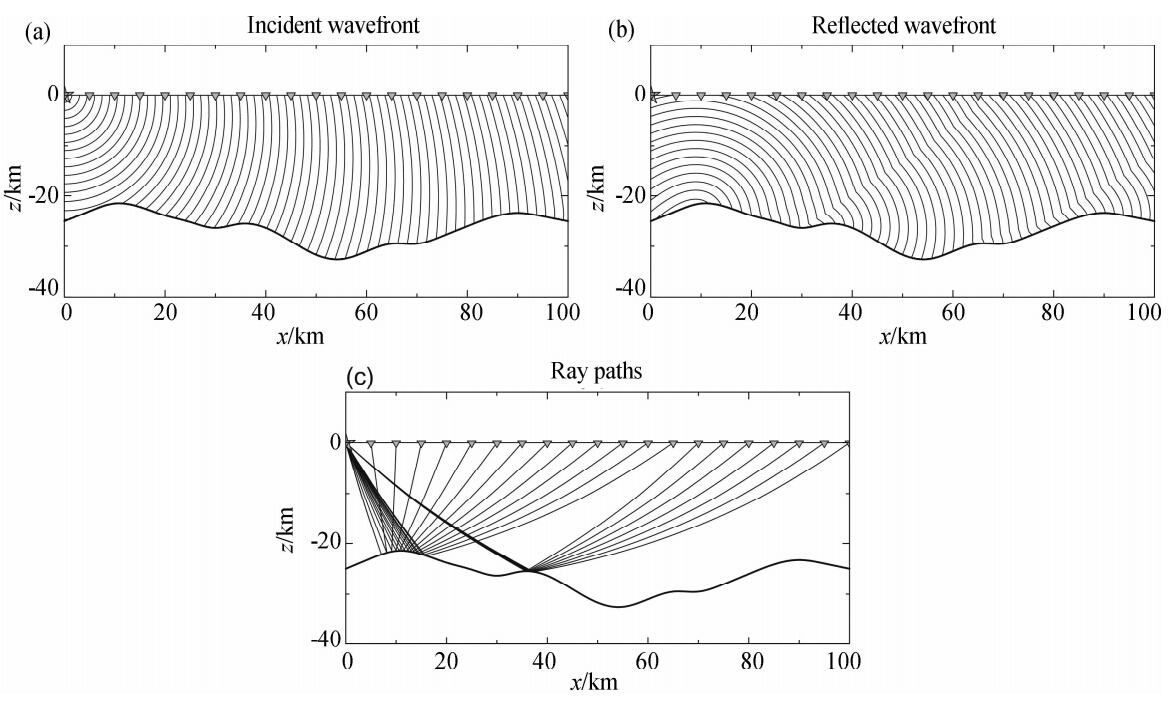 | 图 4 计算单层反射震相的二阶FMM算法(Rawlinson et al., 2004) (a)入射波波前；(b)反射波前；(c)源点到接收点的射线路径. Fig. 4The second-order FMM scheme for a reflected phase in a single layer(Rawlinson et al., 2004)(a)Incident wave front;(b)reflected wave front;(c)source-receiver ray paths. |
Rawlinson等(2006)在反演时采用了子空间迭代算法，将走时残差作为观测数据，以速度场作为未知变量建立目标函数：
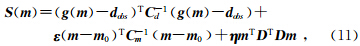
对于目标函数(11)式，由子空间反演方法得到的模型扰动δ m 为
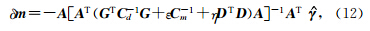
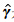是目标函数S(m)的梯度矢量.以模型空间的梯度矢量 γ=C m γ和模型空间的Hessian矩阵 H=C m
H
为基矢量张成n维子空间.反演过程中的搜索方向为
Rawlinson等(2006)利用基于FMM的初至波成像方法采用远震P波相对到时，研究了澳大利亚Northern Tasmania地区的地壳和上地幔地震层析成像，结果显示在Tasmania地区P波速度结构存在明显的侧向扰动.张风雪等(2011)在反演的过程中，改用带阻尼的LSQR算法，提高了反演的精度.郭飚等(2009)采用该方法，利用川西地震台阵记录到的远震P波走时数据，研究了龙门山地区400 km深度范围内的三维P波速度结构.
3 有限频成像方法
实际上，断层滑动产生的地震波的频率是有限的，且地球本身不是完全弹性的，随着地震波传播距离的增加高频成分会被吸收衰减，因此记录到的地震波是有限频率的.实际资料处理也表明，当对地震体波进行不同频率范围的滤波时，所获得体波走时也存在一定的频率相关的变化.Woodward利用Born和Rytov两种不同的近似方法发现中心射线路径周围一定范围内的速度异常对地震波走时变化有贡献(Woodward，1992)，并将这一距离范围确定为第一菲涅尔带.Dahlen等(2000)使用WKBJ近似求得球对称初始介质中的格林函数和波场，它需要远场条件，并要求射线路径远离速度界面.在实际应用中，还需要把中心射线追踪出来，才能用傍轴近似方法在射线中心坐标系中求出中心射线外的Fréchet kernel值，所以不是严格的波动方程层析成像，称之为“射线有限频”理论更合适.Zhao等(2000)用简正振型理论计算的体波波场在球对称初始介质中严格符合波动方程，故在速度界面附近更精确.但因高频体波的简正振型计算量巨大，超出当时的计算机发展水平，故简正振型有限频理论在实际应用上有较大困难.
有限频层析成像基于波动方程，不需要射线理论的无限高频条件，对于任意有限频率的地震波都成立.有限频地震层析成像方法的关键在于灵敏度核的计算，下面我们将具体介绍Dahlen和Hung等提出的有限频层析成像方法灵敏度核的计算.
Dahlen等(2000)和Hung等(2000)将体波传播理论和线性Born单次散射理论结合，近似表达了地震波经非均匀的地球内部任意一散射点到达观测台站的波形扰动，得出有限频率走时变化与中心几何射线附近第一菲涅尔带内的三维速度扰动之间的关系为
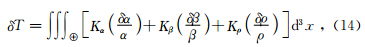
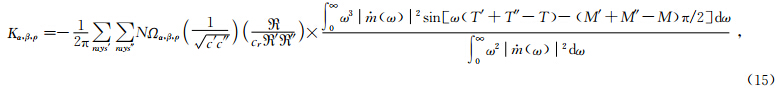
傍轴近似条件下的灵敏度算核的表达式为
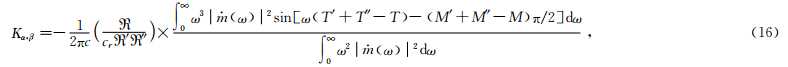
从灵敏度核的具体表达式中可以看出，灵敏度核的计算主要涉及到震源、接收点、散射点三点之间的走时、几何扩散系数、马斯洛夫指数等三个方面的求解问题.此外，灵敏度核Κ不仅是位置x的函数，同时也是频率ω的函数.不同频宽的地震波对速度结构敏感范围不同，有限频“射线”层析成像即在射线路径外Fréchet核(Fréchet kernel)函数范围内的速度扰动异常均对“射线”走时有贡献.核函数的范围大小不仅与位置有关，还和信号频率有关，当频率趋于无穷大时，有限宽度的核(kernel)收缩为无限窄的直线，有限频核函数变为射线(Dahlen et al.， 2000).因此，敏感核函数Κ代表了空间位置处某点的速度异常对走时残差的贡献结果.
有限频成像方法考虑地震波频带本身所具有的有限频宽特性及波前复原效应，克服了射线理论中“无限高频”假设所带来的弊端.而且，由于它考虑到了射线路径外的速度结构对地震波传播走时的影响，因此反演过程中偏导数矩阵的稀疏程度大大降低，有利于反演的稳定性.有限频成像方法提高了对地球内部更为精细的结构的分辨能力，近年来得到了迅速的发展和应用.
与简正振型方法相比，射线求和方法的计算效率比简正振型方法的高，但是该方法需要追踪从震源到介质中各个散射点的射线及各个散射点到接收点的射线，且不适用于转换震相.傍轴近似方法仅需要追踪从震源到接收点的射线路径，需要射线路径相对较少，且用该方法计算灵敏度核适用于震中距在30°~90°间常见的震相(如P，PcP，PP，S，ScS，SS等)，这些震相都是远震体波层析成像研究中常用震相.因此傍轴近似方法是远震体波有限频走时层析成像中经常用到的方法(Dahlen et al.，2000; Hung et al.， 2000; 张风雪，2011).
图 5给出了在震中距为60°的地方，利用三维傍轴近似的Fréchet灵敏度核的有限频层析成像方法得到的远震P波的二维横剖面图(Hung et al.，2000).由于有限频理论的灵敏度核形状像香蕉，横断面像甜面圈(图 5)，因此该理论又被称作香蕉-甜甜圈(Banana-Doughnut)理论(Marquering et al.， 1999).
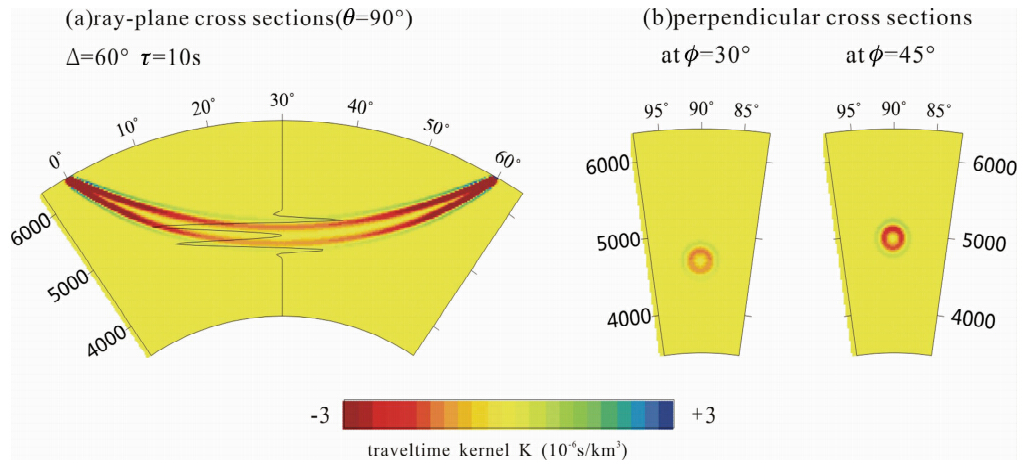 | 图 5 震中距Δ=60°处利用3D傍轴近似灵敏度核Κ得到的远震P波的2D横剖面(Hung et al., 2000)(a)射线平面横剖面；实线表示在拐点处K随着深度的线性变化;(b)在Φ=30°和Φ=45°上的经线方向上的横断面. Fig. 5 2D cross-sections through the 3D paraxial Frechet kernel Κ for a teleseismic P wave at an epicentral distance Δ=60°.(Hung et al., 2000)(b)Longitudinal cross-sections at Φ=30° and Φ=45°. |
实际资料处理表明，有限频成像方法相对射线方法能够更好地反演深部速度异常的强度(Hung et al., 2000).Montelli等(2004)利用有限频层析成像方法得到了全球范围内的地幔最下部1000 km处的P波速度扰动的垂直平均值(图 6)，并通过对速度扰动的分析得到了深层和浅层地幔柱的三维视图(图 7)，左半部分是深层地幔柱的三维视图，右半部分是浅层地幔柱及新发现的地幔柱的三维视图.此外，Yang等(2006)对地震体波走时层析成像中普遍用到的地壳校正所具有的频率依赖性进行了研究；Favier等(2003)考虑了剪切波的有限频特性，由观测的剪切波分裂研究了上地幔的各向异性；Zhao等(2009)、张风雪(2011)还使用远震体波的相对走时残差，利用有限频体波走时层析成像方法反演了华北地壳及上地幔的P波、S波速度结构.Zhao 等(2012)利用升级后的国家地震台网及9个临时排列的约1300个台站记录到的地震体波走时数据，通过有限频成像方法得到了中国东部及其邻区的上地幔的P波、S波速度扰动横剖面图，并计算了P波与S波的速度比，显示了中国东部的地球动力学演化存在一定程度的空间变化性.Liang等(2012)利用设在青藏高原的301个流动台站记录到的P波和S波走时，研究了青藏高原北部上地幔的速度结构，其成像结果显示在青藏高原北部存在深达150 km的均匀低速区，可能为印度板块俯冲的碎块.
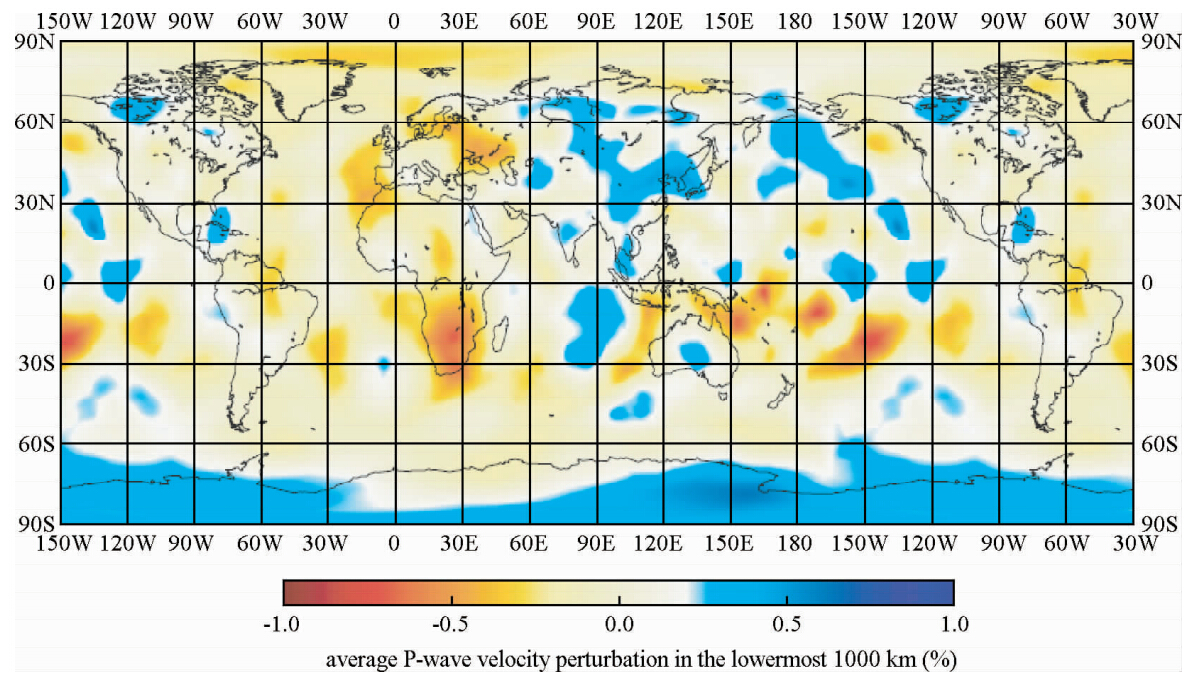 | 图 6 地幔最下部1000 km处相对速度扰动的垂直平均值(Montelli et al., 2004) Fig. 6 Vertical average over the lowermost 1000 km of the mantle of the relative velocity perturbation(Montelli et al., 2004) |
 | 图 7 有限频成像方法揭示的全球地幔柱不同深度结果(Montelli et al., 2004) Fig. 7 Finite-frequency tomography reveals a variety of plumes in the mantle(Montelli et al., 2004) |
地震层析成像方法已经成为地球内部结构探测最重要的方法之一.体波走时层析成像，是研究地球壳幔精细结构的重要途径.目前具有代表性的三种体波走时层析成像方法分别是基于高频近似射线理论的成像方法、基于程函方程数值解的初至波成像方法和有限频成像方法：
第一种方法基于高频近似的射线理论，计算量小，具有较高的计算效率，将长期是体波成像的常规方法之一.
第二种方法是利用地震波场的数值计算方法，尤其是利用FMM求解程函方程得到地震波走时，该算法稳定性好，且适合于各种速度结构，在初至波走时成像方面有优势；由于需要精细的速度网格，因此计算量大.
第三种方法基于波动方程理论，考虑地震波频率的有限性及射线路径外的速度结构对地震波走时的影响.有限频成像方法的理论比射线理论包含更丰富的介质信息，能够更精确地反映地下速度结构，提高了对速度异常的分辨能力，但是由于其计算量大，在目前阶段实现时尚需要引入波场近似.
三种成像方法，基于网格速度模型，速度间断面不专门考虑，多以平均效应来代替，有些方法仅如Moho面等一级速度间断面才专门考虑，且在反演过程中多以先验信息给定，并未参与反演.随着深度探测研究的深入，更精细的壳幔速度成像是重要的研究方向.忽略精细的速度间断面，只考虑平均效应，就会失去壳幔结构的细节，而这有可能恰恰反映了深部过程和动力学演化的内涵，因此，这将是今后需要深入考虑的方向之一.
致 谢 感谢中国科学院地质与地球物理研究所滕吉文院士的悉心指导；感谢赵亮研究员、梁晓峰副研究员有益的讨论和建议.
| [1] | Aki K, Lee W H K. 1976. Determination of three-dimensional velocity anomalies under a seismic array using first P arrival times from local earthquakes: 1. A homogeneous initial model[J]. Journal of Geophysical Research, 81(23): 4381-4399. |
| [2] | Bai C, Li X, Huang G, et al. 2013. Simultaneous Inversion for Velocity and Reflector Geometry Using Multi-phase Fresnel Volume Rays[J]. Pure and Applied Geophysics, 1-17. |
| [3] | Cerveny V. 2001.Seismic Ray Theory[M].Cambridge University Press. |
| [4] | Cerveny V, Soares J E P. 1992. Fresnel volume ray tracing[J]. Geophysics, 57(7): 902-915. |
| [5] | Chen L H, Song Z H. 1990. Crust-upper mantle P wave velocity structure beneath Northern China[J]. Geophysics. (in Chinese), 33(5): 540-546. |
| [5] | Dahlen F A, Hung S H, Nolet G. 2000. Fréchet kernels for finite-frequency traveltimes-I.Theory[J]. Geophysical Journal International, 141(1): 157-174. |
| [6] | Dahlen F A, Tromp J. 1998. Theoretical global seismology[M]. Princeton university press. |
| [7] | Ding Z F, He Z Q, Sun W G, et al. 1999. 3-D crust and upper mantle velocity structure in Eastern Tibetan plateau and its surrounding areas[J]. Geophysics. (in Chinese), 42(2): 197-205. |
| [8] | Duan Y H, Zhang X K, Fang S M. 2002. Three-dimensional finite-difference tomography of velocity structure of the upper crustal in North China[J]. Chinese J. Geophys. (in Chinese), 45(3): 362-369. |
| [9] | Engdahl E R, Lee W H K. 1976. Relocation of local earthquakes by seismic ray tracing[J]. Journal of Geophysical Research, 81(23): 4400-4406. |
| [10] | Favier N, Chevrot S. 2003. Sensitivity kernels for shear wave splitting in transverse isotropic media[J]. Geophysical Journal International, 153(1): 213-228. |
| [11] | Guo B, Liu Q Y, Chen J H, et al. 2009. Teleseismic P-wave tomography of the crust and upper mantle in Longmenshan area, west Sichuan[J]. Chinese J. Geophys. (in Chinese), 52(2): 346-355. |
| [12] | Hole, J.A. 1992. Nonlinear high-resolution three-dimensional seismic travel time tomography[J]. Journal of Geophysical Research, 97(B5): 6553-6562. |
| [13] | Hung S H, Dahlen F A, Nolet G. 2000.Fréchet kernels for finite-frequency traveltimes-II.Examples[J]. Geophysical Journal International, 141(1): 175-203. |
| [14] | Jiang G M, Zhao D P, Zhang G B. 2008. Detailed structure of the subducting Pacific slab beneath the Japan islands and Japan sea[J]. Earth Science Frontiers (in Chinese), 15(1): 222-231. |
| [15] | Jiang G M, Zhao D P, Zhang G B. 2009. Crustal correction in teleseismic tomography and its application[J]. Chinese J. Geophys. (in Chinese), 52(6): 1508-1514. |
| [16] | Jiang Y, Chen X F. 2011. Review on the comparative study between finite-frequency tomography and ray-theoretical tomography[J]. Progress in Geophys. (in Chinese), 26(5): 1566-1575. |
| [17] | Jin A S, Liu F T, Sun Y Z. 1980. Three-dimensional P velocity structure of the crust and upper mantle under Beijing region[J]. Chinese J. Geophys. (in Chinese), 23(2), 172-182. |
| [18] | Julian B R, Gubbins D. 1977.Three-dimensional seismic ray tracing[J]. J. geophys, 43(1): 95-114. |
| [19] | Kayal J R, Zhao D. 1998.Three-dimensional seismic structure beneath Shillong Plateau and Assam Valley, northeast India[J]. Bulletin of the Seismological Society of America, 88(3): 667-676. |
| [20] | Komatitsch D, Liu Q, Tromp J, et al. 2004. Simulations of ground motion in the Los Angeles basin based upon the spectral-element method[J]. Bulletin of the Seismological Society of America, 94(1): 187-206. |
| [21] | Lan H, Zhang Z. 2013a. Topography-dependent eikonal equation and its solver for calculating first-arrival traveltimes with an irregular surface[J]. Geophysical Journal International, 193(2): 1010-1026. |
| [22] | Lan H, Zhang Z. 2013b. A High-Order Fast-Sweeping Scheme for Calculating First-Arrival Travel Times with an Irregular Surface[J]. Bulletin of the Seismological Society of America, 103(3): 2070-2082. |
| [23] | Langan, R.T., Lerche, I., Cutler, R.T. 1985. Tracing of rays through heterogeneous media: Anaccurate and efficient procedure[J]. Geophysics, 50(9): 1456-1465. |
| [24] | Lei J S, Zhou H L, Zhao D P. 2002. 3-D velocity structure of P-wave in the crust and upper-mantle beneath Pamir and adjacent region[J]. Chinese J. Geophys. (in Chinese), 45(6): 802-811. |
| [25] | Lei J S, Zhao D P, Su J R, et al. 2009.Fine seismic structure under the Longmenshan fault zone and the mechanism of the large Wenchuanearthquake[J]. Chinese J. Geophys. (in Chinese), 52(2): 339-345. |
| [26] | Li, C., and van der Hilst, R.D. 2010.Structure of the upper mantle and transition zone beneath South East Asia from travel time tomography[J].Journal of Geophysical Research, 115, B07308, doi:10. 1029/2009JB006882. |
| [27] | Li F, Xu T, Wu Z B, et al. 2013. Segmentally iterative ray tracing in 3-D heterogeneous geological models[J]. Chinese J. Geophys. (in Chinese), 56(10): 3514-3522. |
| [28] | Li F, Xu T, Zhang M, et al. 2013. Seismic traveltime inversion of 3D velocity model with triangulated interfaces[J]. Earthquake Science, 1-10. |
| [29] | Li Z W, Xu Y, Hao T Y, et al. 2006. Seismic tomography and velocity structure in the crust and upper mantle around Bohai Sea area[J]. Chinese J. Geophys. (in Chinese), 49(3): 797-804. |
| [30] | Liang X, Sandvol E, Chen Y J, et al. 2012.A complex Tibetan upper mantle: A fragmented Indian slab and no south-verging subduction of Eurasian lithosphere[J]. Earth and Planetary Science Letters, 333: 101-111. |
| [31] | Liu Q, Gu Y J. 2012. Seismic imaging: from classical to adjointtomography[J]. Tectonophysics, 566: 31-66. |
| [32] | Lv Q T, Jiang M, Ma K Y. 1996. 3-D traveltime inversion and the deep structure in the southern Tibetan plateau[J]. ActaSeismologicasinica (in Chinese), 18(4): 451-459. |
| [33] | Maarten V, van Der Hilst R D. 2005. On sensitivity kernels for 'wave-equation'transmissiontomography[J]. Geophysical Journal International, 160(2): 621-633. |
| [34] | Marquering, H., Dahlen, F.A., Nolet, G. 1999. Three-dimensionalsensitivity kernels for finite-frequency traveltimes: the banana-doughnut paradox[J]. Geophys. J. Int. , 137(3): 805-815. |
| [35] | Montelli R, Nolet G, Dahlen F A, et al. 2004. Finite-frequency tomography reveals a variety of plumes in the mantle[J]. Science, 303(5656): 338-343. |
| [36] | Nolet G. 2008. A breviary of seismic tomography: Imaging the Interior[M]. Cambridge University Press. |
| [37] | Pereyra V. 1992.Two-point ray tracing in general 3D media[J]. Geophysical Prospecting, 40(3): 267-287. |
| [38] | Pratt R G. 1999. Seismic waveform inversion in the frequency domain, Part 1: Theory and verification in a physical scale model[J]. Geophysics, 64(3): 888-901. |
| [39] | Qin F, Luo Y, Olsen K B, et al. 1992. Finite-difference solution of the eikonal equation along expanding wavefronts[J]. Geophysics, 57(3): 478-487. |
| [40] | Rawlinson N, Pozgay S, Fishwick S. 2010. Seismic tomography: a window into deep Earth[J]. Physics of the Earth and Planetary Interiors, 178(3): 101-135. |
| [41] | Rawlinson N, Reading A M, Kennett B L N. 2006. Lithospheric structure of Tasmania from a novel form of teleseismictomography[J]. Journal of Geophysical Research: Solid Earth(1978-2012), 111(B2). |
| [42] | Rawlinson N, Sambridge M. 2004. Multiple reflection and transmission phases in complex layered media using a multistage fast marching method[J]. Geophysics, 69(5): 1338-1350. |
| [43] | Rawlinson N., ReadingA M, Kennett B L N. 2006. Lithospheric structure of Tasmania from a novel form of teleseismictomography[J]. Journal of Geophysical Research: Solid Earth(1978-2012),111(B2). |
| [44] | Rawlinson N, Pozgay S, Fishwick S. 2010. Seismic tomography: A window into deep Earth[J]. Physics of the Earth and Planetary Interiors, 178(3): 101-135. |
| [45] | Sethian J A. 1996. A fast marching level set method for monotonically advancing fronts[J]. Proceedings of the National Academy of Sciences, 93(4): 1591-1595. |
| [46] | Sethian J A, Popovici A M. 1999.3-D traveltime computation using the fast marching method[J]. Geophysics, 64(2): 516-523. |
| [47] | Shearer P M. 2009. Introduction to Seismology[M]. Cambridge University Press. |
| [48] | Teng J W, Liu F T, Quan Y L, et al. 1994. The crust and upper mantle seismic tomography in the orogenic belts and sedimentary basins of the Northwest China[J].Progress in solid Geophysics of China (in Chinese), 66-80. |
| [49] | Teng J W, Zhang Z J, Bai W M. 2003. Lithosphere Physics[J]. Beijing: Science Press. |
| [50] | Tian Y, Liu C, Feng X. 2011. P-wave velocity structure of crust and upper mantle in Northeast China and its control on the formation of mineral and energy[J]. Chinese J. Geophys. (in Chinese), 54(2): 407-414. |
| [51] | Tian Y, Zhao D P, Liu C, et al. 2009.A review of body-wave tomography and its applications to studying the crust and mantle structure in China[J]. Earth Science Frontiers (in Chinese), 16(2): 347-360. |
| [52] | Tian Y, Zhao D P, Sun R M, et al. 2007. The 1992 Landers earthquake: effect of crustal heterogeneity on earthquake generation[J]. Chinese J. Geophys. (in Chinese), 50(5): 1488-1496. |
| [53] | ThurberC H, Ellsworth W L. 1980. Rapid solution of ray tracing problems in heterogeneous media[J].Bulletin of the Seismological Society of America, 70(4): 1137-1148. |
| [54] | Thurber C H. 1983. Earthquake locations and three-dimensional crustal structure in the Coyote Lake area, central California[J]. Journal of Geophysical Research: Solid Earth (1978–2012), 88(B10): 8226-8236. |
| [55] | Tromp J, Komattisch D, Liu Q. 2008. Spectral-element and adjoint methods in seismology[J]. Communications in Computational Physics, 3(1): 1-32. |
| [56] | Um J, Thurber C. 1987.A fast algorithm for two-point seismic ray tracing[J]. Bulletin of the Seismological Society of America, 77(3): 972-986. |
| [57] | Van Der Hilst R D, Maarten V. 2005. Banana-doughnut kernels and mantle tomography[J]. Geophysical Journal International, 163(3): 956-961. |
| [58] | Van der Hilst R D, Widiyantoro S, Engdahl E R. 1997. Evidence for deep mantle circulation from global tomography[J]. Nature, 386(6625): 578-584. |
| [59] | Vidale J. 1988. Finite-difference calculation of travel times[J]. Bulletin of the Seismological Society of America, 78(6): 2062-2076. |
| [60] | Vidale J E. 1990. Finite-difference calculation of traveltimes in three dimensions[J]. Geophysics, 55(5): 521-526. |
| [61] | Virieux J, Farra V. 1991. Ray tracing in 3-D complex isotropic media: An analysis of the problem. Geophysics, 56(12): 2057-2069. |
| [62] | Wang H, Huang D C. 2000. Seismic tomography and its application to rock mass structure study[J]. Journal of engineering geology (in Chinese), 8(1): 109-117. |
| [63] | Woodward M J. 1992.Wave-equation tomography[J]. Geophysics, 57(1): 15-26. |
| [64] | Wu Z B, Xu T, Li F, et al. 2014. Acoustic full-waveform inversion in the finite frequency-domain[J]. See: Chen Y T, eds, the physics of the earth's interior and dynamics in China-to celebrate the 60th anniversary of engaging in the geophysical research of the academician TengJiwen (in Chinese), Beijing: Science press, 306-314. |
| [65] | Xu T, Li F, Wu Z B, et al. 2014. A successive three-point perturbation method for fast ray tracing in complex 2D and 3D geological models[J]. Tectonophysics, doI:10.1016/j.tecto.2014.02.012. |
| [66] | Xu T, Xu G M, Gao E G, et al. 2004. Block modeling and shooting ray tracing in complex 3-D media[J]. Chinese J. Geophys. (in Chinese), 47(6): 1118-1126. |
| [67] | Xu T, Xu G, Gao E, Li Y, Jiang X, Luo K. 2006. Block modeling and segmentally iterative ray tracing in complex 3D media[J]. Geophysics, 71(3): T41-T51. |
| [68] | Xu T, Zhang Z, Gao E, Xu G, Sun L. 2010. Segmentally iterative ray tracing in complex 2D and 3D heterogeneous block models[J]. Bull. Seismol. Soc. Am. , 100(2): 841-850. |
| [69] | Xu Y, Liu F T, Liu J H, et al. 2001. Deep features of continental collision belts in northwestern China and their dynamic implications[J]. Chinese J. Geophys. (in Chinese), 44(1): 41-47. |
| [70] | Xu Y, Liu J H, Hao T Y, et al. 2006. P wave velocity structure and tectonics analysis of lithospheric mantle in eastern China seas and adjacent regions[J]. Chinese J. Geophys. (in Chinese), 49(4): 1053-1061. |
| [71] | Yang G H. 2009. Travel time tomography method with Fresnel volume and its applications[D]. Xiamen University. |
| [72] | Yang T, Shen Y. 2006.Frequency-dependent crustal correction for finite-frequency seismic tomography[J]. Bulletin of the Seismological Society of America, 96(6): 2441-2448. |
| [73] | Zelt C A, Smith R B. 1992. Seismic traveltime inversion for 2-D crustal velocity structure[J]. Geophysical journal international, 108(1): 16-34. |
| [74] | Zhang F X. 2011. Finite-frequency traveltime tomography by body wave and its application in the North China[D]. Institute of Geophysics, China Earthquake Administration. |
| [75] | Zhang F X, Li Y H, Wu Q J, et al. 2011. The P wave velocity structure of upper mantle beneath the North China and surrounding regions from FMTT[J]. Chinese J. Geophys. (in Chinese), 54(5): 1233-1242. |
| [76] | Zhang F X, Wu Q J, Li Y H. 2013. The traveltime tomography study by teleseismic P wave data in the Northeast China area[J]. Geophys. (in Chinese), 56(8): 2690-2700. |
| [77] | Zhao D, Christensen D, Pulpan H. 1995. Tomographic imaging of the Alaska subduction zone[J]. Journal of Geophysical Research: Solid Earth (1978–2012), 100(B4): 6487-6504. |
| [78] | Zhao D, Hasegawa A, Horiuchi S. 1992. Tomographic imaging of P and S wave velocity structure beneath northeastern Japan[J]. Journal of Geophysical Research: Solid Earth (1978–2012), 97(B13): 19909-19928. |
| [79] | Zhao D, Hasegawa A, Kanamori H. 1994. Deep structure of Japan subduction zone as derived from local, regional, and teleseismicevents[J]. Journal of Geophysical Research: Solid Earth (1978–2012), 99(B11): 22313-22329. |
| [80] | Zhao D, Kanamori H, Humphreys E. 1996. Simultaneous inversion of local and teleseismic data for the crust and mantle structure of southern California[J]. Physics of the earth and planetary interiors, 93(3): 191-214. |
| [81] | Zhao D, Wang Z, Umino N, et al. 2007. Tomographic imaging outside a seismic network: Application to the northeast Japan arc[J]. Bulletin of the Seismological Society of America, 97(4): 1121-1132. |
| [82] | Zhao L, Allen R M, Zheng T, et al. 2009. Reactivation of an Archean craton: Constraints from P-and S-wave tomography in North China[J]. Geophysical Research Letters, 36: L17306. |
| [83] | Zhao L, Allen R M, Zheng T, et al. 2012. High-resolution body wave tomography models of the upper mantle beneath eastern China and the adjacent areas[J]. Geochemistry, Geophysics, Geosystems, 13(6). |
| [84] | Zhao L, Jordan T H, Chapman C H. 2000. Three-dimensional Fréchet differential kernels for seismicdelaytimes[J]. Geophysical Journal International, 141(3): 558-576. |
| [85] | Zheng H W, Li T D, Gao R, et al. 2007. Teleseismic P-wave tomography evidence for the Indian lithospheric mantle subducting northward beneath the Qiangtangterrane[J]. Chinese J. Geophys. (in Chinese), 50(5): 1418-1426. |
| [86] | Zheng H W, Li T D, Gao R. 2011. The progress of seismic tomography research in the Tibetan plateau[J]. Geophysical and geochemical exploration, 35(2): 160-164. |
| [87] | 陈立华, 宋仲和. 1990. 华北地区地壳上地幔 P 波速度结构[J]. 地球物理学报, 33(5): 540-546. |
| [88] | 丁志峰, 何正勤, 孙为国, 等. 1999. 青藏高原东部及其边缘地区的地壳上地幔三维速度结构[J]. 地球物理学报, 42(2): 197-205. |
| [89] | 段永红, 张先康, 方盛明. 2002. 华北地区上部地壳结构的三维有限差分层析成像[J]. 地球物理学报, 45(3): 362-369. |
| [90] | 郭飚, 刘启元, 陈九辉, 等. 2009. 川西龙门山及邻区地壳上地幔远震P波层析成像. 地球物理学报, 52(2): 346-355. |
| [91] | 江国明, 赵大鹏, 张贵宾. 2008. 日本列岛下太平洋俯冲板块的精细结构[J]. 地学前缘, 15(1): 222-231. |
| [92] | 江国明, 赵大鹏, 张贵宾. 2009. 远震层析成像中的地壳校正研究及应用[J]. 地球物理学报, 52(6): 1508-1514. |
| [93] | 江燕, 陈晓非. 2011. 有限频与射线层析成像比较研究综述[J]. 地球物理学进展, 26(5): 1566-1575. |
| [94] | 金安蜀, 刘福田, 孙永智. 1980. 北京地区地壳和上地幔的三维P波速度结构[J]. 地球物理学报, 23(2): 172-182. |
| [95] | 雷建设, 周蕙兰, 赵大鹏. 2002. 帕米尔及邻区地壳上地幔 P 波三维速度结构的研究[J]. 地球物理学报, 45(6): 802-811. |
| [96] | 雷建设, 赵大鹏, 苏金蓉, 等. 2009. 龙门山断裂带地壳精细结构与汶川地震发震机理[J]. 地球物理学报, 52(2): 339-345. |
| [97] | 李飞, 徐涛, 武振波, 等. 2013.三维非均匀地质模型中的逐段迭代射线追踪[J]. 地球物理学报, 56(10): 3514-3522. |
| [98] | 李志伟, 胥颐, 郝天珧, 等. 2006. 环渤海地区的地震层析成像与地壳上地幔结构[J]. 地球物理学报, 49(3): 797-804. |
| [99] | 吕庆田, 姜枚, 马开义. 1996. 三维走时反演与青藏高原南部深部构造[J]. 地震学报, 18(4): 451-459. |
| [100] | 滕吉文, 刘福田, 全幼黎. 1994. 中国西北地区造山带及沉积盆地的地壳和上地幔地震层析成像[J]. 见: 陈运泰等主编,中国固体地球物理进展, 66-80. |
| [101] | 滕吉文,张中杰,白武明. 2003. 岩石圈物理学[M]. 北京:科学出版社. |
| [102] | 田有, 刘财, 冯晅. 2011. 中国东北地区地壳、上地幔速度结构及其对矿产能源形成的控制作用[J]. 地球物理学报, 54(2): 407-414. |
| [103] | 田有, 赵大鹏, 刘财, 等. 2009. 体波走时层析成像方法及其在中国壳幔结构研究中的应用评述[J]. 地学前缘, 16(2): 347-360. |
| [104] | 田有, 赵大鹏, 孙若昧, 等. 2007. 1992年美国加州兰德斯地震-地壳构造不均匀性对地震发生的影响[J]. 地球物理学报, 50(5): 1488-1496. |
| [105] | 王辉, 黄鼎成. 2000. 地震层析成像方法及其在岩体结构研究中的应用[J]. 工程地质学报, 8(1): 109-117. |
| [106] | 武振波,徐涛,李飞, 等. 2014. 声波方程的有限频率域全波形反演[J]. 见: 陈运泰等主编, 中国大陆地球内部物理学与动力学研究-庆贺滕吉文院士从事地球物理学研究60周年,北京:科学出版社[M],306-314. |
| [107] | 徐涛, 徐果明, 高尔根, 等. 2004. 三维复杂介质的块状建模和试射射线追踪[J]. 地球物理学报, 47(6): 1118-1126. |
| [108] | 胥颐,刘福田,刘建华, 等. 2001.中国西北大陆碰撞带的深部构造特征和地球动力学意义[J]. 地球物理学报, 44(1): 40-47. |
| [109] | 胥颐, 刘建华, 郝天珧, 等. 2006. 中国东部海域及邻区岩石层地幔的P波速度结构与构造分析[J]. 地球物理学报, 49(4): 1053-1061. |
| [110] | 杨国辉. 2009. 菲涅耳体旅行时层析成像方法及应用研究[D]. 厦门大学. |
| [111] | 张风雪. 2011. 有限频体波走时层析成像及其在华北地区的应用[D]. 中国地震局地球物理研究所. |
| [112] | 张风雪, 李永华, 吴庆举, 等. 2011. FMTT方法研究华北及邻区上地幔P波速度结构[J]. 地球物理学报, 54(5): 1233-1242. |
| [113] | 张风雪, 吴庆举, 李永华. 2013. 中国东北地区远震P波走时层析成像研究[J]. 地球物理学报, 56(8): 2690-2700. |
| [114] | 郑洪伟, 李廷栋, 高锐, 等. 2007. 印度板块岩石圈地幔向北俯冲到羌塘地体之下的远震 P 波层析成像证据[J]. 地球物理学报, 50(5): 1418-1426. |
| [115] | 郑洪伟, 李廷栋, 高锐. 2011. 青藏高原地震层析成像的研究进展[J]. 物探与化探, 35(2): 160-164. |