0 引 言
模拟退火算法(SA)是近几年来应用十分广泛的一种全局优化算法(Kirkpatrick et al,1983),其主要优点是,不用求目标函数的偏导数,不用解大型矩阵方程组,即能找到一个全局最优解,且易于约束条件的加入,方法易于移植,克服了局部反演方法依赖于初始模型的选取以及解容易落入局部极值的缺陷.
SA 已用于解非线性地球物理反演问题,已取得了良好的应用效果(Rothman,1985;Sen,1991;Jerivs,1996),然而,SA 存在着计算效率低的缺陷,Ingber(1989)对模型的扰动方式、接受概率和退火方式上做了改进,提出了非常快速模拟退火算法(VFSA),有效的提高了方法的计算效率;Sen 等(1995)年利用快速模拟退火法对地震数据进行处理,获得了很好的应用效果;张霖斌等(1997)对快速模拟退火法的温度分布进行改进,提高了计算效率;杨辉(1998)以VFSA 为基础,将VFSA 的连续模型空间改为可变的离散化形式,节省了计算量;陈华根等(2006)进一步对VFSA 算法的温度分布进行改进,并对重力和大地电磁资料的联合反演进行了研究,取得了一定效果.迄今为止,快速模拟退火法已经在地震数据处理和联合处理方面得到了广泛的应用(杨辉等,2004;于鹏等,2008;李景叶等,2003).
重力梯度异常能更好的体现密度界面的局部变化,且有效的剔除了地壳和地幔密度差异以及地壳厚度差异所引起的异常,因此本文利用快速模拟退火法对重力梯度异常进行反演来获得密度界面的变化. 1 界面起伏引起的重力梯度异常
本文依据位场基本原理推导密度界面所引起的重力梯度异常表达式(Parker,1972;Oldenburg,1974),单一密度界面在水平面(xoy面)上的引力位为
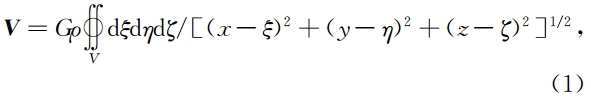
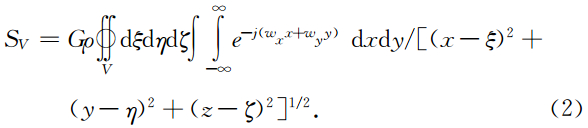
根据Erdelyi(1954)积分表,1/(x2+y2+η2)1/2的波谱为2πe-ωζ/ω,根据傅立叶变换的位移性质,1/[(x-ξ)2+(y-η)2+ζ2]1/2的波谱为 [2πe-ωζe-j(ωxξ+ωyη)]/ω ,上式可变为
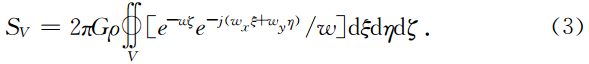
ξ和η的积分限是-∞~∞,而ζ的积分限是(h0+Δh)~h0,其中Δh为界面相对平均深度h0的起伏,界面在h0以上Δh为负,在h0以下Δh为正,而Δh又是ξ和η的函数,故
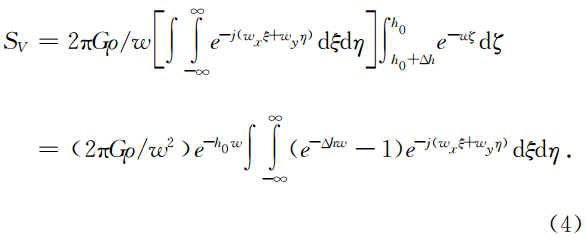
已知重力异常垂直导数波谱与引力位波谱之间的关系为

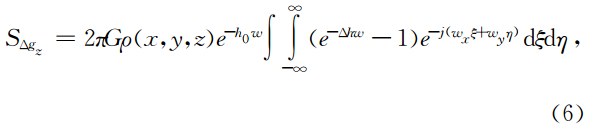
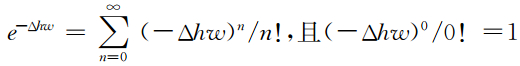 ,所以上式可以改写为离散形式
,所以上式可以改写为离散形式
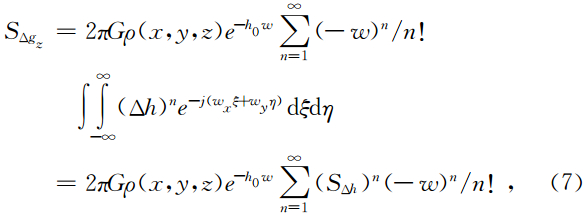
目标函数:采用重力梯度异常单独进行反演的目标函数(于鹏等,2007)为
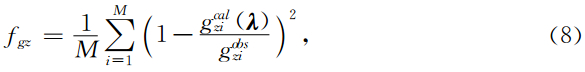
模型扰动为
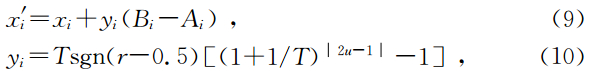
接收概率为
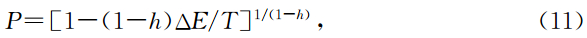
降温方式为

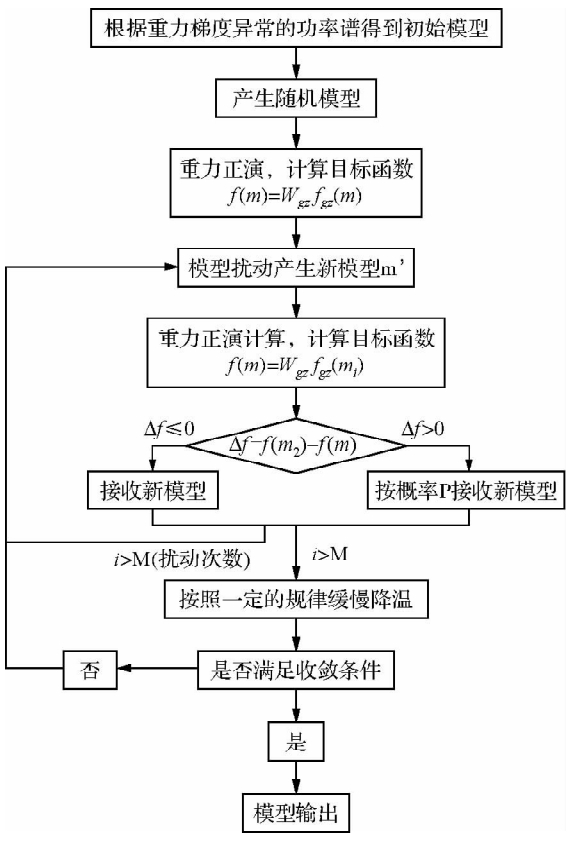 | 图 1 重力梯度数据模拟退火法反演流程图 Fig. 1 The flow chart of using simulated annealing to invert gravity gradient data |
为了试验本文方法的适用性,建立了如下的重力模型(图 2):
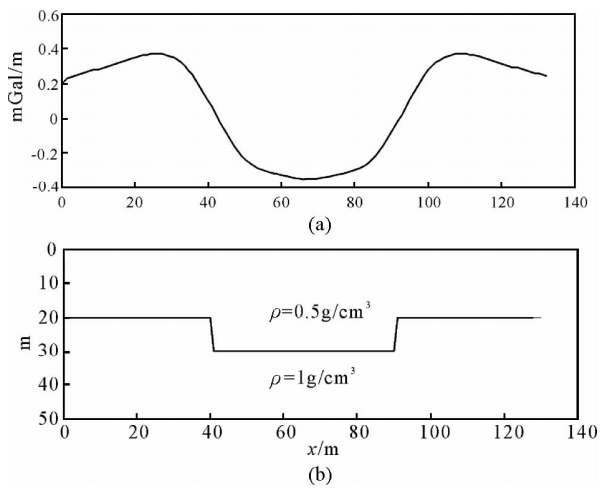 | 图 2 地质模型及其所引起的梯度异常 (a)地质模型所引起的垂直梯度;(b)地质模型. Fig. 2 Geological model and generated gravity gradient anomaly |
计算图 2a所示重力梯度异常的功率谱:
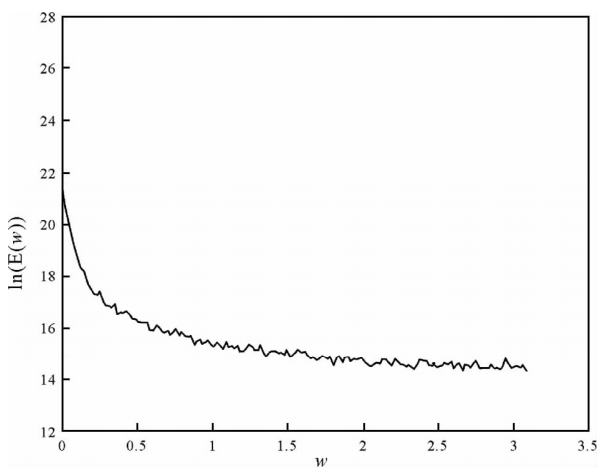 | 图 3 梯度异常的对数功率谱 Fig. 3 Log power spectrum of gradient data |
从功率谱中可以看出界面的平均深度为23.85m,以此建立初始模型,利用快速模拟退火法对异常进行反演(图 4):
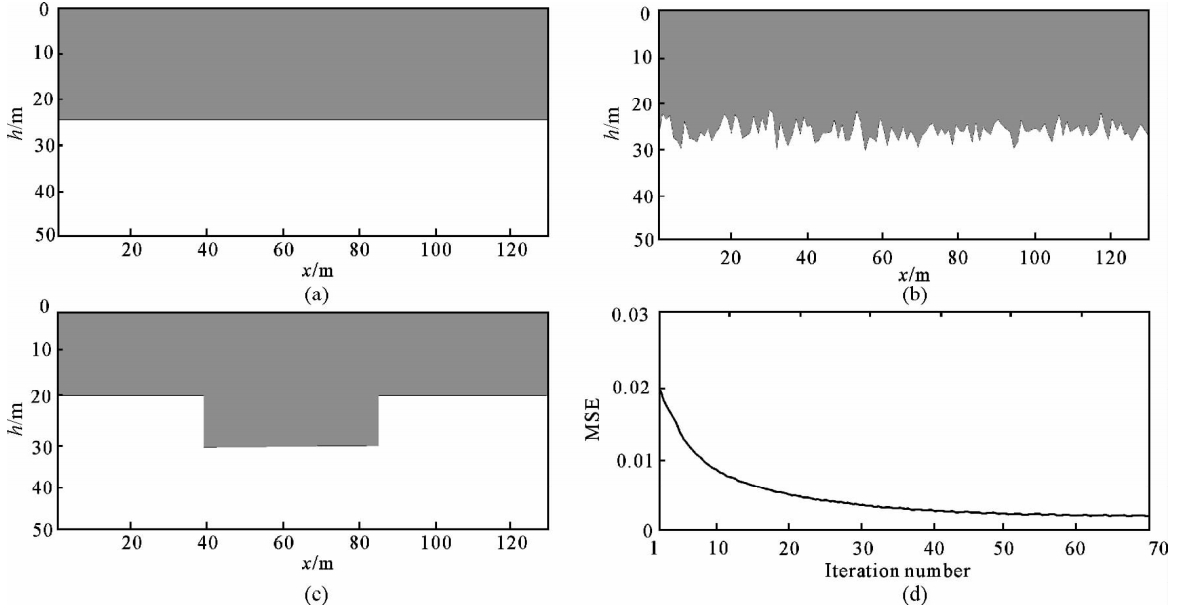 | 图 4 快速模拟退火法反演结果 (a) 初始模型;(b)深度初始扰动模型;(c)利用重力梯度异常反演的结果;(d)反演迭代均方误差曲线. Fig. 4 The inversion results computed by simulated annealing method |
从图 4中可以看出快速模拟退火法能很好的完成界面的反演,其反演结果与实际地质模型几乎一样.以上初始模型的建立是依据功率谱曲线获得的,当初始模型是随意给定时会对结果产生怎样的影响(图 5).
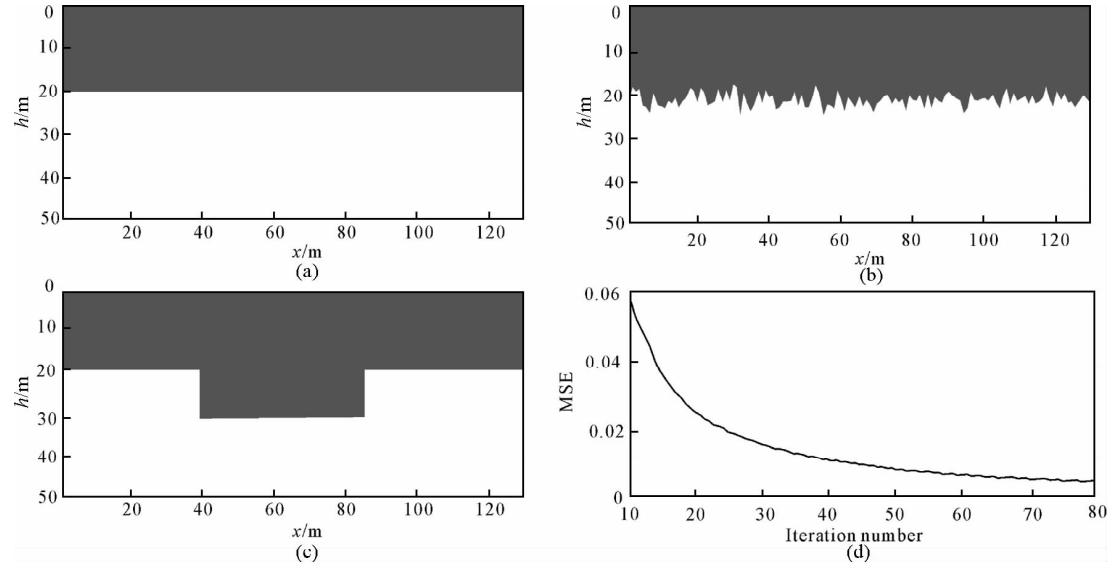 | 图 5 快速模拟退火法反演结果 (a)初始模型;(b)深度初始扰动模型;(c)利用重力梯度异常反演的结果;(d)反演迭代均方误差曲线. Fig. 5 The inversion results of simulated annealing method |
从图 5中可以看出,当初始模型任意给定时,模拟退火算法仍能完成异常的反演工作,但是达到相同的均方差所需要的迭代次数较多.因此在实际数据处理时,为了节省计算时间,需要事先依据功率谱给出大致地初始模型. 4 中国南海海底地形计算
南海是西太平洋最大的边缘海之一,总面积约350万km2,地质构造多样化,油气资源丰富.近些年国内外学者在南海地区进行了大量的地球物理工作,取得了丰硕的成果(李家彪等,2011;郝天珧等,2011; 秦静欣等,2011).本文根据南海地区重力梯度数据利用模拟退火法计算海底地形深度特征.为得到中国南海海域重力垂直梯度,首先利用Geosat,ERS-1/2,T/P,Jason-1,EnviSat-1卫星测高数据采用垂线偏差计算大地水准面的方法计算出高分辨率的海洋大地水准面,然后采用下式计算出重力垂直梯度(Ramillien,1997;Arabelos,1998;Hwang,1999;Wang,2000)
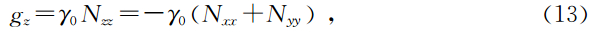
图 6(a)为计算得到的中国南海海域重力垂直梯度异常,采用本文所提出的方法对该异常进行反演来获得中国南海海底地形,其初始模型深度为5647 m,最终迭代均方误差为1.558×10-4 mGal/m,迭代次数为241次.
 | 图 6 中国南海重力梯度异常及其海底地形 (a)中国南海区域的重力垂直梯度异常;(b)模拟退火法反演得到的海底地形;(c)船测海底地形;(d)反演得到的海底地形与实测地形之差. Fig. 6 The seabed terrain and gravity gradient data of South China sea |
将所反演得到的海底地形与船测数据进行比较,其海底形态与实测地形相一致,最大差距为240 m,反演深度与实际深度的均方差为12.5 m. 5 结 论
本文提出采用基于重力垂直梯度的模拟退火法来反演中国南海海域的海底地形.首先通过理论试验证明了利用梯度异常通过模拟退火法反演界面的可行性,然后依据卫星测高数据计算中国南海海域的重力垂直梯度,最终采用该方法计算高分辨率的南海海底地形,并将其与船测海底地形数据相比较,结果显示反演得到的海底地形与实际船测海底地形差距较小,能真实地描述海底地形的特征.因此本文方法对于未知海域海底地形的反演将会有一定的实用价值.
| [1] | Arabelos D. 1998. On the possibility to estimate ocean bottom topography from marine gravity and satellite altimeter data using collocation[J]. Geodesy on the Move, 119: 105-112. |
| [2] | Chen H G, Li L H, Xu H P, et al. 2006. Modified very fast simulated annealing algorithm[J]. Journal of Tongji University (Natural Science) (in Chinese), 34(8): 1121-1125. |
| [3] | Hao T Y, Xu Y, Sun F L, et al. 2011. Integrated geophysical research on the tectonic attribute of conjugate continental margin of South China Sea[J]. Chinese J. Geophys. (in Chinese), 54(12): 3098-3116. |
| [4] | Hwang C. 1999. A bathymetric model for the South China sea from satellite altimetry and depth data[J]. Marine Geodesy, 22(1): 37-51. |
| [5] | Ingber L. 1989. Very fast simulated re-annealing[J]. Journal of Mathematical and Computer Modelling, 12: 967-973. |
| [6] | Jerivs M, Sen M K, Stoffa P. 1996. Prestack migration velocity estimation using nonlinear method[J]. Geophysics, 61(1): 138-150. |
| [7] | Kirkpatrick S, Gelatt C D, Vecchi M P. 1983. Optimization by simulated annealing[J]. Sciences, 220(4598): 671-680. |
| [8] | Li J B, Ding W W, Gao J Y, et al. 2011. Cenozoic evolution model of the sea-floor spreading in South China Sea: new constraints from high resolution geophysical data[J]. Chinese J. Geophys. (in Chinese), 54(12): 3004-3015. |
| [9] | Li J Y, Chen X H. 2003. Inversion of poststack time-lapse seismic data by modified simulated annealing algorithm[J]. OGP (in Chinese), 37(4): 392-395. |
| [10] | Oldenburg D W. 1974. The inversion and interpretation of gravity anomalies [J]. Geophysics, 39(4): 526-536. |
| [11] | Parker R L. 1972. The rapid calculation of Potential anomalies [J]. Geophys. J. Roy. Astron. Soc., 31(2): 447-455. |
| [12] | Qin J X, Hao T Y, Xu Y, et al. 2011. The distribution characteristics and the relationship between the tectonic units of the Moho Depth in South China Sea and Adjacent Areas[J]. Chinese J. Geophys. (in Chinese), 54(12): 3171-3183. |
| [13] | Ramillien G, Cazenave A. 1997. Global bathymetry derived from altimeter data of the ERS-I geodetic mission [J]. Journal of Geodynamics, 23(2): 129-149. |
| [14] | Rothman D H. 1985. Nonlinear inversion, statistical mechanics, and residual statics estimation[J]. Geophysics, 50(12): 2784-2796. |
| [15] | Sen M K, Stoffa P L. 1991. Nonlinear one dimensional seismic waveform inversion using simulated annealing[J]. Geophysics, 56(10): 1624-1638. |
| [16] | Sen M K, Stoffa P L. 1995. Global Optimization Methods in Geophysical Inversion[M]. Elsevier Science Publication. |
| [17] | Tsallis C. 1988. Possible generalization of Boltzmann-Gibbs statistics[J]. J. Stat. Phys., 52(1-2): 479-487. |
| [18] | Wan W F, Li Y F, Zhang J J. 2005. Application of fast simulated annealing algorithm in aquifer parameter identification[J]. Coal Geology & Exploration (in Chinese), 33(6): 56-59. |
| [19] | Wang Y M. 2000. Predicting bathymetry from the Earth’s gravity gradient anomalies [J]. Marine Geodesy, 23(4): 251-258. |
| [20] | Yang H. 1998. Basement density inversion using gravimetric and seismic data and the integrative interpretation[J]. OGP (in Chinese), 3(4): 496-502. |
| [21] | Yang H, Dai S K, Mu Y G. 2004. Joint layer-stripped inversion of 3-D gravity and seismic data[J]. OGP (in Chinese), 39(4): 468-471. |
| [22] | Yu P, Wang J L, Wu J S, et al. 2007a. Constrained joint inversion of gravity and seismic data using the simulated annealing algorithm[J]. Chinese J. Geophys. (in Chinese), 50(2): 529-538. |
| [23] | Yu P, Wang J L, Wu J S. 2007b. An inversion of gravity anomalies by using a 2.5 dimensional rectangle gridded model and the simulated annealing algorithm[J]. Chinese J. Geophys. (in Chinese), 50(3): 882-889. |
| [24] | Yu P, Dai M G, Wang J L, et al. 2008. Joint inversion of gravity and seismic data based on common gridded model with random density and velocity distributions[J]. Chinese J. Geophys. (in Chinese), 51( 3): 845-852. |
| [25] | Zhang L B, Yao Z X, Ji C, et al. 1997. Fast simulated annealing algorithm and its application[J]. OGP (in Chinese), 42(5): 654-660. |
| [26] | 陈华根, 李丽华, 许惠平, 等. 2006. 改进的非常快速模拟退火算法[J]. 同济大学学报(自然科学版), 34(8): 1121-1125. |
| [27] | 郝天珧, 徐亚, 孙福利,等. 2011. 南海共轭大陆边缘构造属性的综合地球物理研究[J]. 地球物理学报, 54(12): 3098-3116. |
| [28] | 李景叶, 陈小宏. 2003. 用改进的模拟退火算法进行叠后时移地震数据反演[J]. 石油地球物理勘探, 38(4): 392-395. |
| [29] | 李家彪, 丁巍伟, 高金耀,等. 2011. 南海新生代海底扩张的构造演化模式: 来自高分辨率地球物理数据的新认识[J]. 地球物理学报, 54(12): 3004-3015. |
| [30] | 秦静欣, 郝天珧, 徐亚,等. 2011. 南海及邻区莫霍面深度分布特征及其与各构造单元的关系[J]. 地球物理学报, 54(12): 3171-3183. |
| [31] | 万伟锋, 李云峰, 张娟娟. 2005. 快速模拟退火算法在含水层参数识别中的应用[J]. 煤田地质与勘探, 33(6): 56-59. |
| [32] | 杨辉. 1998. 重力、地震联合反演基岩密度及综合解释[J]. 石油地球物理勘探, 33(4): 496-502. |
| [33] | 杨辉, 戴世坤, 牟永光. 2004. 三维重力地震剥层联合反演[J]. 石油地球物理勘探, 39(4): 468-471. |
| [34] | 于鹏, 王家林, 吴健生,等. 2007a. 重力与地震资料的模拟退火约束联合反演[J]. 地球物理学报, 50(2): 529-538. |
| [35] | 于鹏, 王家林, 吴健生. 2007b. 二度半长方体组合模型的重力模拟退火反演[J]. 地球物理学报, 50(3): 882-889. |
| [36] | 于鹏, 戴明刚, 王家林,等. 2008. 密度和速度随机分布共网格模型的重力与地震联合反演[J]. 地球物理学报, 51(3): 845-852. |
| [37] | 张霖斌, 姚振兴, 纪晨,等. 1997. 快速模拟退火算法及应用[J]. 石油地球物理勘探, 42(5): 654-660. |
 2014, Vol. 29
2014, Vol. 29

