2. 中国科学院大学, 北京 100049;
3. 中国石油勘探开发研究院, 北京 100083
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Research Institute of Petroleum Exploration and Development, CNPC, Beijing 10083, China
0 引 言
南海是东亚大陆边缘经过多方向扩张形成的大型边缘海(Zhang et al., 1984),也是西太平洋最大的边缘海之一,位于太平洋板块、欧亚板块和印度洋—澳大利亚板块的结合带上(丁巍伟和李家彪,2011),呈菱形展布,南海深海盆分为西北次海盆、西南次海盆和东部次海盆(刘光鼎,1992).平均深度1212 m,最深处有5567 m.南海北部大陆边缘从西往东依次发育了琼东南盆地、珠江口盆地和台西南盆地三个较大的深水盆地(吴时国等,2011),研究区位于113°10′E-118°00′E、18°30′N-23°30′N之间(图 1),跨过珠江口盆地和西北次海盆.珠江口盆地是南海北部陆缘深水区规模最大的盆地(董冬冬等,2009),总面积约17.5×104 km2,与琼东南盆地紧紧相连总体呈NE-SW向展布(宋洋等,2011).西北次海盆是南海三个次级海盆之一,东接东部次海盆,南靠中沙群岛,西临西沙海槽,北依南海北部陆坡.该区域火山十分发育,存在大量岩浆侵入与喷出,采集数据可用以研究南海北部火山活动历史、洋陆过渡带地壳演化、海底扩张、大陆边缘裂解等地球动力学过程;深部结构是大陆边缘演化过程中多种信息的载体与架构,也是认识陆缘构造属性的窗口(郝天珧等,2011),本研究也为深部构造的识别提供一定的借鉴意义.
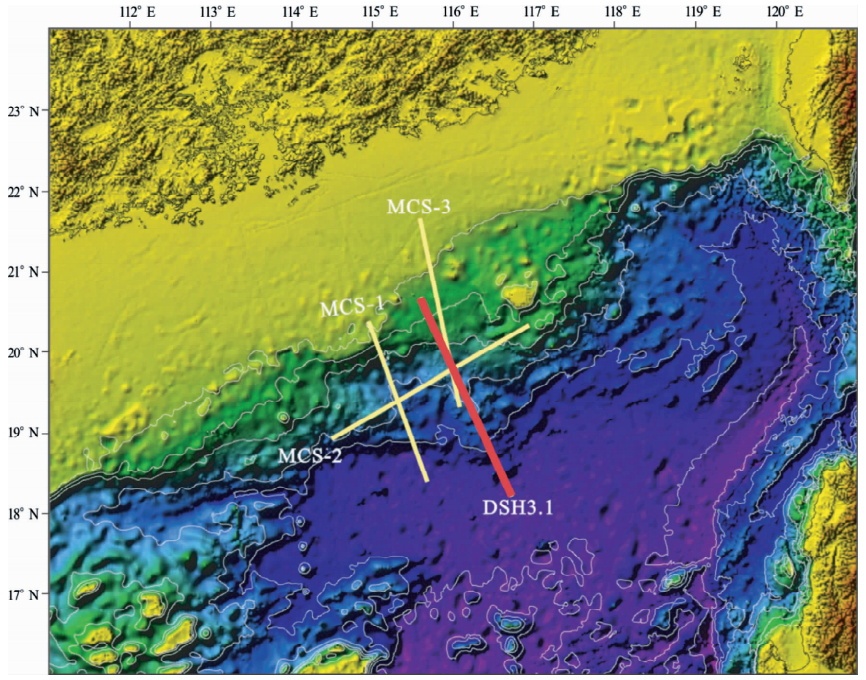 | 图 1 采集测线地理位置 Fig. 1 Geographical location of the acquisition line |
在南海海盆散布着一些由火山组成的高出周围海底上千米的大型海山(阎贫等,2008),这些海山引起的表面多次波能量非常强.另外由于测线穿越了洋陆过渡带,水深变化幅度大,地层具有很大的倾角和横向上的岩性变化,连续性差,海底崎岖,构造复杂,多次波十分发育,极大地降低了采集数据的信噪比与分辨率,难以获得清晰的地层反射与构造细节,也制约了深部信息的识别,因此有必要针对数据特征,研究适合的资料处理方法和流程,以获取更高质量的地震剖面.本文以压制多次波为主要目标,根据数据特征采用组合优化的多种多次波压制技术,形成针对南海深水资料的一套有效衰减多次波的处理方法和流程.
目前,对于多次波问题,主要有两种处理手段,一是把多次波当成噪音进行压制,一是利用多次波,对多次波进行成像(郭书娟等, 2011,2012;Liu et al., 2011;刘伊克等,2004).多次波常与一次波干涉影响剖面分辨率,甚至导致错误解释为深层的一次反射波,因此通常把多次波作为噪声进行压制.然而多次波一定程度上也反映了地下界面的信息,因此多次波成像也成为当前研究的热点,但将其应用到实际生产工作还需要更深入的研究工作.绝大多数地震资料处理均利用一次反射波进行偏移成像,将多次波视为相干噪音进行压制(石颖等,2011).
Weglein(1999)将衰减多次波的方法主要分为两大类:
(1)基于信号分析的滤波类方法;
(2)基于波动方程预测的预测相减法.
滤波类方法,是利用一次波和多次波之间的周期性、速度等差异,在不同变换域中用滤波的方法压制多次波;预测相减法压制多次波分两步,首先进行多次波的预测,然后将预测出的多次波模型从原始数据中减去.根据Weglein的标准,滤波法主要包括共中心点叠加、Radon变换(Wang,2003;Foster and Charles, 1992;郭全仕等,2005)、F-K滤波、预测反褶积(Peacock and Treitel, 1969;渥·伊尔马滋,2006;Egbai et al., 2012)以及聚束滤波方法(洪菲等,2004;胡天跃等, 2000,2002)等;波动方程法主要有波场延拓、逆散射级数(金德刚等,2008;李翔和胡天跃,2009)、反馈迭代、恒定内插法等.
基于滤波法的共中心点叠加,就是将动校正后的共中心点道集叠加,由于多次波与一次波存在动校速度差异,一次波校平而多次波未校平,叠加后可压制部分多次波,但要求动校速度差异大才能获得较好效果,而且此方法只能体现在叠后数据上,不能在道集上进行处理.Radon(Taner,1980)变换包括线性、抛物型、双曲型等,此方法要求一次波与多次波有较大动校时差,对于具有复杂构造的地下介质难以有效应对.预测反褶积基于周期性,能够有效压制海上鸣震,但难以处理深水长周期中远偏移距多次波.对于聚束滤波法,当有效信号较弱而背景噪声较强时,聚束滤波器容易不稳定,导致分辨率降低.预测相减法能适用于复杂的地下结构,需要较少或不需要关于地下结构的假定,能在不损坏一次反射信号的情况下衰减多次波,但其运算量较大(李鹏等,2006).因此,每种方法都有一定的前提假设和缺陷,必须有针对性地研究如何有效地利用和改进多次波压制的方法.
本文首先介绍了研究区域的概况,数据信息和采用的处理流程,然后阐释了从数据体识别多次波并深入分析了多次波压制方法的适用范围,剖析了如何选择适宜的方法并详细介绍了所采纳的方法原理,最后在实际数据上应用了组合优化的方法技术并取得较好的效果,证明了其有效性. 1 数 据
本研究的数据来自2010年和2011年国家自然科学基金委共享航次.利用中国科学院南海海洋研究所“实验2号”科学考察船,先后采集4条二维地震测线数据,共计约1万千米.采集区域位于南海北部陆缘珠江口盆地(图 1).本文抽取了4条二维测线之一的DSH3.1测线数据.DSH3.1测线横过珠江口盆地南部陆坡直至南海西北次海盆,穿过洋陆过渡带,水深变化范围大(400~4000 m),海底崎岖、构造复杂.由于浅水区多次波周期短,多次波与一次波或多次波之间相互干涉导致多次波难以区分;深水区多次波周期长,数据驱动难以准确预测多次波周期和振幅,常规多次波压制处理难以取得很好的结果.采集参数见表 1.
|
|
表 1 DSH3.1测线采集参数 Table 1 Acquisition parameters of the DSH3.1 line |
针对DSH3.1测线这一数据的特点,经过模块试算,形成以下处理流程,如图 2所示.在压制线性噪声过程中采用F-K变换和Radon变换;在压制多次波方面,综合应用了SRME、τ-p域预测反褶积、高分辨率抛物线Radon变换以及叠后压制残余多次波等方法.经过精细压制线性噪声、随机噪声以及多次波后,采用叠前时间偏移技术,通过迭代速度分析提高速度拾取精度,最终获得了较为精细的成果剖面.
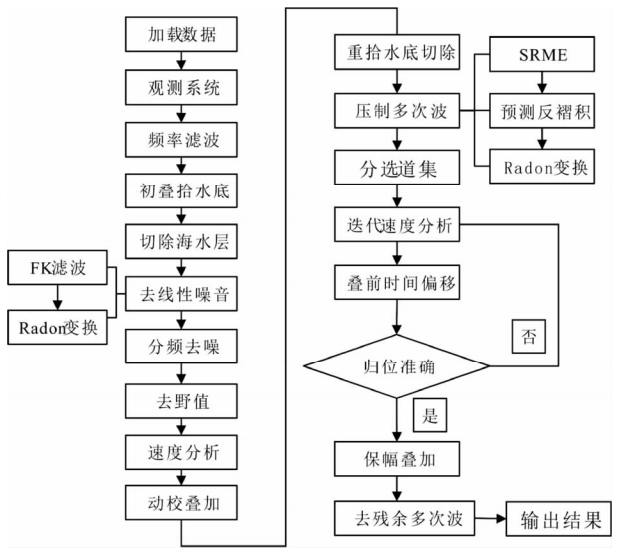 | 图 2 资料处理流程 Fig. 2 Processing flow chart of the data |
由于任何一种多次波压制方法都有其优势和固有缺陷,难以压制所有多次波,因此这里列表分析了方法的特征和适用性,作出如下总结,如表 2和表 3所示:
|
|
表 2 滤波类方法特征 Table 2 Characteristics of the filtering methods |
|
|
表 3 波动理论类方法特征 Table 3 Characteristics of the wave theory methods |
能量较强的全程多次波较易通过时差来识别,然而部分多次波难以肉眼识别.DSH3.1测线数据发育不同类型不同特征的多次波,主要为表面多次波,为了全面处理,我们应用以下方法识别多次波.
1 )从单炮记录上识别多次波.单炮记录上零偏移距处的全程多次波出现的时间约为一次波的整数倍.如图 3所示,零偏移距处海底一次反射波出现在2.2 s附近,一阶海底全程多次波出现在4.4 s附近,二阶全程多次波出现在6.6 s附近.
 | 图 3 单炮记录上的多次波 Fig. 3 Multiple in the CSP(Common Shotpoint)gather |
2)从速度谱和CDP(Common Depth Point)道集上识别多次波.在速度谱上,多次波能量团与相应的一次波能量团对应着相同的或者接近的速度,如图 4所示,左侧速度谱中4.6 s到5.0 s之间的能量团即对应着海底表面多次波.图中CDP道集中的多次波特征类似于单炮记录.在CDP道集上,用一次波速度进行动校正后,一次波将被拉平,多次波仍将有剩余时差.
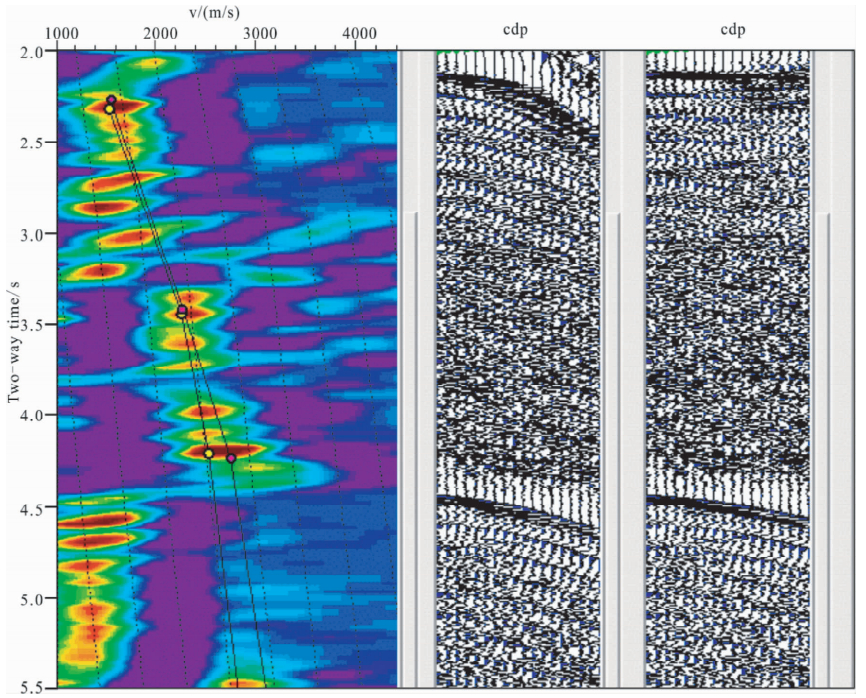 | 图 4 多次波在速度谱和CDP道集上的特征 Fig. 4 Characteristics of multiples in the velocity spectrum and CDP gather |
3 )从初始叠加段上识别多次波.如图 5所示,初步叠加剖面上多次波十分发育,根据时差关系,中深部4.4 s和6.5 s处的多次波分别对应着海底表面的一阶和二阶全程多次波.
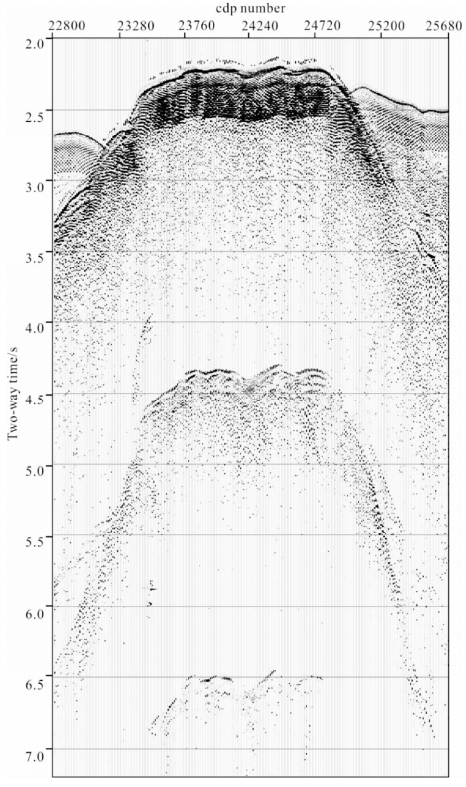 | 图 5 叠加剖面上的多次波 Fig. 5 Multiples in the stacking profile |
4)Radon域识别多次波.用一次波速度动校正后的数据从t-x域变换到Radon域(线性变换、抛物线变换或者双曲线变换等),一次波与多次波能量将显著分离分别聚焦,从而可以在Radon域进行滤波压制多次波.
5 )自相关与互相关识别多次波.根据多次波的周期性,多次波在自相关上表现为子波的续至相位.
6)极性识别多次波.多次波具有与一次波极性相反并且后续多次波极性正负相间的特点. 2.3 组合优化的多次波压制技术
针对DSH3.1测线数据的特点,在压制多次波方面,设计了SRME、τ-p域预测反褶积、高分辨率抛物线Radon变换以及叠后压制残余多次波的方法组合,综合了滤波类方法和波动理论类方法,以期望在多次波压制上达到最佳效果.
根据采集区域相关地质资料和初叠剖面可以知道,研究区水深变化剧烈,海底崎岖,构造起伏变化大,横向不连续性强,发育长周期的全程多次波,主要应以波动理论类方法压制.SRME的主要优点就体现在复杂海底构造情况下多次波的压制,而且完全数据驱动,不需先验信息.
多次波的周期性只体现在零偏移距或者近偏移距道,中远偏移距道不再有严格的周期性.因此,依据周期性的方法对于中远偏移距数据处理效果降低.理论上预测反褶积可以较好地压制周期严格的近道多次波,而τ-p域中多次波具有更好的周期性,采用τ-p域预测反褶积压制近偏移距多次波.
针对远偏移距多次波,采用高分辨率抛物线Radon变换法.这种方法适用于一次波和多次波视速度差异较大情况下远偏移距多次波的压制.
在偏移叠加数据上运用叠后压制残余多次波、绕射多次波等方法,经过以上处理,主要的多次波能量应该已经基本去除. 2.3.1 SRME——自由表面相关多次波衰减法(van Groenestijn et al., 2012;马继涛等,2011;肖二莲等,2010)
荷兰Delft大学Verschuur提出利用SRME方法和能量最小准则来压制与自由表面相关的多次波( Van Borselen et al., 2005).该方法是利用叠前地震数据中的反射波信息来构建地表相关多次波的一种数据驱动的多次波去除方法(Verschuur,2006),它可以实现自适应相减消除多次波.对于多次波模型预测,不需要任何外部模型和先验参数,也不需要知道详细的地下界面信息.预测过程之后的自适应减去法,是通过两步法来实现的.
(1)多次波模型的预测
在时间域中,表面相关多次波模型M的建立是用实际数据D与通过一次波场P获得的算子做褶积得到的,其结果须用震源子波做反褶积进一步计算.公式(1)中的负号代表了自由表面反射(反射系数为-1).多次波模型可表示为



(2)最小平方减去法
从输入的实际数据D中自适应减去多次波模型数据M,即得到一次反射波.这里的自适应性体现在以下计算过程:在一维(时间域)或者二维(空间-时间域)的滑动窗口内,将对应的一维或二维算子f(多次波模型和实际数据间的匹配滤波算子)应用到多次波模型中,以增加多次波模型数据M与输入的实际数据D的相似度(即遵循最小能量假设原则).两步法,第一步,计算匹配滤波算子为



以上两步对于每个窗口是不断重复进行计算的,窗口的大小和重叠范围应根据具体数据进行定义.一次波通过时空域褶积得到多次波,低阶多次波通过时空域褶积构成高阶多次波,多次波的预测算子就是一次波本身,根据褶积记录中的所有波(一次波、多次波),就能够预测出所有自由表面多次波.
2.3.2 τ-p域预测反褶积
τ-p域预测反褶积,基于多次波的周期性特征,对于周期性较强的多次波压制效果最好.由于在t-x域进行τ-p变换很费机时,因此采用频率域τ-p变换.值得注意的是,预测反褶积基于多次波的周期性质,在τ-p域预测反褶积之前的输入数据,必须保证其多次波周期性未受影响,由于Radon变换影响了多次波的周期性,故先做预测反褶积,后做Radon变换.
在t-x域只有水平层状介质下,零炮检距附近的地震道才满足严格周期性,随偏移距增大周期性逐渐变差.不同阶数的多次波其传播角度也不同(图 6),阶数越高,不同阶数传播时间的差别越小.而在τ-p域中,每一个P道上的多次波都具有较好的周期性,如图 7所示,因此可以沿P轴改变预测步长以压制多次波.由于在τ-p域中多次波具有相对更好的周期性,所以在τ-p域用预测反褶积将更为精确更为有效,同时能够提高计算效率.
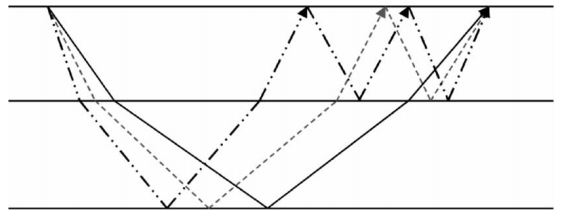 | 图 6 不同阶多次波的传播角度示意图 Fig. 6 Emergence angle of multiples of different orders |
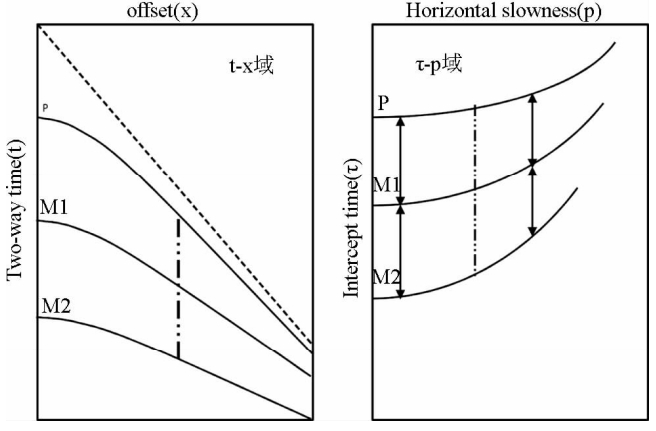 | 图 7 在不同数据域中的多次波周期性特征 Fig. 7 Multiple cycle characteristics in different data domain |
在τ-p域对某一射线参数P,水层多次波和鸣震有严格周期性,可以对各射线参数分别预测反褶积,从而达到压制多次波的目的.每个反褶积处理都需要一个延迟步长,延迟步长应与射线参数所定义射线在第一层的双程旅行时匹配,为一椭圆函数.水平射线参数对应的延迟时间为
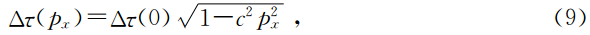

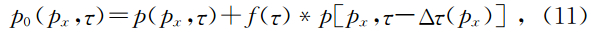
然后参照方程(11)应用一个椭圆延迟自适应滤波器在τ-p域进行预测反褶积.
2.3.3 高分辨率抛物线Radon变换
Hampson(1986)改进了τ- p 变换,将τ- p变换的积分路径t=τ+ph改为t=τ+ph2,给出了抛物线Radon 变换(PRT).
动校正后的双曲线规律的多次波,接近抛物线规律,抛物线路径对其是一种较好的近似.如图 8所示,动校正后一次波被拉平,而多次波存在近似抛物线形态的剩余时差,根据多次波和一次波视速度的差异,通过变换能够将一次波和多次波的能量分离,因此,可以应用抛物线Radon变换压制多次波.图 9所示为Radon变换域一次波与多次波能量分布不同区域,以便准确切除滤波.其中(1)为t-x域数据;(2)为Radon域数据;(3)表示定义的滤波范围;(4)为反变换后的t-x域数据.
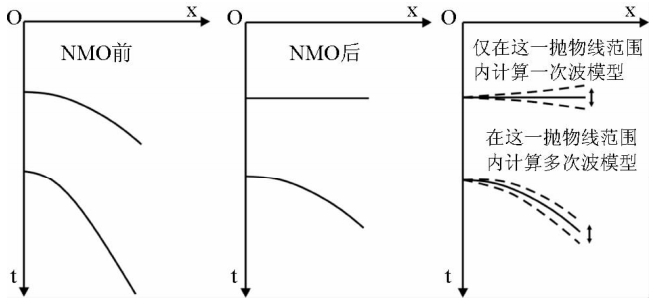 | 图 8 动校正前后的一次波和多次波 Fig. 8 The primary wave and multiples before and after normal moveout correction |
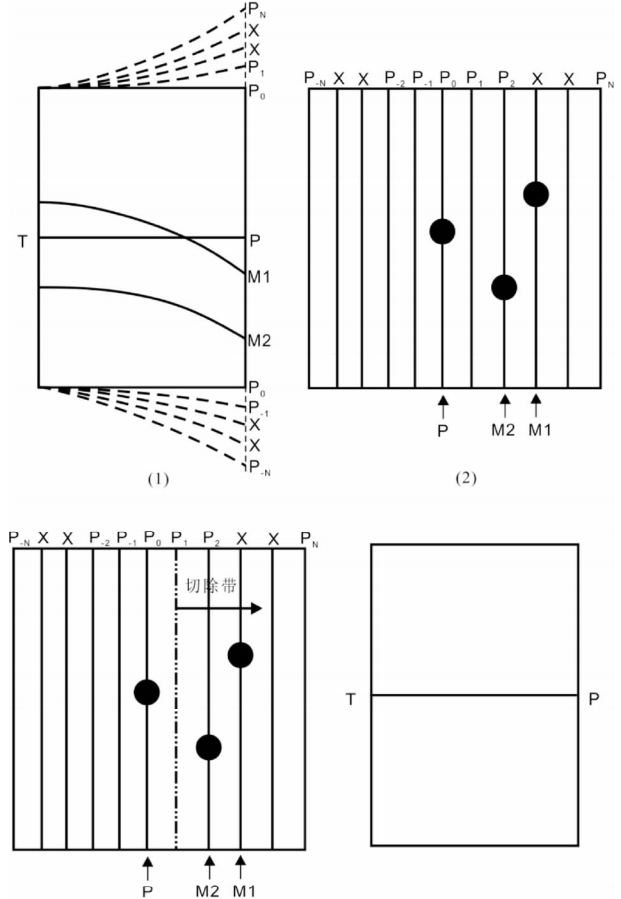 | 图 9 Radon域切除多次波能量 Fig. 9 The filtering of multiple in the Radon domain |
由于地震数据的离散运算,Radon变换存在截断效应,传统的最小二乘约束反演无法有效解决这种截断效应.应用最小二乘方法计算的常规Radon 变换成像存在“蝴蝶”状弥散现象,产生了许多假象.为提高精度和分辨率,应该采用高分辨率Radon变换.高分辨率抛物线Radon 变换在Radon 变换域寻求反射轴的稀疏表示,在Radon 参数和截断时间两方面Radon 变换结果都被稀疏性约束,能够分辨在远道处仅有几毫秒剩余时差的多次波界面(刘喜武等,2004).前人给出了类似的算法(Cary,1998).这种压制多次波的方法能够增加变换域的稀疏性,有效减小采集孔径效应导致的变换域近、远偏移距假象,同时也能很好地聚焦和分开一次波和多次波能量同时去假频,压制多次波效果较常规Radon变换方法更好.值得注意的是,在利用高分辨率Radon变换压制多次波时,Radon变换的曲率参数的确定和Radon变换域中压制区域的确定对于多次波的压制效果影响很大,不合适的参数将会严重影响多次波的压制结果.
2.3.4 叠后压制剩余多次波
经过SRME、τ-p域预测反褶积、高分辨率抛物线Radon变换等处理以后,得到了主要多次波能量压制后的叠前道集.经过迭代速度分析和偏移叠加后的剖面仍有残余多次波,主要是绕射多次波以及其他残余多次波等.绕射多次波主要是由于崎岖海底、以及构造突变等导致的多次反射,它的传播路径既不满足双曲线规律也不满足抛物线规律,因此难以应用SRME和Radon变换等方法进行压制.对于绕射等残余多次波的压制,主要是利用剩余海底多次波的频率和振幅特性,它与一次反射波有较大的差异性.
1 )频率差异:在绕射多次波能量较强的时窗内,绕射多次波的频率高于一次反射波,这也是深水地震资料的特点之一;
2)振幅差异:在绕射多次波能量集中的时窗内,绕射多次波的振幅级别高于一次反射波.
根据频率和振幅的差异性,就可以把绕射多次波的高频能量从原始数据中分离出来进行衰减.然后计算比例系数,将衰减后的高频成分与输入数据相除即可得到.再将计算得到的比例系数应用到输入数据的高频成分上并与其低频部分相加,这就是衰减绕射多次波的主要过程.
3 实际资料对比分析
图 10为多次波压制前后的炮集记录.(a)为原始炮集;(b)为SRME后的炮集;(c)为SRME+高分辨率Radon变换后的炮集;(d)为预测的多次波.多次波主要为海底全程多次波,能量强,周期性较好,图 12也证明了应用多次波周期性的τ-p域预测反褶积效果较为明显.Radon变换后多次波能量几乎都已被压制,仅有极少量残余,这些残余多次波将在叠后数据中予以压制.
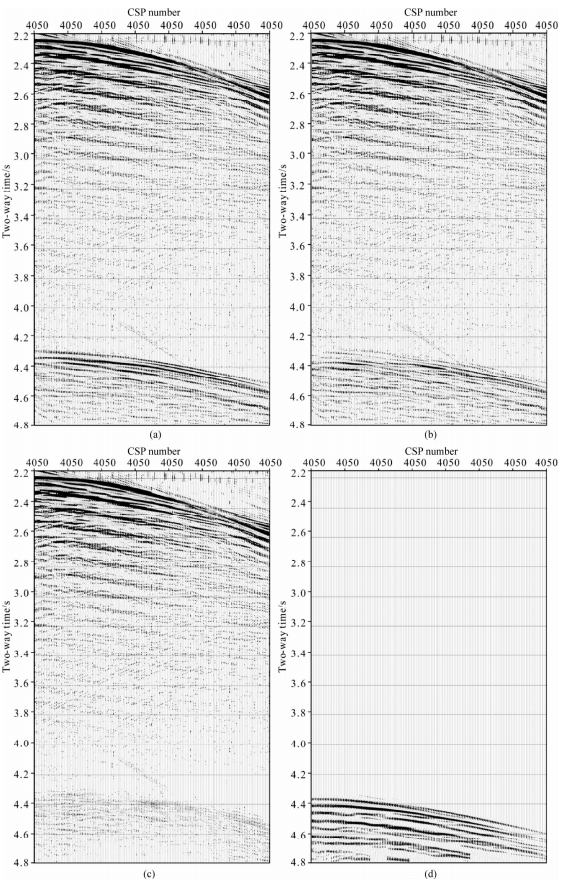 | 图 10 压制多次波前后的共激发点道集 Fig. 10 The Common Shotpoint gather before and after multiple elimination |
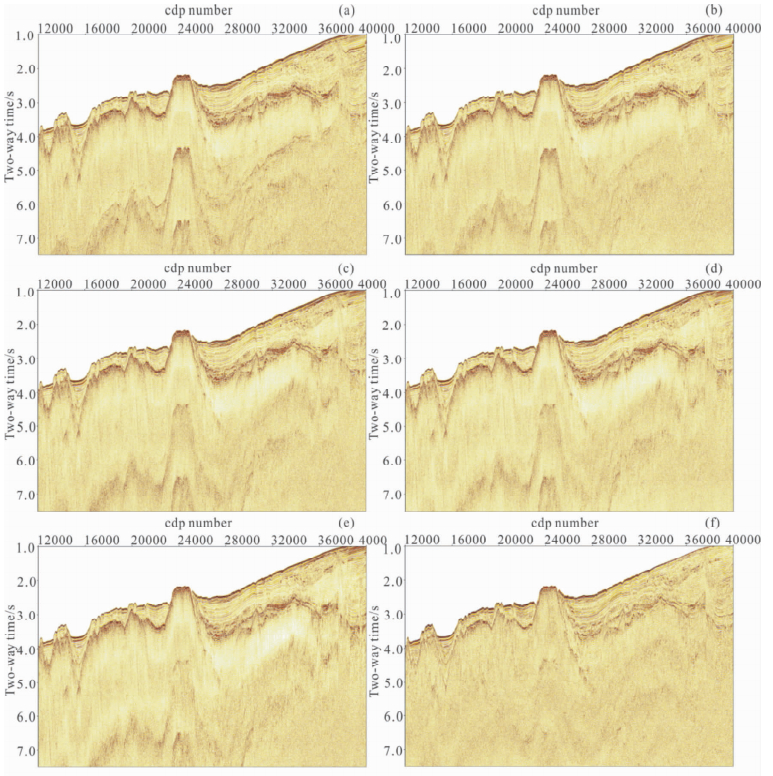 | 图 12 优化组合法压制多次波效果对比 Fig. 12 The effect of multiple elimination with the method of optimum combination |
图 11为多次波压制前后的速度谱和CDP道集.左侧为初次速度分析生成的速度谱和对应CDP道集,右侧为优化组合法压制多次波后的速度谱和对应CDP道集.压制前速度谱多次波能量团十分集中,4.2 s以后几乎没有一次波能量团,速度难以拾取,速度趋势也难以估测,CDP道集上多次波能量覆盖了一次波能量;压制后速度谱上多次波能量已经基本去除,深部的速度得以精确拾取,对应的CDP道集上多次反射能量大部分得到压制,无论是浅部还是深部的有效反射都凸显了出来.
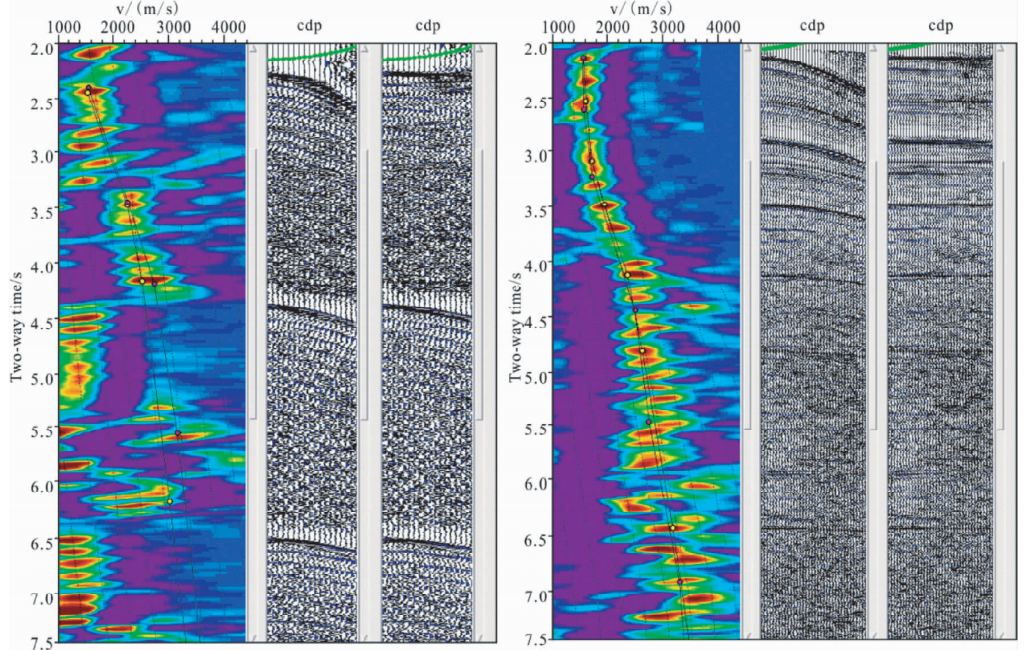 | 图 11 压制多次波前后的速度谱和CMP道集 Fig. 11 The velocity spectrum and Common Midpoint gather before and after multiple elimination |
图 12详细描述了优化组合法压制多次波各个处理步骤的成效.(a)为原始叠加剖面,中深部的全程多次波十分发育,尤其海山区段最为严重,并出现了两阶多次波,足见多次波能量之强;(b)为应用SRME后的叠加剖面,由于海山附近的多次波能量很强,没有明显压制,而海山两侧的海底和基底的全程多次波得到了明显压制;(c)为SRME基础上再做τ-p域预测反褶积的结果,海山的一阶多次波和两侧的海底以及基底多次波得到了进一步压制,但海山二阶多次波没有明显改善;(d)为在前一步基础上再做高分辨率抛物线Radon变换后的结果,多次波压制效果不很明显,原因可能为数据最大偏移距较小,压制远偏移距多次波效果没有得以凸显,同时动校正也切除了部分远偏移距数据;(e)为应用前面三种方法后重拾速度叠加后的结果,浅部同相轴连续性增强,由于深部有效波反射能量较弱,速度精度的提高在深部没有明显体现;(f)为偏移叠加后做叠后压制残余多次波并做增益控制后的结果,残余多次波基本都已压制,深部能量得到补偿,剖面信噪比和分辨率进一步提高,达到了预期目标. 4 结 论
4.1 针对南海北部洋陆过渡带地质特征和数据的具体特点,优选适合的方法并做合理组合,有步骤地做压制多次波处理试验,得出了针对这一海区的合理的方法组合,即SRME+τ-p域预测反褶积+高分辨率抛物线Radon变换+叠后压制残余多次波.
4.2 压制多次波后重拾叠加速度、叠前时间偏移迭代速度分析、构造复杂海底崎岖的区段加密速度分析点,速度精度进一步提高,同相轴连续性将更好,也能增强需要速度信息的Radon变换效果.
4.3 SRME方法在复杂海底构造情况下更能体现其优越性,运用τ-p域预测反褶积压制近偏移距多次波,运用高分辨率Radon变换法压制中远偏移距多次波,在输出的叠后数据上压制残余多次波.
4.4 偏移后的CRP(Common Reflection Point)道集上也可进一步压制残余多次波,下一步研究分析成像空间多次波压制;浅层的层间多次波不易识别,压制效果也不明显,下一步应深入识别和压制浅部层间多次波.
致 谢 本文在撰写和数据处理过程中得到了中国石油勘探开发研究院杭州地质研究院各位研究人员的指导与大力支持,对此表示衷心的感谢!| [1] | Cary P W. 1998. The simplest discrete Radon transform[C]. SEG Annual Meeting. |
| [2] | Ding W W, Li J B. 2011. Seismic stratigraphy, tectonic structure and extension factors across the southern margin of the South China Sea: evidence from two regional multi-channel seismic profiles[J]. Chinese J. Geophys. (in Chinese), 54(12): 3038-3056, doi:10.3969/j.issn.0001-5733.2011.12.006. |
| [3] | Dong D D, Wang D W, Zhang G C, et al. 2009. Cenozoic tectonic and sedimentary evolution of deepwater area, Pearl River Mouth Basin[J]. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese), 33(5): 17-23. |
| [4] | Egbai J C, Atakpo E, Aigbogun C O. 2012. Predictive deconvolution in seismic data processing in Atala prospect of rivers State, Nigeria[J]. Advances in Applied Science Research, 3(1): 520-529. |
| [5] | Foster D J, Mosher C C. 1992. Suppression of multiple reflections using the Radon transform[J]. Geophysics, 57(3): 386-395, doi: 10. 1190/1. 1443253. |
| [6] | Guo Q S, Zhang W H, Huang H C, et al. 2005. High resolution Radon transform method and application[J]. Oil Geophysical Prospecting (in Chinese), 40(6): 622-627. |
| [7] | Guo S J, Li Z C, Tong Z Q, et al. 2011. Joint imaging of primaries and surface-related multiples based on generalized shot-profile migration[J]. Chinese J. Geophys. (in Chinese), 54(4): 1098-1105, doi: 10.3969/j.issn.0001-5733.2011.04.025. |
| [8] | Guo S J, Li Z C, Tong Z Q, et al. 2012. Method and technique for imaging of surface-related multiples[J]. Progress in Geophys. (in Chinese), 27(6): 2570-2576, doi: 10.6038/j.issn.1004-2903.2012.06.034. |
| [9] | Hampson D. 1986. Inverse velocity stacking for multiple elimination[J]. Journal of the Canadian Society of Exploration Geophysicists, 22(1): 44-55. |
| [10] | Hao T Y, Xu Y, Sun F L, et al. 2011. Integrated geophysical research on the tectonic attribute of conjugate continental margin of South China Sea[J]. Chinese J. Geophys. (in Chinese), 54(12): 3098-3116, 10.3969/j.issn.0001-5733.2011.12.011. |
| [11] | Hong F, Hu T Y, Zhang W P, et al. 2004. Attenuating multiples for low signal-to-noise ratio seismic data using optimal beamforming[J]. Chinese J. Geophys. (in Chinese), 47(6): 1106-1110. |
| [12] | Hu T Y, Wang R Q, Wen S L. 2002. Multiple attenuation of seismic data from South China Sea by using beam-forming filtering method[J]. Oil Geophysical Prospecting (in Chinese), 37(2): 18-23. |
| [13] | Hu T Y, Wang R Q, White R E. 2000. Beamforming in seismic data processing[J]. Chinese J. Geophys. (in Chinese), 43(1): 105-115. |
| [14] | Jin D G, Chang X, Liu Y K. 2008. Algorithm improvement and strategy of internal multiples prediction based on inverse scattering series method[J]. Chinese J. Geophys. (in Chinese), 51(4): 1209-1217. |
| [15] | Li P, Liu Y K, Chang X, et al. 2006. Progress on the multiple problems[J]. Progress in Geophys. (in Chinese), 21(3): 888-897. |
| [16] | Li X, Hu T Y. 2009. Surface-related multiple removal with inverse scattering series method[J]. Chinese J. Geophys. (in Chinese), 52(6): 1663-1640, doi: 10. 3969/j. issn. 0001-5733. 2009. 06. 026. |
| [17] | Liu G D. 1992. Geophysical Series Maps in China Sea and Adjacent Regions (in Chinese)[M]. Beijing: Geology Press. |
| [18] | Liu X W, Liu H, Li Y M. 2004. High resolution Radon transform and its application in seismic signal processing[J]. Progress in Geophys. (in Chinese), 19(1): 8-15. |
| [19] | Liu Y K, Chang X, Jin D G, et al. 2011. Reverse time migration of multiples for subsalt imaging[J]. Geophysics, 76(5): 209-216, doi: 10.1190/geo2010-0312.1. |
| [20] | Liu Y K, Sun H C, Chang X. 2004. Multiple removal by wavepath migration[J]. Chinese J. Geophys. (in Chinese), 47(4): 697-701. |
| [21] | Ma J T, Mrinal S K, Chen X H, et al. 2011. OBC multiple attenuation technique using SRME theory[J]. Chinese J. Geophys. (in Chinese), 54(11): 2960-2966, doi: 10. 3969/j. issn. 0001-5733. 2011. 11. 026. |
| [22] | Peacock K, Treitel S. 1969. Predictive deconvolution: theory and practice[J]. Geophysics, 34(2): 155-169, doi: 10. 1190/1. 1440003. |
| [23] | Shi Y, Xing X L, Wu Q J, et al. 2011. Investigation progress on surface-related multiple suppression: review and outlook[J]. Progress in Geophys. (in Chinese), 26(6): 2046-2054, doi: 10. 3969/j. issn. 1004-2903. 2011. 06. 020. |
| [24] | Song Y, Zhao C Y, Zhang G C, et al. 2011. Research on tectono-thermal modeling for Qiongdongnan Basin and Pearl River Mouth Basin in the northern South China Sea[J]. Chinese J. Geophys. (in Chinese), 54(12): 3057-3069, doi: 10. 3969/j. issn. 0001-5733. 2011. 12. 007. |
| [25] | Taner M T. 1980. Long-period sea-floor multiples and their suppression[J]. Geophysical Prospecting, 28(1): 30-48, doi: 10. 1111/j. 1365-2478. 1980. tb01209. x. |
| [26] | Van Borselen R G, Schonewille M A, Hegge R F. 2005. 3D surface-related multiple elimination: Acquisition and processing solutions[J]. The Leading Edge, 24(3): 260-268, doi: 10. 1190/1. 1895310. |
| [27] | Van Groenestijn G, Ross W, Cumaran G. 2012. Connecting deconvolution and SRME[C]. SEG Technical Program Expanded Abstracts, 1-5, doi: 10. 1190/segam2012-1274. 1. |
| [28] | Verschuur D J. 2006. Seismic Multiple Removal Techniques: Past, Present and Future[M]. HOUSTEN: EAGE Publications. |
| [29] | Wang Y H. 2003. Multiple attenuation: coping with the spatial truncation effect in the Radon transform domain[J]. Geophysical Prospecting, 51(1): 75-87, doi: 10. 1046/j. 1365-2478. 2003. 00355. x. |
| [30] | Weglein A B. 1999. Multiple attenuation: An overview of recent advances and the road ahead (1999)[J]. The Leading Edge, 18(1): 40-44, doi: 10. 1190/1. 1438150. |
| [31] | Wu S G, Qin Z L, Wang D W, et al. 2011. Seismic characteristics and triggering mechanism analysis of mass transport deposits in the northern continental slope of the South China Sea[J]. Chinese J. Geophys. (in Chinese), 54(12): 3184-3195, doi: 10. 3969/j. issn. 0001-5733. 2011. 12. 018. |
| [32] | Xiao E L, Chen Y, Wan H, et al. 2010. Surface-related multiple elimination on marine seismic data[J]. Progess in Geophys. (in Chinese), 25(3): 1057-1064, doi: 10. 3969/j. issn. 1004-2903. 2010. 03. 046. |
| [33] | Yan P, Wang Y L, Liu H L. 2008. Topography of oceanic basin in South China Sea and NW-directed faults[J]. Journal of Tropical Oceanography (in Chinese), 27(3): 30-37. |
| [34] | Yilmaz O. 2006. Seismic Data Analysis: Processing, Inversion, and Interpretation of Seismic Data (in Chinese)[M]. Beijing: Press of Petroleum Industry, 122-216. |
| [35] | Zhang Z M, Liou J G, Coleman R G. 1984. An outline of the plate tectonics of China[J]. Geological Society of America Bulletin, 95(3): 295-312, doi: 10. 1130/0016-7606. |
| [37] | 丁巍伟, 李家彪. 2011. 南海南部陆缘构造变形特征及伸展作用: 来自两条973多道地震测线的证据[J]. 地球物理学报, 54(12): 3038-3056, doi:10.3969/j.issn.0001-5733.2011.12.006. |
| [38] | 董冬冬, 王大伟, 张功成,等. 2009. 珠江口盆地深水区新生代构造沉积演化[J]. 中国石油大学学报(自然科学版), 33(5): 17-23. |
| [39] | 郭全仕, 张卫华, 黄华昌,等. 2005. 高精度拉冬变换方法及应用[J]. 石油地球物理勘探, 40(6): 622-627. |
| [40] | 郭书娟, 李振春, 仝兆岐,等. 2011. 基于广义的炮偏移方法实现地表多次波和一次波联合成像[J]. 地球物理学报, 54(4): 1098-1105, doi: 10.3969/j.issn.0001-5733.2011.04.025. |
| [41] | 郭书娟, 李振春, 仝兆岐,等. 2012. 表层多次波成像方法技术研究[J]. 地球物理学进展, 27(6): 2570-2576, doi: 10.6038/j.issn.1004-2903.2012.06.034. |
| [42] | 郝天珧, 徐亚, 孙福利,等. 2011. 南海共轭大陆边缘构造属性的综合地球物理研究[J]. 地球物理学报, 54(12): 3098-3116, doi: 10.3969/j.issn.0001-5733.2011.12.011. |
| [43] | 洪菲, 胡天跃, 张文坡,等. 2004. 用优化聚束滤波方法消除低信噪比地震资料中的多次波[J]. 地球物理学报, 47(6): 1106-1110. |
| [44] | 胡天跃, 王润秋, 温书亮. 2002. 聚束滤波法消除海上地震资料的多次波[J]. 石油地球物理勘探, 37(2): 18-23. |
| [45] | 胡天跃, 王润秋, White R E. 2000. 地震资料处理中的聚束滤波方法[J]. 地球物理学报, 43(1): 105-115. |
| [46] | 金德刚, 常旭, 刘伊克. 2008. 逆散射级数法预测层间多次波的算法改进及其策略[J]. 地球物理学报, 51(4): 1209-1217. |
| [47] | 李鹏, 刘伊克, 常旭,等. 2006. 多次波问题的研究进展[J]. 地球物理学进展, 21(3): 888-897. |
| [48] | 李翔, 胡天跃. 2009. 逆散射级数法去除自由表面多次波[J]. 地球物理学报, 52(6): 1663-1640, doi: 10. 3969/j. issn. 0001-5733. 2009. 06. 026. |
| [49] | 刘光鼎. 1992. 中国海区及邻域地质地球物理系列图集[M]. 北京: 地质出版社. |
| [50] | 刘喜武, 刘洪, 李幼铭. 2004. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 19(1): 8-15. |
| [51] | 刘伊克, Sun H C, 常旭. 2004. 基于波射线路径偏移压制多次波[J]. 地球物理学报, 47(4): 697-701. |
| [52] | 马继涛, Mrinal S K, 陈小宏,等. 2011. 海底电缆多次波压制方法研究[J]. 地球物理学报, 54(11): 2960-2966, doi: 10. 3969/j. issn. 0001-5733. 2011. 11. 026. |
| [53] | 石颖, 邢小林, 吴庆举,等. 2011. 表面多次波压制的研究进展: 回顾与展望[J]. 地球物理学进展, 26(6): 2046-2054, doi: 10. 3969/j. issn. 1004-2903. 2011. 06. 020. |
| [54] | 宋洋, 赵长煜, 张功成,等. 2011. 南海北部珠江口与琼东南盆地构造-热模拟研究[J]. 地球物理学报, 54(12): 3057-3069, doi: 10. 3969/j. issn. 0001-5733. 2011. 12. 007. |
| [55] | 渥·伊尔马滋. 2006. 地震资料分析——地震资料处理、反演和解释[M]. 北京: 石油工业出版社, 122-216. |
| [56] | 吴时国, 秦志亮, 王大伟,等. 2011. 南海北部陆坡块体搬运沉积体系的地震响应与成因机制[J]. 地球物理学报, 54(12): 3184-3195, doi: 10. 3969/j. issn. 0001-5733. 2011. 12. 018. |
| [57] | 肖二莲, 陈瑜, 万欢,等. 2010. SRME多次波衰减方法在海洋地震资料中的应用[J]. 地球物理学进展, 25(3): 1057-1064, doi: 10. 3969/j. issn. 1004-2903. 2010. 03. 046. |
| [58] | 阎贫, 王彦林, 刘海龄. 2008. 南海海盆地形与NW向断裂[J]. 热带海洋学报, 27(3): 30-37. |
 2014, Vol. 29
2014, Vol. 29


