地球物理学进展  2014, Vol. 29 Issue (2): 913-919   PDF    
引用本文
黄建平, 李振春, 林建民, 曹晓莉, 李娜, 田坤.2014, 南印度洋地区双T波现象及形成机制解释[J]. 地球物理学进展, 29(2): 913-919, doi: 10.6038/pg20140259  
HUANG Jian-ping, LI Zhen-chun, LIN Jian-min, CAO Xiao-li, LI Na, TIAN Kun.2014, The double T wave in south Indian Ocean and its generation mechanism. Progress in Geophysics, 29(2): 913-919, doi: 10.6038/pg20140259   
南印度洋地区双T波现象及形成机制解释
黄建平1, 李振春1, 林建民2, 曹晓莉1, 李娜1, 田坤1    
1. 中国石油大学（华东）地球科学与技术学院地球物理系, 青岛 266580;
2. 浙江海洋大学, 舟山 316004
收稿日期: 2013-6-18 修回日期: 2013-10-19 .
基金项目：国家973课题（2011CB202402）、国家自然科学基金（41104069，41274124）和石油大学创新基金联合资助.
作者简介：黄建平，男，1981年生，四川人，博士，副教授，主要从事海洋T波、地震波正演及偏移成像工作.（E-mail：jphuang@mail.ustc.edu.cn）
摘要：T波是由地震激发而在海洋低速层中传播的声波.海洋T波的产生过程相当复杂，对其激发机制的解释,目前存在两种较为流行的模型，倾斜海底反射和海底散射.本文从地震台站（COCO）记录到的印尼苏门答腊半岛的地震信号中，提取出了清晰的T波信号.进一步研究发现，在第一个T波波峰出现后一段时间，又出现了一个明显的T波波峰，即在南印度洋区域存在双T波现象.为解释这一现象，本文通过分析T波信号时域和频域特征，并计算T波理论到时，与实际T波双峰到时比较，推知发生这一独特现象的主要原因可能是狭长海岛的反射作用.
关键词： 海洋低速层     T波     激发机制     散射     双峰    
The double T wave in south Indian Ocean and its generation mechanism
HUANG Jian-ping1, LI Zhen-chun1, LIN Jian-min2, CAO Xiao-li1, LI Na1, TIAN Kun1    
1. China University of Petroleum, Qingdao 266555, China;
2. Zhejiang Ocean University, Zhoushan 316004, China
Abstract: T waves are seismically generated acoustic waves that propagate in low velocity zone of the oceanic sound channel. The mechanism of the T wave generation is extremely complex. At present, there are two popular models to explain the process of the T wave generation: the reflection and scattering theory. In this research, we extract clear double T waves recorded in station (COCO) from the earthquakes occurred at Sumatra Island. In order to explain this strange phenomenon, we firstly calculate the synthetic travel time of the T wave converted from seismic P and S wave, and also the T wave signal both in time and frequency domain. From the comparison between the synthetic and real data, we find out the reflection of the island is the probable reason for the generation of the double T waves.
Key words: low velocity zone     T wave     mechanism     scattering     doublet    

0 引 言

T波是于1946年由Ewing et al.发现的一种由地震波转化而来的声波信号.通常认为，地震信号沿俯冲板块传至海陆交界面时将激发、转换为声波而在水下800~1300 m的海洋低速层中传播 (何怡等，1994;张仁和等，1994;宫在晓等，2005)，并能够被水下探测器记录到( de Groot-Hedlin et al., 1999; de Groot-Hedlin et al., 2001;Minkyu et al., 2001;Robert，2001).目前，有关T 波的激发机制，存在两种理论解释：其一，Johnson 等认为，声波在海面与倾斜海底的多次反射，使得其在海洋中逐渐沿水平传播，从而被低速层俘获形成T波，关键因素是海底的坡度 (Johnson et al., 1966;Johnson，1970).其二，一些研究认为，T波是由地震波在震源附近区域的散射形成的(Walker et al., 1992).在散射模型中，海水深度、震源深度以及俯冲板块的性质将是控制T波的关键因素(Walker et al., 1992).

对T波形成机理和传播规律的研究，已取得了丰硕的成果.在理论研究方面，Groot-Hedlin等计算了不同模态，点源地震所激发的理论T波波场，指出浅源地震，较低模态可激发较为清晰的T波(de Groot-Hedlin et al., 1999; de Groot-Hedlin et al., 2001).Minkyu等发现不同大小模态所对应激发源优势深度存在差异，并指出散射模型是研究海洋T波的关键模型之一(Minkyu et al., 2001).在实际应用方面，Groot-Hedlin(2001)从海洋声纳层中的声波接收仪所记录的东太平洋和北太平洋区域地震信号中，提取出较为清晰的T波信号，并通过T波能量计算，指出：相同震级，正断层和逆断层型地震所激发T波能量，一般要低于走滑断层 (de Groot-Hedlin et al., 1999).此外，也可利用T波包络线长度来推算地震破裂过程和震源时间函数(Johnson，1970)，根据T波的振幅结果计算地震震级(Johnson et al., 1966)，采用T波延时资料结合反演方法计算地震矩震级(Okal et al., 1986)，或者获取T波在频率域内的振幅，进而估算地震震级和矩震级(Hiyoshi et al., 1992;Dziak et al., 1997).与此同时，Dziak(1997)通过不同区域地震计算结果对比给出：海底与俯冲带附近地震所激发的T波机制及能量差别都较大(Dziak et al., 1997).此外，研究还显示T波激发过程与海陆交界面的坡度以及地震震源深度有关(Johnson et al., 1966;黄建平等，2008).Graeber等利用低速声纳层中所记录到的T波，对印度洋东部部分地震震源位置进行了重定位(Graeber et al., 2004).此外一些研究也通过实际地震数据的处理，得到T波的图像及其性质(Lay et al., 1995;Okal et al., 1997;Blackman et al., 2000;Okal，2001;黄建平等，2008；Huang et al., 2010;Huang et al., 2011).

本文将通过陆地地震台(COCO)记录的地震波形，提取高频T波信号，同时经过希尔伯托变换的包络函数处理，得出了T波的包络线图.通过对包络线的研究，我们发现了清晰的T波，且T波信号呈现出较为明显的双峰现象.本文在对南印度洋地区海底地形和T波路径等构造背景及其到时的理论分析基础上，得出海岛反射是该区域产生T波明显双峰记录的一种可能解释. 1 地震数据及T波信号分析

本文研究的区域为南印度洋地区(90°E-120°E，15°S-5°N).地震台站是位于东经96.8349°，南纬12.19°的IRIS数字台站(COCO).我们选取了2002年11月到2005年3月，发生在印尼苏门答腊岛地区，震源深度从10 km到50 km，震级为5级及其以上的地震，地震相关参数如表 1所示.本文选择了IRIS提供的地震P波到时前300 s到后1800 s的地震信号，在这个时间窗口内能够较好的包含研究需要的P、S和T波的信号.

我们首先将表 1中原始地震信号消除线性漂移，同时将所有信号以地震发震时刻为基准零时，如图 1所示.从图 1可以看出，P、S波和T波信号大多数都淹没在噪声中，很难分辨.为了更好的分析波形数据，去除信号中的低频干扰信号，本文将地震信号通过截止频率为2 Hz的高通滤波器，得到如图 2所示的波形.由波形结果可以看出，地震发生后500 s到1500 s之间，出现了两个明显的波峰T1和T2.为了更加清楚地分析两次T波的特征，将地震信号经过希尔伯托变换的包络函数处理，得到了T波包络线(图 3).在图 3中，可以看出较为明显的T波双峰现象.对应于表 1中地震2、5、6，第一个T波的波峰出现在610 s左右，第二个波峰出现在760 s左右，两峰间隔为150 s左右，且第一个波峰的峰值大小为第二个波峰的6.5倍左右.对于表中地震事件1、3、4、7、8、9、10，第一个波峰出现在1090 s，第二个波峰出现在1230 s左右，两峰间隔为140 s左右，且第一个波峰的峰值大小为第二个波峰的3倍左右.

表 1 研究挑选出的地震事件的具体参数包括：地震编号、发震时刻、地震经纬度、深度、地震震级等信息 Table 1 Parameters of the chosen events：the earthquake numbers，seismic moment，the longitude and latitude，depth，magnitude

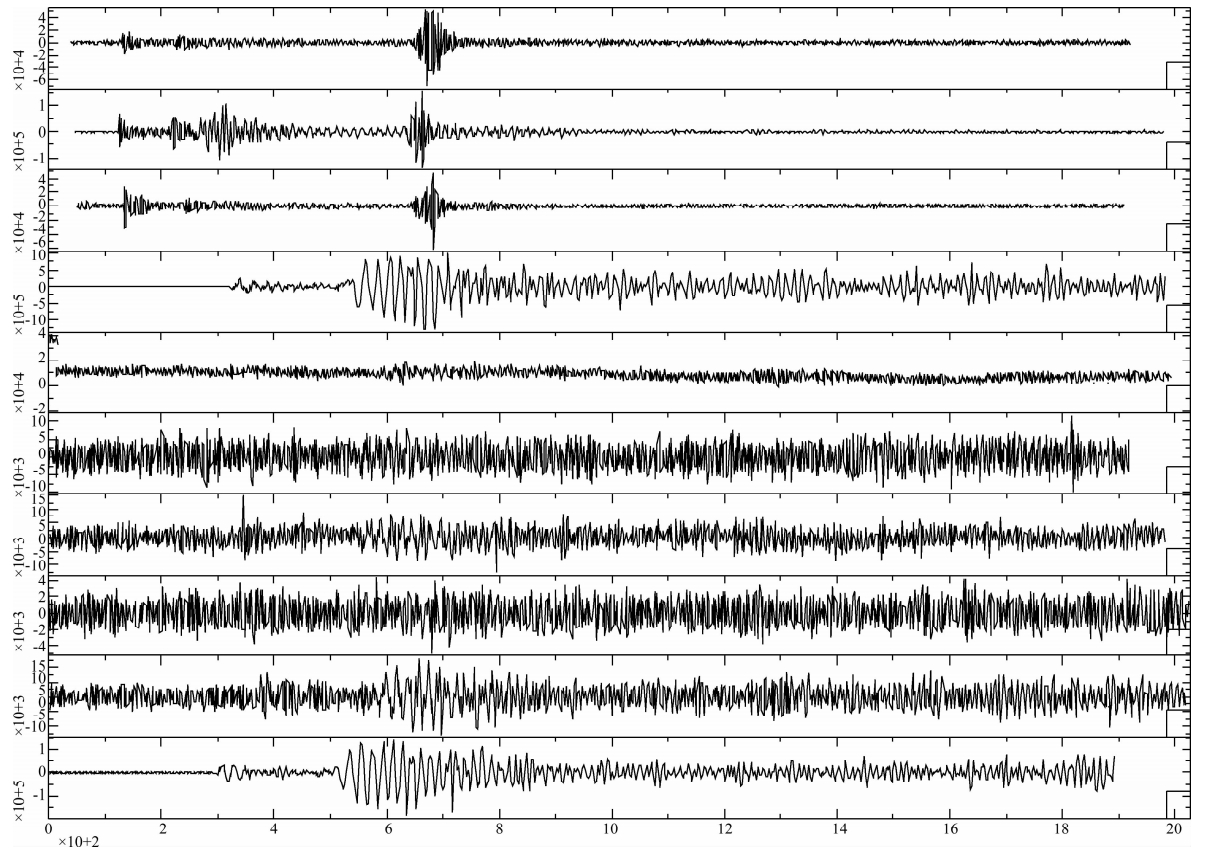图 1 台站(COCO)记录到的原始地震信号(横坐标单位：s)

Fig. 1 The raw seismogram data in station(COCO)


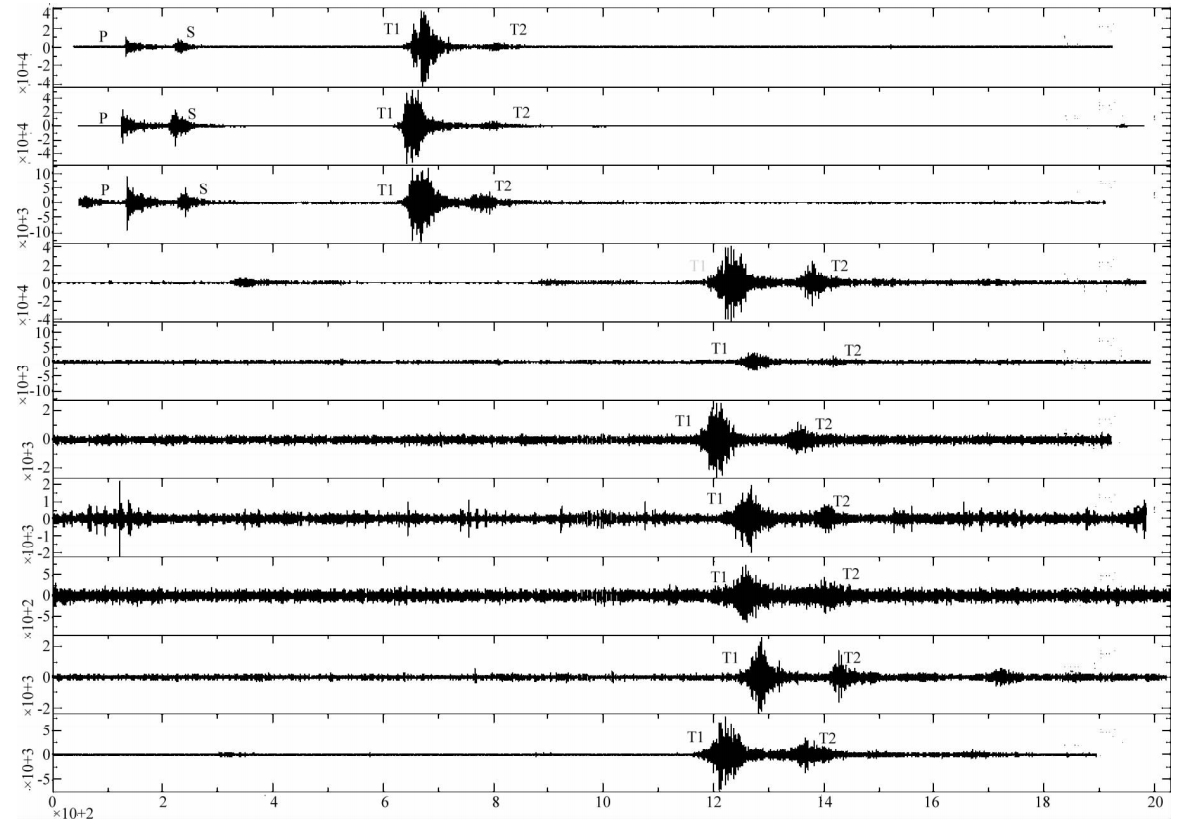图 2 通过高频滤波后得到的T波波形，滤波角频率为2 Hz(横坐标单位：s)

Fig. 2 The T waves generation from high pass filtering the raw data，the corner frequency is 2 Hz


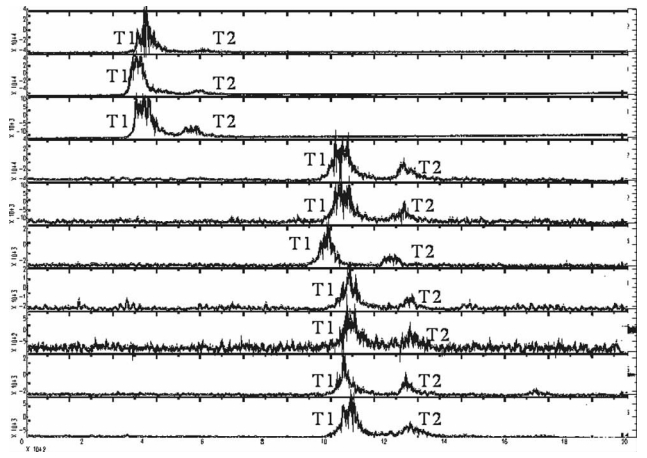图 3 经过处理后的地震T波包络线图(横坐标单位：s)

Fig. 3 The envelope profiles of the T waves

为了更深入认识T波特性，本文选择两个地震聚集区的地震数据1、9为例进行谱分析，研究方法类似于文献( de Groot-Hedlin et al., 2001;Graeber et al., 2004)，得到其频谱随时间变化的关系(图 4).对于地震事件1(图 4(a))，在COCO上有明显的双峰，与之相应在波谱图 4(b)上也存在两个明显的强度较大的区域.通过频谱分布图，从信号的动力学参数特性上发现，双峰较为符合T波波形、能量和相位的主要特征.

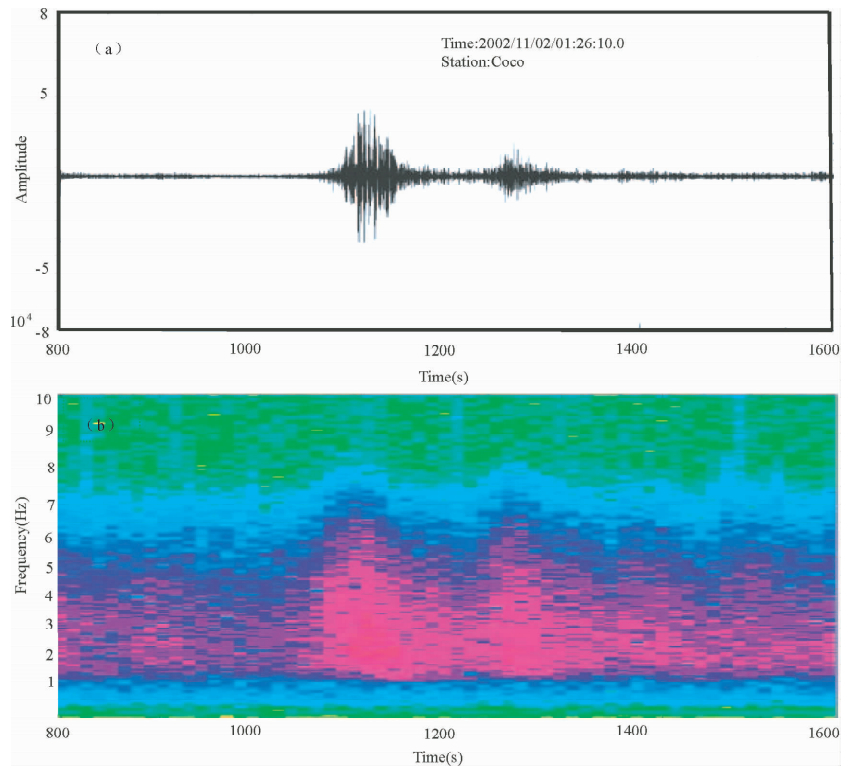图 4(a)地震1在台站(COCO)上处理后的波形图;(b)地震1在台站(COCO)上处理后的频谱随时间变化图.

Fig. 4(a)The seismogram of the T wave in station(COCO)for event 1;

(b)The spectrum of the T wave in station(COCO)for event 1.

2 T波理论走时及双峰现象

观察表 1可见地震主要集中在两个区域，在这两个区域中，震源位置变化不大.由此，本文分别对这两个代表性区域的地震，进行了T波理论到时的计算，其传播路径如图 5所示.图 5中(eve.1)对应地震事件1，(eve.2)对应地震事件9.对这两个地震，(path1)，(path2)分别代表直达及经过海岛反射T波的传播路径.(Sac.1)，(Sac.2)分别代表地震信号沿着上述两条不同路径传播时，在海陆交界处散射点的位置.(Ref-point1)，(Ref-point2)分别表示两个不同事件T波的反射海岛1和海岛2的位置.本文对所选用的地震事件，分别计算了T波沿(path1)和(path2)到达台(COCO)所需的理论走时.计算过程中，P波在陆壳中传播的速度为6.8 km/s(PREM模型)，T波在低速层中传播的速度为1.5 km/s(Lay et al., 1995).T波双峰的实际到时是在T波包络线上读取的.如图 6所示，T1、T2分别为第一和第二个波峰的到达时刻.本文在读取T波到达时刻时，对于不同的包络线图，根据波形的质量，设定了两个误差范围： ±10 s和±5 s，具体数值列于表 2中. 从表 2可以看到，T波经过路径1(直达T波)到达台站(COCO)的理论到时与实际观测T波第一个波峰的到时较为一致，而经过路径2的理论到时(海岛反射波)与第二个波峰的到时较为一致. 由此可见，在该区域T波出现双峰现象可能是海岛的反射作用.

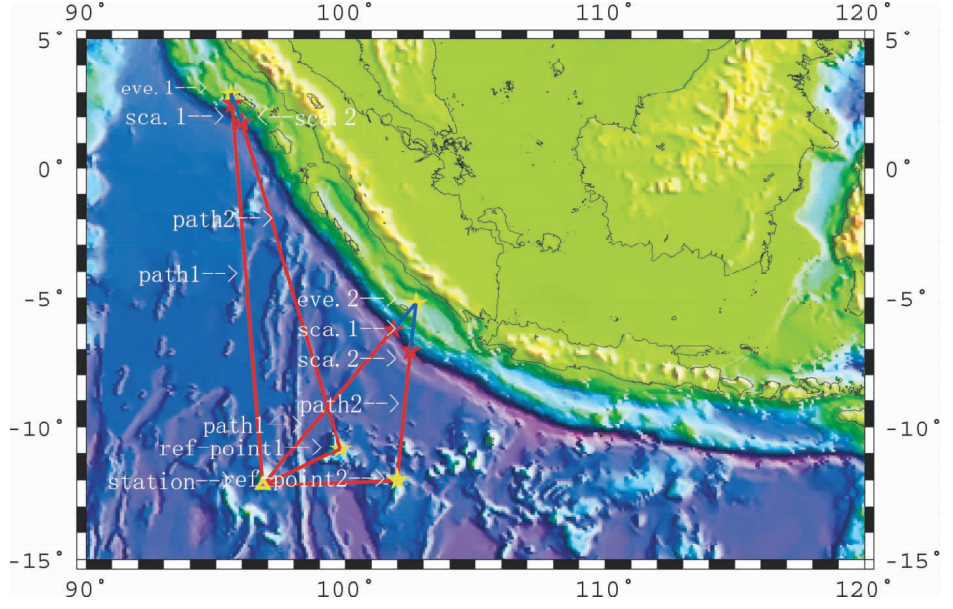图 5 地震激发的T波信号传播过程中海岛反射的路径图(横坐标为经度、纵坐标为纬度)

Fig. 5 The road map of the T wave propagation along the isl and from the different earthquakes


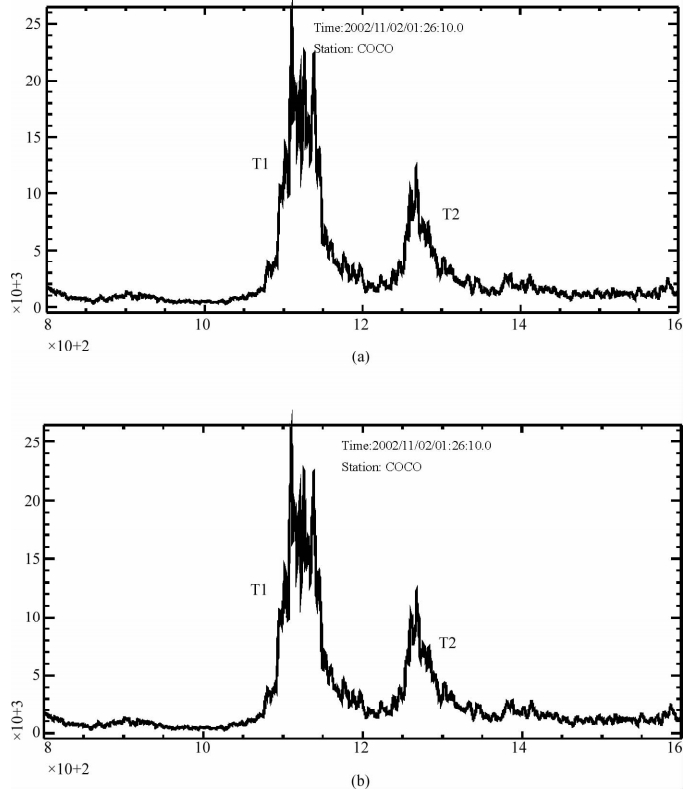图 6 地震1和地震5的T波包络线图(横坐标单位：s)

(a)地震1的T波包络线图;(b)地震5的T波包络线图.

Fig. 6 The envelope profiles for event 1 and event 5

(a)the envelope profile for even 1;(b)the envelope profile for event 5.


表 2 表 1中10个地震事件，经过不同的路径到达台站(COCO)所得到的理论和观测的到时.其中1-10与表 1中的地震事件一一对应.表中“/”的左右分别代表经度和纬度大小 Table 2 The theoretic and observed arriving time of the 10 events in table 1. The two side of “/” in the table refer to the longitude and latitude respectively
3 结论和讨论

本文通过台(COCO)记录到的地震信号的分析处理，得到了清晰的T-波图像，发现了明显的T波双峰现象T1和T2，这与通常观测到的T波图像有很大的差别.同时，在对地震T波信号进行波谱随时间变化分析时，也可以看出两个明显的能量集中的区域.为了探索产生T波双峰现象的可能解释，我们通过计算T波沿不同传播路径的理论走时，并将其与实际观测的T波到时进行比较.结果发现，海岛的反射作用能够解释观测到的T波双峰现象.为了排除震源过程产生T波双峰可能性，本文分析了表 1中地震事件在地震台站(DGAR)上记录到的T波信号，以地震事件6的计算结果为例示于(图 7).可以看出，提取出的T波波形结果中并没有出现双峰现象.由此可知，苏门答腊岛地区地震激发的T波双峰现象，其根源不在地震事件本身.

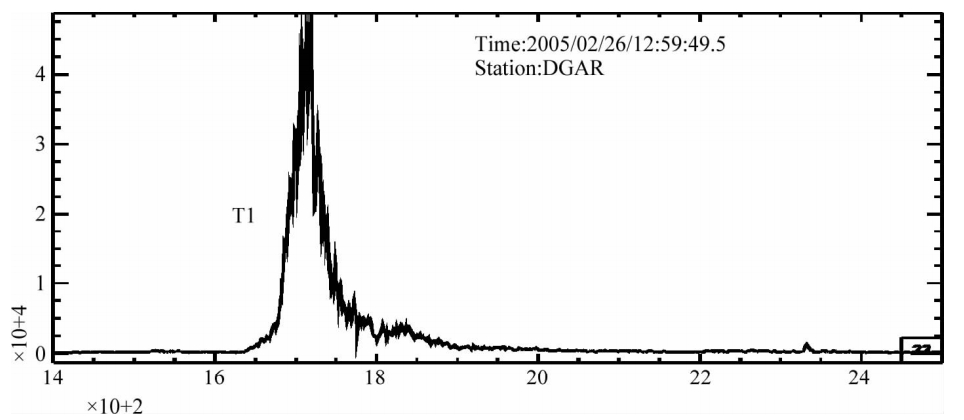图 7 台站(DGAR)记录到的地震10的T-波波形(横坐标单位：s)

Fig. 7 The seismogram of the T wave in station(DGAR)for event 10

当然产生T波双峰现象可能还有别的原因，但分析后我们还是倾向于，南印度洋地区产生T波双峰现象的原因是海岛的反射作用.对于T波两个波峰峰值能量大小的分析发现，对应于不同反射点的T波双峰峰值比为6.5(反射点1)和3(反射点2)左右.究其原因，可能是两反射点对T波的反射效率不同.其反射效率可能不仅与海岛的实际形状、大小等环境因素，同时还可能与反射点岩石的岩性和物性参数有十分密切的关系，这需要进一步结合岩石物理、地震波正演模拟等研究工作加以认识.

致 谢 作者感谢两位匿名审稿人的宝贵意见.同时感谢美国国家地震信息中心(http://neic.usgs.gov/neis/epic/)，地震研究中心联合会(http://www.iris.edu/) Harvard中心矩张量结果中心(http://www.globalcmt.org/)提供的波形和机制解数据.感谢Generic Mapping Tools(GMT)(Wessel and Smith 1995).
参考文献
[1] Blackman D K, Nishimura C E, Orcutt J A. 2000. Seismoacoustic recordings of a spreading episode on the Mohns Ridge[J]. J. Geophys. Res., 105(B5): 10961-10973.
[2] Dziak R P, Fox C G, Matsumoto H, et al. 1997. The April 1992 cape Mendocino earthquake sequence: Seismo-acoustic analysis utilizing fixed hydrophone arrays[J]. Mar. Geophys. Res., 19(2): 137-162.
[3] de Groot-Hedlin C D, John A O. 1999. Synthesis of earthquake-generated T-waves[J]. Geophys. Res. Lett., 26(9): 1227-1230.
[4] de Groot-Hedlin C D, Orcutt J A. 2001. Excitation of T-phases by seafloor scattering[J]. J. Acoust. Soc., 109(5): 1944-1954.
[6] Graeber F M, Piserchia P F. 2004. Zone of T-wave excitation in the NE Indian Ocean mapped using variations in backazimuth over time obtained from multi-channel correlation of IMS hydrophone triplet data[J]. Geophys. J. Int., 158(1): 239-256.
[7] Gong Z X, Zhang R H, Li X L, et al. 2005. Experimental research on sound pulse propagation and channel match in shallow water[J]. Acta Acustica (in Chinese), 30(2): 108-114.
[8] Hiyoshi Y, Walker D A, McCreecy C S. 1992. T-phase data and regional tsunamigenesis in Japan[J]. Bull. Seismol. Soc. Am., 82(5): 2213-2223.
[9] He Y, Zhang R H, Zhu Y. 1994. WKBZ mode approach to pulsed propagation in ocean channels[J]. Acta Acustica (in Chinese), 19(6): 418-424.
[10] Huang J P, Li Z C, Cao X L. 2011. T-wave generation by deep earthquake. Submitted to earthquake science.
[11] Huang J P, Ni S D, Fu R S. 2008. T-phase from the big Sumatra earthquake (2004/12/26) [J]. Process in Geophysics (in Chinese), 23(1): 49-55.
[12] Huang J P, Ni S D. 2008. The relationship between the T phase and the fault parameters of eastern Indian Ocean earthquakes[J]. Journal of University of Science and Technology of China (in Chinese), 38(4): 342-347.
[13] Huang J P, Vanacore E, Niu F L, et al. 2010. Mantle transition zone beneath the Caribbean-South American plate boundary and its tectonic implications[J]. Earth and Planetary Science Letters, 289(1-2): 105-111.
[14] Johnson R H. 1970. Estimating earthquake rupture length from T-waves[C].// Adams W A. Tsunamis in the Pacific Ocean, Proceeding of the International Symposium on Tsunamis and Tsunami Research. Honolulu: East-West Center Press, 253-259.
[15] Johnson R H, Northrop J. 1966. A comparison of earthquake magnitude with T-phase strength[J]. Bull. Seismol. Soc. Am., 56(1): 119-124.
[16] Lay T, Wallace T C. 1995. Modern global seismology[M]. San Diego: Academic Press, 207.
[17] Minkyu P, Robert I O, Soukup D J. 2001. Modal scattering: a key to understanding oceanic T-waves[J]. Geophys. Res. Lett., 28(17): 3401-3404.
[18] Okal E A, Talandier J. 1986. T-wave duration, magnitudes and seismic moment of an earthquake: application to tsunami warning[J]. J. Phys. Earth, 34(1): 19-42.
[19] Okal E A. 2001. T-phase stations for the international monitoring system of the comprehensive nuclear-Test ban treaty: a global perspective[J]. Seismol. Res. Lett., 72(2): 186-196.
[20] Okal E A, Talandier J. 1997. T waves from the great 1994 bolivian deep earthquake in relation to channeling of S wave energy up the slab[J]. J. Geophys. Res., 102(B12): 27421-27437.
[21] Robert P D. 2001. Empirical relationship of T-wave energy and fault parameters of northeast Pacific Ocean earthquakes[J]. Geophys. Res. Lett., 28(13): 2537-2540.
[22] Walker D A, McCreery C S, Hiyoshi Y. 1992. T-phase spectra, seismic moments, and tsunamigenesis[J]. Bull. Seismol. Soc. Am., 82(3): 1275-1305.
[23] Zhang R H, He Y, Liu H. 1994. WKBZ mode approach to sound propagation in horizontally stratified oceans[J]. Acta Acustica (in Chinese), 19(1): 1-12.
[24] 宫在晓, 张仁和, 李秀林,等. 2005. 浅海脉冲声传播及信道匹配实验研究[J]. 声学学报, 30(2): 108-114.
[25] 何怡, 张仁和, 朱业. 1994. 水下声道中脉冲传播的WKBZ简正波方法[J]. 声学学报, 19(6): 418-424.
[26] 黄建平, 倪四道, 傅容珊. 2008. 2004年苏门答腊大地震激发的T-波[J]. 地球物理学进展, 23(1): 49-55.
[27] 黄建平, 倪四道. 2008. 印度洋T波与地震震源参数的相关性[J]. 中国科学技术大学学报, 38(4): 342-347.
[28] 张仁和, 何怡, 刘红. 1994. 水平不变海洋声道中的WKBZ简正波方法[J]. 声学学报, 19(1): 1-12.