地球物理学进展  2014, Vol. 29 Issue (2): 889-894   PDF    
引用本文
朱崇利. 2014,网格剖分对反演的影响[J]. 地球物理学进展, 29(2): 889-894, doi: 10.6038/pg20140256  
ZHU Chong-li. 2014, The influence of the grid subdivision on the inversion. Progress in Geophysics, 29(2): 889-894, doi: 10.6038/pg20140256   
网格剖分对反演的影响
朱崇利    
成都理工大学地球探测与信息技术教育部重点实验室, 成都 610059
收稿日期: 2013-9-15 修回日期: 2013-12-16 .
作者简介：朱崇利，男，1974年生，江苏连云港人，博士研究生，从事地球物理数值模拟与电磁场理论应用研究.（E-mail：zhuchongli@163.com）
摘要：从观测数据中提取更多的有用的地电信息的反演解释才是地球物理工作的终极目的，而反演的精度是勘探地层物性的关键.对于不论是线性反演还是非线性反演算法，研究的重点始终是围绕着如何构建初始模型和提高计算速度.而众多学者大多只是在算法的精度等方面做了相应改进，而研究区域剖分的差异所带来的误差影响，远大于算法等方面的精度的高低.网格剖分的合适与否，为反演结果的精度提供了先决条件.文中用不同的模型不同的反演方法对比验证粗细两种不同的网格对反演精度的影响.经研究表明，两种不同网格剖分方式，从整体上看，在深部粗网格比细网格模拟精度高，但是近地表开始阶段，粗网格与细网格波动幅度都较大，都脱离正常值.粗网格模拟精度不如细网格；整体变化幅度粗网格比细网格缓和，其中对低阻异常体反演精度较好，但对高阻异常体反演精度较差，与真实值相去甚远，奥克姆反演对异常体效果比较差.结果表明，网格剖分对不同反演的精度影响差异很大，进一步说明非线性反演适应性较强且非线性反演能够获取更合理的真实地电模型，精度较高已被广泛的应用于地球物理的各个领域.
关键词： 网格剖分     反演     奥克姆     非线性共轭梯度    
The influence of the grid subdivision on the inversion
ZHU Chong-li    
Key Laboratory of Earth Exploration and Information Techniques of the Ministry of Education, Chengdu University of Technology, Chengdu 610059, China
Abstract: How to extract more useful inversion interpretation of geoelectric information from the observation data,which is the ultimate purpose of geophysical work, And the precision of inversion is the key to the prospecting formation physical property, For both linear inversion and nonlinear inversion algorithm, The focus of the research is how to build the initial model and improve the calculation speed. While many scholars mostly just made corresponding improvement in the precision of the algorithm, etc, the error influence brought by the difference of region subdivision can be far more than the precision of the algorithm, etc. Whether the grid subdivision is suitable provides a prerequisite for the accuracy of the inversion results.In this paper, by using different model different inversion methods we Compared to verify the effects of two different grid on the accuracy of inversion. As a whole, by using the two different ways of grid subdivision, Studies show that the coarse grid is more highly simulation precision than fine grid in the deep, but at the start of near-surface, amplitude of fluctuation of the coarse grid and fine grid is Relatively large, they both break away from the normal value.The simulation accuracy of fine grid is better than coarse grid; The overall change in the coarse grid is more easing than the fine grid, the inversion accuracy of anomalous body of low resistance is better, but for abnormal body of high resistance inversion accuracy is poorer, and widely apart from the real value,the effect of Occam inversion for abnormal body is bad. The results show that the grid subdivision has a great effect on the accuracy of the different inversion. It further shows that the nonlinear inversion has strong compatibility and can obtain a more reasonable truly electric model, It was already used widely in every fields of geophysical exploration as its high precision.
Key words: the grid subdivision     the inversion     occam     nonlinear conjugate gradient    

0 引 言

大地电磁测深(简称MT)法自从50年代初问世以来，在油气的普查与勘探，深部金属矿物勘探与开采，工程勘探，地壳和上地慢电性结构的研究，地热田的调查等方面都得到了成功的应用(张艳飞和徐义贤，2009).由于这种地球物理方法利用天然交变电磁场来探测地下电性结构，它不需要大功率供电设备，却可以研究几十乃至几百公里深度的地壳与上地幔的地电信息，而且高阻屏蔽对它不起作用，由于它的高效、价格低廉、方便等特点，国内外许多学者(陈乐寿，1981；王绪本等，1999；陈小斌等，2000；毛立峰等，2005；马为等，2008；柳建新等，2009)进行了不懈的努力，进行了大量的理论和应用研究.MT法和所有地球物理方法一样通过数据采集处理，然后反演解释，而从观测数据中提取更多的有用的地电信息的反演解释才是地球物理工作的终极目的.当前，大地电磁三维反演是人们热衷探讨的一个课题(吴小平，2005)，但是它离推广应用还有一段路程要走，由于一维的局限性，人们应用最多的还是二维反演(Constable S C et al，1990; Smith J T and Booker J R，1991; 吴小平和徐果明，1998；Rodi W L and Mackie R L，2001；胡祖志等，2005；李永兴等，2010; 程勃和底青云，2012)，但是如何获得最佳初始模型及快速提高运算速度一直是二维研究的重点及有待进一步的完善提高.如大地电磁线性反演算法中的奥克姆(OCCAM)法(Constable，1987)、快速松弛反演法(Smith等，1991、2001)等；非线性反演方法中的非线性共轭梯度(NLCG)反演法(Rodi、Mackie，2001)等．不论线性还是非线性反演算法，研究的重点始终是围绕着如何构建初始模型和提高计算速度.众多学者( 王若和王妙月，2003；汤井田等，2007；王家映， 2007a，b；罗红明等，2009；于鹏等，2009；卞爱飞等，2010；何梅兴等，2011；张季生等，2011；孟小红等，2012；陈华根等，2012)大多只是在算法的精度等方面做了相应改进，而研究区域剖分的差异所带来的误差影响，远大于算法等方面的精度的高低.由于矩形网格剖分在求解地球物理问题中具有典型的一般性及通用性，因此，文中区域选用矩形网格剖分，对于相同的模型分别做不同反演方法对比验证.大地电磁正演的精度对后续反演意义重大，所以文中网格剖分别从正反演两个方面同时结合论证.

我们一般认为细网格剖分总是好于粗网格部分，认为细网格不仅可以提高模型网格化转换的精度，而且可以提高计算求解的精度，进而有利于更好的反演解释.但是，是不是网格越小越好呢？

目前大地电磁的反演方法根据观测数据和模型参数之间的关系，将反演方法分为线性反演和非线性反演法. 1 OCCAM法原理

在二维地电模型中，在给定边界条件后，一般通过有限元法或者有限差分法进行正演模拟，反演问题可表示为：d=F(m)+e式中： d =[d1，d2，…，dN]T为观测数据向量；F(m)为模型正演响应函数，m =[m1，m2，…，mN]T为模型参数向量；e为残差向量.则观测数据与理论模型响应的拟合差可表示为为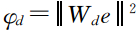.高斯—牛顿法核心思想是将非线性的正演响应函数F(m)线性化，同时通过改善Hessian矩阵的条件数，但由于雅克比矩阵的秩常小于模型参数个数导致方程组病态.而马奎特法通过调整主对角线的系数来改变方程组的矩阵条件数.但是它们都不能对模型进行评价，还是会出现发散的情况.针对这种情况，OCCAM法被Constable等人在1987年提出来，它是针对压制来自非数据的模型构造，达到最小化模型的粗糙度，构造出拟合数据的最小模型.所以目标函数的构建和解的稳定性等方面要同时考虑.对二维构造，Constable等人考虑了模型的横纵向光滑问题，假设模型粗糙度为:分别表示横纵向相邻块的模型参量的粗糙度矩阵.将模型范数项替换为粗糙度矩阵，即为OCCAM法的目标函数和罚函数，对F(m)仍然象GS-N法一样进行泰勒级数一阶展开得到：

J k=(∂ F /∂ m)|m k是在 m k处计算的 N×M 阶灵敏度矩阵，然后根据正则化思想构造一个无约束的函数，由微分建立方程，产生一逼近解的迭代序列，从以上过程看出OCCAM法实质上是一种平滑约束的最小二乘法正则化反演方法，在每次迭代过程中，由正则化参数调控方向和步长；在迭代前期一般拟合差很大，选择最小拟合差模型是最佳方案，而在迭代后期，一般有多个模型满足拟合要求，最小范数模型的选择是首当其冲，这种方案大大提高了反演的稳定性和收敛速度.初始模型的选取对OCCAM反演结果不起决定作用，反演速度不快，但是很稳定. 2 非线性共轭梯度反演

定义：φ(m)=(d -F(m))TU-1(d -F(m))+λ m T w T wm，给定已知数值.正则化因子λ是一个正数.正定矩阵 U表示探测数据的误差.令A表示正演函数F的雅可比矩阵：A ij(m)=∂j F i(m)，i=1，2，…，N，j=1，2，…，M，根据Fletcher和Reeves于1964年提出的利用共轭梯度法求解非线性问题的思想，可以不进行雅可比矩阵 A 的计算而直接求得.算法引用了Polak-Ribiere的非线性共轭梯度方法来求 解式中极小值.它通过非精确的一维搜索确定每一步的步长αk，和线性CG迭代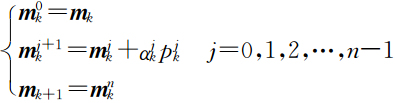 中，步长的精确计算不同，搜索方向迭代如下：p0=-C0g0，pk=-Ckgk+βkpk-1，k=1，2，3，…式中Ck为预条件因子.不同于线性CG的搜索方向迭代，引用PRP非线性共轭梯度算法计算共轭方向向量的加权因子搜索方向没有必要与某些固定矩阵共轭，但是要满足一个条件： p Tk(g k- g k-1)=0则可，NLCG无须计算Hessian矩阵，实践证明，NLCG反演方法是快速、高效、稳定，反演结果具有较高的分辨率，可以进行较大规模反演问题的计算.另外，NLCG反演方法可以进行联合反演，如TE和TM视电阻率和阻抗相位的联合.当然，NLCG反演方法的自身缺陷也是在所难免的，比如对初始模型的选择存在依赖性，正则化参数筛选需要凭经验输入. 3 模型算例

为了更好地验证粗细网格剖分的不同效果，通过奥克姆反演和非线性共轭梯度反演两种方法，笔者计算如下两种模型进行反演结果(文中采用TE模式，因为不仅比TM模式误差波动小，而且基本雷同)分析：

模型一(如图 1所示)，以高阻异常体为例：均匀半空间中有一个电阻率为1000 Ωm，上底埋深为1 km，下底埋深为2 km，长度4 km矩形异常体，背景电阻率为10 Ωm.网格剖分分成两种方式对比验证：粗网格，在反演时正演网格数为40×26，反演网格数为40×26；细网格，在反演时正演网格数为100×60，反演网格数为100×50；

图 1 高阻模型

Fig. 1 High resistance model

从图 2可见奥克姆反演(粗网格)结果中在深度约1000 m下出现高阻异常体，2000 m以下慢慢波动趋于平缓，接近背景电阻率值，但异常体中心电阻率值和实际电阻率值相差较大，而且向两边及向上下略微扩散延伸，略超出实际异常范围，异常体中心位置与初始模型吻合比较好.但细网格反演结果出现挂“面条”现象，不能真实反映地电模型的物性，对异常体的中心位置都难以确定.

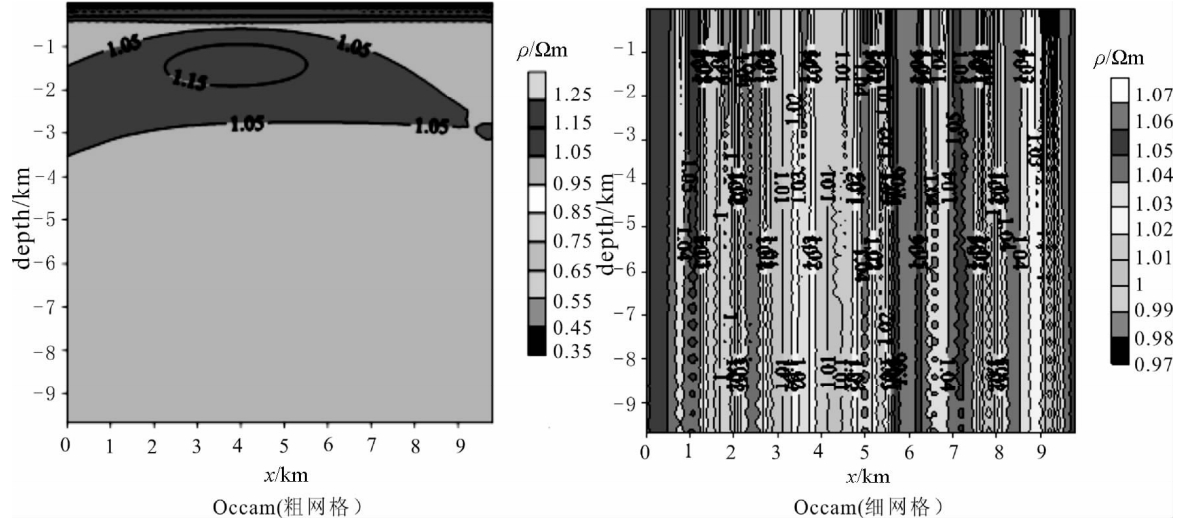图 2 不同网格反演(Occam)

Fig. 2 The inversion of the different grid

从图 3可见NLCG反演结果中在深度约1000 m下出现低阻异常体，2000m以下慢慢波动趋于平缓，接近背景电阻率值，但异常体中心电阻率值和实际出入较大，而且向两边及向上下略微扩散延伸，略超出实际异常范围，异常体中心位置与初始模型吻合比较好.而且从粗细不同网格剖分看出，在低频阶段，粗网格模拟效果比细网格精度明显好得多，这可以从趋肤深度角度得以论证，而在高频阶段细网格模拟精度比粗网格好得多，但是在近地表阶段，两种网格模拟结果波动都比较大.整体可以看出NLCG反演能较好的反映出地电模型的异常体埋深、范围与实际模型比较接近，能比较准确地反映出异常体的中心位置，但是和实际值相差太大.而且从图 2、图 3看出非线性反演有更好的适应性，能更好反映出地电模型的物性.

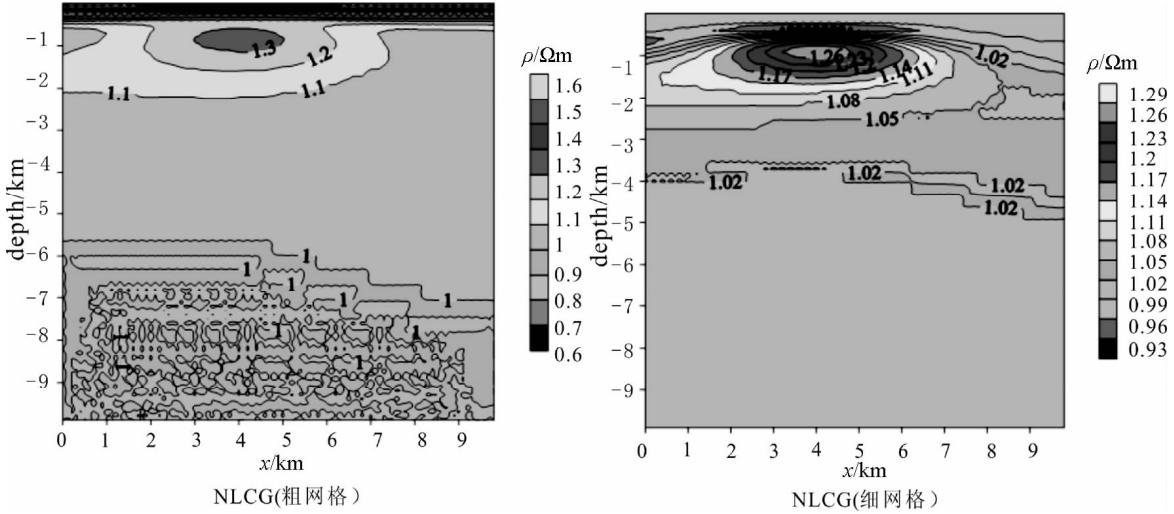图 3 不同网格反演(NLCG)

Fig. 3 The inversion of the different grid

模型二(如图 4所示)，以低阻异常体为例：均匀半空间中有一个电阻率为10 Ωm，上底埋深为1 km，下底埋深为2 km，长度4 km矩形异常体，背景电阻率为100 Ωm.网格剖分分成两种方式对比验证：粗网格，在反演时正演网格数为40×26，反演网格数为40×26；细网格，在反演时正演网格数为100×60，反演网格数为100×50；

图 4 低阻模型

Fig. 4 Low resistance model

从图 5可见奥克姆反演结果中在深度约1000 m下出现低阻异常体，2000m以下慢慢波动趋于平缓，接近背景电阻率值，异常体中心电阻率值和10 Ωm有一定差距，而且向两边及向上下略微扩散延伸，略超出实际异常范围，异常体中心位置与初始模型吻合比较好.而且从粗细不同网格剖分看出，在低频阶段，粗网格模拟效果比细网格精度略微好些，这可以从趋肤深度角度得以论证，而在高频阶段细网格模拟精度比粗网格好，但是在近地表阶段，两种网格模拟结果波动都比较大，但细网格明显精度好得多.整体可以看奥克姆反演能较好的反映出地电模型的物性，能比较准确地反映出异常体的中心位置.

图 5 不同网格反演(Occam)

Fig. 5 The inversion of the different grid

从图 6可见NLCG反演结果中在深度约1000 m下出现低阻异常体，2000m以下慢慢波动趋于平缓，接近背景电阻率值，异常体中心电阻率值比较接近10 Ωm而且向两边及向上下略微扩散延伸，略超出实际异常范围，但粗网格剖分明显比细网格剖分向两侧延伸的范围大得多，异常体中心位置与初始模型吻合比较好.而且从粗细不同网格剖分看出，在低频阶段，粗网格模拟效果比细网格精度明显好得多，这可以从趋肤深度角度得以论证，而在高频阶段细网格模拟精度比粗网格好得多，但是在近地表阶段，两种网格模拟结果波动都比较大，但细网格波动要大.整体可以看出NLCG反演能较好的反映出地电模型的异常体大小、埋深、范围与实际模型比较接近，能比较准确地反映出异常体的中心位置，而且从图 5、图 6看出非线性反演有更好的适应性，能更好反映出地电模型的物性.

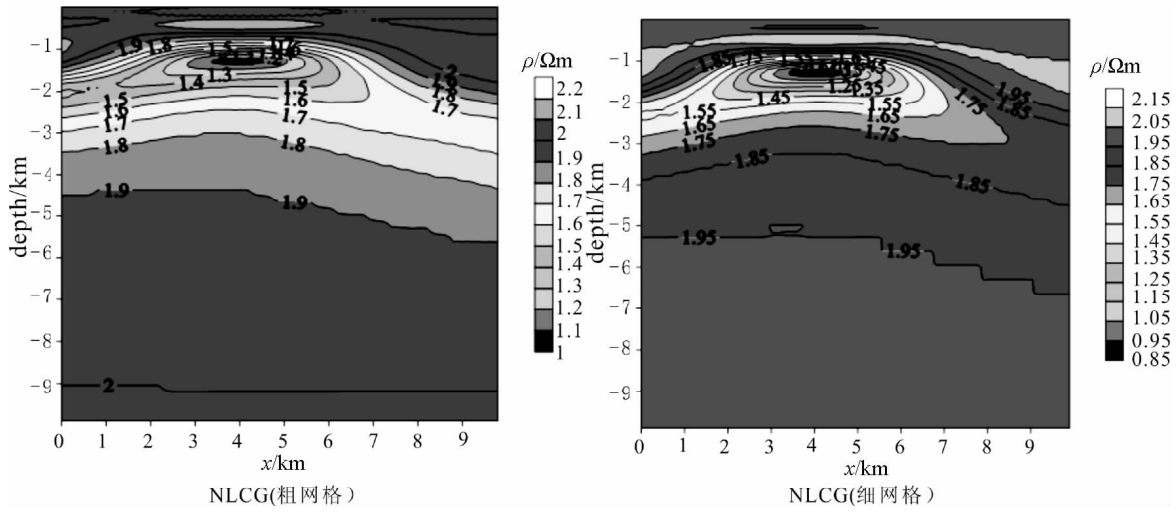图 6 不同网格反演(NLCG)

Fig. 6 The inversion of the different grid
4 结 论

(1)从反演的结果来看，整体趋势深部用粗网格较好，浅部用细网格较好.

(2)在近地表阶段，不论粗网格还是细网格剖分反演结果波动范围都比较大，粗网格变化幅度较细网格略大.

(3)对低阻异常体反演精度较好，但对高阻异常体反演精度较差，从整体上看，奥克姆反演对异常体而言，粗网格效果要好于细网格.

(4)网格在高频时不能剖分太大，防止出现物性变化.

(5)至于反演结果中途细微变化有待进一步探讨.

参考文献
[1] Bian A F,Ling W H,Zhou H W. 2010. Progress in the frequency-domain full waveform inversion method[J].Progress in GeoPhys.(in Chinese),25(3):982-993.
[2] Constable S C et al. 1990. Occam's inversion to generate smooth, two - di2mensional models from magnetotelluric data[J]. Geophysics, 55(12) : 1613-1624.
[3] Chen L S. 1981. Application and improvement of finite-element method in forward calculation of geo-electromagnetic field[J]. geophysical prospecting for petrole, 20(3):84-103.
[4] Chen X B,Zhang X, Hu W B. 2000. Application of finite-element direct iteration algorithm to mt 2-d forward computation[J].oil geophysical prospecting, 35 (4) : 487-496.
[5] Chen H G,Li J X,Wu J S,et al. 2012. Study on simulated-annealing MT-gravity joint inversion[J].Chinese J.Geophys.(in Chinese),55(2):663-670.
[6] Cheng B,DI Q Y. 2012. 2Dinversion of resistivity sounding base on GA and statistic method[J].Progress in Geophys.(in Chinese),27(2):788-795.
[7] Hu Z Z, Hu X Y, Wu W P,et al. 2005. Compared study of two-dimensional magnetotelluric inversion methods[J]. Coal Geology&Exploration,33(1):64-68.
[8] He M X,Hu X Y,Ye Y X,et al. 2011. 2.5 D controlled source audio-frequency magnetotellurics OCCAM inversion[J]. Progress in GeoPhys.(in Chinese), 26(6):2163-2170.
[9] Liu J X,Jiang P F, Tong X Z, et al. 2009. Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling[J]. Journal of central south university, 40 (2) : 484-491.
[10] Li Y X,Qiang J K,Tang J T. 2010. A research on 1-D forward and inverse airborne transient electromagnetic method[J].Chinese J.Geophys.(in Chinese),53(3):751-759.
[11] Luo H M,Wang J Y,Zhu P M,et al. 2009. Quantum geneticalgorithm and its application in magnetotelluric data inversion[J].Chinese J.Geophys.(in Chinese),52(1):260-267.
[12] Mao L F, Wang X B, Gao Y C. 2005. Appraisement on the MT probability tomography[J].Chinese J.Geophys.(in Chinese), 48(2):429-433.
[13] Ma W,Chen X B,Zhao G Z. 2008. A new algorithm for the calculation of auxiliary field in mt 2d forward modeling[J]. Seismology and Geology, 30 (2) : 525-533.
[14] Meng X H,Liu G F,Chen Z X,et al. 2012. 3-D gravity and magnetic inversion for physical properties based on residual Anomaly correlation[J].Chinese J.Geophys.(in Chinese),55(1):304-309.
[15] Rodi W L and Mackie R L. 2001. Nonlinear conjugate gradients algorithm for2 - D magnetotelluric inversion[J]. Geophysics, 66 (1) : 174 -187.
[16] Smith J T and Booker J R. 1991. Rapid inversion of two - and three - di2mensional magnetotelluric data[J]. J. Geophys. Res., 96 : 3905- 3922.
[17] Tang J T,Ren Z Y,Hua X R. 2007. The forward modeling and inversion in geophysical electromagnetic field[J]. Progress in GeoPhys.(in Chinese), 22(4): 1181-1194.
[18] Wang X B,Li Y N, Gao Y C. 1999. Two dimensional topographic responses in magneto telluric sounding and its correction methods[J].computing techniques for giophysical and geochenical exploration, 21(4) :327-332.
[19] Wu X P. 2005. 3-D resistivity inversion under the condition of uneven terrain[J].Chinese J.Geophys.(in Chinese),48(4):932-936.
[20] Wu X P, Xu G M. 1998. Improvement of occam's inversion for mt data[J]. Chinese J.Geophys.(inChinese), 41(4):547-554.
[21] Wang J Y. 2007. Introduction to Geophysical Inverse Problems[J]. Chinese Journal of Engineering Geophysics,4(1):1-3.
[22] Wang J Y. 2007. The Inversion Theory of Geophysics[M].Beijing:Higher Edueation Press.
[23] Wang R, Wang M Y. 2003. Inversion method of controlled source audio-frequency magnetotelluric data[J]. Progress in GeoPhys.(in Chinese), 18(2): 197-202.
[24] Yu P,Dai M G,Wang J L,et al. 2009. Joint inversion of magnetotelluric and seismic data based on random resistivity and velocity distributions[J].Chinese J.Geophys.(inChinese),52(4):1089-1097.
[25] Zhang Y F,Xu Y X. 2009. Study on the feasibility of using the MT rnethod to map the depth of Curie interfaee[J].Progress in GeoPhys.(InChinese),24(6):2003-2011.
[26] Zhang J S,Gao R,Li Q S,et al. 2011. A combined Euler and analytic signal method for an inversion calculation of potential data[J].Chinese J.Geophys.(in Chinese),54(6):1634-1641.
[27] 卞爱飞,龄文辉,周华伟.2010.频率域全波形反演方法研究进展[J].地球物理学进展,25(3):982-993.
[28] 陈乐寿.1981.有限元法在大地电磁场正演计算中的应用与改进[J].石油物探,20(3):84-103.
[29] 陈小斌,张翔,胡文宝. 2000. 有限元直接迭代算法在MT二维正演计算中的应用[J]. 石油地球物理勘探,35(4):487-496.
[30] 陈华根,李嘉虓,吴健生,等. 2012. MT-重力模拟退火联合反演研究[J].地球物理学报,55(2):663-670.
[31] 程勃,底青云.2012.基于遗传算法和统计学的电阻率测深二维反演研究[J].地球物理学进展, 27(2):788-795.
[32] 胡祖志,胡祥云,吴文鹏,等.2005.大地电磁二维反演方法对比研究[J].煤田地质与勘探,33(1):64-68.
[33] 何梅兴,胡祥云,叶益信,等. 2011. 2.5维可控源音频大地电磁法Occam反演理论及应用[J].地球物理学进展,26(6):2163-2170.
[34] 柳建新,蒋鹏飞,童孝忠,等. 2009. 不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用[J].中南大学学报,40(2):484-491.
[35] 李永兴,强建科,汤井田. 2010. 航空瞬变电磁法一维正反演研究[J].地球物理学报,53(3):751-759.
[36] 罗红明,王家映,朱培民,等. 2009. 量子遗传算法在大地电磁反演中的应用[J].地球物理学报,52(1):260-267.
[37] 毛立峰,王绪本,高永才. 2005. 大地电磁概率成像的效果评价[J].地球物理学报,48(2):429-433.
[38] 马为,陈小斌,赵国泽. 2008. 大地电磁测深二维正演中辅助场的新算法[J].地震地质,30(2):525-533.
[39] 孟小红,刘国峰,陈召曦,等. 2012. 基于剩余异常相关成像的重磁物性反演方法[J].地球物理学报,55(1):304-309.
[40] 汤井田,任政勇,化希瑞. 2007. 地球物理学中的电磁场正演与反演[J].地球物理学进展,22(4): 1181-1194.
[41] 王绪本,李永年,高永才. 1999. 大地电磁测深二维地形影响及其校正方法研究[J]. 物探化探计算技术,21(4):327-332.
[42] 吴小平. 2005. 非平坦地形条件下电阻率三维反演[J].地球物理学报,48(4):932-936.
[43] 吴小平,徐果明. 1998. 大地电磁数据的Occam反演改进[J].地球物理学报,41(4):547-554.
[44] 王家映.2007.地球物理反演问题概述[J].工程地球物理学报,4(1):1-3.
[45] 王家映. 2007. 地球物理反演理论[M].北京:高等教育出版社.
[46] 王若,王妙月. 2003. 可控源音频大地电磁数据的反演方法[J].地球物理学进展,18(2):197-202.
[47] 于鹏,戴明刚,王家林,等. 2009. 电阻率和速度随机分布的MT与地震联合反演[J].地球物理学报,52(4):1089-1097.
[48] 张艳飞,徐义贤. 2009. MT探测居里面深度的可行性研究[J].地球物理学进展,24(6):2003-2011.
[49] 张季生,高锐,李秋生,等. 2011. 欧拉反褶积与解析信号相结合的位场反演方法[J].地球物理学报, 54(6):1634-1641.