2014, Vol. 29
为了探测井外断层或反射面(文中称其为界面，井内流体与井外固体的分界面被称为井壁)，起源于地震勘探的偏移成像技术(Claerbout，1971；Schneider，1978；程玖兵等，2009)逐渐被应用于测井领域中(Hornby，1989；Esmersoy et al., 1998；Tang，2004；严建文等，2008；唐晓明和魏周拓，2012)，进而形成了一种新的井下声反射成像技术——单井成像.传统的测井技术(鲁来玉等，2006；胡恒山和何晓，2009；宋若龙等，2010；马明明等，2013)主要是测量井眼周围地层的参数，而单井成像主要是探测井外的断层或裂缝.就获得的结果而言，单井成像与地震勘探类似，都属于成像技术.但是，地震勘探的频率一般都低于100Hz，其主要用于大范围的地质结构探测；单井成像的频率为kHz量级，分辨率比地震成像高的多，探测范围一般在10m左右，主要被用于井眼附近地质结构的局部探测，以便即时指导钻探、开采.单井成像技术在地质导向、储层位置探测等方面有着广泛的应用，其已经成为地下资源勘探、开采的重要工具.
井外的地质构造从宏观上看一般为曲面，但是在局部范围内对其进行成像时，我们可以视其为一个平面(图 1中区域1与2的分界面).在图 1中，z轴为井轴方向，源和接收器均位于井轴上.依据几何关系可知，井内接收到的反射信号都来自于一条反射线(图 1中的线段AB)上.单井成像的目的是判断井外是否有界面，若有，方位角、倾角以及界面与源的距离是多少.图 1中，倾角β∈[0，π/2]是反射线与z轴的夹角；方位角α∈[0，2π]是反射线在X-Y平面的投影与x轴的夹角；d是反射线与源的距离.
 | 图 1 斜界面Fig. 1 The inclined interface |
求倾角和距离的工作可以参照地震成像技术完成.地震成像时，方位角的求解可以借助于在地表设置多条测线来实现；但是在单井成像中，这显然是不现实的，因为测线只能沿井轴排列.可用信息的匮乏是单井成像比地震成像更困难的根本原因.单井成像技术中，方位角α可以通过位移的x和y分量大小来确定，但是其存在多解性(见下式)
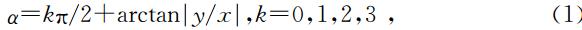
利用同一时刻反射波信号位移x和y分量绝对幅度的比，从式(1)中将得到四个可能的解，其中只有一个解代表界面的真实方位角.由于现有的单井成像技术仅利用了反射信号中的位移与到时，所以方位角不能被唯一确定，通常需要借助一些额外的信息来实现界面的准确定位.即使将图 1的模型简化为二维情况(此时k的取值为0或2)，单井成像依然面临着界面方位如何选取的问题，我们用图 2 来说明这个问题.
 | 图 2 虚界面与真实界面Fig. 2 The false and true interface |
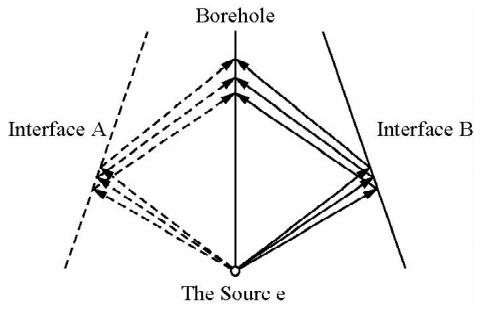
图 2中，位于右侧的实线代表真实界面，左侧的虚线代表虚界面，中间的直线是井轴线，虚界面与真实界面关于井轴对称(虚界面是成像过程中没有消除界面方位模糊性所产生的，它不是真实存在的界面).源所激发的波到达某一接收位置有两条可能路径(不考虑直达波).尽管位于井轴上的阵列接收器接收到的反射波(其路径由图 2中实线给出)均来自右侧的真实界面，但当仅利用幅度和到时信息进行判别时，我们无法排除源激发的波沿左侧虚线所给出的路径达到接收位置的可能性(因为沿两条不同路径到达的反射波在幅度和到时上没有差异)，也就是说我们无法确定界面位于接收阵列的左侧还是右侧.同是成像技术，在地震勘探中，界面位于地下，而接收阵列位于地表，所以其是在半空间内成像；而单井成像时，接收阵列左右两侧均可能存在界面，所以此时要做的是全空间范围内的成像.这是单井成像与地震勘探的一个重要区别，也是单井成像方位模糊性产生的根源.
早期的单井成像给出的是二维结果，虽然此时不需要求解方位角(或者说方位角仅为0或π)，但是其依然需要对界面的方位进行判定，即判断界面在图 2中的左侧还是右侧.通常情况下，可以利用一些其他渠道获得的信息来解决这个问题.如Hornby(1989)利用了倾角钻井记录，Esmersoy等(1998)利用了井的轨迹记录.
偶极测井仪可以提供径向两个正交方向上的反射信号，这为井下三维成像奠定了基础.但是界面方位角的多解性仍然存在，并且由二维成像时的左右两侧二选一演变为三维成像时的四象限选一.Tang(2004)曾经提出过一个解决方案：利用偶极源和单极源的测量结果进行对比.但是这需要偶极系统和单极系统在界面上的入射波必须相同，并且迄今为止未见后续报道.对于一般的偶极测井仪，他利用最小二乘原理得到了两个相差180°的方位角.井间成像(严建文等，2008)不存在界面方位的选择问题，但是其经济成本太高.目前也有国内学者(乔文孝等，2008)试图通过利用相控阵技术来实现方位判别，不过这需要对现有测井仪进行大幅度改装.此外还有通过改变发射装置和接收阵列的位置来实现界面准确定位的技术，如垂直地震剖面成像(孙文博和孙赞东，2010；吴世萍等，2011；刘守伟等，2012).
井外界面的方位模糊性已经引起了国内外学者的高度关注，但是从经济性、实用性上看，目前其还未得到妥善解决.本文的目的就是建立一种仅利用井内接收信号就可以实现界面定位的方法，提供一种解决界面方位模糊性的新思路.
1 利用反射波相位特征进行界面定位
1.1 界面处反射波的相位变化规律 方便起见，本文对两个非周期信号(φ1(t)和φ2(t))的正相似、反相似做如下定义：若 图 3中两个信号(信号1与信号2)间的反相似比较容易判断：信号1有一个最高峰A，两个幅度相等的最低谷；而信号2的情况与之相反. 图 4中信号3与信号4的反相似体现在两个信号中A、B、C、D点(其分别代表最高、次高、最低、次低点)的出现次序上：在信号3中波峰A、B是顺序出现的，波谷C、D的逆序出现的；信号4中则正好与之相反. 本文附录中证明了界面处纵波法应力和位移反射系数间的关系，即：在图 1所示的模型中，x、y方向上，法应力(声压)反射系数与位移(或质点速度)反射系数符号相反.该关系的数学表达为 结合前面给出的关于两个信号正、负相似的定义，我们不难得到一个推论：若反射波法应力与入射波法应力信号正(负)相似，那么反射波位移与入射波位移信号必为负(正)相似.由于上述关系仅在界面上成立，下面先将该结论进行推广，然后给出单井成像技术中界面方位定位的具体方法. 对于该结论需要注意的是：各向同性弹性介质中才成立；反射系数为实数；用质点速度替换位移，结论依然成立；结论与频率无关(详情参见附录A).
1.2 反射波相位变化规律在井下成像时的推广 在前面的信号正、负相似定义中我们在相位特征上有意地忽略了时间延迟，重点关注波形是否反转，其原因主要有两方面.一是界面与接收阵列间总是存在一定距离的，这将不可避免地产生时间延迟；二是测井仪的发射信号总是有限时间信号，并非周期信号.因此这种定义方式有助于我们将(3)式的适用范围推广到波的整个传播路径上. 其次，单井成像中需要考虑井的存在.由于井孔效应(Kurkjian，1985)，井内接收信号中一个重要组成部分为模式波，如单极源激发的斯通利波、偶极源激发的弯曲波以及四极源激发的螺旋波.这些模式波不是在我们所探测的界面上产生的，它们基本上都在反射波提取时被过滤掉了.单井成像利用的信号主要是井外界面上产生的反射纵波与横波，并且即使是转换波(纵波与SV波之间的转换)也被忽略，因为其可以由于到达时间上的差异而被识别.这也是后面数值实验中的前三个模型采用固体-固体模型，不考虑井眼存在的原因之一. 再者，对于体波而言，透射系数总是正数，引起波形反转的主要原因是反射.对于均匀各向同性弹性介质来说，多数情况下反射系数是实数，只有其为负数时才发生波形反转；反射系数也可能是复数(Jayet and Baboux， 1993)，这时将发生相移，不过这主要是由于入射角大于临界折射角造成的.临界反射发生的条件是入射角足够大，并且远离井孔的地层阻抗足够高.在附录的图 18中将看到，入射角是受限的(入射角最大只能是界面倾角的余角)，太大的入射角产生的反射波将不能被测井仪记录. 综上所述，在井径方向上，对测井仪记录的某道反射波而言，其入射路径上各点处的波形与反射路径各点处的波形将满足前小节中的推论：若反射波法应力与入射波法应力正(负)相似，那么反射波位移与入射波位移必为负(正)相似.
1.3 界面定位的实现
前面结论给出的是入射波和反射波间的关系.反射波可以从测井仪记录的信号中提取.界面处的入射波显然是无法记录的，但是从前面的分析讨论中可以看到：在入射方向上，源激发的波与界面处的入射波在本文的定义下为正相似，于是界面的方位选择就可以转化为寻找在相位上与接收到的反射波满足反射波相位变化规律的入射波，或者说是求取正确的入射方向.下面我们将以单极激发、偶极接收的模式为例建立一种利用反射纵波的相位进行界面方位识别的方法.该模式中，一般以井轴线方向为z轴，以偶极接收的两个正交方向分别为x、y轴建立直角坐标系.本方法中提到的波形记录(除非单独声明)均包括声压与径向位移，本方法的最终目标就是将界面限定在X-Y平面的某一象限内. 首先需要给出参照波形.单极激发模式中，对于辐射场来说，声压(法应力)无方向性，位移有方向性并且在井轴上无径向位移.不失一般性，可以将第一象限内某点(本文使用FDTD进行数值模拟，该点的位置为源右侧半个空间网格点)作为参照点，取该点的法应力、位移x分量的波形为参照波形.严格意义上来说，位移的参照波形应该有两个.考虑到井内辐射场的对称性，前面选取的位移x分量与沿y轴正向的入射波位移y分量正相似，所以本文的位移参照波形只有一个.事实上，位移参照波形的确定意味着我们由此假定了一个入射方向(X-Y平面内). 接着从测井仪的记录中提取井外界面上产生的反射纵波信号. 最后将反射波形与对应的参照波形进行对比，判断二者间的相位变化，确定界面的方位.例如，将反射波和对应的参照波形对比，其结果为：声压正相似、位移x分量反相似、y分量正相似.声压正相似，位移x分量反相似，这符合(3)式的结论，说明x方向上的入射方向选取正确，即入射波向右传播，界面在一、四象限.声压正相似，位移y分量正相似，这与(3)式结论不符，要想满足反射波相位变化规律需要改变y方向的入射波传播方向.考虑到单极子辐射场位移的对称性，满足要求的入射方向应为y轴负向，于是界面应该在三、四象限.综合以上结果，界面应该在第四象限.其他情况参见表 1，不再做详细说明.
在表 1中，反射波与参照波形间的相位关系是按照固定顺序排列的：声压、位移x分量、位移y分量.+表示反射波与参照波形正相似，-表示反射波与参照波形反相似.若考虑的是二维模型的界面方位识别，那么接收信号只有声压与位移x分量，则一、四象限表示反射波来自接收阵列右侧，二、三象限表示反射波来自接收阵列左侧. 必须指出：上述界面方位判别法所利用的数据都可以由井内仪器接收、处理后得到，或可以被视为已知条件.源的选择显然是人为的、可控的，于是本方法所使用的参照波形可以由解析解给出，所以其可以看作是已知条件；反射波信号的提取是测井技术中的重要课题，常用的技术有：f-k滤波(Hornby，1989)、参数估计法(Tang，2004)等，但这不是本文的研究重点，所以将文中其视为已知条件；另外，声压和径向位移都可以被现有的测井仪记录.
2 数值实验
本节的主要内容是用数值实验来验证上节中反射系数之间关系的结论，并进行界面方位识别.本节共给出了四个算例，界面两侧介质均为固体，前三个算例使用的模型中无井存在，最后一个使用井孔模型；前两个为二维模型，主要用于验证反射波相位的变化规律，后两个用于验证本文提出的方位识别法的可行性；源都位于坐标系原点，其所在区域记为区域一，界面另一侧远离源的区域记为区域二(参见图 1的区域分划)；数据来自于时域有限差分法(FDTD)的数值模拟，液-固界面处的参数处理参考了Guan和Hu(2011)所使用的方法.质点速度参照波形由图 3a给出，法应力参照波形由图 4a给出，介质参数由表 2给出.
在X-Z平面内，界面控制方程为x=2 m，接收器位置为井轴线上z=2 m处，采用的激励源为单极源，区域一采用介质1的参数.接收信号为x方向上的法应力σxx.由于这里考察的是界面阻抗对反射波的影响，所以区域二中分别采用硬地层、软地层参数，相应的反射波在图 5中均已注明.
采用图 4a与4b间波形的相位比较法，在图 5中可以看到：与法应力的参照波形图相比，软地层的反射波出现了反相似，而硬地层的反射波为正相似.两个算例仅在介质参数上有差异，这说明地层参数确实影响法应力反射系数，进而可以影响反射波的相位.
2.2 界面位置对反射波场相位的影响
本小节实际包含两个算例：界面的控制方程分别为x+z=3 m和z=x+3 m，区别期间，分别记其为界面A和界面B.显然它们关于z轴对称；区域一采用介质1的参数，区域二均采用硬地层参数. 首先考察反射波质点速度x分量相对于其参照波形的相位变化，如图 6所示.与图 6中的参照波形相比，界面A产生的反射波是反相似的，界面B产生的反射波是正相似的.考虑到参照波形表示的是沿x轴正向入射的波，界面B位于z轴左侧，所以界面B上的入射波与参照波形反相似.这就是说界面B产生的反射波与其对应的入射波相比亦是反相似. 图 7、图 8中给出了界面A、B产生的反射波(考察量为法应力的x分量)，但是由于单极源应力场的对称性，二者完全重合了，这符合理论预期.另外，由图 6可以得到井轴上z=2 m处对应的质点速度反射系数为负，而图 7与图 4a的对比表明，该点法应力反射系数为正，这与(3)式的结论吻合.
2.1和2.2节中的算例表明：法应力反射系数的符号与界面方位无关，其只取决于界面两侧介质的波阻抗；质点速度反射系数的符号与界面方位密切相关.关于反射系数的计算，请参阅相关文献，如Aki和Richards(2002)的《定量地震学》.这也是本文给出的界面方位判别法要求测量法应力(声压)信号的原因，因为只有这样才可以先估计出界面两侧介质的阻抗变化，进而用反射波质点速度的相位变化确定界面方位.
2.3 三维模型
尽管对于界面方位判别来说，二维模型与三维模型本质 上都是一样的，但是本文还是通过下面的数值实验进行验证.参照波形、介质参数的选择与前一算例相同，界面的控制方程为x+y+z=4 m，界面位于X-Y平面的第一象限. 图 9给出了反射波法应力的波形，图 10则是质点速度的波形(x分量)，由于本算例中界面的方位角为45°，所以质 点速度y分量的波形将与图 10完全一致，这里不再给出. 图 9与图 4a正相似，图 10与图 3a反相似.由表 1得到，反射波来自第一象限，因此，要探测的界面也位于第一象限，这与设定吻合.
本算例中使用的模型由图 11给出；以单极子为源，其辐射波形由图 12给出，同样取x轴正向半个网格点处的x方 向质点速度为质点速度参照波形；界面方程为z-4x=24 m，位于接收阵列左侧.本算例中使用二维井孔模型，以便验证在有井存在条件下该方法的可行性. 图 13、14给出的是井轴上z=2.5 m处的反射波.这两幅图中的反射波都是由井外界面产生的，前面的是纵波，后面的为横波，由于参照波形的波峰或波谷比较明显，所以明 显可以看出：图 13与图 12中对应的波形正相似，图 14与图 12中对应的波形正相似.在表 1中该情况对应的反射波来自井眼左侧，即界面位于接收阵列的左侧，这与设定吻合. 图 15给出的是z=2.5 m处的全波记录，它对应测井仪实际记录的波形.在最前面的是直达波(首波)，接着是井孔效应产生的斯通利波，最后的两个分别是反射纵波与横波，横波是在纵波遇到界面时解耦后产生的.由于本算例中界面距离源的位置较远，界面产生的两道反射波的到达时差非常显著，只显示图 15中反射波到达后的波形就可以得到图 16.图 13中的反射波是用图 15中的数据减去井外无界面时该点接收到的数据得到的，所以与图 16相比其更光滑.无论怎样，二者间波峰、波谷的相位、到时、幅度都是一致的，这对于本文提出的界面方位相位识别法来讲就已经足够了.
相位、幅度和时差是波形组成的基本要素.其中，幅度和时差主要与传播距离和介质衰减系数相关；相位变化则主要与界面的反射系数相关(忽略相位延迟).长期以来，单井成像都是利用幅度和时差进行偏移成像的，这也使得界面的方位模糊性一直无法得到妥善处理.本文给出了一种基于反射波相位的界面方位判别法，并对于不同阻抗、倾角、方位角的界面进行了数值实验，结果表明对于各向同性弹性介质，仅依靠井内接收到的反射声压和位移信号就可以实现界面方位判定.以单极激发、偶极接收的系统为例，现将该方法的主要思路整理如下： (1)在声源附近选取一个参考位置，以该点处直达波的声压、位移波形分别作为声压参照波形和位移参照波形.文中位移参照波形选取的是x正向距离声源半个差分空间网格处位移x分量的波形. (2)将接收点处记录到的反射声压波形、反射位移波形分别与其对应的参照波形进行对比，判断二者的相位变化. (3)从反射波相位变化情况，按表 1给出的法则判断反射界面位于哪一个象限，进而得到界面方位角的取值范围.
附录 A 正文中给出的界面方位判别方法，利用了如下波动原理：对于界面上产生的反射纵波，在同一方向上，法应力分量的反射系数与位移分量的反射系数符号相反.由于这里研究的是某一反射点处反射系数间的关系，而非反射系数本身，所以将反射系数视为已知常数.任意的入射波信号都可以展开为平面波信号的叠加，所以证明过程将从平面纵波的入射出发，但是最后的结果将表明该原理与频率或波数无关.
首先以界面为z轴，界面法线方向为x轴建立直角坐标系，分析平面纵波在界面上产生的反射纵波，如图 17所示.在本附录中，下标号x、y、z表示方向，对于波场分量，上标号0、1分别表示其为入射波、反射波；对于反射系数，上标号u、v、σ表示其分别为位移、质点速度、法应力的反射系数.
在图 17中位移的表达式为 利用反射定理，在界面x=0处产生的反射纵波位移表达式为 因为 下面考虑更一般的情况：倾角为β，方位角为α的界面，如图 1所示.将该直角坐标系的原点设定为界面上的某一反射点，则入射角为θ，方位角为α的入射波的波矢方向为 由于证明是在任意频率下推导的，而(A-6)不出现频率，这表明结论不随频率变化.需要说明的是，在推导过程中我们用到了一个假设——上述公式中的参数均为实数，这也是本定理的成立条件.当有复参数出现在(A-2)～(A-5)式中时就不再一定有(A-6)式成立，具体情况有待进一步的研究. 总揽整个证明过程，其思路是：先给出纵波位移的平面波表达，然后利用本构关系导出法应力的表达式，最后依据给出的反射系数定义完成整个证明.由于液体、气体的剪切模量为零，它们可以作为固体的一种特例，所以对此不做详细推导.
则实数t0表示两个信号在时间坐标上的相对平移，实数a表示两个信号的幅度比.当a为正数时，称φ1(t)和φ2(t)正相似(此时两个信号的差异仅为时间延迟)；当a为负数时，称φ1(t)和φ2(t)反相似(两个信号的差异还有波形反转).下面给出两个在本文定义下反相似的示例：信号2、信号4分别由信号1、信号3乘以a=－1然后在时间轴上平移t0得到，按照定义式(2)，信号1与信号2反相似(图 3所示)，信号3与信号4反相似(图 4所示).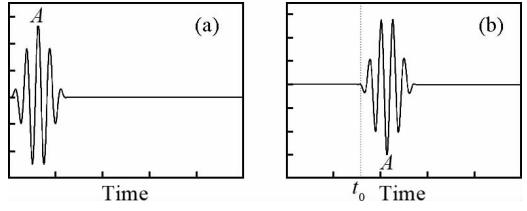
图 3(a)信号1;(b)信号2Fig. 3(a)Signal 1;(b)Signal 2
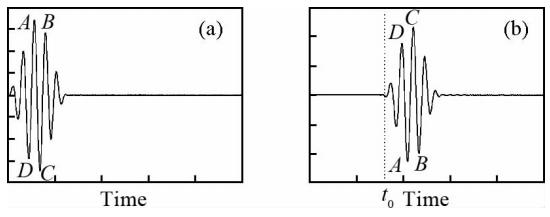
图 4(a)信号3;(b)信号4Fig. 4(a)Signal 3;(b)Signal 4 
其中
为某方向上法应力、位移的反射系数.
表 1 单极激发偶极接收系统界面方位识别表
Table 1 The position determination table of an interface for the monopole exciting and dipole receiving system
表 2 介质参数
Table 2 Parameters of the medium
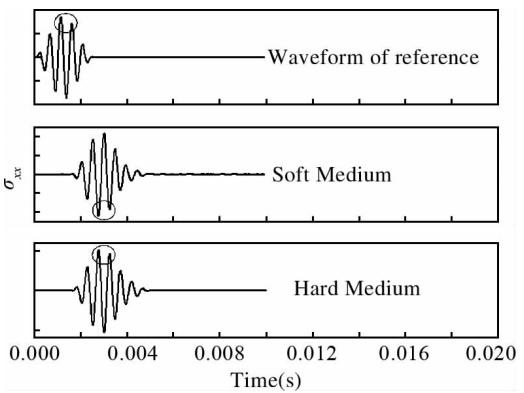
图 5 z=2 m处的反射波(σxx)Fig. 5 The reflected waves at z=2 m(σxx)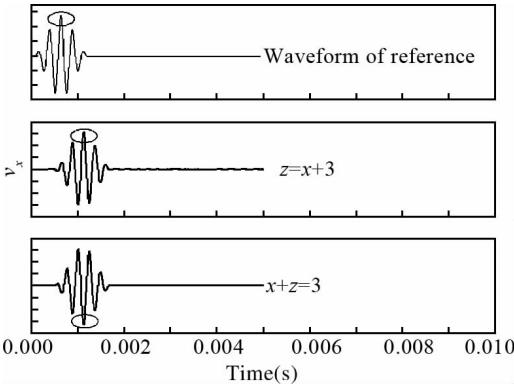 
图 6 z=2 m处的反射波(vx)Fig. 6 The reflected waves at z=2 m(vx)
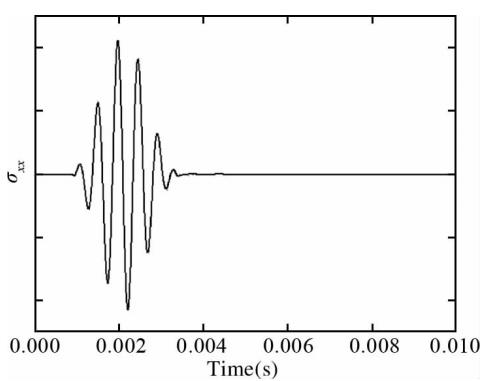
图 7 z=2 m处的反射波(σxx) Fig. 7 The reflected waves at z=2 m(σxx)
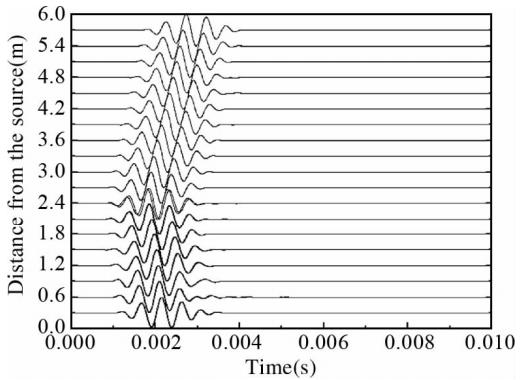
图 8 反射波(σxx)归一化波形Fig. 8 Normalized waveforms(σxx)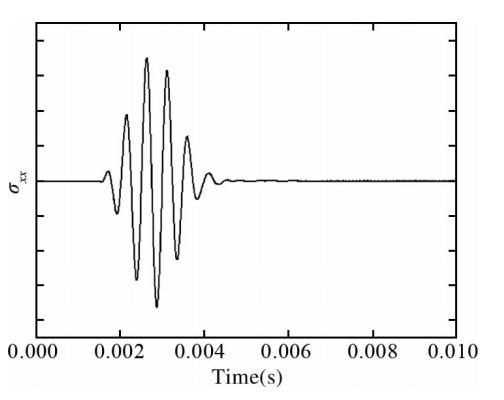 
图 9 z=2 m处的反射波法应力波形(σxx)Fig. 9 The reflected waveform of normal stress at z=2 m(σxx)
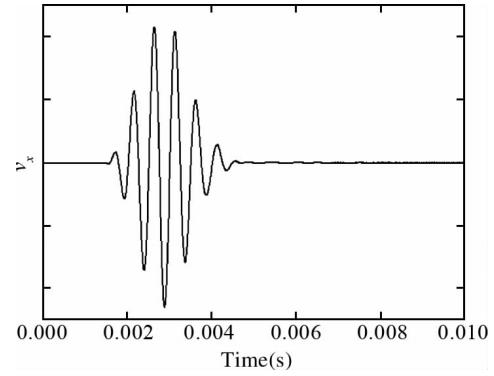
图 10 z=2 m处的反射波质点速度波形(vx)Fig. 10 The reflected waveform of particle movement at z=2 m(vx)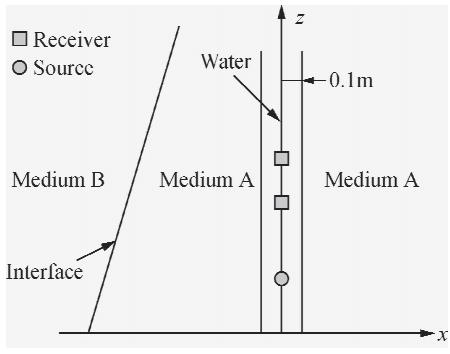 
图 11 井孔模型Fig. 11 A borehole model
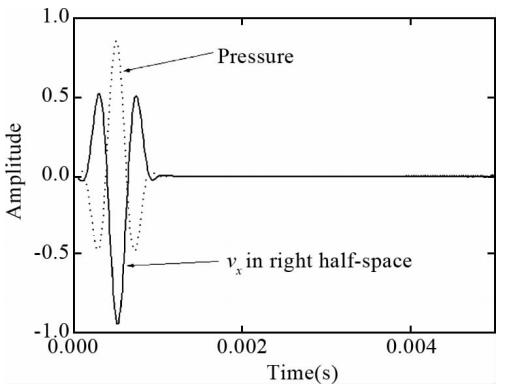
图 12 参照波形Fig. 12 Waveforms of reference
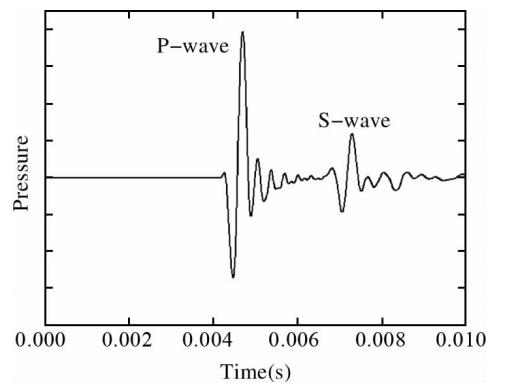
图 13 z=2.5 m处的反射波声压波形 Fig. 13 Reflected waveform of pressure(z=2.5 m)
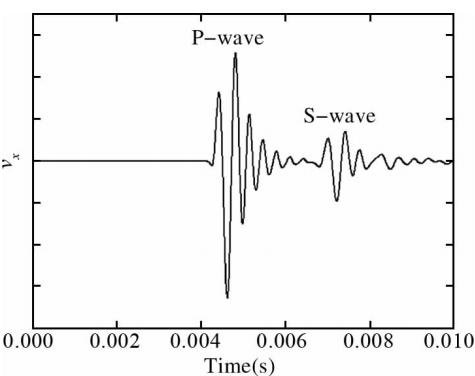
图 14 z=2.5 m处的反射波质点速度波形Fig. 14 Reflected waveform of vx(z=2.5 m)
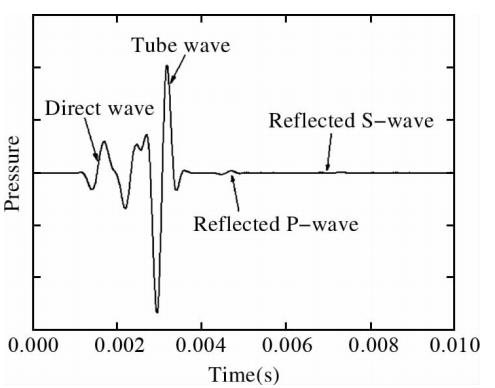
图 15 z=2.5 m处的全波记录(声压)Fig. 15 The full waveform at z=2.5 m(pressure)
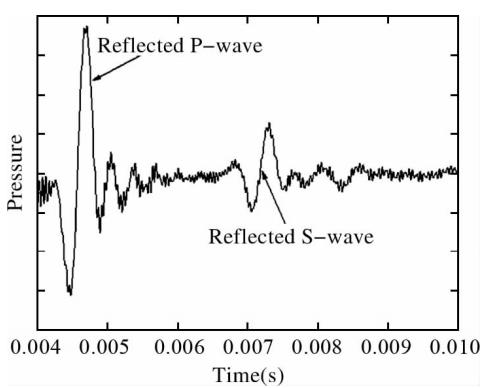
图 16 z=2.5 m处的反射波(声压)Fig. 16 The reflected wave at z=2.5 m(pressure)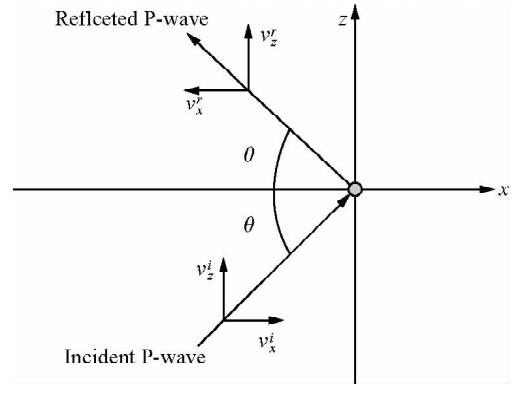 
图 17 纵波在界面上的反射Fig. 17 The reflection of P wave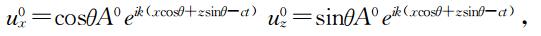 
其中A0是入射波振幅，θ是入射角，i是虚数单位，k是波数，c为纵波速度.
相应地由本构关系可以写出其x方向法应力的表达式(Achenbach，1973)为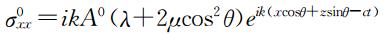
其中λ、μ是拉梅常数.
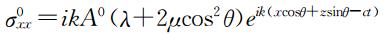
其中A1是反射波振幅.
类似地得到反射波的x方向法应力为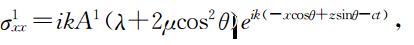
由此得到x方向法应力的反射系数为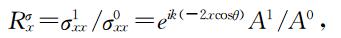
注意到在界面上有x=0，所以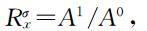
如果定义位移反射系数为入射波位移与反射波位移的比为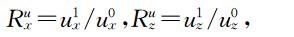
那么在界面上可以得到
上式中的反射系数不仅包含了反射波振幅的变化，也同时反映了其相位变化情况：在界面上，反射波法应力与位移法向分量振幅变化相同，相位相反.
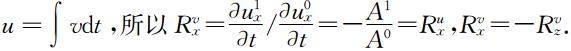所以相同方向上位移的反射系数与质点速度的反射系数相同，这也是可以利用质点速度代替位移进行方位识别的原因.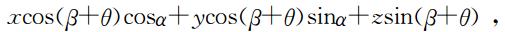
依据反射定理，其反射波的波矢方向为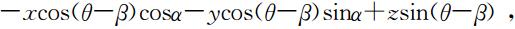
它们的位移分别是：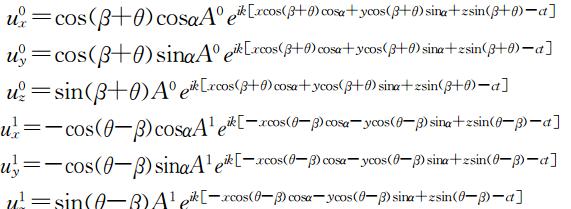
依据前面的反射系数定义，x方向位移反射系数为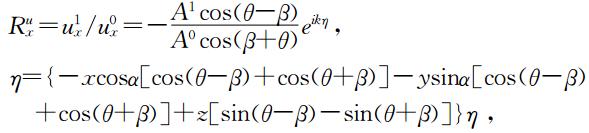
化简后为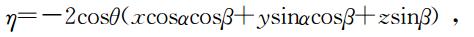
由于界面过坐标系原点，其方程为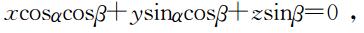
所以在界面上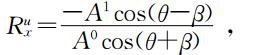
利用几何关系不难发现在图 18中：β+θ∈[0，π/2]，θ－β∈[－π/2，π/2]
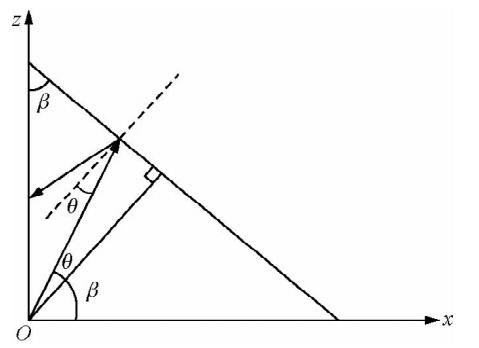
图 18 入射角与倾角间的关系Fig. 18 Relationship between incident and dip angle 
类似地我们可以得到y方向的位移反射系数
x方向入射波、反射波的法应力分别为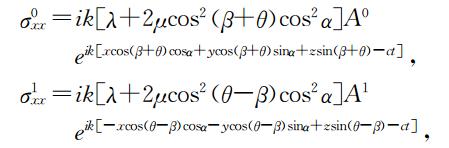
于是反射波x方向法应力的反射系数为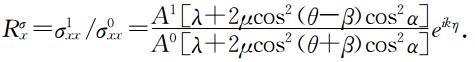
由前面的推导可知在界面上eikη=1，于是：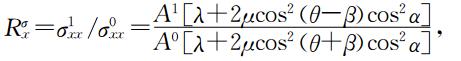
类似地在y方向上有：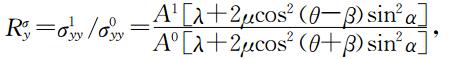
剪切模量μ≥0；实际地质材料的λ均为正数，所以
式说明当拉梅常数为正时，法应力与位移的反射系数总是一正一负，即
这表明：位移分量的反射系数与同一方向法应力的反射系数之乘积小于0.
| [1] | Achenbach J D. 1973. Wave propagation in elastic solids [M]. New York/Amsterdam: North-holland/American Elsevier Publishing Company. |
| [2] | Aki K, Richards P. 2002. Quantitace seismology: Theory and method [M]. Calif: University Science Books. |
| [3] | Cheng J B, Wang N, Ma Z T. 2009. Table-driven 3-D angle-domain imaging approach for Kirchhoff prestack time migration [J]. Chinese J. Geophys. (in Chinese), 52 (3): 792-800. |
| [4] | Claerbout J F. 1971. Toward a unified theory of reflector mapping [J]. Geophysics, 36(3): 467-481. |
| [5] | Esmersoy C, Chang C, Kane M, et al. 1998. Acoustic imaging of reservoir structure from a horizontal well [J]. The Leading Edge, 17(7): 940-946. |
| [6] | Guan W, Hu H S. 2011. The parameter averaging technique in finite-difference modeling of elastic waves in combined structures with solid fluid and porous subregions [J]. Communications in Computational Physics, 10(3): 695-715. |
| [7] | Hornby B E. 1989. Imaging of near-borehole structure using full-waveform sonic data [J]. Geophysics, 54(6): 747-757. |
| [8] | Hu H S, He X. 2009. The low-frequency asymptotic velocity of pseudo Rayleigh, flexural, and screw waves in a transversely isotropic formation [J]. Chinese J. Geophys. (in Chinese), 52(7): 1873-1880. |
| [9] | Jayet Y, Baboux J C. 1993. Change of temporal shape of pulsed ultrasonic Wave-Form by the reflection phenomenon [J]. Ultrasonics, 31(3): 205-206. |
| [10] | Kurkjian A L. 1985. Numerical computation of individual Far-Field arrivals excited by an acoustic source in a borehole [J]. Geophysics, 50(5): 852-866. |
| [11] | Liu S W, Wang H Z, Chen S C, et al. 2012. Joint imaging method of VSP upgoing and downgoing reflection wave [J]. Chinese J. Geophys. (in Chinese), 55(9): 3126-3133. |
| [12] | Lu L Y, Zhang B X, Wang C H. 2006. Experiment and inversion studies on Rayleigh wave considering higher modes [J]. Chinese J. Geophys. (in Chinese), 49(4): 1082-1091. |
| [13] | Ma M M, Chen H, He X, et al. 2013. The inversion of shear wave slowness's radial variations based on the dipole flexural mode dispersion [J]. Chinese J. Geophys. (in Chinese), 56 (6): 2077-2087. |
| [14] | Qiao W X, Che X H, Ju X D, et al. 2008. Acoustic logging phased are array and its radiation directivity [J]. Chinese J. Geophys. (in Chinese), 51(3): 939-946. |
| [15] | Schneider W A. 1978. Intergral formulation for imagration in two and three dimension [J]. Geophysics, 43(1): 49-76. |
| [16] | SONG Ruo-Long, LIU Jin-Xia, YAO Gui-Jin, MA Jun, WANG Ke-Xie.Parallel finite difference modeling of acoustic fields in nonaxisymmetric cased hole[J].Chinese J.Geophys. (in Chinese),2010,53(11): 2767-2775. |
| [17] | Sun W B, Sun Z D. 2010. VSP reverse time migration based on the pseudo-spectral method and its applications [J]. Chinese J. Geophys. (in Chinese), 53(9): 2196-2203. |
| [18] | Tang X M. 2004. Imaging near-borehole structure using directional acoustic-wave measurement [J]. Geophysics, 69(6): 1378-1386. |
| [19] | Tang X M, Wei Z T. 2012. Single-well acoustic reflection imaging using far-field radiation characteristics of a borehole dipole source [J]. Chinese J. Geophys. (in Chinese), 55(8): 2798-2807. |
| [20] | Wu S P, Peng G X, Huang L Z, et al. 2011. Seismic interferometry imaging based on virtual source estimation with complex overburden [J]. Chinese J. Geophys. (in Chinese), 54(7): 1874-1882. |
| [21] | Yan J W, Fang W B, Cao H, et al. 2008. Wave equation migration imaging of cross-well seismic data [J]. Chinese J. Geophys. (in Chinese), 51(3): 908-914. |
| [22] | 程玖兵, 王楠, 马在田. 2009. 表驱三维角度域Kｉｒｃｈｈｏｆｆ叠前时间偏移成像方法 [J]. 地球物理学报, 52 (3): 792-800. |
| [23] | 胡恒山, 何晓. 2009. 横向各向同性地层井孔伪瑞利波、弯曲波、螺旋波的低频极限速度 [J]. 地球物理学报, 52(7): 1873-1880. |
| [24] | 刘守伟, 王华忠, 陈生昌,等. 2012. VSP上下行反射波联合成像方法研究[J]. 地球物理学报, 55(9): 3126-3133. |
| [25] | 鲁来玉, 张碧星, 汪承灏. 2006. 基于瑞利波高阶模式反演的实验研究[J]. 地球物理学报, 49(4): 1082-1091. |
| [26] | 马明明, 陈浩, 何晓,等. 2013. 基于偶极弯曲波频散的横波慢度径向分布反演[J]. 地球物理学报, 56(6): 2077-2087. |
| [27] | 乔文孝, 车小花, 鞠晓东,等. 2008. 声波测井相控圆弧阵及其辐射指向性[J]. 地球物理学报, 51(3): 939-946. |
| [28] | 宋若龙, 刘金霞, 姚桂锦, 马俊, 王克协.非轴对称套管井中声场的并行有限差分模拟[J]. 地球物理学报, 2010,53(11): 2767-2775. |
| [29] | 孙文博, 孙赞东. 2010. 基于伪谱法的VSP逆时偏移及其应用研究[J]. 地球物理学报, 53(9): 2196-2203. |
| [30] | 唐晓明, 魏周拓. 2012. 利用井中偶极声源远场辐射特性的远探测测井[J]. 地球物理学报, 55 (8): 2798-2807. |
| [31] | 吴世萍, 彭更新, 黄录忠,等. 2011. 基于虚源估计的复杂上覆地层下地震相干成像[J]. 地球物理学报, 54(7): 1874-1882. |
| [32] | 严建文, 方伍宝, 曹辉,等. 2008. 井间地震数据的波动方程偏移成像[J]. 地球物理学报, 51(3): 908-914. |