2. 中国石油大学CNPC物探重点实验室, 北京 102249
2. CNPC Key Laboratory of Geophysical Prospecting, China University of Petroleum, Beijing 102249, China
页岩气为近年来在北美地区广泛勘探开发的天然气新目标,在全球非常规油气勘探开发中异军突起,成为突破最晚、近期发展最快的非常规天然气资源.然而,对页岩气储层性质,如干酪根的分布形式对应的地球物理响应特征的认识不足,使得利用地球物理资料进行页岩气识别存在很大的困难(B and yopadhyay, 2009; Goodway et al.,2010;郝建飞等,2012; Guo et al.,2012; 张春等,2013).岩石物理模型是连接地震属性与储层参数的纽带,它的精确与否将直接影响到地震解释的精度.目前,大多数岩石物理模型属于半经验模型,对岩石描述不够准确,而且绝大部分岩石物理模型只适用于各向同性介质,而页岩气藏因其各向异性程度高,不同于传统的构造和岩性圈闭油气藏,并不能用各向同性岩石物理模型来近似,因此建立一个适用性强的各向异性岩石物理模型有较大的理论和实用价值(Bakulin et al.,2003; Mavko et al.,2009; Sondergeld et al.,2011; 孙伟家等,2013).
Vernik和Nur(1992)发现用传统的Backus平均理论(Backus,1962)计算得到的Bakken 页岩沿层面方向的速度无法与实验室测量结果吻合.从特定岩样的电子显微镜扫描图片(SEM)可以看出,富含有机质页岩中的干酪根将粘土颗粒、细砂颗粒以及它们的聚合物彼此分离开来,干酪根在岩石中形成一个连续的网络,而这些被分离开来的非有机成分可看作透镜状的“粘土”薄片,通过引入一个用来控制岩石微观横向连续性的经验常数,Vernik和L and is(1996)提出了改进的Backus平均模型,用该模型计算出的Bakken页岩沿层面方向的速度与实验室测量结果吻合较好.另外,Sayers(2013)采用各向异性等效场理论同样较好地弥补了Backus模型的不足.Vernik和Liu(1997)指出,干酪根在垂向上与横向上都是连续分布的,如果忽视干酪根的垂向连续性,只考虑其横向连续性,会导致预测出的岩石沿层面方向的弹性刚度比实际测量结果坚硬得多.
Hornby(1994)将各向异性自洽模型(SCA)和微分等效介质模型(DEM)结合起来,计算了各向异性页岩等效弹性模量.该模型将粘土矿物看作支撑岩石的连续固体骨架,而其它矿物,如石英,长石,黄铁矿等则看作是嵌在粘土基质中分散的包含物.根据DEM模型的两个准则,如果初始相是连续的,采用DEM模型得到的等效介质也能保证该相连续;如果某一相作为初始相是不连续的,或作为加入相,那么该相在DEM模拟介质中也是不连续的。因此,DEM模型适用于考虑岩石内部连续相与离散相之间的弹性互动.
本文试图探究各向异性DEM模型在模拟有机页岩中的可行性,并分析干酪根含量、分布形式以及成熟度对岩石弹性性质的影响. 1 改进的Backus平均模型
Backus(1962)提出,在长波长极限下,一个由多层横向各向同性(每层的对称轴方向都垂直于层面)材料组成的层状介质,是等效各向异性的,其刚度矩阵中非零元素表示如下:
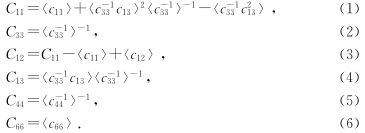
图 1和图 2中的点线和虚线是采用Backus平均公式(1),(2),(5),(6)预测的干酪根和粘土两相混合物的等效弹性刚度分量.假设粘土单层是横向各向同性的,而干酪根单层是各向同性的.计算采用的粘土与干酪根的弹性参数见表 1,这些参数被Vernik和L and is(1996)认为能最好地描述本文的研究对象—Bakken页岩.
需要注意的是,这些值是由实验室测量数据分别外推得到的100%的干酪根和粘土矿物的弹性参数,并不是实际测量的纯干酪根和纯粘土的性质.然而Vernik和L and is并没有给出粘土参数C13,若假设Thomsen各向异性参数满足关系δ=0.5ε,可得到C13=21.1 GPa,由此求出的各向异性参数δ与测量数据一致.
| 表 1 Vernik和L and is给出的Bakken页岩两相模型参数 Table 1 Parameters given by Vernik and L and is for a two-component model of Bakken shale |
图 1和图 2中的各离散点表示由Bakken页岩的密度和速度测量数据(Vernik和Liu,1997)计算出的弹性刚度分量C11,C33,C44和C66. 可以看出,C33和C44(虚线)的预测结果与测量数据一致,但预测得到的C11和C66(点线)与测量数据相比偏高.
Vernik和L and is认为这种差异与构成该类页岩的主要矿物伊利石的构造有关,即伊利石表现出透镜状排列特征,而不是连续的席状分布(图 3).
 | 图 1 高围压(70 MPa)下Bakken页岩实验室测量数据(Vernik和Liu,1997)转化而来的刚度系数C11(圆点)和C33(星号).点线和虚线表示Backus平均模型预测得到的C11和C33,实线为C11的修正. Fig. 1 Elastic stiffness coefficients C11(points) and C33(stars)computed from the ultrasonic measurements reported by Vernik and Liu(1997)in Bakken shale at high confining pressure(70 MPa)versus kerogen content. The dotted and dashed curves show the theoretical predictions for C11 and C33,respectively,whereas the full curve shows the modified C11. |
 | 图 2 高围压(70MPa)下Bakken页岩实验室测量数据(Vernik and Liu, 1997)转化而来的刚度系数C66(圆点)和C44(星号).点线和虚线表示Backus平均模型预测得到的C66和C44,实线为C66的修正. Fig. 2 Elastic stiffness coefficients C66(points) and C44(stars)computed from the ultrasonic measurements reported by Vernik and Liu(1997)in Bakken shale at high confining pressure(70 MPa)versus kerogen content. The dotted and dashed curves show the theoretical predictions for C66 and C44,respectively,whereas the full curve shows the modified C66. |
 | 图 3 富含有机质页岩(干酪根含量大于0.15)的拓扑结构示意图(Vernik and Nur, 1992)显示出在XY平面内由干酪根引起的粘土(伊利石)层的不连续性.Z轴指向介质的对称轴方向. Fig. 3 Schematic fabric topology of kerogen-rich(K>0.15)shales showing discontinuity of some of the clay(illite)layers separated by kerogen in XY plane. Z-direction corresponds to the symmetry axis(Vernik and Nur, 1992). |
为了解决这个问题,可以将等式(1)和(6)替换为
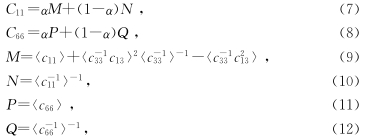
尽管采用改进的Backus平均模型能较好地模拟Bakken页岩,但常数α的选取具有一定的经验性,对其它页岩可能并不适用.另外,Backus平均将岩石各组分等效为纵横比趋近于0的薄片,无法考虑包含物纵横比对岩石弹性性质的影响. 2 各向异性微分等效介质模型
微分等效介质(DEM)理论通过往固体矿物相中逐渐加入包含物相来模拟双相混合物.固体矿物是相1(当相2含量为零),之后逐步加入相2的材料.这个过程一直进行到需要的各成分含量达到为止.DEM公式并不是对称地对待各组成成分.被当做固体矿物或主相的成分可以有不同的选择,且最终的等效模量会依赖于达到最终混合物所采用的路径(Mavko et al.,2009; Wu et al.,2012;李宏兵等,2013).Hornby(1994)给出了各向异性DEM的表达式:
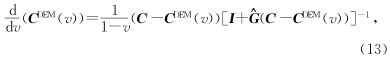
图 4显示了两种不同的干酪根分布形式下岩石的等效刚度系数C11,C33,C44和C66随干酪根含量的变化趋势:(i)干酪根颗粒作为椭球形包含物离散分布在连续的粘土基质中.(ii)粘土颗粒作为椭球形包含物离散分布在连续的干酪根基质中.其中包含物的纵横比α依次取值为0.1,0.2和0.5.干酪根和粘土的弹性模量依然采用表 1中的取值.从图中可以看出,各刚度系数均随干酪根含量的增大而减小.随着包含物纵横比的增大,纵波刚度分量C11和C33,横波刚度分量C44和C66逐渐逼近.当包含物的纵横比足够小时,各向异性 DEM与Backus平均模型的预测结果相似.尽管在很多富含有机质页岩中,SEM研究显示了斑块状的干酪根颗粒离散分布在由非有机质物质形成的岩石基质中(Curtis et al.,2012; Loucks et al.,2009; Sondergeld et al.,2010),Vernik和Landis通过SEM分析,认为针对Bakken页岩,应将干酪根看作岩石基质而非离散分布的包含物.从图中也可以看出,将干酪根看作岩石基质,粘土矿物看作包含物时模型的预测结果与实验室测量数据吻合程度更好.说明采用各向异性DEM模型来预测Bakken页岩是有效可行的.
 | 图 4 采用各向异性DEM模型分别模拟干酪根作为岩石背景基质(实线)与内部包含物(虚线)时岩石的等效刚度分量(a)C11,(b)C33,(c)C44,(d)C66随干酪根含量的变化规律.箭头指向包含物纵横比α增大的方向,α依次取值为0.1,0.2,0.5 Fig. 4 Relationship of the effective stiffness coefficient(a)C11,(b)C33,(c)C44,(d)C66 versus kerogen content using the anisotropic DEM model by treating kerogen as rock background matrix(full curves) and inclusion(dashed curves),respectively. The arrows point in the direction of increasing inclusion aspect ratio α by defining the value of α as 0.1,0.2,0.5. |
 | 图 5 将干酪根看作岩石基质,调整输入参数后各向异性DEM模型预测出的等效介质刚度分量(a)C11和C33,(b)C66和C44 Fig. 5 Stiffness coefficients(a)C11 and C33,(b)C66 and C44predicted by the anisotropic DEM model by treating kerogen as rock matrix after adjusting the input parameters |
 | 图 6 刚度系数(a)C11,(b)C33,(c)C44,(d)C66随含氢指数的变化趋势 Fig. 6 Stiffness coefficients(a)C11,(b)C33,(c)C44,(d)C66versus Hydrogen Index |
| 表 2 两种模型预测结果的相对均方根误差对比 Table 2 Comparison of the relative RMS errors of the two models |
含气页岩的热成熟度越高,表明页岩生气量越大,页岩中赋存的天然气也越多.并且,随着干酪根演化程度的加深,烃类气体的生成将会增大地层压力,从而提高页岩对气体的吸附能力.同时,当压力增大到一定程度时,地层中产生的微裂缝也是页岩气的良好储集空间(周德华等,2012; 宗兆云等,2012).因此,干酪根的热成熟度是页岩气“甜点”预测与评价中的核心参数.
含氢指数HI已被证明是衡量干酪根成熟度的重要标志,其值会随着干酪根成熟度的增大而减小(Kenechukwu et al.,2010).为了考察干酪根的成熟度对页岩弹性性质的影响,我们从Vernik和Nur对Bakken页岩的实验室测量数据中提取HI,密度和速度参数,拟合得到岩石刚度系数随HI的变化规律,如图 6所示.
可以看出,岩石的各刚度系数在总体趋势上均随着HI的增大而减小,说明随干酪根演化程度的加深,岩石将变得更加坚硬.对于Bakken页岩,根据其刚度系数对HI的敏感程度,可将HI的取值区间分为两部分:[50,200]和[250,600].在[50,200]区间内,随HI的增大,岩石的刚度系数下降得更快,即当干酪根的成熟度较高时,其对岩石弹性性质的影响更明显. 4 结论与讨论
为了分析干酪根的含量和分布对有机页岩弹性性质的影响,本文提出利用各向异性DEM模型进行页岩岩石物理建模的方法.以Bakken页岩为例,各向异性DEM模型的预测结果优于先前用于该目标的改进的Backus平均模型,证明了该方法的有效性.数值模拟结果显示,岩石刚度会随着干酪根含量的增加而减小;干酪根作为岩石内部包含物离散分布在非有机物质构成的岩石基质中时,岩石刚度要大于干酪根作为基质时的情形.另外,干酪根的成熟度也是影响岩石弹性性质的重要因素,通过拟合各岩样含烃指数与刚度系数之间的关系,得到岩石刚度与干酪根成熟度具有正相关性.
值得注意的是,许多富含有机质页岩的SEM资料显示出呈斑块状的干酪根颗粒离散分布在非有机物质形成的岩石基质中,不同于本文的考虑对象.因此,各向异性DEM模型的适用性有待进一步验证.
| [1] | Backus G E. 1962. Long-wave elastic anisotropy produced by horizontal layering. Journal of Geophysical Research, 67(11):4427-4440. |
| [2] | Bakulin A, Grechka V. 2003. Effective anisotropy of layered media. Geophysics, 68(6): 1817-1821. |
| [3] | Bandyopadhyay K. 2009. Seismic anisotropy-geological causes and its implications to reservior geophysics. PHD thesis, StanfordUniversity. |
| [4] | Curtis M E, Sondergeld C H, Ambrose R J. 2012. Microstructural investigation of gas shales in two and three dimensions using nanometer-scale resolution imaging. AAPG Bulletin. 96(4): 665-677. |
| [5] | Goodway B, Perez M, Varsek J, et al. 2010. Seismic petrophysics and isotropic–anisotropic AVO methods for unconventional gas exploration. The Leading Edge, 29(12): 1500-1580. |
| [6] | Guo Z Q, Chapman M, Li X Y. 2012. A shale rock physics model and its application in the prediction of brittleness index,mineralogy, and porosity of the Barnett Shale. 82nd Annual International Meeting, SEG, Expanded Abstracts, 1-5. |
| [7] | Hao J F, Zhou C C, Li X, et al. 2012. Summary of shale gas evaluation applying geophysical logging. Progress in Geophysics (in Chinese), 27(1): 1621-1632. |
| [8] | Hornby B E, Schwartz L M, Hudson J A. 1994. Anisotropic effective-medium modeling of the elastic properties of shales.Geophysics, 59(10): 1570-1583. |
| [9] | Kenechukwu M, Prasad M. 2010. Mineralogy and its contribution to anisotropy and kerogen stiffness variations with maturity in the Bakken Shale. 80th Annual International Meeting, SEG, Expanded Abstracts. 2612-2616. |
| [10] | Li H B, Zhang J J, Yao F C. 2013. Inversion of effective pore aspect ratios for porous rocks and its applications. Chinese J. Geophys. (in Chinese), 56(2): 608-615. |
| [11] | Lonardelli I, Wenk H R, Ren Y. 2007. Preferred orientation and elastic anisotropy in shales. Geophysics, 72(2): D33-D40. |
| [12] | Mavko G, Mukerji T, Dvorkin J. 2009. The Rock Physics Handbook. Cambridge University Press. |
| [13] | Sayers C M. 2013. The effect of kerogen on the elastic anisotropy of organic-rich shales. Geophysics, 78(2): D65-D74. |
| [14] | Sondergeld C H, Ambrose R J, Rai C S, et al. 2010. Micro-structural studies of gas shale: SPE 131771. |
| [15] | Sondergeld C H, Rai C S. 2011. Elastic anisotropy of shales. The Leading Edge, 30(3): 324-331. |
| [16] | Sun W J, Fu L Y, Guan X Z, et al. 2013. A study on anisotropic of shale using seismic forward modeling in shale gas exploration. Chinese J. Geophys. (in Chinese), 56(3): 961-970. |
| [17] | Vernik L, Landis C. 1996. Elastic anisotropy of source rocks: Implications for hydrocarbon generation and primary migration.AAPG Bulletin, 80(4): 531-544. |
| [18] | Vernik L, Liu X. 1997. Velocity anisotropy in shales: A petrophysical study. Geophysics, 62(2): 521-532. |
| [19] | Vernik L, Nur A. 1992. Ultrasonic velocity and anisotropy of hydrocarbon source rocks. Geophysics, 57(5): 727-735. |
| [20] | Wu X, Chapman M, Li X Y, et al. 2012. Anisotropic elastic modeling for organic shales. 74th Conference and Exhibition, EAGE,Extended Abstracts. |
| [21] | Zhang C H, Liu X J, He L F, et al. 2013. A study of exploration organic rich shales using Time-Frequency Electromagnetic Method(TFEM). Chinese J. Geophys. (in Chinese), 56(9): 3173-3183. |
| [22] | Zhou D H, Jiao F Z. 2012. Evaluation and prediction of shale gas sweet spots: a case study in Jurassic of Jiannan area, Sichuan Basin. Petroleum Geology and Experiment, 34(2): 109-114. |
| [23] | Zong Z Y, Yin X Y, Zhang F, et al. 2012. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Possion ratio. Chinese J. Geophys. (in Chinese), 55(11): 3786-3794. |
| [24] | 郝建飞, 周灿灿, 李霞, 等. 2012. 页岩气地球物理测井评价综述. 地球物理学进展, 27(1): 1621-1632. |
| [25] | 李宏兵, 张佳佳, 姚逢昌. 2013. 岩石的等效孔隙纵横比反演及其应用. 地球物理学报, 56(2): 608-615. |
| [26] | 孙伟家, 符力耘, 管西竹, 等. 2013. 页岩气地震勘探中页岩各向异性的地震模拟研究. 地球物理学报, 56(3): 961-970. |
| [27] | 张春贺, 刘雪军, 何兰芳, 等. 2013. 基于时频电磁法的富有机质页岩层系勘探研究. 地球物理学报, 56(9): 3173-3183. |
| [28] | 周德华, 焦方正. 2012. 页岩气“甜点”评价与预测—以四川盆地建南地区侏罗纪为例. 石油实验地质, 34(2): 109-114. |
| [29] | 宗兆云, 印兴耀, 张峰等. 2012. 杨氏模量和泊松比反射系数近似方程及叠前地震反演. 地球物理学报, 55(11): 3786-3794. |
 2014, Vol. 29
2014, Vol. 29

