2. 中国石油大学(华东), 青岛 266555
2. China University of Petroleum(East China), Qingdao 266555, China
0 引 言
在地震资料的处理过程中,速度求取的准确与否将直接影响到动校正、叠加、偏移成像、剩余静校正量等,进而影响到资料的分辨率,因此获取准确的速度参数是正确处理和解释地震资料的中心问题.当前地震勘探的重点已转向复杂地表区,这些地区有的地震资料的信噪比太低,CMP道集上反射波同相轴完全无法分辨,速度谱聚焦性差,提取的叠加速度误差较大,直接影响了后续的偏移成像处理(周青春等,2009;符力耘等,2013).针对低信噪比地震资料如何建立更加精确的速度模型,成为当前亟须解决的关键问题.
共散射点(CSP)道集与共反射点(CMP)道集相比,包含了共反射点道集上所有的反射能量和来自反射点的散射能量,充分利用地震信号的有效信息.因此,共散射点道集具有更高的信噪比(曹志勇等,2012;曲寿利等,2012;刘铁华,2012;王芳芳等,2013;宫华泽等,2013),基于CSP道集的速度分析能够提高速度分析的精度.国内外很多专家学者都对基于CSP道集的速度分析方法进行了深入的研究.Bancroft和Wang(1994)提出了基于CSP道集的转换波叠前偏移和速度分析方法;Bancroft(Bancroft et al., 1995;Bancroft and Hugh, 1996)指出CSP道集的形成对初始速度不敏感,1996年他又提出CSP道集具有自然抗假频的作用;王勇等(2000,2005)利用CSP方法对低信噪比地震资料进行速度分析和偏移处理,认为该方法能改善低信噪比资料的速度分析质量和成像效果;王伟(2007)利用基于二维地质模型的波场正演模拟数据,利用CSP方法获得了准确的速度场,成像效果优于常规叠后偏移;张凯(2008)实现了基于等效偏移距的散射波速度分析与成像方法;尹军杰等(2009)进行了散射波成像方法研究,并将其应用到低信噪比资料的处理中(尹军杰等,2010);勾丽敏等(2012)将散射波速度分析方法用于南华北盆地破碎地层发育区的叠前偏移速度模型构建,改善了成像效果.
基于CSP道集的速度分析方法在实际资料的应用中都取得了不错的效果.但是我们也不得不指出该方法尚存的一些问题,如CSP道集上的映射噪音影响速度分析的精度、基于CSP道集的速度分析效率不高等.本文在前人的基础上,对基于CSP道集的速度分析方法从效果与效率上进行了优化,并提出了一种新的映射方法.
1 CSP道集形成原理
根据Huygens-Fresnel原理,地表检波器接收到的地震波都是来自地下任何波阻抗异常点引起的散射波的叠加.反射同相轴可以看作是一些散射点对应的绕射波相互干涉的结果.这些散射波满足的时距曲线的几何关系如图 1所示.
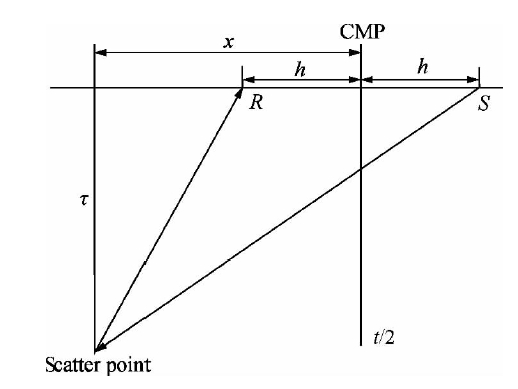 | 图 1 地下介质中任意一个绕射点的时距曲线的几何关系图 Fig. 1 Geometry of the time-distance relationship of one diffraction point underground medium |
对应的公式为
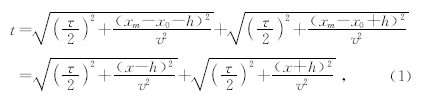
式中x是CMP点与散射点之间的距离,xm是CMP点坐标,x0是绕射点位置的坐标,h是半偏移距.
在几何意义上,由(1)式定义的时距关系是一个Cheop’s Pyramid(基奥普斯椎体)(如图 2所示).
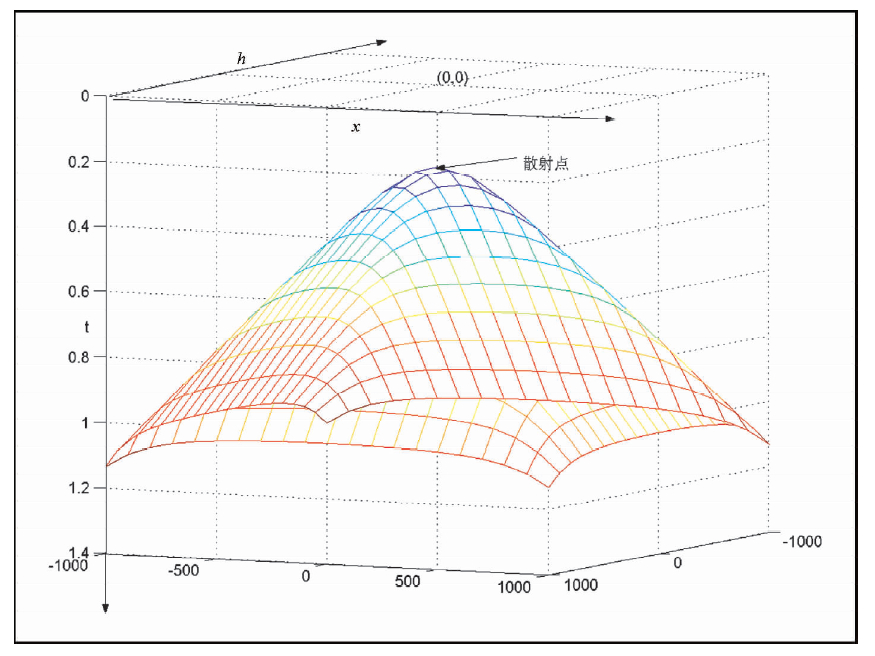 | 图 2 Cheop’sPyramid 代表(1)式定义的对应一个绕射点的绕射波的完整的时距曲线 Fig. 2 Cheop’sPyramid-the complete diffraction wave ’s time-distance relationship of a diffraction point on |
下面引入等效偏移距的概念:如图 3所示,假设地面存在一点E,从震源S到散射点P再到接收点R的旅行时等于从E点到散射点再回到E的旅行时,我们将E点到散射点之间的水平距离定义为等效偏移距(EO),用he表示,则这个关系可以表示为
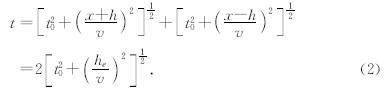
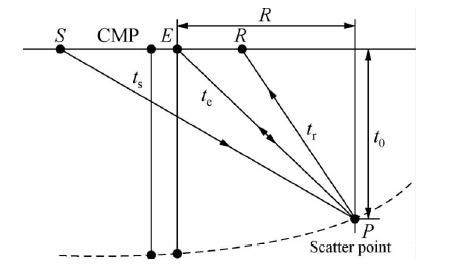 | 图 3 等效偏移距的定义示意图 Fig. 3 Definition diagram of Equivalent offset |
根据公式(2)可以得到等效偏移距的显式公式

由公式(3)可以看到he是关于x和h的函数,它的轨迹也是双曲线,对于一个输入道来说,x和h是已知的常量,这 样我们就可以按照时间采样点对每个输入道映射到相应的等效偏移距道(Wu and Huang, 1992;Bancroft et al., 1994;Bancroft et al., 1995a,b).我们对一个含有一个散射点的常速模型(v=2000.0 m/s)按照这种方式提取cmp=301处的CSP道集,结果如图 4(b)所示.相对于CMP道集(图 4(a)),同相轴清晰可见,资料的信噪比明显提高了.
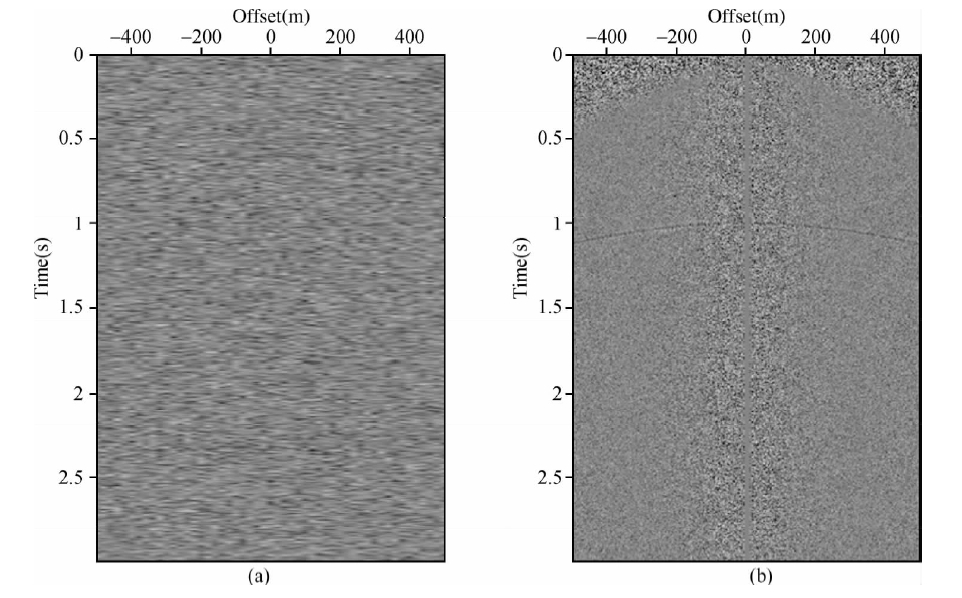 | 图 4(a)CMP=301处CMP道集和(b)相同位置处CSP道集 Fig. 4(a)CMP gathers at CMP=301 and (b)CSP gathers at the same position |
从以上分析可以看到,x与h之间的耦合造成了Cheop’s Pyramid如此复杂.CMP道集到CSP道集映射的本质就是消除或隐藏x与h的耦合作用,把Cheop’s Pyramid转化为一条二维的双曲线,它反映地下绕射点的CRP/CSP时距关系.我们假设x与h之间存在一种线性关系,即令
x=αh,(4)
将(4)式代入(1)式,得到
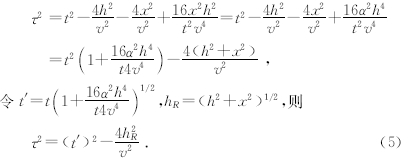
于是,一种新的CMP道集到CSP道集的映射方法就可以定义出来,这样做的一个基本好处是实现起来非常简单.只要沿着图 2中Cheop’s Pyramid顶点为中心,按角度关系来定义(5)式就可以产生每一点的CSP道集. 2 基于CSP道集的速度分析
通过以上分析我们看到,CSP道集的时距关系符合双曲线规律,因此,对于CSP道集,我们可以采用常规速度分析方法—速度扫描来做速度分析(Bancroft and Hugh, 1996;李振春等,2011;秦宁等,2013).但是CSP道集的映射效率以及CSP道集上的映射噪音会给我们速度分析的效率和精度带来很大的影响.因此,我们有必要研究快速映射和消除映射噪音的方法.
2.1 消除映射噪音
朱生旺(2010)提出了一种利用τ-p变换的方法来消除映射噪音,但势必会增加计算量.本文通过在映射公式中加入一个加权系数来消除映射噪音,加权系数的公式为

式中,x是CMP点与散射点之间的距离,he是等价偏移距.
该映射噪音的消除完全在道集映射过程中完成,几乎没有增加计算量.我们用一个四层洼陷模型(cmp=1—3600)验证了方法的有效性(图 5(b)cmp=1800).
 | 图 5(a)某CSP道集未消除映射噪音前和(b)本文方法消除映射噪音后 Fig. 5 A CSP gather(a)before removing conformation noise and (b)after removingthe noise |
在CSP道集的形成过程中,理论上需要计算所有输入采样点对应的等效偏移距,这样CSP道集的映射效率就不高.考虑到对于特定的输入道,等价偏移距存在极值,可以将等效偏移距按等间隔 δhe离散采样.我们对公式(3)变形可以导出
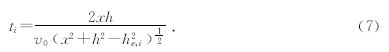
根据公式(7),我们只需计算孔径范围内各离散等效偏移距节点he,i对应的时间节点ti,将ti-1和ti之间的采样点保持时间不变,叠加到等效偏移距道he,i-1上.如图 7所示,左边是一道输入地震道,输入道能映射到输出道的有效采样点范围为tmin到输入道的最大采样点;右侧是一个散射点的按δhe采样的各等效偏移距道(灰色虚竖线),灰色的双曲线是输入道映射到等效偏移距的轨迹,它与各等效偏移距的交点就是时间节点.输入道和输出道颜色等级相同的线段表示的就是输入道的数据段映射到输出道的位置.
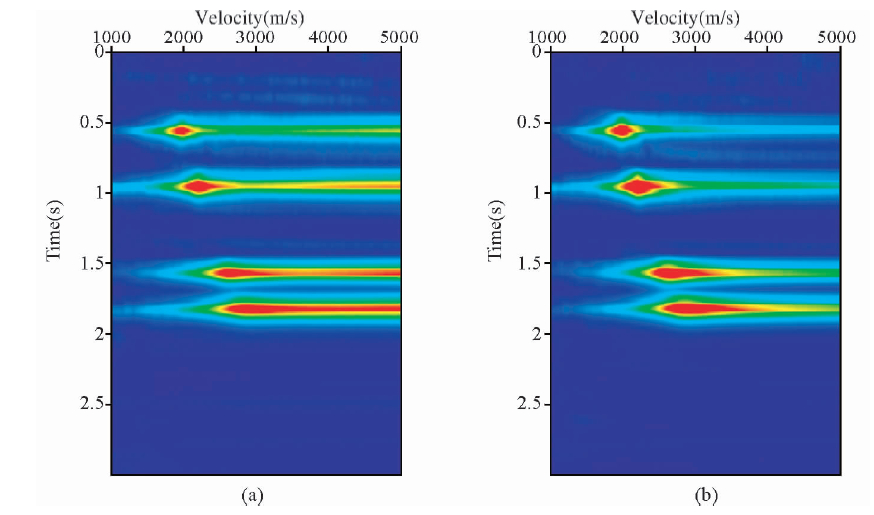 | 图 6(a)某CSP道集速度谱未消除映射噪音前和(b)本文方法消除映射噪音后 Fig. 6 A CSP gather velocity spectrum and (a)before removing conformation noise(b)after removing the noise |
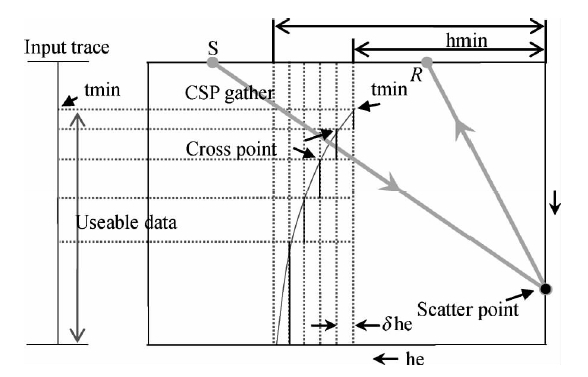 | 图 7 一个输入道快速映射到CSP道集的示意图 Fig. 7 Diagram of an input channel quickly mapped to the CSP gathers |
这里讨论一个问题,在公式(7)中,对于一个特定的输入道,x和h是已知的,则第i个等效偏移距he,i与的映射时间节点ti是一定值,因此速度v0也是一定值.但是速度v0怎么确定呢?我们知道这里的速度v0是散射点到基准面的均方根速度,它是和零偏移距的单程旅行时t0对应的,如果有一种办法可以确定t0的话,v0也就确定了.下面介绍本文采用的一种快速的查表计算速度v0的方法(Bancroft,1999).
从公式(2)可得

结合公式(7)得到如下方程
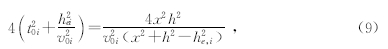
最后解出:
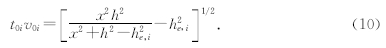
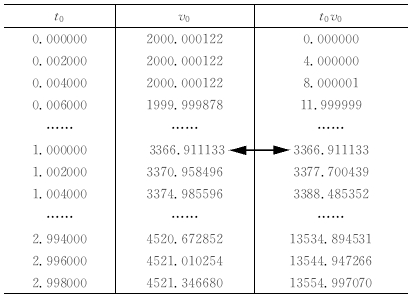
对于一个散射点道集来说各个t0时间的v0是已知的,因此可以提前算出t0v0来,例如表 1计算了采样间隔为2 ms的某个CSP道的1500个采样点的t0v0时间值,假如根据公式(10)计算出的某个等效偏移距对应的t0iv0i的值是3361.91,通过查表就可以得到该等效偏移距对应的v0为3366.91 m/s;如果计算的t0iv0i在t0v0列表里没有对应的值,则可以通过最接近的t0v0值插值得到v0.
|
|
表 1 由t0,v0计算的t0v0值列表 Table 1 t0v0 calculating from t0,v0 |
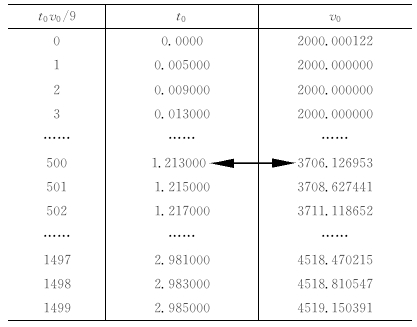
考虑到一个输入道映射到一个CSP道集时对应于每个等效偏移距都可能要查表一次,计算效率较低.一种更好的解决办法是计算出连续的整数t0v0,这样在计算出一个t0iv0i后能直接定位到t0v0值.具体的做法是用计算出的t0v0的最大值除以一个间隔值,得到一个新的t0v0的最大整数值, 构造一个新的列表,这个新列表的t0v0值为从0到新的最大t0v0的整数值,并以1为等间隔采样,并将每个新的列表中 t0v0对应的t0值和v0值通过插值计算出来. 如果通过公式 (10)计算的某一个等效偏移距对应的t0iv0i为4500,则可以用4500除以9(间隔值)直接将表 2中t0v0/9这一列定位在500的位置,进而可以得到速度v0为3706.13 m/s.如果通过公式(10)计算的t0iv0i为3707.0,则可以将t0v0/9定位在500和501之间,并且插值得到t0等于1.214000 s,v0等于3707.37 m/s.图 9(a)是我们用本方法对四层洼陷模型(与图 6中的一样)提取的cmp=1800处的CSP道集.表 3是cmp1800处csp道集映射参数列表,可以看到,快速映射方法的映射时间约为常规映射方法的五分之一,大大减少了映射时间.图 8(a)快速映射方法得到的csp道集,与常规方法得到的csp道集(图 5(b))基本一样,说明了本文提出的快速映射方法是可行的.
|
|
表 2 由t0v0定义的t0,v0列表 Table 2 t0,v0 definited by t0v0 |
|
|
表 3 cmp1800处csp道集映射参数列表 Table 3 Mapping parameter of cmp1800 |
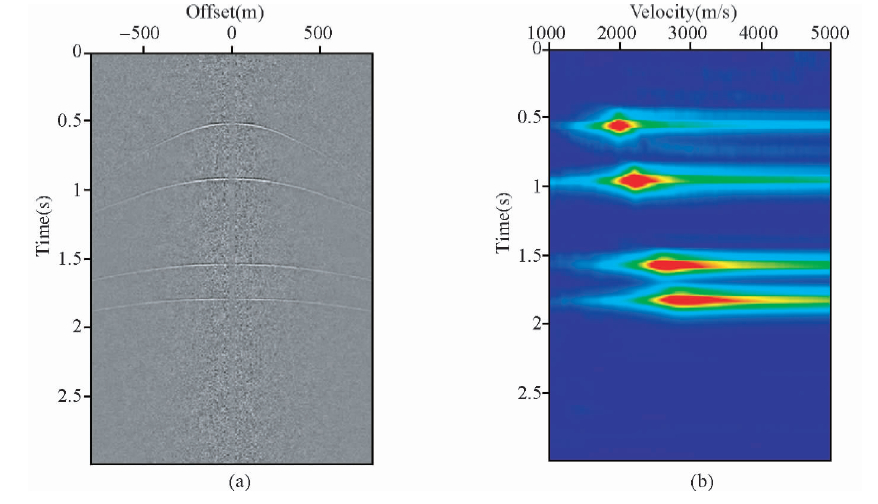 | 图 8(a)快速映射方法某CSP道集和(b)CSP道集速度谱 Fig. 8 fast mapping method(a)A CSP gathers(b)this CSP gathers velocity spectrum |
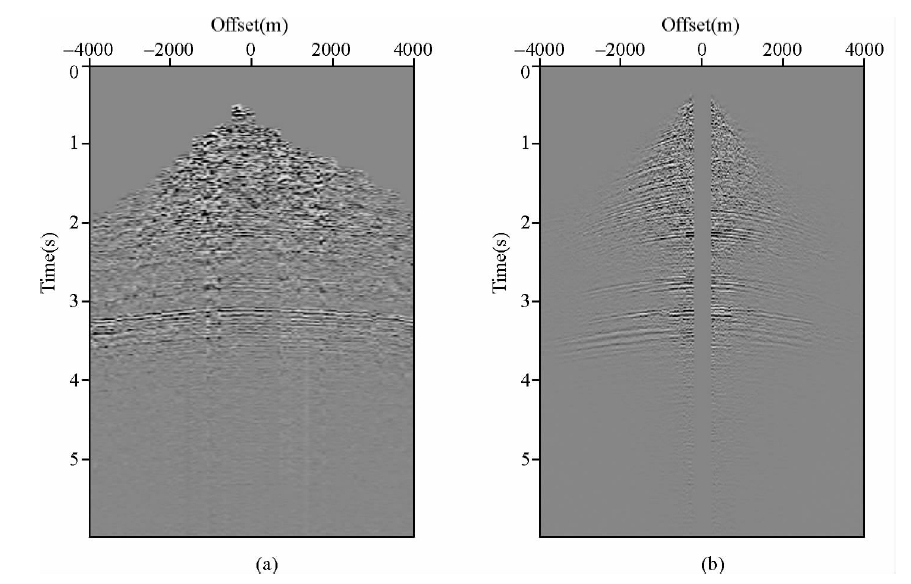 | 图 9(a)CMP=801处CMP道集和(b)相同位置处CSP道集 Fig. 9(a)CMP gathers at CMP=801 and (b)CSP gathers at the same position |
下面对陆上某个探区的三维资料的一条测线做CSP道集速度分析.该探区以山地为主,地表切割剧烈,地表接收条件差异较大,速度横向变化大,深部地质条件复杂,存在着高陡构造、逆掩推覆带等多种复杂构造,地震资料的信噪比较低,常规的速度分析难度很大.该条测线CMP范围为500~1495,CMP间距为25m,采样点数为3000,采样率为2 ms.
图 9(a)和(b)分别为cmp801处的CMP道集和CSP道集.从图中可以看到,由于地表和地下构造的复杂性,CMP道集的信噪比较低,在浅层几乎看不到有效的同相轴,但在我们提取的CSP道集上同相轴清晰可见,CSP道集有更高的覆盖次数(cmp801处CSP道集的覆盖次数为313,CMP道集的覆盖次数为36)和更大的偏移距.基于CSP道集的速度分析得到的速度谱(图 10(b))能量团更加明显,速度谱更加干净,这给我们的速度分析带来了方便.
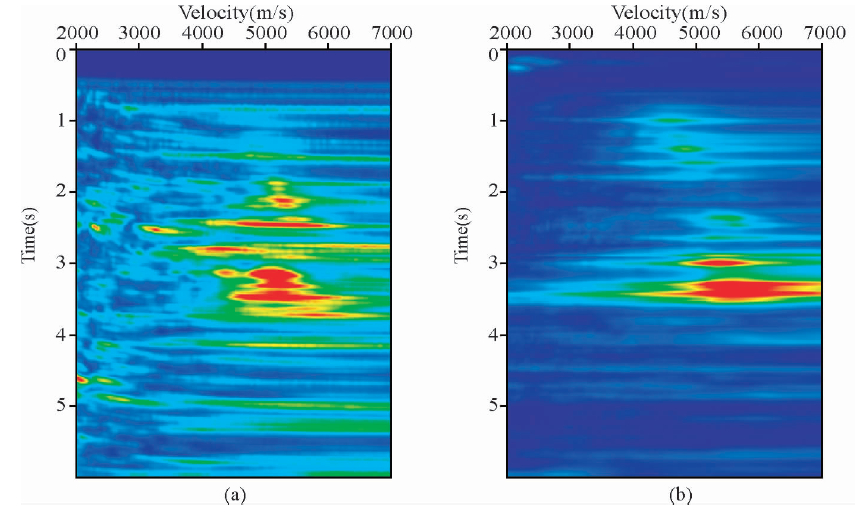 | 图 10(a)速度谱CMP=801处CMP道集和(b)相同位置处CSP道集 Fig. 10 CSP gather spectrum(a)CMP gathers at CMP=801(b)CSP gathers at the same position |
图 11是基于CMP道集利用速度扫描方法得到的速度模型,基于此速度模型我们构建csp道集并进行速度分析,得到速度模型图 11(b).为了更准确的对比,我们在获得速度模型后,未对其做任何的修饰.可以看到,基于CSP道集得到的速度场更加平滑,横向变化平缓,这样的速度模型更接近于我们偏移成像所需要的速度模型.
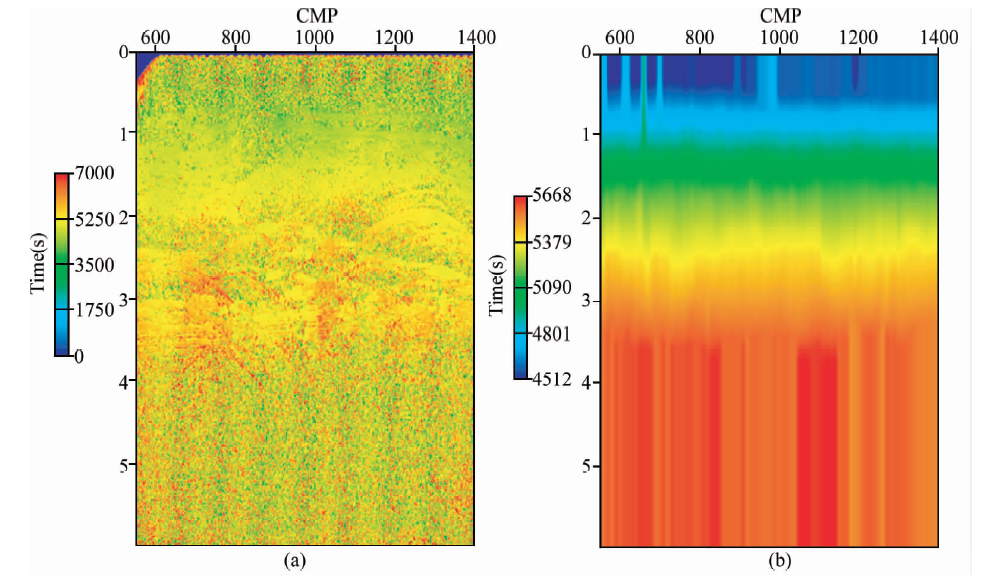 | 图 11(a)速度场由自动CMP扫描建立和(b)由CSP道集建立 Fig. 11 Velocity field(a)build from auto cmp scanning(b)build from csp gathers |
对比两幅剖面,我们可以看到,两张剖面的构造特征基本一致,但是基于CSP道集速度分析得到的速度场的偏移剖面构造更加清晰,反射层更加连续,尤其是在图中的方框中.因此,对于构造复杂、信噪比较低的地震资料,基于散射波道集的速度分析方法是可行的,而且在一定程度上提高了速度分析的精度.
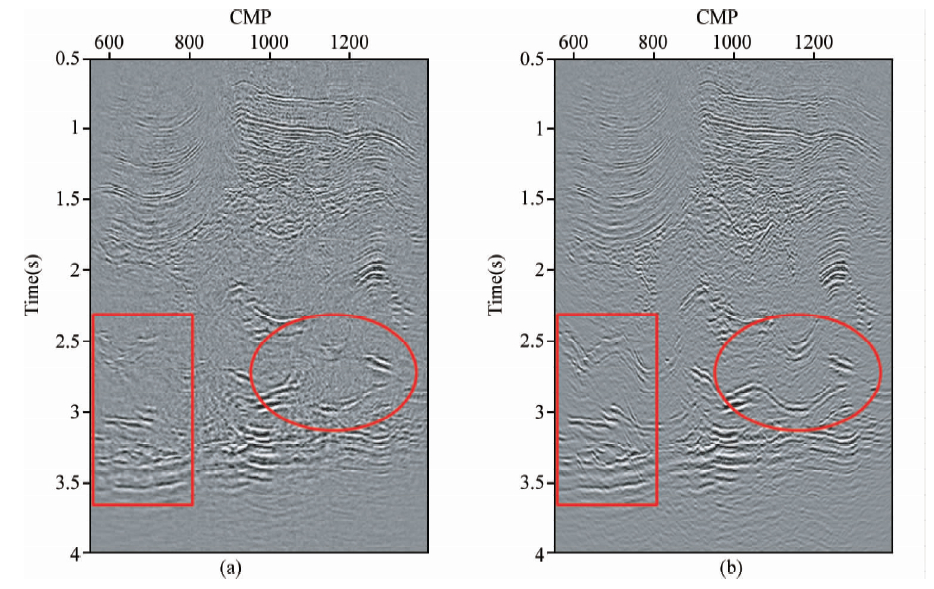 | 图 12(a)基于图 11(a)的速度场偏移结果和(b)图 11(b)速度场偏移结果 Fig. 12 Migration profile based on Fig. 11(a)’ velocity field and Fig. 11(b)’ velocity field |
我们以由CSP道集速度分析得到的时间域均方根速度场(图 11(b))为基础,通过剩余速度分析方法建立更加精细的时间域均方根速度模型(图 13(a)).利用该速度模型进行kirchhoff叠前时间偏移,其结果如图 13(b)所示.相比于图 12,其高陡构造和复杂断裂的成像效果的成像效果得到明显改善.这说明我们通过CSP道集速度分析来建立初始均方根速度模型的方法是正确可行的.
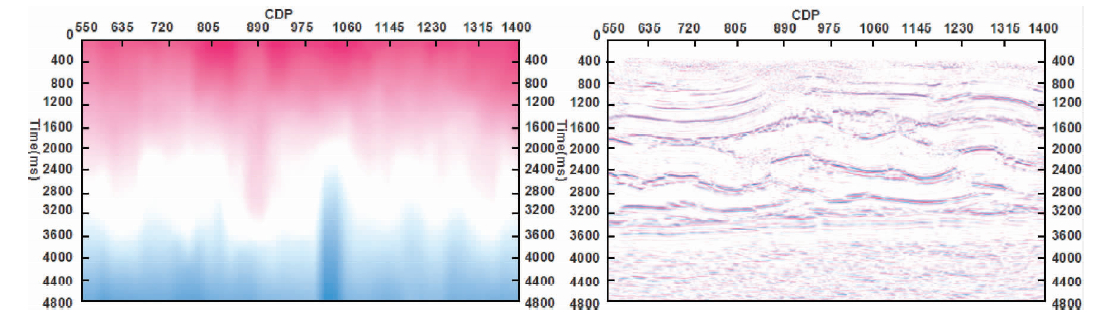 | 图 13(a)由CSP道集建立的均方根速度场和(b)kirchhoff偏移剖面 Fig. 13(a)Velocity field build from CSP gathers and (b)Kirchhoff migration profie |
从CMP道集映射产生CSP道集,然后对CSP道集进行速度分析,能够改善速度分析的质量.对于低信噪比资料,我们可以做两到三次基于CSP道集的速度分析来进一步提高速度分析的精度.本文提出的快速映射和消除映射噪音的方法在实际资料的应用中都取得了较好的效果.通过分析我们可以得出以下结论: 1)CSP道集是一种部分偏移后的道集,道集对应的双曲时距关系不受地层倾角的影响,应用常规的速度谱分析方法即可估算出均方根速度,提高了速度分析的精度; 2)相对于CMP道集,CSP道集拥有更高的覆盖次数和更大的偏移距范围,有利于改善深层同相轴速度谱的聚焦,提高速度分析的精度; 3 )CSP道集的形成对初始速度不敏感,对于难以获得精确初始速度模型的资料很实用;而且CSP道集具有自动插值和反假频效果,对于非规则或稀疏采样的地震数据的速度分析效果明显.
致 谢 感谢中国石化石油物探技术研究院段心标工程师在百忙之中对本文方法实现以及撰写论文过程中的耐心指导,在此表示衷心感谢和深深的敬意.
| [1] | Aki K. 1969. Analysis of the seismic coda of local earthquakes as scattered waves[J]. Geophysics, 74(2): 615-631. |
| [2] | Bancroft J C, Wang S. 1994. Converted-wave pre-stack migration and velocity analysis by equivalent offsets and CSP gathers[R]. CREWES 1994 Research Report. |
| [3] | Bancroft J C, Geiger H D. 1994. Equivalent offsets and CRP gathers for pre-stack migration[C]. 64th. Ann. Internat. Mtg, Geophysics, Expanded Abstracts, 672-675. |
| [4] | Bancroft J C. 1995. Velocity sensitivity for equivalent offset in CSP gathers[R]. CREWES 1995 Research Report. |
| [5] | Bancroft J C, Wang S et al. 1995a. Common scatter point (CSP) pre-stack migration[G]. Expanded Abstracts CSEG 1995 National Convention. Bancroft J C, Geiger H D, Wang S W, et al. 1995b. Pre-stack migration by equivalent offsets and CSP gathers: an Update[R]. CREWES Research Report, Volume 7. |
| [6] | Bancroft J C, Hugh D G. 1996. Pre-stack migration by equivalent offsets and CSP gathers[R]. CREWES Research Report, 29-21. |
| [7] | Bancroft J C. 1999. Efficient computation of the equivalent offset travel-time for EOM[C]. SEG Expanded Abstract. |
| [8] | Cao Z Y, Wang W, Wang Y. 2012. Numerical simulation and imaging of scattered wave of sunk pillar in coal seam[J]. Chinese Journal of Geophysics (in Chinese), 55(5): 1749-1756. |
| [9] | Fu L Y, Xiao Y J, Sun W J, et al. 2013. Seismic imaging studies of complex high and steep structures in Kuqa depression[J]. Chinese Journal of Geophysics (in Chinese), 56(6): 1985-2001. |
| [10] | Gou L M, Liu X W, Liu X L, et al. 2012. Application of scattering wave velocity analysis in broken strata area of the Southern North China Basin[J]. OGP (in Chinese), 47(6): 873-881. |
| [11] | Gong H Z, Shao Y, Wang G J, et al. 2013. Polarimetric and scattering properties of subsurface saline lacustrine deposites in Lop Nur Lake Basin, China using Synthetic Aperture Radar data[J]. Chinese Journal of Geophysics (in Chinese), 56(2): 431-440. |
| [12] | Li Z C, Guo C B, Zhang K, et al. 2011. To obtain accurate seismic velocity field in Karst exploration area[J]. Progress in Geophysics (in Chinese), 26(2): 549-556. |
| [13] | Liu T H. 2012. High precision numerical modeling and dynamic characteristic analysis of seismic scattering wave[J]. Chinese Journal of Geophysics (in Chinese), 55(4): 1318-1324. |
| [14] | Qu S L, Zhu S W, Zhao Q, et al. 2012. Analysis of seismic reflection characters for carbonate Karst reservoir[J]. Chinese Journal of Geophysics (in Chinese), 55(6): 2053-2061. |
| [15] | Qin L, Li Z C, Yang X D, et al. 2013. Pre-stack joint migration velocity modeling with multi-stage optimization[J]. Process in Geophysics (in Chinese), 28(1): 320-327. |
| [16] | Wang F F, Li J Y, Chen X H. 2013. Deghosting method based on inverse scattering series[J]. Chinese Journal of Geophysics (in Chinese), 55(5): 1628-1636. |
| [17] | Wang Y. 2005. New Methods of Seismic Imaging (in Chinese) [M]. Beijing: Petroleum Industry Press. |
| [18] | Wang Y, Zhu Y P, Yang H Z. 2000. Common scatter imaging and its applications in the low signal-to-noise ratio seismic data processing of 3D[J]. Oil Geophysical Processing (in Chinese), 33(1): 20-26. |
| [19] | Wang W, Yin J J, Liu X W, et al. 2007. Equivalent offset method and its application. [J]. Chinese Journal of Geophysics (in Chinese), 50(6): 1823-1830. |
| [20] | Wu R S, Huang L J. 1992. Scattered field calculation in heterogeneous media using a phase-screen propagator: Expanded Abstracts of the Technical Program[C]. SEG 62nd Annual Meeting, 1289-1292. |
| [21] | Yin J J, Xing C Y, Wang W. 2010. Imaging method and application of scattering wave of low signal-to-noise ratio seismic data [J]. Coal Society (in Chinese), 12(12): 2064-2067. |
| [22] | Zhang K. 2008. Pre-Stack Migration Velocity Analysis (in Chinese) [ Ph.D.thesis].Shanghai: Tongji University. |
| [23] | Zhou Q C, Liu H S, Kondrashkov V V, et al. 2012. Research of dual parameters evolving common reflection point stack and velocity analysis method[J]. Chinese Journal of Geophysics (in Chinese), 52(7): 1881-1890. |
| [24] | Zhu S W, Qu S L, Wei X C, et al. 2010. To improving imaging resolution by mapping noise attenuation on CSP gathers[J]. Geophysical Prospecting for Petroleum (in Chinese), 49(2): 107-114. |
| [25] | 曹志勇, 王伟, 王赟. 2012. 煤层陷落柱散射波数值模拟与成像[J].地球物理学报, 55(5): 1749-1756. |
| [26] | 符力耘, 肖又军, 孙伟家,等. 2013.库车坳陷复杂高陡构造地震成像研究[J]. 地球物理学报, 56(6): 1985-2001. |
| [27] | 勾丽敏, 刘学伟, 刘西宁,等. 2012. 散射波速度分析方法在南华北盆地破碎地层发育区的应用[J]. 石油地球物理勘探, 47(6): 873-881. |
| [28] | 宫华泽, 邵芸, 王国军,等. 2013. 罗布泊湖相沉积物极化散射特性及其环境意义[J]. 地球物理学报, 56(2): 431-440. |
| [29] | 刘铁华. 2012. 地震散射波的高精度数值模拟与振幅分析[J]. 地球物理学报, 55(4): 1318-1324. |
| [30] | 李振春, 郭朝斌, 张凯,等. 2011. 论碳酸盐岩探区时间域速度分析. 地球物理学进展, 26(2): 549-556. |
| [31] | 曲寿利, 朱生旺, 赵群,等. 2012. 碳酸盐岩孔洞型储集体地震反射特征分析[J]. 地球物理学报, 55(6): 2053-2061. |
| [32] | 秦宁, 李振春, 杨晓东,等. 2013. 叠前多级优化联合偏移速度建模[J]. 地球物理学进展, 28(1): 320-327. |
| [33] | 王芳芳, 李景叶, 陈小宏. 2013. 基于逆散射级数法的鬼波压制方法[J]. 地球物理学报, 56(5): 1628-1636. |
| [34] | 王勇. 2005. 地震成像新方法[M]. 北京: 石油工业出版社. |
| [35] | 王勇, 朱亚平, 杨慧珠. 2000. 共散射点成像及其在低信噪比三维地震数据处理中的应用[J]. 石油地球物理勘探, 33(1): 20-26. |
| [36] | 王伟, 尹军杰, 刘学伟,等. 2007. 等效偏移距方法及应用[J]. 地球物理学报, 50(6): 1823-1830. |
| [37] | 尹军杰, 邢春颖, 王伟. 2010. 低信噪比地震数据散射波成像方法及应用[J]. 煤炭学报, 12(12): 2064-2067. |
| [38] | 张凯. 2008. 叠前偏移速度分析方法研究[博士论文]. 上海: 同济大学. |
| [39] | 周青春, 刘怀山, Kondrashkov V V,等. 2009. 双参数展开CRP叠加和速度分析方法研究[J]. 地球物理学报, 52(7): 1881-1890. |
| [40] | 朱生旺, 曲寿利, 魏修成,等. 2010. 通过压制共散射点道集映射噪声改善绕射波成像分辨率[J]. 石油物探, 49(2): 107-114. |
 2014, Vol. 29
2014, Vol. 29