大地电磁测深(Magnetotelluric sounding，简称MT)是以天然交变电磁场为场源、以电磁感应理论为基础、通过测量地表电场和磁场分量来探测地球内部电性结构的方法，被广泛应用于固体矿产、油气、地热等资源勘探和上地幔结构研究等方面(石应骏等，1985；魏文博，2002；李墩柱等，2009).大地电磁测深反演的好坏直接影响其在各个领域的应用效果，所以MT反演问题一直是MT研究重点.MT反演分为线性和非线性二大类(冯思臣等，2002；陈清礼等，2003)，目前线性反演已经很成熟且被广泛应用，但是线性反演依赖于初始模型，如果给定的初始模型不合适，容易使其陷入局部极小甚至不收敛；非线性反演虽然不依赖于(或是依赖小)初始模型，但是由于其收敛速度慢等原因而没有广泛应用(陈小斌等，2005；罗红明等，2007；师学明等，2009；曾奇等，2011；陈向斌等，2011；梁宏达，2012).目前MT实际工作中最常用的的是一维、二维反演技术(蔡军涛和陈小斌，2010；秦林江和杨长福，2012；董浩等，2012)，一维反演通常是二维反演的基础.所以，研究一维MT反演的初始模型构建方法对提高一维、二维MT反演效果有着重要意义.

至今，一维MT反演初始模型的构建有二种方法.第一种方法是人工直接给定初始模型(王若等，2001)，包括把初始模型给为均匀半空间模型(电阻率通常给为表层的电阻率)和根据地质等资料给出初始模型.这样构建初始模型很简单，但是把初始模型给为均匀半空间模型，不但需要更多的迭代次数，而且可能导致反演陷入局部极小甚至不收敛；而根据地质等资料给出初始模型一方面比较耗时，另一方面对数据处理人员的水平要求较高.第二种方法是把Bostick反演的结果作为初始模型，苏朱刘等(2002)、戴亦军等(2012)人用Bostick反演的结果作为初始模型在一维MT反演中做了研究，周俊杰(2010)用Bostick反演的结果作为初始模型在一维CSAMT反演中做了研究，均取得了一定的效果.但是Bostick反演的结果很粗糙并且层参数过多，周俊杰等(2010)提出用电阻率对数差和厚度对数差进行初始模型优化，但是用对数差优化时往往较难选择合适的对数差值.为了构建更合理可靠的初始模型，使反演稳定收敛、收敛速度快且期待达到更高的精度，本文提出用Vagin(2012)文献中的控制转换算法构建初始模型参数，然后使用最优分割法优化初始模型.本文首先介绍Bostick反演、控制转换算法、对数差优化和最优分割法等基本原理，然后使用最小二乘反演方法通过模型计算验证本文所提出的构建初始模型方法的效果.

1 构建初始模型的方法

1.1 Bostick反演法

Bostick反演法是Bostick(1977)基于大地电磁测深曲线低频渐进线的性质提出来的一种一维近似反演方法.该方法利用渐进线的交点能反映交点以上底层平均电阻率而与底层电性无关的原理来做近似反演，后来又称为渐近线交点近似方法(周虬，1985；陈乐寿等，1988).Bostick反演公式详细推导可见陈乐寿等(1988)论著，实际反演时常用的公式为

1.2 控制转换算法

Vagin(2012)详细介绍了控制转换算法，他将之称为CTP(controlled transformation program的缩写，下同)，控制转换算法是利用MT实测数据和MT一维正演来光滑实测数据而提出来的，其基本过程如下：

1 )设有一系列实测数据为：T(j)，ρ_a(j)，j=1，…，N. 根据下式计算ρ⁽⁰⁾(j)：

3 )然后开始以下循环：

(1)把ρ^(l)、d^(l)作为正演参数进行MT一维正演，得到正演视电阻率 ρ^m(l)_a ；

(2)然后计算

(4)计算

以上便是控制转换算法的大概过程，其实质为利用二次MT一维正演和实测数据来调整层厚度和层电阻率，使调整后的模型参数响应与实测视电阻率拟合最好.在本文研究过程中发现：

CTP拟合实测曲线的能力是有限的，若是ε给的太小，CTP将达不到这精度，并且ε^(l+1)不一定小于ε^(l)；但是会有一个最佳ε^(l)，于是本文计算时在第3步增加了判断ε^(l+1)是否小于ε^(l)，若不小于则结束循环.从以上看到：在控制转换算法中产生了层参数ρ^(l+1)和d^(l+1)，这就为构建一维MT反演的初始模型提供了条件，于是本文提出把ρ^(l+1)和d^(l+1)经过优化后作为一维MT反演的初始模型. 2 优化初始模型的方法

从构建初始模型的方法中可以看到，无论是Bostick反演法，还是CTP算法，其得到的模型层数都很多，即有多少个频点就有多少层，必须经过层合并优化才可以作为可靠的一维MT反演的初始模型. 2.1 对数差优化

周俊杰等(2010)提出用对数差优化层参数，其基本算法为：从浅层出发，比较相邻二个频点的电阻率，若其对数差小于某一个数(参考数值为0.1~0.9)，则后一个电阻率取前一个电阻率的值；对全部频点进行这样的比较后就对电阻率进行了合并.然后，从浅层出发，比较相邻两层的厚度，若其对数差小于某个数值(参考数值为0.2)，则合并该层.这样合并优化后，会得到一个层数减小的新模型.电阻率对数差和厚度对数差的选取直接影响了初始模型的层数和层参数，若对数差的数值小，产生的模型层数相对较多，相反则产生的模型层数较少.从该算法可以看出：

1 )对优化后模型的层数无法预先估计，即使根据实测视电阻率曲线或其他地质资料可以判断出模型的层数，往往也较难选择合适的电阻率对数差和厚度对数差使优化后的模型的层数为我们所想要的层数；

2)优化后的模型的电阻率参数进行了二次近似，这势必使优化后的模型更偏离真实模型. 2.2 最优分割法

最优分割法在地质学科中应用广泛(刘承祚，1980；倪鹏等，2012)，主要用于对地质体的分层、分段、分带等.最优分割法的基本思路为：对于给定的一列数据，根据某个指标或几个指标，将这列数据分为几组，使组内离差平方和最小，而组间差平方和最大.

因为电法勘探主要根据电阻率差异来区分异常，所以这里仅介绍一个指标的最优分割法.设有一列有序电阻率数据为：ρ_j，j=1，…，N.其中这列有序电阻率数据记为ρ.用{i，…，j}表示由第i个电阻率开始至第j个电阻率终止电阻率段，其中1≤i≤j≤N，引入

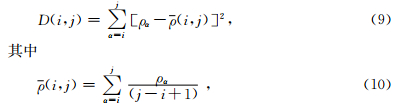
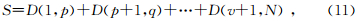
本文采用经典的最小二乘反演法.反演程序设计的关键有三点(阮百尧，1999)：一是偏导数的求取；二是模型参数的处理；三是线性方程组的求解.雅克比矩阵的求取采用差分代替微分的方式；用参数的对数值进行反演解决了视电阻率数据和电阻率模型参数变化范围大的问题，并将方程进行无量纲化；采用共轭斜量法中的Fletcher-Reeves方法求解方程组(Nocedal and Wright， 2006).反演中将电阻率、层厚度等参数同时反演.

3.1 优化初始模型的方法对比

下面以Bostick反演法构建初始模型，比较对数差优化和最优分割法优化的初始模型对反演的影响.设置模型为H型，参数分别为ρ₁=ρ₃=100 Ωm，ρ₂=10 Ωm，h₁=200 m，h₂=100 m，第三层为无穷厚.图 1(a)为反演迭代RMS曲线对比图，图 1(b)为真实模型与反演结果对比图.

图 1

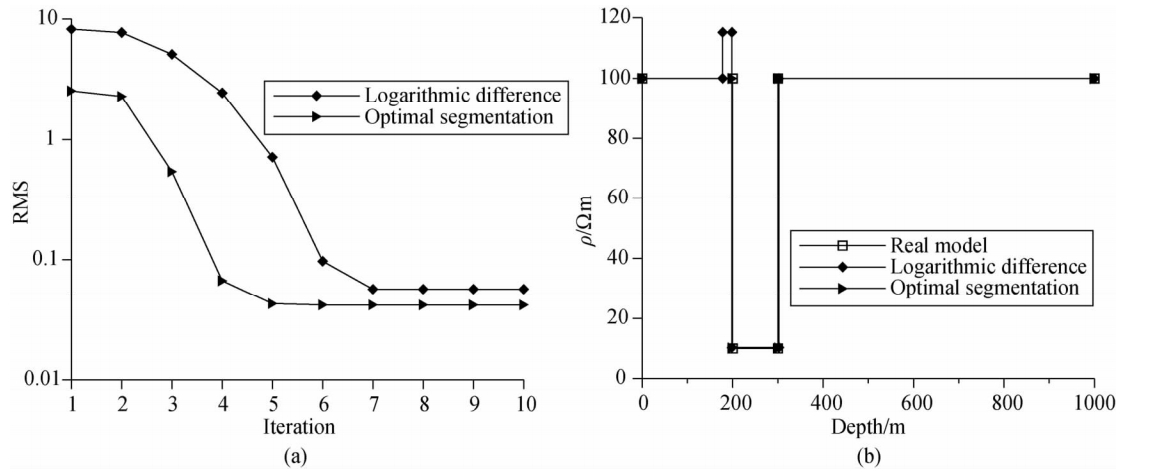图 1 优化初始模型的方法对比 (a)反演迭代RMS曲线对比图；(b)真实模型与反演结果对比图.Fig. 1 Comparison of the methods of optimizing initial model

从图 1(a)看到：二种方法的反演迭代RMS曲线均稳定减小，说明是稳定收敛的；但是最优分割法只需要迭代5次就趋于稳定，对数差优化需要迭代7次才趋于稳定，并且趋于稳定时最优分割法的RMS(0.042)比对数差优化的RMS(0.057)小，表明最优分割法优化的初始模型使反演达到的精度更高.

从图 1(b)看到：二种方法都能较好地恢复真实模型，但是仔细对比可以看到，对数差优化的结果为四层模型，第二层为电阻率偏高的薄层.这就是用对数差优化初始模型的缺点：往往较难选择合适的对数差值使优化后的初始模型层数为我们想要的层数，在这个模型计算中，作者对电阻率对数差值和厚度对数差值选择了一系列值进行尝试，均不能使对数差优化后的模型为三层，而最优分割法可以很容易达到这一点.从以上分析可见：最优分割法优化初始模型的能力比对数差优化初始模型能力强. 3.2 构建初始模型的方法对比

下面以最优分割法优化初始模型，比较均匀半空间、Bostick反演法和CTP法构建的初始模型对反 演的影响.设置了二个模型.

第一个模型为H型，参数分别为ρ₁=ρ₃=100 Ωm，ρ₂=10 Ωm，h₁=200 m，h₂=100 m，第三层为无穷厚.图 2(a)为 其反演迭代RMS曲线对比图，从图 2(a)可以看到：三种初始模型的反演均稳定收敛，但是CTP法收敛最快，只需要迭代4次，次之为Bostick反演法，需要迭代5次，最慢的是以均匀半空间为初始模型的反演，需要迭代8次.并且当反演趋于稳定时，RMS由大到小依次为：均匀半空间、Bostick反演法、CTP法，说明用CTP法构建的初始模型使反演达到的精度最高.

图 2

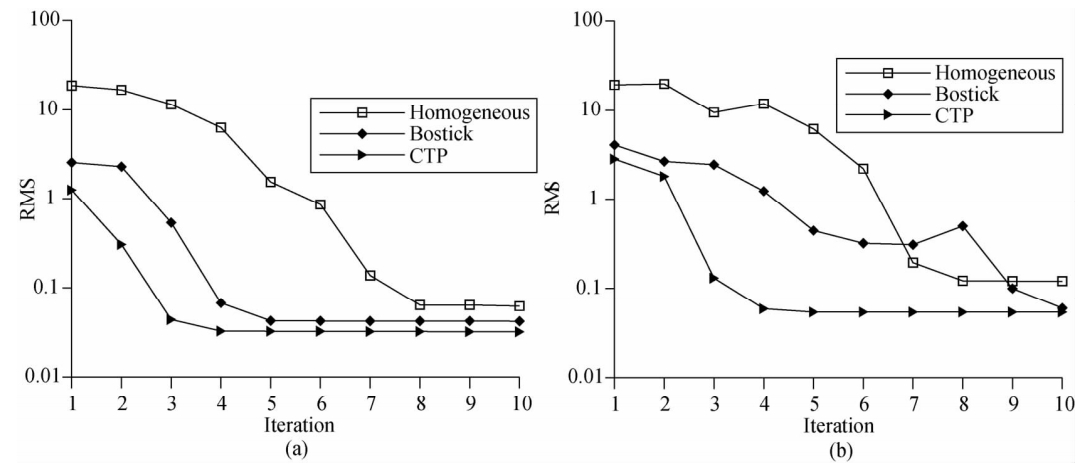图 2 构建初始模型的方法对比(a)H型反演迭代RMS曲线对比图；(b)HK型反演迭代RMS曲线对比图.Fig. 2 Comparison of the methods of building initial model

表 1为H型反演结果，从表 1看到：初始模型平均相对误差由大到小依次为：均匀半空间(195.00%)、Bostick反演法(124.78%)、CTP法(49.82%)，表明CTP法构建的初始模型偏离真实模型最小.反演结果的平均相对误差由大到小依次为：均匀半空间(1.38%)、Bostick反演法(0.94%)、CTP法(0.71%)，表明CTP法构建的初始模型使反演达到的精度最高.

表 1(Table 1)

表 1 H型反演结果 Table 1 Inversion results of H model ρ1(Ωm) ρ2(Ωm) ρ3(Ωm) h1(m) h2(m) 平均相对误差(%) 真值 100.00 10.00 100.00 200.00 100.00 — 初始模型1 100.00 100.00 100.00 150.00 150.00 — 初始模型1相对误差(%) 0.00 900.00 0.00 25.00 50.00 195.00 反演结果1 100.04 10.29 100.01 198.93 103.41 — 反演结果1相对误差(%) 0.04 2.94 0.01 0.53 3.41 1.38 初始模型2 113.65 31.25 98.00 155.84 473.61 — 初始模型2相对误差(%) 13.65 212.56 2.00 22.08 372.62 124.78 反演结果2 100.02 10.20 100.01 199.28 102.30 — 反演结果2相对误差(%) 0.02 1.98 0.01 0.36 2.30 0.94 初始模型3 104.41 23.15 100.23 186.28 206.19 — 初始模型3相对误差(%) 4.31 131.53 0.23 6.86 106.19 49.82 反演结果3 100.02 10.15 100.01 199.45 102.74 — 反演结果3相对误差(%) 0.02 1.50 0.01 0.27 1.74 0.71 注：1为均匀半空间初始模型，2为Bostick反演法构建的初始模型，3为CTP法构建的初始模型.

表 1 H型反演结果 Table 1 Inversion results of H model

模型二为HK型，参数分别为ρ₁=100 Ωm，ρ₂=10 Ωm，ρ₃=500 Ωm，ρ₄=10 Ωm，h₁=h₂=100 m，h₃=500 m，第四层为无穷厚.图 2(b)为其反演迭代RMS曲线对比图，从图 2(b)可以看到：均匀半空间为初始模型的反演在第4次迭代时不稳定，Bostick反演法在第8次迭代时不稳定，只有CTP法是稳定收敛的；CTP法收敛最快，只需要迭代4次，次之为均匀半空间的，需要迭代8次，最慢的是以Bostick反演法，需要迭代10次.当反演趋于稳定时，RMS由大到小依次为：均匀半空间、Bostick反演法、CTP法，其中，CTP法的RMS仅略小于Bostick反演法的RMS.表 2为HK型反演结果，从表 2看到：初始模型平均相对误差由大到小依次为：均匀半空间(171.43%)、CTP法(46.37%)、Bostick反演法(45.88%)，表明CTP法构建的初始模型偏离真实模型的程度与Bostick法构建的结果相当.反演结果的平均相对误差由大到小依次为：均匀半空间(10.74%)、Bostick反演法(8.20%)、CTP法(7.44%)，表明CTP法构建的初始模型使反演达到的精度最高.HK型三种反演结果的平均相对误差均较大的原因可能为本文反演程序本身精度不是很高所致，但这不作为本文讨论内容.

表 2(Table 2)

表 2 HK型反演结果 Table 2 Inversion results of HK model ρ1(Ωm) ρ2(Ωm) ρ3(Ωm) ρ4(Ωm) h1(m) h2(m) h3(m) 平均相对误差(%) 真值 100.00 10.00 500.00 10.00 100.00 100.00 500.00 — 初始模型1 50.00 50.00 50.00 50.00 200.00 200.00 200.00 — 初始模型1相对误差(%) 50.00 400.00 90.00 400.00 100.00 100.00 60.00 171.43 反演结果1 99.93 9.68 209.37 9.99 100.65 90.92 519.80 — 反演结果1相对误差(%) 0.07 3.21 58.13 0.06 0.65 9.08 3.96 10.74 初始模型2 126.33 23.23 53.99 11.40 78.48 120.92 429.86 — 初始模型2相对误差(%) 26.33 132.33 89.20 14.04 21.52 20.92 14.03 45.48 反演结果2 99.98 9.86 260.15 9.996 100.26 94.76 512.50 — 反演结果2相对误差(%) 0.02 1.42 47.97 0.04 0.25 5.22 2.50 8.20 初始模型3 124.69 21.73 273.10 12.23 78.19 155.95 314.33 — 初始模型3相对误差(%) 24.69 117.30 45.38 22.33 21.81 55.95 37.13 46.37 反演结果3 99.97 9.86 281.95 9.997 100.27 95.34 510.59 — 反演结果3相对误差(%) 0.03 1.41 43.61 0.03 0.27 4.65 2.12 7.44 注：1为均匀半空间初始模型，2为Bostick反演法构建的初始模型，3为CTP法构建的初始模型.

表 2 HK型反演结果 Table 2 Inversion results of HK model

本文实测资料来自哈密市某地MT观测数据.该区地貌单元属于山前冲洪积倾斜平原区，地势平坦开阔，主要为戈壁景观，北距天山脚下10 km.区内地层由中生界侏罗系、新生界第四系组成.资料采集采用的是加拿大凤凰公司生产的V5-2000大地电磁测深仪器.选取该区一条大地电磁测线上的一个测点的MT资料进行反演，反演时采用CTP法和Bostick法构建初始模型、最优分割法优化初始模型.图 3是其反演结果对比图.从图 3(a)反演迭代RMS曲线对比图看到：CTP法和Bostick法的反演趋于收敛时的RMS基本是一致的，但是CTP法在第3次迭代时收敛，Bostick法在第5次迭代时收敛，可见CTP法收敛速度比Bostick法快.这里没有对比均匀半空间作为初始模型的结果是因为对于该实测数据，测试不同的均匀半空间模型，其反演结果要么不稳定收敛，要么反演精度很低，反演结果具有较强的主观性；其原因一是给的初始模型偏离真实模型太大，二是可能为本文反演程序本身精度不是很高，后者不是本文讨论的重点，故这里仅对比CTP法和Bostick法的结果.从图 3(b)实测曲线与反演曲线对比图看到：CTP法和Bostick法的结果拟合实测数据均较好，仅在高频段少有偏离；反演结果与地质资料一致.

图 3

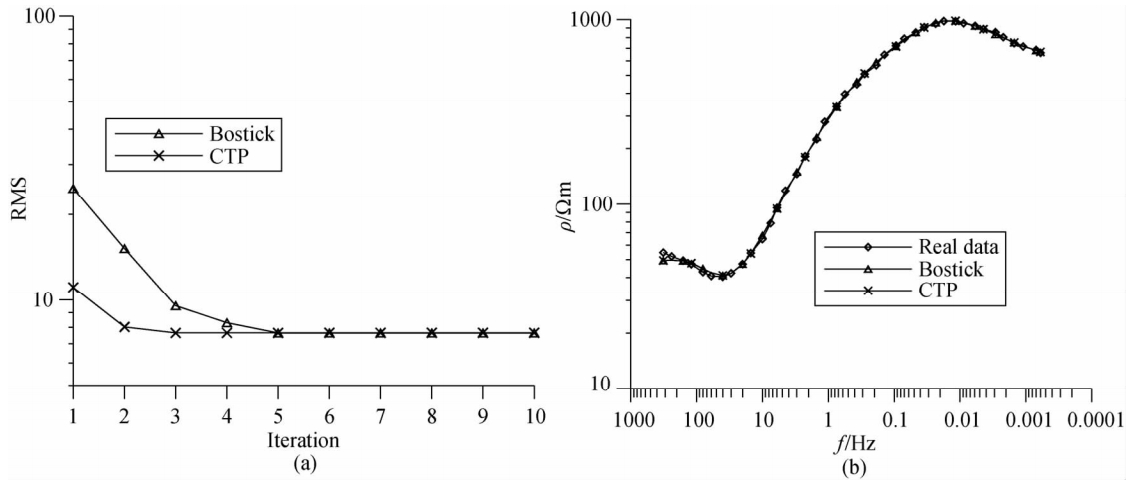图 3 实测数据反演结果对比(a)反演迭代RMS曲线对比图;(b)实测曲线与反演曲线对比图.Fig. 3 Comparison of the inversion results of real data

通过层状模型和实测数据计算对比分析Bostick反演法、CTP法构建初始模型和对数差优化、最优分割优化初始模型对MT一维反演的影响.得到以下结论：

(1)最优分割法比对数差优化初始模型更有效，可以容易得到我们预先所想要的模型层数，且电阻率仅是一次近似，更适合用于初始模型的优化.

(2)用CTP法构建初始模型参数、最优分割法优化后的结果作为MT一维反演的初始模型可以使反演稳定收敛且收敛速度快.同样使用最小二乘反演算法，该方法的反演迭代次数比用Bostick反演结果作为初始模型的反演迭代次数少20%以上，比均匀半空间作为初始模型的反演迭代次数少100%以上；并且反演精度也有了一定的提高.

(3)本文提出的构建初始模型的方法不但对提高MT一维反演效果有意义，而且对构建其他勘探方法的反演初始模型也具有一定的参考价值.