0 引 言
大地电磁测深法(MT)具有穿透深度大(可探测至上地幔)、不受高阻层屏蔽、对低阻层反映灵敏、等值范围较窄及分辨能力较高等特点(黄文彬,2009;王辉等,2013;叶高峰等,2013).目前已广泛应用于石油、天然气、地热勘探;沉积盆地构造、地壳和上地幔结构的探测;监视地下深部岩石电阻率的变化,提供地震前兆的信息等.但由于大地电磁使用天然场源,抗干扰能力较弱,所以测深资料极易受到噪声干扰,特别是人文噪声干扰,随着人类活动的日益增强,人文噪声干扰范围广、强度大,MT数据采集不可能完全避开人类活动区域,所以要采集到高质量的数据并不容易.如何减少噪声干扰、提高资料信噪比、消除非构造因素对反演结果的影响,是目前MT工作中首先考虑的问题(张全胜和杨生,2002).
针对大地电磁测深资料的去噪,汤井田等(汤井田等, 2012a,b)利用数学形态学对实测大地电磁信号进行噪声压制,有效地剔除了大尺度干扰及基线漂移,较好地还原了大地电磁信号的原始特征,修正了标准形态算子所产生的统计偏倚现象;景建恩等(景建恩等,2012)定义了利用离散广义S变换时频谱计算大地电磁场分量功率谱公式,并在此基础上研究了基于S变换时谱频的大地电磁测深数据Robust处理方法;尹曜田等(尹曜田等,2012)提出基于遗传算法的大地电磁阻抗张量分解方法,该方法取得了较好的应用效果,但是由于该方法本身的性质所决定,GB分解都有一些不可确定的畸变参数,这就导致完成GB分解后的大地电磁响应函数中仍然包含静位移的影响;杨云飞等(杨云飞等,2001)采用正交多项式逼近去白噪的方法对观测数据进行回归处理,并使它们的整体误差达到最小.该方法有利于从整体上约束数据的变化趋势,但正交多项式拟合去噪方法基于传统的统计学理论,是当训练样本数趋向无穷大时的解决方案.然而在实际工作中,由于训练样本数的限制,基于经验风险最小化原则的学习机器普遍存在推广能力不足的问题,以致求取的多项式不能反映系统本身的特性.杨迪琨等(杨迪琨和胡祥云,2007)采用基于概率分析的去噪方法,“先反演,再去噪”,这种方法对被高噪声淹没的信息有较好的恢复能力,但在随机行走和边缘概率计算环节运算量偏大.目前对大地电磁测深资料处理比较流行的做法是采用Robust变换(张帆等,2012)与人工筛选相结合的方法来提高数据质量,有时还需要用到远参考,此法在实际应用中效果比较理想,但当数据量大且受干扰严重时,人工筛选耗时耗力,对编译人员的素质要求较高.
统计学习理论是一种专门研究小样本情况下机器学习规律的基本理论和数学构架,也是小样本统计估计和预测学习的最佳理论.由Vapnik根据统计学习理论提出的支持向量机(Vapnik,1995)目前广泛应用于解决分类和回归问题(邓小英和李月,2007;张军等,2009;龚灏等,2011;邓小英等,2011;张尔华等,2011;邴萍萍等,2012),该方法是基于结构风险最小化原则的学习机器,具有良好的推广能力,较好地解决了小样本、非线性、高维数和局部极值等实际问题(徐飞和徐卫亚,2010).本文利用支持向量机的上述优良特性,将ε-支持向量机回归引入大地电磁测深资料的去噪中,通过对实测数据的处理,表明该方法是行之有效的. 1 ε-SVR基本原理
支持向量机回归(GUNN S,1998;边肇祺和张学工等,1998)(SVR)的基本思想是通过一个非线性映射φ将数据映射到高维特征空间,并在这个空间进行线性回归.设给定的训练样本为
(x i,y i),x i∈ R d,y i∈ R,i=1,…,n,其中 x i为输入值,y i为对应的目标值,n为样本个数.
回归的目标就是求回归函数
f(x)=< W,φ(x)>+b,(1)
优化问题是最小化:
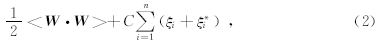
约束为
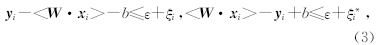
式(1)中,W和b分别为回归函数的权重向量与偏置.式(2)中C为惩罚因子,是预先给定的,用于控制模型的复杂程度和逼近误差的折中,C越大,则对数据的拟合程度越高,ξ、ξ*i表示松弛因子.式(3)中ε为不敏感惩罚系数,用于控制回归逼近误差管道的大小,从而控制支持向量的个数和泛化能力,其值越大,则支持向量越少,但精度会越低.这是一个二次优化问题,将其转化为相应的对偶问题为
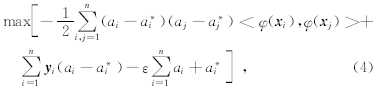
约束为
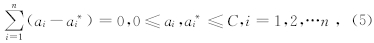
式(5)中ai为各样本对应的拉格朗日系数.解这个二次优化,可以得到ai,a*i的值,于是 W 的表达式为
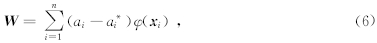
从而回归函数f(x)的表达式为
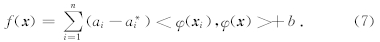
可以看到,在上面的优化中需要进行高维特征空间中的内积运算,如果找一个核函数 k(x,y)代替高维空间中的内积,就可以避免复杂的高维计算问题. 已经证明对于<φ(x),φ(y)>,对称函数 k(x,y)只要满足Mercer条件,即可满足要求,这就避免了明确知道φ(x),从而巧妙地解决了在高维空间中的运算.按照Kuhn -Tucker 定理,可得b的计算式为
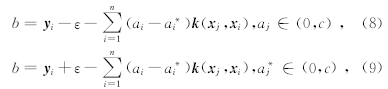
可以通过任意一个满足条件的样本计算出b的值.这样就得到目标的回归方程:
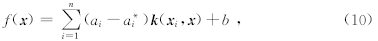
式(10)中 k(x,y)为核函数,目前,最常用的核函数主要有:
(1)多项式核函数:
k(x i,x)=(
(2)径向基核函数:
k(x i,x)=exp(-λ|| x-x i||2),λ为核参数,(12)
(3)Sigmoid函数:
k(x i,x)=tanh(v< x i,x >+c),(13)
(4)线性核函数:
k(x i,x)=x i x T .(14)
本文选用应用较多且效果较好的径向基函数作为核函数(Pontil and Verri, 1998).对于支持向量机回归模型来说,不敏感系数ε,核函数的参数λ以及误差惩罚参数C的选择对于模型的性能有至关重要的影响,对 SVM 参数的选择目前还没有一种有效的方法,实际操作时往往凭借经验、试验对比、大范围搜寻或者利用软件包提供的交互检验功能进行寻优.本文是在经验值内经过多次实验对比找出一组最优组合.
2 应用实例
文章所应用的数据为湖南某地区的宽频大地电磁测深数据,测区内两条测线分别为南北走向和东西走向,长80 km,成十字交叉型,每条测线有5个测深点,其中交叉点即中间点为两条测线的共用点,故测点总数为9个.使用的仪器为加拿大凤凰公司的V5-2000型大地电磁仪.测区地势复杂,丘陵起伏,盆地密布,水系发达,采集环境恶劣.区内高压电网、信号塔、矿场等密布,人文干扰十分严重,致使实测电阻率曲线受噪声影响严重.
本文选取南北测线上的S20和S40点、东西测线上的W20和W40点及中间点MID共五个测深点,利用ε-SVR算法对其视电阻率资料进行去噪处理,同时利用S20和S40点评估模型的应用效果及稳健性.对于SVR参数的选择,小样本数据回归模型参数经验(陈果等,2008)一般为ε取(0.0001~0.01),C取(1~1000),经过多次实验对比最终选取c=400,ε=0.01,λ=0.01为本次研究的参数.
2.1 ε-SVR模型去噪效果分析
通过对W20点、W40点及中心点MID的去噪处理,改善了上述三个测深点的数据质量.
图 1、图 2分别是点W20点和W40点去噪前后的TE和TM视电阻率曲线,由图可以看出这两个测深点整体都受到噪声干扰,但高频部分受噪声影响相对较小,中低频部分受影响比较大.经ε-SVR去噪后,视电阻率曲线整体形态得到改善,中低频部分的改善尤为明显.
通过对中心点去噪前后视电阻率曲线的对比,可以看出ε-SVR 对消除类似于近场干扰的局部畸变也有较好的效果,通过ε-SVR 去噪后,噪声影响被消除,中低频段的畸变得到了校正,整体曲线变得比较合理,呈现出较为真实的变化规律.
2.2 ε-SVR模型优势与稳健性评估
分别对S20点利用常规处理方法及ε-SVR算法进行处理,通过对比发现后者的去噪效果明显优于前者,且由于后者是由算法自动实现,比起常规方法更加省时省力.对S40点原始测深数据人为加入10%噪声,处理结果显示ε-SVR模型具有较强的稳健性.
图 4(a)是经过Robust变换得到的TE和TM视电阻率曲线图,从图中可以看出数据高频段质量比较好,中低频段受噪声影响依然很严重,不能用于反演解释,必须进一步消除噪声影响.图 4(b)是经过人工筛选后得到的是电阻率曲线图,可以看出中低频段数据质量已有明显改善,但数据还有继续改善的空间,然而受限于解释人员的素质及个人主观因素,同时考虑到时间消耗,人工筛选只能在一定程度上改善数据质量,很难做到尽善尽美.图 4(c)是经过ε-SVR算法去噪后得到的曲线图,从图中可以看出整个频段的数据质量都有大幅提升,曲线的整体形态及平滑程度均优于人工筛选.
图 5是用S40点评估模型稳健性得到的对比图,其中图 5(a)及图 5(c)是S40点原始资料去噪前后的视电阻率曲线图,通过对比可以看出,经过ε-SVR模型去噪后,整个频段的数据质量均得到明显改善,曲线形态变得合理,曲线光滑程度大幅提升.图 5(b)和图 5(d)则用来验证模型的稳健性,对S40点原始视电阻率资料的中高频段人为加入10%的噪声,如图 5(b)所示;再利用ε-SVR模型进行去噪处理,得到图 5(d)所示结果,通过对比图 5(c)和图 5(d),可以看出,二者基本上是一致的,只在中低频段曲线下掉部分二者TM曲线有细微差别.
从图 5可以直观的去评价模型的稳健性能,而从表 1则可以定量评价模型应用于去噪时的稳健性.测区内所有测点数据均取到80个频点,随机取S40中高频部分的8个频点加入噪声,如图 5(b)所示,然后再用模型对其进行去噪处理,表 1所示数据即为加噪前后的处理结果及误差,其中最大绝对误差为54.093,最小绝对误差为0,相对误差百分比最大值和最小值分别为9.209%和0,同时计算可得绝对误差的均方差为9.454,相对误差的均方差为1.61%,说明模型具有良好的稳健性和较强的泛化能力.
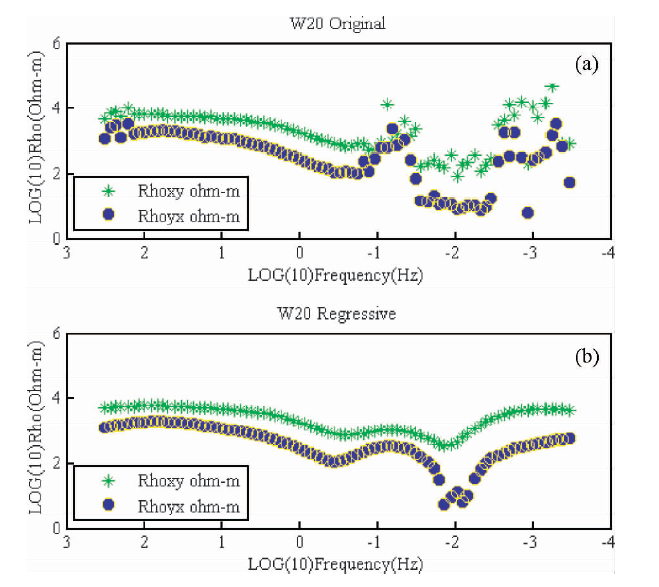
图 1 W20点去噪前(a)去噪后(b)视电阻率曲线对比图
Fig. 1 The comparison apparent resistivity curves before denoising(a) and after denoised(b)of W20 point
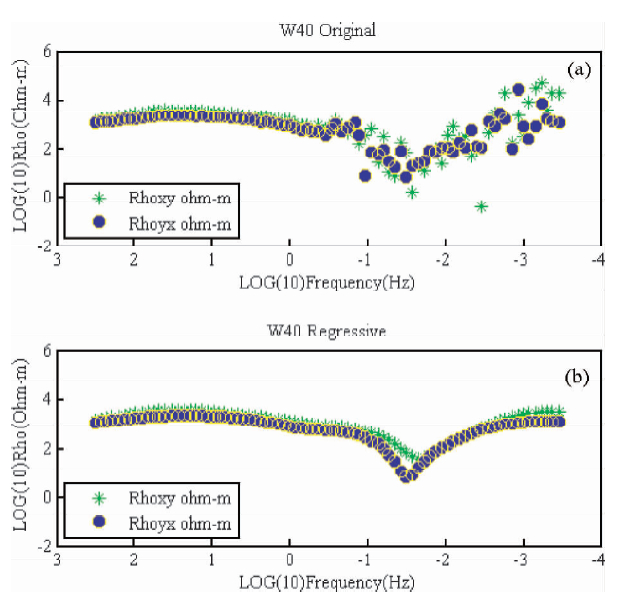
图 2 W40点去噪前(a)去噪后(b)视电阻率曲线对比图
Fig. 2 The comparison apparent resistivity curves before denoising(a) and after denoised(b)of W40 point
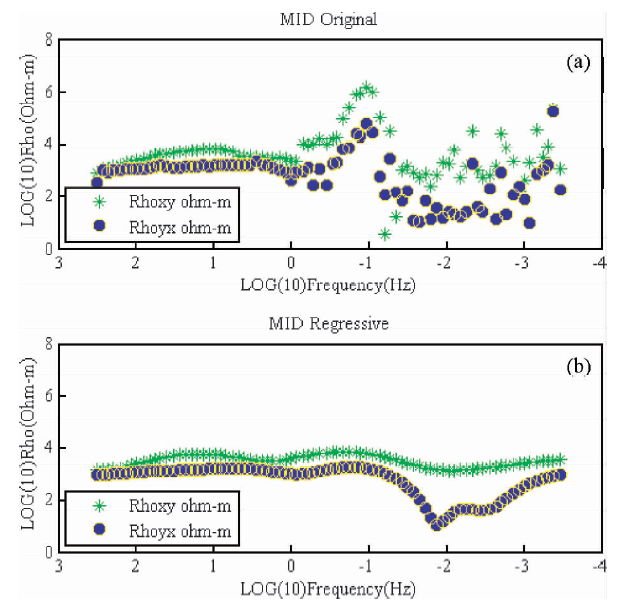
图 3 中心点MID去噪前(a)去噪后(b)
视电阻率曲线对比图
Fig. 3 The comparison apparent resistivity curves before
denoising(a) and after denoised(b)of MID point
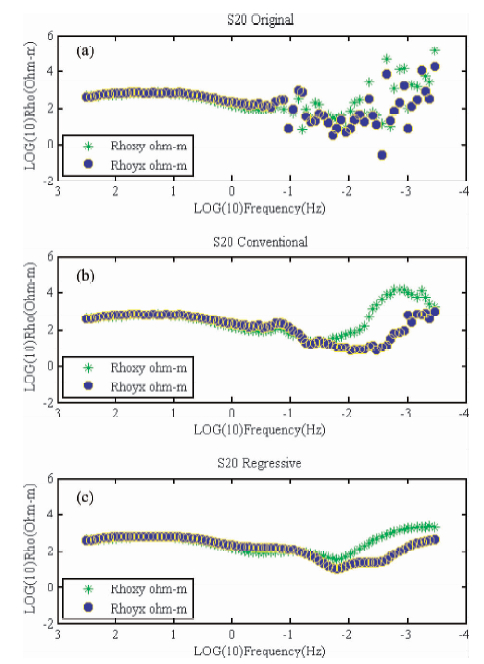
图 4 S20点去噪前(a)、人工筛选(b)及模型去噪(c)对比图
Fig. 4 The comparison apparent resistivity curves before denoising(a),artificial selection(b) and model denoised(c)of S20 point
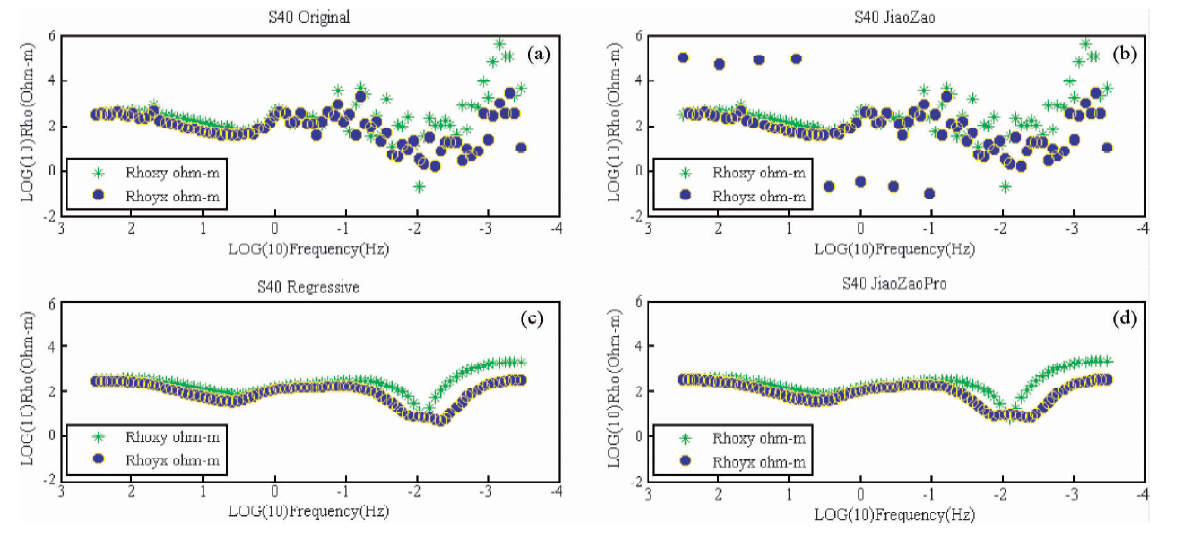
图 5 S40点加入噪声前(a)和(c),(b)和(d)模型去噪对比图
Fig. 5 The comparison model denoising curves before adding noise(a)和(c) and after adding noise(b) and (d)of S40 point
![]()
表 1 S40点加入噪声前后模型去噪误差
Table 1 The model denoising error before and after adding noise of S40 point
| [1] | Bian Z Q, Zhang X G. 1998. Pattern Recognition[M]. Beijing: Tsinghua University Press, 284-304. |
| [2] | Bing P P, Cao S Y, Lu J T. 2012. Non-linear AVO inversion based on support vector machine[J]. Chinese J. Geophys. (in Chinese), 55(3): 1025-1032. |
| [3] | Chen G, Zhou J. 2008. Research on Parameters and Forecasting Interval of Support Vector Regression Model to Small Sample[J]. Acta Metrologica Sinica (in Chinese), 29(1): 92-96. |
| [4] | Chen Q N. 2005. Study on Observation Construction Mechanics Simulation for Non-Symmetry Arch Tunnel in Highway (in Chinese)[D]. Chongqing: Chongqing University. |
| [5] | Deng X Y, Li Y. 2007. Study of parameters setting for least square support vector machine based on Ricker wavelet kernel in the denoising applications of seismic prospecting signals[J]. Progress in Geophysics (in Chinese), 22(3): 953-959. |
| [6] | Deng X Y, Liu T, Luo Y. 2011. Robustness of least squares support vector regression filtering method with Ricker wavelet kernel[J]. Chinese J. Geophys. (in Chinese), 54(3): 845-853. |
| [7] | Gong H, Lin Y H, Zhou Z L, et al. 2011. De-noising of the metallic ore deposit seismic data based on the theories of wavelet package and support vector machine[J]. Progress in Geophysics (in Chinese), 26(6): 2190-2195. |
| [8] | Gunn S. 1998. Support Vector Machines for Classification and Regression[R]. Technical Report of University of Southampton . |
| [9] | Huang W B. 2009. Research of Magnetic Parameters Effect in the Magnetotelluric Sounding (in Chinese)[D]. Chengdu: Chengdu University of Technology. |
| [10] | Jing J E, Wei W B, Chen H Y, et al. 2012. Magnetotelluric sounding data processing based on generalized S transformation. Chinese J. Geophys. (in Chinese), 55(12): 4015-4022. |
| [11] | Pontil M, Verri A. 1998. Support vector machines for 3D object recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20(6): 637-646. |
| [12] | Tang J T, Xu Z M, Xiao X, et al. 2012a. Effect rules of strong noise on magnetotelluric (MT) sounding in the Luzong ore cluster area[J]. Chinese J. Geophys. (in Chinese), 55(12): 4147-4159. |
| [13] | Tang J T, Li J, Xiao X, et al. 2012b. Mathematical morphology filtering and noise suppression of magnetotelluric sounding data[J]. Chinese J. Geophys. (in Chinese), 55(5): 1784-1793. |
| [14] | Vapnik V N. 1995. The Nature of Statistical Learning Theory[M]. New York: Springer-Verlag, 52-123. |
| [15] | Wang H, Ye G F, Wei W B, et al. 2013. High-precision acquisition technology of telluric field on magnetotellurics[J]. Progress in Geophysics. (in Chinese), 28(3): 1199-1207. |
| [16] | Xu F, Xu W Y. 2010. Prediction of displacement time series based on support vector machines-Markov chain[J]. Rock and Soil Mechanics (in Chinese), 31(3): 944-948. |
| [17] | Yan G H, Zhu Y S. 2009. Parameters selection method for support vector machine regression[J]. Computer Engineering (in Chinese), 35(13): 218-220. |
| [18] | Yang D Q, Hu X Y. 2007-10-01. Magnetotelluric data denoising based on probability analysis (in Chinese)[C]. 8th China International Geo-electromagnetic Workshop Essays. |
| [19] | Yang Y F, Wang H Z, Cao J Z. 2001. Using orthogonal polynomials for e-liminating white noise[J]. Oil Geophysical Prospecting (in Chinese), 36(6): 704-706. |
| [20] | Ye G F, Wang H, Guo Z Q, et al. Data acquisition and processing technology of long-period magnetotellurics. Progress in Geophysics. (in Chinese), 28(3): 1219-1226. |
| [21] | Yin Y T, Wei W B, Ye G F, et al. 2012. An improved GB decomposition method based on genetic algorithm[J]. Chinese J. Geophys. (in Chinese), 55(2): 671-682. |
| [22] | Zhang E H, Guan X W, Zhang Y G. 2011. Support vector machine in volcanic reservoir forecast: East slope in Xujiaweizi depression[J]. Chinese J. Geophys. (in Chinese), 54(2): 428-432. |
| [23] | Zhang F, Wei W B, Jin S, et al. 2012. Ocean coast effect on land-side magnetotelluric data in the vicinity of the coast[J]. Chinese J. Geophys. (in Chinese), 55(12): 4023-4035. |
| [24] | Zhang J, Li H Q, Guo H F, et al. 2009. Abnormal amplitude checking method of log data based on SVM[J]. Progress in Geophysics (in Chinese), 24(6): 2181-2185. |
| [25] | Zhang Q S, Yang S. 2002. An application study of noise elimination for magnetotelluric sounding data[J]. Geophysical Prospecting for Petroleum (in Chinese), 41(4): 493-499. |
| [26] | 边肇祺, 张学工等. 1998. 模式识别[M]. 北京: 清华大学出版社. |
| [27] | 邴萍萍, 曹思远, 路交通. 2012. 基于支持向量机的非线性AVO反演[J]. 地球物理学报, 55(3): 1025-1032. |
| [28] | 陈果, 周伽. 2008. 小样本数据的支持向量机回归模型参数及预测区间研究[J]. 计量学报, 29(1): 92-96. |
| [29] | 陈秋南. 2005. 非对称连拱隧道动态施工力学模拟研究[D]. 重庆: 重庆大学 . |
| [30] | 邓小英, 李月. 2007. Ricker子波核最小二乘支持向量机在地震勘探信号去噪应用中的参数设置研究[J]. 地球物理学进展, 22(3): 953-959. |
| [31] | 邓小英, 刘涛, 罗勇. 2011. Ricker子波核最小二乘支持向量回归滤波方法的稳健性研究[J]. 地球物理学报, 54(3): 845-853. |
| [32] | 龚灏, 蔺远洪, 周仲礼等. 2011. 基于支持向量机和小波包的金属矿床地震数据去噪[J]. 地球物理学进展, 26(6): 2190-2195. |
| [33] | 黄文彬. 2009. 大地电磁测深中磁参数的影响研究[D]. 成都: 成都理工大学 . |
| [34] | 景建恩, 魏文博, 陈海燕等. 2012. 基于广义S变换的大地电磁测深数据处理[J]. 地球物理学报, 55(12): 4015-4022. |
| [35] | 汤井田, 徐志敏, 肖晓等. 2012a. 庐枞矿集区大地电磁测深强噪声的影响规律[J]. 地球物理学报, 55(12): 4147-4159. |
| [36] | 汤井田, 李晋, 肖晓等. 2012b. 数学形态滤波与大地电磁噪声压制[J]. 地球物理学报, 55(5): 1784-1793. |
| [37] | 王辉, 叶高峰, 魏文博等. 2013. 大地电磁测深中大地电场的高精度采集技术[J]. 地球物理学进展, 28(3): 1199-1207. |
| [38] | 徐飞, 徐卫亚. 2010. 基于支持向量机-马尔可夫链的位移时序预测[J]. 岩土力学, 31(3): 944-948. |
| [39] | 闫国华, 朱永生. 2009. 支持向量机回归的参数选择方法[J]. 计算机工程, 35(13): 218-220. |
| [40] | 杨迪琨, 胡祥云. 2007-10-01. 基于概率分析的大地电磁数据去噪方法[C]. 第8届中国国际地球电磁学讨论会论文集. |
| [41] | 杨云飞, 王华忠, 曹景忠. 2001. 正交多项式逼近去白噪[J]. 石油地球物理勘探, 36(6): 704-706. |
| [42] | 叶高峰, 王辉, 郭泽秋等. 2013. 长周期大地电磁测深数据采集及处理技术[J]. 地球物理学进展, 28(3): 1219-1226. |
| [43] | 尹曜田, 魏文博, 叶高峰等. 2012. 基于遗传算法的大地电磁阻抗张量分解方法研究[J]. 地球物理学报, 55(2): 671-682. |
| [44] | 张尔华, 关晓巍, 张元高. 2011. 支持向量机模型在火山岩储层预测中的应用——以徐家围子断陷徐东斜坡带为例[J]. 地球物理学报, 54(2): 428-432. |
| [45] | 张帆, 魏文博, 金胜等. 2012. 海岸效应对近海地区大地电磁测深数据畸变作用研究[J]. 地球物理学报, 55(12): 4023-4035. |
| [46] | 张军, 李洪奇, 郭海峰等. 2009. 基于支持向量机的测井资料幅度异常验收方法研究[J]. 地球物理学进展, 24(6): 2181-2185. |
| [47] | 张全胜, 杨生. 2002. 大地电磁测深资料去噪方法应用研究[J]. 石油物探, 41(4): 493-499. |
 2014, Vol. 29
2014, Vol. 29

