2. 吉林省冶金研究院, 长春 130012
2. Metallurgical Research Institute of Jilin Province, Changchun 130012, China
电磁波在大气层传播过程中,其速度和方向将发生变化,由此引起大气折射效应.针对不同测量技术,大气折射主要有测角、测距和测速三个研究方向.目前,大气折射理论研究不仅具有提高归算精度的作用,而且在地球内部物理结构和动力学变化、航空和航天定位、现代高新武器的精确制导,甚至包括地球表面运动、大气和海洋变化的监测等科学研究、国民经济和国防建设上均具有重要现实意义(严豪健,2006).在推导天文大气折射时,一般假设大气是球对称分布的球壳层模型,由此利用球面斯涅耳定律(普遍情况下的折射反射定律)来推导天文大气折射的原理性公式(冒蔚,2004).在精度要求不高和小天顶距观测的情况下,可假设大气是平面平行层模型.依据平面平行层大气模型导出的天文大气折射公式和1976美国标准大气模型资料(中国大百科全书出版社大气科学卷,1987),可知在距离地球表面高度72 km以上的大气对天文大气折射角的贡献约为3.0毫角秒.Saastamoinen(1972a,b;1973)把测角和测距的大气折射效应以视天顶距为引数进行级数展开,其成果得到了广泛采用.Marini(1972)首次把测距效应变为了连分式形式,并在其后的空间测地技术中得到了普遍推广.黄捷(1999)给出了测距和测速技术的大气折射原理性公式,并研究了大气折射指数理论公式的非全球适应性.冒蔚等(2009)研究了建立适合本地大气折射模型的必要性,给出了一种能直接测定蒙气差的有效方法,并建立了适应于本地随方位和光谱型而异的模型.张捍卫等(2010a,b)给出了映射函数形式的天文大气折射理论公式,以及适用于当代的光学和近红外波段的大气群折射率差理论公式.
本文在以上研究工作的基础上,重新研究了不同观测目标和测量技术的大气折射效应.指出天文大气折射角就是射线弯曲角,它与假设大气是球对称的壳层模型,采用普遍折射和反射定律推导的结果是等价的.同时,在不依赖于任何大气模型的情况下,给出了适合于测角、测距和测速的大气折射原理性公式.1 测角技术的大气折射原理性公式
如图 1所示,设目标P处有一光源.由于大气折射,此光源发出的光线只有沿着直线Ⅰ方向传播时,才能沿着射线路径Rg到达测站A1点,射线在A1点处的切线方向是直线Ⅳ,直线Ⅳ称为目标视方向.假设不存在大气,则测站A1点接收到的是沿着直线Ⅱ方向传播的光线,直线Ⅱ称为目标真方向.直线Ⅲ是目标P点的地心向径,直线Ⅴ是测站A1点的地心向径.在A1点处,直线Ⅰ与直线Ⅴ的夹角是![]() ,直线Ⅳ与直线Ⅴ、直线Ⅰ的夹角分别是z1、τP;直线Ⅱ与直线Ⅴ、直线Ⅰ夹角分别是ξP、θP,直线Ⅱ和直线Ⅳ的夹角是εy .显然有以下关系
,直线Ⅳ与直线Ⅴ、直线Ⅰ的夹角分别是z1、τP;直线Ⅱ与直线Ⅴ、直线Ⅰ夹角分别是ξP、θP,直线Ⅱ和直线Ⅳ的夹角是εy .显然有以下关系

式中,ξP称为目标P的“真天顶距”.εy 称为仰角误差.设目标P处于大气层边缘,并有一平面电磁波入射于P点处,其传播方向用直线Ⅰ表示,入射角是zP(直线Ⅲ与直线Ⅰ的夹角),经过大气折射沿着射线路径Rg到达测站A1点,此时
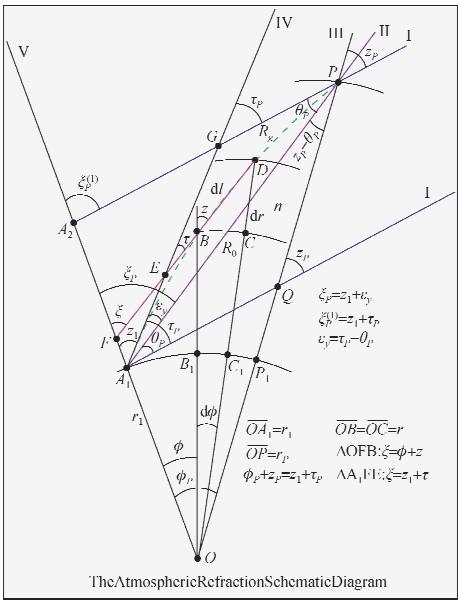 | 图 1 大气折射示意图 Fig. 1 Schematic diagram of the atmospheric refraction |
在射线路径上任意点B处,电磁波的入射角是z;在点B处射线的切线方向与视方向的夹角称为射线弯曲角τ;点B与测站A1点对地心的张角是.对于P点来说,入射角是zP,射线弯曲角是τP,对地心的张角是P.显然有
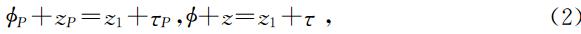
因此,在这条射线路径上,以上参数满足如下微分关系

另外,在无限小的平面直角三角形ΔBCD中可看出
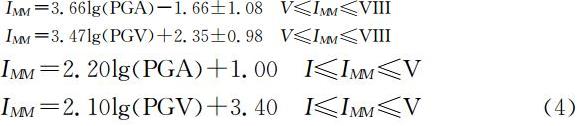
同时布格公式为(严豪健,2006)
nrsinz=n1r1sinz1,
式中,n和r分别为射线路径上某点的电磁波位相折射指数和地心距,带下标1的表示测站A1点对应的参数.对布格公式求微分,并利用

上式从测站A1沿着射线路径Rg积分到P点,就是P点处的射线弯曲角τP,它就是测站与目标两处射线的切线之交角.由此得
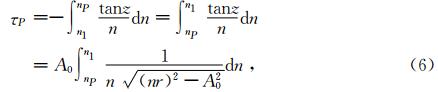
式中,A0=n1r1sinz1.如果nP=1,则τP就称为天文大气折射角. 1.2 地心张角和水平距离
根据rd=drtanz,可得目标点和测站点对地心的张角为
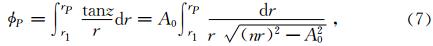
水平距离则是
仰角误差εy 为在测站A1处目标P的真方向与视方向之差,即
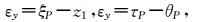
求解仰角误差εy有两种方法.第一种方法求ξP,由图 1的ΔOA1 P中的正弦定理可知
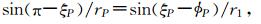
于是有

由此解得ξP,进而求出仰角误差εy=ξP-z1.
第二种方法求θP,由平面三角形ΔOA1P中的正弦定理
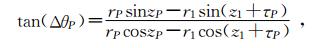
利用布格公式nPrPsinzP=n1r1sinz1后,就有
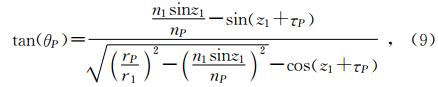
由此解得θP,进而求出仰角误差εy=τP-θP.2 测距技术的大气折射原理性公式
以无线电观测为基础的雷达测距、人卫多普勒测量、甚长基线干涉测量、全球定位系统和以激光观测为基础的月球激光测距和人卫激光测距等空间大地测量学技术,不仅涉及电磁波传播方向的改变,还涉及传播路径和传播时间的延长. 2.1 视在距离
视在距离Re等于电磁波沿着射线路径Rg的单程传播时间t与真空中的光速c之积,即
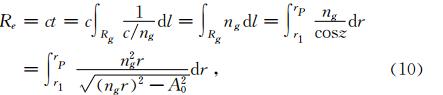
式中,ng为群折射指数.
2.2 距离误差
距离误差ΔL定义为视在距离与几何距离之差

3 测速技术的大气折射原理性公式
在空间大地测量学技术中,有时需要知道由大气折射引起的目标速度误差,也就是视在距离变化率与真实距离变化率的关系.对式(9)式和(6)分别求时间导数,由于与时间有关的参数仅为上限rP及射线视方向(含在A0中),故其导数为
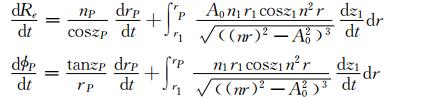
注意到nPrPsinzP=n1r1sinz1=A0,则有

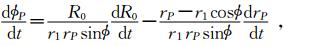
从图 1中可看出
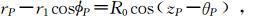
把上式代入到前一式中,就有
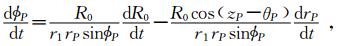
另外,根据ΔOA1P中的正弦定理

可得到:
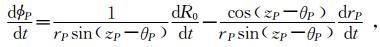
把上式代入到(11)式,由于A0=nPrPsinzP,则有
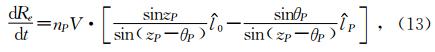
式中,已考虑到

可证明
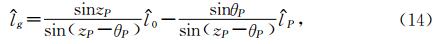
这样(12)式可表示为

那么

就是由大气折射引起的速度误差.
设信号源发出的频率为f0,信号源在不同时刻发出的电磁波到达地面接收机时,接收机接收到的频率fr是(黄捷,1999):

可见,上式与真空中的关系式是一样的,只是将原来的dR0/dt变成了dRe/dt.上式就是视在距离变化率与视在多普勒频移的关系式.
4 小 结
本文在推导不同测量技术中的大气折射原理性公式时,完全没有采用普遍情况下的折射和反射定律,也没有对大气分布模型做任何要求.基于一个原理图,给出了适合于测角、测距和测速的大气折射原理性公式.
在(5)式中,如果nP=1,则τP就称为经典天体测量中的天文大气折射角(无穷远观测目标的真天顶距与视天顶距之差).由于大气折射指数与气体质量密度成正比,距离地面高度72 km处的大气密度约为地面的10-5倍,因此求解天文大气折射角时,只需考虑对流层、平流层和部分中层就可以了.实际上,仰角误差εy=τP-θP就是人造地球卫星目视观测中的大气折射修正角,其中利用(8)式求θP,此时可令nP=1,τP就是天文大气折射角.
根据(9)和(10)式可知
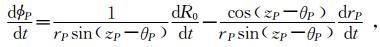
式中,dX是A1点和P点之间几何直线R0的线元.ΔL1称为大气折射延迟主项,δL称为大气折射路径弯曲改正.
| [1] | Huang jie.The radio-wave refractive error correct[M]. Beijing: National defense industry press, 1999 (in Chinese). |
| [2] | Mao wei, tie qiong-xian yang lei. Astronomical refraction and building a local obervational model[J], Acta Astronomica Sinica, 2009, 50(2):180-188 (in Chinese) . |
| [3] | Mao Wei, TIE Qiong-xian YANG Lei. The astronomical atmospheric refraction[M], Kunming: Yunnan science and technology press, 2004 (in Chinese). |
| [4] | Marini J W. Correction of Satellite tracking data for an arbitrary troposphere profile[J]. Radio Science, 1972, 7(2): 223-231. |
| [5] | Saastamoinen J. Contributions to the Theory of Atmospheric Refraction, part I, Astronomical refraction[J]. Bulletin Géodésique, 1972a, 105: 279-299. |
| [6] | Saastamoinen J. Contributions to the Theory of Atmospheric Refraction, part II, Refraction Corrections in Satellite geodesy[J]. Bulletin Géodésique, 1973, 107:13-34. |
| [7] | Saastamoinen J. Introduction to Practical Computation of Astronomical Refraction[J]. Bulletin Géodésique, 1972b, 106:383-397. |
| [8] | The Editorial committee of Encyclopedia Sinica. Encyclopedia Sinica-Atmospheric Sciences[M]. Beijing: Encyclopedia Sinica press, 1987 (in Chinese). |
| [9] | Yan Hao-jian, FU Yang, HONG Zhen-jie. The introduction of modern atmospheric refraction[M], Shanghai science and technology education press, 2006. (in Chinese) |
| [10] | Zhang Han-wei, LI Ai-guo, GUO Zeng-zhang. Astronomical refraction theoretical formula in mapping function form[J]. Progress in Geophysics, 2010, 25(4): 1240-1246 (in Chinese). |
| [11] | Zhang Han-wei, LI Ai-guo, WANG Qing-lin. Theoretical formula of atmospheric group refractivity at optical and near-infrared wavelengths[J]. Progress in Geophysics, 2010, 25(1): 179-185. (in Chinese) |
| [12] | 黄捷. 电波大气折射误差修正[M]. 北京: 国防工业出版社, 1999. |
| [13] | 冒蔚, 铁琼仙, 杨磊. 天文大气折射[M]. 昆明: 云南科技出版社, 2004. |
| [14] | 冒蔚, 杨磊, 铁琼仙.测定瞬时天文大气折射值和建立本地实测模型[J]. 天文学报, 2009, 50(2):180-188. |
| [15] | 严豪健, 符养, 洪振杰. 现代大气折射引论[M], 上海: 上海科技教育出版社, 2006. |
| [16] | 张捍卫, 李爱国, 郭增长.映射函数形式的天文大气折射理论公式[J]. 地球物理学进展, 2010a, 25(4): 1240-1246. |
| [17] | 张捍卫, 李爱国, 王庆林. 光学和近红外波段的大气群折射率差理论公式[J]. 地球物理学进展, 2010b, 25(1): 179-185. |
| [18] | 中国大百科全书编辑委员会.中国大百科全书-大气科学卷[M]. 北京:中国大百科全书出版社.1987. |
 2014, Vol. 29
2014, Vol. 29

