近些年来，GPS在经典的大地测量(殷海涛等，2009；姜卫平等，2012；廖华等，2013)、地球动力学(熊熊等，2004；张培震等，2004；朱守彪和蔡永恩，2006；陈祖安等，2009；陈光齐等，2013)、地球形变监测(王琪等，2002；江在森等，2003；黄立人等，2003；姚宜斌，2008；薄万举，2013)以及大气电离层活动监测(温晋等，2010；李强等，2012)等科学实验中，均发挥了举足轻重的作用.GPS定位的基本原理是：观测站的GPS接收机同时接收到4颗以上GPS卫星发出的信号，根据电磁波在空间传播的时间测得各卫星至GPS接收机的距离，当卫星的空间位置是已知的情况下，就可以确定GPS接收机的空间位置(中国地震局监测预报司，2003；李征航和黄劲松，2005).于是精确获取GPS卫星轨道坐标是GPS定位首要解决的问题.

获取GPS卫星轨道坐标的途径有两种(李征航和黄劲松，2005；邱蕾等，2008)：一种是根据广播星历计算出星历参数，进而求出卫星的空间坐标，另一种是根据精密星历直接插值得到卫星的轨道坐标.广播星历每两小时更新一次，实时发送给用户，精度仅为2 m；而事后精密星历由IGS组织发布(International GNSS Service)，有12～18天的延迟，精度可达2.5 cm，被广泛应用于事后高精度定位.

IGS提供SP3(St and ard Product 3)格式的精密星历文件，包含文件头和数据记录两个部分.数据记录部分每15分钟更新一次卫星的空间位置坐标(精确到mm)和钟差(精确到ps)，有时还提供卫星的瞬时速度等物理量(李征航和黄劲松，2005；Spofford et al., 2008).然而15分钟的时间间隔难以满足实时监测的需求，需进行插值才能得到所需历元的卫星的轨道坐标.为满足实时监测的需要，特别是GPS高频GPS技术进行强震地面活动的监测技术的兴起(Chen，1998)，GPS接收机也正朝着高采样率的方向发展，Trimble公司的NetR8(Trimble Navigation Limited，2008)、NetR9(Trimble Navigation Limited，2010)等接收机目前已支持50 Hz的超高频采样率.对于高频采样，由于数据量巨大，快速而准确地对精密星历进行插值就成为高频GPS数据处理的一项重要工作.

常用的插值算法有拉格朗日多项式插值(Lagrange Polynomial Interpolation)(王世儒等，1996；徐萃薇和孙绳武，2002；William et al., 2007)、牛顿多项式插值(Newton Polynomial Interpolation)(王世儒等，1996；徐萃薇和孙绳武，2002)、内维尔逐次线性插值(Neville Successive Linear Interpolation)(William et al., 2007)以及三角函数插值(Trigonometric Function Interpolation)(张守建等，2007)等.选用何种插值方法、选用几次多项式对GPS卫星的空间坐标进行插值，使得插值的精度最高，许多学者均对此做了研究：邱蕾(2008)认为当插值点位于节点中央时，9阶以上拉格朗日插值以及内维尔插值可获得与精密星历相当的精度，同时多项式的次数最好为奇数，待插值的时刻位于节点的中间，插值的误差也最小；张守建(2007)认为10阶拉格朗日多项式内插精度最高，11阶的三角函数多项式插值内插精度最好；马俊(2011)认为拉格朗日、牛顿以及内维尔插值在16阶精度最高；何玉晶(2011)认为9阶拉格朗日插值的精度最高.

虽说众学者的看法不尽相同，但均认为在进行多项式插值时，适当提高多项式的次数，可以提高插值的精度，但在插值节点两端附近高次多项式插值，容易产生龙格(Runge)现象(王世儒等，1996；徐萃薇和孙绳武，2002)，特别是拉格朗日多项式插值，会影响插值的精度，故盲目地提高插值多项式的次数是不可取的.

本文简要介绍四种常用插值算法的基本原理，分别对不同阶次多项式的精度、各插值算法的理论运算量以及实际运行时间进行详细的科学分析和总结，为实际应用中选用何种插值算法提供依据.

1 插值算法的数学模型

下面讨论当已知t₀，t₁，…，t_n时刻卫星三维坐标(x₀，y₀，z₀)，(x₁，y₁，z₁)，…，(x_n，y_n，z_n)的情况下(精密星历提供)，求出插值区间内任意历元卫星轨道的三维空间坐标.对于某些特殊领域还可能要对卫星钟差、卫星速度等物理量进行插值.不失一般性，现假定要对N种物理量(记为w)m个历元进行插值.

CPU进行乘/除法的时间远超过加/减法，所以通常估计算法的运算量往往只估计乘/除法运算量.

1.1 拉格朗日多项式插值

拉格朗日多项式插值的表达式为

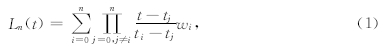
拉格朗日多项式插值模型简单，是经典的插值算法.但当精度不够而需要增加新的插值节点时，原来的插值多项式，包括连续乘积项都不能使用，必须重新构造一个插值多项式.

1.2 牛顿多项式插值

定义w_[t0，t1]= w_(t1)－w_(t0) t₁－t₀ 为函数w(t)在t₀，t₁两点的一阶差商；w_{[t0，t1，…，tn]}= w_{[t1，t2，…，tn]}－w_{[t0，t1，…，tn－1}] t_n－t₀ 为函数w(t)在t₀，t₁，…，t_nn+1个点的n阶差商.根据差商的定义可列出差商表，如表 1所示，表中共有n(n+1)/2个差商，各差商项中均不显含历元时间t，当进行m个历元插值时，各物理量的差商表只要计算一次.

表 1(Table 1)

表 1 牛顿差商表 Table 1 Table of Newton divided difference 时间 坐标 一阶差商 二阶差商 … n阶差商 t0 w(t0) t1 w(t1) w[t0，t1] t2 w(t2) w[t1，t2] w[t0，t1，t2] … … … … … … tn w(tn) w[tn－1，tn] w[tn－2，tn－1，tn] … w[t0，t1，…，tn]

表 1 牛顿差商表 Table 1 Table of Newton divided difference

根据(2)式，易得牛顿插值多项式的递推关系为

1.3 内维尔逐次线性插值

内维尔插值是一种由两个n-1次插值多项式构造一个n次多项式的线性逐次插值方法.

令0阶插值结果为w_i，0=y(t_i)，下一阶插值结果通过上一阶线性插值得到的，第j阶的插值公式为

在实际应用中，当第j阶插值结果w_j，j与第j-1阶插值结果w_j-1，j-1小于限差时，即可终止插值.显然，增加新的插值节点，原先计算得到的插值多项式仍然有用，只要在表中添加一行，计算出w_n+1，1，w_n+1，2，…，w_n+1，n+1即可，这一点与牛顿插值颇似.

表 2(Table 2)

表 2 地应力预测地震实例 Table 2 Examples of earthquake prediction based on field stress measurement 时间 坐标 一阶多项式 二阶多项式 … n阶多项式 t0 w0，0=y(t0) w1，1 t1 w1，0=y(t1) w2，2 w2，1 … wn，n t2 w2，0=y(t2) … … … … tn wn，0=y(tn)

表 2 地应力预测地震实例 Table 2 Examples of earthquake prediction based on field stress measurement

对于n次多项式，有

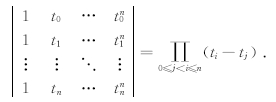
当t_i互异时，该行列式的值非零，线性方程组的根存在且惟一(事实上精密星历每15分种提供一组数据，(6)式定有惟一解).通过高斯消去法，求出各物理量的多项式系数，再代入(5)式可求出插值区间内任意历元卫星轨道的三维空间坐标.

高斯消去法通过对线性方程组的系数矩阵进行初等行变换，先将系数矩阵逐步化为上三角矩阵(消元过程)，最后再获得方程组的解(回代过程).消元过程要进行n³/3+(1+N/2)n²+(2/3+N/2)n次乘/除法运算；回代过程要进行Nn²/2+3Nn/2+N次乘/除法运算.于是高斯消去法乘/除法运算的总次数为n³/3+(1+N)n²+(2/3+2N)n+N.

对于(5)式的n次多项式求值的最优算法莫过于秦九韶算法，仅需n次乘法和n次加法即可.

综上多项式系数求解法对N种物理量m个历元进行插值需要n³/3+(1+N)n²+(2/3+2N)n+N+mNn 次乘/除法运算.

2 插值算法的比较 2.1 不同阶次多项式插值精度的比较

考虑到GPS卫星运行轨道的周期性，选用下列函数作为理论曲线进行比较：

y(t)= b₀+b₁sin(ωt)+b₂cos(ωt)+…+b_p－1sin(pωt/2)+b_pcos(pωt/2)，(7)

表 3(Table 3)

表 3 各种插值算法的标准偏差 Table 3 The st and ard deviation of the interpolation algorithms 阶数 标准偏差(10-8) 拉格朗日插值 牛顿插值 内维尔插值 多项式系数求解 9 0.7977 0.7977 0.7976 0.7977 11 0.0025 0.0023 0.0022 0.0022 13 0.0048 0.0013 0.0013 0.0011 15 0.0130 0.0048 0.0048 0.0048 17 0.0406 0.0190 0.0195 0.0202

表 3 各种插值算法的标准偏差 Table 3 The st and ard deviation of the interpolation algorithms

(1)四种插值算法9阶的插值精度均不理想；

(2)四种插值算法中拉格朗日插值的精度最差，其它三种插值算法精度相差不大；

(3)除了拉格朗日多项式插值外，其它三种插值算法在13阶时插值精度最高.

图 1给出各插值算法在9阶(左)与13阶(右)的绝对误差分布.在9阶多项式插值中，各算法绝对误差分布完全重合、且误差较大；而在13阶多项式插值中，虽然拉格朗日多项式在插值区间两端附近仍然存在明显的龙格现象，但在插值区间的中央区域四种插值算法的绝对误差均很小.也就是说，当待插值的历元位于插值节点中央时，无论采用哪种算法进行插值，都能取得较满意的结果.

2.2 理论运算量的比较

表 4列出四种插值算法对N种物理量m个历元进行插值的浮点乘/除法理论运算量.

表 4(Table 4)

表 4 各插值算法理论运算量的比较 Table 4 Comparison of computation of interpolation algorithms 插值算法 N维m个历元插值乘/除法运算量 拉格朗日多项式插值 m[2n2+(N+2)n+N] 牛顿多项式插值 Nn2/2+(Nm+m+N/2)n 内维尔逐次线性插值 3Nmn2/2+3Nmn/2 多项式系数求解法 n3/3+(1+N)n2+(2/3+2N)n+N+mNn

表 4 各插值算法理论运算量的比较 Table 4 Comparison of computation of interpolation algorithms

首先考察维数N对算法运算量的影响，由于拉格朗日插值重复利用了连续乘积项，增长因子仅为n，而其它算法均为n².其次考察历元数m的影响：牛顿插值、多项式系数求解法的增长因子仅为n，主要是因为牛顿插值对差商项的重复利用，而多项式系数求解法对多项式求值使用了秦九韶算法.

图 1

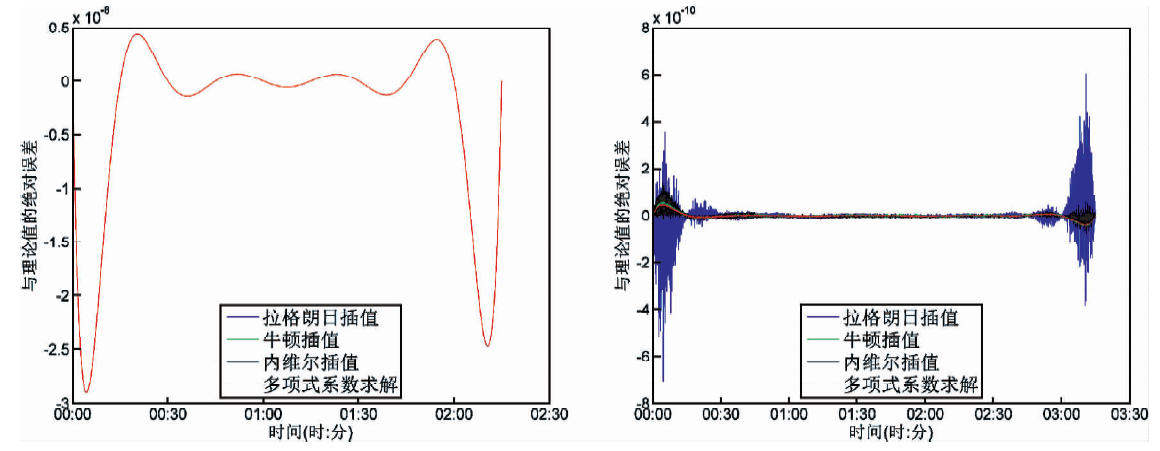图 1 各插值算法的计算值与理论值之间的绝对误差分布 Fig. 1 Distribution of absolute tolerance between interpolation algorithms calculated value and theoretical value

图 2给出各种算法在13阶的理论运算量.图中不带圈的曲线代表N=1的理论运算量；带圈的曲线为N=3的理论运算量.显然，拉格朗日插值对N极不敏感.拉格朗日和内维尔插值的运算量比另外两种算法要高出一个量级.而牛顿插值与多项式系数求解算法在m=90(历元间隔10秒)附近出现一个交替，当m<90时，牛顿插值的运算量是最少的.

图 2

图 2 各种插值算法在13阶的理论运算量 Fig. 2 Distribution of computation of 13-order interpolation algorithms

若不考虑插值精度等因素的影响，仅考虑算法的运算量，当需要插值的物理量很多时，应优先选择拉格朗日插值；当插值的历元数很多时，应优先选择牛顿插值或多项式系数求解法.

2.3 实际卫星空间坐标计算结果的比较

从IGS网站(ftp://garner.ucsd.edu)下载2013年2月14日卫星轨道数据igs17274.sp3精密星历(延迟至2013年3月1日公布).卫星号为8的GPS卫星的三维空间轨道坐标如图 3所示.

选用前14个历元(0时至3时15分，图 3左侧阴影区域)作为插值节点，对插值节点的中央区域(1时30分至1时45分，左侧阴影区域内的粗线)进行13阶多项式插值，插值历元的时间间隔为1 s，历元总数为900个.

图 3

图 3 卫星号为8的GPS卫星轨道 Fig. 3 Orbit coordinates of satellite PRN. 8

由于插值时刻卫星轨道的精确坐标是未知的，只能通过比较四种插值算法间的离散程度.图 4给出各插值算法间最大偏差的分布(左中右三幅图分别代表x，y，z坐标最大偏差分布).诚然，四种插值算法间的偏差均很小(最大仅为2.5×10^-11，而精密星历提供的原始数据精度为10^-6)；x坐标拟合效果较差；各算法yz坐标拟合值偏差分布比较均匀.

图 4

图 4 四种插值算法间离散程度 Fig. 4 Distribution of absolute tolerance deviation between interpolation algorithms and average value

当需插值的历元位于插值节点的中央(见图 3)时，无论使用何种算法，计算结果均可取.

2.4 实际运行时间的比较

测试平台为I5 3.1 GHZ的CPU、4 G内存、Win 7操作系统；代码编译环境为MinGW GCC.

分别对不同采样率(从实际应用较广的30 s逐渐增加到超高频的50 Hz)的历元进行插值，表 5和图 5给出这四种不同插值算法的实际运行时间.

图 5

图 5 各插值算法的实际运行时间曲线 Fig. 5 Running time of different interpolation algorithms

表 5(Table 5)

表 5 各插值算法完成不同采样率插值的实际运行时间(ms) Table 5 Running time of different interpolation algorithms for various different sampling rate 采样率 30 S 20 S 10 S 5 S 2 S 1 Hz 2 Hz 5 Hz 10 Hz 20 Hz 50 Hz 插值历元数m 30 45 90 180 450 900 1800 4500 9000 18000 45000 程序重复运行次数 100000 50000 50000 20000 20000 10000 10000 5000 2000 1000 500 拉格朗日插值 0.0624 0.0955 0.1878 0.3760 0.9407 1.8830 3.7643 9.4224 18.8290 37.6740 94.1000 牛顿插值 0.0087 0.0134 0.0243 0.0453 0.1108 0.2199 0.4352 1.0888 2.1685 4.3360 10.8880 内维尔插值 0.0754 0.1129 0.2253 0.4493 1.1248 2.2511 4.4990 11.2508 22.4875 45.0060 112.4460 多项式系数求解 0.0144 0.0184 0.0268 0.0445 0.0983 0.1888 0.3682 0.9142 1.8170 3.6350 9.0800

表 5 各插值算法完成不同采样率插值的实际运行时间(ms) Table 5 Running time of different interpolation algorithms for various different sampling rate

据表 5和图 5对GPS卫星轨道的三维空间坐标进行插值，有如下几个特点：

(1)内维尔逐次线性插值算法的运行效率最低，其次是拉格朗日多项式插值；

(2)当插值历元的采样率低于5 s时(15分钟总历元数m=180)，牛顿多项式插值的运行效率最高；而当插值历元的采样率高于5 s时，则是多项式系数求解法占优；

(3)多项式系数求解法、牛顿插值算法的运行时间仅为拉格朗日、内维尔插值的1/10左右.

3 结 论

3.1 当增加插值节点时，拉格朗日插值和多项式系数求解法必须重新计算，而牛顿和内维尔插值却可以利用先前的计算结果.

3.2 当需插值的历元位于插值节点中央时，无论采用哪种算法进行插值，都能取得满意的结果.当需插值的历元位于插值节点区间两端附近时，牛顿多项式插值和多项式系数求解法最为稳定，而拉格朗日插值极易产生龙格现象.

3.3 无论是理论的浮点乘/除法运算量，还是实际的运行时间，多项式系数求解法、牛顿多项式插值算法均比拉格朗日多项式插值、内维尔逐次线性插值少一个数量级.

3.4 至于实际应用中，多项式系数求解法和牛顿多项式插值如何取舍.图 2给出的理论运算次数建议历元间隔低于10 s采用牛顿多项式插值，而图 5给出的实际运行时间则建议历元间隔低于5 s就可以使用牛顿多项式插值.造成二者不协调的主要原因是一方面多项式系数求解法需要构造一个范德蒙德系数矩阵，另一方面在高斯消去法求解线性方程组的消元和回代过程中频繁地对矩阵进行寻址.

致 谢 感谢审稿专家的指导帮助.