2. 中国科学院寒区旱区环境与工程研究所, 兰州 730000
2. Cold and Arid Regions Environment and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000, China
研究表明,全球性地震活动进入活跃期.位于亚洲西南部的伊朗伊斯兰共和国,国土面积约164.6万km2,绝大部分在伊朗高原上,大地构造位置上以印度板块和阿拉伯板块之间的伊朗板块为主.进入20世纪至今(1900-2013年),伊朗地区共发生6.7级以上的地震近三十次,其中6.7~7.0级多于7.0~8.0级,是亚欧地震带上地震活动频繁的地区之一.伊朗人口众多,分布密集,有时震级不是很大的地震都会引起大量的人员伤亡和严重的经济损失.
李均之等(2007)认为可公度信息系作为信息预测方法中的一种,主要用来研究物理体系中的特性.孙宗扬(2009)认为对称性是物理学中的第一原理,并且透过外表来研究本质是对称性方法的威力.Noether(1971)证明对于力学体系的每一个连续的对称变换,都有一个守恒量与之对应.空间平移的对称变换与线性动量的守恒律对应;空间转动的对称变换与角动量守恒对应;时间平移的对称变换与能量守恒定律对应.徐一鸿(2005)认为发现一个对称比发现一个特定的现象意义大的多.而可公度正是时空对称性的一种表现,由此,延军平等(2011)认为看似简单的时空对称性研究或许正揭示了重大自然灾害的时空分布规律.翁文波(1996)将可公度性应用到预测科学中,使其从理论和方法上得到很大发展.它可应用于微观、宏观、宇观中许多自然现象的科学研究.
研究伊朗地区地震活动趋势判断,对于最大限度减少灾害损失,保护人民生命财产安全,对于阿拉伯相对向北运动控制欧亚大陆的板块活动的研究以及对地震趋势判断(Hu H,2005;孙加林和章瑞,2007)和可公度方法的应用研究有重要意义.
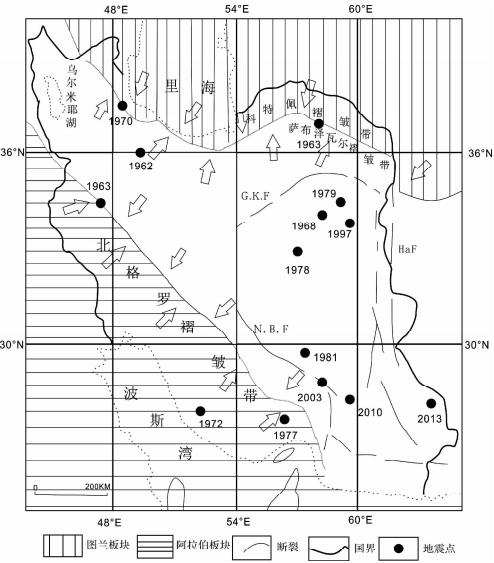 | 图 1 伊朗地区地震研究区域示意图Fig. 1The subduction of earthquake in Iran |
Bertr and和Dortz(2007)认为亚速尔群岛和伊朗之间的阿尔卑斯-亚洲地震带西部地区内存在优势的大地震东向迁移;Berberian(1984)认为发生在最近的过去和负责东部和西倾断层下盘地区共同形成细长的冲积物填充洼地.Walker等(2010)认为Gowk 故障是在伊朗东部区域构造应力住宿的最重要的结构之一,而在过去的30a中,已经产生了五个Gowk故障破坏性地震.没有历史地震记录的这一地区构成了相当大的剩余危险,而2013年的7.8级地震正是发生在东部.原为一体的伊朗微板块与阿拉伯板块发生了分离,导致现今伊朗南部扎格罗山脉以南的波斯湾(Persaingulf)和阿曼湾(Gulf of Oman)及其沿岸地区均陷为阿拉伯板块北缘,形成了伊朗乃至中东地区大量的油田,气田;而脱离阿拉伯板块的伊朗微板块则向北漂移,并与欧亚次大陆的图兰板块发生碰撞,然后拼贴在欧亚次大陆的南缘,形成一条相当于由现今伊朗北部的科佩特山南侧至里海南岸一带的北伊朗缝合带.与此同时,在伊朗东部地区围绕现今的卢特高原形成了卡维尔(G. K. F)、 巴夫特(N. B. F)和哈里河(HaF)3条环形深大断裂(李锦平和吴良士,2008).阿拉伯板块与欧亚大陆板块之间主要碰撞带在阿富汗地壳块贯穿的伊朗微板块之东缘,地震活动主要沿着微板块的边缘.多次地震都是延断层的走向滑移位移所造成的.而阿拉伯板块沉入伊朗板块会造成灾难性地震.图 1为伊朗地震研究区域示意图.
根据《全球地震目录》等相关资料,从1900年至今113a的时间内,伊朗地区发生≥6.7级强震的年份为n=24a,平均每4.7a就会发生一次≥6.7级的破坏性地震.其中前六十年平均6a一次,而1961年至2013年53a中,每3.8a就会发生一次.后半个世纪开始至今强震的震源深度明显减小,较靠近地面,灾害损失更大.就地区分布而言,27次地震中有5次发生在克尔曼,5次发生在呼罗珊,而且1981年至今发生在克尔曼地区≥6.6级地震就有6次,并且伤亡惨重.
| | 表 1 伊朗地区1961年以来≥6.7级强震参数 Table 1 The parameters of MS≥6.7 earthquake in Iran |
可公度性是自然界中的一种秩序(延军平等,2010),也是周期性的扩张(翁文波,1981),揭示了系统中某种因素的可共同量度的秩序体系,从数据中的可公度性可抽提出并非偶然的信号,通过利用周期性演变过程中存在的这一离差信息进行分析应用.重大自然灾害绝不是一个孤立事件,应该是一个有时空联系的灾害事件群(李双双等,2013).根据可公度性(徐道一等,2007;延军平等,2011)的信息理论,可建立三元~五元可公度性公式进行伊朗地区强震趋势判断. 2.1 三元可公度趋势判断
对伊朗地区≥6.7级强震的14个数据进行统计分析,公式为
Xy=Xi+Xj-Xp,i,j,p,y为指标,i,j,p∈[1,14],y为要判断的第15个年份,即y=15,且同时满足y=i+j-p.
设:X1=1961;X2=1962;X3=1963;X4=1968;X5=1972;X6=1977;X7=1978;X8=1979;X9=1981;X10=1990;X11=1997;X12=2003;X13=2010;X14=2013;求:X15=?
满足上式的最近高频年份结果为2014年和2016年,都有4次,具体算法为
| X2+X14-X1=X15=2014; X4+X13-X2=X15=2016; X3+X14-X2=X15=2014 ; X7+X13-X5=X15=2016; X7+X14-X6=X15=2014 ; X11+X11-X7=X15=2016; X8+X14-X7=X15=2014 ; X14+X14-X13=X15=2016. |
还是对该数据,Xy=Xi+Xj-Xp-Xq,i,j,p,q,y为指标,i,j,p,q∈[1,14],y为要判断的第15个年份.其中,y =i+j-p-q,与三元算法相对应,满足上式的最近频率较高的年份是2016年19次,具有可公度性即未来有可能发生强震的年份是2016年.
具体算法为
| X1+X5-X2-X4=X15=2016 X1+X7-X4-X4=X15=2016 X2+X5-X3-X4=X15=2016 X2+X6-X4-X4=X15=2016 X4+X6-X1-X9=X15=2016 X4+X7-X2-X9=X15=2016 X4+X8-X3-X9=X15=2016 X4+X11-X5-X10=X15=2016 X4+X13-X5-X12=X15=2016 X5+X5-X2-X8=X15=2016 X5+X5-X3-X7=X15=2016 X5+X6-X4-X7=X15=2016 X5+X7-X4-X8=X15=2016 X6+X8-X5-X9=X15=2016 X7+X7-X5-X9=X15=2016 X10+X11-X9-X12=X15=2016 X11+X11-X9-X13=X15=2016 X12+X12-X10-X14=X15=2016 X12+X13-X11-X14=X15=2016 |
同样,对伊朗地区≥6.7级强震进行五元可公度法计算出信号较强的为2015年137次和2016年123次,依然具有很强的可公度性. 2.4 时间序列图的分析 2.4.1 蝴蝶结构图
重大自然灾害一经发生,极易借助地球各圈层之间相互依存制约的关系,产生连锁效应,由一种灾害引发出一系列灾害(郭增建,2007).自然灾害的时间对称性构造出的蝴蝶结构是一种周期共振的表现,从周期上可以理解为是长时间作用力累加而形成的交变应力,从时间上可以看做是一种过去地震释放的能量对将来产生的蝴蝶效应,形状类似蝴蝶双翼,故名蝴蝶结构图.图 3是伊朗地区的蝴蝶结构图,共包括14个年份,四套周期的时间序列组合,用曲线连接年份并表明周期,反映出所选年份等时间间隔的特点以及周期平移后不变的时空对称性.由图 3可以看出,该地区强地震发生的时间间隔有一定规律性,以1年、3年、6年、9年、13年和26 年最为显著,并且可套合到2016年的周期有3年、6年、13年和26年,从而进一步说明该地区在2016年可能发生强震.
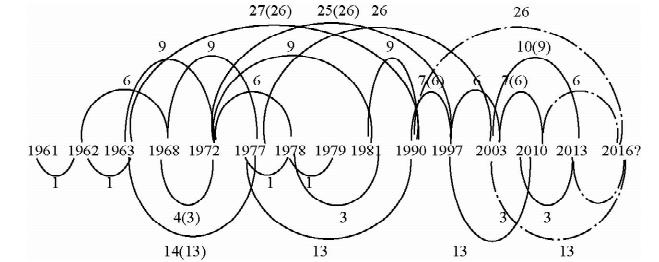 | 图 3 伊朗地区≥6.7级强震时间序列蝴蝶结构图 Fig. 3 The butterfly structure diagram MS≥6.7 earthquake in Iran |
如果将伊朗地区≥6.7级强震的年份作为一组数列,那么在其中我们可以找出几组具有相同公差的子数列,例如“1963、1972、1981、1990”、“1968、1977”、“2003、2013”、“1977、1990”、“1997、2010”等(部分年份的误差在正负一年以内).如图 4所示,可公度结构系也是验证 可公度法的有效途径之一,它能清楚地展现各个灾害发生年之间的相互关系,由此我们可以根据上述计算得出的统计规律,对今后可能发生的地震年份进行推测,可以看出2016年有强烈的地震灾害信号.
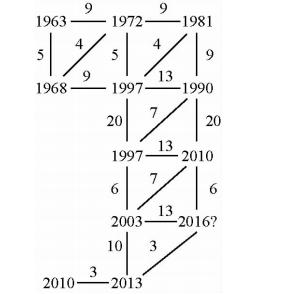 | 图 4 伊朗地区≥6.7级强震时间序列可公度结构系 Fig. 4 The commensurability structure system MS≥6.7 earthquake in Iran |
伊朗地区几年来强震震源多发生在地下12 km处,基本处于同一震源深度,在地下具有平衡的对称性.图 5为1961年至今强震震中纬向、经向迁移图.从图中可以看出,纬向有南北较对称分布,而经向有从西到东的明显迁移;并且纬向震中的迁移与经向震中的迁移有共同的突变性.震中处于该区域中心位置的情况下,当强震震中向北迁移时,经向震中向东迁移;当强震发生在该地区边境的情况下,当强震震中向南迁移时,经向震中向东迁移.
从伊朗地区强震震中的迁移来看,其纬向对称轴在31°N左右,经向对称轴在54°E左右.假设伊朗地区强震空间分布有良好的对称性,那么下次区域强震很有可能向西北方向迁移,在北纬34°N左右,落在伊朗东北部.
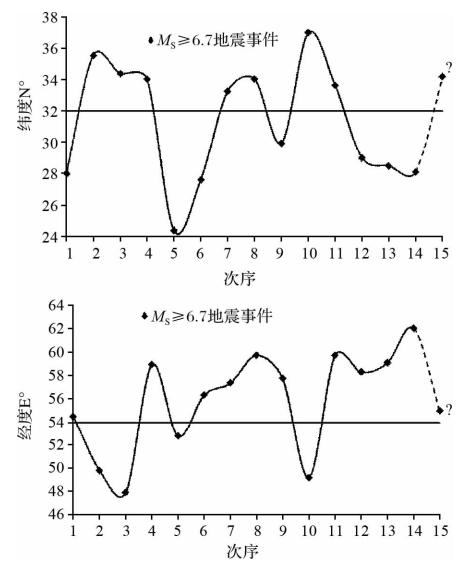 | 图 5 伊朗地区MS≥6.7强震纬向、经向迁移 Fig. 5 The MS≥6.7 earthquake f longitudinal and latitudinal migration in Iran |
很多专家学者研究表明(秦四清,2010),太阳黑子活动周期与地球环境有着某种联系,在此根据太阳黑子平均11年的周期活动,将伊朗地区发生强震事件所对应的年份绘制于太阳黑子活动事件图中(图 2),图中深色线段部分为太阳黑子活动的单周年,浅色线段部分为双周年.分析可得该地区强震活动的活跃期与太阳黑子活动的11年周期有对应关系.我们首先可以看出,太阳黑子数较多的周期,地震事件也发生得多;其次,在1965年之前,单周年为强震的平静期,双周年为强震的活跃期;而在1966-1976这个单周年周期突变为活跃期并且为近一百年来伊朗地区强震最活跃的时期,随后的双周年则表现出进入平静期,单周年为活跃期,完成一次转换;我们还可以发现,在这十个周期中,有7次峰值年份或者附近年份位置都出现了强震,并且强震易发生在地震活跃期及其相对应的太阳黑子活动周期的衰退阶段.而判断出的伊朗地区未来发生强震信号最强的年份2016年正是新的周期峰值附近,更进一步增强了趋势判断的可能性.
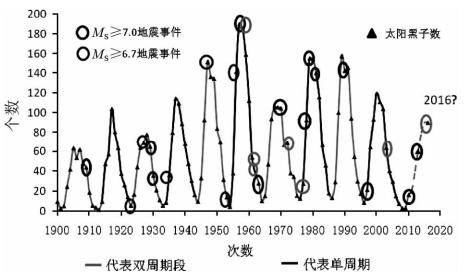 | 图 2 太阳黑子活动与伊朗地区强震时序分布 Fig. 2 Sunspot activity and earthquake sequence’s regional distribution in Iran |
5.1 强震事件后半个世纪比前半个世纪明显增多,强震的震源深度明显减小,较靠近地面,灾害损失更大.目前该地区地震灾害带来的人员伤亡和经济损失仍旧十分严重.
5.2 1961年来伊朗地区≥6.7级地震呈现较好的可公度特征,经过三元、四元和五元可公度法计算得出,2015年和2016年的强震信号较强,有可能发生较大地震级的地震,其中由蝴蝶图和可公度结构系进一步分析出2016年发生强震的信号要强于2015年.
5.3 太阳黑子数多的周期里强震也多,在前半个世纪中呈现太阳黑子活动双周年为强震活跃期,在后半个世纪变为单周年为强震活跃期,并且强震多处于太阳黑子活动的峰值和下降期,判断出的2016年正是峰值附近.
5.4 震中空间迁移经纬向呈现明显的对称性和同步的突变性.对称性表现为震中纬度南北对称,经度东西对称,整体上呈现西北-东南向对称.同步的突变性表现为震中处于区域中心位置情况下,当强震震中向北迁移时,经向震中向东迁移;当强震发生在地区边境情况下,当强震震中向南迁移时,经向震中向东迁移.其中对称轴在31°N左右,经向震中迁移的对称轴在54°E左右.未来强震震中很有可能向西北方向迁移,在北纬34°N左右,落在伊朗东北部.
致 谢 感谢各位审稿老师的宝贵指导意见.
| [1] | Berberian M, Jackson J A, Ghorashi M, et al. 1984. Field and teleseismic observations of the 1981 Golbaf-Sirch earthquakes in SE Iran[J]. Geophysical Journal International, 77(3): 809-838. |
| [2] | Bertrand M, Le Dortz K. 2007. Strike-slip kinematics in Central and Eastern Iran: Estimating fault slip-rates averagedover the Holocene[J]. Kristell Tectonics, 26(5), doi: 10.1029/2006TC002073. |
| [3] | Guo A N, Guo J Z. 2010. A discussion on the retrospective of the Ms 8. 0 we chuan earthquake in 2008 by means of earthquake source models[J]. Seismology and Geology (in Chinese), 32(1): 115-126. |
| [4] | Guo Z J. 2007. Acupuncture theory and Geophysical disaster chain[J]. Progress in Geophysics (in Chinses), 22(4): 1370-1374. |
| [5] | Guo Z J, Qin B Y. 1983. Rebiew of earthquake migration[J]. Recent Developments in World Seismology (in Chinese), (1): 8-10. |
| [6] | Hu D L. 2013. Solar variation and earth chlimate[J]. The Tide of Science & Technology (in Chinese), (3): 58-61. |
| [7] | Hu H, Han Y B. 2005. Prediction of the Hualian Earthquakes in Taiwan and an extended discussion on the method of commensurability[J]. Applied Geophysics, 2(3): 194-197. |
| [8] | Li J P, Wu L S. 2008. Metallogenic and Geological structure in Iran[J]. Mineral Deposits (in Chinese), 27(1): 120-121. |
| [9] | Li J Z, Su C, Xia Y Q. 2007. Application of commensurability information system in the earthquake prediction[J]. Journal of Beijing University of Thchnology (in Chinese), 33(1): 109-112. |
| [10] | Li S S, Yan J P. 2012. Space-time symmertry of Ms(8 earthquake In north-western pacific plate subduction[J]. Prosress in Geophysics (in Chinese), 27(3): 960-966. |
| [11] | Li S S, Yan J P, Liu Y S, et al. 2013. Spatiotemporal symmetry and tendency judgment of the Ms(7. 8 strong earthquake in Indonesia[J]. Journal of Natural Disasters (in Chinese), 22(1): 190-197. |
| [12] | Lin H, Su Y J, Han Y B, et al. 2009. Commensurability of earthquakes in Kun lun area of Xinjiang[J]. Journal of Natural Disasters (in Chinese), 18(5): 189-191. |
| [13] | Long X X, Yan J P, Sun H, et al. 2006. Study on earthquake tendency in Sichuan-yunnan region based on commensurability[J]. Journal of Catastrophology (in Chinese), 21(3): 81-84. |
| [14] | Mirzaei N, Gao M T, Chen Y T, et al. 1997. For seismic risk analysis of a unified Iran earthquake catalogue[J]. Acta Seismologica Sinica (in Chinese), 19(6): 574-585. |
| [15] | Noether E. 1971. Invariant variation problems[J]. Transport Theory and Statistical Physics, 1(3): 186-207. |
| [16] | Peng G H, Ma J Q, He Y B, et al. 2013. Based on the theory of commensurability using association rule algorithm in drought prediction and research. South to North Water[J]. Transfers and Water Science & Technology (in Chinese), 11(2): 1-4. |
| [17] | Qin S Q, Xu X W, Hu P, et al. 2010. Brittle failure mechanism of multiple locked patches in a sesmogenic fault system and exploration on a new way for earthquake, prediction[J]. Progress in Geophysics (in Chinese), 53(4): 1001-1014. |
| [18] | Qin S S, Xue L, Wang Y Y, et al. 2010. Further verifications on the brittle failure theory of multiple locked patches along a seismogenic fault and discussions on some science issues[J]. Progress in Grophysics (in Chinese), 25(4): 749-748. |
| [19] | Sun J L, Zhang R. 2007. Complexity of the 5th seismc active period in Mainland China since the 20th Century and its true nature[J]. Earthquake (in Chinese), 27(2): 30-40. |
| [20] | Walker R T, Talebian M, Sloan R A, et al. 2010. Holocene slip-rate on the Gowk strike-slip fault and implications for the distribution of tectonic strain in eastern Iran[J]. Geophysical Journal International, 181(1): 221-228. |
| [21] | Wang T, Yan J P. 2013. Analysis of the influence of solar activities and ENSO events on the drought and flood in river Hanjiang valley[J]. Journal of Arid Land Resources and Environment (in Chinese), 27(7): 107-112. |
| [22] | Weng W B. 1981. Commensurability[J]. Acta Geophysica Sinica (in Chinese), 24(2): 151-154. |
| [23] | Xu D Y, Wang M T, Geng Q G, et al. 2007. The creativity of informative forecasting theory and significance[J]. Progress in Geophysics (in Chinese), 22(4): 1375-1279. |
| [24] | Xu S S. 2007. Commen-surability of strong earthquake activity in Sichuan Province[J]. Earthquake Research in Sichuan (in Chinese), (2): 8-10. |
| [25] | Yan J P, Bai J, Su K H, et al. 2011. Research on symmetry and tendency of several major natural disasters[J]. Geographical Research (in Chinese), 30(7): 1169-1168. |
| [26] | Yan J P, Yan J H, Bai J, et al. 2010. Discussion on trends of major natural disasters in Shaanxi province and its vicinities based on commensurable method[J]. Journal of Catastrophology (in Chinese), 25(2): 18-20. |
| [27] | Yan J P, Yan J H. 2011. Trend of seismicity in Ka Shi area of Xinjiang a commensurability-based research[J]. Journal of Natural Disasters (in Chinese), 20(6): 177-180. |
| [28] | 郭安宁, 郭增建. 2010. 从震源模式讨论2008年汶川8级地震的回顾性预测[J]. 地震地质, 32(1): 115-126. |
| [29] | 郭增建, 秦保燕. 1983. 地震迁移问题(综述)[J]. 国际地震动态, (1): 8-10. |
| [30] | 郭增建. 2007. 穴位论与地球物理灾害链[J]. 地球物理学进展, 22(4): 1370-1374. |
| [31] | 胡德良. 2013. 太阳活动变化与地球气候[J]. 科技潮, (3): 58-61. |
| [32] | 李锦平, 吴良士. 2008. 伊朗地质构造及其区域成矿[J]. 矿床地质, 27(1): 120-121. |
| [33] | 李均之, 苏成, 夏雅琴. 2007. 可公度信息系在强震预报中的应用[J]. 北京工业大学学报, 33(1): 109-112. |
| [34] | 李双双, 延军平. 2012. 西太平洋俯冲带北部地区Ms(8强震时空对称特征[J]. 地球物理学进展, 27(3): 960-966. |
| [35] | 李双双, 延军平, 刘栎杉等. 2013. 印度尼西亚Ms7. 8强震时空对称特征及其趋势判断[J]. 自然灾害学报, 22(1): 190-197. |
| [36] | 林辉, 苏有锦, 韩延本等. 2009. 新疆昆仑地震的可公度性[J]. 自然灾害学报, 18(5): 189-191. |
| [37] | 龙小霞, 延军平, 孙虎等. 2006. 基于可公度方法的川滇地区地震趋势研究[J]. 灾害学, 21(3): 81-84. |
| [38] | Mirzaei N, 高孟潭, 陈运泰等. 1997. 用于地震危险性分析的统一的伊朗地震目录[J]. 地震学报, 19(6): 574-585. |
| [39] | 彭高辉, 马建琴, 贺渊博等. 2013. 基于可公度理论的相关联规则算法在干旱中的预测研究[J]. 南水北调与水利科技, 11(2): 1-4. |
| [40] | 秦四清, 徐锡伟, 胡平等. 2010. 孕震断层的多锁固段脆性破裂机制与地震预测新方法的探索[J]. 地球物理学进展, 53(4): 1001-1014. |
| [41] | 秦四清, 薛雷, 王媛媛等. 2010. 对孕震断层多锁固段脆性破裂理论的进一步验证及有关科学问题的讨论[J].. 地球物理学进展, 25(4): 749-748 |
| [42] | 孙加林, 章瑞. 2007. 中国大陆20世纪以来第五地震活跃期的复杂性及其本质问题[J]. 地震, 27(2): 30-40. |
| [43] | 孙宗扬. 2009. 物理学中的对称性[M]. 合肥: 中国科学技术大学出版社, 5: 33. |
| [44] | 王腾, 延军平, 张涛涛等. 2013. 太阳活动与ENSO事件对汉江谷地旱涝灾害影响分析[J]. 干旱区资源与环境, 27(7): 107-112. |
| [45] | 翁文波. 1981. 可公度性[J]. 地球物理学报, 24(2): 151-154. |
| [46] | 翁文波. 1996. 预测学[M]. 北京: 石油工业出版社, 20-24. |
| [47] | 徐道一, 王明太, 耿庆国等. 2007. 翁文波院士的信息预测理论体系的创新性及其意义[J]. 地球物理学进展, 22(4): 1375-1279. |
| [48] | 徐一鸿. 2005. 可畏的对称性[M]. 北京: 清华大学出版社, 15: 68-69. |
| [49] | 徐水森. 2007. 四川强地震活动的可公度性初探[J]. 四川地震, (2): 8-10. |
| [50] | 延军平, 闫军辉, 白晶等. 2010. 基于可公度方法的陕西及邻近地区重大自然灾害发生趋势探讨[J]. 灾害学, 25(2): 18-20. |
| [51] | 延军平, 白晶, 苏坤慧等. 2011. 对称性与部分重大自然灾害趋势研究[J]. 地理研究, 30(7): 1169-1168. |
| [52] | 延军平, 闫军辉. 2011. 新疆喀什地区地震活动趋势-基于可公度方法的研究[J].. 自然灾害学报, 20(6): 177-180 |
 2014, Vol. 29
2014, Vol. 29

