2. 烽火通信科技股份有限公司网络产出线研发部, 武汉 430073
2. R&D Department/Network Business Unit, Fiberhome Telecommunication Technologies Co., Ltd., Wuhan 430073, China
地震勘探是一种重要的物探方法(付燕,2002).通过人工激发地震波,分析地震子波在地层中的传播规律,从而获得不同地层间的反射强度,了解地层结构,达到勘探的目的.由于真实的地质结构非常复杂,因此通过地层剖面来分析地质结构是非常困难的.稀疏分解方法一经提出,许多研究学者就将其应用到地震数据解释中.
在传统的人工地震记录(徐伯勋等,2001)中,是把大地地层看成一个线性系统,即假设激发震源产生一个尖脉冲,经过地层传播后仍然保持脉冲的波形不变.然而,在实际的地震记录中情况是非常复杂的.激发震源所产生的尖脉冲经地层介质的吸收后,尖脉冲的波形将会被拉长,这种具有时延的单个反射波被称为地震子波.从而实际的地震记录 x(t)由反射系数γ(t)和地震子波w(t)褶积组成(陈玉东,2006),公式为
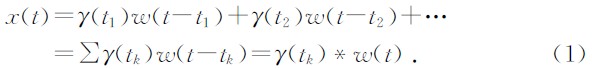
由于震源信号经过地层传播时,信号在地层间的反射是有所差别的,从而地层反射系数γ(t)可以抽象为一有限长序列γ(n).不同地层之间对震源信号的反射系数可以简化为γ(n)上的非零数值,而同一地层内相对较小的反射系数则简化为0(Charles等,2005).因此地震记录的离散化公式为
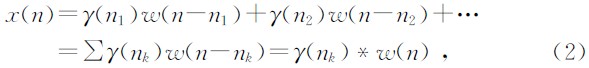
信号稀疏分解的思想最早是由Mallat和Zhang(Mallat et al.,1993)在1993年提出来的,信号稀疏分解是信号在过完备原子库上根据信号特点选取最佳匹配原子,用选取的最佳原子的线性叠加得到一个非常简洁的稀疏表达式的过程.稀疏分解以其灵活、简洁、稀疏这一优良特性已经被广泛应用到地震资料的解释中,如地震信号的去噪(赵天资等,2008)、谱分解(张显文等,2010;Wang et al.,2007)、反演(Ismael et al.,2012)、存储预测(武国宁等,2012)、快速分解(陈发宇等,2007; 张繁昌等,2012)、滤波(李学良等,2013;石颖等,2013)等方面.
目前,在地震信号处理中常用的稀疏分解算法是匹配追踪(Matching Pursuit,MP)算法(王建英等,2006).Chakraboty等(1995)最早将MP算法用于地震信号时频属性分析;Liu等(2004)提出基于Ricker小波匹配算法的地震信号分解;王成梅等(王成梅等,2010)提出了改进的Ricker子波的地震信号MP分解,降低信号分解后的均方误差.以上方法应用MP对地震信号进行处理,取得了比较好的效果,但MP选取的原子间存在相关性,因而信号的分解不够稀疏.为了克服上述问题,本文采用正交匹配追踪(Orthogonal Matching Pursuit,OMP)方法(杨福生,2006)对信号进行稀疏分解,要求在每步选取的最佳原子必须与已选取的原子正交,来提高信号分解的稀疏度.与MP比较, OMP中添加了正交化过程,但同时增加了算法的计算复杂度.为了降低计算复杂度,采用一种全局搜索算法—重复加权提升搜索(Repeated Weighted Boosting Search,RWBS)算法,来快速搜索最佳匹配原子.
目前稀疏分解的算法很多,大多是先建立一个过完备原子库,再通过一定的准则从过完备原子库中选取与观测信号最佳匹配的原子,最后利用选取的最佳原子进行线性叠加得到与原始信号最佳逼近的稀疏表达式.
雷克子波(Ricker Wavelet)是人工合成地震记录时常用的零相位子波,并在地震信号滤波处理中得到广泛应用(邓小英等,2011).Ricker子波在时间域上的表达式为
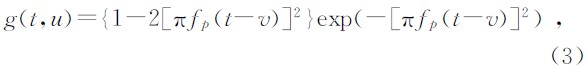
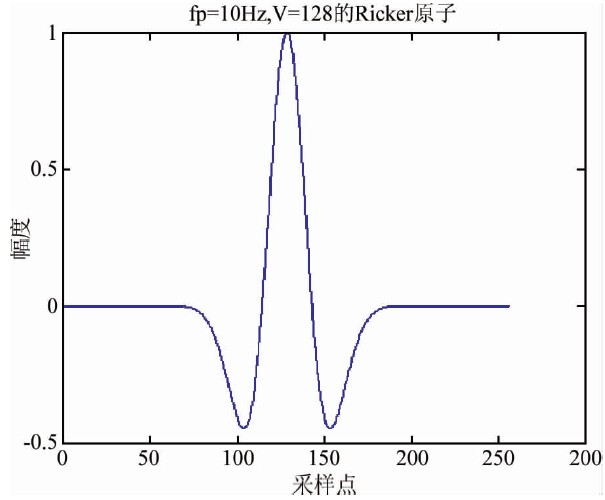 | 图 1 一个Ricker原子 Fig. 1 A Ricker atom |
设 G={g ri} r i∈Γ为建立的过完备原字库, g ri为过完备原字库中的原子, r i这个指标与构建原子的参数及参数个数有关,Γ为由ri这个指标组成的集合.一般将情况下需对原字库中的所有原子进行归一化处理,即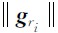 =1.假设研究的信号是 y ,信号的长度为n,构建过完备原子库的原子为零相位Ricker子波.
=1.假设研究的信号是 y ,信号的长度为n,构建过完备原子库的原子为零相位Ricker子波.
首先,在过完备原字库 G 中寻找与待分解信号y最佳匹配的原子,记作 g n1,其满足条件

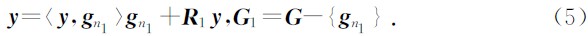
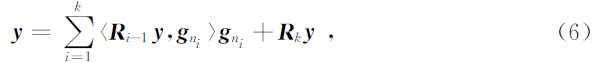
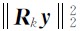 小于或等于某个给定阈值ξ1(在对加性噪声信号进行分解时,ξ1的值一般要比加性噪声方差稍大一些;在无噪声情况下,ξ1的取值要尽量小)时停止迭代.选取的原子数目愈少时,信号就分解的越稀疏.
小于或等于某个给定阈值ξ1(在对加性噪声信号进行分解时,ξ1的值一般要比加性噪声方差稍大一些;在无噪声情况下,ξ1的取值要尽量小)时停止迭代.选取的原子数目愈少时,信号就分解的越稀疏.由于在MP算法过程中,只能保证 R k y与g nk正交,但不能确保 R k y与g n1, g n2,…, g nk-1正交,因此所得到的结果是次最优的,即信号分解不是最稀疏的.研究MP的改进算法来减少分解所需要的原子个数已成为信号稀疏分解的热点.
与MP算法相比较,OMP算法在MP算法每选取一个最佳匹配原子之后,即寻找下一个最佳匹配原子之前,将原字库中剩余原子与已选取原子所张成的子空间的一组基做Gram-Schmidt正交归一化处理.第一次提取的原子 g n1就是第一个正交基 e 1,它所张成的空间记作V1.则y在e1方向上的投影为 P V1y=〈 y,e 1〉 e 1,剩余原字库为 G1=G-{g n1}.
设在第k次选取最佳匹配子时,需要将剩余原字库 G k-1中所有的原子与已得到的一组正交基 e1,e2,…,e k-1 做Gram-Schmidt正交归一化处理,即有
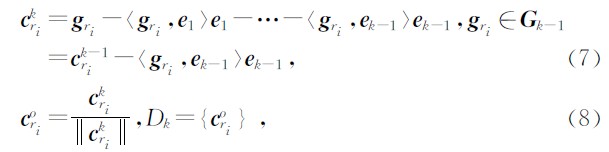
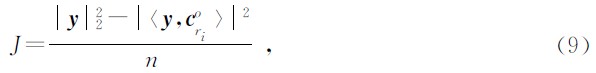
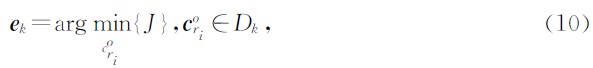
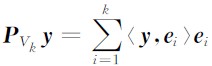 ,就得到新的残余和剩余原字库,即为
,就得到新的残余和剩余原字库,即为
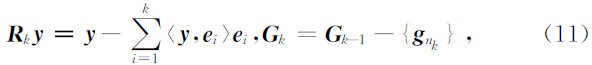
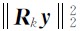 小于或等于某个给定的阈值ξ1(ξ1的取法同上)时,就停止迭代.
小于或等于某个给定的阈值ξ1(ξ1的取法同上)时,就停止迭代.由上面MP和OMP算法的介绍可知,MP和OMP算法的区别在于OMP算法选取的所有原子都是两两相互正交的,而MP算法没有正交过程.正因为原子得到了正交化处理,所以若达到相同的重构精度,OMP算法的分解的步数应该比MP算法的少,但同时也增加算法的计算复杂度.此外,MP和OMP的分解效果都与建立的过完被原子库的大小有关,当原子库越大时,分解的结果越稀疏但速度较慢;当原子库越小时,分解的速度提高了但不够稀疏.为了克服这些问题,本文提出了基于RWBS的正交匹配追踪算法.
由于基于匹配追踪算法的稀疏分解的每一步,实际上是解一个最优化问题,所以可以将寻找最佳匹配原子的过程转化为利用智能算法求函数最优化的问题.选取最佳匹配原子的搜索方法有很多,如人工鱼群算法(舒伟杰等,2009)、模拟退火算法(徐帅等,2008)、遗传算法(张静等,2008)等等.本文将应用RWBS算法,它是一种新的全局搜索算法,易于实现.在使用该算法时,需要设定一些参数.为了方便下面算法的描述,设定了如下参数: Ps为种群初始个数,NG为外部循环迭代次数,NB为内部循环迭代最大次数,ξ为内部循环终止条件之一.
RWBS的内部循环是一个加权提升搜索过程.它先结合信号的先验信息,随机的产生Ps个种群:{ u ′ i|i=1,2,…,Ps},根据(3,7-9)式计算J(u).再寻找当前最优和最差种群,将其分别记作 u best=argminJ(u), u worst=argmaxJ( u ).对种群{ u ′ i|i=1,2,…,Ps}用凸组合的方式产生一个新的种群 u ′ Ps+1,同时利用镜像原理产生一个 u ′ Ps+1关于 u best的对称点 u ′ Ps+2.最后用 u ′ Ps+1和 u ′ Ps+2中使得J( u)最小种群来替换u worst.该过程重复进行直到达到最大迭代步数NB,或 u ′ Ps+2- u ′ Ps+1 2≤ξ时停止迭代.
图 2是一个简单的说明加权提升搜索算法的二维例子,在这个例子中Ps=3, u1,u2,u3是三个初始种群,且由图可知u best= u1,u worst= u2.u4是u1,u2,u3加权组合得到的种群,u5是u 4的镜像,且J( u 4)>J( u5),因此用u5来代替u2.在下一步循环中的三个种群就是u1,u3,u 5,按照上面的过程循环,直到达到终止条件.在这个过程中加权组合的方式很关键,关于它的具体说明可以参考文献Ron等(2003).
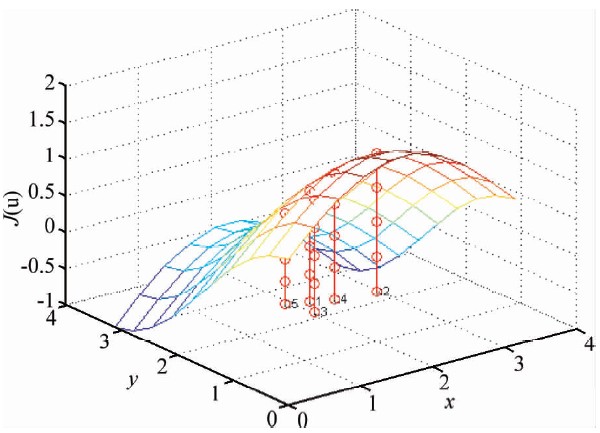 | 图 2 简单加权搜索最优化过程 Fig. 2 The optimization process of a simple weighted search |
加权提升搜索属于局部最优化过程,对初始选择的种群依赖性很强.为了克服局部最优的特性,将加权提升搜索过程重复多次来得到一个全局最优解.这种得到全局最优解的过程就是RWBS算法,关于RWBS算法的更多细节可以参考文献Sheng等(2005).当用RWBS搜索第k个匹配原子时,算法流程如图 3.
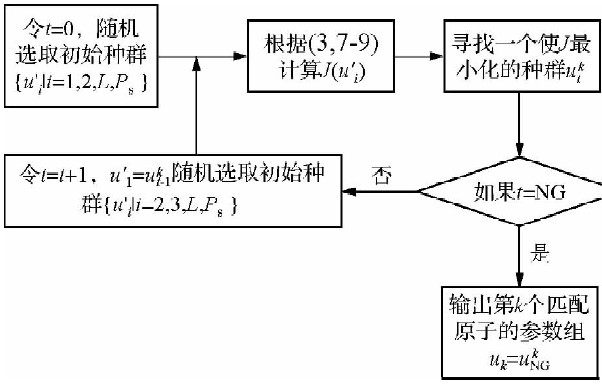 | 图 3 用RWBS寻找第k个匹配原子的算法流程图 Fig. 3 The algorithm flow chart of looking for the kth matching pursuit atom by RWBS |
RWBS采用加权提升搜索最优过程来寻找一个较优的种群 u kt,t=0,1,…,NG-1,然后将其融入下一步循环中.保留全局最优值 u kNG作为新选择的匹配原子参数组,删除其余的种群.
本文提出的基于RWBS的快速分解算法步骤如下:
步骤1 给定参数Ps,NG,NB以及ξ的值,以及最终的迭代终止阈值ξ1的值,置初始残余 R o y=y,k =1;
步骤2 利用RWBS 寻找与 R k-1 y最佳匹配的原子,记作u k,再将 R k-1 y沿着u k的方向投影,就得到残余信号 R ky;
步骤3 当 R k y 小于阈值ξ1时,停止迭代;否则令k=k+1,返回到步骤2.
传统的信号质量评价指标一般是重构信号与原始信号间的均方误差(Mean Square Error,MSE)和信噪比(Signal to Nose Ratio,SNR).
MSE定义为
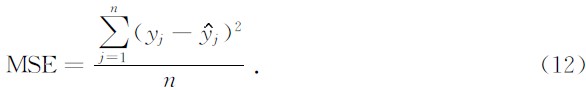
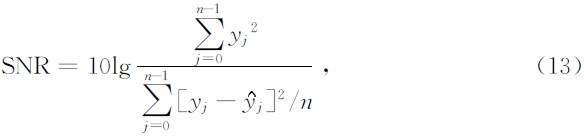
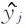 分别为原始信号和分解重构信号的第j个分量,n为信号长度.
分别为原始信号和分解重构信号的第j个分量,n为信号长度.
按照 (2) 式,构建一个长度为244的系数矩阵,与Ricker子波做卷积,其中Ricker子波的主频参数fp取20 Hz,t在区间[-0.2,0.2]上等间隔采取257个点,v取0,这样构造的地震信号如图 4,其长度为500,此信号即为待分解的原始信号,用y表示.
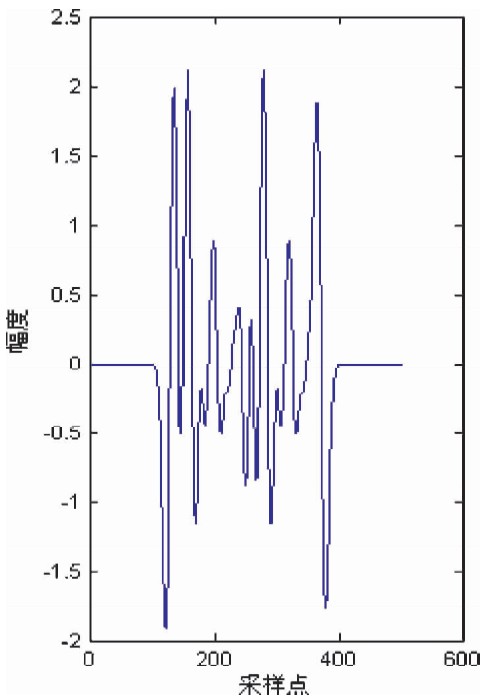 | 图 4 人工合成的原始地震信号 Fig. 4 Synthetic original seismic signal |
地震信号稀疏分解选取Ricker子波来构建原子库,Ricker子波的表达式如(3)式所示.MP、OMP是在相同的固定原子库上对信号稀疏分解,位移参数v的搜索范围是[0,n-1],间隔为1,主频参数fp的搜索范围是利用快速傅里叶变换来确定.从图 5的原始地震信号y的幅度谱图可以看出信号y的能量分布在0~110 Hz频率范围内,频率间隔取为1.1 Hz.上述两种算法构造的原子库的大小为50000.算法终止阈值设为0.0001.RWBS算法在理想地震信号稀疏分解实验中的三个参数NG=8,Ps=40,NB=15.在带有加性噪声的地震信号进行稀疏分解时,算法最外层迭代终止阈值设为高斯白噪声的方差,RWBS过程的三个参数的设定根据具体情况调节.
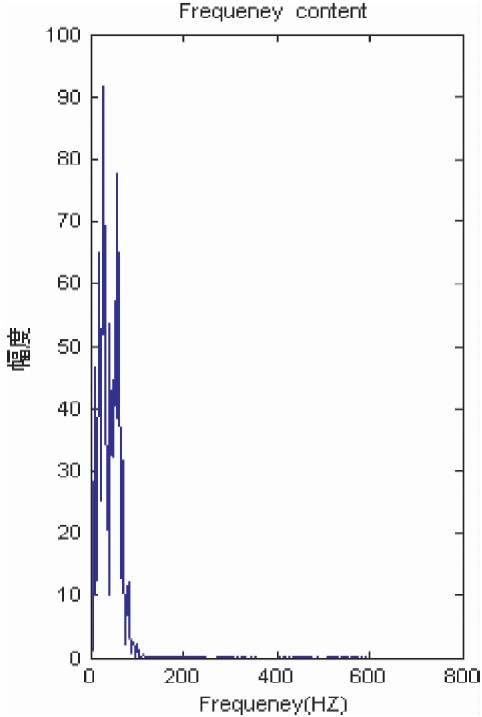 | 图 5 原始地震信号的幅度谱 Fig. 5 The amplitude spectrum of original seismic signal |
(1)理想地震信号稀疏分解
通过对3.2节中地震信号的稀疏分解来分析MP、OMP以及RWBS对信号进行分解的性能,本文主要从运行时间、重构精度以及分解的稀疏度来评价算法的性能.
表 1是采用MP、OMP以及RWBS算法对理想地震信号稀疏分解所得到的三种性能指标的结果.MP、OMP是采用相同的原子库对地震信号进行稀疏分解,由表 1可以知道, OMP与MP在保证重构精度相差不大的条件下, OMP稀疏分解所需的原子个数明显小于MP所需的.OMP算法存在的不足是它的运行时间是MP算法的4倍多,这种运行速度是难以忍受的.与OMP算法相比较,RWBS算法所需要的运行时间减少了87%;与MP算法相比较,RWBS算法所需要的运行时间减少了49%.与MP和OMP算法相比较,本文提出的基于RWBS的快速分解算法不仅所需的运行时间最少,分解的稀疏度最高,而且残差信号的MSE值与MP和OMP算法相差不大.
|
|
表 1 地震信号稀疏分解的算法效果比较 Table 1 The effect comparison of Seismic signal sparse decomposition algorithm |
对如图 4所示的信号,分别用MP和OMP算法在相同原子库上进行稀疏分解,图 6给出了这两种算法分解此信号的迭代步数对比.图中横轴表示的是分解所需的迭代步数,纵轴是归一化残差范数的对数.从图 6中可以看出,在相同的归一化残差下,迭代10次后,OMP所需的迭代步数明显少于MP,即OMP的收敛速度比较快.
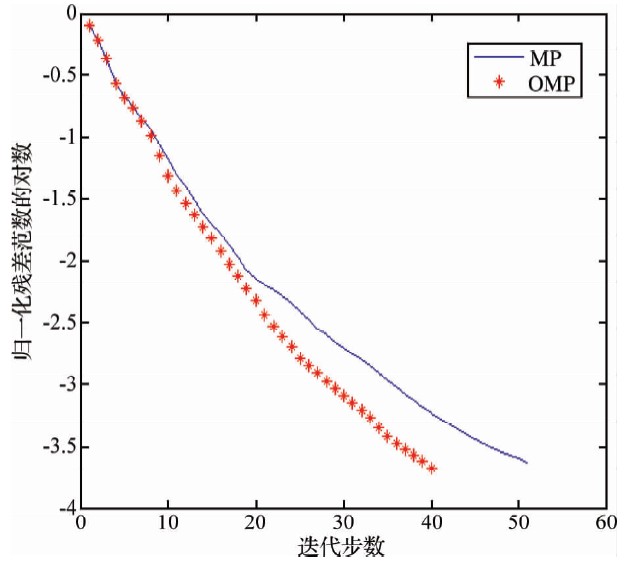 | 图 6 无噪声背景下的MP、OMP算法迭代步数比较 Fig. 6 The iterative steps comparison of MP, OMP algorithm without noise |
(2)加性噪声背景下的地震信号稀疏分解
在实际的地震勘探中,观测到的人工地震信号会受到不同程度的噪声干扰,这就要求用于地震信号稀疏分解的算法具有较好的鲁棒性能.为检验改进算法对受到噪声干扰的地震信号稀疏分解的性能,将上述构造的地震信号作为原始地震信号,在此原始信号的基础上加入长度为500的均值为零,标准差为0.05的高斯白噪声.然后采用MP、OMP以及RWBS算法对地震信号进行稀疏分解,来比较算法鲁棒性和稀疏度.
表 2是MP、OMP以及RWBS对带有噪声的地震信号的稀疏分解效果.从表 2中可以知道,OMP、RWBS和MP算法的鲁棒性强度差不多,但OMP和RWBS算法分解的稀疏度明显提高了.与OMP算法相比较,RWBS大大提高了算法的运行速度,运行时间减少了约90%,而且比MP的运行速度要快.
|
|
表 2 加性噪声背景下的地震信号稀疏分解的 算法效果比较 Table 2 The algorithm effect comparison of seismic signal sparse decomposition with additive noise |
对带有噪声的地震信号分别用MP和OMP算法在相同原子库上进行稀疏分解,图 7给出了这两种算法分解此信号的迭代步数比较.图中横轴表示的是分解所需的迭代步数,纵轴是归一化残差范数的对数.从图 7中可以看出,在相同的归一化残差下,迭代10次后,OMP所需的迭代步数明显少于MP.
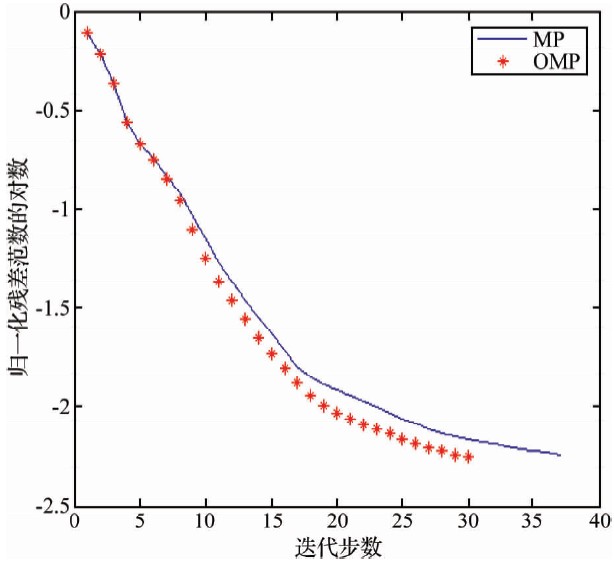 | 图 7 噪声背景下的 MP、OMP算法迭代步数比较 Fig. 7 The iterative steps comparison of MP, OMP algorithm with noise |
从上面的两个仿真实验结果中可以得到,无论是在理想背景下还是在加性噪声背景下,用RWBS算法对地震信号进行稀疏分解,与MP和OMP算法相比较,不仅在稀疏度方面得到了提高,而且在运行速度方面也得到了提升.
(3) 实际地震信号稀疏分解
图 8是一道长度为256的实际地震信号,其采样率为1 ms.采用MP、OMP和RWBS三种方法对其进行稀疏分解.图 9是实际地震信号的幅度谱图,从图中可以看出信号的能量主要集中在0~150 Hz频率范围内,频率间隔取为1.5 Hz.位移参数v的搜索范围是[0,n-1],间隔为1,构建的原子库大小为25600.把信号稀疏分解后得残差信号的MSE作为迭代终止条件,本文中选取代终止阈值为10.
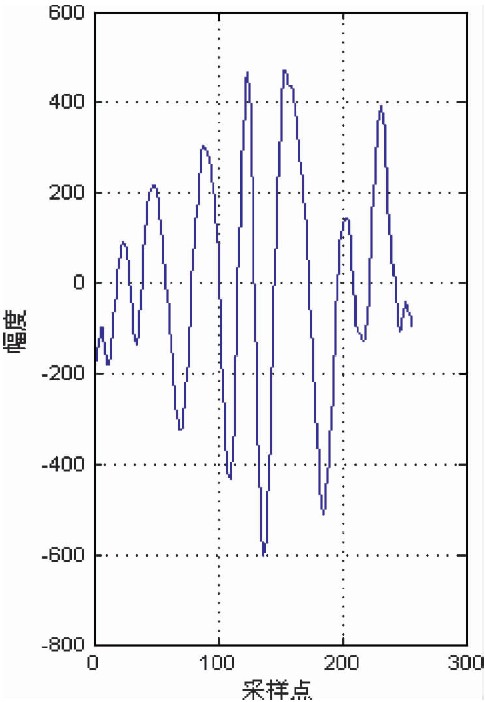 | 图 8 实际地震信号 Fig. 8 The real seismic signal |
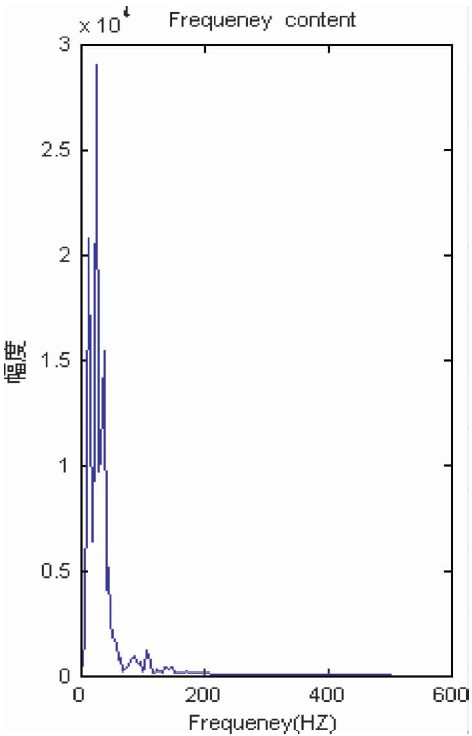 | 图 9 实际地震信号的幅度谱 Fig. 9 The amplitude spectrum of practical seismic signal |
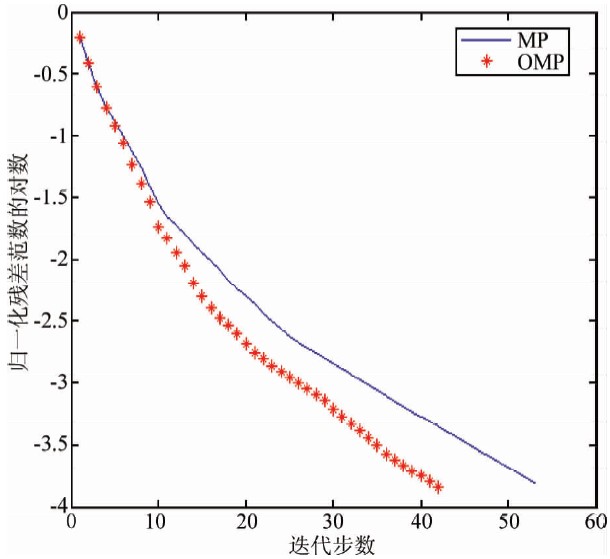 | 图 10 关于实际地震信号稀疏分解的MP、 OMP算法迭代步数比较 Fig. 10 The iterative steps comparison of MP, OMP algorithm about sparse decomposition of the real seismic signal |
表 3是实际地震信号在相同迭代阈值下采用上面提到的三个算法进行稀疏分解的结果,从表 3中可以知道,三种算法的怒棒性差不多,但OMP和RWBS算法分解的稀疏度也明显提高了.与OMP算法相比较,RWBS大大提高了算法的运行速度,运行时间减少了约86%,而且比MP的运行速度要快.
|
|
表 3 实际地震信号稀疏分解的算法效果比较 Table 3 The algorithm effect comparison of real seismic signal sparse decomposition |
针对现有的基于MP算法的地震信号稀疏分解方法稀疏度不够高的局限性,提出了结合OMP和RWBS的改进算法.该算法不仅有效地提高信号分解的稀疏度,而且降低了OMP算法的运行速度.无论是对人工合成的地震信号还是对实际的地震信号,改进算法对地震信号的分解都比MP更加稀疏,而且对受噪声污染的信号具有较好的鲁棒性.
匹配追踪方法的思想是选择与待分解信号最佳匹配的原子,进行信号的稀疏分解.但匹配追踪的难点在于如何选取核模型,如果与构成原始信号的子波波型相近,则不仅会反应出信号的一些有用的特征,而且还会提高分解的稀疏度.因此,如何构建更好的核模型来进行信号的稀疏分解是接下来研究的重点.
| [1] | Chakraborty A, Okaya D. 1995. Frequency-time decomposition of seismic data using wavelet-based methods[J]. Geophysics, 60(6): 1906-1916. |
| [2] | Charles D, Stephane M C, Ecole P. 2005. Sparse spike deconvolution with minimum scale [C]. Proceeding of Signal Processing with Adaptive Sparse Structure Representations, 123-126. |
| [3] | Chen F Y, Yang C C. 2007. Seismic signal’s decomposition based on matching pursuit method[J]. Progress in Geophysics (in Chinese), 22(6): 1692-1697. |
| [4] | Chen Y D. 2006. Geophysical information processing foundation (in Chinese)[M]. Beijing: Geological Press. |
| [5] | Deng X Y, Liu T, Luo Y. 2011. Robustness of least squares support vector regression filtering method with Ricker wavelet kernel[J]. Chinese J. Geophys.(in Chinese), 54(3): 845-853. |
| [6] | Fu Y. 2002. Research on de-noising methods of seismic data (in Chinese)[D]. Xi’an: The Doctoral Dissertation of Northwest Industry University. |
| [7] | Ismael V R, Mauricio S, Yu J G. 2012. Simultaneous recovery of origin time, hypocentre location and seismic moment tensor using sparse representation theory[J]. Geophysical Journal International, 188(3): 1188-1202. |
| [8] | Li X L, Sun C, Yuan Y M, et al. 2013. Diffracted wave separation by applying self-adaptive least square filtering method[J]. Progress in Geophysics (in Chinese), (2): 777-784, doi:10.6038/pg20130226. |
| [9] | Liu J L, Wu Y F, Li X G. 2004. Time-Frequency decomposition based on Ricker wavelet[C]. Expanded Abstracts of 74th SEG Annual International Meeting, 1937-1940. |
| [10] | Mallat S G, Zhang Z F. 1993. Matching pursuits with time frequency dictionaries [J]. IEEE Transactions on Signal Processing, 41(12): 3397-3415. |
| [11] | Ron M, Gunnar R. 2003. An introduction to boosting and leveraging[C]. // Mendelson S, Smola A. Advanced Lectures in Machine Learning. New York: Springer Verlag, 119-184. |
| [12] | Sheng C, Wang X X, Harris C J. 2005. Experiments with repeating weighted boosting search for optimization in signal processing applications [J]. IEEE Transactions on Systems Man Cybernetics B, Cybernetics, 35(4): 682-693. |
| [13] | Shi Y, Wang J M, Jing H L, et al. 2013. Suppressing surface-related multiple by multi-trace adaptive matching filter approach[J]. Progress in Geophysics (in Chinese), (2): 785-792, doi:10.6038/pg20130227. |
| [14] | Shu W J, Yuan Z G, Yin Z K. 2009. Signal MP-based sparse decomposition with artificial fish-swarm algorithm[J]. Application Research of Computers (in Chinese), 26(1): 66-67. |
| [15] | Wang C M, Yang S L. 2010. Seismic signal’s MP decomposition based on Ricker wavelet[J]. Computer Knowledge and Technology (in Chinese), 6(4): 976-978. |
| [16] | Wang J Y, Yin Z K, Zhang C M. 2006. Signal and image sparse decomposition and preliminary Application (in Chinese)[M]. Chengdou: Southwest Jiaotong University Press. |
| [17] | Wang Y H. 2007. Seismic time frequency spectral decomposition by matching pursuit[J]. Geophysics, 72(1): 13-20. |
| [18] | Wu G N, Cao S Y, Sun N. 2012. Matching pursuit method based on complex seismic traces and its application of hydrocarbon exploration[J]. Chinese J. Geophys. (in Chinese), 55(6): 2027-2034. |
| [19] | Xu B X, Bai X B, Yu C Q. 2001. Seismic information technology - extraction, analysis and Prediction (in Chinese)[M]. Beijing: Earthquake Press. |
| [20] | Xu S, Zhao Y L, Zhang J Q. 2008. Research of signal sparse decomposition based on simulated annealing[J]. Communications Technology (in Chinese), 41(11): 188-190. |
| [21] | Yang F S. 2006. The principle and application of independent component analysis (in Chinese)[M]. Beijing: Tsinghua University Press. |
| [22] | Zhang F C, Li C H. 2012. Orthogonal time-frequency atom based fast matching pursuit for seismic Signal[J]. Chinese J. Geophys.(in Chinese), 55(1): 277-283. |
| [23] | Zhang J, Fang H, Wang J Y, et al. 2008. Improved GA-based MP algorithm for signal aparse decomposition[J]. Computer Engineering and Applications (in Chinese), 44(29): 79-81. |
| [24] | Zhang X W, Han L G, Wang Y, et al. 2010. Seismic spectral decomposition fast matching pursuit algorithm and its application[J]. Geophysical Prospecting for Petroleum (in Chinese), 49(1): 1-6. |
| [25] | Zhao T Z, Song W, Wang S X. 2008. Time-frequency filtering de-noise method based on matching pursuit algorithm[J]. Geophysical Prospecting for Petroleum (in Chinese), 47(4): 367-371. |
| [26] | 陈发宇, 杨长春. 2007. 基于MP方法的地震信号快速分解算法[J]. 地球物理学进展, 22(6): 1692-1697. |
| [27] | 陈玉东. 2006. 地球物理信息处理基础[M]. 北京: 地质出版社. |
| [28] | 邓小英, 刘涛, 罗勇. 2011. Ricker子波核最小二乘支持向量回归滤波方法的稳健性研究[J]. 地球物理学报, 54(3): 845-853. |
| [29] | 付燕. 2002. 人工地震信号去噪方法研究[D]. 西安: 西北工业大学. |
| [30] | 李学良, 孙晨, 袁义明,等. 2013. 利用最小二乘自适应滤波实现绕射波分离[J]. 地球物理学进展, (2): 777-784, doi:10.6038/pg20130226. |
| [31] | 石颖, 王建民, 井洪亮,等. 2013. 多道自适应匹配滤波方法压制表面多次波[J]. 地球物理学进展, (2): 785-792, doi:10.6038/pg20130227. |
| [32] | 舒伟杰, 袁志刚, 尹忠科. 2009. 利用人工鱼群算法实现MP的信号稀疏分解[J]. 计算机应用研究, 26(1): 66-67. |
| [33] | 王成梅, 杨胜利. 2010. 基于改进的Richer子波的地震信号MP稀疏分解[J]. 电脑知识与技术, 6(4): 976-978. |
| [34] | 王建英, 尹忠科, 张春梅. 2006. 信号与图像的稀疏分解及初步应用[M]. 成都: 西南交通大学出版社. |
| [35] | 武国宁, 曹思远, 孙娜. 2012. 基于复数道地震记录的匹配追踪算法及其在储层预测中的应用[J]. 地球物理学报, 55(6): 2027-2034. |
| [36] | 徐伯勋, 白须滨, 于常青. 2001. 地震勘探信息技术-提取、分析、预测[M]. 北京: 地震出版社. |
| [37] | 徐帅, 赵云龙, 张江泉. 2008. 基于模拟退火的信号稀疏分解研究[J]. 通信技术, 41(11): 188-190. |
| [38] | 杨福生. 2006. 独立分量分析的原理与应用[M]. 北京: 清华大学出版社. |
| [39] | 张繁昌, 李传辉. 2012. 基于正交时频原子的地震信号快速匹配追踪[J]. 地球物理学报, 55(1): 277-283. |
| [40] | 张静, 方辉, 王建英,等. 2008. 基于GA和MP的信号稀疏分解算法的改进[J]. 计算机工程与应用, 44(29): 79-81. |
| [41] | 张显文, 韩立国, 王宇,等. 2010. 地震信号谱分解匹配追踪快速算法及其应用[J]. 石油物探, 49(1): 1-6. |
| [42] | 赵天资, 宋炜, 王尚旭. 2008. 基于匹配追踪算法的时频滤波去噪方法[J]. 石油物探, 47(4): 367-371. |
 2014, Vol. 29
2014, Vol. 29

