2. 中国石化石油物探技术研究院, 南京 211103
2. SINOPEC Geophysical research institute, Nanjing 211103, China
偏移成像正由传统的纵波成像向着弹性波、转换波成像发展.转换波成像可以综合利用纵横波信息,得到高质量的转换波成像剖面,进而可以为地震资料解释、流体识别、储层预测提供有效支持(Granli et al., 1999; Han et al., 2014;李振春等,2018;岳玉波等,2018;公绪飞,2018;Li et al., 2019).各向异性介质中,采用传统的各向同性算法,会导致成像归位不准确,能量不聚焦等问题(段新意等,2014;韩建光等,2015;刘强,2017).当前,众多学者对转换波进行了研究,包括转换波成像、转换波分辨率以及转换波成像条件等(Thomsen, 1999; Meier and Lee, 2009; Shabelansky et al., 2017; 李振春等,2018;Li et al., 2018; Gong et al., 2018),其研究多是基于各向同性假设.因此,有必要研究各向异性转换波偏移成像,进一步推动转换波勘探技术发展,以满足复杂介质地质目标勘探的要求.
转换波勘探的概念起源于20世纪70年代,随后,经过近20年的发展,逐步建立起相应的处理技术流程(李振春等,2018;Kuo and Dai, 1984).同SS波成像相比,转换波成像不仅可以节约采集成本,而且在分辨率、信噪比等方面具有优势(Stewart et al., 2002).同PP波成像相比,它可以综合利用纵横波波场信息,得到分辨率较高的偏移剖面(李振春等,2018).转换波成像可以分为矢量波成像和标量波成像(Wang et al., 2016).矢量波成像利用地震波的振幅矢量进行偏移,其实现方式有两种,一种应用多分量波场同时进行偏移,在成像中解决非本型波引起的串扰噪音;另一种是目前矢量偏移考虑的方式,在叠前进行波场分离,然后利用真振幅的单波波场进行偏移成像;而标量波成像是基于声学场理论进行成像(芦俊等,2018;Liu et al., 2019).本文研究中采用的思路是先在叠前进行波场分离,然后基于标量波成像条件进行转换波成像.当前,随着研究的深入,转换波偏移也由时间偏移向着深度偏移发展.转换波深度偏移主要包括基于射线理论的转换波深度偏移(Dai and Li, 2006)和基于波场延拓理论的转换波深度偏移,后者又包括单程波偏移和RTM成像(Du et al., 2017; 芦俊等,2018).转换波Kirchhoff偏移作为一种经典的基于射线理论的偏移方法,其继承了射线类偏移的灵活性和高效性,在生产中得以较多运用(Dai and Li, 2006).但是,作为一种单一波至的Kirchhoff偏移,无法对多值走时进行成像,且存在阴影区、焦散区等问题;而传统的单程波偏移受角度限制,难以适用于复杂构造成像(芦俊等,2018);转换波RTM偏移成像方法,具有较高的成像精度,但其对速度模型的准确性要求较高,且需要较大的计算成本,因而,在一定程度上限制了它在生产中的应用(李振春等,2018).与此同时,学者们研究了一种兼具成像质量与成像效率的高斯束偏移成像方法(岳玉波,2011;蔡杰雄等,2017).高斯束方法最初由Červeny等(Červeny, 1972; Červeny et al., 1982)引入到地球物理学中.随后,Hill(1990, 2001),Nowack等(2003),Gray(2005)等学者将其应用到偏移中.近年来,国内外的学者们提出了控制束(Casasanta and Grion, 2012)、快速束(Tanushev et al., 2017)、最小二乘高斯束(Hu et al., 2006; Yue et al., 2019, 2021a, b)、高斯束逆时偏移(肖建恩等,2019)、时间域高斯束(吕庆达等,2018;秦宁,2020)以及时空域高斯束偏移(胡自多等,2020)等方法.随着研究的深入,学者们相继提出了各向异性介质叠后(Alkhalifah, 1995)和叠前声波高斯束偏移成像方法(Zhu et al., 2005, 2007;段新意等,2014;韩建光等,2015;刘强等,2016).同时,针对不同波类型,学者们研究了弹性波(岳玉波,2011;Yang et al., 2018; Han et al., 2020)、转换波(Han et al., 2014;李振春等,2018)高斯束偏移成像方法,推动了高斯束成像方法的发展.然而,以上研究均基于构建高斯束传播算子,其成像质量受到高斯束初始束宽影响(Zhu, 2013),不好兼顾浅表层与中深层成像质量.针对常规高斯束偏移中存在的问题,Nowack(2008, 2011)通过修改传播算子,提出了动态聚焦束偏移方法.该方法可以使得波束在传播过程中能量保持聚焦,从而有助于解决高斯束偏移中初始束宽引起的问题,而其研究局限在各向同性介质声波成像,没有考虑更为复杂的介质.
本文通过求解各向异性介质qPqSV转换波运动学和动力学射线追踪方程,获得转换波中心射线走时、路径及动力学信息;并通过修改动态聚焦型传播算子,构建出各向异性介质动态聚焦束,提出了一种各向异性介质转换波动态聚焦束偏移成像方法.模型试算的结果表明,本文提出的方法可使射线束的形态和能量得到较好保持,在保证浅层成像质量的前提下,提高了深层反射轴能量,同常规的高斯束偏移相比,该方法更有助于解决深层地质目标勘探问题.
1 基本原理 1.1 各向异性介质转换波射线追踪 1.1.1 运动学射线追踪各向异性介质声波运动学射线追踪主要包括基于弹性参数的运动学射线追踪(Červeny, 1972; Alkhalifah, 1995;段新意等,2014;韩建光等,2015)和基于相速度的运动学射线追踪(Zhu et al., 2007; 刘强等,2016).前者计算较为复杂且需要开辟较大的内存空间;后者求解更为简洁,计算效率更高;为此,本文在前人研究基础上,进一步给出了各向异性介质转换波运动学射线追踪方程:
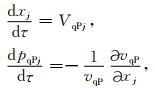
|
(1a) |
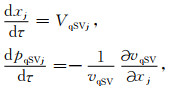
|
(1b) |
式中xj为射线路径,τ为走时;VqPj,vqP,pqPj分别为笛卡尔坐标系下qP波群速度分量、相速度和慢度分量(j=1,2,3),而VqSVj,vqSV和pqSVj为qSV波对应的三个参量.
1.1.2 动力学射线追踪动力学射线追踪广泛应用在高频近似下地震波场计算和地震反演中(Červeny, 2001).本文在Zhu等(2007)研究的基于相速度的声波动力学射线追踪方程基础上,发展了各向异性介质转换波动力学射线追踪方程:
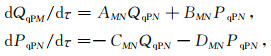
|
(2a) |
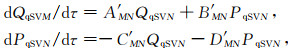
|
(2b) |
式中:Q和P为动力学射线追踪参数,M,N分别取1,2.Q表示从射线坐标系(γ1,γ2,γ3)的坐标γ1,γ2,γ3到射线中心坐标系(q1, q2, q3)的坐标q1,q2,q3之间的转换关系;P表示从射线坐标系(γ1,γ2,γ3)的坐标γ1,γ2,γ3到射线中心坐标系(q1, q2, q3)的慢度p1q,p2q,p3q之间的转换关系,上标q表示射线中心坐标系,射线坐标系(γ1,γ2,γ3)中γ1为射线出射的倾角i0,γ2为射线出射的的方位角ϕ0,γ3为射线的传播方向的弧长s(Červeny,2001).系数AMN, BMN, CMN, DMN和A′MN, B′MN, C′MN, D′MN由式(3)给出:
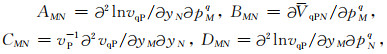
|
(3a) |
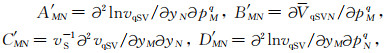
|
(3b) |
式中,VqPN表示射线中心坐标系下qP波群速度,VqSVN表示射线中心坐标系下qSV波群速度.
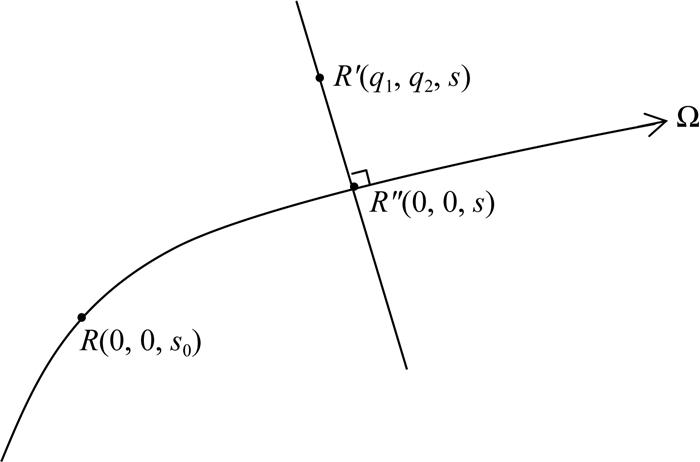
1.2 动态聚焦传播算子构建 1.2.1 中心射线复值走时计算如图 1所示,在射线追踪的基础上,可进一步计算出中心射线附近的复值的走时(Červeny,2001):
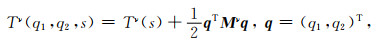
|
(4) |
|
图 1 射线中心坐标系(Červeny,2001) Fig. 1 Ray center coordinate system (Červeny, 2001) |
式中,ν表示不同类型波,即:qP波和qSV波;q3选取为射线弧长s;2×2复数矩阵Mν为不同类型波对应的走时关于坐标q1和q2的二阶偏导数.二维介质中,Mν(s)可表示为下式所示的形式:
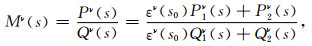
|
(5) |
式中,εν(s0)为复常数,s0为出射点位置,Pν(s)和Qν(s)为动力学射线追踪参数,表达式如下:
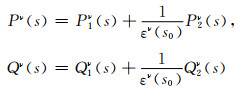
|
(6) |
研究表明(Červeny,2001),复变量M的实部影响着高斯束的波前曲率等几何特性,M的虚部影响着高斯束的轮廓.根据Nowack(2008)的研究,将复常数εν(s0)调整为复值参数εν(s),实现地震波束聚焦:
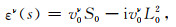
|
(7) |
式中,i为虚数单位,v0ν表示不同类型波对应的初始速度,S0表示束腰距离射线初始点的位置,L0为束腰处束的有效半宽度.聚焦型传播算子只能对某一特定位置处波束进行聚焦,因而在应用中有一定局限性.为此,学者们(Nowack, 2011; 杨继东等,2015)进一步修改复值参数εν(s),构建起动态聚焦型传播算子:
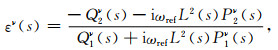
|
(8) |
式中,ωref为参考频率,L(s)为地下某点处束腰宽度:
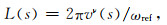
|
(9) |
通过构建动态聚焦型传播算子来调整复值参数MDFBν(s):
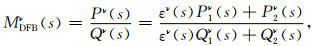
|
(10) |
将调整后的参数MDFBν(s)代入高斯束表达式,将地震波束能量约束在一定范围内,进而表征出动态聚焦束,得到射线中心坐标系下动态聚焦束位移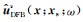
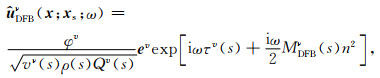
|
(11) |
式中,xs为出射点位置,x为计算点位置;ϕv为复常数;vν(s)为相速度;ρ(s)为密度;τν(s)为走时;Qν(s)为动力学射线追踪参数;n为射线在射线中心坐标系n方向分量,有:n=xcosθ-zsinθ,x,z为笛卡尔坐标系中的射线坐标位置,θ表示射线的出射角;ev为x处动态聚焦束的极化矢量,对于qP波,eqP=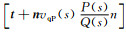
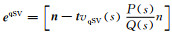
在前人研究基础上(李振春等,2018;岳玉波,2011),可将震源xs处qP波位移波场通过动态聚焦束位移矢量表示,得到各向异性介质动态聚焦束波场正向延拓公式:
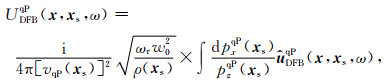
|
(12) |
式中ωr为动态聚焦束的参考频率;w0为动态聚焦束的初始宽度;ρ(xs)为xs处介质密度;x为计算点位置,vqP(xs)为震源xs处qP波相速度;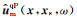
局部平面波分解后(Hill, 1990, 2001),利用qSV波位移矢量波场进行波场延拓,经过相移校正处理(李振春等,2018),令ρ(xr)≈ρ(xL),可得到束中心xL处qSV波反向延拓公式:
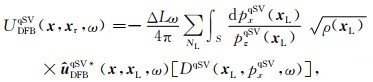
|
(13) |
式中NL为束中心的数目;xr为接收点位置;ΔL为束中心间隔;pxqSV(xL),pzqSV(xL)分别为qSV波慢度矢量x和z分量;DqSV(xL, pxqSV, ω)为局部倾斜叠加:
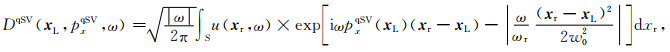
|
(14) |
式中,u(xr, ω)为地震记录.
1.3.4 qPqSV波成像公式根据互相关成像条件(Claerbout, 1971),可得各向异性介质qPqSV转换波互相关成像公式:
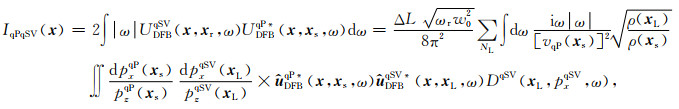
|
(15) |
式中vqP(xs)为震源xs处qP波相速度;*表示复值共轭.
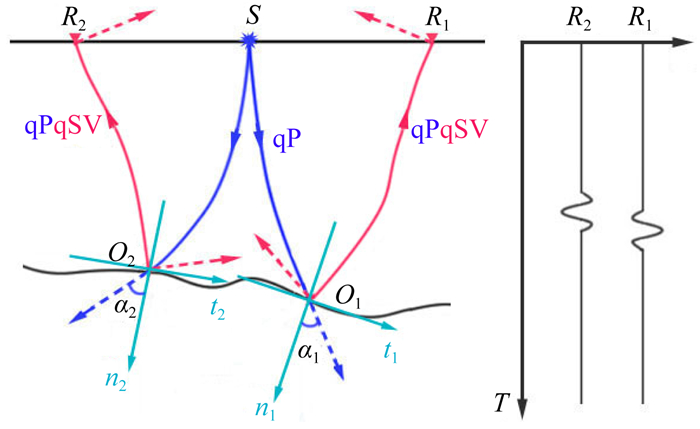
利用式(15),可以实现各向异性介质qPqSV波转换波成像.然而,转换波偏移成像会出现极性反转现象.为此,本文采用岳玉波(2011)、李振春等(2018)给出的研究思路,根据qP波入射角度的正负,通过符号函数sgn(α)校正极性反转问题.如图 2所示,入射qP波具有不同符号的入射角,导致R1点和R2点处的x分量地震记录极性相反.因此,可以根据qP波入射角α的正负对成像结果进行校正(岳玉波,2011;李振春等,2018),得到校正后的各向异性介质qPqSV转换波成像公式为
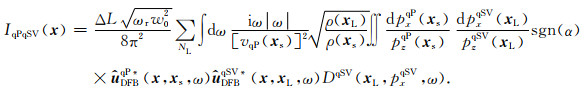
|
(16) |
|
图 2 qPqSV转换波在反射界面处的偏振(岳玉波,2011;李振春等,2018) Fig. 2 Polarization of qPqSV converted waves at the reflector |
本文进行地震波束数值模拟和模型测试,进一步说明本文方法在深层地质目标勘探中的潜在优势.
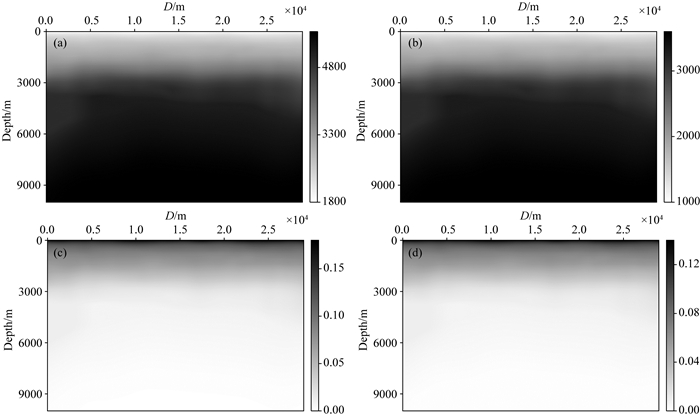
2.1 各向异性介质地震波束数值模拟本文采用各向异性速度场和各向异性参数场(如图 3),分别构建出高斯束、聚焦束以及动态聚焦束,进行地震波束数值模拟.横纵向采样点2901×2500,采样间隔10 m×4 m.结合式(5)—(11),计算出不同类型波的地震波束(如图 4).本文参考了Hill(2001)文中给出的经验公式,同时,为了形象地说明不同类型波地震波束的传播形态,测试中没有根据经验公式选取偏移中采用的初始束宽,最终数值计算采用的参考频率为35Hz,高斯束初始束宽为100 m.聚焦束束腰宽度L0为25 m,动态聚焦束束宽L(s)利用式(9)计算得到.
|
图 3 各向异性介质速度场及各向异性参数场 Fig. 3 The velocity and anisotropic parameters in anisotropic media (a) vp; (b) vs; (c) Epsilon; (d) Delta. |
|
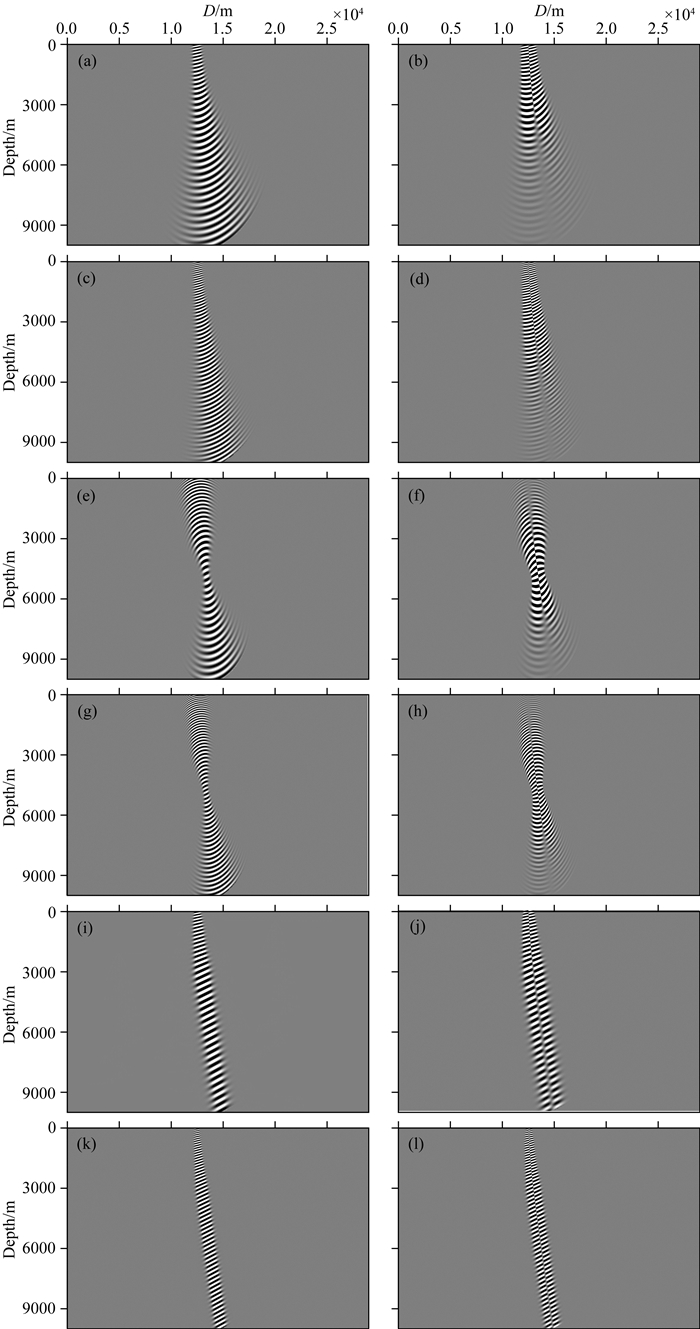
图 4 各向异性介质不同类型波地震波束 (a) qP波高斯束主分量;(b) qP波高斯束次分量;(c) qSV波高斯束主分量;(d) qSV波高斯束次分量;(e) qP波聚焦束主分量(5000 m);(f) qP波聚焦束次分量(5000 m);(g) qSV波聚焦束主分量(5000 m);(h) qSV波聚焦束次分量(5000 m);(i) qP波动态聚焦束主分量;(j) qP波动态聚焦束次分量;(k) qSV波动态聚焦束主分量和;(l) qSV波动态聚焦束次分量. Fig. 4 Seismic beams in anisotropic media (a) The principal component of qP wave Gaussian beam; (b) The additional component of qP wave Gaussian beam; (c) The principal component of qSV wave Gaussian beam; (d) The additional component of qSV wave Gaussian beam; (e) The principal component of qP wave focused beam (5000 m); (f) The additional component of qP wave focused beam(5000m); (g) The principal component of qSV wave focused beam (5000 m); (h) The additional component of qSV wave focused beam (5000 m); (i) The principal component of qP wave dynamically focused beam; (j) The additional component of qP wave dynamically focused beam; (k) The principal component of qSV wave dynamically focused beam; (l) The additional component of qSV wave dynamically focused beam. |
对比可以发现:随着传播距离的增加,图 4a、4b、4c和4d所示,qP波和qSV波的主分量和次分量高斯束在形态上都会发散较快,尤其初始束宽较窄时,高斯束束宽随传播距离增加而快速增大,这样会导致传到深部的能量发散,尤其对于次分量,中深层能量衰减明显;而图 4e、4f、4g和图 4h所示的聚焦束在地下某一位置处(5000 m处),可以将该处的波束收敛在束腰宽度内,从而使得该点处能量更加聚焦和收敛,但远离聚焦点时,形态上仍然会出现随传播距离增大而快速发散的现象.而图 4i、4j、4k和图 4l所示的动态聚焦束在传播过程中,将波束约束在中心射线附近一定范围内,从而使得能量保持收敛,有助于传播到深层,进而将为深层地质目标勘探提供解决思路.
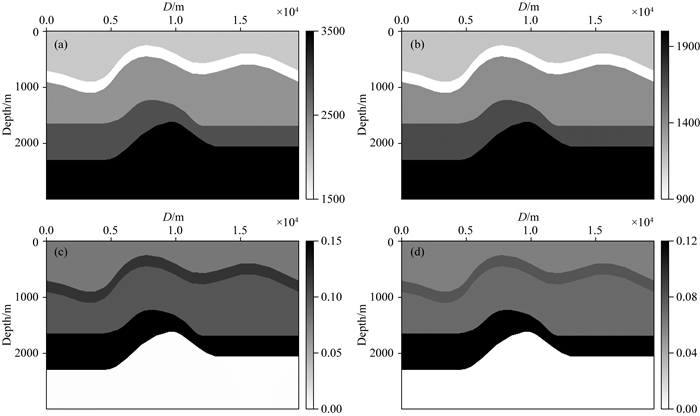
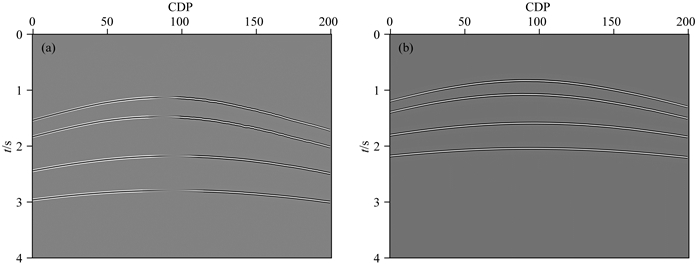
2.2 VTI低速异常模型为了说明本文研究方法的正确性,采用VTI介质低速异常模型进行测试.该模型的具体参数如下:横纵向采样点1951×300,采样间隔10 m×10 m.图 5a、5b、5c、5d分别给出了模型速度场和各向异性参数场.模型中存在低速异常区,伴有多个起伏构造,介质存在较为复杂各向异性.该地震数据采用各向异性介质转换波高斯束正演方法进行正演模拟,采取中间激发,双边接收的方式.地震记录共计311炮,炮间距为50 m;每炮201道接收,道间隔为20 m;地震记录采样时间为4.0 s,时间采样间隔为1 ms.正演模拟中考虑反射系数影响(Jílek, 2002),得到图 6所示的地震记录,该数据同相轴信息丰富,但受射线入射和反射角度关系影响,随着地层起伏的变化,浅层地震记录有效偏移距较小,导致远偏移距地震信息缺失,将会对偏移成像带来一定影响.图 7分别为运用各向同性转换波动态聚焦束偏移、各向异性转换波高斯束偏移以及各向异性转换波动态聚焦束偏移的成像结果.
|
图 5 VTI介质低速异常模型速度场及各向异性参数场 Fig. 5 The velocity and anisotropic parameters of low velocity model in VTI media (a) vp; (b) vs; (c) Epsilon; (d) Delta. |
|
图 6 地震记录 (a) x分量;(b) z分量(第3炮). Fig. 6 Seismic records (a) x component; (b) z component (third). |
|
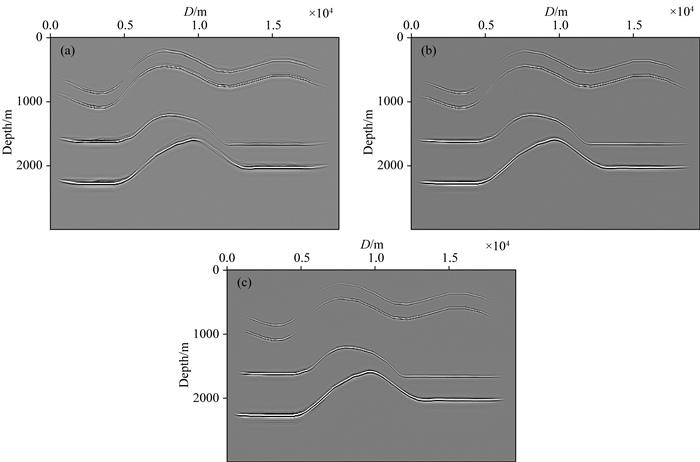
图 7 各向异性VTI介质低速异常模型偏移成像结果 (a) 各向同性介质转换波动态聚焦束偏移; (b) 各向异性介质转换波高斯束偏移; (c) 各向异性介质转换波动态聚焦束偏移. Fig. 7 The imaging results of low velocity model in VTI media (a) Isotropic converted wave dynamically focused beam migration; (b) Anisotropic converted wave Gaussian beam migration; (c) Anisotropic converted wave dynamically focused beam migration. |
对比分析可知,由于不考虑各向异性,各向同性转换波动态聚焦束偏移的结果,低速异常区及下覆地层,反射波没有准确归位,剖面两侧出现上翘的假象(即中远偏移距道集上翘),能量聚焦性较差,同相轴连续性不理想,整体信噪比较低.各向异性转换波高斯束和本文方法的偏移剖面,低速异常区及其下覆地层同相轴连续性增强,成像质量有效改善,但水平距离5000 m左右浅层低速异常区成像欠佳,分析原因为采用射线类正演模拟方法得到的地震数据远偏移距信息缺失,且受到偏移孔径影响,导致局部区域成像效果有待提升.本文研究方法在能量聚焦性上优于各向异性高斯束成像方法,成像质量更高.
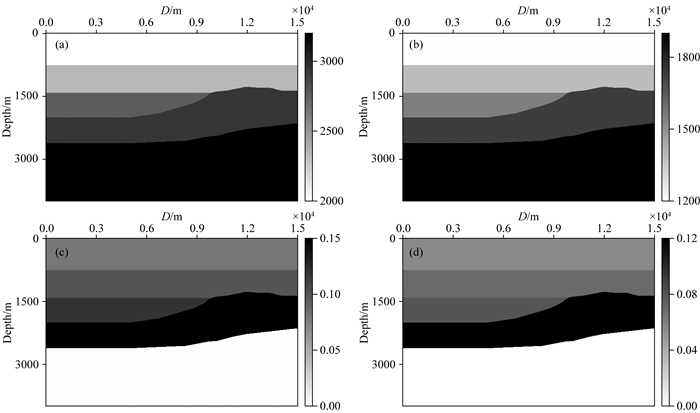
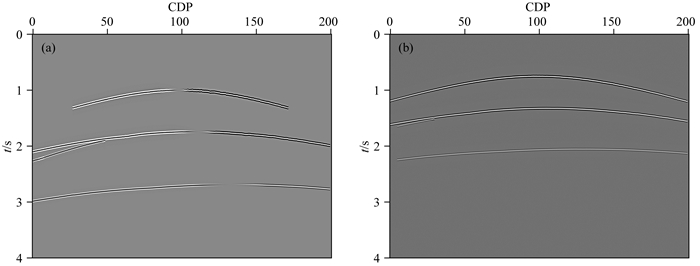
2.3 VTI多层构造模型为了进一步测试方法对存在各向异性的地质构造的有效性,本文采用VTI介质多层构造模型进行试算.为提高模型的合理性,本文参考文献(张雪莹等,2020)的研究设计了图 8所示的速度模型及各向异性参数模型,最终采用的速度及各向异性参数值如表 1所示,具体参数如下:横纵向采样点1501×400,采样间隔10 m×10 m.该模型伴有断层、断裂发育,地下介质为复杂各向异性.本文运用各向异性介质转换波高斯束正演模拟方法进行正演模拟,并将反射系数的影响引入到正演模拟中(Jílek, 2002).图 9给出了第166炮地震记录,其震源横向位置位于10.26 km,最大偏移距2 km.该地震数据共计221炮,炮间隔50 m;每炮201道接收,道间隔20 m;地震记录时间4 s,采样间隔为1 ms.图 10分别为运用各向同性转换波动态聚焦束、各向异性高斯束以及各向异性动态聚焦束偏移的成像结果.
|
图 8 VTI介质多层构造模型速度场及各向异性参数场 (a) vp; (b) vs; (c) Epsilon; (d) Delta. Fig. 8 The velocity and anisotropic parameters of VTI multilayers structure model |
|
|
表 1 多层构造模型速度及各向异性参数值 Table 1 The velocity and anisotropic parameters of VTI multilayer structure model |
|
图 9 地震记录 (a) x分量;(b) z分量(第166炮). Fig. 9 Seismic records (a) x component; (b) z component (166th). |
|
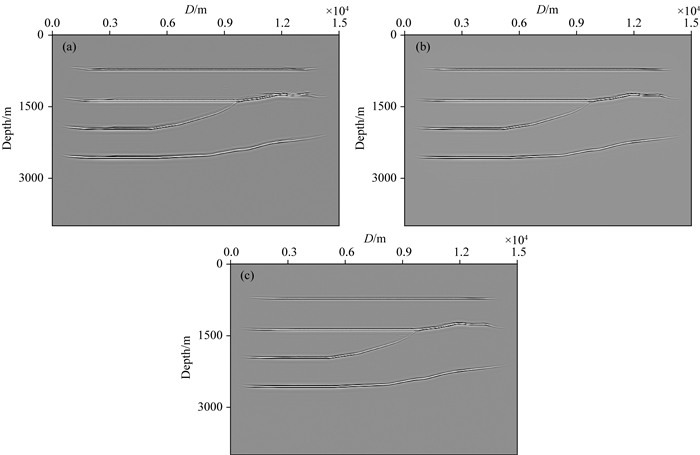
图 10 VTI介质多层构造模型偏移成像结果 (a) 各向同性介质转换波动态聚焦束偏移; (b) 各向异性介质转换波高斯束偏移; (c) 各向异性介质转换波动态聚焦束偏移. Fig. 10 The imaging results of VTI multilayer structure model (a) Isotropic converted wave dynamically focused beam migration; (b) Anisotropic converted wave Gaussian beam migration; (c) Anisotropic converted wave dynamically focused beam migration. |
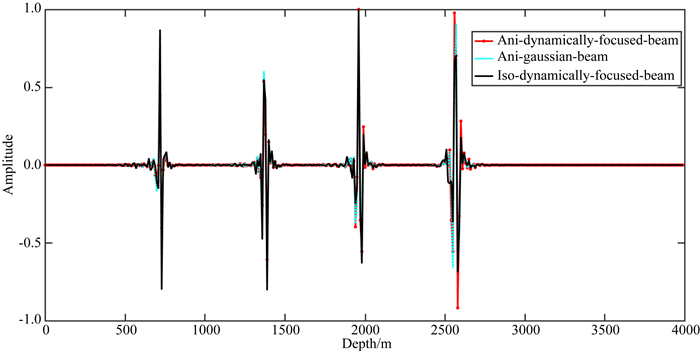
对比成像结果可以发现:运用各向同性转换波动态聚焦束偏移得到的结果,无论浅层还是中深层,成像归位不准确,绕射波收敛不完全,同相轴两侧出现上翘假象(即中远偏移距归位不准确),能量聚焦性不理想,整体成像质量欠佳.而运用各向异性转换波高斯束和本文方法得到的结果,反射波归位更加准确,同相轴能量更加收敛,连续性增强,断层、断裂等构造均得到较好的成像,整体成像质量明显提升;结合图 11所示的振幅曲线可知,本文方法得到的结果,能量更加均衡,中深层同相轴振幅能量聚焦性方面优于各向异性高斯束方法.模型试算的结果进一步说明了本文方法对复杂各向异性介质地质构造的适应性.
|
图 11 VTI介质多层构造模型单道振幅曲线对比(CDP=400) Fig. 11 The amplitude comparison for one trace of VTI multilayer structure model (CDP=400) |
试算的结果表明,本文研究方法能够综合运用纵横波波场信息,对低速异常区等复杂介质地质构造有效成像,得到分辨率较高的成像结果.
3 结论本文通过求解各向异性介质转换波运动学和动力学射线追踪方程,获得转换波中心射线走时、路径及动力学信息;并通过修改传播算子,构建起动态聚焦束,提出了一种各向异性介质动态聚焦束偏移成像方法.
复杂介质不同形态的地震波束数值模拟的结果表明:本文研究的转换波动态聚焦束可以使得波束在传播过程中能量保持聚焦,提高中深层能量的聚焦性,这将为解决深层地质目标成像提供新的研究思路.同时,本文运用VTI介质低速异常模型和多层构造模型进行试算,结果表明:本文研究方法能够有效利用纵横波波场信息,能够对存在低速异常区、断层等复杂构造成像.同其他方法相比,本文研究方法可使反射波归位更加准确,绕射波更加收敛,有助于提高中深层能量聚焦性.
当然,本文研究也存在一定的局限性,对转换波地震勘探中存在的分辨率、吸收衰减、三维成像等问题没有进行探讨.同时,由于正演模拟条件以及实际资料限制,没有对复杂模型和实际资料进行测试.接下来将进一步考虑吸收衰减对转换波成像振幅的影响等,提高方法的适应性.
致谢 感谢审稿专家和编辑部老师提出的宝贵意见!感谢各位专家、学者以及编辑部老师们对本文的指导与帮助!感谢Seismic Unix开源软件提供的技术支持!
Alkhalifah T. 1995. Gaussian beam depth migration for anisotropic media. Geophysics, 60(5): 1474-1484. DOI:10.1190/1.1443881 |
Cai J X, Wang H Z, Chen J, et al. 2017. Traveltime tomography in the image domain based on the Gaussian-beam-propagator. Chinese J. Geophys. (in Chinese), 60(9): 3539-3554. DOI:10.6038/cjg20170921 |
Casasanta L, Grion S. 2012. Converted-wave controlled-beam migration for vector-offset volumes. //64th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 1-5.
|
Červeny V. 1972. Seismic rays and ray intensities in inhomogeneous anisotropic media. Geophys. J. Int., 29(1): 1-13. DOI:10.1111/j.1365-246X.1972.tb06147.x |
Červeny V, Popov M M, Pšeník I. 1982. Computation of wave fields in inhomogeneous media-Gaussian beam approach. Geophys. J. Int., 70(1): 109-128. DOI:10.1111/j.1365-246X.1982.tb06394.x |
Červeny V. 2001. Seismic Ray Theory. Cambridge: Cambridge University Press.
|
Claerbout J F. 1971. Toward a unified theory of reflector mapping. Geophysics, 36(3): 467-481. DOI:10.1190/1.1440185 |
Dai H C, Li X Y. 2006. The effects of migration velocity errors on traveltime accuracy in prestack Kirchhoff time migration and the image of PS converted waves. Geophysics, 71(2): S73-S83. DOI:10.1190/1.2187788 |
Du Q Z, Guo C F, Zhao Q, et al. 2017. Vector-based elastic reverse time migration based on scalar imaging condition. Geophysics, 82(2): S111-S127. DOI:10.1190/geo2016-0146.1 |
Duan X Y, Li Z C, Huang J P, et al. 2014. A prestack Gaussian beam depth migration in common-shot domain for anisotropic media. Geophys. Prospect. Pet. (in Chinese), 53(5): 579-586. |
Gong X F, Du Q Z, Zhao Q. 2018. SP- and SS- imaging for 3D elastic reverse time migration. Geophysics, 83(1): A1-A6. DOI:10.1190/geo2017-0286.1 |
Gong X F. 2018. Study on converted wave imaging for 3D elastic reverse-time migration [Ph. D. thesis] (in Chinese). Qingdao: China University of Petroleum (East China).
|
Granli J R, Arntsen B, Sollid A, et al. 1999. Imaging through gas-filled sediments using marine shear-wave data. Geophysics, 64(5): 668-677. |
Gray S H. 2005. Gaussian beam migration of common-shot records. Geophysics, 70(4): S71-S77. DOI:10.1190/1.1988186 |
Han J G, Wang Y, Xing Z T, et al. 2014. Gaussian beam prestack depth migration of converted wave in TI media. J. Appl. Geophys., 109: 7-14. DOI:10.1016/j.jappgeo.2014.07.008 |
Han J G, Wang Y, Zhang X B, et al. 2015. Gaussian beam prestack depth migration in VTI media. Oil Geophys. Prospect. (in Chinese), 50(2): 267-273. |
Han J G, Lü Q T, Gu B L, et al. 2020. 2D anisotropic multicomponent Gaussian-beam migration under complex surface conditions. Geophysics, 85(2): S89-S102. DOI:10.1190/geo2018-0841.1 |
Hill N R. 1990. Gaussian beam migration. Geophysics, 55(11): 1416-1428. DOI:10.1190/1.1442788 |
Hill N R. 2001. Prestack Gaussian-beam depth migration. Geophysics, 66(4): 1240-1250. DOI:10.1190/1.1487071 |
Hu H, Liu Y K, Zheng Y C, et al. 2006. Least-squares Gaussian beam migration. Geophysics, 81(3): S87-S100. |
Hu Z D, Lü Q D, Han L H, et al. 2020. Elastic space-time Gaussian beam method for seismic depth imaging. Chin. J. Geophys. (in Chinese), 63(2): 652-665. DOI:10.6038/cjg2020M0542 |
Jílek P. 2002. Converted PS-wave reflection coefficients in weakly anisotropic media. Pure Appl. Geophys., 159(7): 1527-1562. DOI:10.1007/s00024-002-8696-9 |
Kuo J T, Dai T F. 1984. Kirchhoff elastic wave migration for the case of noncoincident source and receiver. Geophysics, 49(8): 1223-1238. DOI:10.1190/1.1441751 |
Li X L, Mao W J, Shi X C, et al. 2018. Elastic 3D PS converted-wave Gaussian beam migration. Geophysics, 83(3): S213-S225. DOI:10.1190/geo2017-0122.1 |
Li Y Y, Guo Q, Li Z C, et al. 2019. Elastic reflection waveform inversion with variable density. Geophysics, 84(4): R553-R567. DOI:10.1190/geo2017-0722.1 |
Li Z C, Liu Q, Han W G, et al. 2018. Angle domain converted wave Gaussian beam migration in VTI media. Chin. J. Geophys. (in Chinese), 61(4): 1471-1481. DOI:10.6038/cjg2018K0455 |
Liu Q. 2017. The research of Gaussian beam migration methods in Transversely Isotropic (TI) media [Master's thesis] (in Chinese). Qingdao: China University of Petroleum (East China).
|
Liu Q, Zhang M, Li Z C, et al. 2016. Common-shot domain Gaussian beam migration in anisotropic media. Oil Geophys. Prospect. (in Chinese), 51(5): 930-937. |
Liu Y S, Xu T, Wang Y H, et al. 2019. An efficient source wavefield reconstruction scheme using single boundary layer values for the spectral element method. Earth Planet. Phys., 3(4): 342-357. DOI:10.26464/epp2019035 |
Lu J, Wang Y, Ji Y X, et al. 2018. Imaging techniques of multi-component seismic data. Chin. J. Geophys. (in Chinese), 61(8): 3499-3514. DOI:10.6038/cjg2018L0031 |
Lü Q D, Huang J P, Li Z C, et al. 2018. Efficient Gaussian beam method in time domain for anisotropic media. Prog. Geophys. (in Chinese), 33(6): 2428-2434. DOI:10.6038/pg2018BB0466 |
Meier M A, Lee P J. 2009. Converted-wave resolution. Geophysics, 74(2): Q1-Q16. DOI:10.1190/1.3074303 |
Nowack R L, Sen M K, Stoffa P L. 2003. Gaussian beam migration for sparse common-shot and common-receiver data. //73th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 1114-1117.
|
Nowack R L. 2008. Focused Gaussian beams for seismic imaging. //78th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 2376-2380.
|
Nowack R L. 2011. Dynamically focused Gaussian beams for seismic imaging. Int. J. Geophys., 2011: 316581. |
Qin N. 2020. Time-domain Gaussian beam prestack depth migration for acoustic anisotropic media. Oil Geophys. Prospect. (in Chinese), 55(4): 813-820. |
Shabelansky A H, Malcolm A, Fehler M. 2017. Converted-wave seismic imaging: amplitude-balancing source-independent imaging conditions. Geophysics, 82(2): S99-S109. DOI:10.1190/geo2015-0167.1 |
Stewart R R, Gaiser J E, Brown J R, et al. 2002. Converted-wave seismic exploration: methods. Geophysics, 67(5): 1348-1363. DOI:10.1190/1.1512781 |
Tanushev N, Popovici A M, Hardesty S. 2017. Fast, high-resolution beam tomography and velocity-model building. Lead. Edge, 36(2): 140-145. DOI:10.1190/tle36020140.1 |
Thomsen L. 1999. Converted-wave reflection seismology over inhomogeneous, anisotropic media. Geophysics, 64(3): 678-690. DOI:10.1190/1.1444577 |
Wang C L, Cheng J B, Arntsen B. 2016. Scalar and vector imaging based on wave mode decoupling for elastic reverse time migration in isotropic and transversely isotropic media. Geophysics, 81(5): S383-S398. DOI:10.1190/geo2015-0704.1 |
Xiao J E, Li Z C, Zhang K, et al. 2019. Angle-domain reverse time migration with Gaussian beams for TI media. Oil Geophys. Prospect. (in Chinese), 54(5): 1067-1074. |
Yang J D, Huang J P, Wu J W, et al. 2015. Accuracy factors of Green function constructed with different seismic wave beams. Oil Geophys. Prospect. (in Chinese), 50(6): 1073-1082. |
Yang J D, Zhu H J, Huang J P, et al. 2018. 2D isotropic elastic Gaussian-beam migration for common-shot multicomponent records. Geophysics, 83(2): S127-S140. DOI:10.1190/geo2017-0078.1 |
Yue Y B. 2011. Study on Gaussian beam migration methods in complex medium [Ph. D. thesis] (in Chinese). Qingdao: China University of Petroleum (East China).
|
Yue Y B, Li Z C, Qian Z P, et al. 2018. Optimized imaging schemes of PS-wave Kirchhoff prestack time migration. Chin. J. Geophys. (in Chinese), 61(3): 1188-1195. DOI:10.6038/cjg2018L0196 |
Yue Y B, Save P, Qian Z P, et al. 2019. Least-squares Gaussian beam migration in elastic media. Geophysics, 84(4): S140-S340. |
Yue Y B, Liu Y, Li Y, et al. 2021a. Least-squares Gaussian beam migration in viscoacoustic media. Geophysics, 86(1): S17-S28. DOI:10.1190/geo2020-0129.1 |
Yue Y B, Liu Y J, Gray S H. 2021b. Accelerating least-squares Kirchhoff time migration using beam methodology. Geophysics, 86(3): S221-S234. DOI:10.1190/geo2020-0629.1 |
Zhang X Y, Sun P Y, Ma X J, et al. 2020. Exact reflection coefficients of orthorhombic anisotropic media. Oil Geophys. Prospect. (in Chinese), 55(5): 1060-1072. |
Zhu T F, Gray S, Wang D L. 2005. Kinematic and dynamic raytracing in anisotropic media: theory and application. //75th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 96-99.
|
Zhu T F, Gray S H, Wang D L. 2007. Prestack Gaussian-beam depth migration in anisotropic media. Geophysics, 72(3): S133-S138. DOI:10.1190/1.2711423 |
Zhu T F. 2013. Complex-beam migration: formulation and comparisons. //83th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 3687-3691.
|
蔡杰雄, 王华忠, 陈进, 等. 2017. 基于高斯束传播算子的成像域走时层析成像方法. 地球物理学报, 60(9): 3539-3554. DOI:10.6038/cjg20170921 |
段新意, 李振春, 黄建平, 等. 2014. 各向异性介质共炮域高斯束叠前深度偏移. 石油物探, 53(5): 579-586. DOI:10.3969/j.issn.1000-1441.2014.05.011 |
公绪飞. 2018. 三维弹性逆时偏移转换波成像方法研究[博士论文]. 青岛: 中国石油大学(华东).
|
韩建光, 王赟, 张晓波, 等. 2015. VTI介质高斯束叠前深度偏移. 石油地球物理勘探, 50(2): 267-273. |
胡自多, 吕庆达, 韩令贺, 等. 2020. 二维弹性多波时空域高斯束偏移方法. 地球物理学报, 63(2): 652-665. DOI:10.6038/cjg2020M0542 |
李振春, 刘强, 韩文功, 等. 2018. VTI介质角度域转换波高斯束偏移成像方法研究. 地球物理学报, 61(4): 1471-1481. DOI:10.6038/cjg2018K0455 |
刘强, 张敏, 李振春, 等. 2016. 各向异性介质共炮域高斯束偏移. 石油地球物理勘探, 51(5): 930-937. |
刘强. 2017. TI介质高斯束深度偏移成像方法研究[硕士论文]. 青岛: 中国石油大学(华东).
|
芦俊, 王赟, 季玉新, 等. 2018. 多分量地震数据的成像技术. 地球物理学报, 61(8): 3499-3514. DOI:10.6038/cjg2018L0031 |
吕庆达, 黄建平, 李振春, 等. 2018. VTI介质时间域高斯束偏移. 地球物理学进展, 33(6): 2428-2434. DOI:10.6038/pg2018BB0466 |
秦宁. 2020. 声波各向异性时间域高斯束叠前深度偏移. 石油地球物理勘探, 55(4): 813-820. |
肖建恩, 李振春, 张凯, 等. 2019. TI介质角度域高斯束逆时偏移方法. 石油地球物理勘探, 54(5): 1067-1074. |
杨继东, 黄建平, 吴建文, 等. 2015. 不同地震波束构建格林函数的精度影响因素分析. 石油地球物理勘探, 50(6): 1073-1082. |
岳玉波. 2011. 复杂介质高斯束偏移成像方法研究[博士论文]. 青岛: 中国石油大学(华东).
|
岳玉波, 李振春, 钱忠平, 等. 2018. 转换波Kirchhoff叠前时间偏移的成像优化方案. 地球物理学报, 61(3): 1188-1195. DOI:10.6038/cjg2018L0196 |
张雪莹, 孙鹏远, 马学军, 等. 2020. 正交各向异性介质反射系数精确解. 石油地球物理勘探, 55(5): 1060-1072. |
 2021, Vol. 64
2021, Vol. 64


