地球物理学报  2021, Vol. 64 Issue (9): 3021-3029   PDF    
引用本文
邱封钦, 潘雄, 罗小敏, 等. 2021. 综合半参数核估计和自回归补偿的全球电离层总电子含量预报模型. 地球物理学报, 64(9): 3021-3029, doi: 10.6038/cjg2021O0436.  
Qiu F Q, Pan X, Luo X M, et al. 2021. Global ionospheric TEC prediction model integrated with semiparametric kernel estimation and autoregressive compensation. Chinese J. Geophys. (in Chinese), 64(9): 3021-3029, doi: 10.6038/cjg2021O0436.  
综合半参数核估计和自回归补偿的全球电离层总电子含量预报模型
邱封钦, 潘雄, 罗小敏, 赖祖龙, 蒋可, 王广兴     
中国地质大学(武汉)地理与信息工程学院, 武汉 430078
收稿日期 2020-11-11, 2021-06-19 收修定稿
基金项目: 国家自然科学基金（41874009）资助
第一作者简介: 邱封钦, 男, 1997年生, 硕士生, 主要从事电离层建模与预报方法研究.E-mail: qiufengqin@cug.edu.cn
通讯作者: 王广兴, 男, 1987年生, 讲师, 主要从事GNSS精密单点定位研究.E-mail: wanggx@cug.edu.cn
摘要：针对电离层半参数球谐函数模型中窗宽参数选择引起的估计偏差，本文在传统的电离层球谐函数模型中引入半参数核估计和自回归（Autoregressive model，AR）模型，分别用于分离球谐函数模型的系统误差和窗宽参数引起的估计偏差，提出一种全球电离层总电子含量（Total Electron Content，TEC）组合预报模型.首先，利用多项式拟合法剔除球谐系数的趋势项；然后利用频谱分析法提取球谐系数的周期，引入半参数核估计平差模型求解模型参数，建立半参数球谐函数（Semiparametric-Spherical Harmonic，Semi-SH）模型；最后将Semi-SH模型拟合残差用AR模型补偿预报.实验结果表明，组合预报模型相比单一的Semi-SH模型有较大的提升，全球TEC预报值与欧洲定轨中心（Center for Orbit Determination in Europe，CODE）发布的TEC值相比，单天预报残差小于1 TECU、3 TECU和5 TECU占比分别为54.30%、93.40%和98.61%；组合模型滑动预报5天相对精度在低、中、高纬度地区分别提高了2.14%、1.32%和2.32%.
关键词: 电离层TEC      半参数模型      自回归模型      组合预报     
Global ionospheric TEC prediction model integrated with semiparametric kernel estimation and autoregressive compensation
QIU FengQin, PAN Xiong, LUO XiaoMin, LAI ZuLong, JIANG Ke, WANG GuangXing     
School of Geography and Information Engineering, China University of Geosciences, Wuhan 430078, China
Abstract: Aiming at the estimation deviation caused by the selection of window width parameters in the ionospheric semi-parametric spherical harmonic function model, the semi-parametric kernel estimation and the autoregressive (AR) model are introduced to the traditional ionospheric harmonic function model, which are used to separate the systematic error of spherical harmonic function model and the estimation deviation of window width parameters respectively. A combined model for the forecasting of global ionospheric total electron content (TEC) is proposed in this paper. Firstly, the trend term of the ionospheric spherical harmonic coefficient is eliminated by polynomial fitting. Secondly, the spectral analysis method is used to extract the period of the ionospheric spherical harmonic coefficient, and the semiparametric kernel estimation adjustment model is introduced to solve the model parameters. Based on the aforementioned work, the semiparametric-spherical harmonic model (Semi-SH) is established. Finally, the prediction is carried out after using the AR model to compensate the Semi-SH model fitting residual error. The results indicate that the combined forecasting model based on the semi-parametric kernel estimation and the AR model shows certain advantages than the ordinary Semi-SH model. For validation, the TEC values obtained with the proposed model are compared with those issued by the Center for Orbit Determination in Europe (CODE), and the daily forecasting residuals of global TEC less than 1 TECU, 3 TECU and 5 TECU account for 54.30%, 93.40%, and 98.61% respectively. For the 5-day sliding forecast, the relative accuracy of the combined model are improved by 2.14%, 1.32% and 2.32% in low-, mid- and high-latitude regions respectively.
Keywords: Ionospheric TEC    Semiparametric model    AR model    Combined forecast    
0 引言

电离层延迟是卫星导航定位系统的一项重要误差来源，电离层对卫星伪距和载波信号产生时延效应，最大可达数十米，在实时单频导航定位中必须对电离层延迟加以改正.电离层总电子含量(Total Electron Content, TEC)直接影响电离层延迟的大小，为了降低电离层对于卫星信号的影响，需要对电离层TEC进行精确预报(张强等，2014；章红平等，2006).

电离层预报模型分为经验模型和非经验模型.经验模型有Klobuchar、IRI、Bent等模型(袁运斌等，2017)；非经验模型有球谐函数模型、多项式模型等(李志刚等，2007；安家春等，2015；蔡成辉等，2015).这些模型计算简单，使用方便，但电离层受到太阳活动、灾害性天气等很多因素影响，模型无法精确反映电离层不规则扰动，且模型本身具有不合理性，例如Klobuchar模型将夜间TEC视为常数，导致经验模型预报精度不高(Pongracic et al., 2019；周仁宇等，2019).球谐函数模型通过预报电离层球谐函数系数，将预报得到的球谐系数代入球谐函数模型中，计算出格网点的TEC预报值(Li et al., 2019；Schaer, 1999).该模型可计算全球任意经纬度的电离层TEC值，但是模型观测数据存在系统误差以及模型误差的影响.对此，王喜江等(2020)提出了一种基于半参数核估计的电离层球谐函数模型(Semiparametric-Spherical Harmonic, Semi-SH)，将系统误差及小周期项归入到非参数分量部分，有效地削弱了系统误差对预报精度的影响.

在半参数核估计理论中，窗宽参数是一个非常关键的平滑因子，窗宽参数的选取直接影响参数估计和非参数估计的精度，作为权衡核估计偏差和方差之间的参数，它不能使参数估计偏差和非参数估计偏差同时变小(赵春茹，2011；李文涛等，2020；Yan et al., 2020).颜雄(2019)在利用半参数核估计模型预报北斗钟差时，分析了不同核函数和窗宽参数选取对模型误差的影响，发现选取不同核函数及窗宽参数建模对钟差数据的有用信息均存在提取不充分的情况.所以半参数球谐函数模型对电离层TEC预报依然存在偏差.鉴于此，本文利用半参数球谐函数模型对15阶球谐系数预报，拟合残差建立自回归(Autoregressive model, AR)模型进行补偿预报，提出一种组合预报模型，减小因窗宽参数选取导致的估计偏差，提高电离层预报精度.

1 模型构建 1.1 半参数球谐函数模型

电离层球谐函数各阶次球谐系数随时间具有周期性变化特性，利用频谱分析法对各阶次球谐系数时间序列三角级数分解，建立球谐函数频谱分析模型，即可对球谐系数拟合和预报，进而预报全球TEC值.

电离层球谐系数时间序列可表示为

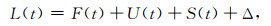
(1)

其中, L(t)为球谐系数时间序列；F(t)为趋势项，可表示为式(2)的多项式回归方程；U(t)为周期项，可表示为式(3)的三角级数形式；S(t)为模型的随机信号，与球谐系数无确定关系，是非参数分量；Δ为观测噪声.

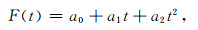
(2)

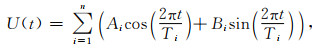
(3)

式(3)中，n为提取的球谐系数周期个数，Ti为提取的球谐系数周期，Ai、Bi为模型的待估参数.将式(3)化为矩阵形式：

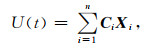
(4)

其中

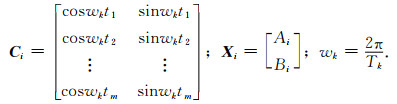
式(4)的误差方程为

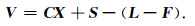
(5)

为了求解待估参数和非参数分量，假设 X 已知，基于{tk, (Lk－Fk)－CkX }k=1n可对非参数分量S(ti)做核估计如下：

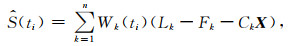
(6)

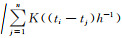
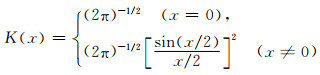
Wk(ti)为选取的核权函数，对时间点ti有Wk(ti)=K((ti－tk)h－1) ，式中k, j=1, 2, …, n；n为球谐系数时间序列长度；K(·)为选取的核函数；h为采用最小均方误差法(MSE法)选取的窗宽参数(潘雄等，2016；赵春茹，2011；杨玉锋等，2020).

(7)

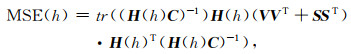
(8)

式(8)中，tr(·)为矩阵的迹；H(h)为影响矩阵，H(h)= CT(I-W)T(I-W)；当MSE(h)取值最小时，确定对应的窗宽参数.

结合式(5)和式(6)，利用最小二乘原则可求得待估参数 X 和非参数分量 S 的估值：

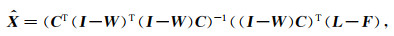
(9)

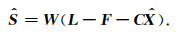
(10)

最后将拟合的趋势项、解算的待估参数和随机信号代入式(1)，建立半参数球谐函数模型，实现对球谐系数的拟合和预报.

1.2 综合半参数核估计与自回归补偿预报模型

由式(8)、式(9)和式(10)可知，窗宽参数的合理选择对半参数球谐函数模型的预报结果影响较大.半参数球谐函数模型中，窗宽参数作为一个惩罚因子，在分离参数分量和非参数时，会出现估计偏差，需对拟合残差中的有用信号进一步分离.将球谐系数观测值减去半参数球谐函数模型拟合值，得到的球谐系数残差序列Y采用AR模型进行拟合和预报.

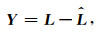
(11)

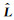
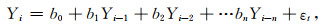
其中，L为球谐系数序列，为半参数球谐系数拟合值.AR模型是一种平稳时间序列预报方法，球谐系数残差序列 Y 的AR模型可表示为

(12)

其中，b0为常数项，b1, b2, …, bn为自回归模型系数；i=1, 2, …, N；N为残差序列长度；n为AR模型阶数；εt是均值为0，方差为σ2的白噪声.令

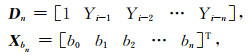
将式(12)转化为矩阵形式：

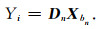
(13)

i时刻的残差值是由该时刻之前的n个时刻的残差值进行估计，将残差序列代入式(13)组成观测方程, 根据式(14)最小二乘原则可求得AR模型参数，建立残差AR模型，实现对半参数球谐函数模型残差的补偿预报.

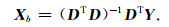
(14)

改进的组合模型预测值采用串联式组合，如式(15)所示：

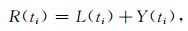
(15)

式中，R(ti)为组合预报模型预测值；L(ti)和Y(ti) 分别为半参数球谐函数预测值和AR模型残差预测值.

将半参数球谐函数模型预报值与AR模型残差预报值求和，即得到组合预报模型的球谐系数预报值.将各阶次球谐系数预报值代入全球电离层电子含量球谐函数模型，即可求得全球电离层TEC格网值.模型方程如式(16)所示：

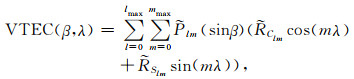
(16)

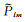
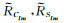
其中，β为地磁纬度；λ为日固地磁系下的经度；为缔合勒让德多项式；为预报得到的球谐系数；l, m分别为球谐系数的阶数和次数.

2 算例分析 2.1 数据来源

利用欧洲定轨中心(Center for Orbit Determination in Europe, CODE) 发布的高精度全球电离层球谐系数数据作为样本序列，选取2018年1月1日至2018年2月4日共计35天的15×15阶共计256个球谐函数系数作为观测值，采样频率为1 h.为了验证组合模型的有效性，分别利用Semi-SH模型和组合模型进行预报，将预报结果与CODE所发布的高精度全球电离层TEC格网值(CODG值)进行对比. CODG值是经差为5°、纬差为2.5°(87.5°N—87.5°S) 共计5183个高精度的全球格网值.本文采用的精度评定指标为均方根误差(RMS)和平均相对精度(P)

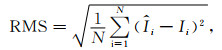
(17)

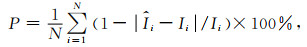
(18)

式中，N表示TEC数据个数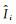；为第i个预报的TEC值；Ii为CODE发布的第i个格网值.

2.2 单天预报

利用2018年1月1日—1月30日共计30天的球谐系数，预报2018年1月31日1天内逐小时的球谐函数系数，根据球谐函数模型计算预报的总电子含量，实现全球TEC单天预报.

为了检验预报精度，将CODE发布的一天预报产品(C1PG值)、Semi-SH模型预报值和组合模型预报值与CODG值24 h的全球格网值进行比较，其差值图分布如图 1(a、b、c)所示.

图 1 C1PG值(a)、Semi-SH模型(b)和组合模型(c)单天预报残差全球分布图 Fig. 1 The global map of residuals of C1PG (a), Semi-SH (b) and combined model (c) value with respect to CODG value

图 1可以看出，Semi-SH模型和组合模型相比C1PG模型精度有明显提升，在0~16 h精度提升较大，两种模型的预报精度均随预报时间长度降低.在南极地区，C1PG模型预报精度较低.组合模型预报残差大部分在±3 TECU以内，说明了组合模型的有效性.从图 1b和1c可以看出，组合模型在前半天对单一的Semi-SH模型的改正效果较显著，主要表现在赤道附近残差较大区域；在后半天改正较小，这与自回归模型相关性逐渐减弱，模型趋稳有关.预报精度较低地区主要分布在南北纬20°左右，在赤道两侧呈驼峰状，与电离层赤道异常现象相关(田耀宇等，2019；黄江等，2013；Balan et al., 2018).

表 1是C1PG模型、Semi-SH模型、组合模型三种模型的预报残差分析.由表 1可知，组合模型预报精度高于单一的Semi-SH模型，预报均方根误差为1.59 TECU，C1PG模型精度最低；在北半球地区，三种模型的预报精度都比南半球地区的预报精度高，这可能是南半球处于夏季，电离层电子活跃度高于北半球，以及南半球海洋面积广阔，地基观测站观测数据密度小，导致预报精度降低.

表 1 C1PG模型、Semi-SH模型和组合模型预报值残差分析 Table 1 C1PG model, Semi-SH model and combined model prediction residual analysis

组合模型预报差值在1 TECU以内占比54.30%、在3 TECU以内占比93.40%，普遍高于C1PG模型和单一的Semi-SH模型；三种模型预报差值在5 TECU以内占比均达到98%以上，其中组合模型预报差值在5 TECU以内占比98.61%，优于CIPG模型和单一的Semi-SH模型.

2.3 多天预报

利用2018年1月1日—1月30日共计30天的球谐系数，单次预报一天，滑动预报2018年1月31日—2月4日共计5天的球谐系数，根据球谐函数模型计算预报的总电子含量，实现全球TEC预报，预报结果与COGD值进行检验.

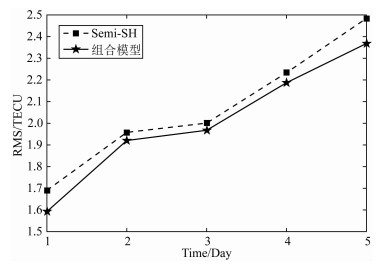
图 2为Semi-SH模型和组合模型滑动5天预报值与CODG值对比的均方根误差统计.因C1PG为CODE发布的一天预报产品模型，与滑动5天预报结果可比性不强，故未引入比较.从图中可以看出，组合模型预报精度均高于Semi-SH模型.随着预报时长增加，两种模型的预报精度都逐步降低.

图 2 Semi-SH模型和组合模型预报RMS统计 Fig. 2 RMS statistics of Semi-SH value and combined model value relative to CODG value

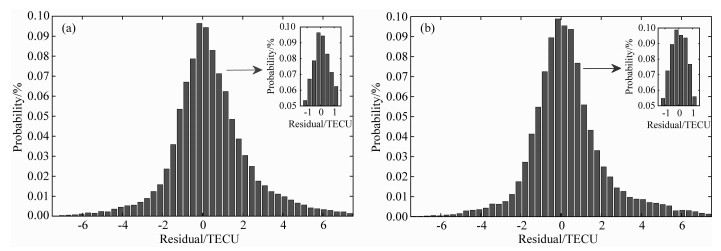
取滑动预报5天每天00 ∶ 00 h共计25915(71×73×5) 个全球格网点预报残差数据进行统计，图 3a和3b分别是Semi-SH模型和组合模型滑动5天预报残差概率密度统计图.从图 3中可以看出，两种模型预报残差主要分布在±3 TECU以内，大于5 TECU的残差值所占比例较小，说明两种模型用于全球电离层TEC预报的可靠性.组合模型预报残差值小于1 TECU占比53.43%，Semi-SH模型小于1 TECU占比49.83%，组合模型有明显提高.

图 3 Semi-SH模型(a)和组合模型(b)预报残差密度统计 Fig. 3 Semi-SH model (a) and combined model (b) forecast residual probability density statistics

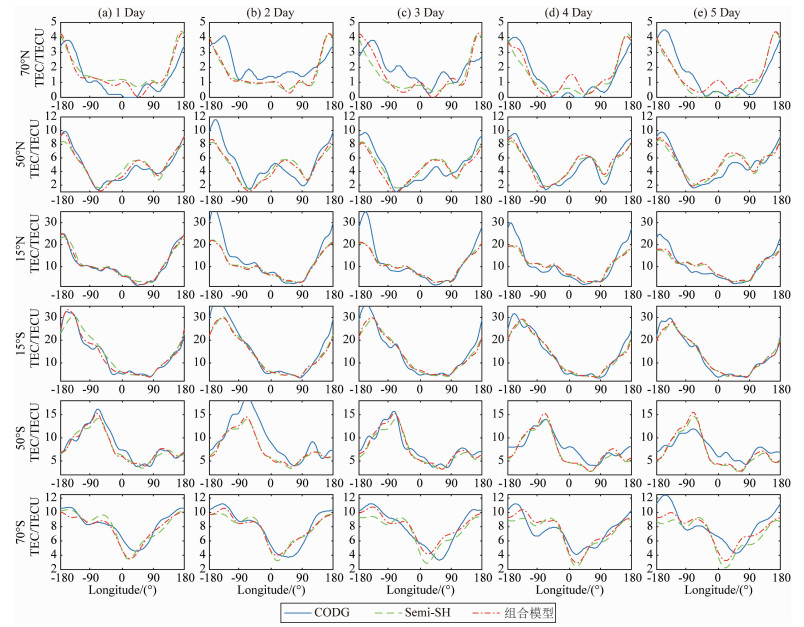
为了分析不同纬度下组合模型的预报精度，根据滑动预报5天的总电子含量数据，分别选取不同纬度TEC值进行分析.图 4a—4e分别为Semi-SH模型和组合模型滑动预报5天00 ∶ 00 h的总电子含量与CODG格网值比较，从上至下依次为70°N、50°N、15°N、15°S、50°S和70°S六个纬度数据.

图 4 Semi-SH模型、组合模型预报值与CODG值对比 Fig. 4 Comparison of Semi-SH model, combined model forecast value with CODG value

从图 4可以看出Semi-SH模型和组合模型预报值都能较好反映出真实总电子含量及其变化趋势，组合模型的改进效果随着预报时间的增长而下降，这与预报误差滑动积累有关.白天中低纬度预报残差较大，这与白天中低纬度地区电离层电子活跃度高有关.在中低纬度地区，第2天的CODE-TEC值与其他天有一定区别，导致该天Semi-SH模型和组合模型的预测误差较大，这可能是当天该时刻地磁环境出现扰动造成的.组合模型在中高纬度地区以及预报前期比Semi-SH模型更加接近CODG值，后期与Semi-SH模型预报结果相近，改正效果减弱.

受季节因素影响，北半球高纬度地区夜间电离层电子浓度较低，该区域CODG值含有较多零值，相对精度失去评定意义，故只统计南半球15°S、50°S和70°S三个纬圈两种模型滑动预报5天的预报精度，结果见表 2.从表中可以看出，组合模型滑动预报5天精度在低、中、高纬度下均高于Semi-SH模型.组合模型在高纬度地区的改正效果最好，相对精度提高了2.32%；其次是低纬度地区，相对精度提高了2.14%；在中纬度地区改正效果较小，相对精度提高了1.32%.两种模型预报结果的均方根误差大致随着纬度的提高而减小.

表 2 Semi-SH模型和组合模型预报精度对比 Table 2 Comparison between the prediction accuracies of the Semi-SH model and the combined model
3 结论

本文对发布的15阶电离层球谐系数进行建模与预报，利用自回归模型对残差进行建模，实现对窗宽参数选取产生的估计偏差的补偿修正，提出一种全球电离层TEC组合预报模型，并通过实验，得出以下结论：

1) 组合预报模型在2018年1月31日当天的预报均方根误差为1.59 TECU，预报差值小于3 TECU的格网点占90%以上，表明组合预报模型的可行性；

2) 与Semi-SH模型相比，组合模型单天预报差值小于1 TECU、3 TECU和5 TECU的格网点分别占54.30%、93.40%和98.61%，均高于Semi-SH模型，且组合预报模型的预报精度优于单一Semi-SH模型；

3) 在滑动预报5天中，组合模型预报精度优于Semi-SH模型，组合模型对高纬度和低纬度地区改正效果明显，在中纬度地区改正较小.

致谢  感谢CODE提供的电离层数据产品.
References
An J C, Ning X G, Wang Z M, et al. 2015. Antarctic ionospheric prediction based on spherical cap harmonic analysis and time series analysis. Geomatics and Information Science of Wuhan University (in Chinese), 40(5): 677-681.
Balan N, Liu L B, Le H J. 2018. A brief review of equatorial ionization anomaly and ionospheric irregularities. Earth and Planetary Physics, 2(4): 257-275. DOI:10.26464/epp2018025
Cai C H, Liu L L, Li J Y, et al. 2015. Establishment of region ionospheric delay model in China based on a polynomial model with restrictive conditions. Journal of Geodesy and Geodynamics (in Chinese), 35(6): 1007-1011.
Huang J, Deng B C, Huang L F, et al. 2013. Analysis of the asymmetry of the equatorial ionization anomaly in north-south direction using TEC data of ground IGS observation. Acta Scientiarum Naturalium Universitatis Sunyatseni (in Chinese), 52(4): 130-137.
Li B F, Wang M M, Wang Y L, et al. 2019. Model assessment of GNSS-based regional TEC modeling: polynomial, trigonometric series, spherical harmonic and multi-surface function. Acta Geodaetica et Geophysica, 54(3): 333-357. DOI:10.1007/s40328-019-00262-8
Li W T, Yan X, Xia L, et al. 2020. Abnormal data detection and process by using BDS satellite offset semiparametric adjustment model. Acta Geodaetica et Cartographica Sinica (in Chinese), 49(1): 55-64.
Li Z G, Cheng Z Y, Feng C G, et al. 2007. A study of prediction models for ionosphere. Chinese Journal of Geophysics (in Chinese), 50(2): 327-337. DOI:10.3321/j.issn:0001-5733.2007.02.001
Pan X, Lv Y T, Wang Y, et al. 2016. Research of the location and valuation of gross error based on semi-parametric adjustment model. Geomatics and Information Science of Wuhan University (in Chinese), 41(11): 1421-1426.
Pongracic B, Wu F L, Fathollahi F, et al. 2019. Midlatitude klobuchar correction model based on the k-means clustering of ionospheric daily variations. GPS Solutions, 23(3): 80. DOI:10.1007/s10291-019-0871-x
Schaer S. 1999. Mapping and predicting the Earth's ionosphere using the global positioning system[Ph. D. thesis]. Berne, Switzerland: University of Bern.
Tian Y Y, Hao Y Q, Zhang D H, et al. 2019. Single crest phenomenon in the equatorial ionospheric anomaly region and its longitudinal distribution caused by nonmigrating tides. Chinese Journal of Geophysics (in Chinese), 62(11): 4067-4081. DOI:10.6038/cjg2019M0645
Wang X J, Bian S F, Li Z S, et al. 2020. Prediction of global ionospheric TEC using the semiparametric kernel estimation method. Chinese Journal of Geophysics (in Chinese), 63(4): 1271-1281. DOI:10.6038/cjg2020N0143
Yan X. 2019. Research on theory and method of BDS clock offset prediction model based on semi-parameter estimation [Master's thesis](in Chinese). Wuhan: China University of Geosciences.
Yan X, Li W T, Yang Y F, et al. 2020. BDS satellite clock offset prediction based on a semiparametric adjustment model considering model errors. Satellite Navigation, 1: 11. DOI:10.1186/s43020-019-0007-z
Yang Y F, Pan X, Qing C X, et al. 2020. Detection and repair of outliers in BDS satellite clock offset based on semiparametric mean drift model. Chinese Journal of Scientific Instrument (in Chinese), 41(8): 47-54.
Yuan Y B, Huo X L, Zhang B C. 2017. Research progress of precise models and correction for GNSS ionospheric delay in China over recent years. Acta Geodaetica et Cartographica Sinica (in Chinese), 46(10): 1364-1378.
Zhang H P, Ping J S, Zhu W Y, et al. 2006. Brief review of the ionospheric delay models. Progress in Astronomy (in Chinese), 24(1): 16-26.
Zhang Q, Zhao Q L, Zhang H P, et al. 2014. Evaluation on the precision of Klobuchar Model for BeiDou navigation satellite system. Geomatics and Information Science of Wuhan University (in Chinese), 39(2): 142-146.
Zhao C R. 2011. Semiparametric kernel estimation theory and its application in deformation monitoring [Master's thesis](in Chinese). Wuhan: China University of Geosciences.
Zhou R Y, Hu Z G, Su M D, et al. 2019. Preliminary performance evaluation of BeiDou global ionospheric delay correction model. Geomatics and Information Science of Wuhan University (in Chinese), 44(10): 1457-1464.
安家春, 宁新国, 王泽民, 等. 2015. 利用球冠谐函数和时间序列分析预报南极地区电离层. 武汉大学学报(信息科学版), 40(5): 677-681.
蔡成辉, 刘立龙, 黎峻宇, 等. 2015. 基于附有限制条件的多项式模型建立中国区域电离层模型. 大地测量与地球动力学, 35(6): 1007-1011.
黄江, 邓柏昌, 黄林峰, 等. 2013. 基于IGS的TEC赤道异常南-北不对称性分析. 中山大学学报(自然科学版), 52(4): 130-137.
李文涛, 颜雄, 夏磊, 等. 2020. BDS卫星钟差半参数平差模型异常数据探测与处理. 测绘学报, 49(1): 55-64.
李志刚, 程宗颐, 冯初刚, 等. 2007. 电离层预报模型研究. 地球物理学报, 50(2): 327-337. DOI:10.3321/j.issn:0001-5733.2007.02.001
潘雄, 吕玉婷, 汪耀, 等. 2016. 基于半参数平差模型的粗差定位与定值研究. 武汉大学学报(信息科学版), 41(11): 1421-1426.
田耀宇, 郝永强, 张东和, 等. 2019. 非迁移潮作用下的电离层赤道异常区单峰现象及其经度分布. 地球物理学报, 62(11): 4067-4081. DOI:10.6038/cjg2019M0645
王喜江, 边少锋, 李子申, 等. 2020. 利用半参数核估计法预报全球电离层总电子含量. 地球物理学报, 63(4): 1271-1281. DOI:10.6038/cjg2020N0143
颜雄. 2019. 基于半参数估计的BDS钟差预报模型的理论与方法研究[硕士论文]. 武汉: 中国地质大学.
杨玉锋, 潘雄, 卿晨昕, 等. 2020. 基于半参数均值漂移模型的BDS卫星钟差异常探测与修复. 仪器仪表学报, 41(8): 47-54.
袁运斌, 霍星亮, 张宝成. 2017. 近年来我国GNSS电离层延迟精确建模及修正研究进展. 测绘学报, 46(10): 1364-1378. DOI:10.11947/j.AGCS.2017.20170349
章红平, 平劲松, 朱文耀, 等. 2006. 电离层延迟改正模型综述. 天文学进展, 24(1): 16-26. DOI:10.3969/j.issn.1000-8349.2006.01.002
张强, 赵齐乐, 章红平, 等. 2014. 北斗卫星导航系统Klobuchar模型精度评估. 武汉大学学报(信息科学版), 39(2): 142-146.
赵春茹. 2011. 半参数核估计理论及其在变形监测中的应用研究[硕士论文]. 武汉: 中国地质大学.
周仁宇, 胡志刚, 苏牡丹, 等. 2019. 北斗全球系统广播电离层模型性能初步评估. 武汉大学学报(信息科学版), 44(10): 1457-1464.