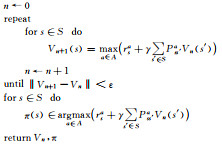在地震勘探层析成像、静校正、速度分析、AVO分析和地质解释中地震数据走时信息起着重要的作用,众多地球物理学家提出了许多算法,用以进行走时的拾取,这些方法都有各自的优缺点以及适用范围.所以,走时自动拾取算法的研究有其现实意义,算法的稳定性和准确性在经济上具有重要价值.传统走时拾取算法大体可分为两类:滑动时窗法和相干法(Molyneux and Schmitt, 1999).在滑动时窗方法中,地震信号序列其属性在连续或重叠的移动窗口中计算(Coppens,1985;Spagnolini,1991;Sabbione and Velis, 2010).相干类方法依赖于使用一些相似度测量技术比较单个或多个波形(López and Aldana, 2009).同时,近几年来,人工智能技术迅猛发展,机器学习算法在地球物理勘探领域的应用越来越广泛(Jia and Ma, 2017;Shi et al., 2020).
走时拾取工作是地震数据处理的重要一步,也是人工智能算法应用较为广泛的一个领域.比如,传统的神经网络(Artifical Neural Network,ANN)算法就已广泛应用于地震(微震)事件的自动分类识别中(Turhan et al., 1988;Veezhinathan and Wagner, 1990;Murat and Rudman, 1992;McCormack et al., 1993;Scarpetta et al., 2005;Esposito et al., 2006, 2013;Langer et al., 2006;AitLaasri et al., 2013;Vallejos and McKinnon, 2013;Maity et al., 2014;Riggelsen and Ohrnberger, 2014;Mousavi and Langston, 2016).但早期用于地震(微震)信号识别的网络结构受限于计算机能力一般设计比较浅,其泛化能力比较欠缺(Murat and Rudman, 1992).此外,Mousavi和Langston(2016)指出传统ANN算法常以工程特征(Engineered features)作为网络的输入,通过分析不同特征对自动化地震事件识别精度的影响,认为从原始数据中提取工程特征包含过多不确定性.卷积神经网络(CNN)一般包括卷积、池化和全连通层,是一种能力强大的深度学习算法(LeCun et al., 1995;于子叶等,2018;李薇薇等,2021).CNN使用其多个卷积层直接从图像或信号中提取不同的特征或属性,然后通过完全连接的层对其进行分类,将特征提取与分类放在同一网络结构中,这样很大程度上降低了提取工程特征对走时拾取精度的影响.Yuan等(2018)将CNN直接应用于地震初至走时中,将二维原始地震数据作为输入,相比单道输入,考虑了波形的空间横向连续性特征.为了进一步证明CNN算法在海量数据支持下,具有很强的分类能力,Loginov等(2019)以5000个训练样本训练包含4个隐藏层的CNN网络并用其完成了某3D地震数据(450万道)的初至走时拾取工作,正确率达到了95%.神经网络类方法,属于有监督学习,大量的标签样本产生不仅耗时,同时也会引入人的先验认识.无监督学习算法(比如模糊聚类分析、支持向量机等)直接根据特征属性将地(微)震信号自动分为几类,不但能够完成走时拾取工作,还能够为有监督学习提供标签样本(Chen,2000;蒋一然和宁杰远,2019;许鑫等,2020).Ma等(2019)基于强化学习理论,在能量比谱上自动化全局寻优实现初至走时拾取,但该方法缺乏对奖励函数和初始状态选择的详细描述,难以适应复杂波形.还有部分研究人员在传统走时拾取算法(Sabbione and Velis, 2010)的基础上,使用人工智能算法实现窗函数/拾取策略的自适应选取、质量监控等(Duan et al., 2018;Hollander et al., 2018;Mezyk and Malinowsk, 2018).总之,人工智能算法的引入,提高了拾取地震走时信息的自动化程度和精度,为地震数据处理提供了很大帮助.
在本文中,我们将初至拾取看作高维特征属性空间内带约束的Markov决策过程(Constrained Markov Decision Processes,CMDPs),在一定全局寻优准则的约束下获得积累奖励值最大的路径,从而自动化的拾取地震数据的初至信息.文中首先介绍了约束Markov决策理论,通过引入折扣因子γ、受空间几何信息约束的动作和转移概率,CMDPs算法能够自动获取地震数据的初至信息.接着,基于合成地震数据,分析了文中算法的抗噪能力以及常规MDPs和约束MDPs算法对参数的敏感程度,说明CMDPs算法不仅降低了对起始状态和折扣因子选择的难度,同时考虑地震数据的空间横向连续性,自动的回避地震数据中的坏道信息,具有一定QC功能,保证初至拾取更加准确和自动化.最后,实际地震数据的测试结果,证明CMDPs方法能准确地实现地震初至事件的自动拾取,特别是对弱初至信号或浅层相邻复杂波形的拾取.
1 约束Markov决策理论 1.1 Markov决策过程马尔科夫链(Markov chains),指在随机过程中,下一个状态仅取决于当前状态,和之前(历史)其他状态无关,即:
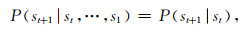
|
(1) |
其中,P(st+1|st)为状态转移概率,表示从状态st到st+1的概率.
马尔科夫决策过程(Markov Decision Processes,MDPs)即为在满足马尔科夫链前提下,一个智能体(Agent)采取行动(Action)从而改变自己的状态(State)获得奖励(Reward)与环境(Environment)发生交互的循环学习过程.其一般由五元组〈S, A, T, P, r〉描述(Sigaud and Buffet, 2013):
·S:有限状态集;
·A:控制状态发生变化的所有可能动作的集合;
·T:随机演变的时间(空间)序列;
·P:状态转移;
·r:状态转移时的奖励函数(瞬时).
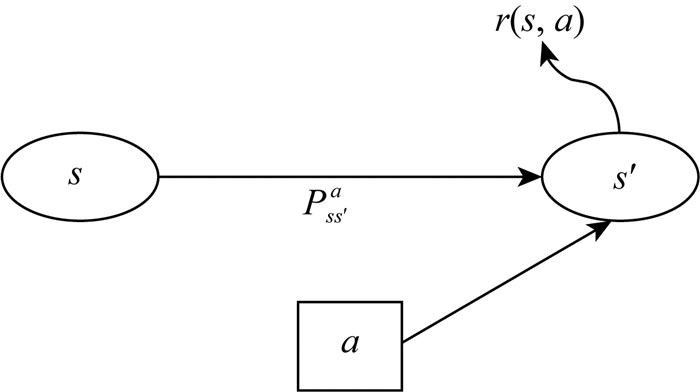
图 1为Markov决策过程的示意图.在每个时间步t和当前状态s下,执行动作at后,状态s有p(s′|s, a)的概率转移到下一个状态s′.r为实现该过程应获得的瞬时奖励值.
|
图 1 Markov决策过程示意图(Sigaud and Buffet, 2013) Fig. 1 Sketch showing Markov decision processes(Sigaud and Buffet, 2013) |
Markov决策过程使我们能够模拟一个随机系统的状态演化过程,在每一个时间步t,选取合适的动作at,最终完成合适的系统演化.这一系列的动作统称为策略,常记作π.对于给定策略π,我定义状态值函数Vγπ(s),用以表征任何两个状态之间的联系:
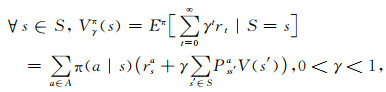
|
(2) |
其中,π(a|s)表示状态s下执行某种动作的概率,每个状态s都有这样一个π(a|s),所有的π(a|s)就构成整体策略π.Pss′a表示在状态s执行动作a后能够转移到状态s′的概率.rsa则是成功转移后的瞬时奖励值.γ称为折扣因子,其保证距离越远的奖励值对当前的影响越小,基于该特性能够很自然的回避由坏道引起的错误初至拾取结果(异常值或奇异点).Markov决策过程,就是希望寻找一个合适的策略,能够产生最大的积累奖励值,即:
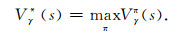
|
(3) |
根据Bellman equation方程(2),当γ<1时,Vγ*(s)存在唯一解.根据Sigaud和Buffet(2013)所述,值函数迭代法是求解Markov决策过程最常用的方法之一,其大体过程见表 1.
|
|
表 1 值函数迭代法—折扣策略 Table 1 Value iteration algorithm-discounted criterion |
如何将初至识别问题,提炼成一个包含〈S, A, T, P, r〉五个元素的Markov决策过程?以图 2中合成2D地震数据为例,状态空间S和时间序列T定义为
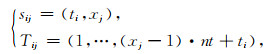
|
(4) |
其中,i=1, …, nt; j=1, …, nx;sij表示时空域地震数据每一点的位置,ti和xj分别为时间和偏移距/道索引,i和j分别为时间和空间采样点.
基于Markov决策理论,在奖励值空间(高维特征属性集合)中根据一定的准则全局寻优获得一条累积奖励值最大的路径,便对应着初至走时的子集.为了降低Markov决策过程的非线性程度,一个合适的奖励函数的选取是至关重要的.对于奖励函数的设计,一般以“生成与初至走时相关性高的属性”为目标,需对相应的地震数据进行分析,构造一个包含多个属性的特征空间.因此,我们能够定义瞬时奖励函数为
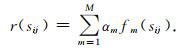
|
(5) |
由式(5)可知,奖励值函数可以由多个属性组成.fm(sij)表示第m种特征属性,αm为加权因子,用于调节多个特征属性之间的权重.对于初至拾取,其能量变化属性一般可以认为是相关度较高的敏感属性.如图 2中地震数据,采用STA/LTA算法(Trnkoczy,1999)得到对应的归一化奖励函数(能量比)谱(图 2b).接着,需选取合适起始状态,设计合适的全局寻优准则.Ma等(2019)基于强化学习理论,将远偏移距的初至到达时位置作为初始状态,由下至上进行全局寻优,但当遇到地震数据信噪比较低的情况时,自动化的选取初始状态位置则会出现困难.考虑到地震数据近偏移距的浅层信噪比往往高于远偏移距,因此,本文采用由上至下的全局寻优策略并结合后续空间结构信息,以此弱化种子点选择的困难,相应的动作集合函数A和执行某种动作的概率π(a|s)可以写为
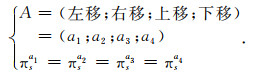
|
(6) |
式(6)表明,MDPs只存在四个动作,并且执行每种动作的概率相等.在此基础上,概率转移Pss′a表示为
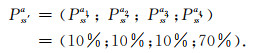
|
(7) |
式(7)说明,在状态s执行不同动作a后能够转移到状态s′的概率可能不同,且选取由上往下全局寻优策略,故向下移动的概率最大,为70%.根据上述公式,将初至拾取定义为一个特征属性空间内的Markov决策寻优过程后,求解相应(3)式,便能够获得初至走时的子集(图 2中绿点所示).
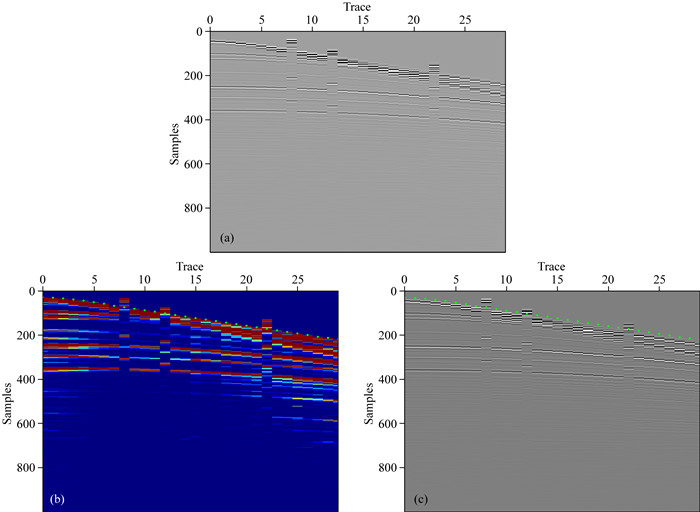
|
图 2 常规MDPs方法拾取初至走时示意图 (a) 合成2D地震数据;(b) 自动拾取结果覆盖于奖励值空间上;(c) 自动拾取结果覆盖于地震数据上.绿点,自动拾取结果. Fig. 2 Schematic diagram of picking up first breaks by traditional MDPs method (a) Synthetic seismic data (2D); (b) Auto-picking result overlaid on the reward value function; (c) Auto-picking result overlaid on seismic data. Green dots: auto-picking result. |
这里需要指出,奖励函数是采用STA/LTA算法定义而得,奖励值大的地方(初至信息)理论上对应地震信号的起跳位置.通过分析图 2结果,可发现采用Markov决策理论进行初至自动化的拾取,考虑了地震道之间的横向连续性,让拾取结果更加的平滑合理.同时,由于其状态值函数Vγπ(s)中引入了折扣因子γ,因此能够很自然的回避由坏道引起的错误初至拾取结果(异常值或奇异点).
1.3 约束Markov决策过程为了进一步的提高Markov理论自动拾取初至信息的精度,处理更加复杂的情况,本文在常规Markov决策理论的基础上,结合图像分割技术(Luo et al., 2018),引入地震数据的空间结构信息dip(s),式(6)重新写为
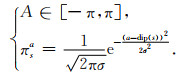
|
(8) |
对比式(6),式(8)引入了与构造信息dip(s)相关并服从高斯分布的全新动作概率函数πsa,使沿先验结构方向执行动作的概率最大.假定(0, π)表示笛卡尔坐标系的第一、二象限,相应的概率转移可写为
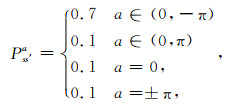
|
(9) |
其中,当a∈(0, -π)时,状态发生转移的概率较大,从而能够保证从上而下的寻优准则.改进后的式(8)、(9),使全局寻优过程不仅保留常规MDPs的特点,还能一定程度上受空间结构先验信息的约束,后续数值试验的结果也表明了约束Markov理论的优势.值得注意的是,空间几何信息的获取,除了文中提到的图像分割技术(Luo et al., 2018),也能采用其他方法技术.
2 数值试验 2.1 抗噪能力测试如图 3所示,对比了不同初至拾取算法的抗噪能力.本试验所采用合成地震数据共36道,纵向701个采样点,采样间隔为1 ms.对其添加不同级别的高斯白噪声(White Gaussian Noise,WGN),生成不同信噪比的模拟地震数据,所使用信噪比公式可表示为
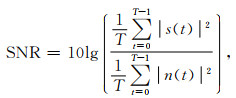
|
(10) |
|
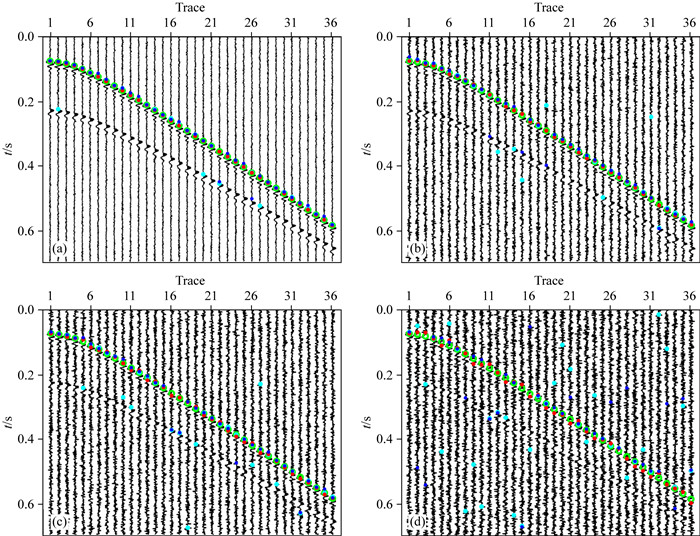
图 3 不同信噪比下四种方法初至拾取结果示意图 (a) SNR=5 dB;(b) SNR=-2 dB;(c) SNR=-6 dB;(d) SNR=-10 dB.青色:STA/LTA;蓝点:MER;红点:常规MDPs;绿圈:约束MDPs. Fig. 3 First-breaks picked by four methods with different SNR (a) SNR=5 dB; (b) SNR=-2 dB; (c) SNR=-6 dB; (d) SNR=-10 dB. Cyan dots: STA/LTA; Blue dots: MER; Red dots: traditional MDPs; Green circles: constrained MDPs. |
其中,s(t)为原始有效信号,n(t)为高斯白噪声.按公式(10)计算图 3a—d的信噪比依次为5 dB、-2 dB、-6 dB和-10 dB.图 3中,将四种不同的初至拾取算法的结果覆盖在地震数据上,其中青色圆点为经典的STA/LTA方法(Trnkoczy,1999);蓝色圆点为MER(Modified Energy Ratio)算法(Wong et al., 2009);红色圆点为常规MDPs算法;绿色圆圈为本文改进的CMDPs方法.对比不同信噪比下,四种算法的拾取结果可知,传统基于单道处理的算法,忽视了地震数据所包含的空间特征(横向连续性),从而导致难以识别信噪比低的弱初至信号,而常规MDPs和CMDPs算法,均基于Markov理论,在高维空间进行初至拾取,并考虑与距离相关的折扣因子γ,很自然的回避掉异常拾取结果,能够抓住弱初至信号,使拾取结果更加符合物理,故基于Markov决策理论的两种算法抗噪能力强于传统单道拾取算法.同时,对比常规MDPs方法和本文改进的CMDPs算法,由于CMDPs算法引入了先验结构约束,其结果比常规MDPs算法更加稳健.图 4定量显示了不同信噪比下四种算法的性能,根据定义的拾取误差函数:
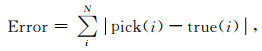
|
(11) |
|
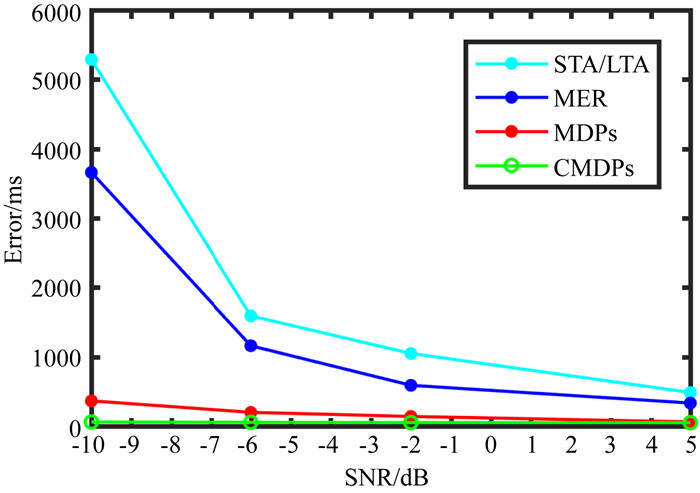
图 4 不同信噪比下四种方法初至拾取结果误差曲线图 Fig. 4 Error curves of first break picking using four methods with different SNRs |
式中,Error代表算法的拾取误差,即所有N道的拾取误差(测量值与真实值之差的绝对值)之和,单位为ms,第i道的真实值true(i)通过CMDPs算法在原始有效信号s(t)上拾取所得.如图 4所示,MER和STA/LTA两种基于单道拾取的算法其拾取积累误差明显高于考虑地震数据横向连续性的算法(MDPs和CMDPs).CMDPs(绿线)误差增加最为缓慢,进一步说明在考虑空间结构先验信息后,CMDPs算法的性能要好于常规MDPs算法.
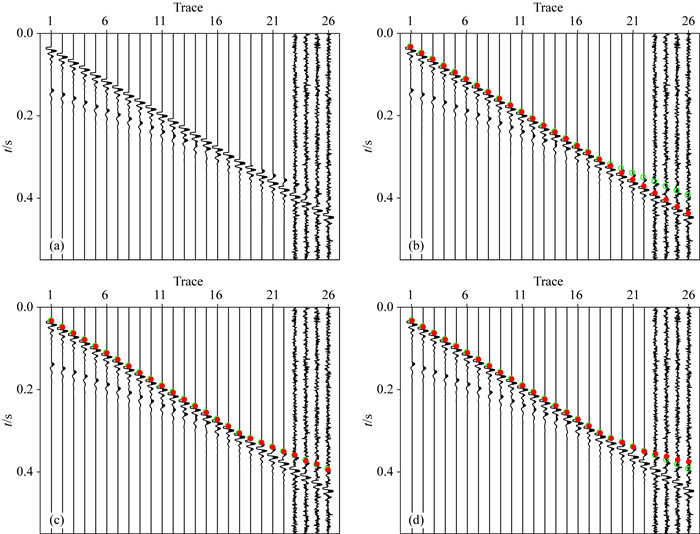
2.2 折扣因子γ敏感性测试当奖励函数和起始状态确定后,基于Markov决策理论拾取地震数据初至信息,需要考虑折扣因子γ,用以回避由坏道引起的错误初至拾取结果(异常值或奇异点).但是,常规MDPs和本文改进的约束MDPs算法对其敏感程度存在差异.如图 5a所示,为理论合成地震数据,共26道,其中第23~26道信噪比较低,初至能量弱于相邻直达波能量.图 5b—d为考虑不同折扣因子γ情况下常规MDPs和CMDPs的初至拾取结果.当γ设置较大为0.6时,MDPs算法对浅层相邻复杂波形识别能力较弱,出现拾取错误(图 5b中红点),这是因为γ越大,远处的状态奖励值影响越大,全局寻优时自然难以忽视强直达波能量.随着γ值逐渐减小到0.2,MDPs算法能获得较准确的初至信息(图 5c中红点,远偏移距仍存在轻微抖动);但是当γ值进一步减小为0.1时,根据公式(2)可知,当前状态只受相邻很近的状态奖励值影响,从而再次出现拾取偏差(图 5d中红点).而图 5b—d中绿色圆圈为本文改进的约束Markov决策理论初至拾取结果,可见在不同折扣因子下,CMDPs由于空间趋势的约束,拾取结果基本一致,说明其对γ的取值并不敏感.总体来说,折扣因子γ越小,常规MDPs拾取结果应该更加平缓,即相邻初至走时变化小.当地震数据的浅层信噪比较高时,常规MDPs和CMDPs的折扣因子γ的选取还是比较容易的,两者的拾取效果也相当.但是,当出现数值试验中所展示的复杂波现象后,约束MDPs的优势就得到了体现.
|
图 5 常规MDPs与约束MDPs在不同折扣因子γ情况下初至拾取结果对比图 (a) 理论合成地震数据;(b) γ=0.6时初至拾取结果;(c) γ=0.2时初至拾取结果;(d) γ=0.1时初至拾取结果.绿圈,约束MDPs;红点,常规MDPs. Fig. 5 Comparison of first-breaks picking results between traditional MDPs and constrained MDPs under different discount factors (a) Noisy synthetic seismic data; (b) γ=0.6; (c) γ=0.2; (d) γ=0.1. Green circles: constrained MDPs; Red dots: traditional MDPs. |
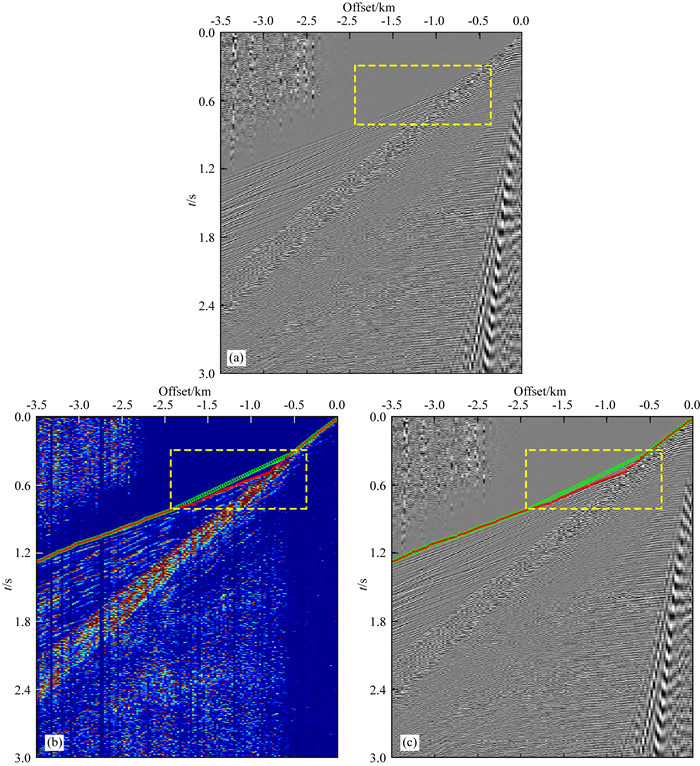
前面理论数据试验,分析了约束Markov理论在初至拾取工作中的特点.在本节,选取南海某OBC实际地震数据(图 6)说明CMDPs算法在实际资料初至拾取中的效果.如图 6a所示,该地震数据为气枪震源激发,道间距25 m,共计185道,最大偏移距3.5 km,时间采样间隔2 ms,采样时间为3 s,图中黄框处显示邻近弱初至波的下方存在强能量的折射波.针对该数据,采用STA/LTA算法生成状态奖励值空间(图 6b),选取折扣因子γ为0.3,分别采用常规MDPs算法和约束MDPs算法自上而下进行初至走时的拾取.图 6b为拾取结果覆盖在奖励值空间上,图 6c则是拾取结果覆盖在地震数据上.对比两种方法的拾取效果,可以发现如果采用常规MDPs方法进行全局寻优自动拾取初至走时,在经过黄框处时容易忽略较弱的初至波,得到错误的拾取结果(图 6b、c中红色圆点).因此,在常规MDPs的基础上,本文改进的CMDPs算法引入结构信息dip(s),相当于在状态s执行动作a后能够转移到状态s′的概率同时受到dip(s)的约束.图 6b、c中绿色圆圈即为约束MDPs算法得到的拾取结果,其在黄框处仍然能拾取准确的弱初至信号,说明CMDPs方法包含了常规MDPs和空间几何信息的优点,能够更加精确的自动化拾取初至信息,特别是在处理相邻较近复杂波现象时,存在明显优势.
|
图 6 (a) OBC数据;(b) 自动拾取结果覆盖于奖励值空间上;(c) 自动拾取结果覆盖于地震数据上绿圈,约束MDPs;红点,常规MDPs. Fig. 6 (a) Real data (from the OBC); (b) Auto-picking result overlaid on the reward value function; (c) Auto-picking result overlaid on seismic data >Green circles: constrained MDPs; Red dots: traditional MDPs. |
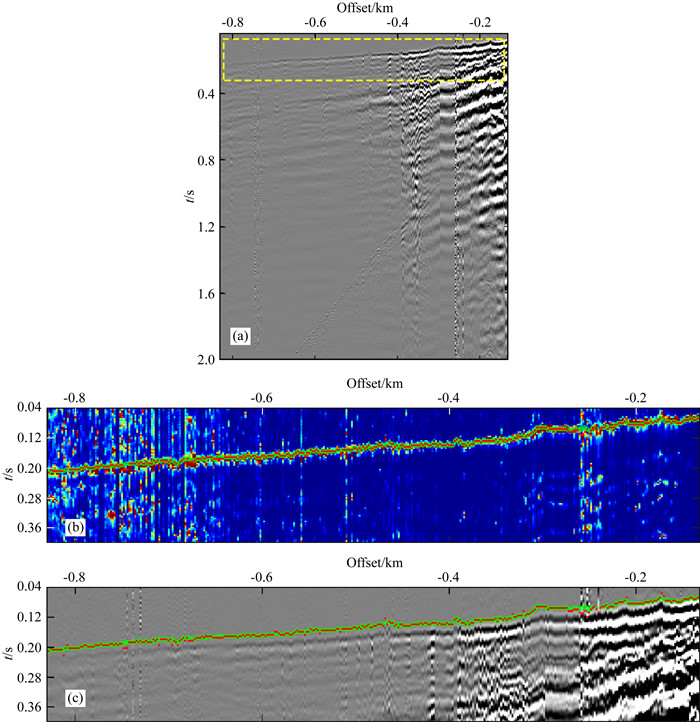
海上地震数据信噪比一般会比陆上复杂地区数据信噪比高一些,同时由于地表高程影响,海上数据的道间时差变化也相对缓慢一点.为了进一步说明本文算法在实际应用中的普适性,如图 7a所示,为西部某山前带地区实际地震资料.该数据主要用于近地表建模,因此使用炸药震源,小道间距(2 m)采集,共351道,最大偏移距为830 m,时间采样点数为501,采样间隔4 ms.由于山前带地区地表存在起伏,地震数据道间时差相对平原地区变化更为剧烈,为了更好地适应陆上山前带复杂地震数据,对于该实际资料,基于2.2节的分析,假如选择较小的折扣因子,会导致常规MDPs算法难以适应道间时差变化大的情况,因此,这里常规MDPs和CMDPs算法相较于OBC数据(图 6)均选取更大的折扣因子γ(取值为0.5)使其拾取结果允许一定程度的抖动,状态奖励值空间仍然采用STA/LTA构建.通过放大图 7a中黄框区域,图 7b、c更加清晰的展示了两种算法自上而下拾取的效果,其中红色圆点为常规MDPs的拾取结果,绿色圆圈为CMDPs的拾取结果.相比于图 6b的状态奖励值空间,图 7b中状态奖励值空间能量变化更加剧烈,远偏移距上信噪比更低,在采用较大折扣因子后,常规MDPs算法在信噪比低或坏道处(图 7b、c中红色圆点)出现了少量错误拾取,而约束MDPs算法由于引入了空间构造信息的约束,受折扣因子的影响更小,拾取结果更加合理稳健,说明本文改进的CMDPs算法,考虑空间横向连续性并受先验空间信息约束,能够适应道间时差变化大的情形,相比于常规MDPs,CMDPs对参数依赖程度更低,适用范围更广,拾取精度也更高.
|
图 7 (a) 山前带数据;(b) 自动拾取结果覆盖于奖励值空间上(图 7a黄框区域放大显示);(c) 自动拾取结果覆盖于地震数据上(图 7a黄框区域放大显示)绿圈,约束MDPs;红点,常规MDPs. Fig. 7 (a) Data from complex foothills; (b) Auto-picking result overlaid on the reward value function enlarged view with the yellow box in Fig. 7a; (c) The auto-picking result overlaid on the shot gather enlarged view with the yellow box in Fig. 7a Green circles: the constrained MDPs; Red dots: the traditional MDPs. |
通过第2节的数值试验分析,考虑空间横向连续性的Markov决策过程比传统基于单道初至拾取的算法抗噪能力更好,同时引入先验空间几何信息约束后,相较于常规MDPs算法,约束MDPs方法对折扣因子的依赖程度更低,其拾取结果更稳健.海上和陆上实际地震资料初至拾取结果也表明,CMDPs算法比常规MDPs算法适用性更广,初至拾取精度更高.
在约束Markov决策理论进行初至拾取过程中,折扣因子的选取、状态奖励值空间构建以及空间几何信息的获取这几个方面需要注意.折扣因子选取方面,通过第2.2节的数值试验,说明CMDPs算法比常规MDPs算法对折扣因子的依赖程度低,一般根据地震数据的信噪比以及道间时差变化情形选择一个适中的值即可.关于状态奖励值空间的构建,文中只提及了STA/LTA算法,这是因为能量的变化对初至比较敏感,文中所涉及的地震数据使用STA/LTA方法生成的奖励值空间已经能够满足CMDPs需求.但是,理论上,构建奖励值函数的方式有很多,并且选取的奖励函数越合适,CMDPs算法的非线性程度越低,初至拾取的精度也就越高.对于空间几何信息的提取,文中使用的是图像分割技术,也能够依靠其他更先进的构造提取算法.总之,CMDPs算法可以看作一套地震数据初至识别技术的流程框架,与其相关的一些重要组成部分,可以根据处理人员对数据的认识程度进行调整,以期获得更加精确合理的初至信息.
任何初至拾取算法均有其适用性,CMDPs算法在遇到比文中信噪比更低,道间时差变化更剧烈的实际地震资料时,也需要进行必要的地震数据预处理,比如去噪、地表一致性校正以及静校正等.同时,本文数值试验均使用二维数据,从第1节的理论分析可知,CMDPs理论也能直接构建3D的状态奖励值空间、状态转移动作、转移概率以及空间结构信息,从而很自然的将约束Markov理论拓展到3D情形,但是,3D情况下的全局寻优难度更高效率更低,因此在实际地震资料处理中,选择在2D空间还是在3D空间进行地震数据的初至拾取工作,需要结合实际生产需求设计合理方案.
4 结论本文提出了一种基于马尔科夫决策过程(MDPs)的无监督学习算法,用于地震数据初至信息的自动拾取.相较于有监督学习算法拾取初至信息,无监督算法节省了生成大量标签样本的时间,不仅能够更加自动化的获取初至信息,还能为后续有监督学习算法提供标签信息.文中给出的约束MDPs算法,继承了常规MDPs理论的优点,在高维特征属性空间中进行初至信息的自动拾取,考虑了地震数据之间的横向连续性,同时,折扣因子γ的设计,使寻优过程能够很自然的修正由坏道/噪声引起的错误初至信息,使拾取结果更加的合理.在此基础上,引入由空间几何信息dip(s)约束的动作a和转移概率Pss′a,弱化了选取起始状态和折扣因子的难度,提高了算法的精度和自动化程度,能够适应信噪比更低、道间时差变化大的数据,使CMDPs算法的适用范围更广.根据实际数据的测试结果对比,约束MDPs方法能更好的进行初至走时的自动拾取,特别是面对弱初至信号或浅层相邻的复杂波现象(相干噪声/折射波).但是,本文未对奖励函数做更具体的分析,理论上越合适的奖励函数(高维特征属性空间),全局寻优的线性化程度越好,拾取结果会更加精确,这也是今后进一步研究需要探讨的问题.
致谢 感谢中国石油勘探开发研究院及西北分院、中海油研究院和湛江分公司、中国石化物探技术研究院和胜利油田分公司对波现象与智能反演成像研究组(WPI)研究工作的资助与支持.感谢审稿专家提出的修改意见.
AitLaasri E H, Akhouayri E S, Agliz D, et al. 2013. Seismic signal classification using multi-layer perceptron neural network. International Journal of Computer Applications, 79(15): 35-43. DOI:10.5120/13821-1950 |
Chen Y K. 2020. Automatic microseismic event picking via unsupervised machine learning. Geophysical Journal International, 222(3): 1750-1764. DOI:10.1093/gji/ggaa186 |
Coppens F. 1985. First arrival picking on common-offset trace collections for automatic estimation of static corrections. Geophysical Prospecting, 33(8): 1212-1231. DOI:10.1111/j.1365-2478.1985.tb01360.x |
Duan X D, Zhang J, Liu Z Y, et al. 2018. Integrating seismic first-break picking methods with a machine learning approach. //SEG International Exposition and 88th Annual Meeting. SEG, 2186-2190.
|
Esposito A M, D'Auria L, Giudicepietro F, et al. 2013. Neural analysis of seismic data: applications to the monitoring of Mt. Vesuvius. Annals of Geophysics, 56(4). |
Esposito A M, Giudicepietro F, Scarpetta S, et al. 2006. Automatic discrimination among landslide, explosion-quake, and microtremor seismic signals at Stromboli volcano using neural networks. Bulletin of the Seismological Society of America, 96(4A): 1230-1240. DOI:10.1785/0120050097 |
Hollander Y, Merouane A, Yilmaz O. 2018. Using a deep convolutional neural network to enhance the accuracy of first-break picking. //SEG International Exposition and 88th Annual Meeting. SEG, 4628-4632.
|
Jia Y N, Ma J W. 2017. What can machine learning do for seismic data processing? An interpolation application. Geophysics, 82(3): V163-V177. DOI:10.1190/geo2016-0300.1 |
Jiang Y R, Ning J Y. 2019. Automatic detection of seismic body-wave phases and determination of their arrival times based on support vector machine. Chinese Journal of Geophysics (in Chinese), 62(1): 361-373. DOI:10.6038/cjg2019M0442 |
Langer H, Falsaperla S, Powell T, et al. 2006. Automatic classification and a-posteriori analysis of seismic event identification at Soufrière Hills volcano, Montserrat. Journal of Volcanology and Geothermal Research, 153(1-2): 1-10. DOI:10.1016/j.jvolgeores.2005.08.012 |
LeCun Y, Bengio Y, Hinton G. 2015. Deep learning. Nature, 521(7553): 436-444. DOI:10.1038/nature14539 |
Li W W, Gong R B, Zhou X G, et al. 2021. UNet++: a deep-neural-network-based seismic arrival time picking method. Progress in Geophysics (in Chinese), 36(1): 187-194. DOI:10.6038/pg2021EE0152 |
Loginov G, Anton D, Litvichenko D, et al. 2019. The first-break detection for real seismic data with use of convolutional neural network. //81st EAGE Conference and Exhibition. EAGE, 1-5.
|
López C C, Aldana M. 2009. Automatic first break picking in VSP data using fuzzy logic systems. //SEG Technical Program Expanded Abstracts 2009. SEG, 4189-4193.
|
Luo F, Wang H Z, Wu C L, et al. 2018. Automatic first-breaks picking algorithm under the constraint of image segmentation. //SEG International Exposition and 88th Annual Meeting. SEG, 2762-2766.
|
Ma Y, Fei T, Luo Y. 2019. A new insight into automatic first-arrival picking based on reinforcement learning. //81st EAGE Conference and Exhibition. EAGE, 1-5.
|
Maity D, Aminzadeh F, Karrenbach M. 2014. Novel hybrid artificial neural network based autopicking workflow for passive seismic data. Geophysical Prospecting, 62(4): 834-847. DOI:10.1111/1365-2478.12125 |
McCormack M D, Zaucha D E, Dushek D W. 1993. First-break refraction event picking and seismic data trace editing using neural networks. Geophysics, 58(1): 67-78. DOI:10.1190/1.1443352 |
Mezyk M, Malinowski M. 2018. Deep neural network and multi-pattern based algorithm for picking first-arrival traveltimes. //80th Annual Conference and Exhibition, EAGE, 1-5.
|
Molyneux J B, Schmitt D R. 1999. First-break timing: Arrival onset times by direct correlation. Geophysics, 64(5): 1492-1501. DOI:10.1190/1.1444653 |
Mousavi S M, Langston C. 2016. Fast and novel microseismic detection using time-frequency analysis. //2016 SEG International Exposition and Annual Meeting. October, Dallas, Texas: SEG, 2632-2636.
|
Murat M E, Rudman A J. 1992. Automated first arrival picking: A neural network approach. Geophysical Prospecting, 40(6): 587-604. DOI:10.1111/j.1365-2478.1992.tb00543.x |
Riggelsen C, Ohrnberger M. 2014. A machine learning approach for improving the detection capabilities at 3C seismic stations. Pure and Applied Geophysics, 171(3-5): 395-411. DOI:10.1007/s00024-012-0592-3 |
Sabbione J I, Velis D. 2010. Automatic first-breaks picking: New strategies and algorithms. Geophysics, 75(4): V67-V76. DOI:10.1190/1.3463703 |
Scarpetta S, Giudicepietro F, Ezin E C, et al. 2005. Automatic classification of seismic signals at Mt. Vesuvius volcano, Italy, using neural networks. Bulletin of the Seismological Society of America, 95(1): 185-196. DOI:10.1785/0120030075 |
Shi S Z, Liu Z Y, Feng J, et al. 2020. Using 3D seismic exploration to detect ground fissure. Advances in Geo-Energy Research, 4(1): 13-19. DOI:10.26804/ager.2020.01.02 |
Sigaud O, Buffet O. 2013. Markov Decision Processes in Artificial Intelligence. Hoboken, NJ: John Wiley & Sons.
|
Spagnolini U. 1991. Adaptive picking of refracted first arrivals. Geophysical Prospecting, 39(3): 293-312. DOI:10.1111/j.1365-2478.1991.tb00314.x |
Trnkoczy A. 1999. Understanding and parameter setting of STA/LTA trigger algorithm. //IASPEI New Manual of Seismological Observatory Practice, Vol. 2. GeoForschungsZentrum Potsdam, 1-20.
|
Turhan Taner M, Lu L, Baysal E. 1988. Unified method for 2-D and 3-D refraction statics with first break picking by supervised learning. //1988 SEG Annual Meeting. November, Anaheim, California: SEG, 772-774.
|
Vallejos J A, McKinnon S D. 2013. Logistic regression and neural network classification of seismic records. International Journal of Rock Mechanics and Mining Sciences, 62: 86-95. DOI:10.1016/j.ijrmms.2013.04.005 |
Veezhinathan J, Wagner D. 1990. A neural network approach to first break picking. //IJCNN International Joint Conference on Neural Networks. San Diego, CA, USA: IEEE, 235-240.
|
Wong J, Han L J, Bancroft J C, et al. 2009. Automatic time-picking of first arrivals on noisy microseismic data. CREWES Research Report. |
Xu X, Zhang K, Wang F Y, et al. 2020. New method of first break picking based on seismic DNA algorithm. Progress in Geophysics (in Chinese), 35(5): 1894-1901. DOI:10.6038/pg2020DD0333 |
Yu Z Y, Chu R S, Sheng M H. 2018. Pick onset time of P and S phase by deep neural network. Chinese Journal of Geophysics (in Chinese), 61(12): 4873-4886. DOI:10.6038/cjg2018L0725 |
Yuan S Y, Liu J W, Wang S X, et al. 2018. Seismic waveform classification and first-break picking using convolution neural networks. IEEE Geoscience and Remote Sensing Letters, 15(2): 272-276. DOI:10.1109/LGRS.2017.2785834 |
蒋一然, 宁杰远. 2019. 基于支持向量机的地震体波震相自动识别及到时自动拾取. 地球物理学报, 62(1): 361-373. DOI:10.6038/cjg2019M0442 |
李薇薇, 龚仁彬, 周相广, 等. 2021. 基于深度学习UNet++网络的初至波拾取方法. 地球物理学进展, 36(1): 187-194. DOI:10.6038/pg2021EE0152 |
许鑫, 张凯, 王非翊, 等. 2020. 基于地震DNA算法的一种新的初至拾取方法. 地球物理学进展, 35(5): 1894-1901. DOI:10.6038/pg2020DD0333 |
于子叶, 储日升, 盛敏汉. 2018. 深度神经网络拾取地震P和S波到时. 地球物理学报, 61(12): 4873-4886. DOI:10.6038/cjg2018L0725 |
 2021, Vol. 64
2021, Vol. 64