致密砂岩气已成为我国非常规油气增储上产的重要资源，广泛分布于鄂尔多斯盆地苏里格地区、四川盆地广安地区、塔里木盆地库车地区等.其中，塔里木盆地库车坳陷致密气资源赋存潜力大，尤其在侏罗系、白垩系地层深层勘探获得突破性进展.然而，致密砂岩储层具有物性差、孔隙结构复杂、非均质性强等特征，天然气对测井响应贡献小，气水层识别难度大.为此，前人采用并改进了多种智能算法进行致密砂岩储层的流体识别，例如Fisher判别(凡睿等，2015)、神经网络(Tan et al., 2013；陈俊等，2019)、贝叶斯判别(晏信飞等，2012；洪忠等，2015)等.但在实际应用中，上述智能算法受限于训练集、超参数等因素，模型训练难度大、可靠性不好，需要探索和构建新的智能算法.

近年来，国内外很多学者采用多种智能算法集成的思想来提升智能模型的整体性能，这种联合算法被称为集成学习或委员会机器(王飞等，2015；王黎雪，2017).这种思想来源于人类的委员会机制，在算法框架中体现为由输入层、专家层、组合器和输出层组成的复合系统(Ansari，2014).其中，专家层联合多种专家(智能算法)进行输入数据的训练或预测，组合器利用投票机制将上述专家的输出模型或结果组合起来，得到最终输出(Horrocks et al., 2015).这种集成策略有利于提高分类准确度和模型稳定性，但专家自身性能无法被提升，即集成模型的性能提升空间受限，因此称之为静态分类委员会机器.在上述委员会机器的基础上，在输入层和组合器间并列增加门网络可以构建门网络委员会机器.然而，这种方法存在收敛难、可解释性差的问题.因此，针对测井智能流体识别的实际需求，本文构建了动态分类委员会机器方法.该方法针对输入数据距离特征划分子数据集，再利用专家训练子模型，最后通过组合器对子模型组合进行优化，达到训练任务“分而治之”的效果(Shazeer et al., 2017).这种学习方式通过简化数据结构来简化子模型，有助于提升专家训练模型性能，从而提高分类系统整体的准确率和稳定性，适合于致密砂岩储层的测井解释工作.

委员会机器(committee machine，CM)是Nilsson(1965)为克服多层感知器无自适应学习规则而提出的，后来在不同领域的应用中发展出了多种改进模型，通常由输入层、专家层、组合器和输出层组成(Ghiasi-Freez et al., 2012; Barzegar et al., 2016; Dashti et al., 2018).而门网络委员会机器是Jacobs和Jordan(1991)在委员会机器的输入层和组合器间并列增加门网络构建的学习框架，使其能够自适应的计算各专家加权系数，提升模型的精度(图 1).然而，原方法专家层采用的是相同的单层网络，专家性能受限，组合效果不佳.而如果仅仅简单替换专家为不同的、性能更好的专家，又会导致收敛难、可解释性差的问题.本文在上述学习框架的基础上，与测井流体识别实际问题相结合，针对实际预测任务对各层进行了算法设计与改进，构建了针对致密砂岩含气性预测的动态分类委员会机器(DCM).

图 1

Fig. 1

图 1 静态委员会机器基础上引入门网络的动态委员会机器学习框架(Jacobs et al., 1991a, b，有修改) Fig. 1 Dynamic committee machine learning framework that introduces gate network to static committee machine (Jacobs et al., 1991a, b, modified)

输入层既是委员会机器数据导入的端口，也承担输入数据预处理的任务.针对数据预处理问题，由于不同测井方法对不同流体的测井响应存在较大差异，敏感程度不同，筛选对流体敏感的测井系列作为训练输入有利于后续专家训练.测井解释中常用的敏感测井系列筛选方法有图版法(周永娇等，2018)、降维分析(丁世村，2014)等，然而这些方法很难表征非线性关系，实际应用效果不好.因此，本研究基于智能算法自身输入层与输出层间的响应关系构建了新的敏感性评价指标，即平均影响值(MIV).假设输入数据的组别序号为i，维数序号为j，则每个元素可表示为x_ij.首先利用该数据集作为输入，训练得到一个初始预测模型I.然后对数据集X中的第j维数据进行一定比例的正扰动和负扰动，得到数据集X₊和X_-，将两个扰动数据集作为模型I的输入，得到预测输出Y₊和Y_-.最后根据式(1)得到对应j维度的平均影响值.

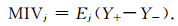
(1)

通过上述步骤逐次计算全部测井系列的输入端变化对输出端影响程度大小的平均值，可以对不同类型测井数据对初始训练模型的敏感程度进行评价.

门网络委员会机器中，门网络一般采用模糊C均值聚类算法(FCM聚类)，位于输入层和组合器之间(Rambabu et al., 2020).针对致密砂岩流体识别问题，在动态分类委员会机器中，为了加快网络收敛，提升组合过程可解释性，将门网络前置于输入层和专家层间，同时，依然保留门网络与组合器间的连通.作为一种典型的门网络算法，FCM聚类是在硬C均值聚类的基础上引入模糊集合理论发展而来，其通过式(2)反复迭代聚类中心V和隶属度矩阵U来优化目标函数J，得到最佳聚类结果(魏友华等，2012).

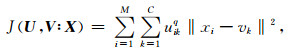
(2)

式中，M为数据集大小，C为聚类类别，q为模糊指数，u_ik为第i组数据属于k类的隶属度，x_i为第i组数据，v_k为第k类聚类簇的质心，‖·‖²为2范数.利用式(3)和式(4)循环迭代U和V可以使J达到极小值或满足终止条件停止迭代.

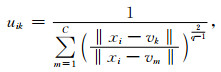
(3)

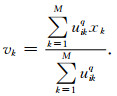
(4)

FCM聚类结果即为目标函数最优状态下的隶属度矩阵U和聚类中心V.此外，为了专家层能够识别输入数据，利用隶属度最大原则进行反模糊化可以得到明确划分的子数据集.同时，由于隶属度表征的是数据点与聚类中心的模糊关系，后续步骤需要考虑重新恢复两者的模糊关系，构建出足够稳健的组合策略(Xing and Hua, 2008).

专家层是动态分类委员会机器的主要组成部分，主要承担子模型训练和专家预测结果输出的工作.专家层一般由相同类型的专家组成，比如AdaBoost算法(Guo et al., 2016；杨笑等, 2019)和bagging算法(柴明锐等，2017)，门网络委员会机器也是采用了相同的单层神经网络.实际上，专家也可以由不同智能算法组成.研究表明，异质专家往往比同质专家的集成效果更好(周志华，2016).而且，专家间存在足够的差异，有利于动态分类委员会机器专家训练的子模型组合最优化.因此，本文采用5种不同的智能算法，即BP神经网络、概率神经网络、决策树、最近邻算法和贝叶斯分类算法建立专家层.

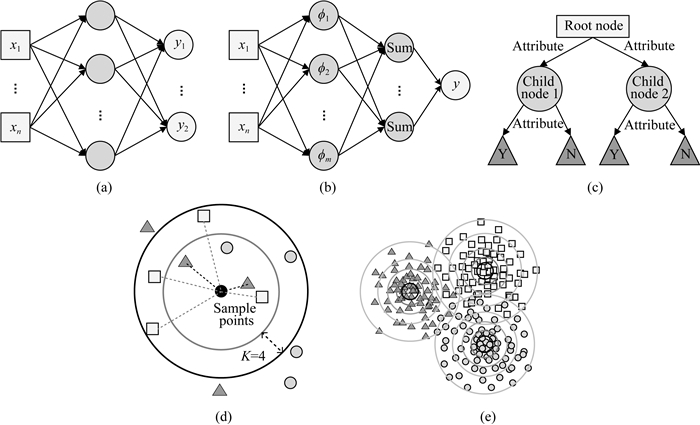
BP神经网络也被称为反向前馈神经网络，是一种应用最广的智能算法.该算法以MP神经元模型作为基本构成，数据前向传播而误差反向传播，通过梯度下降法不断更新权重和偏置使得代价函数最小，主要用于逼近和分类问题(图 2a).概率神经网络是在径向基函数神经网络的基础上结合贝叶斯算法构建而成，省去了模型参数的迭代步骤，加快收敛的同时仍能保证任意的非线性逼近，主要用于模式分类问题(图 2b).决策树通过递归的方式逐层建立反映属性与对象值关系的树状结构，每个决策节点通过信息增益或增益率来选择划分属性，从而得到能够直观表征映射关系的树状模型(图 2c).最近邻算法通过记录样本点附近属于某类样本数量最多的类别作为该样本类别，是一种依托特征空间距离的算法，特别适合多分类问题(图 2d).贝叶斯分类算法首先假设各属性相互独立，然后利用概率统计规律计算某个样本属于某一类的概率，最后选择概率最大的类作为判别结果，在分布独立假设成立时具有显著的预测效果(图 2e).

图 2

Fig. 2

图 2 动态委员会机器专家层构成 (a) BP神经网络; (b) 概率神经网络; (c) 决策树; (d) 最近邻算法; (e) 贝叶斯分类算法. Fig. 2 Dynamic committee machine expert layer composition (a) BP neural network; (b) Probabilistic neural network; (c) Decision tree; (d) Nearest neighbor algorithm; (e) Bayesian classification.

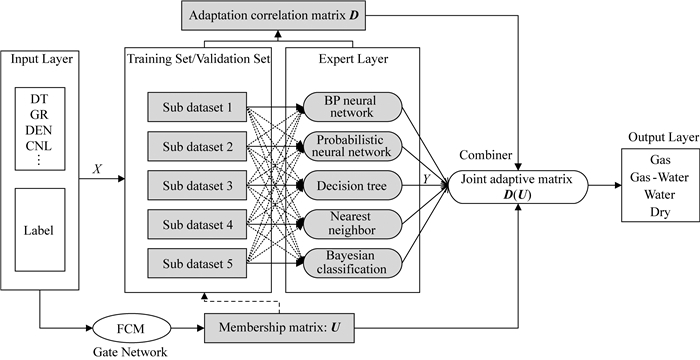
组合器是动态分类委员会机器的核心，一般进行专家权重的计算和分配.本文针对实际测井流体识别问题，为其增加数据集-专家适应关系及联合适应性评价功能.首先，它要对不同专家训练的子模型进行评估，得到子数据集与专家间的适应关系矩阵D.其次，由于FCM聚类输出的子数据集是模糊集合，而专家训练是利用了最大隶属度准则转换得到的明确划分的子数据集，因此组合器需要利用上述隶属度矩阵重新构建数据集间的模糊关系，与适应关系矩阵共同构建得到子模型的联合适应性矩阵D(U).

针对致密砂岩测井解释流体识别问题，采用上述步骤构建出能够进行动态流体识别的分类委员会机器(图 3).该委员会机器首先对输入数据进行预处理，包括归一化和测井系列敏感性分析；然后对整理好的数据集进行FCM聚类，得到隶属度矩阵和对应子数据集；之后将这些子数据集输入到专家层中，训练得到N个子模型或预测得到N个输出序列y_n；在此过程中，组合器实时记录并更新子数据集与专家间的适应关系矩阵D；最后根据得到的适应关系矩阵D和隶属度矩阵U计算得到子模型和专家间的联合适应性矩阵D(U)，作为权重进行加权组合得到最终输出Y_DCM.

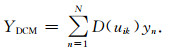
(5)

图 3

Fig. 3

图 3 针对测井流体识别的动态分类委员会机器流程 Fig. 3 Dynamic classification committee machine structure for logging fluid identification

塔里木盆地北缘库车坳陷巴什基奇克组为一套扇三角洲前缘亚相砂泥互层沉积，是重要的产气储层.该地层以岩屑长石砂岩为主，主要矿物包括石英、斜长石、方解石、钾长石和黏土矿物，孔隙度介于1.5%~7.5%，渗透率介于1.0×10^-5μm²~5.0×10^-4μm²，属于低孔特低渗储层，物性较差.而且，黏土矿物、氯盐、地应力、地层倾角等因素导致该地区电阻率异常，增加了储层流体判别难度.筛选该地区大北、克深、博孜3个研究区块共8口井98层1696组测井数据，测井系列包括自然伽马测井(GR)、阵列感应测井(RT10、RT20、RT30、RT60、RT90)、声波测井(DT)、补偿密度测井(DEN)和中子密度测井(CNL)，作为训练目标的流体类型包括气层、气水同层、水层和干层.其中，流体类型标签数据为测试数据或已明确流体类型地层的数据.随机划分上述数据集中的80%作为训练输入以得到流体识别模型，其余20%作为验证集验证模型性能，利用该模型以BZ9井为例进行了流体类型判别.

数据预处理有利于提高智能算法训练效率和模型性能.由于阵列感应测井系列数值上相近，在智能算法训练中容易造成特征冗余，只取更能反映地层电阻率的RT90作为输入阵列感应测井数据.而且，还引入能够反映地层流体特征的阵列感应测井幅度差，即ΔRT=RT90-RT10.因此，输入层共包含6种类型的测井数据.利用上述测井数据和标签数据构建得到1696×6的输入数据集，采用平均影响值法对其进行测井系列敏感性分析结果如表 1所示.平均影响值表示输入样本数值成比例的变化对输出的影响程度，输入样本变化程度不同，影响程度也不同.实验结果表明，随着输入端扰动率从±10%提高到±50%，智能算法输出的变化也逐渐增大，且变化趋势相同.

表 1 (Table 1)

表 1 不同测井系列在不同扰动率下的平均影响值 Table 1 Mean influence value with different disturbance rates of various logging series GR RT90 ΔRT DT DEN CNL ±10% 0.073 0.126 0.134 0.108 0.114 0.093 ±20% 0.143 0.251 0.268 0.212 0.223 0.183 ±30% 0.211 0.374 0.401 0.307 0.326 0.268 ±40% 0.274 0.494 0.532 0.391 0.418 0.346 ±50% 0.332 0.610 0.660 0.466 0.499 0.418 Mean 0.206 0.371 0.399 0.297 0.316 0.262 注：表中为不同测井系列归一化后计算的平均影响值，无量纲.

表 1 不同测井系列在不同扰动率下的平均影响值 Table 1 Mean influence value with different disturbance rates of various logging series

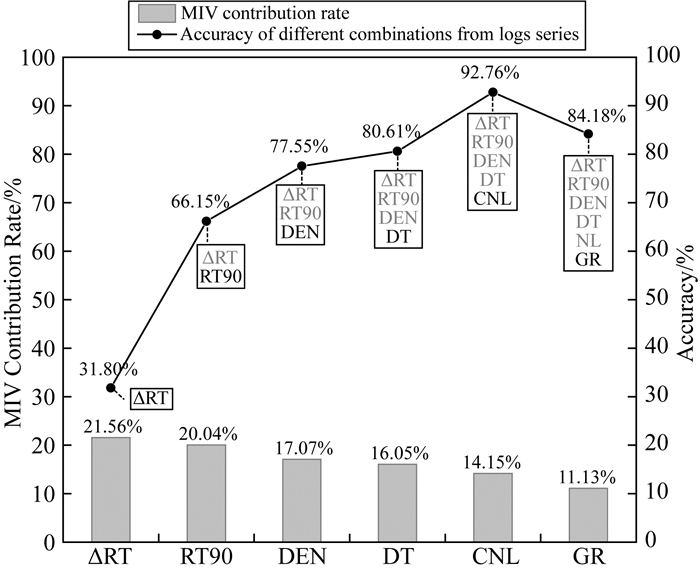
对不同扰动率的影响值求均值，计算不同测井系列影响值的贡献率，得到反映测井系列对训练目标(流体类型标签)敏感程度贡献的相对大小.根据敏感程度贡献从大到小依次采用不同测井系列组合进行动态委员会机器的训练，并取训练模型验证准确率最高的组合作为训练集输入(图 4).敏感程度从大到小依次为ΔRT、RT90、DEN、DT、CNL、GR.其中，GR对模型输出端敏感程度最小，是由于GR虽然反映了储层岩性变化，但训练模型是针对储层进行的(流体类型标签只分布在储层段)，敏感性分析同样也只针对储层，因此，GR可被认为对储层流体不敏感.而且，按平均影响值从大到小依次将不同测井系列组合作为动态分类委员会机器输入进行训练，验证集准确率分别为31.80%、66.15%、77.55%、80.61%、92.76%、84.18%.优选准确率最高的测井系列组合，即ΔRT、RT90、DEN、DT、CNL共5个系列，和对应的流体类型标签共同构建训练集.预处理后共得到1696×5的训练数据，其中气层数据478组，气水同层数据387组，水层数据352组，干层数据479组.

图 4

Fig. 4

图 4 不同测井系列的平均影响值贡献率及测井系列组合训练模型性能对比 Fig. 4 Contribution rate of mean influence value of various logging series and combination performance of various logging series training model

此外，考虑到量纲和测井数值的差异会对训练过程产生较大影响，对输入数据进行了归一化处理.而且，归一化可以使误差梯度下降更快，加快智能算法的收敛速度.

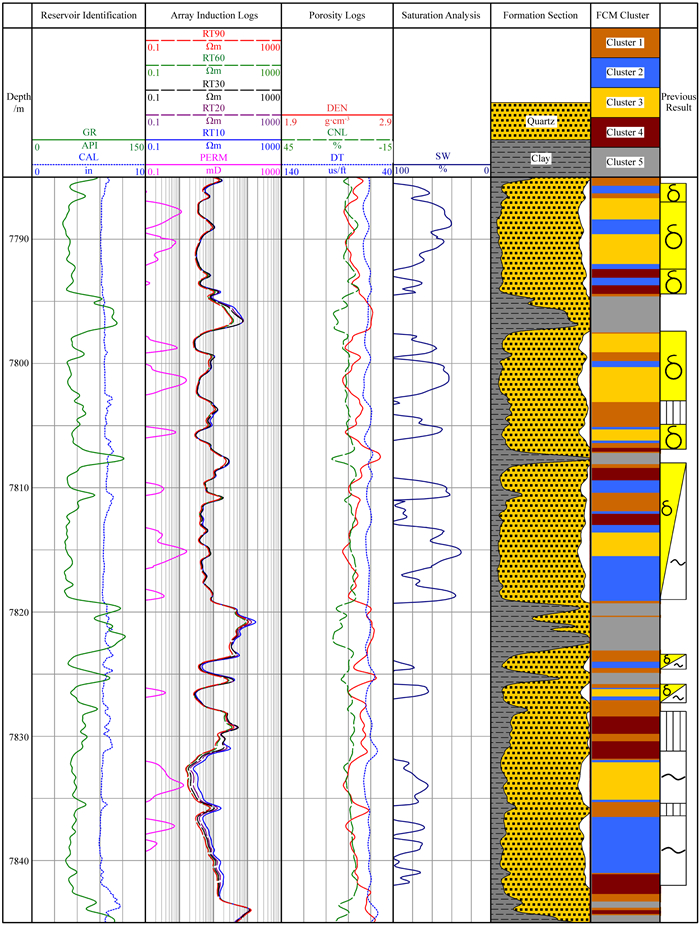
以BZ9井为例，首先使用门网络，即FCM聚类算法对训练输入和BZ9井测井数据进行聚类分析，聚类簇数量设定为5，分别对应气层、气水同层、水层、干层和非储层.聚类输出为隶属度矩阵，采用最大隶属度原则将其转化为聚类簇得到聚类结果(表 2).将聚类结果与测井流体识别结果进行对应性分析，结果显示聚类簇1主要对应干层、聚类簇2主要对应水层、聚类簇3主要对应气层、聚类簇4对应关系不明显、聚类簇5主要对应非储层(图 5).总体来看，聚类结果与流体类型的匹配率仅为60.59%，表明利用无监督的聚类算法无法精细表征储层流体类型，而将聚类结果进一步通过有监督学习的方式进行调整，能够有效实现储层流体的精细表征.

表 2 (Table 2)

表 2 聚类隶属度矩阵及聚类簇划分部分结果(井BZ9) Table 2 Partial results of membership matrix and clusters (Well BZ9) Depth (m) ΔRT (Ωm) RT90 (Ωm) 改为DEN (g·cm-3) DT (μs/ft) CNL (%) Membership matrix Cluster 7772.9 -1.5 5.915 2.596 61.318 7.998 [0.907 0.034 0.006 0.014 0.039] 1 7799.4 -2.292 8.517 2.601 60.574 8.376 [0.829 0.075 0.013 0.024 0.059] 1 7772.8 -1.429 5.951 2.593 61.379 8.273 [0.822 0.060 0.014 0.030 0.073] 1 7808.8 -1.065 10.13 2.615 59.018 5.065 [0.035 0.929 0.003 0.008 0.025] 2 7669.7 -2.4 10.197 2.601 59.172 6.152 [0.048 0.911 0.003 0.008 0.029] 2 7669.8 -2.797 11.07 2.604 59.002 6.181 [0.056 0.901 0.004 0.009 0.030] 2 7854.9 -0.958 42.918 2.695 60.076 14.037 [0.028 0.017 0.925 0.014 0.016] 3 7821 -48.762 87.149 2.71 60.295 12.692 [0.036 0.022 0.905 0.017 0.019] 3 7807.9 -6.063 23.45 2.728 61.574 14.499 [0.033 0.022 0.905 0.019 0.020] 3 7715.4 -0.52 2.893 2.502 65.655 9.363 [0.003 0.002 0.001 0.988 0.007] 4 7702 -0.347 2.928 2.494 65.859 9.117 [0.006 0.004 0.002 0.973 0.016] 4 7717.4 -0.51 2.944 2.51 65.21 9.456 [0.007 0.004 0.002 0.969 0.018] 4 7711.8 -0.215 4.043 2.535 62.676 7.066 [0.015 0.011 0.002 0.019 0.954] 5 7838.4 -3.016 5.69 2.534 62.127 6.938 [0.017 0.013 0.002 0.016 0.952] 5 7697.8 -0.219 4.197 2.549 62.201 6.935 [0.025 0.017 0.002 0.016 0.941] 5

表 2 聚类隶属度矩阵及聚类簇划分部分结果(井BZ9) Table 2 Partial results of membership matrix and clusters (Well BZ9)

图 5

Fig. 5

图 5 井BZ9的FCM聚类结果与测井解释结论对应关系 Fig. 5 Correspondence between FCM clustering results and logging interpretation in Well BZ9

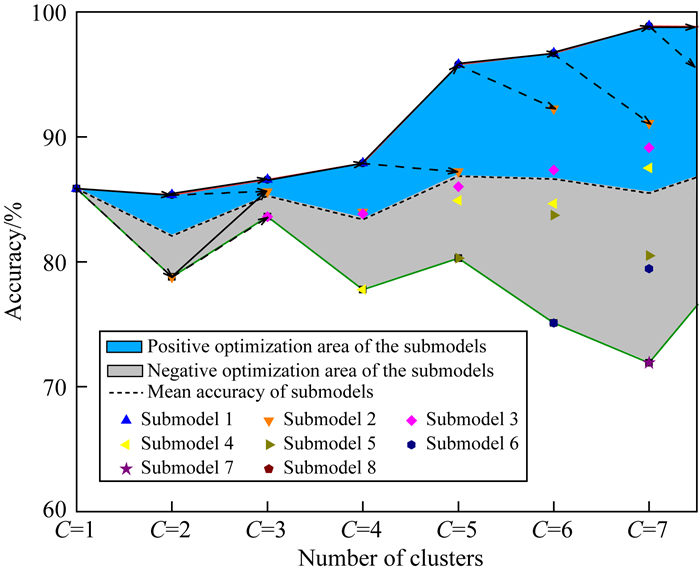
利用FCM聚类后，初始数据集被划分为5个子数据集，将这些子数据集作为输入进行有监督学习，可以得到子模型.由于子数据集中的数据结构相对简单，数据方差小，更容易构建出高精度、高稳定的子模型.图 6是智能算法为决策树时，随着聚类簇数量的增加，子数据集不断分裂，利用这些分裂的子数据构建的子模型性能发生分化.一些性能较好的子模型得到保留，而表现较差的子模型被淘汰.实际上，该过程是将与决策树适应性好的数据筛选出来，利用这些自动构建的子数据集实现决策树训练性能的提升.

图 6

Fig. 6

图 6 决策树子模型在不同聚类簇数量时的准确率分布 Fig. 6 Accuracy distribution of decision tree submodels under different numbers of clusters

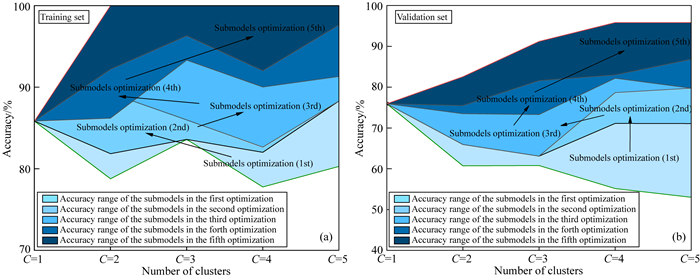
当决策树算法无法利用图中负向更新区域的数据集训练得到较好的子模型时，采用其他智能算法进行替换，可以改善模型训练效果.图 7显示了分别使用决策树、概率神经网络、贝叶斯分类、BP神经网络、最近邻算法共5种类型的智能算法对子模型组优化的结果.其中，每种类型的智能算法准确率填充范围的下限为子模型的最小准确率，上限为子模型的最大准确率.子模型组共进行了5次优化，每次优化都有一些子模型的性能更优，性能较差的子模型被替换，子模型组准确率范围得到提升.最终，针对训练集，在聚类簇数量为5的情况下，最优化的流体识别子模型组的准确率范围分布在97.63%~100%之间；针对验证集，最优化的子模型组准确率范围分布在86.83%~95.83%之间.表 3显示了当聚类数为5时，不同专家针对不同子数据集构建子模型准确率的变化，通过5个专家构建的25个子模型的最优组合可以实现流体识别模型性能最大程度的提升.

图 7

Fig. 7

图 7 多智能算法联合下的子模型组合最优化(不同聚类簇数量的优化趋势) (a)训练集；(b)验证集. Fig. 7 Optimization of submodel combination when multiple intelligent algorithms are integrated (the optimization trend of different numbers of clusters) (a) Training set; (b) Validation set.

表 3 (Table 3)

表 3 训练集和验证集中的不同专家子模型准确率(C=5) Table 3 Accuracy of submodels from different experts in the training and validation set (C=5) Decision tree (%) Probabilistic neural network (%) Bayesian classification (%) BP neural network (%) Nearest neighbor algorithm (%) Training set Submodel 1 87.23 92.70 85.29 94.53 100.00 Submodel 2 86.01 88.31 86.88 100.00 89.80 Submodel 3 85.29 91.31 82.65 88.24 97.63 Submodel 4 95.79 94.86 88.24 100.00 92.70 Submodel 5 80.29 95.30 100.00 94.63 95.30 Validation set Submodel 1 72.75 49.28 81.59 56.52 87.53 Submodel 2 83.02 72.35 87.21 89.53 88.37 Submodel 3 77.06 62.35 79.73 51.76 86.83 Submodel 4 91.67 95.83 87.23 91.67 95.83 Submodel 5 52.99 71.08 87.84 59.73 81.08

表 3 训练集和验证集中的不同专家子模型准确率(C=5) Table 3 Accuracy of submodels from different experts in the training and validation set (C=5)

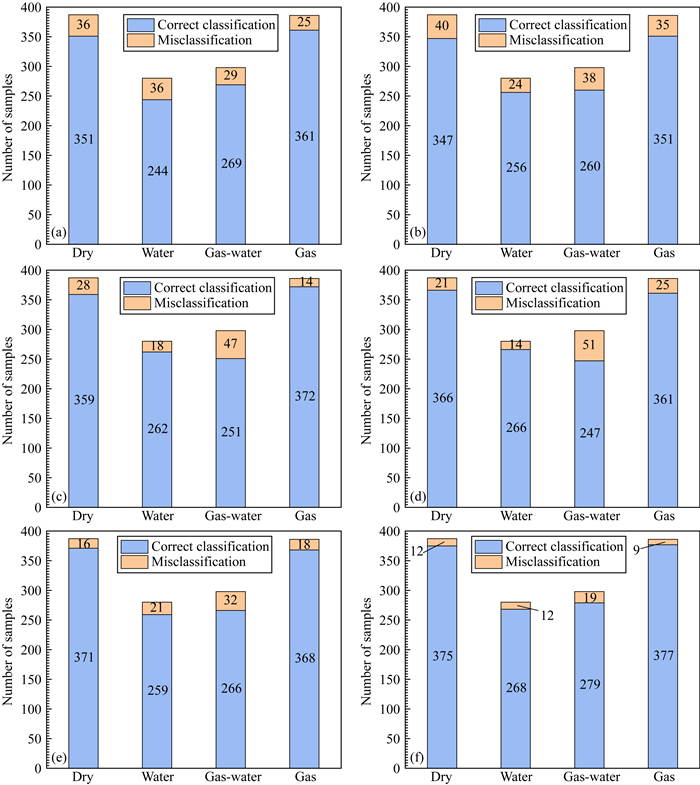
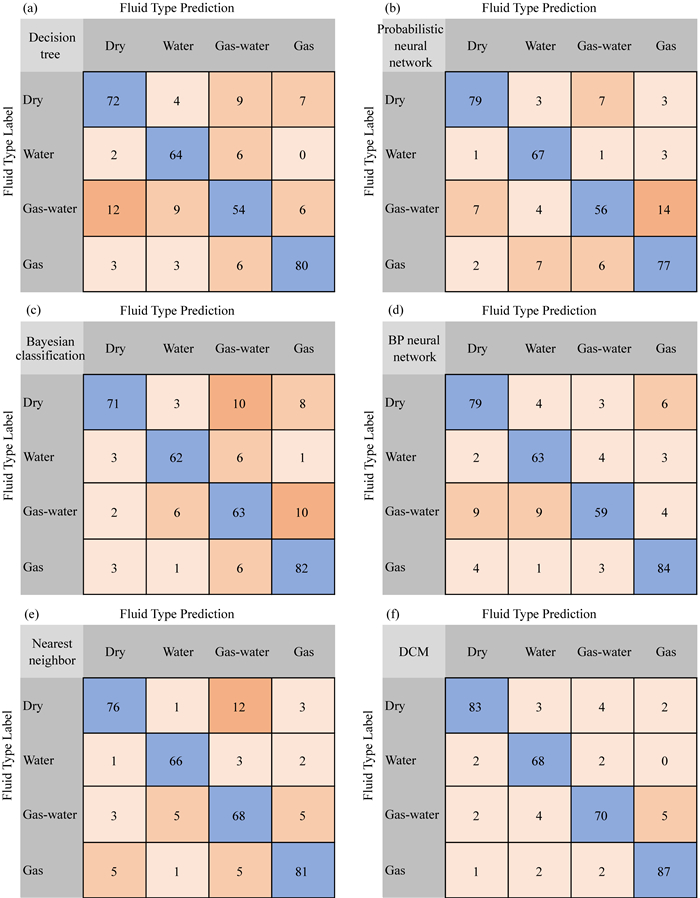
上述过程完成了动态分类委员会机器子模型的训练、组合和优化过程.其中，由于动态分类委员会机器的门网络采用了模糊聚类算法，在组合器中将隶属度矩阵与适应关系矩阵组合构建的联合适应关系矩阵作为加权因子，对上述最优化的子模型组合进行加权，建立关于子模型的模糊关系并实现动态分类委员会机器的最终输出.动态分类委员会机器训练模型的性能采用训练集和验证集准确率来评价，其中，训练集准确率可以表征模型的拟合能力，验证集准确率可以表征模型的泛化能力.根据测井流体识别实际问题，构建了如图 8、图 9所示的训练模型性能表征方法.图 8的性能表示方法简单直接，其表示的分类准确率信息对模型在训练集中的性能评估是足够的.对于验证集，由于其预测结果更能表征模型性能，采用图 9中能够反映更丰富模型信息的混淆矩阵是更为合适的.因此，如图 8所示，展示了训练集中各专家与动态分类委员会机器在气层、气水同层、水层和干层的训练结果对比.蓝色柱状表示正确分类样本数量，橘色柱状表示错误分类样本数量.其中，决策树分类模型的准确率为90.81%，概率神经网络分类模型的准确率为89.99%，贝叶斯分类模型的准确率为92.22%，BP神经网络分类模型的准确率为91.92%，最近邻算法分类模型的准确率为93.70%，动态分类委员会机器的准确率为96.29%.图 9显示了验证集中，各专家与动态分类委员会机器输出的混淆矩阵.蓝色方块表示正确分类样本数量，橘色方块表示错误分类样本数量.横向表示各层标签样本数量(真实样本数量)，纵向表示各层预测样本数量.通过不同层的标签样本数量和预测样本数量，可以计算准确率、精确率、召回率和特异度.为方便对比，当只考虑准确率时，决策树分类模型的准确率为80.12%，概率神经网络分类模型的准确率为82.79%，贝叶斯分类模型的准确率为82.49%，BP神经网络分类模型的准确率为84.57%，最近邻算法分类模型的准确率为86.35%，动态分类委员会机器的准确率为91.39%.

图 8

Fig. 8

图 8 训练集中专家和动态分类委员会机器的分类结果对比 (a) 决策树；(b) 概率神经网络；(c) 贝叶斯分类；(d) BP神经网络；(e) 最近邻算法；(f) 动态分类委员会机器. Fig. 8 Classification results comparison of the experts and dynamic classification committee machine in the training set (a) Decision tree; (b) Probabilistic neural network; (c) Bayesian classifier; (d) BP neural network; (e) Nearest neighbor algorithm; (f) Dynamic classification committee machine.

图 9

Fig. 9

图 9 验证集中专家和动态分类委员会机器的分类结果对比 (a) 决策树；(b) 概率神经网络；(c) 贝叶斯分类；(d) BP神经网络；(e) 最近邻算法；(f) 动态分类委员会机器. Fig. 9 Classification results comparison of the experts and dynamic classification committee machine in the validation set (a) Decision tree; (b) Probabilistic neural network; (c) Bayesian classifier; (d) BP neural network; (e) Nearest neighbor algorithm; (f) Dynamic classification committee machine.

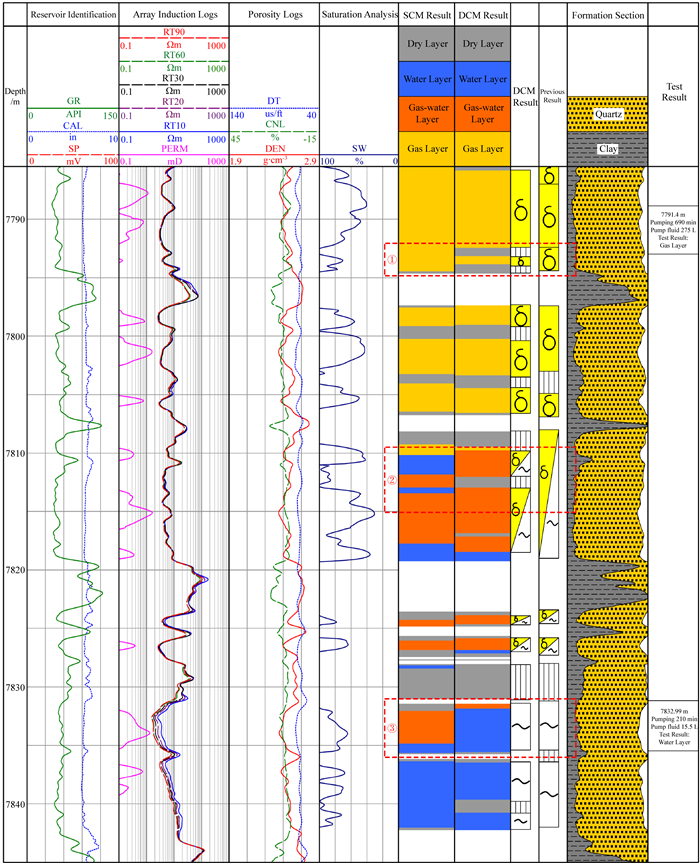
为了对比流体识别模型效果，分别利用静态委员会机器(验证集准确率为85.94%)与上述构建的动态分类委员会机器对BZ9井进行流体类型预测，预测结果如图 10所示.第6道为静态委员会机器(SCM)流体识别结果，第7道为动态分类委员会机器(DCM)流体识别结果，黄色填充为气层，橘色填充为气水同层，蓝色填充为水层，灰色填充为干层，无填充为非储层.第8道为对应的动态分类委员会机器解释结论，第9道为测井解释结论，第11道为测试结果.其中，SCM与DCM流体识别结果在图中序号1~3处存在差异.位置1为7792.30~7794.60 m处，SCM与DCM在干层识别上存在差异，根据饱和度分析可知DCM识别结果更为合适；位置2为7809.30~7813.50 m处，SCM识别结果为气层、气水同层和水层相互混杂，DCM识别为气水同层，更符合气水分布规律；位置3为7831.70~7834.80 m处，SCM识别为气水同层，7832.99 m深度处的MDT测试结论判断为水层，与DCM的流体识别结论一致.

图 10

Fig. 10

图 10 井BZ9动态分类委员会机器(DCM)测井流体识别结果 Fig. 10 Logging fluid identification results of dynamic classification committee machine in Well BZ9

利用上述流体识别模型在大北、克深、博孜3个研究区块5口井进行了流体类型识别，共有测试层数11个，判别结果符合率为100%(表 4).结果表明，利用动态分类委员会机器可以对致密砂岩储层进行快速的流体识别，识别准确率高，在该地区应用效果显著.

表 4 (Table 4)

表 4 库车大北、克深、博孜区块5口井智能流体识别符合率 Table 4 Coincidence rate of intelligent fluid identification for 5 wells in Dabei, Keshen and Bozi of Kuqa Depression Well Depth (m) Fluid identification results of DCM Test results Accuracy (%) BZ9 7785.70~7792.30 Gas Gas 100 7831.30~7835.40 Water Water DB1101 6580.00~6592.30 Gas Gas 100 DB1102 5856.80~5862.10 Gas Gas 100 5865.90~5870.20 Gas-water Gas-water 5926.80~5931.20 Water Water 5961.90~5970.50 Water Water KS503 6858.70~6865.90 Gas Gas 100 6994.80~7001.10 Water Water KS1003 6552.40~6561.60 Gas Gas 100 6637.50~6640.30 Water Water

表 4 库车大北、克深、博孜区块5口井智能流体识别符合率 Table 4 Coincidence rate of intelligent fluid identification for 5 wells in Dabei, Keshen and Bozi of Kuqa Depression

本文针对致密砂岩储层流体识别难题构建了分类委员会机器动态模型，与其他智能算法相比，该方法克服了智能算法实际应用中数据集质量差或智能算法调优难导致的预测结果准确率低、稳定性差、泛化性能不佳等问题.而且，由于将模糊聚类算法和多智能算法两种无监督和有监督学习模式很好的结合在一起，在实际模型训练和预测中，能够有效避免人为因素的影响，实现测井资料的动态分析和解释.然而，上述过程是通过专家对FCM算法聚类得到的子数据集进行训练，且多次优化对应子模型的组合模式，这一过程依赖于模型评价指标对所有子模型的遍历(如训练集准确率或验证集准确率)，如何采取更有效的方式更新子模型组合是需要继续研究的内容.

本文针对致密砂岩储层，采用门网络，即模糊聚类得到子数据集，通过多种专家多次优化子模型，构建了动态分类委员会机器，能够根据输入数据自动对自身结构进行调整.利用该方法在塔里木盆地库车坳陷大北、克深、博孜地区致密砂岩流体类型预测中显示了较高的准确度、稳定性和泛化能力.

(1) 平均影响值是表示测井系列对流体敏感性的指示因子，它通过智能算法输入端变化对输出端影响程度的大小来指示敏感性，与智能算法耦合性高，结果直观可靠；

(2) 门网络算法采用模糊C均值聚类算法，能够较好的实现复杂学习任务的模糊分割，简化数据结构，便于后续子模型训练；

(3) 多专家联合能够有效避免单一智能算法预测结果不可靠的问题.利用模糊聚类指导专家联合，改进了投票策略，进一步提升了预测结果的准确率和动态分类委员会机器的泛化能力；

(4) 组合器对不同专家构建的子模型性能进行评估，采用“优胜劣汰”的策略优化子模型组合，有利于全局最优，比投票法组合效率更高，效果更好；

(5) 动态分类委员会机器在数据预处理、输入层、门网络、专家层、组合器等阶段采用了动态的数据处理、训练和预测方式，避免了人为因素的影响，实现了致密砂岩流体类型的准确预测.