2. 北京白家疃地球科学国家野外科学观测研究站, 北京 100095;
3. 日本数理统计研究所, 东京 190-8562
2. Beijing Baijiatuan Earth Sciences National Observation and Research Station, Beijing 100095, China;
3. The Institute of Statistical Mathematics, Research Organization of Information and Systems, Tokyo 190-8562, Japan
地球物理反演技术是研究地壳内部结构和性质的重要工具.由于地球物理反演问题先天具有多解性,通常反演结果在数学上适定,但可能与实际地质情况并不相符(Li and Oldenburg, 1998; Williams et al., 2004; Howe, 2009; Dirian et al., 2016).现今在很多研究热点地区,利用多种手段获得的地壳结构模型和认识越来越多.如何充分融合已有的模型,发挥各种地球物理手段的优势,减小反演结果的不确定性,无疑是地球物理联合反演研究要解决的核心问题(Welford et al., 2018; Yang et al., 2012).
如果将所有已有模型解释结果看作先验认识,当今地学家面临的首要挑战是如何从已有模型数据中提取尽可能多的有用信息以获取新的见解.与常规技术相比,数据同化提供了一套新模式,用于发现常规技术不容易揭示的数据和模型结构之间的关系(Bergen et al., 2019).数据同化将观测数据、计算模型和先验推断集成到一个系统中,通过对系统中不确定性的估计和控制,来提高后验估计模型的精度.在当今这个大数据时代中,数据同化方法已成功地应用到了多个科学领域的建模、数据分析和预测中(Riggelsen et al., 2007; de Wit et al., 2013).
重力反演是探测地球深部构造的有效手段之一,具有对地下物质密度变化敏感、水平分辨能力强、成本低等优势(Kearey et al., 2002; Hinze et al., 2013).然而,由于观测数据误差和核函数算子本身的性质,重力反演具有多解性(Green, 1975; Fedi and Rapolla, 1999).除了通过增加观测数据和减小观测误差,在一定程度上降低反演的多解性.之外,在反演中加入先验信息进行约束是更有效的方法(Li and Oldenburg, 1998;陈石等,2010;李红蕾等,2016).近年来,重力约束条件越来越受到重视,许多地球物理学者都提出了各种各样的约束条件以及相应的反演方法.约束总体上可以分为两类,即数学结构约束和参考模型约束.前者包括最小构造约束(Last and Kubik, 1983)、深度加权约束(Li and Oldenburg, 1998)、平坦度和光滑度约束(Boulanger and Chouteau, 2001)等,后者主要包括地震波速转化密度约束(王新胜等,2013)、地质约束(Nabighian et al., 2005)、岩性约束(Geng et al., 2019)等.在传统的三维重力反演算法中,上述约束和参考都是通过阻尼因子被引入到反演方程中,并通过广义交叉验证(GCV)(Golub et al., 1979)或L曲线准则(Hansen,2001)获取的单个阻尼因子实现对观测数据和先验信息权重的平衡.然而,当在先验假设(光滑先验、深度加权)和参考权重设置增多的情况下,传统算法很难依据数据特征实现对多个约束信息权重参数的优选,这很容易造成反演结果偏离实际(Li and Oldenburg, 1998, 2000; Williams, 2008).
Akaike(1977)最早利用贝叶斯方法来解决气象领域的数据同化问题.这种方法已成为数据同化的重要手段,其是以数据驱动模式量化反演参数,通过最小化Akaike贝叶斯信息量(ABIC)实现对观测数据及先验约束不确定性的估计与控制,从而显著提高模型估计精度,减少模型不确定性.同样方法随后成功应用到时-空传染型余震序列模型(ETAS模型)的参数估计(Ogata and Katsura, 1993)、三维地震层析成像、应力图像反演(Terakawa and Matsu′ura, 2008)、GPS断层数据反演(Fukahata et al., 2004; Fukahata and Wright, 2008)、重力平差参数优化(Chen at al., 2019)等多个地球物理学领域.
本文探索通过数据同化手段,将贝叶斯同化策略引入到传统的重力约束反演中,设计一种可以融合多种先验推断的重力异常贝叶斯同化反演算法,以期得到更加准确的最大后验概率意义下的模型参数估计.文中第2部分给出了三维重力贝叶斯同化反演的求解方程和ABIC目标函数的构建;第3部分设计了两个综合实验模型,测试了该方法在解决多种已知先验参考约束和深度加权约束中超参数和后验模型估计问题的优化效果,验证了该方法的可行性和有效性;第4部分和第5部分是应用该方法和龙门山及周边地区2′×2′的高精度WGM2012布格重力异常数据反演了该区的地壳密度模型, 并对龙门山地区地壳内低密度分布、隆升变形机制、强震震源区环境等进行了深入分析;最后,第6部分对本文研究方法和认识进行了总结和讨论.
1 方法原理一般空间域三维重力位场正演问题,可以离散化并线性化为:
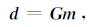
|
(1) |
其中,G为N×M的二维核函数矩阵或格林函数矩阵,矩阵中每个元素值与模型中待计算密度单元和观测点的位置相关,m为M×1的一维密度单元矩阵,d为N×1的一维观测矩阵.方程(1)中已知异常d求解m则称为重力反演问题,一般观测N≪M,直接反演在数学上是没有唯一解的.Tikhonov and Arsenin(1977)引入最小模约束后,求解方程(1)可以变为:
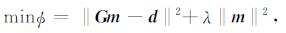
|
(2) |
其中λ是阻尼因子.
公式(2)具有数学上的唯一解.当有最小构造、光滑度、深度加权、参考模型等多个约束存在时,传统反演方法通过式(3)将其加入到反演目标函数中:
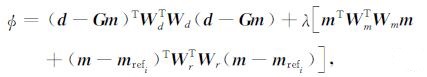
|
(3) |
其中,d为数据,m为模型,mrefi为参考模型,WmTWm=αsWrTWr+αxWrTWxTWxWr+αyWrTWyTWyWr+αzWrTWzTWzWr,Ws为单位阵,Wx、Wy、Wz为有限差分近似求解的方向梯度光滑算子矩阵,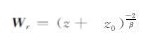
为解决上述问题,我们提出了重力贝叶斯同化反演算法,其是在综合考虑重力观测数据误差及模型约束不确定性的基础上,通过引入ABIC准则实现最大化边际概率分布的数据及模型权重超参数自动优选的反演方法.算法的基本原理如下:给定特定模型下重力观测数据的条件概率分布和模型的先验概率分布,根据贝叶斯公式,结合了观测数据,模型的后验概率密度函数(pdf)表示为:
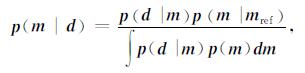
|
(4) |
其中,p(*|*)为条件概率密度函数.如果数据和模型误差都以正态分布,则重力观测数据的条件概率为:
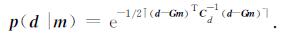
|
(5) |
考虑最小模型和多个先验约束的模型先验概率分布可表示为:
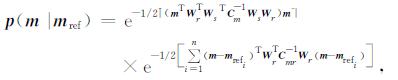
|
(6) |
其中,Cd为向量(d-Gm)的方差矩阵,Cm为模型约束算子方差矩阵.Cmr为(m-mrefi)量的方差矩阵.在λd、λms、λri已知的情况下,最大化后验分布概率求解m等价于最小化:
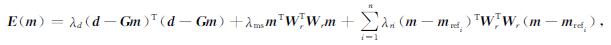
|
(7) |
式中λ0、λms、λri为数据和模型权重系数,又称为反演超参数,其可以通过引入ABIC准则来求解,即最小化统计量:
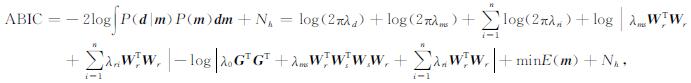
|
(8) |
其中Nh为超参数的个数.从而将传统的反演目标函数最大似然解问题转为最大化后验分布和最小化反演系统不确定性的ABIC最优问题.最小化目标函数可以通过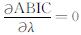
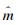
为测试上述方法的可行性和有效性,我们分别设计了两组仿真测试模型,来检验贝叶斯同化反演策略的实际效果.
2.1 参考模型约束引入适当的参考模型约束能在垂向分层上改善重力异常反演结果.通常认为参考模型越准确,反演结果越接近真实情况.但在实际问题中,可参考的模型不止一个,其误差、不确定性差异都不尽相同,同时不同参考模型之间也往往不一致.对于多参考模型约束问题,特别是在先验参考模型误差未知情况下,如何分配每个参考模型的权重问题一直是研究热点(Hansen, 1994; Vogel, 1996).下面就本文提出的方法如何分配权重和改善反演结果进行测试.
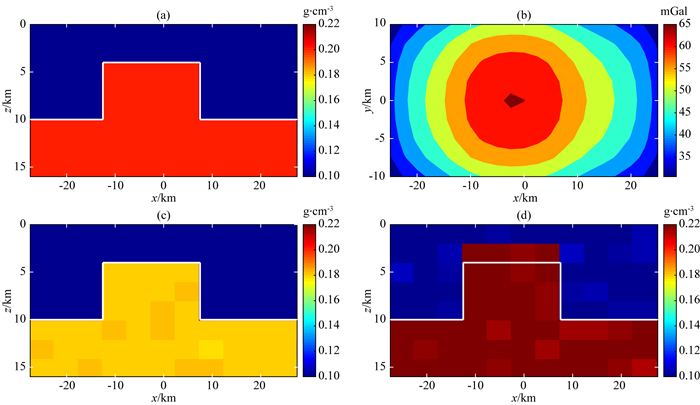
这个数值实验中,真实模型在y方向没有变化,在y=0处的垂直切片,模型起伏界面上方蓝色部分密度为0.1 g·cm-3,下方红色部分密度为0.2 g·cm-3,起伏界面上下密度差为0.1 g·cm-3(如图 1a).图 1b是仿真的重力异常数据,在理论真实模型正演异常的基础上,加入了5%的高斯误差.
|
图 1 不同参考模型约束下反演算法测试 (a) 真实模型;(b) 正演重力异常;(c) 参考模型M1;(d) 参考模型M2. Fig. 1 Tests of inversion algorithm on different reference models with constraints (a) True model; (b) Forward modeling gravity anomaly; (c) Reference model M1; (d) Reference model M2. |
在测试中,设计了两个简单的参考模型,每个模型与真实模型都存在一定的误差.其中,参考模型M1密度起伏界分界面形态与真实模型一致,但界面两侧的密度差比真实模型小10%,如图 1c所示;参考模型M2中的密度起伏界面位置与真实模型不一致,界面两侧的密度差真实模型大10%,如图 1d所示.此外,参考模型1和2中还分别加入了2%和1%高斯误差.
在模型测试过程中,我们选择了四种不同的反演方案,方案1是仅有参考模型M1优化约束反演;方案2是仅有参考约束模型M2优化约束反演;方案3是参考模型M1和M2联合非优化约束反演;方案4是参考模型M1和M2联合优化约束反演.每种反演都实现了模型异常与数据异常的拟合,但反演的模型结果差异性显著,详见图 2所示.
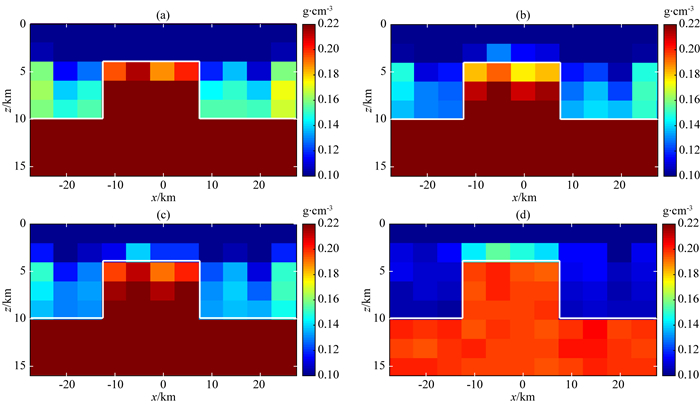
|
图 2 不同参考模型约束下反演结果 (a) 参考模型M1约束反演结果; (b) 参考模型M2约束反演结果; (c) 参考模型M1和M2联合非优化约束反演结果; (d) 参考模型M1和M2联合优化约束反演结果,白色实线为真实模型密度分界面. Fig. 2 Inversion results of different reference models with constraints (a) Reference model M1; (b) Reference model M2; (c) Reference models M1 and M2 combined with non-optimization constraint; (d) Reference models M1 and M2 combined with optimization constraint. The white solid line is the real model density interface. |
从图 2中的结果可以看出,图 2a的反演模型相比图 2b结果界面更清晰,但上下密度差偏差较大,图 2b的界面凸起部分效果比图 2a差.图 2c的联合反演结果,相比前两个无论在界面起伏和上下密度差方面都有一定程度改善,而与图 2d的贝叶斯同化联合反演结果相比,在上下界面位置和密度差方面图 2d明显优于图 2c.
在该模型测试中,参考模型1和2的归一化权重参数分别为λ1和λ2.图 2a—d的反演结果,对应的参数详见表 1.从表 1中的结果可以看出,在图 2d的最优化过程中,参考模型1的权重更大,对应的ABIC值也最小.
|
|
表 1 不同参考约束下反演统计参数及ABIC参数特征 Table 1 Inversion statistical parameters and ABIC parameter characteristics under different reference constraints |
结合表 1中的反演统计参数结果来看,参考模型1约束反演优化得到的超参数λ1为129.055,以此计算得到的ABIC值为-1355.069;参考模型2约束反演优化得到的超参数λ2为160.062,计算得到的ABIC值为-1406.770;将上述两个模型单独优化得到的超参数直接代入多模型约束,计算得到的ABIC值为-3217.861;将两个模型同时优化反演得到的最优λ1和λ2分别为1798.5和1094.8,最小化ABIC值为-3700.195.
将表 1反演统计参数与图 2中的反演结果结合来看,与单个参考模型和非优化权重的多个参考模型约束反演相比,ABIC最小化(ABIC最小值为-3700.195)给出的最优超参数可有效降低反演的卡方值,提高反演的准确性和精度.与手动指定的模型约束权重进行反演计算得到的反演结果(图 2c)相比,基于优化ABIC的反演算法可依据观测数据来选择提取不同参考之间的有用信息,并实现不同参考模型与反演结果之间的数据同化.
2.2 深度加权约束在式(1)的核函数矩阵G中,每个元素数值大小都与观测点和模型单元之间的距离平方成正比,在不同深度位置上,模型单元的核函数大小数值差异明显,浅层单元的数值远大于深层.体现在反演结果中,常常会出现异常的变化仅集中在浅部模型单元上,通常称之为重力位场反演的趋肤效应(Li and Oldenburg, 1998).
Li和Oldenburg(1998)通过模型实验提出将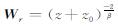
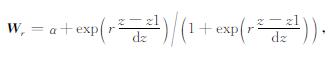
|
(9) |
其中,dz为垂向间隔,α和r的大小直接决定了近地表顶层压制作用的大小,然而在实际应用中α和r的值也主要根据经验指定(Commer, 2011; 秦朋波和黄大年,2016).
本文简化Li和Oldenburg (1998)文章中的深度加权函数表现形式为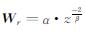
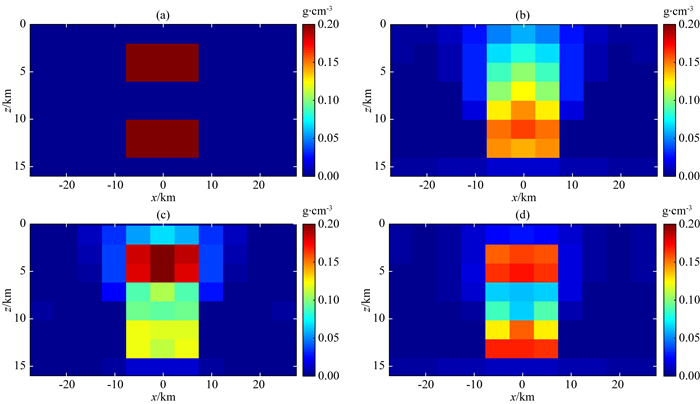
本节的测试模型如图 3所示,与图 2模型在y方向设置相同,即在y方向没有变化,抽取模型在y=0处的垂直切片如图 3a所示.真实模型在深度方向由两个规则长方体组成,周边蓝色区域密度为零,每个长方体的密度大小同为0.2 g·cm-3,长方体的顶面埋深分别为2 km和11 km,厚度均为4 km.
|
图 3 深度加权参数优化反演算法测试 (a) 真实模型;(b) 过衰减加权系数反演结果;(c) 欠衰减加权系数反演结果;(d) 优化加权系数反演结果. Fig. 3 Tests of inversion algorithm with depth weighted parameter optimization (a) Real model; (b) Inversion result of over-attenuation weighted coefficient; (c) Inversion result of under-attenuation weighted coefficient; (d) Inversion results of optimized weighted coefficient. |
我们将在真实模型正演重力异常的基础上添加了5%白噪声的模拟数据作为观测重力异常.由于重力反演很难分辨深度方向上的异常体,因此,需要给定一定的先验信息作为参考模型.在本次测试中,我们选择了局部参考模型作为约束,即假设在x=0位置处的单元体密度为已知.一般在实际地壳结构反演中,测井或接收函数方法可以提供此类的局部模型信息.
该模型测试中,我们给出了三种不同深度加权参数的反演结果,分别对应了三种不同的深度加权参数,如表 2中α、β参数值所示,表 2中不同的深度加权参数值分别对应了图 3b、c、d的反演结果.当表 2中加权参数α值过大时,得到的反演结果图 3b中高密度部分主要集中在底部,异常体的深度与真实模型埋深存在一定的差异;而当加权参数β过大时,得到的图 3c的反演结果其高密度主要集中在浅部,异常体埋深同样存在较大差异.通过本文算法得到的最优化深度加权参数反演结果如图 3d所示,异常体的深度信息较为准确,得到的反演结果埋深和形态与真实模型基本一致.由此可得,与主观指定的深度加权参数反演结果相比,本文提出的贝叶斯同化反演方法,在已知局部参考信息下,给出的深度加权更合理,反演的异常体深度与真实模型更加一致.
|
|
表 2 不同深度超参数约束下反演统计及ABIC参数特征 Table 2 Inversion statistics and ABIC parameter characteristics under different depth hyperparameter constraints |
综合以上两个模型的测试结果,可以认为本文算法具备同化多个参考模型和优化深度加权参数的能力.下面我们进一步应用该方法,选择地球物理观测资料丰富、地壳结构参考模型较多的龙门山地区进行实际数据测试.
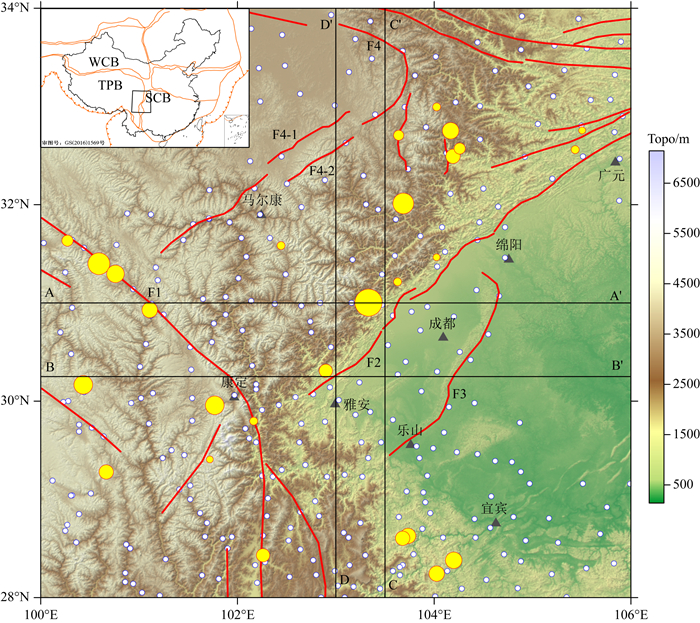
3 龙门山地壳模型 3.1 龙门山构造背景龙门山地区位于南北地震带中南部位,拥有复杂的构造边界条件、活动断层系统.其西部是活跃的青藏高原边界,东部是稳定的华南地台,是青藏高原主体向东挤出构造边界,地壳变形强烈,结构复杂.地块内部褶皱断裂广泛发育,其中包括了多个大地构造区边界断裂和控制强震活动的活断层:鲜水河断裂带、龙门山断裂带、东昆仑断裂带、龙泉山断裂带、龙日坝断裂带、毛尔盖分支断层等(徐锡伟等,2008).此外,沿着龙门山断裂带,还存在着约5 km的强烈高程梯度带(如图 4所示).
|
图 4 龙门山地区主要构造特征与地震活动 红色实线为断裂,四条黑色实线为跨震中研究剖面,黄色圈为5级以上地震位置,白色实心圆为中国地震观测网台站位置,F1:鲜水河断裂带;F2:龙门山断裂带;F3:龙泉山断裂带;F4-1:龙日坝断裂带;F4-2:毛尔盖分支断层;F4:东昆仑断裂带(徐锡伟等,2008). Fig. 4 Main tectonic features and seismic activity in and around the Longmenshan area The red solid lines represent faults, black solid lines are profiles through epicenters, yellow circles represent earthquakes of M5 or greater, and white solid circles are stations of China earthquake observation network. F1: Xianshuihe fault zone; F2: Longmenshan fault zone; F3: Longquanshan fault zone; F4-1: Longriba fault zone; F4-2: Maoergai branch fault; F4: East kunlun fault zone (Xu et al., 2008). |
同时,该地区也属于中国地震科学实验场区,过去几十年中以中国地震科学台阵项目为代表的大规模地球物理观测相继开展,已积累了大量的地球物理探测工作成果(如Yao et al., 2008; Li et al., 2011; Zhang et al., 2011; 王绪本等,2018).这些深部成果对该区的壳幔结构及其相关动力学问题达成了部分共识,但在一些基本问题上依旧存在争议,如在该区的地壳上地幔变形机制的解释上,就有壳幔连续变形机制(England and Molnar, 1997)、块体挤出机制(Tapponnier et al., 1982, 2001)、下地壳流机制(Clark and Royden, 2000;Royden et al., 1997)等多种模式.
此外,龙门山地区地震多发,如2008年汶川8.0级和2013年芦山7.0级强震.虽然国内外研究学者对该区大震震源区的深部孕震结构等进行了大量的研究,但对于地震孕育深部地壳结构特征及相关动力学机制还存在分歧.如:Zhang等(2011)通过地震层析结果,认为龙门山断裂带两侧高低速异常的边界是该区强震的凹凸区;而房立华等(2013)和王夫运等(2015)的地震测深剖面显示断裂带下方中滑脱层是产生研究区地震的主要原因;张培震等(2008)、杨文采等(2015)和王绪本等(2018)的多种研究结果表明研究区强震的发生与地壳内部存在的低速高导层有关.
密度作为地球内部构造最重要的参数之一,能够很好地反应地下物质的运动和变化,高精度的地壳三维密度结构对该区构造形成及演化、地震孕育等深部动力学过程的深入认识具有重要作用.虽然前人已经在该研究区内进行了一定的重力密度探测研究工作,这些探测成果为我们理解和认识研究区地幔变形及强震风险源区的地壳结构和物性特征研究提供了重要的深部资料(姜文亮和张景发,2011;申重阳等, 2015),但这些成果主要集中在二维.已有三维地壳密度数据分辨率和精度较低(方剑和许厚泽,1997; 杨文采等; 2015;李红蕾等,2017;Li et al., 2017).不足以识别地壳和上地壳深度的细节特征,也不能为解决该区壳幔变形、地震孕育及相关动力学过程争议提供很好的论据(王椿镛等, 2016).
3.2 研究区已有地壳结构众所周知,重力数据水平分辨率高,但垂向分辨率低,在实际反演过程中,要想得到有地质意义的结果,还需要添加深部参考约束.相对重力方法来讲,地震成像方法具有较好的垂向分辨率,重力反演中将地震成像结果作为参考约束,可以集两种数据之长,提高重力深部结构的探测能力.本文选择的研究区,在地震学研究方面,已有体波成像(如Zhang et al., 2011; Wang et al., 2017)、面波成像(如Yao et al., 2008; Li et al., 2011)、接收函数反演(如Bao et al., 2015; Liu et al., 2014)、地震测深成像(如张先康等, 2007; 王夫运等, 2008)等多个结果.然而,由于不同学者使用的研究数据及方法不同,获得的参考地震模型结果在数据分布、分辨率、误差及物性等方面常存在较大差异,如表 3所示.
|
|
表 3 研究区内已有部分地震波速成果 Table 3 Partial seismic wave velocities in the study area available |
如果将已有的模型解释结果看作先验认识,那么如何根据这些先验去改进反演模型的估计?这是本文提出的重力异常贝叶斯同化反演新算法应该回答的问题.我们将以多种不同类型的地震速度转换密度作为已知先验参考,利用高精度的卫星重力场模型数据,通过新算法实现对不同先验参考约束的取长补短,剔除偏差数据在反演计算中的作用,以期得到同时符合计算系统不同先验假设的最优高精度地壳结构模型.同时测试算法在实际重力资料反演中的效果,为研究该区的地壳变形机制、强震孕育环境及相关动力学提供有益参考.
3.3 参考模型建立地震层析成像和接收函数是探测地下介质结构和物性的两种主要手段.层析成像对介质的平均地震波速度敏感;而接收函数对台站下方介质的分层速度变化敏感,但对绝对速度的约束较差(Ammon et al., 1990; Yao et al., 2008).本文选择研究区最新公开发表的地震层析成像资料,构建全局反演参考模型.该模型水平分辨率为0.25°,垂直分辨率为5 km.此外,我们又选择中国科学台阵仪器位置下方的一维接收函数结果(王夫运等, 2015; 郑晨等,2018)为局部地壳速度模型参考.两者都采用相同的速度-密度经验关系式ρ=1.6612Vp-0.4712Vp2+0.067Vp3-0.0043Vp4+0.000106Vp5(Brocher, 2005)转换得到初始参考密度模型.
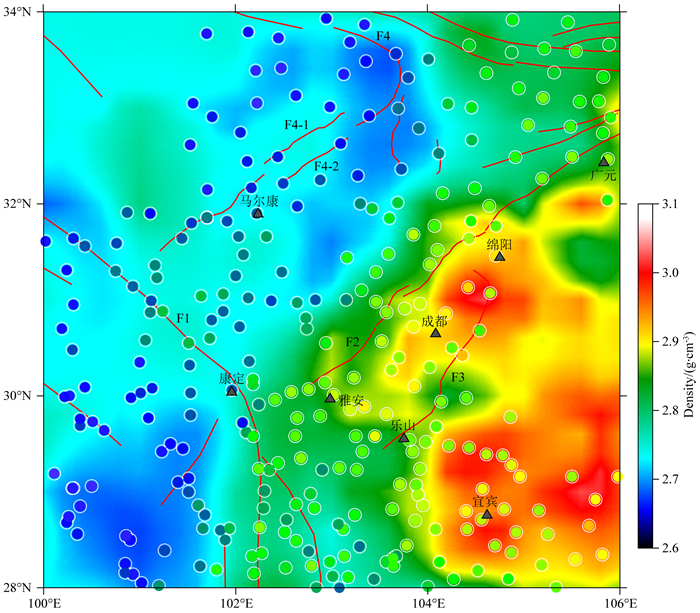
转换为密度的两个参考模型信息在30 km深度切片密度结构如图 5所示.图中给出了接收函数转换密度(圆点)和地震层析结果模型(底图)之间的横向密度信息差异.在图 5中,地震层析成像和接收函数资料有明显差异,具体表现在马尔康以西、成都以东、康定以南层析成像转换密度结果与接收函数转换密度结果异常大小及分布相差较大.
|
图 5 地震层析成像和接收函数转换密度结果(30 km水平切片) 实心圆填充的颜色代表接收函数转换密度,底图是层析成像转换密度. Fig. 5 Transformed density model from tomography and receive function (horizontal section at 30 km depth) The colors of solid circles represent the transformed density of the receiving function result, and the base map is the transformed density of the tomographic result. |
本研究的三维密度结构反演,布格重力异常选择最新的WGM2012模型数据,该模型空间分辨率高达2′.BGI(Bureau Gravimétrique Internationa)官方给出的WGM2012模型资料显示,该模型融合了多种重力数据,同时使用了高分辨率的ETOPO1高程数据进行地形改正,考虑了异常计算过程中的多种不确定性,评估显示在高原地区的平均精度优于5 mGal(Balmino et al., 2012).
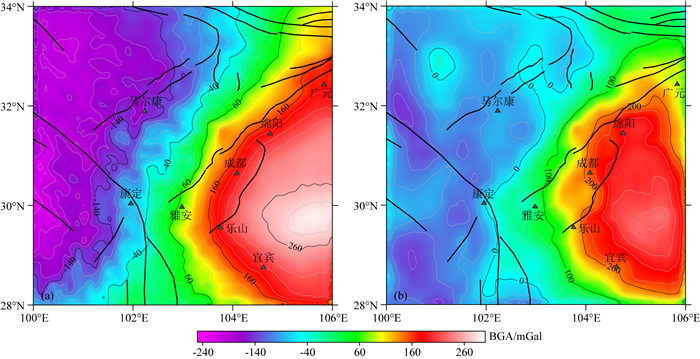
图 6a为我们基于WGM2012模型采用50 km高斯低通滤波得到的该区布格重力异常.下面将使用该布格重力异常进行反演,同时在研究区下方0~60 km深度,以水平间隔5′×5′(约为8 km)和垂向间隔4 km的分辨率构建三维密度模型空间,该模型初始局部参考约束分别来自于3.3节地震层析成像和接收函数转换密度结构(图 5).图 6b是地震层析成像速度结果转换得到的密度模型正演得到重力异常.
|
图 6 (a) 布格重力异常;(b) 层析成像转化密度模型正演重力异常 Fig. 6 (a) Bouguer gravity anomalies; (b) Forward modeling gravity anomalies from the topography transformed density model |
图 6a结果显示了与深部壳幔界面过渡的相一致的东西向特征,总的来看青藏高原东南部川西高原地区都为负异常区,四川盆地整体呈现结构清晰的正异常带,与构造边界线符合良好,即沿龙门山断裂带附近有一条横贯的重力梯级带,其走向与地表断裂位置符合较好.相比图 6b的速度转换密度结构正演重力异常,布格重力异常(图 6a)在水平向上反映出了更多的短波长特征,这可能与地壳内部介质密度横向结构的变化相关.
4 反演结果与分析根据上一节构建的两个参考密度模型和布格重力异常,我们完成了贝叶斯同化重力反演.下面我们分别对从结果的可靠性和剖面特征两方面进行论述.
4.1 可靠性分析(1) 模型残差
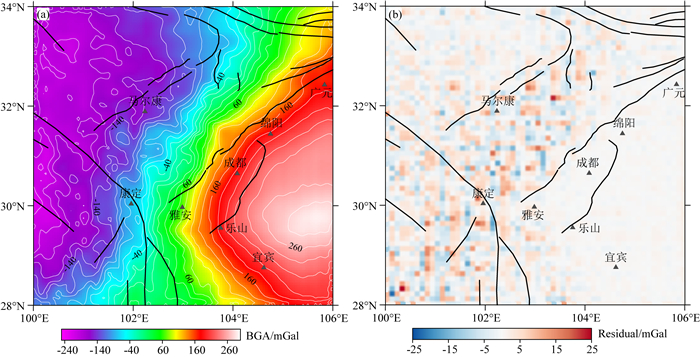
通过前文所述的反演方法,我们通过贝叶斯优化,获得了ABIC最小值对应的反演结果,模型中四个超参数分别为:λ1=139.254、λ2=122.965、α=31.337、β=0.45.图 7中给出了反演模型的正演异常值和其与观测值的差异特征,图 7b的异常残差结果标准差为±2.5 mGal.
|
图 7 (a) 反演模型结果正演重力异常;(b) 观测异常和反演模型正演异常的差异特征 Fig. 7 (a) Forward gravity anomalies from the inversion model; (b) The difference between the observed anomalies and forward modeling anomalies from the inversion model |
从图 7a中可以看出,最终密度异常正演所得异常理论值与观测剩余值形态具有较好的一致性,与地震模型正演结果相比有更多短波长特征.图 7b中观测异常和反演密度模型正演理论异常得到数据拟合剩余残差主要是高频误差,标准差略优于WGM20121布格异常的5 mGal精度.
(2) 水平结构
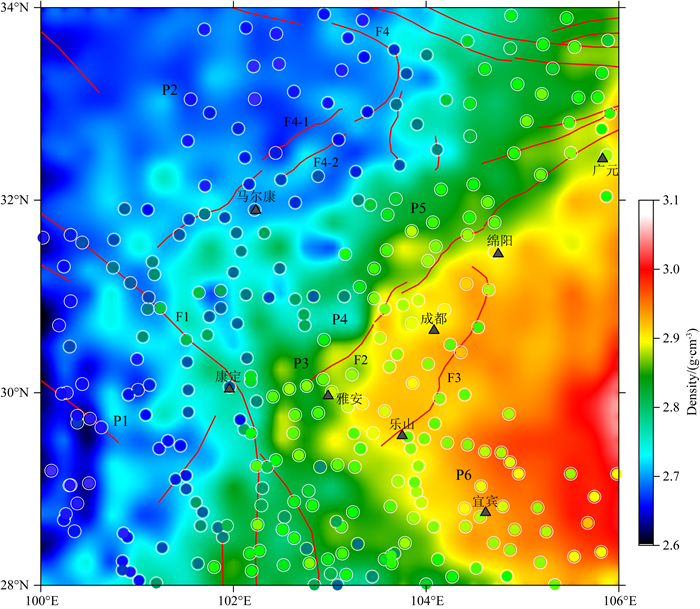
为了进一步检验反演结果的可靠性,我们仿照图 5的结果,取30 km深度切片,对比接收函数转换密度结果与反演结果之间的差异,如图 8所示.可以看出:以龙门山断裂带为界(F2),川西高原与四川盆地高低密度分界清晰.与地震层析结果相比,联合反演所得密度分布形态与接收函数具有较好的一致性;此外,川西高原显著低密度异常的背景下出现了星状分布的小尺度横向密度差异特征,四川盆地内部密度相对川西呈高密度结构特点,也伴随小尺度相间分布的结构特征.
|
图 8 基于ABIC重力异常贝叶斯同化反演密度结果(30 km水平切片) Fig. 8 Density inversion result derived from the Bayesian assimilation of gravity anomalies based on ABIC (horizontal slice at 30 km depth) |
(3) 垂直结构
在垂向分层结构的检测方面,我们在不同构造区,分别挑选了6个接收函数台站位置下方的一维垂向密度结构进行比较.图 9a—f给出了接收函数参考模型(蓝色实线)、地震层析参考模型(红色实线)和同化反演模型(黑点)的一维结果.总体来说,三者结果差异不大,最终反演结果在不同深度位置综合了两种参考模型信息,可说明重力同化反演结果的垂向分辨能力可以从参考模型中获得.

|
图 9 反演模型与参考模型点垂向对比 (a) P1点;(b) P2点;(c) P3点;(d) P4点;(e) P5点;(f) P6点.蓝色折线为接收函数转化密度结果;红色折线为层析成像转化密度结果;黑色空心圆为反演密度结果,黑色短线为密度估计误差. Fig. 9 Vertical comparison between the inversion model and the reference model (a) Point 1; (b) Point 2; (c) Point 3; (d) Point 4; (e) Point 5; (f) Point 6. The blue step-lines are the transformed density result from receiving function. The red broken lines are the transformed density result from tomography. The black hollow circles are the inversion density result. The black short lines are the density estimation errors. |
具体分析图 9,在上地壳浅部位置,反演结果与各参考分层差异不大,但在深部中下地壳深度,P3和P6点反演结构更多地参考了接收函数参考模型结果,由此可见具体同化重力反演的结果,并非为简单的参考模型平均,而是在实际重力异常、参考模型特点等先验信息基础上,给出的最大后验概率估计优选的结果.
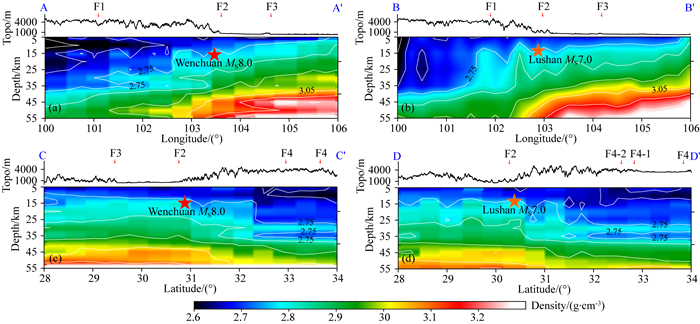
4.2 剖面特征在反演模型结果综合对比分析基础上,我们进一步通过图 4过震中位置的四条垂直剖面特征,来分析本文结果给出的地壳密度垂向结构特征.图 10分别是AA′、BB′、CC′和DD′剖面位置(图 4)的密度结构,采用相同比例色标,红色表示高密度、蓝色表示低密度.从图 10给出的结果来看,地壳密度结构纵向分层界面清晰,不同活动地块下密度分成界面构造形态存在显著差异.龙门山断裂带(F2)下方的密度等值线变化剧烈,可能反映了该区地壳内部密度结构复杂、变形强烈,该地区的密度变化特征较好的刻画了盆山耦合环境下的壳幔接触前缘.对比图 10a、b和图 10c、d,可发现地壳横向密度不均匀特征明显,剖面下方东西向密度变化剧烈(AA′和BB′剖面),构造变形多,结构复杂;南北向密度变化则相对较缓(CC′和DD′剖面),壳幔构造变形及结构相对简单,这与GPS观测得到的青藏高原主要以向东运动和地表体现的隆升变形特征相一致(张培震等,2008).
|
图 10 沿AA′、BB′、CC′和DD′密度结果剖面图(剖面位置如图 4所示) Fig. 10 Density results along profiles AA′, BB′, CC′and DD′ sections(Profile positions are shown in Fig. 4) |
从图 10的局部特征看,壳内低密度层刻画的也很明显.例如,鲜水河断裂带(F1)、东昆仑断裂带(F4)、龙日坝断裂带(F4-1)和毛尔盖断裂带(F4-2)下方中地壳内存在带状低密度层分布(AA′、CC′和DD′剖面).综合地震层析(雷建设等, 2009)、接收函数(郑晨等,2016)、大地电磁测深(王绪本等,2018)等结果在该区低波速、高泊松比、低电阻率等的认识,可将这些低密度层解释为与中地壳的黏滞性地壳流从高原腹地自北西向南东运移过程有关.
图 10a、b所示的AA′和BB′剖面结果显示,龙门山断裂带(F2)下方地壳密度变化强烈,地层发生强烈的揉皱变形.从AA′剖面可以看出,汶川地震断层为高角度断层,该地震所在的断层从地面切割向下延伸至约30 km,断裂形态与密度分层界面突变跳跃的位置一致.同时,断层下方约35 km深度处存在中地壳高低密度接触前缘.从BB′剖面可以看出,芦山地震同样发生在密度分层界面陡变带向下的延伸面上,芦山地震断裂向下延伸面与10~30 km深度的密度差异界面具有较好的吻合特征.
5 结论与讨论本文基于贝叶斯原理,通过引入ABIC准则替代传统的目标函数最小化方法,给出了一种可以有效同化多个参考模型和优选深度加权参数的重力反演新方法.随后经过多组模型测试了该方法的可行性、收敛性和有效性.测试结果表明,通过新方法得到的反演模型与真实模型之间差异性最小,反演结果合理.最后应用该方法对龙门山地区的布格重力异常进行反演,其结果对于地壳垂向分层、局部密度分布特征及深大断裂孕震特征都有较好地反映.本文得到的主要研究结论如下:
(1) 基于综合模型测试结果表明,无论是在全局参考模型还是在局部参考模型情况下,贝叶斯同化反演算法均可实现ABIC最小化,并获得最优的参数估计结果.在参考模型较多、模型参数增多的情况下,不但可以减小人为调参的难度,还可以更多地吸取多个参考模型的有效信息,获得多个先验约束下的最优反演结果.这对于在已有先验约束较丰富的地区开展综合反演研究无疑是十分必要的.
(2) 从实际资料的反演测试结果看,龙门山地区整体地壳密度变化显著,与南北向密度变化相比,东西向密度变化更加剧烈,构造变形更加复杂.此外下地壳低密度层呈现局部分布特征,结合地震、大地电磁等研究成果认为这些局部分布的下地壳低密度层反映了黏滞性地壳流从高原腹地自北西向南东流入东缘的轨迹,支持了该地区下地壳流隆升变形假设.
(3) 通过实际跨震中剖面特征的分析上来看,在龙门山断裂带下方,芦山地震和汶川地震断层形态与中上地壳密度分层界面陡变位置具有较好的吻合性.据此推断,该区大地震容易发生在中上地壳强烈的密度界面陡变位置.与芦山地震相比,汶川地震断裂带下方分布有低密度松潘甘孜地块中地壳俯冲前缘,该俯冲前缘中地壳低密度层的存在可能是造成不同地震发震机制的主要原因.
综上所述,本文提出的贝叶斯反演算法,反演过程不依赖人的主观认识,完全依靠数据说话,通过非线性优化算法可以实现全自动化地反演参数调节和模型同化,提取不同先验约束之间的有效信息,可以充分发挥地震学方法的垂向分辨能力优势和重力异常蕴含的水平密度结构变化特征.
在对强震震源区的结构研究方面,本文得到的密度剖面结果显示,芦山和汶川震中区位置都存在显著的中地壳密度界面陡变特征,其断层位置与密度分层界面陡变区都具有较好的一致性.同时龙门山断裂带下方滑脱层的存在与该断裂带下方密度分层界面也有较好的对应(房立华等, 2013; 王夫运等, 2015),因此,此类高精度的地壳密度结构无疑更有益于研究大地震孕育环境的结构与物性特征.
本文提出的贝叶斯重力反演新算法,是解决多种不同分辨率和时空尺度先验参考模型同化反演的有效手段,但新算法中仍存在一些难题尚需解决,比如:新算法中多个超参数优选过程的计算量远远大于传统单个超参数优化的计算量;当新算法中优化超参数增多、参考模型之间矛盾较大时,算法可能存在一定的不收敛风险.未来,我们将继续针对优化反演算法,提升模型计算能力等方面做进一步的改进和深入研究.
致谢 感谢中国科学台阵项目提供的地震数据,感谢中国地震局地球物理研究所王兴臣博士提供的川滇地壳接收函数结果,感谢中国地震局地球物理研究所李永华研究员和两位匿名审稿人提供的宝贵建议和帮助.
Akaike H. 1977. On entropy maximization principle.//Applications of Statistics. Amsterdam: North-Holland, 27-41.
|
Ammon C J, Randall G E, Zandt G. 1990. On the nonuniqueness of receiver function inversions. Journal of Geophysical Research, 95(B10): 15303-15318. DOI:10.1029/JB095iB10p15303 |
Balmino G, Vales N, Bonvalot S, et al. 2012. Spherical harmonic modelling to ultra-high degree of Bouguer and isostatic anomalies. Journal of Geodesy, 86(7): 499-520. DOI:10.1007/s00190-011-0533-4 |
Bao X W, Sun X X, Xu M J, et al. 2015. Two crustal low-velocity channels beneath SE Tibet revealed by joint inversion of Rayleigh wave dispersion and receiver functions. Earth and Planetary Science Letters, 415: 16-24. DOI:10.1016/j.epsl.2015.01.020 |
Bergen K J, Johnson P A, de Hoop M V, et al. 2019. Machine learning for data-driven discovery in solid Earth geoscience. Science, 363(6433): eaau0323. DOI:10.1126/science.aau0323 |
Boulanger O, Chouteau M. 2001. Constraints in 3D gravity inversion. Geophysical Prospecting, 49(2): 265-280. DOI:10.1046/j.1365-2478.2001.00254.x |
Brocher T M. 2005. Empirical relations between elastic wavespeeds and density in the Earth's crust. Bulletin of the Seismological Society of America, 95(6): 2081-2092. DOI:10.1785/0120050077 |
Chen S, Wang Q S, Lu H Y, et al. 2010. A new method of gravity inversion——theory and model test of harmonic density imaging. Progress in Geophysics (in Chinese), 25(6): 1917-1925. DOI:10.3969/j.issn.1004-2903.2010.06.005 |
Chen S, Zhuang J C, Li X Y, et al. 2019. Bayesian approach for network adjustment for gravity survey campaign: methodology and model test. Journal of Geodesy, 93(5): 681-700. DOI:10.1007/s00190-018-1190-7 |
Chen X B, Wu Y Q, Du P S, et al. 1988. Crustal velocity structure at the two sides of Longmenshan tectonic belt.//Developments in the Research of Deep Structure of China's Continent. Beijing: Geological Publishing House, 97-113.
|
Clark M K, Royden L H. 2000. Topographic ooze: Building the eastern margin of Tibet by lower crustal flow. Geology, 28(8): 703-706. DOI:10.1130/0091-7613(2000)28<703:TOBTEM>2.0.CO;2 |
Commer M. 2011. Three-dimensional gravity modelling and focusing inversion using rectangular meshes. Geophysical Prospecting, 59(5): 966-979. |
de Wit R W L, Valentine A P, Trampert J. 2013. Bayesian inference of Earth's radial seismic structure from body-wave traveltimes using neural networks. Geophysical Journal International, 195(1): 408-422. DOI:10.1093/gji/ggt220 |
Dirian Y, Foffa S, Kunz M, et al. 2016. Non-local gravity and comparison with observational datasets. Ⅱ. Updated results and Bayesian model comparison with ΛCDM. Journal of Cosmology and Astroparticle Physics, 2016: 068. |
England P, Molnar P. 1997. Active deformation of Asia: From kinematics to dynamics. Science, 278(5338): 647-650. DOI:10.1126/science.278.5338.647 |
Fang J, Xu H Z. 1997. Three-dimensional lithospheric density structure beneath Qinghai-Tibet and its adjacent area. Acta Geophysica Sinica (in Chinese), 40(5): 660-666. |
Fang L H, Wu J P, Wang W L, et al. 2013. Relocation of the mainshock and aftershock sequences of Ms7.0 Sichuan Lushan earthquake. Chinese Science Bulletin, 58(28): 3451-3459. |
Fedi M, Rapolla A. 1999. 3-D inversion of gravity and magnetic data with depth resolution. Geophysics, 64(2): 452-460. DOI:10.1190/1.1444550 |
Fukahata Y, Nishitani A, Matsu'ura M. 2004. Geodetic data inversion using ABIC to estimate slip history during one earthquake cycle with viscoelastic slip-response functions. Geophysical Journal International, 156(1): 140-153. DOI:10.1111/j.1365-246X.2004.02122.x |
Fukahata Y, Wright T J. 2008. A non-linear geodetic data inversion using ABIC for slip distribution on a fault with an unknown dip angle. Geophysical Journal International, 173(2): 353-364. DOI:10.1111/j.1365-246X.2007.03713.x |
Geng M, Welford J K, Farquharson C G, et al. 2019. 3-D gravity inversion using a constrained probabilistic method: Applications to crustal-scale models of rifted continental margins, offshore Newfoundland, eastern Canada. Acta Geologica Sinica-English Edition, 93(S1): 300-301. DOI:10.1111/1755-6724.14106 |
Golub G H, Heath M, Wahba G. 1979. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics, 21(2): 215-223. DOI:10.1080/00401706.1979.10489751 |
Green W R. 1975. Inversion of gravity profiles by use of a Backus-Gilbert approach. Geophysics, 40(5): 763-772. DOI:10.1190/1.1440566 |
Hansen P C. 1994. Regularization tools: a Matlab package for analysis and solution of discrete ill-posed problems. Numerical Algorithms, 6(1): 1-35. DOI:10.1007/BF02149761 |
Hansen P C. 2001. The L-curve and its use in the numerical treatment of inverse problems.//Computational Inverse Problems in Electrocardiology: Advances in Computational Bioengineering, Vol. 5. Southampton: WIT Press, 119-142.
|
He C S, Dong S W, Wang Y H. 2019. Lithospheric delamination and upwelling asthenosphere in the Longmenshan area: insight from teleseismic P-wave tomography. Scientific Reports, 9: 6967. DOI:10.1038/s41598-019-43476-0 |
Hinze W J, Von Frese R R B, Saad A H. 2013. Gravity and Magnetic Exploration: Principles, Practices, and Applications. Cambridge: Cambridge University Press.
|
Howe B. 2009. Constrained potential field inversions in areas under cover: Examples from Gawler Craton IOCG prospects. ASEG Extended Abstracts, 2009(1): 1-10. |
Jiang W L, Zhang J F. 2011. Deep structures of Sichuan-Yunnan region derived from gravity data. Progress in Geophysics (in Chinese), 26(6): 1915-1924. DOI:10.3969/j.issn.1004-2903.2011.06.004 |
Kearey P, Brooks M, Hill I. 2002. An Introduction to Geophysical Exploration. 3rd ed. New York: John Wiley and Sons.
|
Last B J, Kubik K. 1983. Compact gravity inversion. Geophysics, 48(6): 713-721. DOI:10.1190/1.1441501 |
Lei J S, Zhao D P, Su J R, et al. 2009. Fine seismic structure under the Longmenshan fault zone and the mechanism of the large Wenchuan earthquake. Chinese Journal of Geophysics (in Chinese), 52(2): 339-345. |
Li H L, Fang J, Braitenberg C. 2017. Lithosphere density structure beneath the eastern margin of the Tibetan Plateau and its surrounding areas derived from GOCE gradients data. Geodesy and Geodynamics, 8(3): 147-154. DOI:10.1016/j.geog.2017.02.007 |
Li H L, Fang J, Wang X S, et al. 2016. Density inversion of gravity gradient tensor based on ART. Progress in Geophysics (in Chinese), 31(1): 54-60. DOI:10.6038/pg20160106 |
Li H L, Fang J, Wang X S, et al. 2017. Lithospheric 3-D density structure beneath the Tibetan plateau and adjacent areas derived from joint inversion of satellite gravity and gravity-gradient data. Chinese Journal of Geophysics, 60(6): 2469-2479. DOI:10.6038/cjg20170634 |
Li Y G, Oldenburg D W. 1998. 3-D inversion of gravity data. Geophysics, 63(1): 109-119. DOI:10.1190/1.1444302 |
Li Y G, Oldenburg D W. 2000. Joint inversion of surface and three-component borehole magnetic data. Geophysics, 65(2): 540-552. DOI:10.1190/1.1444749 |
Li Z W, Xu Y, Huang R Q, et al. 2011. Crustal P-wave velocity structure of the Longmenshan region and its tectonic implications for the 2008 Wenchuan earthquake. Science China Earth Sciences, 54(9): 1386-1393. DOI:10.1007/s11430-011-4177-2 |
Liu Q Y, Van Der Hilst R D, Li Y, et al. 2014. Eastward expansion of the Tibetan Plateau by crustal flow and strain partitioning across faults. Nature Geoscience, 7(5): 361-365. DOI:10.1038/ngeo2130 |
Nabighian M N, Ander M E, Grauch V J S, et al. 2005. Historical development of the gravity method in exploration. Geophysics, 70(6): 63ND-89ND. DOI:10.1190/1.2133785 |
Ogata Y, Katsura K. 1993. Analysis of temporal and spatial heterogeneity of magnitude frequency distribution inferred from earthquake catalogues. Geophysical Journal International, 113(3): 727-738. DOI:10.1111/j.1365-246X.1993.tb04663.x |
Qing P B, Huang D N. 2016. Integrated gravity and gravity gradient data focusing inversion. Chinese Journal of Geophysics (in Chinese), 59(6): 2203-2224. DOI:10.6038/cjg20160624 |
Riggelsen C, Ohrnberger M, Scherbaum F. 2007. Dynamic Bayesian networks for real-time classification of seismic signals.//European Conference on Principles of Data Mining and Knowledge Discovery. Berlin, Heidelberg: Springer, 565-572.
|
Royden L H, Burchfiel B C, King R W, et al. 1997. Surface deformation and lower crustal flow in eastern Tibet. Science, 276(5313): 788-790. DOI:10.1126/science.276.5313.788 |
Shen C Y, Yang G L, Tan H B, et al. 2015. Gravity anomalies and crustal density structure characteristics of profile Weixi-Guiyang. Chinese Journal of Geophysics (in Chinese), 58(11): 3952-3964. DOI:10.6038/cjg20151106 |
Shen W S, Ritzwoller M H, Kang D, et al. 2016. A seismic reference model for the crust and uppermost mantle beneath China from surface wave dispersion. Geophysical Journal International, 206(2): 954-979. DOI:10.1093/gji/ggw175 |
Tapponnier P, Peltzer G, Le Dain A Y, et al. 1982. Propagating extrusion tectonics in Asia: New insights from simple experiments with plasticine. Geology, 10(12): 611-616. DOI:10.1130/0091-7613(1982)10<611:PETIAN>2.0.CO;2 |
Tapponnier P, Xu Z Q, Roger F, et al. 2001. Oblique stepwise rise and growth of the Tibet Plateau. Science, 294(5547): 1671-1677. DOI:10.1126/science.105978 |
Terakawa T, Matsu'ura M. 2008. CMT data inversion using a Bayesian information criterion to estimate seismogenic stress fields. Geophysical Journal International, 172(2): 674-685. DOI:10.1111/j.1365-246X.2007.03656.x |
Tikhonov A N, Arsenin V Y. 1977. Solutions of Ill Posed Problems. Washington, DC: Winston.
|
Vogel C R. 1996. Non-convergence of the L-curve regularization parameter selection method. Inverse Problems, 12(4): 535. DOI:10.1088/0266-5611/12/4/013 |
Wang C Y, Li Y H, Lou H. 2016. Issues on crustal and upper-mantle structures associated with geodynamics in the northeastern Tibetan Plateau. Chinese Science Bulletin, 61(20): 2239-2263. DOI:10.1360/N972016-00160 |
Wang F Y, Duan Y H, Yang Z X, et al. 2008. Velocity structure and active fault of Yanyuan-Mabian seismic zone-The result of high-resolution seismic refraction experiment. Science in China Series D: Earth Sciences, 51(9): 1284-1296. DOI:10.1007/s11430-008-0098-0 |
Wang F Y, Zhao C B, Feng S Y, et al. 2015. Seismogenic structure of the 2013 Lushan MS7.0 earthquake revealed by a deep seismic reflection profile. Chinese Journal of Geophysics (in Chinese), 58(9): 3183-3192. DOI:10.6038/cjg20150914 |
Wang X B, Zhang G, Zhou J, et al. 2018. Crust and upper mantle electrical resistivity structure in the Longmenshan tectonic belt and its relationship with Wenchuan and Lushan earthquakes. Chinese Journal of Geophysics (in Chinese), 61(5): 1984-1995. DOI:10.6038/cjg2018M0233 |
Wang X C, Ding Z H, Zhu L P. 2016. Lithospheric structure of the northeastern North China craton imaged by S receiver functions. Pure and Applied Geophysics, 173(8): 2727-2736. DOI:10.1007/s00024-016-1293-0 |
Wang X C, Li Y H, Ding Z P, et al. 2017. Three-dimensional lithospheric S wave velocity model of the NE Tibetan Plateau and western North China Craton. Journal of Geophysical Research: Solid Earth, 122(8): 6703-6720. DOI:10.1002/2017JB014203 |
Wang X S, Fang J, Hsu H T. 2013. 3D density structure of lithosphere beneath northeastern margin of the Tibetan Plateau. Chinese Journal of Geophysics (in Chinese), 56(11): 3770-3778. DOI:10.6038/cjg20131118 |
Welford J K, Peace A L, Geng M X, et al. 2018. Crustal structure of Baffin Bay from constrained three-dimensional gravity inversion and deformable plate tectonic models. Geophysical Journal International, 214(2): 1281-1300. DOI:10.1093/gji/ggy193 |
Williams N C. 2008. Geologically-constrained UBC-GIF gravity and magnetic inversions with examples from the Agnew-Wiluna greenstone belt, Western Australia[Ph.D. thesis]. Vancouver: The University of British Columbia.
|
Williams N C, Lane R, Lyons P. 2004. Regional constrained 3D inversion of potential field data from the Olympic Cu-Au province, South Australia. Preview, 109: 30-33. |
Xu X W, Wen X Z, Ye J Q, et al. 2008. The MS8.0 Wenchuan earthquake surface ruptures and its seismogenic structure. Seismology and Geology (in Chinese), 30(3): 597-629. |
Yang W C, Hou Z Z, Yu C Q. 2015. Three-dimensional density structure of the Tibetan plateau and crustal mass movement. Chinese Journal of Geophysics (in Chinese), 58(11): 4223-4234. DOI:10.6038/cjg20151128 |
Yang Y J, Ritzwoller M H, Zheng Y, et al. 2012. A synoptic view of the distribution and connectivity of the mid-crustal low velocity zone beneath Tibet. Journal of Geophysical Research, 117. DOI:10.1029/2011JB008810 |
Yao H J, Beghein C, van der Hilst R D. 2008. Surface wave array tomography in SE Tibet from ambient seismic noise and two-station analysis-. Crustal and upper-mantle structure. Geophysical Journal International, 173(1): 205-219. DOI:10.1111/j.1365-246X.2007.03696.x |
Yao H J, Yang Y, Wu H X, et al. 2019. Crustal shear velocity model in Southwest China from joint seismological inversion. CSES Scientific Products. doi: 10.12093/02md.02.2018.01.v1.
|
Zhang X K, Yang Z X, Xu Z F, et al. 2007. Upper crust structure of eastern A'nyemaqen suture zone: results of Barkam-Luqu-Gulang deep seismic sounding profile. Acta Seismologica Sinica (in Chinese), 29(6): 592-604. DOI:10.1007/s11589-007-0628-4 |
Zhang Z, Xu X W, Wen X Z, et al. 2008. Slip rates and recurrence intervals of the Longmen Shan active fault zone and tectonic implications for the mechanism of the May 12 Wenchuan earthquake, 2008, Sichuan, China. Chinese Journal of Geophysics (in Chinese), 51(4): 1066-1073. DOI:10.3321/j.issn:0001-5733.2008.04.015 |
Zhang Z J, Deng Y F, Teng J W, et al. 2011. An overview of the crustal structure of the Tibetan plateau after 35 years of deep seismic soundings. Journal of Asian Earth Sciences, 40(4): 977-989. DOI:10.1016/j.jseaes.2010.03.010 |
Zheng C, Ding Z F, Song X D. 2016. Joint inversion of surface wave dispersion and receiver functions for crustal and uppermost mantle structure in Southeast Tibetan Plateau. Chinese Journal of Geophysics (in Chinese), 59(9): 3223-3236. DOI:10.6038/cjg20160908 |
Zheng C, Ding Z F, Song X D. 2018. Joint inversion of surface wave dispersion and receiver functions for crustal and uppermost mantle structure beneath the northern north-south seismic zone. Chinese Journal of Geophysics (in Chinese), 61(4): 1211-1224. DOI:10.6038/cjg2018L0443 |
陈石, 王谦身, 卢红艳, 等. 2010. 三维重力反演新方法——调和密度成像理论与模型测试. 地球物理学进展, 25(6): 1917-1925. DOI:10.3969/j.issn.1004-2903.2010.06.005 |
方剑, 许厚泽. 1997. 青藏高原及其邻区岩石层三维密度结构. 地球物理学报, 40(5): 660-666. DOI:10.3321/j.issn:0001-5733.1997.05.007 |
房立华, 吴建平, 王未来, 等. 2013. 四川芦山MS7.0级地震及其余震序列重定位. 科学通报, 58(20): 1901-1909. |
姜文亮, 张景发. 2011. 川滇地区重力场与深部结构特征. 地球物理学进展, 26(6): 1915-1924. DOI:10.3969/j.issn.1004-2903.2011.06.004 |
雷建设, 赵大鹏, 苏金蓉, 等. 2009. 龙门山断裂带地壳精细结构与汶川地震发震机理. 地球物理学报, 52(2): 339-345. |
李红蕾, 方剑, 王新胜, 等. 2016. 基于代数重构算法的重力梯度张量反演. 地球物理学进展, 31(1): 54-60. DOI:10.6038/pg20160106 |
李红蕾, 方剑, 王新胜, 等. 2017. 重力及重力梯度联合反演青藏高原及邻区岩石圈三维密度结构. 地球物理学报, 60(6): 2469-2479. DOI:10.6038/cjg20170634 |
秦朋波, 黄大年. 2016. 重力和重力梯度数据联合聚焦反演方法. 地球物理学报, 59(6): 2203-2224. DOI:10.6038/cjg20160624 |
申重阳, 杨光亮, 谈洪波, 等. 2015. 维西-贵阳剖面重力异常与地壳密度结构特征. 地球物理学报, 58(11): 3952-3964. DOI:10.6038/cjg20151106 |
王椿镛, 李永华, 楼海. 2016. 与青藏高原东北部地球动力学相关的深部构造问题. 科学通报, 61(20): 2239-2263. |
王夫运, 段永红, 杨卓欣, 等. 2008. 川西盐源-马边地震带上地壳速度结构和活动断裂研究——高分辨率地震折射实验结果. 中国科学: 地球科学, 38(5): 611-621. DOI:10.3321/j.issn:1006-9267.2008.05.008 |
王夫运, 赵成彬, 酆少英, 等. 2015. 深反射剖面揭示的芦山7.0级地震发震构造. 地球物理学报, 58(9): 3183-3192. DOI:10.6038/cjg20150914 |
王绪本, 张刚, 周军, 等. 2018. 龙门山构造带壳幔电性结构特征及其与汶川、芦山强震关系. 地球物理学报, 61(5): 1984-1995. DOI:10.6038/cjg2018M0233 |
王新胜, 方剑, 许厚泽. 2013. 青藏高原东北缘岩石圈三维密度结构. 地球物理学报, 56(11): 3770-3778. DOI:10.6038/cjg20131118 |
徐锡伟, 闻学泽, 叶建青, 等. 2008. 汶川MS8.0地震地表破裂带及其发震构造. 地震地质, 30(3): 597-629. DOI:10.3969/j.issn.0253-4967.2008.03.003 |
杨文采, 侯遵泽, 于常青. 2015. 青藏高原地壳的三维密度结构和物质运动. 地球物理学报, 58(11): 4223-4234. DOI:10.6038/cjg20151128 |
张先康, 杨卓欣, 徐朝繁, 等. 2007. 阿尼玛卿缝合带东段上地壳结构——马尔康-碌曲-古浪深地震测深剖面结果. 地震学报, 29(6): 592-604. DOI:10.3321/j.issn:0253-3782.2007.06.004 |
张培震, 徐锡伟, 闻学泽, 等. 2008. 2008年汶川8.0级地震发震断裂的滑动速率、复发周期和构造成因. 地球物理学报, 51(4): 1066-1073. DOI:10.3321/j.issn:0001-5733.2008.04.015 |
郑晨, 丁志峰, 宋晓东. 2016. 利用面波频散与接收函数联合反演青藏高原东南缘地壳上地幔速度结构. 地球物理学报, 59(9): 3223-3236. DOI:10.6038/cjg20160908 |
郑晨, 丁志峰, 宋晓东. 2018. 面波频散与接收函数联合反演南北地震带北段壳幔速度结构. 地球物理学报, 61(4): 1211-1224. DOI:10.6038/cjg2018L0443 |
 2021, Vol. 64
2021, Vol. 64



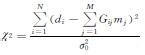 为模型卡方值,超参数λ1、λ2和AIBC由最小化公式(8)得到.
为模型卡方值,超参数λ1、λ2和AIBC由最小化公式(8)得到.