0 引言

地球深部圈层及沉积盆地是一种多层分区非均匀介质系统，其中大尺度不规则边界的反射和透射决定了地震波的传播特征，而小尺度层内随机非均匀介质引起波的散射和衰减.近一个多世纪以来，针对这种复杂介质系统地震波传播的理论和数值研究得到了极大的发展，有限差分法、有限元法和谱元法等普适的全数值模拟技术得到了广泛应用.然而，这些数值模拟方法均需对研究区域进行空间离散，有限尺寸的空间离散对不规则边界和体非均匀介质的近似程度有限，影响了地震模拟的精度，而半解析的数值模拟方法处理这些问题具有巨大的优势，能根据介质非均质程度和计算波长来调整模拟精度.本文拟综合几种半解析数值模拟方法，利用其优势，形成多层分区非均匀介质地震波传播模拟的最佳解决方案.

大多数半解析的地震数值模拟方法的建立源于边界积分方程，其优势在于精确刻画不规则边界和解析实施地层界面边界条件，实现对不规则界面反射、透射和散射的精确模拟.这些半解析数值模拟方法主要分为三类：早期的Aki-Larner方法(Aki and Larner, 1970; Bard, 1982)、Bouchon-Campillo离散波数方法(Bouchon, 1982, 1985; Campillo and Bouchon, 1985; Kawase, 1988; Bouchon et al., 1989)和直接(Dravinski, 1983; 符力耘和牟永光, 1994; Fu et al., 2002)与间接(Sánchez-Sesma and Esquivel, 1979; Sánchez-Sesma and Campillo, 1991; Ba and Liang, 2010; Ba and Xiao, 2016)的边界元法.基于含有边界积分与体积分的广义Lippmann-Schwinger积分方程，这些半解析数值方法进一步拓展至模拟含有不规则边界和体非均匀性的层状介质地震波传播(Fu, 2002; Fu and Bouchon, 2004; 管西竹等，2011).然而，基于积分方程的全波形数值解数据存储和计算耗时巨大，不适用于超大模型模拟和高频记录合成.为此，发展了基于波场连接技术的积分方程数值模拟方法(Fu and Wu, 2001; Ge et al., 2005)和各种积分方程逼近求解地震模拟方法(Hu et al., 2009; Yu et al., 2010; Yu and Fu, 2012, 2013, 2014).这些逼近方法以损失多次散射的模拟精度为代价来有效提高计算效率，适用于介质速度横向变化不大的地震模拟.通过积分方程的频率-波数域表征，上述半解析积分方程数值模拟方法可转换为高效率的R/T递推传播矩阵法.该发展方向的主要贡献源于Kennett (1974)极大发展了早期的Thomson-Haskell矩阵方法(Gilbert and MacDonald, 1960)，形成水平层状介质地震模拟的经典方法(Kennett, 1983; Luco and Apsel, 1983; Maupin and Kennett, 1987)，在地震学领域得到广泛应用.该方法进一步拓展至模拟不规则边界地层，形成不规则边界均匀地层广义R/T递推传播矩阵法(Chen, 1990, 1995, 1996; Cao et al., 2004; Ge and Chen, 2007, 2008)，其优势在于精确刻画不规则地层界面，精确模拟界面的反射、透射和散射效应.最近，Liu等(2020)在该方法基础上，利用广义Lippmann-Schwinger积分方程的频率-波数域表征(Fu, 2006)，结合R/T递推传播矩阵算法，采用薄板离散技术，建立了非均质地层薄板化全局广义R/T递推传播矩阵法.其优势在于：可根据地震模拟波长来调整薄板厚度或根据速度横向变化程度采用高阶薄板近似，准确模拟地层内部随机非均质体散射引起的地震波衰减效应.但由于采用薄板离散，该方法弱化了对不规则地层界面的精细刻画，对界面反射和透射的模拟精度有待研究.

本文拟吸收上述两种广义R/T递推传播矩阵方法各自的优势，形成一种非均匀介质、不规则边界的全局广义R/T递推传播矩阵混合方法，采用该混合方法求解二维情况下边界不规则、层内非均质的复杂模型中SH地震波场，特别是用于起伏近地表复杂介质地震波场的模拟.重点研究与波长相关的纵/横向离散精度以及与非均质强度相关的模拟精度，并开展了与边界元法的比较研究.

1 两种全局广义R/T递推传播矩阵地震模拟方法

均匀介质的不规则边界全局广义R/T递推传播矩阵(GGRTM)法(Chen, 1990, 1995, 1996)将积分方程的位移项和应力项在边界上展开，使对位移项的求解转换为对展开系数的求解，再通过引入全局广义反射/透射系数矩阵并建立该矩阵与界面相关参数矩阵的联系来实现波场中任意位置位移的求解.非均匀介质全局广义R/T递推传播矩阵法是不规则边界均匀介质广义R/T递推传播矩阵法在非均匀介质情况下的推广，其基本原理为：首先将整个计算模型进行薄层离散，之后将对含不规则边界的薄层边界积分与对非均匀介质薄层的体积分相结合，利用积分方程的离散矩阵同位移和应力及上下行波的关系获得修正反射/透射矩阵，最后将修正反射/透射矩阵转换为全局广义反射/透射矩阵并结合震源层的上下行波实现波场求解.本文方法的推导过程详见附录.

不规则界面全局广义R/T递推传播矩阵方法的计算流程包含以下几个步骤：第一步，将模型按各不规则界面进行分层.对于不规则层，将其分为上、中、下三部分，确定每一层中每一部分的最浅和最深深度(例如，对于第j个界面，其最浅和最深深度分别为z_up^(j)=ξ_min^(j)和z_low^(j)=ξ_max^(j))、剪切模量μ^(j)、密度ρ^(j)，并确定震源的位置；第二步，计算积分方程离散参数矩阵和全局修正反射/透射系数矩阵，并推导出全局广义反/透射系数矩阵；第三步，结合广义反射/透射矩阵与震源层的上下行波来计算任意深度的地震波场并合成理论地震图.

非均匀介质全局广义R/T递推传播矩阵方法基于广义Lipmann-Schwinger积分方程.第一步，先将模型划分成数个厚度很小的水平薄层.对于积分方程中的边界积分项直接使用虚拟边界上的物理参数进行计算；而对于体积分部分，若模型为一般的沉积地层，在地震勘探频带范围内采用一阶Born近似，利用每个薄层上下界面的边界积分来近似替代体积分，实现体积分项的降次，同时也可以满足模拟精度要求.而对于横向速度变化大的薄板(含盐丘)可采用二阶或高阶Born近似.第二步，将边界积分项和体积分项进行离散并组装成矩阵方程组.第三步，将通过矩阵方程组和相邻薄层间的位移和应力关系，将矩阵方程组转换成全局修正反射/透射矩阵，并进一步转换至全局广义反射/透射矩阵.第四步，利用震源层的总上下行波振幅和全局广义反射/透射矩阵，在层间使用迭代关系进行任意位置的波场求解.

以上两种全局广义R/T递推传播矩阵地震模拟方法均属于半解析的地震数值模拟方法，其原理和计算流程相似.不规则界面全局广义R/T递推传播矩阵方法的优势在于能准确描述模型中的不规则界面，实现了对界面的反射、透射及散射效应的精确模拟，但其并未考虑内部介质的非均匀性.而非均匀介质全局广义R/T递推传播矩阵法的优势恰恰在于能更好地描述地层内部随机非均质体散射对地震波衰减的影响，但该方法在实施过程中采用薄层近似来处理含不规则界面的地层，弱化了对不规则地层界面的精细刻画，因此根据计算模型的特点采用以上两种方法混合求解有利于充分发挥两种方法的优势.在实际情况中，地层中不规则界面与非均匀介质往往是同时存在的，当需研究的模型主要由不规则界面地层构成且含有随机非均匀介质层(如岩性强非均质的冲积山谷)时，对该非均质层可采用基于薄层近似的非均匀介质全局广义R/T递推传播矩阵法，其他地层则采用传统的不规则界面全局广义R/T递推传播矩阵方法求解，从而通过混合实施两种方法能实现对同一模型中不规则界面与介质非均匀性的准确模拟.

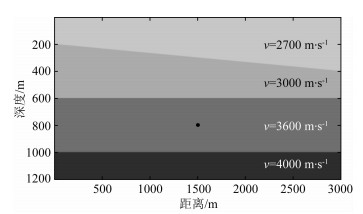
2 模拟精度分析

在本节中，我们对多种工况进行了正演计算，比较了不同剖分精度以及内部介质不同速度扰动量情况下的模拟结果.图 1给出了一个已知各地层背景速度的二维层状模型，该模型第一、二层分界面为倾斜界面，模型从上至下各层速度分别为2700 m·s^-1、3000 m·s^-1、3600 m·s^-1和4000 m·s^-1，地震子波采用主频为15 Hz的雷克子波，震源位于模型横向距离1500 m，深度800 m处，101个检波器以30 m的间隔均匀分布在地表.为了讨论本文方法在不同剖分精度下的计算情况，我们首先对图 1所示的模型根据单波长内不同单元数量来进行离散.

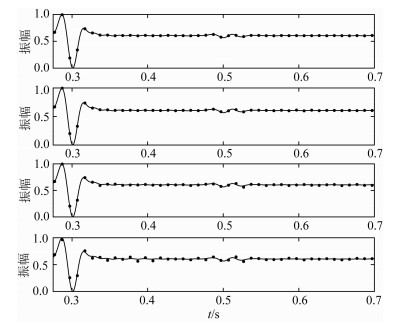
在本节的研究中，我们分别考虑了横向和纵向的离散精度.首先考虑均匀介质情形下的横向离散精度.对于图 1所示模型，各地层中最低波速为2700 m·s^-1，当震源主频为15 Hz时相应的最短波长为180 m.一般情况下，单位波长内单元剖分数量为3个即可保证计算精度(Campillo, 1987; Fu, 2002)，即剖分精度为60 m时可满足条件.为揭示不同离散精度下计算结果的差异，我们将单个波长内单元剖分的数量分别取为10、5、3、2，并分别计算这四种情况下的地震波场.为方便对比，这里抽取了位于模型正中的第51道的振幅曲线进行比较，如图 2所示.我们首先计算了单个波长内单元剖分数量为25的结果，在图 2中以黑色实线表示，进而给出了单波长内单元剖分数量为10、5、3、2四种情况下同一道的振幅与其进行比较，在图 2中以离散点表示.

由图 2可以看出，黑色实线所示的单波长内单元剖分数量为25的振幅曲线最为精确，横向剖分精度为每波长10、5、3个单元时同一道的振幅与该计算结果非常吻合，进一步说明单波长内单元剖分数为3时就已有足够的计算精度.而当剖分精度为每波长2个单元时，同一道振幅与该计算结果有较为明显的差异，说明在此单元剖分数情况下已难以保证计算精度.

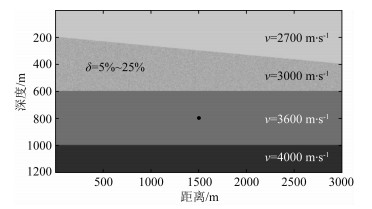
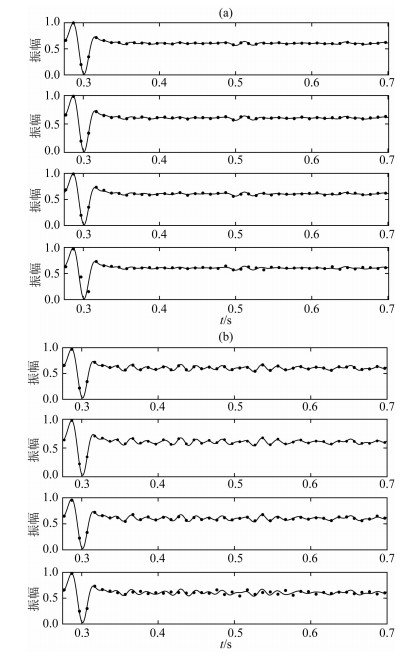
为了研究非均匀介质情况下本文方法的模拟精度，我们对图 1所示模型中的第二层介质加入两种不同程度的波速扰动，使其体现不同程度的介质非均匀性，如图 3所示.研究中分别考虑了介质弱扰动和强扰动两种情形，弱扰动对应所示模型中第二层介质5%的速度扰动，对于背景速度为3000 m·s^-1的第二层介质，加入5%的速度扰动意味着每个体积元的速度分布在2850 m·s^-1至3150 m·s^-1.类似地，强扰动对应该层25%的速度扰动，即每个体积元的速度分布在2250 m·s^-1至3750 m·s^-1.我们分别计算了两种情况下不同薄层离散厚度(即纵向离散精度)下第51道的单道记录结果，而两种情况下横向离散精度在满足采样定理的前提下保持相同，同为单个波长下6个体积元.与均匀介质精度研究类似，首先计算单个波长内薄层剖分数量为25的结果，在图 4中以黑色线表示，单波长内薄层剖分数为10、5、3、2四种情况在图 4中以离散点表示.需要特别说明的是，在本节中为了方便比较，我们将所有情况下的振幅曲线都进行了归一化处理(即振幅分布从0至1).图 4中给出了弱扰动和强扰动两种情况下不同单波长内薄层剖分数量时的中间道振幅曲线的比较.

由图 4可知，当以黑色实线所示的单波长内薄层剖分数量为25的振幅曲线作为比较对象时，在内部介质弱扰动情况下，纵向剖分精度满足10、5、3个薄层每波长时，同一道的振幅与该计算结果仍非常吻合，而当剖分精度仅满足每波长2个薄层时，同一道振幅与该计算结果存在着一定的差异，说明介质弱扰动情形接近于均匀介质的计算结果.在介质强扰动情况下，纵向剖分精度为5、3个薄层每波长时同一道的振幅与该计算结果已出现轻微的偏离，而当剖分精度仅满足每波长2个薄层时，同一道振幅与该计算结果差异非常大，表明介质的强扰动对保证计算精度所需的最低单元剖分数已产生明显的影响，对于含有强扰动的非均匀介质，保证计算精度需采用更大的单波长内的薄层剖分数.

3 混合法实施

本节中我们针对一个包含着不规则边界的层状介质，混合使用不规则界面全局广义R/T递推传播矩阵方法和非均匀介质全局广义R/T递推传播矩阵方法进行地震模拟，并与边界元法(Fu, 2002)的计算结果进行比较.边界元方法在均质情况下进行地震波场计算时需要对整个模型的所有地层进行边界的剖分，分别计算边界单元之间的相互影响，即格林函数，组装成参数矩阵后统一进行求解.而在非均质情况进行计算还需要对内部介质进行剖分，再计算体积元与边界单元以及体积元与体积元之间的相互影响之后统一组装成矩阵，再进行矩阵方程组的求解.

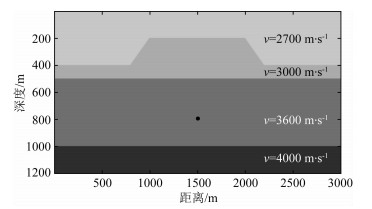
首先考虑内部介质均匀的情况，如图 5中的模型所示，该模型第一、二层界面为不规则界面，模型从上至下各层的速度分别为2700 m·s^-1、3000 m·s^-1、3600 m·s^-1和4000 m·s^-1，地震子波采用主频为15 Hz的雷克子波，震源位于模型横向距离1500 m，深度800 m处，101个检波器以30 m的间隔均匀分布在地表.

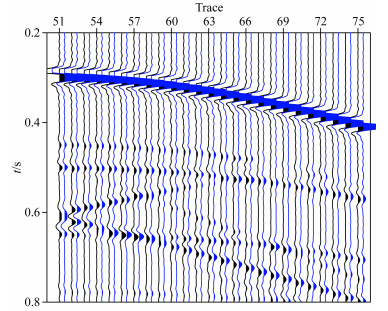
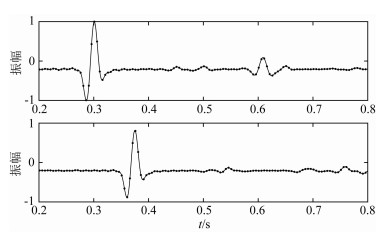
图 6为对以上模型分别使用混合法和边界元法得到的单炮记录的比较图，图中黑线为混合法的计算结果，蓝线为边界元法的计算结果.从中可以看出两种方法的计算结果基本一致.我们从两种方法的计算结果中抽取第51道和第71道的记录进行波形和相位的比较，如图 7所示.从图中可以看出，采用混合法和边界元法的计算结果几乎完全一致，表明了混合方法在处理非规则界面均匀介质问题时的准确性.

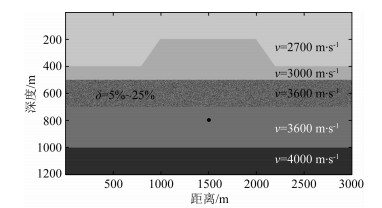
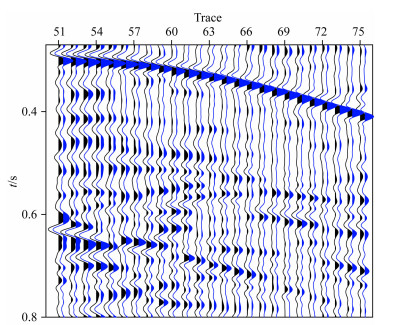
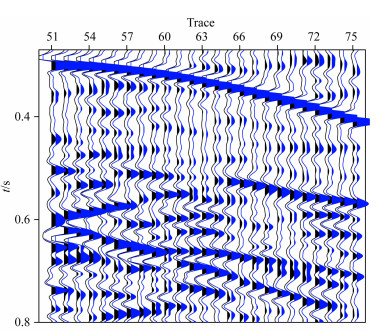
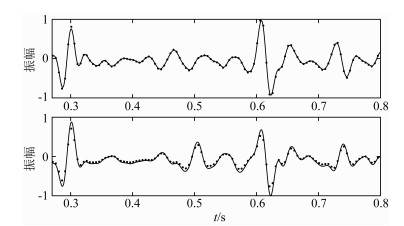
进一步考虑介质非均匀的情况，我们在图 5所示模型中震源位置的上方增加了一个200 m厚的水平非均质层，如图 8所示.非均质层分布在深度500 m至700 m，其背景速度仍为3600 m·s^-1，在实际内部介质剖分中，首先按照非均质层的体积元个数生成一个元素为-1到1的随机数矩阵，乘以速度扰动(如：5%)，并利用此矩阵和背景速度生成实际速度场，得到每个体积元的实际速度.与第2节中的数值算例类似，我们在这里也分别考虑该非均质层为弱扰动或强扰动两种情况，在该层中分别加入5%和25%的速度扰动，并和边界元法的计算结果进行比较，如图 9和图 10所示，同样针对弱、强两种扰动情况，我们从中抽取了第51道的记录进行振幅比较，结果如图 11所示.从图 9的地震记录比较图中可以看出，在弱扰动情况下，混合法计算出的波场仍能和边界元法保持较好的一致；而在图 10中所示强扰动情况下，混合法的计算结果已经和边界元法的计算结果有一定的差异，这是由于在强扰动情况下横向速度变化变大，而混合法中的非均匀介质全局广义R/T递推传播矩阵方法基于一阶Born近似，对于体积分的计算精度不够所致.而从图 11中的同一道地震记录比较可以看出，弱扰动的情况下，单道记录的波形也基本相似，而对于强扰动情况，反射波的相位和振幅已经和边界元的计算结果发生了偏差，而多次波部分也存在相位和振幅差异.

4 结论

本文将常规的不规则边界R/T递推传播矩阵方法进行了拓展，建立了一种用于求解二维SH波情况下含不规则边界、多层非均匀介质波传播问题的全局广义R/T递推传播矩阵混合方法.这一方法将不规则边界、多层非均匀介质内传播的地震波分解为入射波、边界散射波和体散射波三个部分，总波场采用广义Lippmann-Schwinger积分方程进行精确叠加求解.该方法的关键在于将不规则边界与介质的非均匀性进行了解耦，对半空间内不规则边界产生的散射波，通过将半空间划分为一系列水平非均质薄层，计算含不规则边界的薄层的传播算子来求解；对于考虑介质非均匀性的一般的沉积地层，直接采用边界积分替代体积分，即对每个薄层进行一阶Born近似并获得传播算子求解，而对于速度横向变化大的薄板(含盐丘)可采用二阶或高阶Born近似来提高模拟精度.需要说明的是，对于介质速度空间平缓变化的情况，我们沿用了前人的方法(Fu，2002；Fu and Bouchon, 2004)，将非均匀介质波动方程简化为均匀背景介质波动方程，该简化可直接将半空间均匀介质的格林函数作为波动方程的解.采用本文发展的混合方法，模型中任一位置的地震波场均可通过震源项和整个半空间的广义传播矩阵经过迭代实现求解.本文重点研究了非均质地层薄板化R/T传播矩阵法的模拟精度，包括与波长相关的纵/横向离散精度以及与非均质强度相关的模拟精度，并与边界元的计算结果进行了比较.对同时含有不规则边界地层和随机非均质地层的复杂模型采用混合方法进行地震波传播数值模拟，结果表明本文提出的混合法是一种解决复杂模型高精度地震模拟的有效方法.

作为一种可以替代有限差分或有限元的高效数值计算方法，本文提出的全局广义R/T递推传播矩阵混合法在计算速度和精度上都有很大优势.该方法根据采样定理进行薄板离散，其极限精度取决于薄板离散的个数，随着薄板(层)个数的增加，计算量也会相应增大.然而该方法提供了一种灵活的选择，即在广域均质区域可以通过增大薄板厚度以提高计算速度，在非均质区域则可通过减小薄板厚度以提高计算精度.这样的变剖分精度的方法尤其适用于含非均匀层的层状介质模型数值求解，在计算精度、效率上相比有限元、有限差分方法有明显的优势，在未来地震学相关研究中用于处理不规则边界和非均匀介质波场计算有广泛的应用前景.需要指出的是本文只考虑SH波情形，将本文方法用于P-SV波波场求解尚待进一步的研究工作.

附录

本文方法的推导过程分为如下几个步骤：第一步，通过整个模型的物理性质，获得广义Lippmann-Schwinger积分方程表达式，进而转换到频率域下并进行横向离散与薄层离散；第二步，使用Waterman(1975)的波场展开方法将积分方程组转换成关于位移和应力的矩阵方程组；第三步，将矩阵方程组中的参数矩阵转换成修正R/T矩阵进而转换成全局广义R/T矩阵，从震源层出发，利用震源层的上下行波和全局广义R/T矩阵实现波场中任一点的波场求解.以上三步的详细推导过程如下：

A  频率域下广义Lippmann-Schwinger积分方程的推导及离散

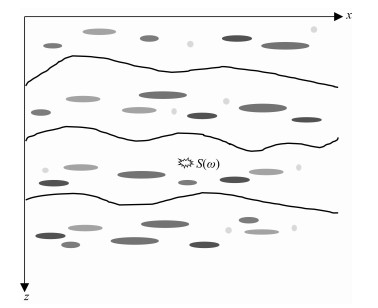
图A1中为一散射介质模型，假设震源S(ω)位于r₀处，则此散射介质中的地震响应满足以下标量Helmholtz波动方程：

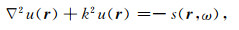
(A1)

其中ω为角频率，k=ω/v(r)为波数.

根据(A1)式，在r处的地震响应u(r)可表示为入射波场u⁽⁰⁾(r)、边界散射u⁽¹⁾(r)和体积散射u⁽²⁾(r)三部分，其表达式分别为：

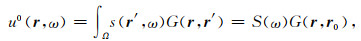
(A2)

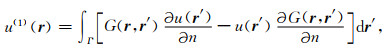
(A3)

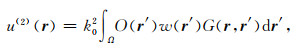
(A4)

其中G(r, r′)为格林函数, 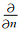为边界法向导数，O(r′)为速度扰动量，k₀为背景波数，w(r′)为介质内地震响应.

综合式(A2)至(A4)，可以得到广义Lippmann-Schwinger积分方程，即：

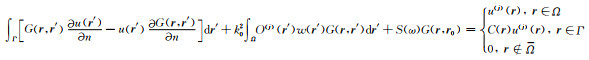
(A5)

其中C(r)为与边界几何特征相关的参数.

为了求解以上积分方程，我们使用离散波数法对公式(A5)中的边界积分项和体积分项进行离散.假设介质具有局部非均匀性，介质按长度L在水平方向上按周期性分布n次，则任意层内的格林函数的离散波数形式为：

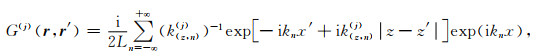
(A6)

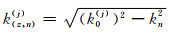
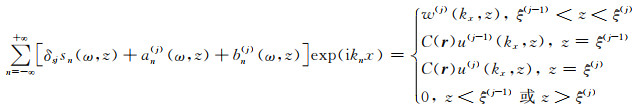
其中k_n=2πn/L为水平波数，为垂向波数且满足Im[k_{(z, n)}^(j)]>0.把公式(A6)代入公式(A5)中可以得到广义Lippmann-Schwinger积分方程的离散波数表达式(Fu, 2004)：

(A7)

式中相应参数的表达式为：

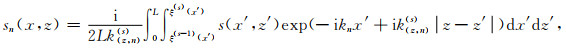
(A8)

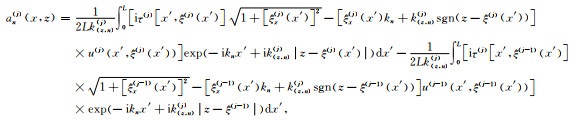
(A9)

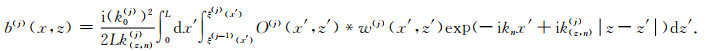
(A10)

其中ξ^(j)和ξ^(j-1)分别为第j层的上下界面深度，ξ_x^(j)为边界曲线的法向导数.

特别地，在求解式(A10)中的体积分项时采用梯形法则来进行简化，将非均质层划分成多个薄层并采用上下边界的边界积分来近似代替体积分，相当于对每一个薄层做一次一阶Born近似，近似后得到的表达式为：

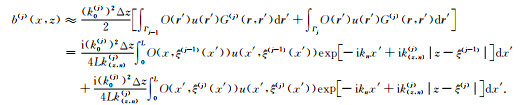
(A11)

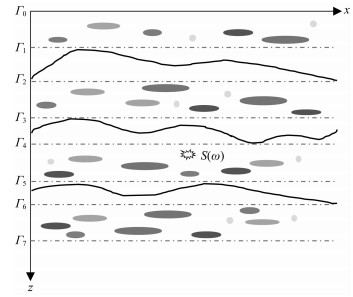
至此，我们就可以针对图A1中的原始模型进行薄层剖分，并对薄层类型进行分类，如图A2所示.

举例来说，对图A2所示的分层模型，若由Γ₁与Γ₂以及两侧的人工边界围成的薄层中包含着不规则边界，则使用不规则界面全局广义R/T递推传播矩阵方法来进行计算；若由Γ₂与Γ₃以及两侧的人工边界围成的薄层中包含着非均匀介质，则使用非均匀介质全局广义R/T递推传播矩阵方法进行计算.其中，含不规则边界的层中的广义Lippmann-Schwinger积分方程仅含有a^(j)(x, z)项，而含非均质薄层的方程则同时包含a^(j)(x, z)和b^(j)(x, z)项.我们将每个薄层对应的方程组分成两类，分别使用适合该薄层类型的方法进行混合求解.

B  矩阵方程组的转化

根据式(A7)中的表达式，提取其中的位移项α与应力项β，将与位移项和应力项相乘的参数归为三类：(1)与位移项相乘的边界参数Q；(2)与应力项相乘的边界参数P；(3)与位移项相乘的内部介质参数M.根据Waterman(1975)的波场展开，并分别考虑被观测点相对于薄层的相对位置，式(A7)可以分为如下两种情况：

① 当z＜ξ^(j-1)且δ_sj=0时：

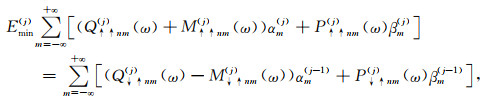
(B1)

② 当z＞ξ^(j)且δ_sj=0时：

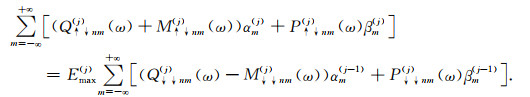
(B2)

其中，E_min^(j)和E_max^(j)分别为与相邻薄层的最小深度差和最大深度差相关的参数，参数Q, P, M的下标中的两个箭头分别代表波的传播方向和被观测点与薄层的相对位置关系，这些参数的详细表达式为：

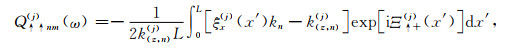
(B3)

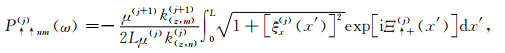
(B4)

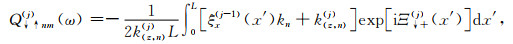
(B5)

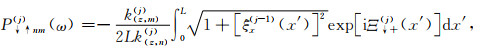
(B6)

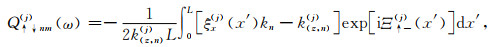
(B7)

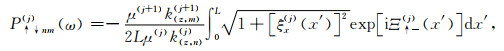
(B8)

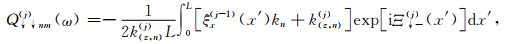
(B9)

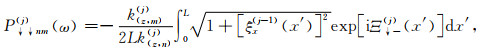
(B10)

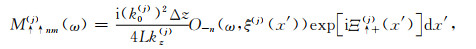
(B11)

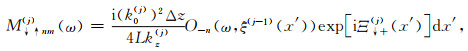
(B12)

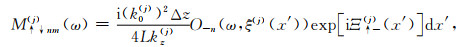
(B13)

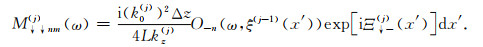
(B14)

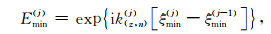
(B15)

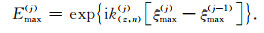
(B16)

式中，Δz为薄层厚度，公式(B3)至(B14)中，Ξ_↑+^(j)(x′), Ξ_↓+^(j)(x′), Ξ_↑-^(j)(x′)和Ξ_↓-^(j)(x′)为与薄层剖分深度ξ^(j)以及起伏界面的最大深度ξ_max^(j)和最小深度ξ_min^(j)的相关参数，其详细表达式分别为：

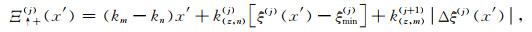
(B17)

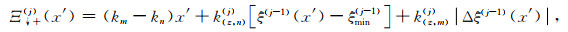
(B18)

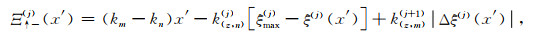
(B19)

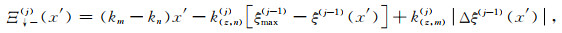
(B20)

其中，Δξ^(j)(x′)为表述界面起伏的参数.需要注意的是，仅在处理不规则界面部分时才需要计算公式(B17)至(B20)部分，在处理非均质部分时，由于界面起伏为0，公式(B3)至(B14)中的积分项的值都为1，仅需要计算积分项前的系数.

C  全局修正反射/透射矩阵及全局广义反射/透射矩阵的推导

根据Luco和Apsel(1983)，任意剖分薄层中的总波场都可表示为总上行波和总下行波之和.根据上述推导，以第j层与第j+1层为例，上行波a_↑^(j)和下行波a_↓^(j+1)与第j界面的位移α^(j)和应力β^(j)存在以下关系：

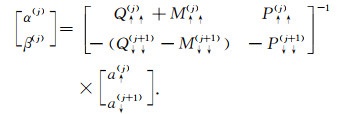
(C1)

同时，层内的上下行波和修正反射/透射矩阵满足以下条件：

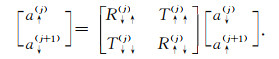
(C2)

其中，R_↓↑^(j), R_↑↓^(j)是修正反射系数因子，T_↑↑^(j), T_↓↓^(j)是修正透射系数因子.结合公式(C1)和(C2)以及公式(B1)和(B2)形成的矩阵方程，修正反射/透射矩阵可表示为：

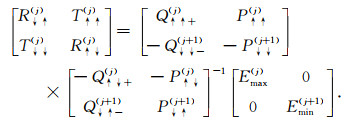
(C3)

其中，Q_↑↓+^(j), Q_↑↑+^(j), Q_↓↑-^(j+1)和Q_↓↓-^(j+1)分别用来代表Q_↑↓^(j)+M_↑↓^(j), Q_↑↑^(j)+M_↑↑^(j), Q_↓↑^(j+1)-M_↓↑^(j+1)和Q_↓↓^(j+1)-M_↓↓^(j+1).

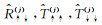
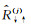
在得到了全局修正反射/透射矩阵之后，为方便计算，引入全局广义反射/透射因子，其对应反射/透射算子和满足以下关系：

① 当薄层位于震源层之上时，有：

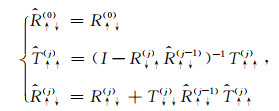
(C4)

② 当薄层位于震源层之下时，有：

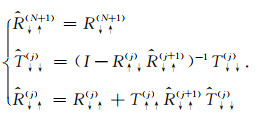
(C5)

至此，模型中任意一点的波场可以通过从震源层出发的上下行波与全局广义R/T矩阵通过迭代关系获得.