2. 天地(常州)自动化股份有限公司, 江苏常州 213015;
3. 同济大学海洋地质国家重点实验室, 上海 200092;
4. 阿里巴巴集团, 杭州 311121
2. Tiandi(Changzhou) Automation Co., Ltd., Changzhou Jiangsu 213015, China;
3. State Key Laboratory of Marine Geology, Tongji University, Shanghai 200092, China;
4. Alibaba Group, Hangzhou 311121, China
各向异性在地下介质中广泛存在,在地震波传播中各向异性会同时影响信号的相位和振幅.对于大偏移距数据,不考虑各向异性会导致速度估计发生很大误差.这促使近年来学术界和工业界在研究基于地震波的反演、成像以及储层建模技术时,必须将算法从各向同性拓展到各向异性(Tsvankin et al.,2010).因此面向各向异性参数估计的层析成像技术成为现代地震反演与成像技术中的一个重要组成部分.然而,由于各向异性层析成像方法引入了更多未知参量,使得参数估计的不确定性和复杂度都大大增加,因此长期以来一直是一个非常有挑战的研究课题.
基于走时的各向异性层析成像已经有大量研究工作(Chapman and Pratt, 1992;Zhou et al., 2008; Wang and Tsvankin, 2013;卢明辉等, 2005;刘玉柱等,2014;黄光南等,2015).20世纪末以来,一种全新的层析成像算法——立体层析,开始为学术界和工业界所知.立体层析将局部相干同相轴在炮集与检波点道集内的射线参数(或P参数)水平分量,以及炮点坐标和检波点坐标都纳入到反演的数据空间之中,重新定义了层析反演的数据分量和模型分量,使得立体层析成为射线类层析反演方法中唯一一种可以同时反演速度结构、反射点位置与反射层局部形态的方法(Billette and Lambare, 1998).国内外学者在各向同性立体层析的理论和实践方面已有很多研究工作(Chauris et al., 2002; Billette et al, 2003; Alerini et al., 2007, 2008; 倪瑶等, 2013, 2014;任丽娟等,2014;李振伟等,2014).Prieux等(2013)利用立体层析为全波形反演建立了优秀的初始模型.Li等(2015)将块状约束加入立体层析FRECHET导数矩阵的建立过程,使得反演结果更具有地质一致性.王宇翔等(2016)将结构张量算法用于P参数水平分量的搜索,实现了高密度的二维立体层析反演.杨锴等(2016)基于非降阶汉密尔顿算子实现了三维直角坐标系下的立体层析反演方法.Xing等(2017)并将其用于实际资料处理.Xiong等(2017)将结构张量用于成像域,将人工拾取与运动学反偏移相结合,制定了更为合理的成像域数据点拾取策略,形成了一种更为实用的两步法策略.
各向异性立体层析方面的研究则相对较少,Barbosa等(2008)讨论了椭圆与非椭圆各向异性介质中PP波立体层析的FRECHET导数求取问题.Nag等(2010)推导了基于PP/PS波数据空间、适用于一般各向异性的立体层析FRECHET导数公式.Tavakoli等(2017)则将上述工作在伴随状态法的理论框架下进行了初步实现.
前人实施各向异性立体层析方法各异,但尚未有人在三角网格模型下予以讨论.使用三角网格模型是考虑到它一种非常稀疏的模型描述方式,利用三角网格来描述模型空间将可以大幅压缩层析矩阵的规模,在提高求解精度的同时压缩了计算成本.Yang等(2017),邵炜栋等(2017)基于慢度平方三角剖分模型实现了二维各向同性立体层析.他们采用地质界面约束下的慢度平方模型三角网格剖分描述地质模型(Hale and Cohen, 1991),能够自然的在模型描述中引入地质界面,该建模方法能够以最稀疏的方式描述块体内的缓变与剧变的波阻抗界面,从而极大的压缩层析反演的模型空间.考虑到各向异性对地震波运动学特征的影响属于次级效应,如果想要保证各向异性参数的反演精度,采用尽可能稀疏的模型表达方式不仅是必要的,而且在实践中更是必须的.慢度平方三角网格模型描述的另一个好处是射线追踪有解析解,使得计算更为高效,从正演的角度对节省计算成本也做出了贡献.
在Yang等(2017)、邵炜栋等(2017)工作的基础上,本文基于考虑界面的各向异性射线扰动理论(Farra, 1989), 将模型空间从各向同性扩展到VTI介质,并逐一求取了反演所需的各个数据空间分量对任一模型空间分量的偏导数,从而建立起慢度平方三角网格剖分下二维VTI介质中的qP波各向异性立体层析所需的FRECHET导数矩阵.本文所使用的各向异性参数化方式为ε以及η=δ-ε,也就是说需要反演的各向异性参数为ε和η.背景介质定义为椭圆各向异性VTI介质,即η=0的情况.由于在慢度平方椭圆各向异性介质中的射线追踪有解析解,基于射线扰动理论从背景椭圆各向异性介质扰动到非椭圆各向异性介质时能够获得半解析解,这使得射线追踪以及FRECHET导数的建立变得简洁高效.可以认为是本文方法最显著的一个优势.
本文展示的敏感度测试表明,慢度平方三角剖分模型下建立的立体层析FRECHET导数矩阵中的元素具有较好的敏感度,可以用于二维VTI介质QP波各向异性立体层析反演.由于模型空间参数的增加,对所有参数进行同时反演变得相当困难,因此本文设计了相应的分步骤反演工作流程,首先反演除了各向异性参数之外的其他模型空间分量如慢度、界面信息、反射点位置等,在获得比较可靠的上述初始模型空间信息基础上,再反演各向异性参数获得各类模型参数信息,来保证各向异性参数反演可以得到稳定的结果,理论算例证实了上述观点,为后续的实际应用奠定了理论基础.
1 各向异性射线理论简介为保证文章的自洽性,首先对各向异性介质射线理论做一简介.Christoffel方程是各向异性射线理论研究的起点.
1.1 Christoffel方程Christoffel方程由各向异性弹性波动方程代入平面波解之后导出(Červený,2001),对密度归一化后其形式为
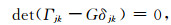
|
(1) |
其中G(x, p)=1,是方程的特征值,对应的方程特征向量为相应波的极化矢量. Γjk是Christoffel矩阵的元素, Γjk=piplcijkl,密度归一化后的弹性参数aijkl=cijkl/ρ.其中cijkl是各向异性弹性参数, pi=∂T/∂xi表示相慢度各分量.T为走时,ρ表示密度.
由于弹性刚度常数的对称性,可以将这个系统写成Voigt矩阵形式.弹性刚度矩阵元素带有两个下标,即:cijkl=Cmn(m, n=1, 2, …, 6).其对应关系如下:11→1,22→2,33→3,23和32→4,13和31→5,12和21→6.由此,原本3×3×3×3的弹性刚度系数矩阵cijkl可以用6×6的矩阵Cmn表示.本文将使用前文提及的密度归一化后的弹性参数aijkl及其对应的6×6的矩阵Amn.
常见的横向各向同性介质(TI介质)具有柱对称轴.在这种介质中,方程(1)存在三个独立的解: 一个qP波和两个不同方向的qS波.由于地球内部大部分沉积岩都表现出TI介质的各向异性,因此以对称轴垂直时的VTI模型为基础的各向异性TI介质研究显得尤为重要.该模型常常被用于描述由周期性的薄互层、岩石内部结构和平行排列的微裂隙引起的各向异性.本文研究以对称轴沿着z轴方向即垂直于各向同性平面介质(VTI介质).在此类介质中方程(1)中三个特征值可以解析表达为(2)式:
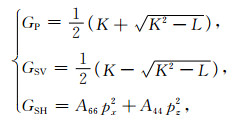
|
(2) |
其中
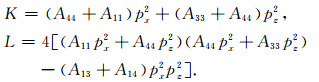
|
Farra(1989)据此定义了各向异性介质中的Hamiltonian:
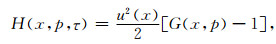
|
(3) |
其中对qP波:u2=A33-1,对于qS波:u2=A44-1;积分变量τ与走时的关系:dT=u2dτ.(3)式可自然退化到各向同性Hamiltonian:
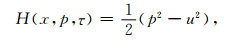
|
(4) |
其中对P波:u=vP-1;对S波: u=vS-1.
根据(3)式所示的各向异性Hamiltonian,可得对应的运动学射线追踪方程:
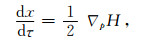
|
(5a) |
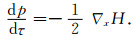
|
(5b) |
本节回顾Farra(1989)在背景介质为VTI椭圆各向异性下导出的qP波射线追踪方程.由于该方程形式简洁,使得在背景介质求取关于ε的FRECHET导数变得相当容易.
根据Thomsen参数表征有:
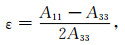
|
(6) |
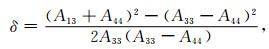
|
(7) |
结合(2)式,可以得到如下关系:
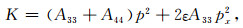
|
(8) |
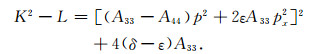
|
(9) |
在实际地质情况中各向异性通常较弱,因此对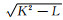
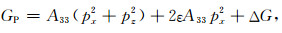
|
(10) |
其中
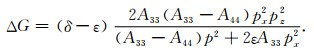
|
(11) |
在椭圆各向异性介质(δ-ε=0)情况下,显然有ΔG=0,这时将(10)式代回(3)式可以得到椭圆各向异性介质下的qP波Hamiltonian:
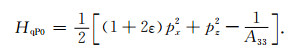
|
(12) |
显然可以将ΔG视为由η=δ-ε的小扰动造成的变量,将(11)式代入(3)式,得到对应的由椭圆各向异性扰动至非椭圆各向异性的ΔH:
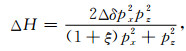
|
(13) |
其中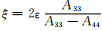
令H=HqP0+ΔH,即可得到本文使用的VTI介质中的qP波Hamlitonian:
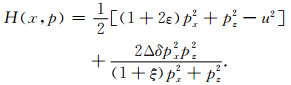
|
(14) |
将(12)式所示的椭圆各向异性背景下qP波Hamiltonian重写为
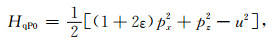
|
(15) |
其中u2=A33-1.
注意在慢度平方三角网格描述下,每个三角形内填充固定的各向异性参数以及固定的纵横向梯度,因此其慢度平方u2(x)=u02+Γx.其中Γ为梯度.当ε为常数时,得到这时的射线追踪方程:
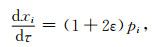
|
(16a) |
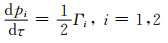
|
(16b) |
显然,方程(16)的解析表达式如下:
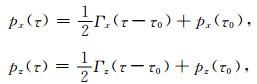
|
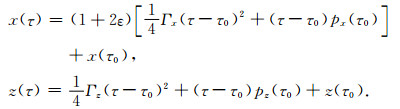
|
(17) |
走时可由积分变量τ与走时T的关系dT=u2du得到:
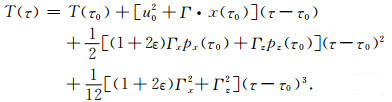
|
(18) |
如果仅仅在椭圆各向异性介质下实施立体层析反演,通过(17)、(18)式即可容易求得数据空间中X坐标,走时T,射线参数P关于ε的偏导数:
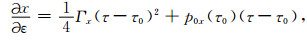
|
(19a) |
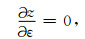
|
(19b) |
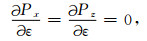
|
(19c) |
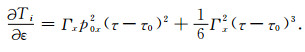
|
(19d) |
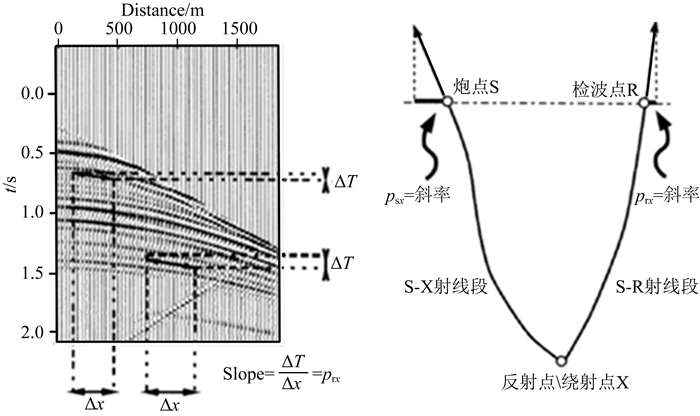
考虑到文章的自洽性,首先利用图 1展示常规二维各向同性立体层析中数据空间与模型空间的各个分量.对于二维空间的一个射线对而言,假设地表水平,那么地表能观测到的数据为d =(Sx, Rx, Tsr, Psx, Prx), 其中Sx, Rx为炮检点的X坐标;Tsr为这个射线对的总走时;Psx, Prx为炮检点处的射线参数水平分量.这些数据分量与地下的模型空间m =(x0, z0, θs, θr, V)有关,其中x0, z0为地下反射点坐标, θs, θr代表从炮点与检波点一侧出射的地下散射角, V代表地下介质速度信息.其中共炮点道集和共检波点道集内的局部相干同相轴的斜率等同于检波点处和炮点处慢度矢量的水平分量(Billette and Lambaré,1998).
|
图 1 二维立体层析数据空间各分量与模型空间各分量 Fig. 1 The model-space components and the data-space components in 2D stereotomography |
而在慢度平方三角网格下VTI介质中讨论二维QP波各向异性立体层析时,数据空间分量不变,其模型空间变为:m=(x0, z0, θs, θr, xn, zn, u2, ε, η)其中xn和zn是构成界面的节点的横、纵坐标, u2表示慢度平方.ε和η是之前定义过的各向异性参数.数据空间的残差Δd与模型空间残差Δm之间的关系由射线扰动理论建立,这里可以简写为
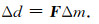
|
(20) |
(20) 式代表了一个矩阵方程,其系数矩阵F即为立体层析FRECHET偏导数矩阵.在慢度平方介质下的完整形式可以表达如下:
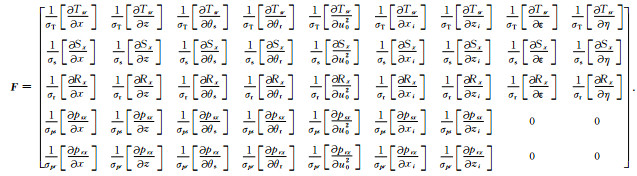
|
(21) |
在这个矩阵中,显然有:
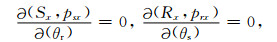
|
(22) |
其次,根据费马原理,走时T在速度结构、激发点与接收点位置都固定时,已经是最小走时.因此可以认为散射角对走时T不存在一阶扰动影响.即可认为
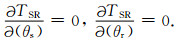
|
(23) |
由于在该理论方法下,层内各向异性参数被设为常数(即每个三角形网格中也为常数),因此射线相慢度p对各向异性参数并没有一阶影响,即
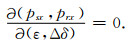
|
将上述关系代入(21)式,可以得到简化后的三角网格立体层析矩阵(24)式.(24)式中σ的含义为针对各类数据的尺度加权因子,用于平衡不同类型的数据对于立体层析反演的误差泛函的贡献比例,避免由于物理量纲不同造成数据类型量级之间差别过大的问题,参数的大小需要通过做具体的测试得到.
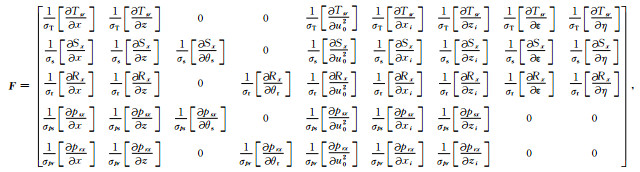
|
(24) |
立体层析反演的理论基础是射线扰动理论(Farra and Madariaga, 1987).射线扰动理论的重要性在于,它在傍轴射线追踪和汉密尔顿传播算子的基础上建立了速度扰动与描述射线传播的相空间各参数扰动量之间的一阶线性关系.三角网格剖分由于在模型描述中引入了界面,因此需要在扰动理论中考虑界面扰动对立体层析数据空间的影响.Farra等(1989)提出的考虑界面扰动的射线扰动理论恰恰是建立三角网格立体层析FRECHET导数矩阵所需要的.Yang等(2017),邵炜栋等(2017)基于该理论建立了各向同性介质下三角网格立体层析FRECHET导数矩阵.由于各向异性参数的加入,本文不仅仅利用传统的射线扰动理论,同时也结合解析公式引入了数据空间分量关于各向异性参数的FRECHET导数.第3、4节根据上述认识逐一建立三角网格VTI介质QP波二维立体层析中数据空间分量对模型空间分量之间的一阶线性扰动关系.
3 三角网格慢度平方模型下VTI介质二维QP波各向异性立体层析FRECHET导数求取在上文列出的FRECHET导数矩阵中,前9列对应于各向同性二维三角网格立体层析层析FRECHET导数,其推导方法请参考邵炜栋等(2017),这里不再重复.本文重点讨论与各向异性参数ε和η相关的这部分导数,即(24)式中的最后两列如何导出.
3.1 基于射线扰动理论推导数据空间关于ε和η的一阶扰动关系以下基于射线扰动理论推导数据空间各分量关于各向异性参数ε和η的一阶扰动公式.我们首先定义一个新的Hamiltonian表达式:
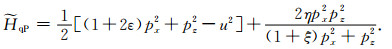
|
(25) |
其公式形式和(14)式完全一致,称之为新Hamiltonian的理由是后面在推导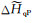
按照射线扰动理论可以写出
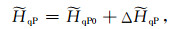
|
(26) |
式中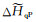
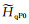
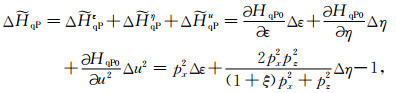
|
(27) |
公式(26)的另一种更为简洁的写法为
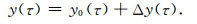
|
(28) |
为推导数据空间关于各向异性参数ε、η与初始相空间扰动的一阶扰动关系,不妨令初始相空间扰动为Δy0=(Δx0, Δp0),需要考察的扰动为各向异性参数的扰动Δε和Δη,慢度的扰动Δu.对(28)式进行微分即有
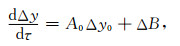
|
(29) |
其中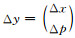
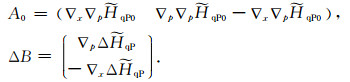
|
利用传播矩阵(Gilbert and Backus, 1966),可以得到式(29)的传播矩阵解:
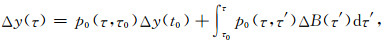
|
(30) |
其中右端第二项中ΔB的计算如下:
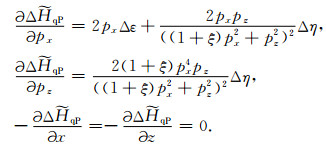
|
(31) |
公式(30)中的传播矩阵P0在椭圆各向异性介质中有很简洁的形式,因为椭圆各向异性背景介质中的扰动射线方程有解析解,其形式为:
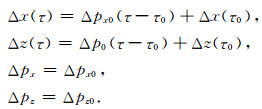
|
(32a) |
将(32a)式整理为与传播矩阵的乘积形式
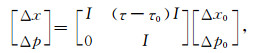
|
(32b) |
即可看出其传播矩阵P0矩阵的形式确实非常简单.
基于(31),(32)式展开(30)式即可获得地表数据空间中观测坐标X、射线参数P关于各向异性参数的一阶扰动关系,如(33)式所示.由于本文将一个地质块内的各向异性参数设定为常数,在这种情况下地表观测的P参数对各向异性参数没有敏感度.
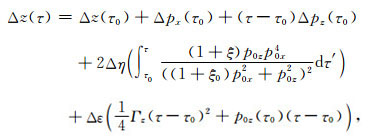
|
(33a) |
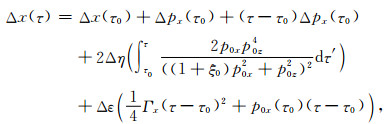
|
(33b) |
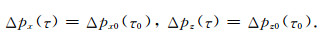
|
(33c) |
因此很容易写出地面观测时,坐标X、射线参数Px关于各向异性参数η的Frechet导数为
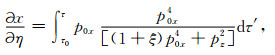
|
(34a) |
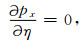
|
(34b) |
而X、Px关于ε的偏导数,容易看出其形式与(19a)(19c)式完全相同,这里不再重复.
关于走时T、η的一阶扰动关系,Farra等(1989)定义了如下走时扰动公式:
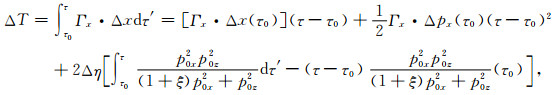
|
(35) |
因此很容易写出T关于η的FRECHET导数为
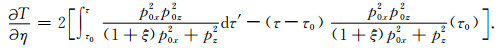
|
(36) |
从(35)式可以看出,走时ΔT与ε无关.因此ΔT关于ε的偏导数依靠背景椭圆各向异性公式即可求得,与(19d)式相同,这里也不再重复.
至此当射线在一个地质块内传播时,立体层析数据空间关于ε和η的偏导数已经全部得到.
3.2 非椭圆各向异性VTI介质中的半解析射线追踪及上述一阶扰动关系的数值验证由于非椭圆各向异性介质中的走时计算公式可以理解为背景椭圆各向异性计算公式(18)与扰动量计算公式(35)之和(Farra et al., 1989),因此有如下走时半解析公式:
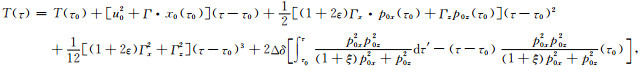
|
(37) |
显然坐标与慢度矢量在非椭圆各向异性介质下的半解析射线追踪方程亦可以同样的形式写出:
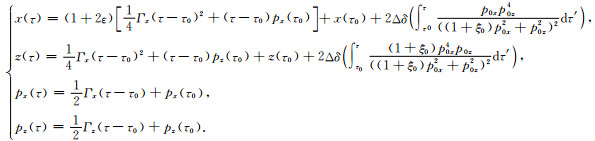
|
(38) |
(38) 式即为本文采用的慢度平方VTI介质中的各向异性射线追踪方程.本文方法实现下的射线追踪方程在层内计算时可以直接得出层位出射点的射线坐标与慢度的解析解,加之以层位之间的连续性条件(Shao et al., 2017)即可实现模型内完整的射线追踪.
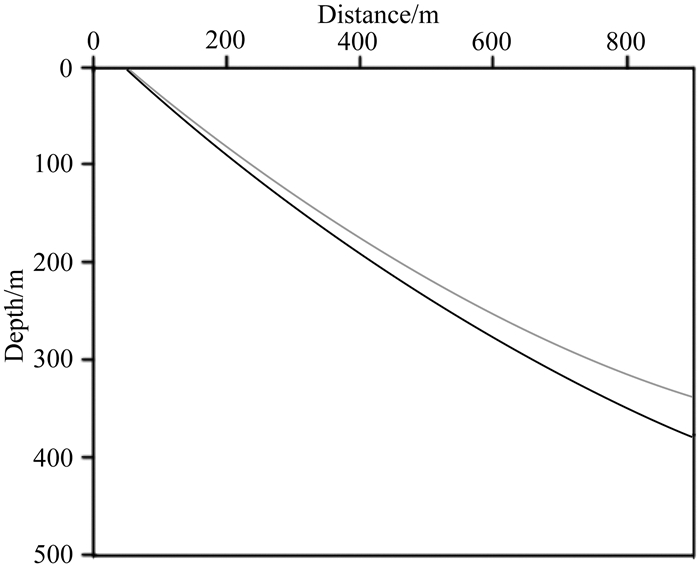
与传统的射线追踪相比,该法计算量大大减少.为验证公式(38)的精度,首先进行了一个扰动测试.图 2所示浅色曲线为椭圆各向异性介质下的射线追踪,旁边的深色曲线为在椭圆各向异性上加以δ的扰动的小扰动计算得到的射线,注意我们还利用龙格库塔算法在真实介质中也追出一根射线作为比较,可以看出龙格库塔算出的射线和利用公式(38)算出的射线几乎是完全重合.计算图 2所用的模型参数为:s02 = 1/3000/3000 s2·m-2; kz=-1×10-8; ε=0.3;A33=9.0;A44=5.19;Sx=500; Sz=0.4; 出射角θ=30°.各向异性参数扰动η=δ-ε=-0.2.
|
图 2 黑色曲线展示了椭圆各向异性介质下的射线追踪,灰色曲线为在椭圆各向异性上加以δ的扰动的小扰动计算得到的射线.其中s02=1/3000/3000 s2·m-2; kz=-1×10-8; ε= 0.3;A33=9.0;A44=5.19;Δδ=-0.2;Sx=500 m; Sz=0.4 m; θ=30° Fig. 2 The dark curve shows ray tracing in elliptical anisotropic media, when the gray curve shows the perturbed ray with small perturbation δ in elliptical anisotropic media. Parameters are given as s02=1/3000/3000 s2·m-2; kz= -1×10-8; ε=0.3;A33=9.0; A44=5.19;Δδ=-0.2; Sx=500 m; Sz=0.4 m; θ=30° |
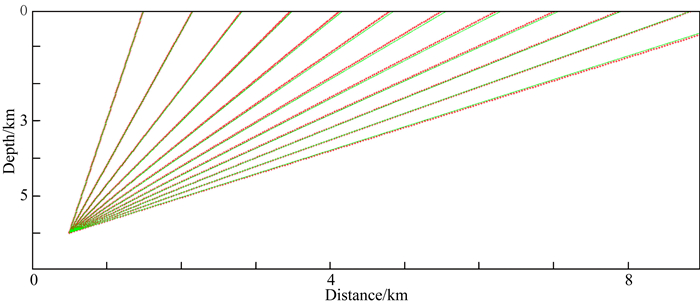
图 3显示了利用(38)式在非椭圆各向异性介质中以不同的出射角度进行射线追踪的精度比较,如图 2,红色线为(38)式射线追踪结果,绿色实线为相同参数情况下的龙格库塔射线追踪结果.这里使用的模型参数为s02=0.11 s2·m-2; ε=0.2;η=δ-ε=0.1; 出射角从15°变化到55°.各向异性参数扰动η=δ-ε=-0.2,扰动达到了60%以上,这个扰动范围基本达到了实际反演的要求.综合以上两个数值实验可以看出,(38)式的射线追踪具有很好的精度,可以用于慢度平方三角网格模型下的立体层析.
|
图 3 半解析射线追踪公式(38)精度测试 红色点线表示由(38)式计算的射线路径,而绿色实线则是表示常规龙格库塔方法解得的射线追踪.测试参数u02 = 0.11;2ε2=0.2;η=δ-ε2=0.1. Fig. 3 Precision test of semi-analytical ray tracing equation The red dotted line represents the ray calculated by equation (38), when the green solid line represents the ray calculated by Runge-Kutta methods. Parameters are given as u02= 0.11;ε=0.2; η=δ-ε=0.1. |
如上一节所述,公式(19)、(36)表达了当射线在一个地质块内传播时,立体层析数据空间关于ε和η的偏导数.然而地下介质一般而言不可能是单个地质块组成的,也就是说射线一般会穿越多个地质界面达到地表.因此公式(19)、(36)还需要做与通过界面有关的某种修正才可以用于多层三角网格模型.这个问题并非是慢度平方各向异性立体层析所独有,邵炜栋等(2017)在建立慢度平方各向同性立体层析FRECHET导数时就已经仔细考虑过.这里简要回顾他们的处理方式,并将其用于本文在射线穿越多个界面时的各向异性参数的FRECHET导数求取.根据邵炜栋等(2017)中的推导,过界面后射线扰动量与过界面前傍轴射线末端的扰动量关系如下:
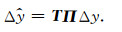
|
(39) |
(39) 式代表了射线过一个界面时,根据矩阵Π和矩阵T即可求得过界面之后的过界面之后的扰动量.其中Π矩阵表示计算中心射线到达地表时对应的傍轴射线的信息,而T矩阵则表示考虑Snell定律和参数连续性后得到的过界面后的傍轴射线信息.在计算下一层的傍轴扰动量时,便可把此次扰动量作为下一层的初始扰动量进行计算.各向异性下这部分的推导与各向同性一致,但具体计算时需要代入式(25)所示的各向异性Hamiltonian,T矩阵和Π矩阵的具体形式请参考邵炜栋等(2017).
由(39)式,可以将射线穿越n个界面时(19,36)式中X关于各向异性参数的偏导数改写为:
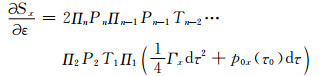
|
(40a) |
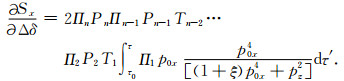
|
(40b) |
走时T并不属于(39)式定义的射线相空间元素,因此在射线穿越多个界面时其偏导数形式并没有变化.
4.2 与各向异性参数ε和η有关FRECHET导数敏感度测试在得到三角网格二维QP波各向异性立体层析所需的数据空间各分量与模型空间各分量之间的一阶线性扰动关系之后,以下基于三角网格理论模型中的一个射线对信息,来测试不同数据分量与不同模型分量之间的敏感度.图 4a展示了一个三层慢度平方模型,射线穿过2个界面,3个地层,共5个节点.数据空间信息依然通过射线正演获得,射线的出射点在(1.8 km,2 km)处,在z=0 m处可观测到数据空间(Sx, Rx, Tsr, Psx, Prx).由于邵炜栋等(2017)已经展示了各向同性下的数据分量与不同模型分量之间的偏导数敏感度,这里不再重复.这里仅展示数据空间分量Psx, Tsr对与各向异性参数相关的模型空间分量ε和η的偏导数敏感度测试.

|
图 4 敏感度测试模型以及三角网格立体层析中Sx, T关于ε和η的敏感度测试 (a) 模型和射线对;(b) Sx/ε; (c) Sx/η; (d) Tsr/ε; (e) Tsr/η. Fig. 4 Sensitivity test of Frechet derivatives for some selected data components (Sx, T) and selected model components (ε, η) of triangulated stereotomography (a) Test model and a ray pair; (b) Sx/ε; (c) Sx/η; (d) Tsr/ε; (e) Tsr/η. |
图 4b,4c,4d,4e展示了数据空间分量炮点坐标Sx和走时T关于各向异性参数ε, η的偏导数测试.在初始参数上加以±20%的扰动,从而计算得到这些曲线.以图 4b为例,偏导数∂Sx (ε)/∂ε是由傍轴射线追踪算得,可以清楚看到直线Sx(ε0)+(∂Sx(ε)/∂ε)Δε与在真实介质中射线追踪得到的曲线Sx(ε0+Δε)相切, 图 4证明了Sx, T和ε, Δη在模型空间中的敏感性是存在的,根据(40)、(19)式计算得到的FRECHET导数结果是正确的.
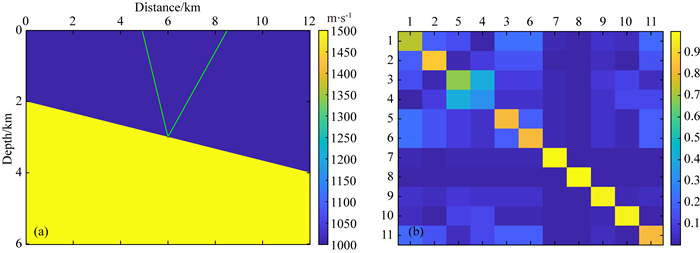
为测试多参数联合反演的可行性,这里采用了模型分辨率矩阵进行验证.模型分辨率矩阵是分析多参数反演耦合特性的有效工具,其计算公式如(41)所示.其中F为Frechet矩阵,λ可取0.将R归一化后,R如果接近单位阵I,则说明各个模型空间之间是解耦的.如果对角线外有值,便可以根据横纵坐标的信息查看具体的模型分量之间的耦合性.
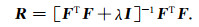
|
(41) |
选取一个简单的两层模型,在(6, 2.99)km处分别以140°、200°出射两条射线,计算出数据空间关于模型空间各个分量的Frechet矩阵进行上述运算,再套用公式(41)即可得到如图 5b所示的模型分辨率矩阵.注意图 5b从左到右依次为界面的两个节点的纵坐标;两个反射点的横、纵坐标;两个散射角、一层的背景慢度,两个各向异性参数,从上到下有同样的参数顺序.可以看出该矩阵呈现出较好的对角化程度.值得关注的是最后两个各向异性参数显然在本文方法下可以进行较为稳定的反演,这也证明了最后实现多参数联合反演的可行性.
|
图 5 模型分辨率矩阵 (a) 用于测试模型分辨率速度模型; (b) 模型分辨率矩阵测试结果. Fig. 5 Model resolution matrix (a) Test Vp0 model of model resolution matrix; (b) Result of test of model resolution matrix. |
由于模型空间加入了各向异性参数,使得直接进行多参数同时反演变得尤为困难.本节首先设计一个简单三层模型的理论试验,且只反演各向异性参数.用来检验在速度、节点等其他模型空间分量位置都设置为正确值的情况下,各向异性参数的反演精度.本次实验共计使用了40根射线,并由这些射线来生成本次反演所需的的数据空间分量(Sx, Rx, T).图 6a, 6d分别展示了真实的各向异性参数模型ε和η,图 6b, 6e为两者所对应的初始模型,均设为0(即为各向同性),而图 6c, 6f则为反演迭代5轮后得到的最终各向异性参数模型ε和η.
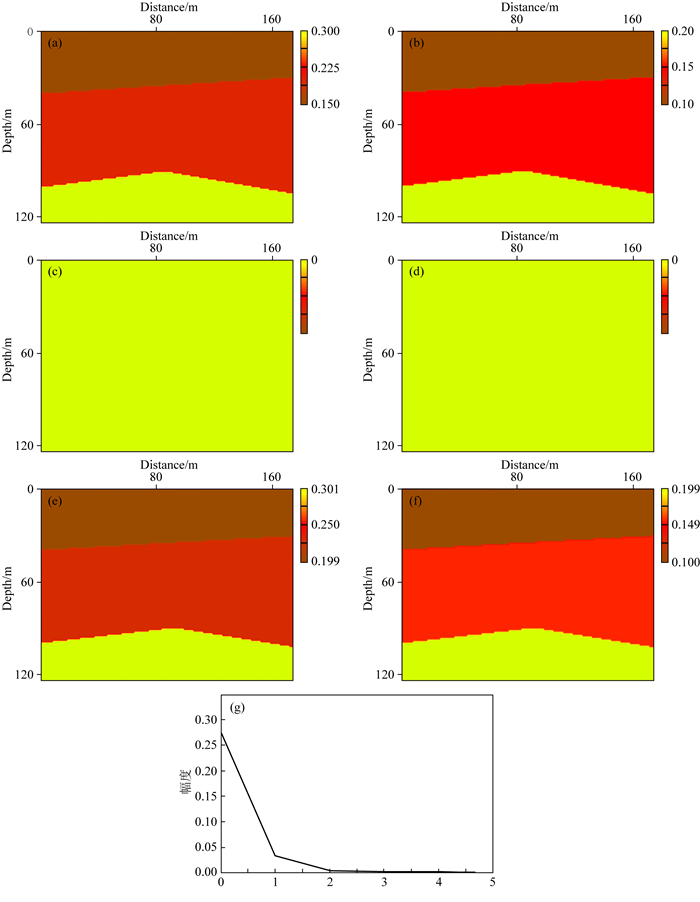
|
图 6 三层模型各向异性参数反演测试 (a) 真实ε模型;(b) 真实η模型;(c) 初始ε模型;(d) 初始η模型;(e) 5轮迭代反演后得到的ε模型;(f) 5轮迭代反演后得到的η模型;(g) 泛函下降曲线. Fig. 6 Inversion test of three-layer model (a) True ε model; (b) True η model; (c) Initial ε model; (d) Initial η model; (e) ε model after 5th inversion; (f) η model after 5th inversion; (g) Decline of the cost function during the iterations. |
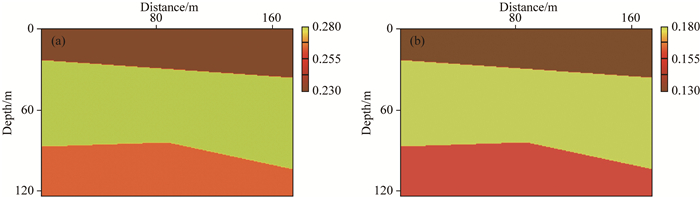
图 6g展示了泛函下降曲线,反演第二轮就已接近真实值,证明了之前推导的关于ε和η的偏导数的正确性.然而,对于任何一种各向异性层析反演方法来说,同时反演所有模型参数都是非常困难的.图 7展示了当界面信息不准时,即便速度为真实值时各向异性参数的反演结果.
|
图 7 层位信息不对时反演得到的结果 (a) 反演得到的ε模型;(b) 反演得到的η模型. Fig. 7 The inversion when other information is incorrect (a) Final ε model; (b) Final η model. |
根据图 7的结果可以看出,层位信息对反演结果有着非常重要的影响,若将较差的层位信息直接用于与各向异性参数的联合反演,得到的结果将不符合精度要求.同理,如果VP0不准确时,对各向异性参数的反演精度同样会产生负面影响.为了保证其稳健性,设计一个多步骤反演工作流程是非常必要的.本文给出了一个实用的二维三角网格下各向异性qP波立体层析的基本工作步骤:
(1) 对原始数据做叠前深度偏移(PSDM);
(2) 在初始PSDM结果上拾取层位信息,通过运动学反偏移得到立体层析数据空间;
(3) 利用拾取的层位节点信息建立三角网格模型,初始各向异性参数为常数.
(4) 基于手头的数据空间信息,进行常规二维各向同性三角网格立体层析反演,得到除各向异性参数以外的参数的初始模型;
(5) 固定其他参数不变,单独反演慢度平方u2, ε和η来作为各向异性参数的初始模型;
(6) 通过步骤(4)和(5)得到的较好的模型,可以进行慢度平方、界面节点位置、反射点位置、散射角和各向异性参数的联合反演.
由于适用于各向异性介质的运动学反偏移正在研究之中,因此在5.2节的联合反演测试中,我们并没有真的使用运动学反偏移来获得数据空间,我们的数据空间依然是采取从界面出发向上进行射线追踪到达地表获得的.也就是说5.2节的反演是直接从第4步开始的,第4步是一个各向同性介质下的三角网格立体层析,具体实现过程可参考邵炜栋等(2017).
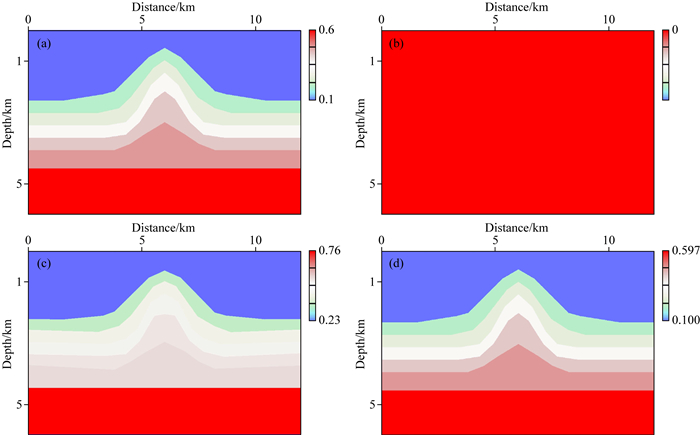
5.2 理论数据联合反演测试为了验证5.1节提出的工作流程的有效性,本实验在如图 8a所示的穹状速度模型中进行,横向12 km,纵向6 km,分为7个地质块体,中间有6个界面.该测试仅使用了180个射线对来生成实验所需的模型空间.根据5.1节所示工作流程,首先暂时忽略各向异性带来的影响,利用图 9b所示的Vp0和节点的初始模型,先进行常规二维各向同性三角网格立体层析反演,得到除各向异性参数以外的慢度、节点位置等更为贴近真实模型的初始模型(如图 9c).可以看出相对于图 9b所示的最初始模型,经过几轮常规各向同性立体层析反演后,图 8c所示模型两侧上翘部分得到了明显改善,但与真实模型(图 9a)仍有差距.这时使用常规各向同性立体层析反演得到的较好的速度和节点模型(图 9c),固定模型空间所有其他参数,仅仅进行两个各向异性参数ε和η的同时反演,就可以得到如图 10c和图 11c所示的ε和η模型的反演中间结果.最后再用图 9c, 10c, 11c, 的模型进行速度、节点、各向异性参数的多参数联合反演,就得到如图 9d、10d、11d所示的最终联合反演后的速度、节点、各向异性参数模型.从图 12所示的模型残差上可以看出,最终的反演结果与真实模型已经比较接近.可以证实5.1节提出的工作流程的有效性和之前推导的偏导数的正确性.

|
图 8 三角网格剖分建立的真实模型 Fig. 8 True triangulated model |

|
图 9 VP0和节点位置的反演 (a) VP0和节点真实模型;(b) VP0和节点初始模型;(c) 控制各向异性参数不变,单独反演速度和节点;(d) 联合反演得到最终的VP0和节点. Fig. 9 Estimation of VP0 and the interface location (a) Exact model; (b) Very initial model before step (4); (c) Initial model for joint inversion after step (4); (d) Final output model after joint inversion. |

|
图 10 关于ε反演结果展示 (a) ε真实模型; (b) ε初始模型; (c) 用单独反演的速度和界面信息反演得到的ε; (d) 联合反演得到最终ε. Fig. 10 Estimation of ε (a) Exact model; (b) Very initial model before step (5); (c) Iinitial model for joint inversion after step (5); (d) Final output model after joint inversion. |
|
图 11 关于η反演结果显示 (a) η真实模型; (b) η初始模型; (c) 用单独反演的速度和界面信息反演得到的η; (d) 联合反演得到最终η. Fig. 11 Estimation of η (a) Exact model; (b) Very initial model before step (5); (c) Initial model for joint inversion after step (5); (d) Final output model after joint inversion. |
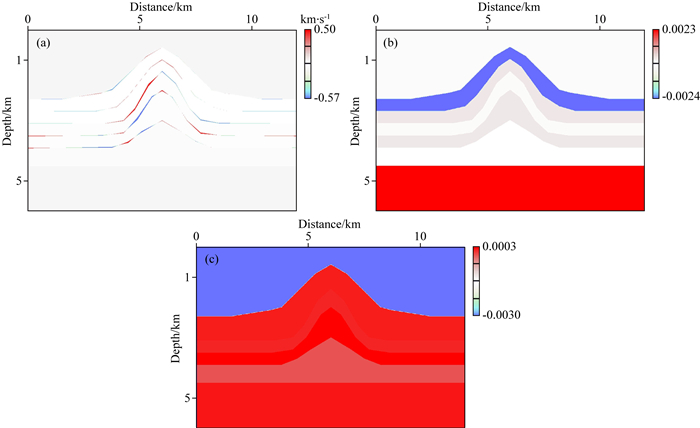
|
图 12 模型残差显示 (a) 真实VP0-反演最终VP0; (b)真实ε-反演最终ε; (c)真实η-反演最终η. Fig. 12 The misfit between the exact model and the final output model (a) Exact VP0-the final output VP0; (b) Exact ε-the final output ε; (c) Exact η-the final output η. |
慢度平方三角网格剖分模型下实施立体层析具有自然描述界面、同时更新慢度和界面、射线追踪有解析等优势.本文在Yang等(2017)、邵炜栋等(2017)实现了慢度平方三角网格二维立体层析反演方法的基础上,进一步发展了慢度平方三角剖分模型下的VTI介质QP波二维立体层析反演方法.本文所使用的各向异性参数化方式为ε以及η=δ-ε.背景介质定义为椭圆各向异性VTI介质,即η=0的情况.由于在慢度平方椭圆各向异性介质中的射线追踪有与各向同性介质下形式相近的解析解,使得到非椭圆各向异性介质情形下亦能获得半解析解,这使得射线追踪以及FRECHET导数的求取变得简洁高效.这是本文方法相对于其他方法最为显著的一个优势.
在上述理论前提下,我们逐一求取了反演所需的各个数据空间分量对任一模型空间分量的偏导数,从而建立起慢度平方三角网格剖分下二维VTI介质中的QP波各向异性立体层析所需的FRECHET导数矩阵.严格的敏感度测试和理论数据的算例一证实了我们推导的FRECHET导数矩阵中的元素具有较好的敏感度,可以用于二维VTI介质QP波各向异性立体层析反演.由于模型空间参数的增加,对所有参数进行同时反演变得相当困难,因此设计了相应的工作流程,首先反演除了各向异性参数之外的其他模型空间分量如慢度、界面信息、反射点位置等,在获得比较可靠的上述初始模型空间信息基础上,再反演各向异性参数获得各类模型参数信息,保证了各向异性参数反演可以得到稳定的结果.理论算例二证实了上述观点.后续将基于各向异性波动方程正演模拟的理论数据和实际数据进一步发展本方法,使得本文提出的算法真正具有实用价值.
致谢 作者感谢自然科学基金面上项目(41874118)对于这项研究的支持.
Alerini M, Lambaré G, Baina R, et al. 2007. Two-dimensional PP/PS-stereotomography: P- and S-waves velocities estimation from OBC data. Geophysical Journal International, 170(2): 725-736. DOI:10.1111/j.1365-246X.2007.03439.x |
Alerini M, Lambaré G, Baina R, et al. 2008. 2D PP/PS-stereotomography: Application to a real 2D-OBC dataset. Geophysical Prospecting, 56(2): 213-227. DOI:10.1111/j.1365-2478.2008.00681.x |
Barbosa B, Costa J, Gomes E, et al. 2008. Resolution analysis for stereotomography in media with elliptic and anelliptic anisotropy. Geophysics, 73(4): R49-R58. DOI:10.1190/1.2917853 |
Billette F, Lambaré G. 1998. Velocity macro-model estimation from seismic reflection data by stereotomography. Geophysical Journal International, 135(2): 671-690. DOI:10.1046/j.1365-246X.1998.00632.x |
Billette F, Le Bégat S, Podvin P, et al. 2003. Practical aspects and applications of 2D stereotomography. Geophysics, 68(3): 1008-1021. DOI:10.1190/1.1581072 |
Červený V. 2001. Seismic Ray Theory. Cambridge: Cambridge University Press.
|
Chapman C H, Pratt R G. 1992. Traveltime tomography in anisotropic media-I Theory. Geophysical Journal International, 109(1): 1-19. DOI:10.1111/j.1365-246X.1992.tb00075.x |
Chauris H, Noble M S, Lambaré G, et al. 2002. Migration velocity analysis from locally coherent events in 2D laterally heterogeneous media: I. Theoretical aspects. Geophysics, 67: 1202-1212. |
Farra V, Madariaga R. 1987. Seismic waveform modeling in heterogeneous media by ray perturbation theory. Journal of Geophysical Research: Solid Earth, 92(B3): 2697-2712. DOI:10.1029/JB092iB03p02697 |
Farra V. 1989. Ray perturbation theory for heterogeneous hexagonal anisotropic media. Geophysical Journal International, 99(3): 723-737. DOI:10.1111/j.1365-246X.1989.tb02054.x |
Farra V, Virieux J, Madariaga R. 1989. Ray perturbation theory for interfaces. Geophysical Journal International, 99(2): 377-390. DOI:10.1111/j.1365-246X.1989.tb01695.x |
Gilbert F, Backus G. 1966. Propagator matrices in elastic wave and vibration problems. Geophysics, 31(2): 326-332. DOI:10.1190/1.1439771 |
Hale D, Cohen J. 1991. Triangulated Models of the Earth's Subsurface: Cener for Wave Phenomena Colarado School of Mines. //Project review, Consortium Project on Seismic Inverse Methods for Complex Structures.
|
Li Z W, Yang K, Ni Y, et al. 2014. Migration velocity analysis with stereo-tomography inversion. Geophysical Prospecting for Petroleum (in Chinese), 2014, 53(4): 444-452.
|
Liu Y Z, Wang G Y, Dong L G, et al. 2014. Joint inversion of VTI parameters using nonlinear traveltime tomography. Chinese Journal of Geophysics (in Chinese), 57(10): 3402-3410. DOI:10.6038/cjg20141026 |
Lu M H, Tang J H, Yang H Z, et al. 2005. P-wave traveltime analysis and Thomsen parameters inversion in orthorhombic media. Chinese Journal of Geophysics (in Chinese), 48(5): 1167-1171. |
Prieux P, Lambaré G, Operto S, et al. 2013. Building starting models for full waveform inversion from wide-aperture data by stereotomography. Geophysical Prospecting, 2013, 61(S1): 109-137.
|
Shao W D, Yang K, Xing F Y, et al. 2017. Stereo-tomography in squared-slowness triangulated model. Chinese Journal of Geophysical (in Chinese), 60(9): 3574-3586. DOI:10.6038/cjg20170923 |
Tsvankin I, Gaiser J, Grechka V, et al. 2010. Seismic anisotropy in exploration and reservoir characterization: An overview. Geophysics, 75(5): 75A15-75A29. DOI:10.1190/1.3481775 |
Nag S, Alerini M, Ursin B. 2010. PP/PS anisotropic stereotomography. Geophysical Journal International, 181(1): 427-452. DOI:10.1111/j.1365-246X.2010.04501.x |
Wang XX, Tsvankin I. 2013. Ray-based gridded tomography for tilted transversely isotropic media. Geophysics, 78(1): C11-C23. DOI:10.1190/geo2012-0066.1 |
Ni Y, Li Z W, Wang L X et al. 2014. The preliminary practice of stereotomography. //Proceedings of the CPS/SEG Beijing 2014 International Geophysical Conference (in Chinese), Beijing: CPS/SEG.
|
Ren L J, Sun X D, Li Z C, 2014. The Stereotomography based on eigen-wave attributes. //Proceedings of the CPS/SEG Beijing 2014 International Geophysical Conference (in Chinese), Beijing: CPS/SEG.
|
Li Z W, Yang K, 2015, Towards an Edge-preserving Stereotomography with a Practical Model Regularization Technique, //Proceeding of the 77th EAGE Conference & Exhibition. Madrid, Spain: EAGE.
|
Wang Y X, Yang K, Yang X C, et al. 2016. A high-density stereo-tomography method based on the gradient square structure tensors algorithm. Chinese Journal of Geophysics (in Chinese), 59(1): 263-276. DOI:10.6038/cjg20160122 |
Tavakoli R, Zhang H. 2017. A nonmonotone spectral projected gradient method for large-scale topology optimization problems. Numerical Algebra Control & Optimization, 2(2): 395-412. |
Xing F Y, Yang K, Xue D, et al. 2017. Application of 3D stereotomography to the deep-sea data acquired in the South China Sea: A tomography inversion case. Applied Geophysics, 14(3): 142-153. |
Xiong K, Yang K, Wang Y X. 2017. Extracting a high-quality data space for stereo-tomography based on a 3D structure tensor algorithm and kinematic de-migration. Journal of Geophysics and Engineering, 14(4): 792-801. DOI:10.1088/1742-2140/aa68bf |
Yang K, Xing F Y, Li Z W, et al. 2016. 3D stereo-tomography based on the non-reduced Hamiltonian. Chinese Journal of Geophysics (in Chinese), 59(9): 3366-3378. DOI:10.6038/cjg20160920 |
Yang K, Shao W D. 2017. Stereotomography in triangulated models. //87th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
|
Zhou B, Greenhalgh S A, Green A. 2008. Nonlinear traveltime inversion scheme for crosshole seismic tomography in tilted transversely isotropic media. Geophysics, 73(4): D17-D33. DOI:10.1190/1.2910827 |
李振伟, 杨锴, 倪瑶, 等. 2014. 基于立体层析反演的偏移速度建模应用研究. 石油物探, 53(4): 444-452. DOI:10.3969/j.issn.1000-1441.2014.04.010 |
刘玉柱, 王光银, 董良国, 等. 2014. VTI介质多参数联合走时层析成像方法. 地球物理学报, 57(10): 3402-3410. DOI:10.6038/cjg20141026 |
黄光南, ZHOU Bing, 邓居智, 等. 2015. 各向异性TI介质qP反射波走时层析成像. 地球物理学报, 58(06): 2035-2045. |
卢明辉, 唐建侯, 杨慧珠, 等. 2005. 正交各向异性介质P波走时分析Thomsen参数反演. 地球物理学报, 48(5): 1167-1171. DOI:10.3321/j.issn:0001-5733.2005.05.026 |
倪瑶, 杨锴, 陈宝书. 2013. 立体层析反演方法理论分析与应用测试. 石油物探, 52(2): 121-130. |
倪瑶, 李振伟, 王立歆等. 2014. 立体层析反演的初步实践. SPE/SEG2014年国际地球物理会议论文集. 北京: 中国石油学会, 美国勘探地球物理学家学会.
|
任丽娟, 孙小东, 李振春. 2014. 基于特征波属性参数的立体层析速度反演方法研究. CPS/SEG北京2014国际地球物理会议摘要.
|
邵炜栋, 杨锴, 邢逢源, 等. 2017. 慢度平方三角网格立体层析反演方法. 地球物理学报, 60(9): 3574-3586. DOI:10.6038/cjg20170923 |
王宇翔, 杨锴, 杨小椿, 等. 2016. 基于梯度平方结构张量算法的高密度二维立体层析反演. 地球物理学报, 59(1): 218-276. DOI:10.6038/cjg20160122 |
杨锴, 邢逢源, 李振伟, 等. 2016. 基于非降阶汉密尔顿算子的三维立体层析反演. 地球物理学报, 59(9): 3366-3378. DOI:10.6038/cjg20160920 |
 2021, Vol. 64
2021, Vol. 64


