裂缝控制了岩石电流路径和流动特性(Renshaw,1996;Berkowitz et al., 2000),因此可以通过测量岩石的电学性质来探测裂缝.Stesky(1986)说明了裂缝性岩石的电导率不仅是岩石结构和内部流体电导率的函数,还与裂缝的开度、表面几何形状等有关.Sandler等(2009)通过实验证明,岩石是否含有裂缝导致不同频率下岩样电阻率随含水饱和度的变化特征有显著差异.沈金松等(2009)以水平裂缝分布的裂缝性储层模型为基础,讨论了裂缝开度、裂缝密度和裂缝粗糙度等裂缝特征参数对裂缝性储层电各向异性的影响.Li(2015)研究了在不同孔隙度、渗透率和岩性的岩石中裂缝对不同频率电阻率与含水饱和度的函数的影响,得到利用不同频率电阻率检测和评估裂缝的方法.刘智颖等(2018)通过岩电实验对数值模拟结果进行检验得出裂缝的产状、宽度和密度等参数对岩石电阻率的影响,并提出适用于裂缝型储层含气饱和度计算公式.上述研究均集中在复电阻率的实部,未涉及与介电常数有关的复电阻率的虚部.仅利用复电阻率实部而不考虑复电阻率虚部来观察裂缝对于岩石电学性质的影响是不够的.在单独研究介电常数或复电阻率虚部的工作中,蔡军等(2016)采用1 GHz高频同轴实验测量泥质砂岩的介电常数,验证了李玉玲和张宇晓(1994)提出的仿阿尔奇公式.Han和Yang(2018)利用数值模拟方法,研究了105~109Hz频率范围内裂缝性多孔碳酸盐岩的介电特性及与填充裂缝的流体类型、裂缝连通性的关系,但未进行定量研究.在多年复电阻率岩石物理研究取得的成果基础上,近年柯式镇团队重点进行了1 GHz以下岩石复电阻率频谱实验,讨论了泥质砂岩、人工岩心复电阻率的频率依赖性(邹德鹏等,2018;马雪瑞等,2019),并通过复电阻率研究推测岩石孔隙度、渗透率等各种参数(Li et al., 2019).综上所述,目前尚缺少对岩石,尤其是对裂缝性岩石从饱和度角度进行复电阻率的相关研究.
裂缝性岩石的电性受孔隙结构和孔隙流体分布的强烈影响,在高含水饱和度下符合阿尔奇公式,但在低含水饱和度下,阿尔奇公式中的饱和度指数n与系数b发生了变化.阿尔奇公式中的参数不是常数,这些参数取决于孔隙度和流体饱和度(郑庆林等,2006).应用平行板电容器法(肖毅等,2009)测量岩石阻抗,通过低频段的阻抗实部计算出岩样的电阻率;通过阻抗虚部,即容抗(在低频时阻抗中的容抗远大于感抗,所以可忽略感抗的影响)可计算出岩样的介电常数.由于平行板内的电场为似稳场,所以不考虑磁导率的影响(苏庆新,1999).因为激发极化的影响以及介电常数本身就是频率的函数,所以不同裂缝特性的裂缝性岩样会产生不同的复电阻率频散现象.
本文采用同一种均匀岩样制造裂缝性岩石,调整人工裂缝的宽度、密度、倾角进行复电阻率的测量,并与有限元模拟结果进行对比,得到了裂缝对于岩样复电阻率频散曲线的影响.并根据裂缝对电阻增大率-含水饱和度图和介电常数变化率-含水饱和度图的影响,研究了阿尔奇公式以及仿阿尔奇公式中饱和度指数n和系数b分别与裂缝特征参数的关系,从而在实际裂缝性气藏评价研究中提高对裂缝和含气性的识别.
1 实验测量 1.1 岩样复电阻率测量系统本文建立的岩样饱和度与复电阻率测量装置(图 1)主要包括TH2829C型阻抗分析仪、高精度电子天平、岩样夹持器、计算机等部分.通过计算机软件完成岩样阻抗与质量数据的自动记录.

|
图 1 岩样复电阻率与重量测量装置 Fig. 1 Measuring device for complex resistivity and weight of the rock samples |
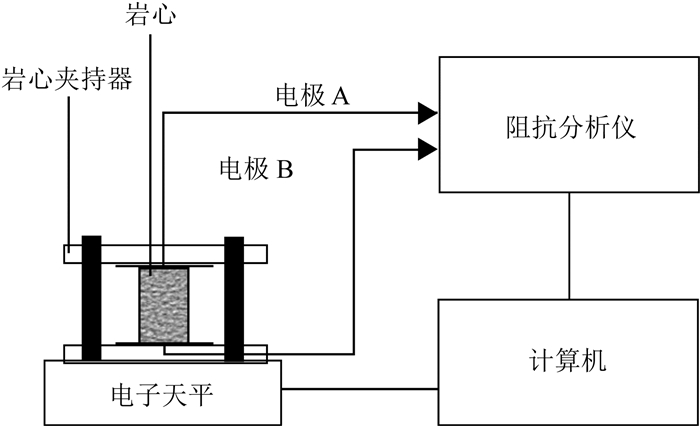
高精度电子天平通过USB端口连接到计算机,软件以5 min为间隔采集岩样在蒸发过程中质量的变化,从而得到作为时间函数的饱和度.同时阻抗分析仪也通过USB端口连接到计算机,在不同频率下以5 min为间隔采集阻抗数据(图 2).
|
图 2 岩样复电阻率与重量测量系统示意图 Fig. 2 Schematic diagram of rock sample complex resistivity and weight measurement system |
在完成天然长样实验测量之后,对岩石进行二次同样的测量,验证了测量系统的重复性.再用岩样切割器对岩样进行切割,人工制造裂缝.测量并研究在多个频率下不同裂缝宽度、密度、倾角的岩石复电阻率随含水饱和度变化规律.
1.2 实验岩样本文使用三组含泥质非常少的砂岩样构造出不同裂缝宽度、密度和倾角的裂缝性岩样,图 3为切割前后岩样照片与编号.

|
图 3 岩样及裂缝构造示意图 (a) KD-1;(b) KD-2;(c) KD-3;(d) KD-4;(e) MD-1;(f) MD-2;(g) MD-3;(h) QJ-1;(i) QJ-2;(j) QJ-3;(k) 环形塑料垫片. Fig. 3 Schematic diagrams of the rock samples and fracture structures |
第一组岩样KD-1(图 3a)用来构造一条水平缝,切割后的裂缝性岩样KD-2见图 3b.通过增加环形塑料垫片的数量改变裂缝宽度,环形塑料垫片为中心掏空的环形绝缘片(图 3k),厚度为0.04 mm,没有垫片的水平裂缝的宽度定义为垫片的一半,即0.02 mm.因此,KD-2裂缝宽度为0.02 mm,KD-3为0.04 mm(图 3c),KD-4为0.08 mm(图 3d).
第二组岩样MD-1(图 3e)用来构造不同裂缝密度,MD-2岩样为MD-1岩样切割一条水平裂缝(图 3f),MD-3岩样为MD-2岩样再切割一条水平裂缝(图 3g).
第三组岩样(图 3h、i、j)用来构造不同倾角的裂缝.QJ-1为一条0°水平缝岩样,QJ-2为一条30°斜缝岩样,QJ-3为一条60°斜缝岩样.为防止测量过程中岩样受到夹持器的压力发生沿裂缝错动影响测量效果,采用热缩膜对岩样进行包裹,并使热缩膜的长度小于岩样的长度,防止与电极接触影响测量结果.在构造裂缝性岩样过程中,岩样会因切割损失部分体积,但由于岩样比较均匀,基本不会影响文中电阻增大率IR与介电常数变化率Iε的研究.表 1为这三组岩样及其裂缝参数表.
|
|
表 1 岩石样品的尺寸和物理性质 Table 1 The dimensions and the physical properties of the rock samples |
首先对岩样进行洗盐、烘干,测量岩样几何参数与干重.将岩样抽真空后用1%NaCl溶液(室温条件下,电阻率为0.65 Ωm)加压饱和岩样,直到岩样被100%饱和.采用图 1所示装置以等时间间隔自动测量蒸发过程中岩样的阻抗及重量,研究饱和度和岩样复电阻率的关系:
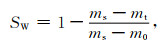
|
(1) |
式中,SW为含水饱和度,小数;mt为测量过程中某一记录时刻岩石的质量,g;m0为岩石的干重,g.mS为岩石的完全饱和时湿重,g.实验采用阻抗分析仪,基于两极法测量岩样的阻抗.电极为网状电极,网状电极可以减小电极极化和接触阻抗的影响(莫婉玲等,2017;Padmaraj et al., 2011).将岩样以稳定的力量夹在夹持器内,两端的网状电极向岩样施加多个频率的交流电压,测量得到岩石阻抗Z:
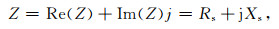
|
(2) |
式中,j为复数单位,j=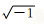
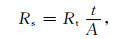
|
(3) |
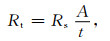
|
(4) |
式中,Rt为蒸发过程中岩石电阻率,Ωm;A为岩样的横截面积,m2;t为岩样的长度,m.
为了更好地研究油气对岩样电阻率的影响,用电阻增大率IR表示(Archie,1942):
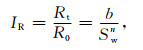
|
(5) |
式中,R0为100%含水岩石的电阻率,Ωm;n为饱和度指数;b为系数.
因为导电介质的容抗作用远大于感抗作用(苏庆新,1999),所以电抗主要为容抗:
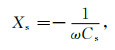
|
(6) |
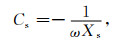
|
(7) |
式中,Cs为蒸发过程中岩石的串联电容,F;ω为交流电的角频率,ω=2πf,f是测量频率.一个充满电介质的理想平行板电容器,其并联电容为
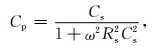
|
(8) |
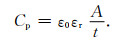
|
(9) |
依据岩石的几何尺寸可计算出介电常数εr:
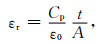
|
(10) |
式中,ε0为真空介电常数,近似为8.854187817×10-12F·m-1;εr为岩样的相对介电常数.
对岩石介电常数进行类似式(5)的处理,Iε定义为介电常数变化率(李玉玲和张宇晓,1994;蔡军等,2016):
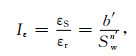
|
(11) |
式中,εS为100%含水岩石的相对介电常数;n′为类似饱和度指数的介电饱和度指数,b′为系数.由于构造裂缝的需求,岩样长度远大于平行板电容方法实际测量介电常数所需要的长度,这样计算出来的介电常数并不是实际中定义的介电常数,该介电常数的对象是离子导体中离子与绝缘材料组成的电容,其整体特性以介电常数的形式表示.由于极板之间的距离很小,此介电常数比传统的介电常数大几个数量级(刘红岐等,2009).并且实际岩样并非理想的平行板电容器,测量结果受到岩样几何形态的影响,对于比值Iε来说,εr与εS所受的影响相同,因此几何形态的影响基本被消除.
2 岩石复电阻率数值模拟 2.1 模拟方法为了分析饱和水状态下裂缝对于岩样复电阻率的影响,利用Comsol Multiphysics软件中交流电模块,使用准静态应用模式,研究简单裂缝模型.从麦克斯韦方程和连续性方程的时间谐波形式,我们得到
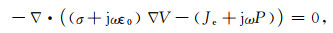
|
(12) |
其中,ε0为自由空间的介电常数,V为电势,σ为电导率,ω为角频率,Je为外部电流密度,P为电极化矢量.这是求解准静态时间谐波信号的方程.
模型是长宽为2.5 cm,高为15 cm的立方体,为了增大裂缝对于研究的影响,设置裂缝单位宽度为0.04 cm.裂缝嵌入均匀盐水饱和的砂岩(假设盐水完全连通),孔隙度φ=10%,裂缝中充满与饱和砂岩孔隙相同的盐水.通过求解理论模型,计算了没有裂缝的砂岩基质的复介电常数εuf*(Asami,2002;Han and Yang, 2018)
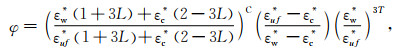
|
(13) |
其中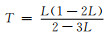
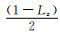
|
|
表 2 有限元模拟中采用的裂缝性岩石的成分的介电特性 Table 2 Dielectric properties of the ingredients for the fractured rock samples employed in the finite element simulation |
岩样的计算得到的频率范围为102~106Hz的背景砂岩的复介电常数,再算出复电阻率,以及填充裂缝的流体(含表 2所列介电特性的盐水)的恒定介电特性,然后用作有限元的输入参数进行数值模拟.
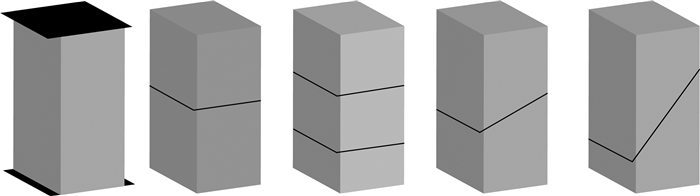
有限元数值模拟计算模型根据图 4建立.图中长方体为岩心,岩心中的加粗黑线表示裂缝,黑色平面代表电极.裂缝性岩石的裂缝宽度为h,h=0.04 cm. 裂缝面与xoy平面的夹角即为裂缝倾角θ.夹在电极间的电压为1 V.岩心四周绝缘.
|
图 4 有限元模拟模型 Fig. 4 Finite element simulation models |
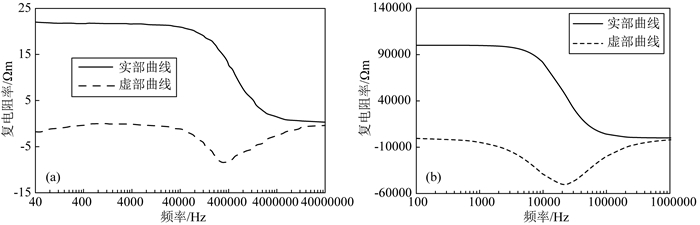
均质岩样的复电阻率实部和虚部通常随测量频率改变.在40 Hz~11 MHz之间,随着频率增加,复电阻率实部先缓慢减小,然后迅速下降,复电阻率虚部先增大,在减小,达到最小值后再增大(马雪瑞等,2019).
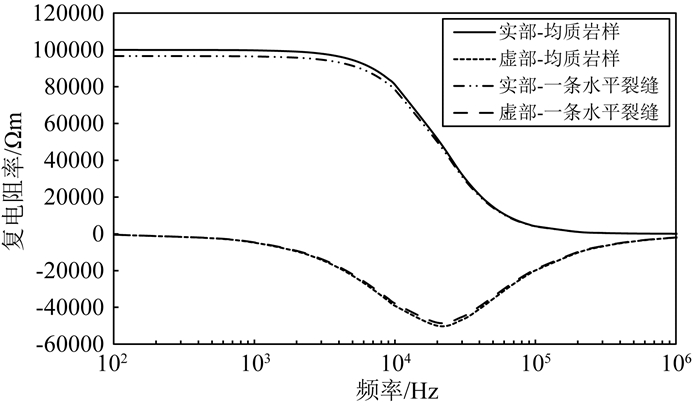
当裂缝中充满盐水时,裂缝性岩样的复电阻率实部明显低于均质砂岩的复电阻率实部.裂缝的加入,增加了电解质,使得岩样的复电阻率实部降低,复电阻率虚部的幅值减小.
|
图 5 (a) 典型岩心电阻率频散曲线(马雪瑞等,2019);(b)背景砂岩复电阻率频散曲线 Fig. 5 (a) Typical core resistivity dispersion curve (Ma et al., 2019); (b) Complex resistivity dispersion curve of background sandstone |
|
图 6 均质砂岩与有一条水平裂缝砂岩复电阻率频散曲线 Fig. 6 Complex resistivity dispersion curves of homogeneous sandstone and sandstone with a horizontal fracture |
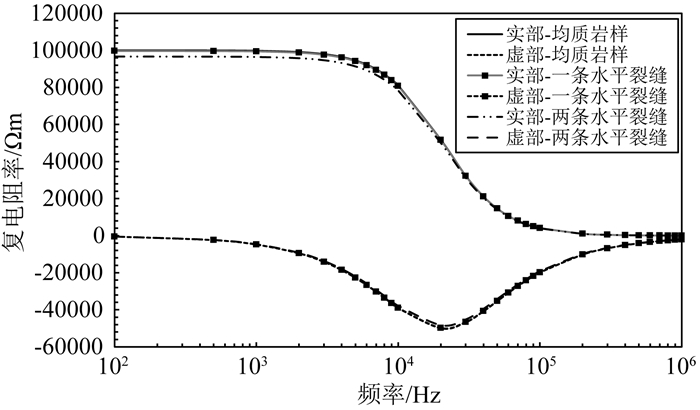
裂缝宽度相同时,随着裂缝密度的增加同样导致岩样的复电阻率实部降低,复电阻率虚部的幅值减小(图 7).
|
图 7 不同裂缝密度砂岩复电阻率频散曲线 Fig. 7 Complex resistivity dispersion curves of sandstone with different fracture densities |
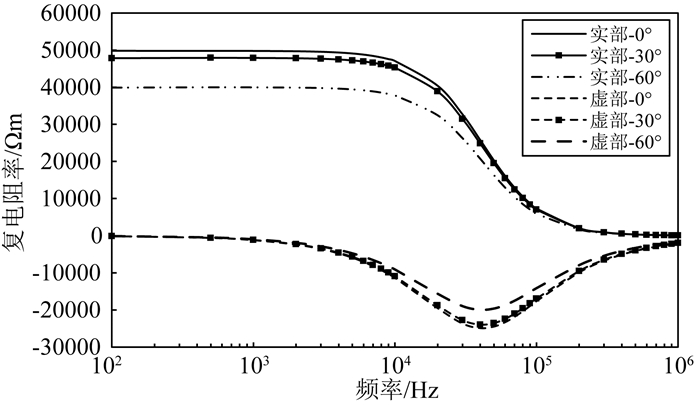
当裂缝倾角从0°变化到60°时,裂缝在岩心中占据的体积分数变大,内含的电解质增加,使得岩样的复电阻率实部降低,复电阻率虚部的幅值减小(图 8).
|
图 8 不同裂缝倾角砂岩复电阻率频散曲线 Fig. 8 Complex resistivity dispersion curves of sandstones with different fracture dip angles |
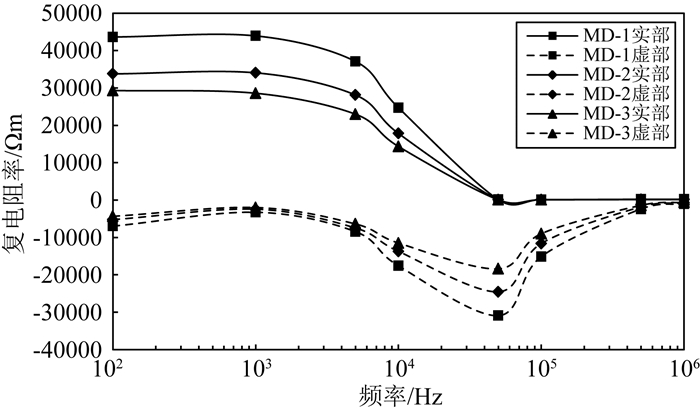
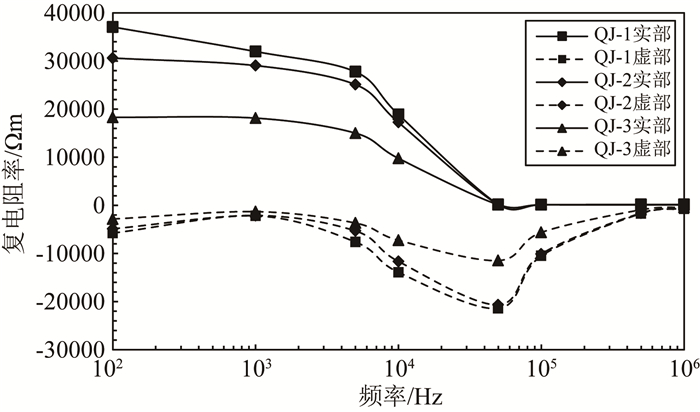
从实验中可以得到与数值模拟相同的实验现象.当裂缝中充满盐水时,裂缝性岩石的复电阻率实部明显低于均质岩样,复电阻率虚部幅值明显低于均质岩样(图 9).随着裂缝密度和裂缝倾角的增加,岩石的复电阻率实部降低,复电阻率虚部幅值降低(图 10、图 11).

|
图 9 均质岩样KD-1与裂缝性岩样KD-2的复电阻率频散曲线 Fig. 9 Complex resistivity dispersion curves of the homogeneous rock sample KD-1 and the fractured rock sample KD-2 |
|
图 10 不同裂缝密度(MD-1、MD-2、MD-3) 岩样的复电阻率频散曲线 Fig. 10 Complex resistivity dispersion curves of the rock samples with different fracture densities (MD-1, MD-2, MD-3) |
|
图 11 不同裂缝倾角(QJ-1、QJ-2、QJ-3)岩样的复电阻率频散曲线 Fig. 11 Complex resistivity dispersion curves of the rock samples with different fracture dip angles (QJ-1, QJ-2, QJ-3) |
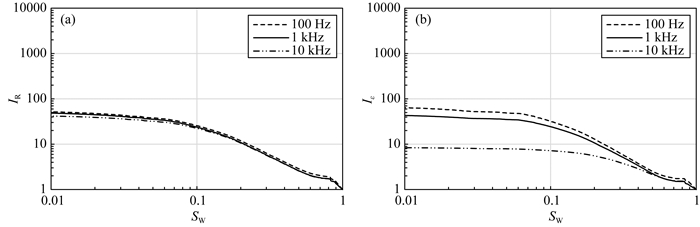
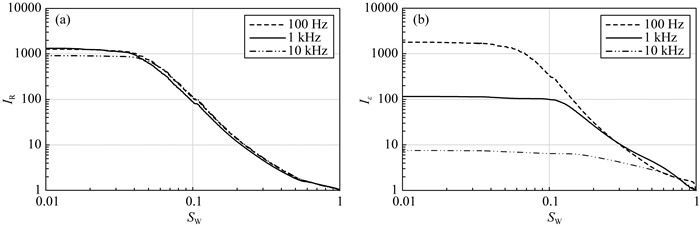
由阿尔奇公式可知,其他条件不变,岩石电阻率随着含水饱和度的减小而增大.图 12和图 13为100 Hz、1 kHz、10 kHz下均质岩样KD-1和MD-1的双对数坐标下IR-SW和Iε-SW图.均质岩样的电阻增大率IR几乎没有分离(图 12a、图 13a).根据IR-SW曲线的斜率变化划分2个区间.在含水饱和度大于0.15时,满足Archie公式,拟合得到饱和度指数n1和系数b1.当含水饱和度SW较小时,曲线趋于平缓,说明电阻增大率不再随着含水饱和度有太大的变化,阿尔奇公式中饱和度指数n与系数b发生变化,拟合得到饱和度指数n2和系数b2.
|
图 12 均质岩样KD-1在不同频率下IR-SW图(a)和Iε-SW图(b) Fig. 12 IR-SW diagram (a) and Iε-SW (b) diagram of the homogeneous rock sample KD-1 at different frequencies |
|
图 13 均质岩样MD-1在不同频率下IR-SW图(a)和Iε-SW图(b) Fig. 13 IR-SW diagram (a) and Iε-SW (b) diagram of the homogeneous rock sample MD-1 at different frequencies |
均质岩样的介电常数变化率Iε受到频率影响(图 12b、图 13b),不同岩样分离特征不同.根据曲线的斜率变化划分2个区间.在高饱和度区域,介电常数变化率Iε与含水饱和度SW满足仿Archie公式,即式(11),通过拟合可以得到不同频率下介电饱和度指数n′ 1和系数b′ 1.当含水饱和度SW较小时,曲线趋于平缓,仿阿尔奇公式中饱和度指数n′ 2和系数b′2明显与n′ 1和b′ 1不同.
3.2.2 不同裂缝宽度的单条水平裂缝岩样KD-1切割一条水平裂缝构成了裂缝性岩样KD-2.KD-2中间加不同数量的环形塑料垫片,从而改变裂缝宽度.图 14a、c、e显示了不同频率下不同裂缝宽度的IR-SW曲线,图 14b、d、f显示了相应的Iε-SW曲线.

|
图 14 不同频率下三种裂缝宽度岩样的IR-SW图和Iε-SW图 (a) KD-2(裂缝宽度=0.02 mm)IR-SW图;(b) KD-2(裂缝宽度=0.02 mm)Iε-SW图;(c) KD-3(裂缝宽度=0.04 mm)IR-SW图;(d) KD-3(裂缝宽度=0.04 mm)Iε-SW图;(e) KD-4(裂缝宽度=0.08 mm)IR-SW图;(f) KD-4(裂缝宽度=0.08 mm)Iε-SW图. Fig. 14 IR-SW diagrams and Iε-SW diagrams of three fractured rocks with different fracture widths at different frequencies (a) KD-2 (fracture width =0.02 mm) IR-SW; (b) KD-2 (fracture width =0.02 mm)Iε-SW; (c) KD-3 (fracture width =0.04 mm)IR-SW; (d) KD-3 (fracture width =0.04 mm) Iε-SW; (e) KD-4 (fracture width =0.08 mm) IR-SW; (f) KD-4 (fracture width=0.08 mm)Iε-SW. |
当含水饱和度大于约0.15时,电阻增大率IR几乎没有受到频率的影响.然而,当含水饱和度小于约0.15时,10 kHz的IR-SW曲线分裂出来,电阻增大率IR随着频率的降低而增加,随着含水饱和度SW的降低,频率对电阻增大率的影响越来越大.在低含水饱和度下,可以很容易观察到裂缝引起的分离变化.
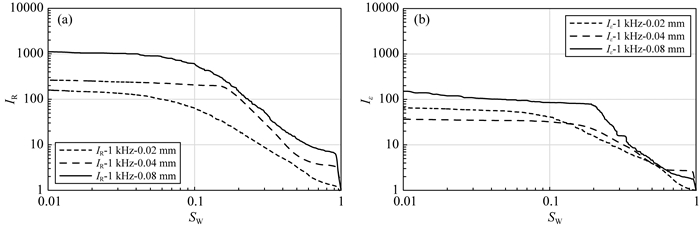
将相同频率(以1 kHz为例)下的不同裂缝宽度岩样的IR-SW和Iε-SW曲线进行对比(图 15).在含水饱和度大于0.9时,IR和Iε有一个突变点,随着裂缝宽度的增加,突变点值增加,这与Li等(2015)实验现象一致(图 15).随着裂缝宽度的增大,相同频率下Iε-SW曲线发生分离,且分离程度增加(图 15b).
|
图 15 不同裂缝宽度岩样1 kHz下IR-SW图(a)和Iε-SW(b)图 Fig. 15 IR-SW (a) diagram and Iε-SW (b) diagram of the rock samples with different fracture widths at 1 kHz |
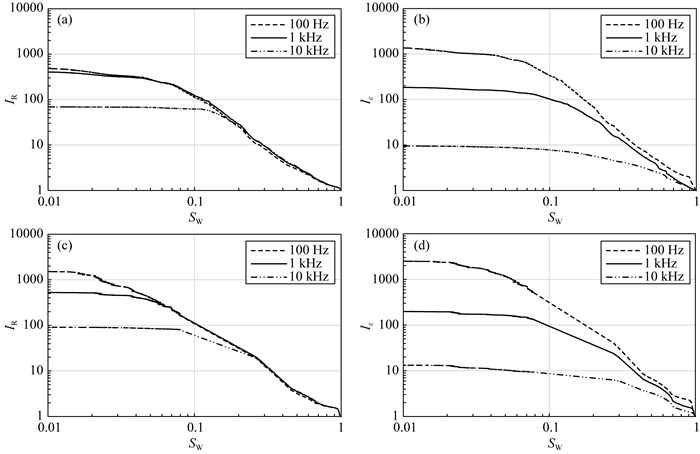
图 16a、b显示有一条裂缝的岩样MD-2的IR-SW和Iε-SW图,图 16c、d显示有两条裂缝的岩样MD-3的IR-SW和Iε-SW图.随着裂缝密度的增加,100 Hz和1 kHz曲线分离程度增加(图 16a、c).
|
图 16 不同频率下两种裂缝密度岩样的IR-SW图和Iε-SW图 (a) MD-2(一条裂缝)IR-SW图;(b) MD-2(一条裂缝)Iε-SW图;(c) MD-3(两条裂缝)IR-SW图;(d) MD-3(两条裂缝)Iε-SW图. Fig. 16 IR-SW diagrams and Iε-SW diagrams of two fractured rock samples with different fracture densities at different frequencies (a) MD-2 (one fracture) IR-SW; (b) MD-2 (one fracture) Iε-SW; (c) MD-3 (two fractures) IR-SW; (d) MD-3 (two fractures) Iε-SW. |
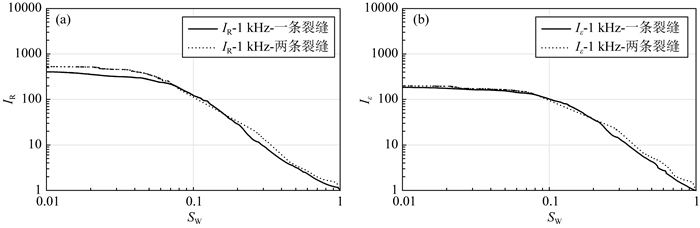
图 17是1 kHz下不同裂缝密度岩样的IR-SW和Iε-SW图.裂缝密度的改变对1 kHz和10 kHz的IR-SW和Iε-SW曲线的整体斜率无显著影响,但是裂缝密度的变化对于高含水饱和度下IR和Iε的突变点值有影响(图 17).
|
图 17 1 kHz下不同裂缝密度岩样的IR-SW图(a)和Iε-SW(b)图 Fig. 17 IR-SW diagram (a) and Iε-SW (b) diagram of the rock samples with different fracture densities at 1 kHz |
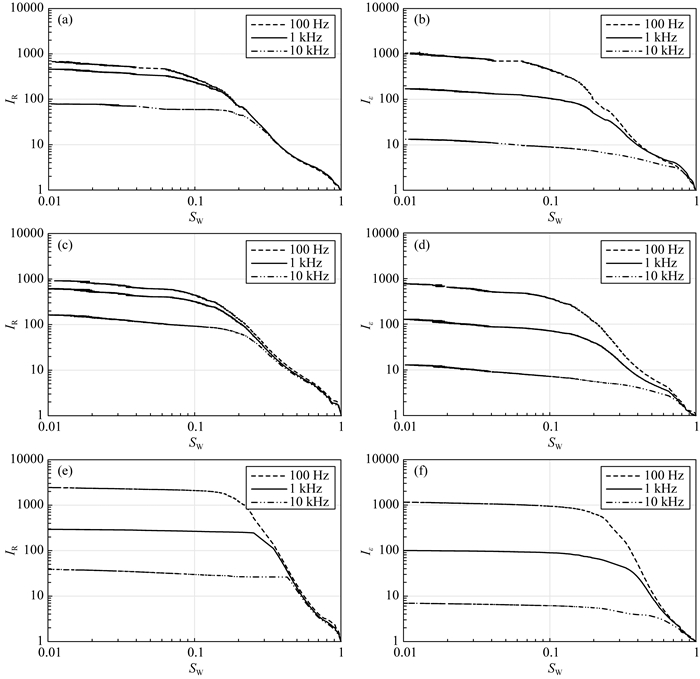
按照产状,裂缝可分为高角度、斜交和低角度缝.由于高角度裂缝岩样制造与测量困难,本文主要讨论低角度缝和斜交缝.随着岩样裂缝角度(0°~60°)的增加,岩样的IR-SW曲线分离程度增加(图 18a、c、e),Iε-SW曲线分离程度增加(图 18b、d、f).
|
图 18 不同频率下三种裂缝倾角岩样的IR-SW图和Iε-SW图 (a) QJ-1(0°)IR-SW图;(b) QJ-1(0°)Iε-SW图;(c) QJ-2(30°)IR-SW图;(d) QJ-2(30°)Iε-SW图;(e) QJ-3(60°)IR-SW图;(f) QJ-3(60°)Iε-SW图. Fig. 18 IR-SW diagrams and Iε-SW diagrams of three rock samples with different dip angles at different frequencies |
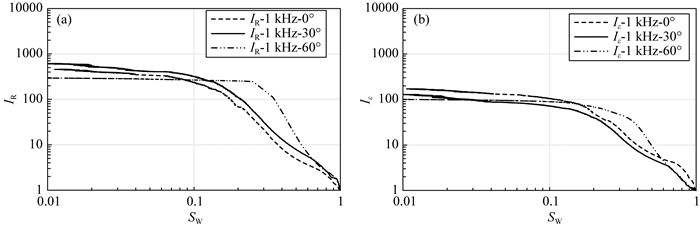
裂缝角度从0°到60°过程中,裂缝在岩心内占据的体积分数发生了变化,即裂缝孔隙度变大,导致岩样电阻率发生变化,类似裂缝宽度的变化.裂缝倾角为0°和30°的岩样的IR-SW曲线以及Iε-SW曲线规律基本是一致的,而到裂缝倾角为60°时,规律发生了明显的变化(图 19).至于发生这种变化开始的角度,还需要进一步实验测量.
|
图 19 1 kHz下不同裂缝倾角岩样的IR-SW图(a)和Iε-SW图(b) Fig. 19 IR-SW diagram (a) and Iε-SW (b) diagram of the rock samples with different fracture dip angles at 1 kHz |
岩石的导电和极化机理较复杂,一般认为岩石的导电发生在岩石孔隙的电解质流体中(苏庆新和柯式镇等,1999).裂缝的加入,增加了岩样的导电路径以及电解质,使得岩样复电阻率频散曲线受到裂缝的影响——复电阻率实部减小且复电阻率虚部幅值减小.饱含水的裂缝性岩石随着裂缝密度的增加以及裂缝倾角的变大,裂缝中含有的电解质增加,所以复电阻率实部逐渐减小,复电阻率虚部的幅值减小.简单的有限元数值模拟也表现出同样的现象.
岩样中矿化水蒸发过程中,岩样含水饱和度减小,孔隙空间中导电的水被不导电的空气占据,导电通道减小,岩石导电能力下降,电阻率升高,介电常数减小.加入裂缝之后,裂缝中的矿化水蒸发较快,在高含水饱和度时,100 Hz、1 kHz和10 kHz频率下IR-SW曲线没有分离,含水饱和度减小到一定程度,气体位于孔隙中心,盐水附着在岩石颗粒表面,大量水的蒸发导致先前通过相邻水接触连接的区域分离,导致100 Hz、1 kHz和10 kHz频率下IR-SW曲线发生分离,Iε-SW曲线分离程度变大.随着裂缝宽度的增加,高含水饱和度时,电阻增大率IR以及介电常数变化率Iε的突变点值增加,100 Hz、1 kHz和10 kHz频率下IR-SW曲线以及Iε-SW曲线的分离程度变大.随着裂缝密度的增加,高含水饱和度时,电阻增大率IR以及介电常数变化率Iε的突变点值增加,100 Hz、1 kHz和10 kHz频率下IR-SW曲线以及Iε-SW曲线的分离程度变大.随着裂缝倾角的增加,100 Hz、1 kHz和10 kHz频率下IR-SW曲线以及Iε-SW曲线的分离程度变大.因此可以利用电阻率增大率以及介电常数变化率与含水饱和度的分离现象判断是否有裂缝.
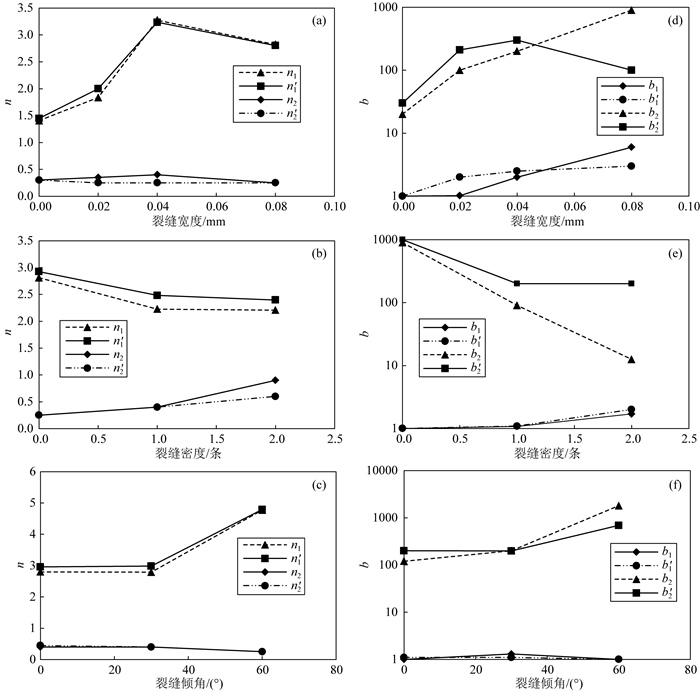
在高含水饱和度区域,由IR-SW和Iε-SW曲线得到100 Hz下阿尔奇公式(5)以及仿阿尔奇公式(11)中的饱和度指数n1、n′1、系数b1和b′ 1,结果见表 3.可以看出同一块裂缝性岩石的饱和度指数n1与n′1值基本接近.随着裂缝宽度的增加,n1和n′1先增大后减小(图 20a),系数b1和b′ 1增大(图 20d);随着裂缝密度的增加,n1和n′1减小(图 20b),b1和b′ 1增大(图 20e);随着裂缝倾角的增大,n1和n′1增大(图 20c),b1和b′ 1基本不变(图 20f).
|
|
表 3 高含水饱和度100 Hz下n1与n′1、b1与b′1值 Table 3 n1, n′ 1, b1 and b′ 1 under 100 Hz with high water saturation |
|
图 20 100 Hz下阿尔奇公式以及仿阿尔奇公式中的n和b值与不同裂缝类型关系交会图 (a) n与裂缝宽度交会图;(b) n与裂缝密度交会图;(c) n与裂缝倾角交会图;(d) b与裂缝宽度交会图;(e) b与裂缝密度关系交会图;(f) b与裂缝倾角关系交会图. Fig. 20 Plots of n and b vs. different fracture types under 100 Hz (a) n vs. fracture width; (b) n vs. fracture density; (c) n vs. fracture dip angle; (d) b vs. fracture width; (e) b vs. fracture density; (f) b vs. fracture dip angle. |
在低含水饱和度区域,由IR-SW和Iε-SW曲线得到100 Hz下阿尔奇公式(5)以及仿阿尔奇公式(11)中的饱和度指数n2、n′2、系数b2和b′2,结果见表 4.裂缝性岩石的饱和度指数n2与n′2值基本接近.随着裂缝宽度的增加,n2和n′2基本不变(图 20a),系数b2增大,b′2先增大后减小(图 20d);随着裂缝密度的增加,n2和n′2增大(图 20b),b2和b′2减小(图 20e);随着裂缝倾角的增大,n2和n′2减小(图 20c),b2和b′2增大(图 20f).
|
|
表 4 低含水饱和度100 Hz下n2与n′2、b2与b′2值 Table 4 n2, and n′2, b2 and b′2 under 100 Hz with low water saturation |
裂缝的存在会导致阿尔奇公式(5)以及仿阿尔奇公式(11)中的饱和度指数n、介电饱和度指数n′、系数b和b′明显不同于均质岩石,这些参数在高饱和度区域与低饱和度区域有着十分明显的差别.n和n′的规律基本一致,但b和b′差别较大.因此在利用(5)以及(11)式计算含水饱和度时,要依据含气的程度以及复电阻率测量频率选择参数.
5 结论通过有限元模拟和实验测量多频下均质岩样和裂缝性岩样的复电阻率含水饱和度,发现多频率下岩石复电阻率包含了裂缝和含气的信息,并形成了以下认识:
(1) 裂缝的产生,增加了岩样中电解质和导电路径,导致岩样复电阻率实部减小,复电阻率虚部幅值减小.
(2) 饱含水均质岩样蒸发过程中频率对电阻增大率IR影响较小,基本不发生分离.介电常数变化率Iε发生分离.
(3) 当含水饱和度小于特定值时,随着频率的降低裂缝性岩石电阻增大率减小.裂缝宽度以及裂缝密度的增加会导致不同频率下IR-SW和Iε-SW曲线的分离程度增加.裂缝角度增加,使不同频率下IR-SW和Iε-SW曲线分离程度增加.
(4) IR-SW和Iε-SW曲线可以分为两个区域.裂缝的存在引起Archie公式中n1、n2和b1变化类似阿尔奇公式中n′1、n′2和b′1的变化.但低饱和度区域b2和b′2值相差较大.
目前三个不同倾角的岩样尚不能完全揭示裂缝角度对岩样电阻率和介电常数与饱和度关系的影响,下一步将通过加工更多不同裂缝倾角的岩样进行深入研究.除此以外针对岩石裂缝性质相关研究仍具有巨大的潜力和空间,比如说将岩石总饱和度区分为基质饱和度和裂缝饱和度,以及建立裂缝性岩石统一的饱和度方程,而不是分高低饱和度区域等.砂岩中含有泥质,同样会对复电阻率频散曲线以及阿尔奇公式产生很大的影响,下一步可以通过制造人工砂岩,只研究裂缝对复电阻率和饱和度的影响.
Archie G E. 1942. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME, 146: 54-67. DOI:10.2118/942054-G |
Asami K. 2002. Characterization of heterogeneous systems by dielectric spectroscopy. Progress in Polymer Science, 27(8): 1617-1659. DOI:10.1016/S0079-6700(02)00015-1 |
Berkowitz B, Bour O, Davy P, et al. 2000. Scaling of fracture connectivity in geological formations. Geophysical Research Letters, 27(14): 2061-2064. DOI:10.1029/1999GL011241 |
Cai J, Zeng S J, Wu H S, et al. 2016. Experimental saturation model based on dielectric logging and its applications. Well Logging Technology (in Chinese), 40(2): 132-136. DOI:10.16489/j.issn.1004-1338.2016.02.002 |
Han T C, Clennell M B, Pervukhina M. 2015. Modelling the low-frequency electrical properties of pyrite-bearing reservoir sandstones. Marine and Petroleum Geology, 68: 341-351. DOI:10.1016/j.marpetgeo.2015.08.037 |
Han T C, Yang S. 2018. Dielectric properties of fractured carbonate rocks from finite-difference modeling. Geophysics, 48(1): 37-44. DOI:10.1190/geo2018-0003.1 |
Ke S Z, Feng Q N, Sun Y R. 1999. A dispersion model of rock complex resistivity and it's parameters algorithm. Well Logging Technology (in Chinese), 23(6): 416-418. DOI:10.3969/j.issn.1004-1338.1999.06.003 |
Li J J, Ke S Z, Yin C F, et al. 2019. A laboratory study of complex resistivity spectra for predictions of reservoir properties in clear sands and shaly sands. Journal of Petroleum Science and Engineering, 177: 983-994. DOI:10.1016/j.petrol.2019.01.061 |
Li K W, Pan B Z, Horne R. 2015. Evaluating fractures in rocks from geothermal reservoirs using resistivity at different frequencies. Energy, 93(1): 1230-1238. DOI:10.1016/j.energy.2015.09.084 |
Li Y L, Zhang Y X. 1994. Method of determining water saturation with dielectric constant and its application. Well Logging Technology (in Chinese), 18(3): 172-177. DOI:10.16489/j.issn.1004-1338.1994.03.004 |
Liu H Q, Deng Y M, Xia H Q, et al. 2009. A study of a new method of exploration based on reservoir capacitivity. Advances in Earth Science, 24(9): 1051-1056. DOI:10.3321/j.issn:1001-8166.2009.09.012 |
Liu Z Y, Zhang C G, Tang J, et al. 2018. Influence of fracture on rock resistivity and its application in saturation calculation. Lithologic Reservoirs (in Chinese), 30(2): 120-128. DOI:10.12108/yxyqc.20180213 |
Ma X R, Ke S Z, He Q L, et al. 2019. A study of complex resistivity experiments and a saturation model of rock. Petroleum Science Bulletin (in Chinese), 4(2): 134-144. |
Mo W L, Sun Z H, Xu Y, et al. 2017. Research on the measurement of interfacial polarization voltage by the extrapolation method. Geophysical and Geochemical Exploration (in Chinese), 41(3): 484-488. DOI:10.11720/wtyht.2017.3.13 |
Padmaraj D, Miller J H Jr, Wosik J, et al. 2011. Reduction of electrode polarization capacitance in low-frequency impedance spectroscopy by using mesh electrodes. Biosensors and Bioelectronics, 29(1): 13-17. DOI:10.1016/j.bios.2011.06.050 |
Renshaw C E. 1996. Influence of subcritical fracture growth on the connectivity of fracture networks. Water Resources Research, 32(6): 1519-1530. DOI:10.1029/96WR00711 |
Sandler J, Li Y Z, Horne R N, et al. 2009. Effects of fracture and frequency on resistivity in different rocks. //EUROPEC/EAGE Conference and Exhibition. Amsterdam, The Netherlands: SPE, 591-594.
|
Shen J S, Su B Y, Guo N C. 2009. Study on the anisotropic characteristics of the electric response to fractured reservoir. Chinese Journal of Geophysics (in Chinese), 52(11): 2903-2912. DOI:10.3969/j.issn.0001-5733.2009.11.026 |
Stesky R M. 1986. Electrical conductivity of brine-saturated fractured rock. Geophysics, 51(8): 1585-1593. DOI:10.1190/1.1442209 |
Su Q X. 1999. Relation between the electrical model and dielectric frequency dispersion of rock at low frequency. Well Logging Technology (in Chinese), 23(2): 127-132. DOI:10.3969/j.issn.1004-1338.1999.02.011 |
Su Q X, Ke S Z, Feng Q N, et al. 1999. An experimental study on the impedance spectra of rocks saturated with oil and water in frequency 100 Hz~10 MHz. Progress in Geophysics (in Chinese), 14(1): 93-103. |
Xiao Y, Ke S Z, Deng H W, et al. 2009. Cause for dielectric highs measured on wet rocks at low frequencies and an improved measurement. Progress in Geophysics (in Chinese), 24(2): 657-662. DOI:10.3969/j.issn.1004-2903.2009.02.039 |
Zheng Q L, Wang Y L, Zhao Y. 2006. Improvement of Archie water-saturation model for the low porosity formation. Well Logging Technology (in Chinese), 30(1): 57-59. DOI:10.16489/j.issn.1004-1338.2006.01.016 |
Zou D P, Ke S Z, Li J J, et al. 2018. Experimental study on resistivity dispersion of highly clay mineral content core. Well Logging Technology (in Chinese), 42(3): 261-266. DOI:10.16489/j.issn.1004-1338.2018.03.003 |
蔡军, 曾少军, 吴洪深, 等. 2016. 介电实验测量与饱和度模型建立及应用. 测井技术, 40(2): 132-136. DOI:10.16489/j.issn.1004-1338.2016.02.002 |
柯式镇, 冯启宁, 孙艳茹. 1999. 岩石复电阻率频散模型及其参数的获取方法. 测井技术, 23(6): 416-418. DOI:10.3969/j.issn.1004-1338.1999.06.003 |
李玉玲, 张宇晓. 1994. 介电常数确定含水饱和度的方法研究与应用. 测井技术, 18(3): 172-177. DOI:10.16489/j.issn.1004-1338.1994.03.004 |
刘红岐, 邓友明, 夏宏泉, 等. 2009. 基于电容率法的矿藏勘探新方法研究. 地球科学进展, 24(9): 1051-1056. DOI:10.3321/j.issn:1001-8166.2009.09.012 |
刘智颖, 章成广, 唐军, 等. 2018. 裂缝对岩石电阻率的影响及其在含气饱和度计算中的应用. 岩性油气藏, 30(2): 120-128. DOI:10.12108/yxyqc.20180213 |
马雪瑞, 柯式镇, 贺秋利, 等. 2019. 人工岩心电频谱实验及饱和度评价模型研究. 石油科学通报, 4(2): 134-144. |
莫婉玲, 孙中华, 徐娅, 等. 2017. 界面极化电压的外推法测量研究. 物探与化探, 41(3): 484-488. DOI:10.11720/wtyht.2017.3.13 |
沈金松, 苏本玉, 郭乃川. 2009. 裂缝性储层的电各向异性响应特征研究. 地球物理学报, 52(11): 2903-2912. DOI:10.3969/j.issn.0001-5733.2009.11.026 |
苏庆新. 1999. 低频下岩石的电学模型和介电频散的关系. 测井技术, 23(2): 127-132. DOI:10.3969/j.issn.1004-1338.1999.02.011 |
苏庆新, 柯式镇, 冯启宁, 等. 1999. 100 Hz~10 MHz频段含油水两相岩石电阻抗的研究. 地球物理学进展, 14(1): 93-103. |
肖毅, 柯式镇, 邓宏文, 等. 2009. 低频含水岩石介电高值成因及改进测量方法. 地球物理学进展, 24(2): 657-662. DOI:10.3969/j.issn.1004-2903.2009.02.039 |
郑庆林, 王钰森, 赵雨. 2006. 低孔隙度条件下阿尔奇含水饱和度解释模型改进. 测井技术, 30(1): 57-59. DOI:10.16489/j.issn.1004-1338.2006.01.016 |
邹德鹏, 柯式镇, 李君建, 等. 2018. 含黏土矿物岩心电频散特性实验研究. 测井技术, 42(3): 261-266. DOI:10.16489/j.issn.1004-1338.2018.03.003 |
 2021, Vol. 64
2021, Vol. 64


