地球物理学报  2021, Vol. 64 Issue (1): 289-297   PDF    
引用本文
韩学辉, 张浩, 毛新军, 等. 2021. 基于岩心室应力应变和不确定度分析的致密储层氦孔隙度测量方法. 地球物理学报, 64(1): 289-297, doi: 10.6038/cjg2021O0345.  
Han X H, Zhang H, Mao X J, et al. 2021. A method of gas porosity measurement for tight reservoirs based on mechanical analysis of core chamber. Chinese J. Geophys. (in Chinese), 64(1): 289-297, doi: 10.6038/cjg2021O0345.  
基于岩心室应力应变和不确定度分析的致密储层氦孔隙度测量方法
韩学辉1, 张浩2, 毛新军3, 徐登辉1, 郭慧英4, 江佳洋5, 罗兴平2, 王振林2, 刘智桢1, 李靖1, 罗振1     
1. 中国石油大学(华东)地球科学与技术学院, 青岛 266580;
2. 新疆油田公司勘探开发研究院, 克拉玛依 834000;
3. 中国石油股份有限公司新疆油田公司勘探事业部, 克拉玛依 834000;
4. 新疆油田实验检测研究院, 克拉玛依 834000;
5. 克拉玛依市昂科能源科技有限公司, 克拉玛依 834000
收稿日期 2020-09-05, 2020-11-25 收修定稿
基金项目: 国家科技重大专项（2017ZX05009001）和国家自然科学基金（U1562108）联合资助
第一作者简介: 韩学辉, 男, 1974年生, 博士, 副教授, 主要研究方向为岩石物理.E-mail:hanxuehui@upoc.edu.cn
摘要：致密油气层的物性（孔隙度和渗透率）较差.针对致密储层，目前常用的氦气法孔隙度测量方法存在两个不足：器壁压变性参数G定义不明确；膨胀前压力设置普遍偏小.本次基于氦气法孔隙度测量装置岩心室的应力应变力学分析和不确定度理论分析，开发了一种面向致密储层的氦孔隙度测量方法.本次提出的方法给出了器壁压变性参数G的解析式，并基于G的解析式推导出了新的孔隙度计算公式，将刻度系数减少到1个，简化了刻度过程.其次，基于不确定度理论得到的孔隙度测量不确定度表明：氦气法测量致密储层孔隙度的膨胀前压力大于2 MPa基本可以将孔隙度绝对误差控制在0.5%以内.与高压压汞法孔隙度测量结果对比发现，该方法测量孔隙度的相对偏差在14%以内，远低于常规氦气法测量孔隙度的相对偏差（50%）.
关键词: 氦气法孔隙度      致密储层      应力应变力学分析      不确定度      测量压力     
A method of gas porosity measurement for tight reservoirs based on mechanical analysis of core chamber
HAN XueHui1, ZHANG Hao2, MAO XinJun3, XU DengHui1, GUO HuiYing4, JIANG JiaYang5, LUO XingPing2, WANG ZhenLin2, LIU ZhiZhen1, LI Jing1, LUO Zhen1     
1. School of Geoscience, China University of Petroleum(East China), Qingdao 266580, China;
2. Research Institute of Petroleum Exploration and Development, Xinjiang Oilfield Company, PetroChina, Karamay 834000, China;
3. Exploration Department of Xinjiang Oilfield Company, PetroChina, Karamay 834000, China;
4. Research Institute of Experiment and Detection of Xinjiang Oilfield, Karamay 834000, China;
5. Karamay OnCores Energy Technology Company Limites, Karamay 834000, China
Abstract: The physical properties (i.e.,porosity and permeability) of tight reservoirs are poor. For the samples of the tight reservoirs,the conventional helium method has the following two shortcomings: The definition of parameter G is not clear and the pro-pressure in the measurement is usually low. Based on the analysis of stress-strain in the helium porosity measurement device and uncertainty analysis theory,a method for measuring helium porosity of the tight reservoir is developed. This method derives the formula of G and proposes the new expression of porosity,which decreases the number of the calibration parameters and simplifies the calibration process. The porosity measurement based on uncertainty theory demonstrates that the absolute porosity error can be within 0.5% when the pressure before expansion is higher than 2 MPa. Compared with the high-pressure mercury method,the relative error of the new helium method is lower than 14%,which is much lower than 50% of the traditional helium method.
Keywords: Helium porosity    Tight reservoir    Analysis of stress-strain mechanics    Uncertainty    Measurement pressure    
0 引言

岩石孔隙度是油气勘探和开发过程中评价储层的重要参数之一(Bustin et al, 2008；李彤，2013；刘畅等，2013；李新等，2015).对于物性普遍较差的致密油气储层，由于孔隙度低，孔隙度测量的相对误差更大，孔隙度的准确测量显得尤为重要(柯式镇等，2007).实验室测量是目前常用的确定储层孔隙度的方法，方法包括：氦气法、高压压汞法、核磁共振法(NMR)、扫描电镜(SEM)、等温吸附法等(Sondergeld et al, 2010；肖立志，2007；Sun et al, 2011).针对致密储层(如致密页岩气、页岩油储层)，最近提出一系列方法来提高孔隙度的测量精度，包括注气孔隙度测定法(GIP)(Sun et al, 2016)、水浸法(WIP)(Kuila et al, 2014)、原子力显微镜(AFM)法等(Yao et al, 2010；Sondergel et al, 2010；Javadpour et al, 2012；Etminan et al, 2014).这些方法都有一定的应用效果，但是存在设施复杂、样品要求较高等弊端，难以满足致密储层孔隙度的实验测量需求.氦气法具有操作简单、成本低、时间短等优点，有必要深入研究以满足大量的致密储层孔隙度测量需求.

氦气法测量致密储层的孔隙度时不确定度高，主要有以下两个原因：一个是刻度参数和刻度过程带来的测量误差.氦气法测量孔隙度需要考虑器壁压变性系数G和标准室体积Vk两个参数的刻度，繁琐的刻度过程会引起误差传递而增大氦气法孔隙度的实验测量误差(柯式镇等，2007).依据不确定度理论，常规氦气法孔隙度测量的不确定度为

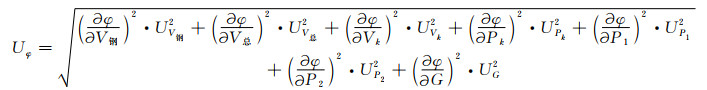
(1)

式中，V钢是钢块体积, 单位为cm3；V总是岩心总体积, 单位为cm3; Pk是膨胀前压力，单位为MPa; P1是装满钢块时的膨胀后压力，单位为MPa; P2为装岩心时的膨胀后压力，单位为MPa.

压力和体积计量的不确定度很小，可以忽略不计，式(1)可以简化为

(2)

图 1为孔隙度分别为5%、10%时G和Vk绝对不确定度对常规氦气法测量致密储层孔隙度的不确定度的影响.其中，G不确定度的增大会近似线性增加孔隙度的不确定度，并且会随着孔隙度变小而带来更大的绝对不确定度，G对致密储层氦气法孔隙度测量的影响较大，需要想办法减小或者消除.

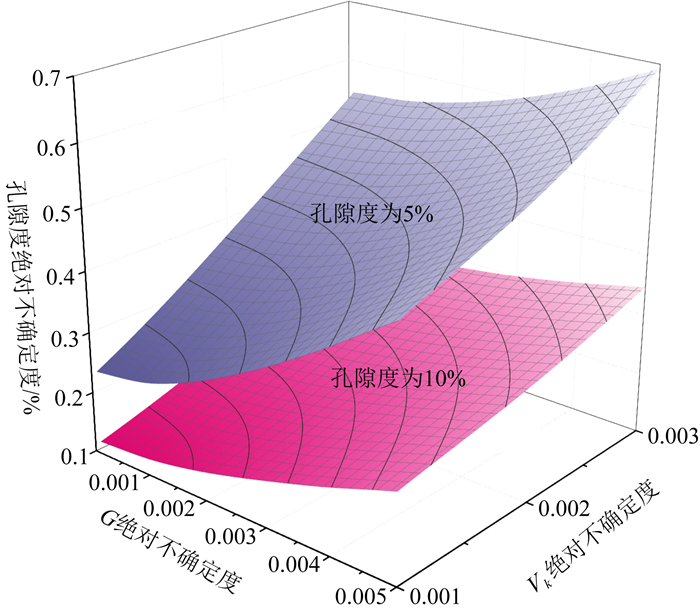
图 1 G及Vk不确定度对常规氦气法测量致密储层孔隙度不确定度的影响 Fig. 1 Effect of uncertainties of G and Vk on the porosity uncertainty of conventional helium measurement of tight reservoirs

另一个导致致密储层氦气法孔隙度测量不确定较高的原因是膨胀前压力的设置缺乏指导，一般偏小(实验室设置一般在0.5 MPa左右)，难以填满微小孔隙.致密储层孔喉半径小，孔隙结构复杂，达西流和低速非达西渗流较弱，气体扩散是气体进出孔隙的主要机制(温晓红等，2010；王小波等，2015).在氦气法测量孔隙度时，较小的标准室膨胀前压力会导致气体进入孔隙困难，膨胀后压力下降小，导致测量孔隙度偏小.田华等(2012)、王磊等(2015)认为标准室的膨胀前压力对致密储层氦气法孔隙度测量的影响较大，理论考察后建立了压力区分度函数，得到了以下认识：平衡前标准室压力越大，取出标准块体积越小，样品体积越小压力区分度越高，孔隙度测量精度则越大.但是，这些研究并没有针对致密储层样品给出合适的膨胀前压力确定方法，且实际测量时不可能随时调节样品室和标准室的体积，得到的结论和认识难以有效地提高氦气法孔隙度的测量精度和准度.

本次研究，为了减少刻度参数G、膨胀前压力对孔隙度测量的影响，基于氦气法孔隙度测量系统的岩心室的应力应变分析推导得到了器壁压变性参数G的解析式，进而提出了无需刻度G的孔隙度测量方法，最后基于不确定理论给出了致密储层样品氦气法孔隙度测量的膨胀前压力设定阈值，提高了致密储层氦气法孔隙度的测量精度.

1 基于应力应变力学分析的器壁压变性系数G的解析式

氦孔隙度测量装置的标准室和岩心室近似为一个封闭的圆筒形介质.根据测量得到的尺寸，对于岩心室及标准室的应力应变力学分析可以简化为弹性力学中的厚壁圆筒问题(皮萨连科等, 1981；朱务学和查子初，1987).

图 2中，Pi为厚壁圆筒承受的内压，单位为MPa；P0为厚壁圆筒承受的外压，单位为MPa；Ri为厚壁圆筒的内径，单位为cm；R0为外径，单位为cm；σθ为微元体受到的切向应力，单位为GPa；σr为微元体受到的径向应力，单位为GPa；r为微元内壁到中心的距离，单位为cm；dr为微元径向长度，单位为cm.

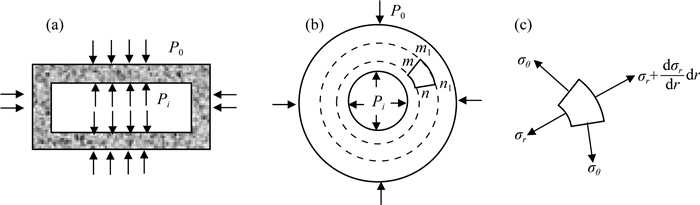
图 2 厚壁圆筒中的应力分析 (a)厚壁圆筒纵切面图；(b)厚壁圆筒横切面图；(c)微元受力分析图. Fig. 2 Analysis of stress in thick-wall cylinder (a) Longitudinal section of the thick-walled cylinder; (b) Transverse section of the thick-walled cylinder; (c) Force analysis of the micro element.

根据图 2d中的微元应力分析，可以得到以下平衡方程：

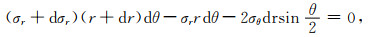
(3)

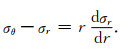
(4)

图 3描述了厚壁圆筒受力后微元体的位移情况.图中，mnm1n1代表微元的初始位置，m′n′m′1n′1代表受力后微元的位置，w为圆筒内壁的位移，单位为cm; w+dw为圆筒外壁的位移, 单位为cm.根据图 3中厚壁圆筒中微元体的位移分析，可以得到径向应变和周向应变分别为

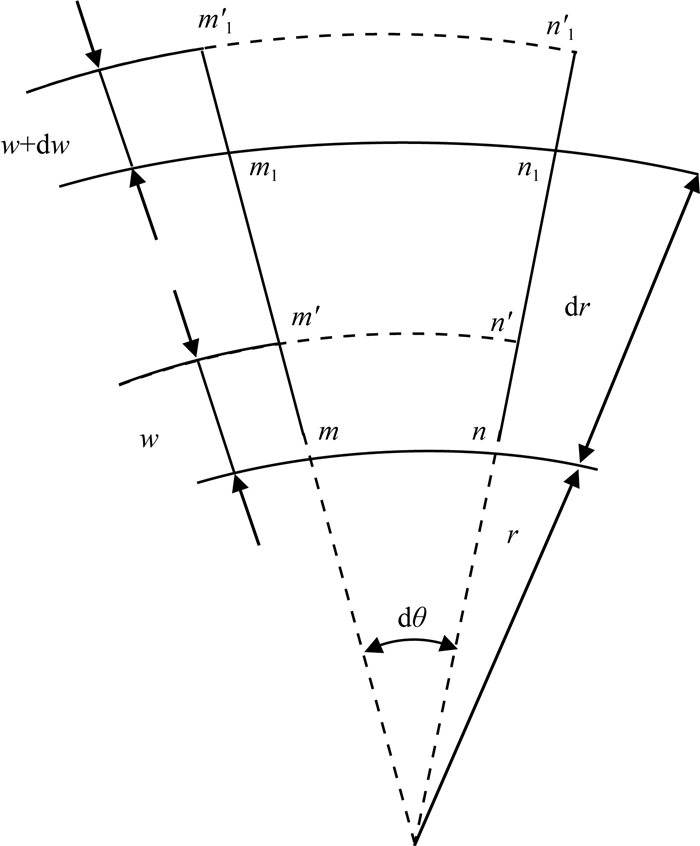
图 3 厚壁圆筒中微元体的位移 Fig. 3 Displacement of micro element in thick-wall cylinder

径向应变：

(5)

周向应变：

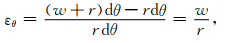
(6)

根据公式(5)和公式(6)可以得到变形协调方程：

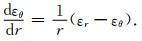
(7)

根据广义胡克定律中应力和应变的关系，可以建立本构方程组：

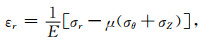
(8)

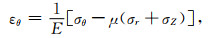
(9)

式中，σz为微元体受到的轴向应力，单位为GPa; μ为厚壁圆筒的泊松比.

最终，通过综合厚壁圆筒微元的平衡方程、几何方程和本构方程，可以得到应力应变微分方程并对其进行求解，具体过程如下：

由公式(8)和公式(9)可得：

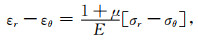
(10)

将公式(10)代入公式(8)，得到式(11)，有：

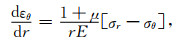
(11)

对公式(10)求导得到式(12)：

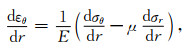
(12)

联立式(11)和(12)，得到式(13)：

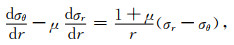
(13)

综合式(4)和式(12)，可以得到微分方程(14)：

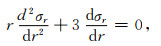
(14)

解微分方程(14)，可以得到两个微分方程的解：

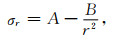
(15)

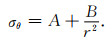
(16)

对于厚壁圆筒，边界条件为：当r=Ri时，σr=-Pi；当r=R0时，σr=-P0.由此可以得到积分常数A和B分别为

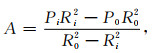
(17)

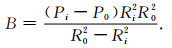
(18)

最终，根据微分方程结果可以得到厚壁圆筒周向应力、径向应力和轴向应力的表达式(朱务学和查子初，1987)：

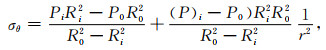
(19)

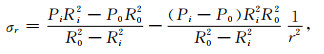
(20)

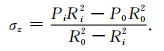
(21)

将公式(19)—(21)代入公式(9)，可以得到厚壁圆筒的径向应变，表达式为

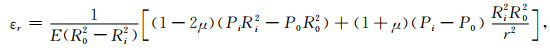
(22)

将式(22)对r积分即可得到岩心室在半径为r的微元体处径向位移的表达式：

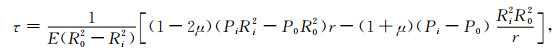
(23)

分别将岩心室及标准室的内外径代入公式(23)中，内压力为Pi外压力为P0时的标准室及岩心室内壁的径向位移表达式为

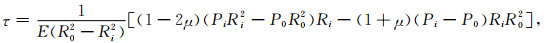
(24)

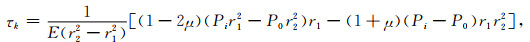
(25)

式中，τ为岩心室的径向形变，单位为cm; τk为标准室的径向形变，单位为cm; Ri和R0分别为岩心室的内径和外径，单位为cm; r1和r2分别为标准室的内径和外径, 单位为cm.

根据式(24)和式(25)，可以得到内压力为Pi时，岩心室和标准室的体积变化：

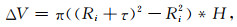
(26)

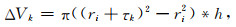
(27)

式中，ΔV为岩心室的体积变化，单位为cm3; ΔVk为标准室的体积变化，单位为cm3; H为岩心室的内部高度，单位为cm; h为标准室的内部高度, 单位为cm.

根据波义耳定律(例如柯式镇等，2007)，常规氦气法测量装置中的体积-压力关系为

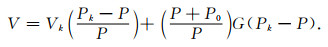
(28)

根据上述孔隙度测量系统的应力应变分析，式(28)可以变换为

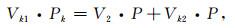
(29)

式中Pk为膨胀前压力，单位为MPa; P为膨胀后压力，单位为MPa; Vk1为内压为Pk时的标准室体积，单位为cm3, 表达式为

(30)

Vk2为内压为P时的标准室体积，单位为cm3, 表达式为

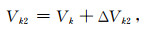
(31)

V2为内压为P时的岩心室体积，单位为cm3, 表达式为

(32)

根据式(29)和式(32)，有：

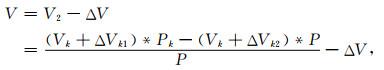
(33)

根据式(28)—(33)，可以得到G的表达式为

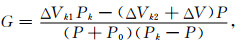
(34)

式(34)给出了器壁压变性系数G的解析式，可以根据实验压力等参数计算得到，不再需要通过实验刻度确定了.

2 无需刻度G的致密储层氦气法孔隙度测量方法

在得到器壁压变性系数G的解析式后，对常规氦气法的测量原理和测量流程就可以得到氦气法孔隙度测量的方法，常规氦气法的测量装置如图 4所示.

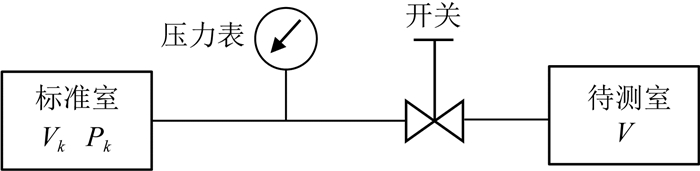
图 4 氦气法孔隙度测量装置示意图 Fig. 4 Schematic diagram of porosity measurement device by helium method

氦气从已知体积Vk与压力Pk的标准室等温膨胀到体积为V的未知室中，膨胀后测量装置的最终平衡压力为P.根据波义耳定律，未知体积V与最终平衡压力P的关系为

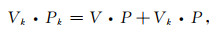
(35)

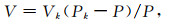
(36)

综合式(35)、式(36)以及器壁压变系数G表达式(34)，可以得到V的表达式：

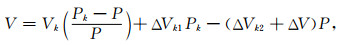
(37)

式中，ΔVk1以及ΔVk2可用公式(27)计算得到，ΔV可用公式(26)计算得到.

式(37)即为无需刻度器壁压变系数G的氦气法孔隙度中骨架体积的确定方法，再测量得到岩样的总体积后即可以得到孔隙度.由式(37)可知，当Vk、Pk一定时，待测体积V是平衡压力P的函数.应用已知体积的钢块进行两次刻度即可得到标准室体积Vk的值.

具体测量步骤如下：

(1) 将总体积为Vb的四块钢块全部装入样品室，记录膨胀前压力为Pof时的膨胀后平衡压力Pf.

(2) 将体积为Vb2的二号钢块取出，记录膨胀前压力为Pob时的膨胀后平衡压力Pb.

(3) 将样品放入岩心室记录膨胀前压力为Pk2时的膨胀后平衡压力P.

根据式(28)可以得到步骤(1)、步骤(2)及步骤(3)的岩心室体积V1、V2及V3：

(38)

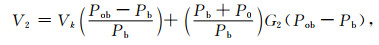
(39)

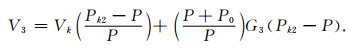
(40)

根据式(38)和(39)可以得到标准室的体积Vk，代入式(40)即可得到V3.综合式(38)及(40)，样品孔隙度的表达式为

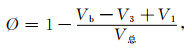
(41)

式中，V总为样品的总体积, 单位为cm3.

3 致密储层氦气法孔隙度测量的膨胀前压力确定方法

样品孔隙度φ、氦气法孔隙度测量膨胀前压力Pk对孔隙度测量不确定度的影响最大.样品的孔隙度是岩石的固有参数，因此在实际测量中只能通过控制膨胀前压力提高氦气法孔隙度的测量精度.以下从致密储层氦气法孔隙度测量方法出发，对孔隙度测量结果的不确定度做了理论分析，重点讨论了样品孔隙度φ以及膨胀前压力Pk对氦气法孔隙度测量不确定度的综合影响，给出了膨胀前压力确定方法.

3.1 氦气法孔隙度不确定度公式

(1) 直接测量不确定度的计算方法

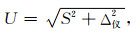
(42)

式中，为标准差；Δ仪是仪器误差，一般按仪器最小分度的一半计算，但是游标卡尺和角游标按最小分度计算，也可按仪器级别计算或查表.

(2)间接测量不确定度的合成方法

间接测量参数N=f(x, y, z, …)的平均值公式为N=f(x, y, z, …)，其不确定度合成公式为

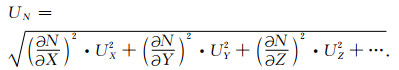
(43)

根据上述直接不确定度和间接不确定度的计算方法，氦气法测量孔隙度φ的合成不确定度为

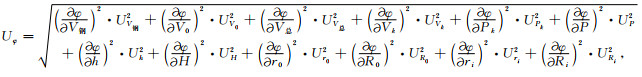
(44)

式中，根号内Ux代表的是相应参数的直接测量不确定度，各个下标的意义如下：V钢代表岩心室放入钢块的体积，单位为cm3；V0代表岩心室的原始体积，单位为cm3；V总代表岩心的总体积，单位为cm3；Vk代表参考室的原始体积，单位为cm3；Pk代表膨胀前压力，单位为MPa；P代表膨胀后压力，单位为MPa；H为岩心室的内部高度，单位为cm；h为参考室的内部高度，单位为cm；R0和Ri分别为岩心室的外径和内径，单位为cm；r0和ri分别是参考室的内径和外径，单位为cm.

将上述各参数的直接测量不确定度代入式(44)中，即可得到氦气法孔隙度测量的不确定度.

3.2 膨胀前压力确定方法

基于式(44)考察了膨胀前压力对孔隙度测量不确定的影响，计算结果见表 1.不确定度分析中用到的参数指标如下：压力表：0.1级，量程为5 MPa；游标卡尺的测量精度为0.01 cm.标准室内径为2.350 cm，外径为2.725 cm，高度为5.817 cm，岩心室与标准室参数一致，样品总体积设为15 cm3，参考室及岩心室材料的杨氏模量设为210 GPa.为了考察不同孔隙度条件下膨胀前压力对孔隙度测量不确定度的影响，设置孔隙度φ变化范围为2%~10%，膨胀前压力Pk的变化范围为0.5~3 MPa.

表 1 不同膨胀前压力、孔隙度下氦气法孔隙度绝对不确定度计算结果表 Table 1 Results of porosity uncertainty of porosity measurement by helium under different pre-expansion pressures and porosities

为了更直观的体现出样品孔隙度和膨胀前压力对氦气法孔隙度不确定度的影响，图 5给出了孔隙度测量绝对不确定度随膨胀前压力Pk和样品孔隙度Φ的变化.相同膨胀前压力下，孔隙度测量绝对不确定度随样品孔隙度减小逐渐增大，膨胀前压力越小越明显.膨胀前压力为常用的0.5 MPa时，孔隙度为10%的绝对不确定度为1.54%，孔隙度为2%的不确定度为1.81%.相同孔隙度情况下，孔隙度测量绝对不确定度随膨胀前压力增大而减小.当膨胀前压力增大到1~1.5 MPa时，孔隙度测量绝对不确定度出现明显的降低.当膨胀前压力为2 MPa时，孔隙度从10%减小到2%，孔隙度绝对不确定度从0.26%增加到0.45%，都已经符合氦气法孔隙度行业标准中对测量误差的要求(孔隙度绝对不确定度小于0.5%).因此，可以选取2 MPa作为致密储层氦气法测量的膨胀前压力.

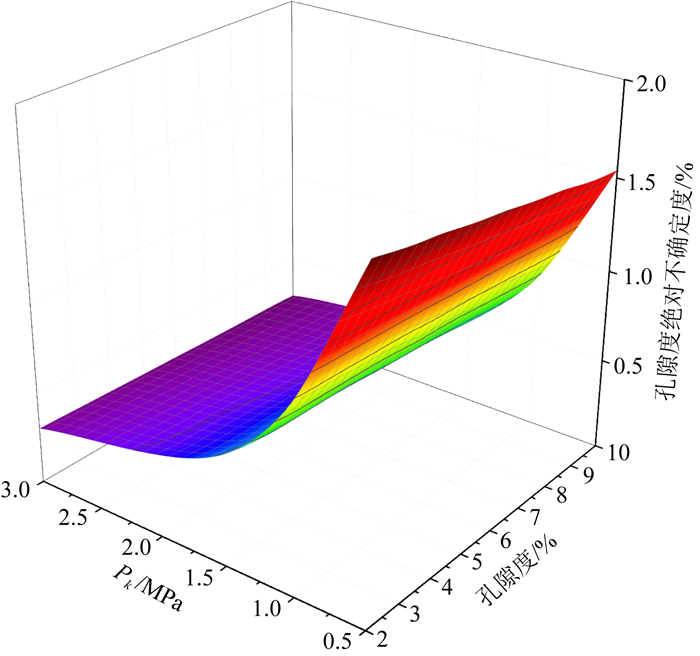
图 5 孔隙度绝对不确定度随膨胀前压力和样品孔隙度变化图 Fig. 5 Variation of relative uncertainty of porosity with pre-expansion pressure and sample porosity
4 氦气法孔隙度测量方法效果分析

为了考察氦气法孔隙度测量新方法的应用效果，选取了来自X致密储层的20块样品，分别应用常规氦气法、新氦气法以及高压压汞法测量了样品的孔隙度(表 2).其中：高压压汞法是一种常用的致密储层孔隙度测量方法，测量压力最大可达455.07 MPa，可识别的孔隙尺度最低可达0.001 μm，也可以同时提供平均孔喉半径、渗透率等参数，如表 2所示；常规氦气法膨胀前压力为0.54 MPa，新氦气法的膨胀前压力统一设定为2 MPa.

表 2 X致密储层常规氦气法、本次提出的氦气法与高压压汞法测量数据 Table 2 Measurement data by conventional helium method, new helium method and high pressure mercury injection method for tight reservoir X

图 6是常规氦气法、氦气法和高压压汞法测量孔隙度结果对比.当孔隙度较大(本例中大于7.5%)时，常规氦气法、新氦气法和高压压汞法测量孔隙度相差很小(本例中不超过0.85%)，表明器壁压变性系数G的不确定度和膨胀前压力对氦气法孔隙度测量影响较小.当孔隙度较小(本例中小于7.5%)，常规氦气法测量孔隙度明显小于高压压汞法的孔隙度，而新氦气法测量孔隙度与高压压汞法孔隙度偏差很小(本例中不超过0.76%).分析认为，当孔隙度较小时，由于平均孔喉半径较小(本例中小于0.5 μm)，常规氦气法测量压力较低(本例中为0.54 MPa)，测量气体更难填充微小孔隙，加上器壁压变性系数G的影响而导致测量孔隙度偏小，平均孔喉半径越小偏差越大.新氦气法消除了器壁压变性系数G的影响，采用了更高的膨胀前压力(本例中为2 MPa), 微小孔隙的填充度高，测量结果更接近于压汞法的孔隙度.

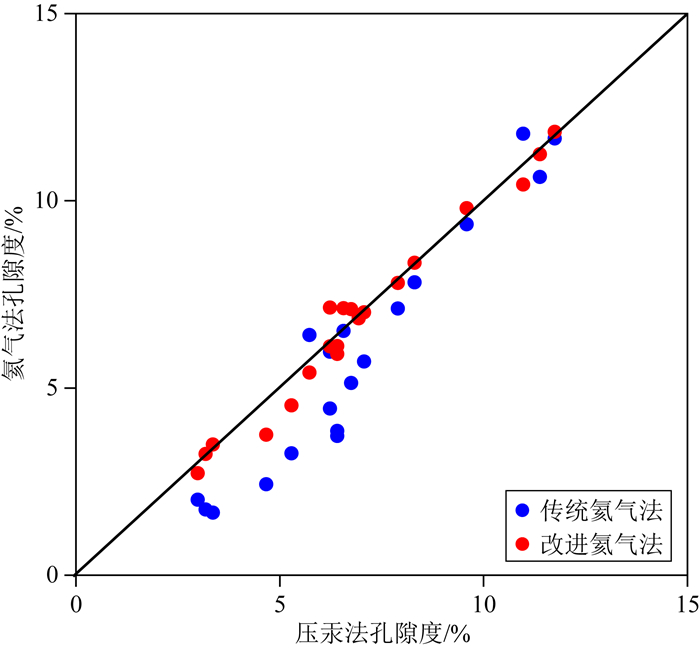
图 6 常规氦气法和新氦气法测量孔隙度与压汞法孔隙度差异对比图 Fig. 6 Comparison of porosity measured by conventional and new helium method with that measured by mercury injection method

总体上，新氦气法在致密储层的孔隙度测量结果与压汞法孔隙度的测量结果接近，能够满足致密储层孔隙度测量的要求.

5 结论

本文通过氦气法孔隙度测量装置的应力应变分析给出了器壁压变性系数G的表达式，简化了常规氦气法的刻度过程，提出了一个免刻度G的氦孔隙度测量方法.基于该方法，通过分析氦气法孔隙度测量的不确定度明确了膨胀前压力对孔隙度测量不确定度的影响，并给出了致密储层样品氦气法孔隙度测量的膨胀前压力设定阈值，提高了致密储层氦气法孔隙度测量的精度.与压汞法孔隙度结果的对比发现：本次改进的氦气法相比常规氦气法孔隙度测量不确定度更小，测量精度更高.

致谢  感谢审稿专家提出的宝贵意见.
References
Bustin R M, Bustin A M M, Cui A, et al. 2008. Impact of shale properties on pore structure and storage characteristics.//74th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2008: 1-28.
Etminan S R, Javadpour F, Maini B B, et al. 2014. Measurement of gas storage processes in shale and of the molecular diffusion coefficient in kerogen. International Journal of Coal Geology, 123: 10-19.
Javadpour F, Farshi M M, Amrein M. 2012. Atomic-force microscopy:A new tool for gas-shale characterization. Journal of Canadian Petroleum Technology, 51(4): 236-243.
Ke S Z, He Y C, Wang J Y. 2007. Uncertainty analysis of gas porosity measurement of rock. Acta Metrologica Sinica (in Chinese), 28(2): 177-179.
Kuila U, McCarty D K, Derkowski A, et al. 2014. Total porosity measurement in gas shales by the water immersion porosimetry (WIP) method. Fuel, 117: 1115-1129.
Li T. 2013. Research on test methods for rock parameters in tight OIL-GAS reservoirs[Master's thesis] (in Chinese). Langfang: University of Chinese Academy of Sciences-Institute of Porous Flow and Fluid Mechanics.
Li X, Liu P, Luo Y Y, et al. 2015. Analysis of influencing factors on porosity measurement of shale gas reservoir core. Progress in Geophysics (in Chinese), 30(5): 2181-2187. DOI:10.6038/pg20150525
Liu C, Zhang Q, Pang G Y, et al. 2013. Quantitative prediction of porosity of tight sandstone reservoir:A case study from Chang 8 oil reservoir set in Jiyuan area, Ordos Basin. Lithologic Reservoirs (in Chinese), 25(5): 70-75.
Liu W X, Wang Y B, Guo L, et al. 2006. Application of SEM/SEM in oil and gas geology. Journal of Chinese Electron Microscopy Society (in Chinese), 25(S1): 321-322.
Sondergeld C H, Ambrose R J, Rai C S, et al. 2010. Micro-structural studies of gas shales.//80th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
Sun J M, Dong X, Wang J J, et al. 2016. Measurement of total porosity for gas shales by gas injection porosimetry (GIP) method. Fuel, 186: 694-707.
Tian H, Zhang S C, Liu S B, et al. 2012. Parameter optimization of tight reservoir porosity determination. Petroleum Geology and Experiment (in Chinese), 34(3): 334-339.
Wang L, Li K W, Zhao N, et al. 2015. Methods research of porosity determination for tight oil reservoir. Petroleum Geology and Recovery Efficiency (in Chinese), 22(4): 49-53.
Wang X B, Chen J F, Li J, et al. 2015. Discussion on role of gas diffusion and its contribution in low porosity-permeability tight sandstone gas reservoirs. Journal of China University of Petroleum (in Chinese), 39(5): 58-64.
Wen X H, Zhou T, Hu Y, et al. 2010. Experimental study of properties and influencing factors of gas flow in tight core. Petroleum Geology and Experiment (in Chinese), 32(6): 592-595.
Xiao L Z. 2007. Some important issues for NMR logging applications in China. Well Logging Technology (in Chinese), 31(5): 401-407.
Yao Y B, Liu D M, Che Y, et al. 2010. Petrophysical characterization of coals by low-field nuclear magnetic resonance (NMR). Fuel, 89(7): 1371-1380.
Zhu W X, Zha Z C. 1987. An elasti-plastic analysis of autofrettaged thick-walled cylinders. Acta Mechanica Sinica (in Chinese), 19(S1): 245-255.
Писаренко Г С. 1981. Handbook of Mechanics of Materials (in Chinese). Zhu Z C, trans. Beijing: China Architecture & Building Press.
柯式镇, 何亿成, 王界益. 2007. 岩石气体孔隙度测量不确定度分析. 计量学报, 28(2): 177-179.
李彤. 2013.致密油气储层岩石参数测试方法研究[硕士论文].廊坊: 中国科学院研究生院(渗流流体力学研究所).
李新, 刘鹏, 罗燕颖, 等. 2015. 页岩气储层岩心孔隙度测量影响因素分析. 地球物理学进展, 30(5): 2181-2187. DOI:10.6038/pg20150525
刘畅, 张琴, 庞国印, 等. 2013. 致密砂岩储层孔隙度定量预测——以鄂尔多斯盆地姬塬地区长8油层组为例. 岩性油气藏, 25(5): 70-75.
刘伟新, 王延斌, 郭莉, 等. 2006. 扫描电镜/环境扫描电镜在油气地质研究中的应用. 电子显微学报, 25(S1): 321-322.
皮萨连科Г С, 亚科符列夫Α Π, 马特维也夫B B. 1981.材料力学手册.朱祖成译.北京: 中国建筑工业出版社.
田华, 张水昌, 柳少波, 等. 2012. 致密储层孔隙度测定参数优化. 石油实验地质, 34(3): 334-339.
王磊, 李克文, 赵楠, 等. 2015. 致密油储层孔隙度测定方法. 油气地质与采收率, 22(4): 49-53.
王小波, 陈践发, 李剑, 等. 2015. 扩散在低孔渗致密砂岩气成藏中的作用和贡献探讨. 中国石油大学学报(自然科学版), 39(5): 58-64.
温晓红, 周拓, 胡勇, 等. 2010. 致密岩心中气体渗流特征及影响因素实验研究. 石油实验地质, 32(6): 592-595.
肖立志. 2007. 我国核磁共振测井应用中的若干重要问题. 测井技术, 31(5): 401-407.
朱务学, 查子初. 1987. 自增强厚壁圆筒的弹塑性应力应变分析. 力学学报, 19(S1): 245-255.