2. 青岛黄海学院智能制造学院, 山东青岛 266427
2. Intelligence and Manufacture College, Qingdao Huanghai University, Qingdao Shandong 266427, China
近年来,全波形反演的发展对频率域模拟方法提出了更高的要求,高精度的频率域模拟是未来发展的必然趋势(Qu et al., 2020a).与时间域模拟相比,频率域模拟有其自身的优势.首先,在多炮数值模拟的情况下,每个频率分量的阻抗矩阵只需计算一次,通过并行计算可以大大提高计算效率;其次,从方程本身来看,频率域易于模拟衰减效应;另外,频率域模拟是计算区域内所有网格点的总时间,误差将分布到计算涉及的所有网格点,不存在类似于时间域模拟的累积误差,便于进行长时间模拟(梁昊, 2016).鉴于频率域模拟的卓越优势,本文在回顾其发展背景的基础上,研究了一种高精度的频率域模拟方法.
1972年,Lysmer和Drake(1972)用有限元方法首次实现了频率域地震波数值模拟;随后,Marfurt(1984)指出在频率域模拟地震波,能够非常有效地模拟出各向异性介质中波的传播以及衰减效应,而且适合多炮并行模拟;1990年, Pratt和Worthington(Pratt, 1990; Pratt and Worthington, 1990)对频率域正演进行了深入的研究,应用常规二阶差分法(5点有限差分格式)对声波方程进行了离散化处理,构建了阻抗矩阵,并得到每个波长至少取13个网格点时,相速度误差可以控制在1%以内的结论,为频率域正演奠定了基础,但由于数值频 散严重和计算量较大等问题,频率域正演并没有得到广泛的应用.旋转9点差分格式的提出使每个波长内只需4个网格就可以达到1%的精度要求,极大地促进了频率域正演的发展(Jo et al., 1996; Shin, 1995);在旋转9点差分格式的基础上,Shin(2001, 2017)又将9点差分格式扩充到25点,将单个波长内的网格点减少到2.5个,提高了模拟精度;2004年, Hustedt等(2004)对频率域模拟的效率进行了研究,他指出,频率域模拟的主要计算量集中在对阻抗矩阵的分解算法上,在单频波场的求解中,LU分解约占用88%的机时.吴国忱等(梁锴等, 2007;吴国忱等, 2007;殷文, 2008, 殷文等, 2006)率先开始国内关于频率域正演的探索,并将25点最优化加权平均差分算子成功运用到弹性波和各向异性介质中的高精度有限差分模拟研究中;随后,任浩然等(2009)对吸收边界条件和大型稀疏矩阵存储技术进行了研究,有效地减少了计算所需的存储量,推动了频率域正演的发展.近年来,为提高频率域模拟精度,多种差分格式被提出并应用(曹书红和陈景波, 2012; Chen, 2014; Jo et al., 1996; Kim et al., 2011;刘璐等, 2013; Moreira et al., 2014; Qu and Li., 2019, 2020b; Shin et al., 2017; Sourbier et al., 2011; Takekawa and Mikada, 2019;吴建鲁和吴国忱, 2018; Zhao and Sen, 2019).提高频率域模拟精度的方式总体分为两种:提高有限差分算子阶数和增加剖分网格数目,然而,精确的差分格式往往导致巨额的计算量,模拟精度和计算效率无法兼得,这也是目前限制频率域模拟方法发展的重要因素.
正演边界条件方面的研究则相对成熟.到目前为止,Berenger(1994)在电磁波模拟时提出的完全匹配层(PML)吸收边界条件仍是使用最广泛的边界条件(Liu et al., 2019).Chew和Weedon(1994)引入复伸展坐标系,将PML边界公式化,为其数值模拟奠定了基础.近年来,PML边界因其卓越的优势被广泛用于声波和弹性波模拟(董士琦等, 2018; Higdon, 1991).在PML吸收边界的基础上,Kuzuoglu和Mittra(1996)等提出了复频移PML(C-PML)边界条件来改善PML边界对某些介质的不稳定性;在此基础上,一些学者研究并实现了非分裂形式的C-PML边界,增强了C-PML边界的简捷性和实用性(Komatitsch and Martin, 2007; Qin et al., 2009;张显文等, 2009);Meza-Fajardo和Papageorgiou(2008)在分析PML边界不稳定原因的基础上,提出在几个正交的方向上同时进行吸收衰减的方式来增强吸收效果,并提高了其在各向异性介质中的适用性,这种边界条件被称之为多轴完全匹配层(M-PML) (Bécache et al., 2003).田坤等(田坤, 2014;田坤等, 2013, 2014)将C-PML和M-PML相结合,在时间域模拟中实现了非分裂的MCPML,具有吸收效果好,便于实现的优点.对于频率域模拟,考虑阻抗矩阵分解时的内存占用问题,对边界条件的吸收能力提出了更高的要求,相比于传统的PML边界,MCPML具有更强的适用性.本文在研究MCPML原理的基础上,实现了频率域的MCPML,提高了频率域模拟的精度和效率.
综上所述,要提高频率域模拟精度和效率,除提高网格阶数和增加网格数目外,需探索更优的模拟方法.在边界吸收问题上,MCPML边界吸收能力强,更适合频率域模拟.基于这两点认识,本文构建了波数补偿的声波方程,结合MCPML边界,得到了精度较高的频率域模拟结果.
1 基于优化的声波方程压制数值频散和时间域正演一样,频率域正演也存在数值频散问题.数值频散是利用有限差分法对时间和空间进行离散时,引入的一种影响模拟精度的现象.数值频散主要表现为不同波数分量的地震波波形散开,形成模拟的“重影”,严重的数值频散会导致地震波正演失败(刘璐等, 2013, 田坤, 2014).较为粗糙的网格或是不够精确的有限差分算法都会导致数值频散的发生.为压制数值频散,一般会提高网格密度或增加网格点数,此二者皆会使分解阻抗矩阵的内存占用量急剧增大,计算效率严重降低.本文从波动方程本身出发,从理论上分析了数值频散产生的原因,在此基础上,推导了对高波数补偿的声波方程,并测试了其数值频散压制效果.
1.1 频率域正演频率域声波方程为
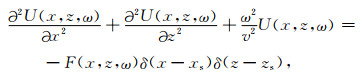
|
(1) |
其中,v是声波速度,ω是角频率,U(x, z, ω)是频率域波场,F(x, z, ω)是震源,δ(x-xs)δ(z-zs)代表震源位置.
求解公式(1)即可得到频率域波场,为离散化公式(1),需将其Laplace项进行差分近似,并使用0°坐标系和45°坐标系进行加权优化:
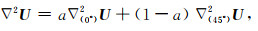
|
(2) |
其中,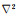
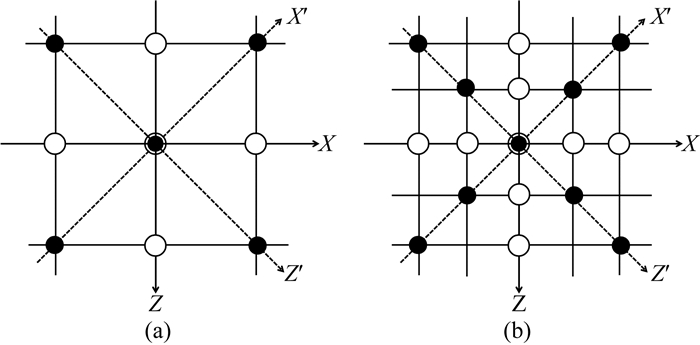
在二阶9点网格中(图 1a),中心点利用网格中的9个点进行加权:
|
图 1 (a) 9点差分网格;(b) 17点差分网格 Fig. 1 (a) The 9-point difference grid; (b) The 17-point difference grid |
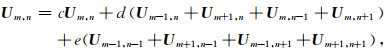
|
(3) |
其中,
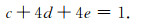
|
(4) |
将(2), (3)和(4)代入公式(1)并推导得到9点差分格式的离散声波方程:
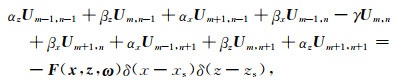
|
(5) |
其中,
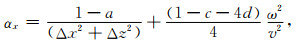
|
(6) |
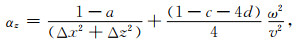
|
(7) |
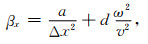
|
(8) |
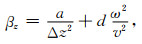
|
(9) |
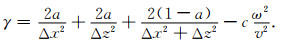
|
(10) |
公式(6)—(10)中,Δx,Δz是网格间距,v是声波速度,ω是角频率,a, c, d为最优化差分系数,取值为:a=0.5461; c=0.6248; d=0.09381.
同理可得,四阶17点差分(图 1b)格式的方程(董士琦等, 2018):
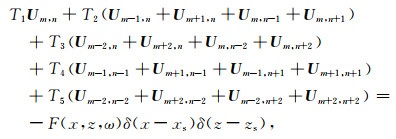
|
(11) |
其中,
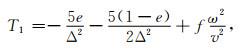
|
(12) |
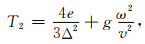
|
(13) |
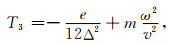
|
(14) |
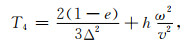
|
(15) |
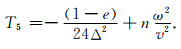
|
(16) |
式(11)—(16)中,Δ=Δx=Δz是网格间距,v是声波速度,ω是角频率;最优化差分系数的取值为:e=1.0673; f=0.8875; g=0.0251; h=0.0237; m=-0.0204; n=-0.000275.T2,T3表示0°坐标系上的点(图 1b中白色的点),T4,T5表示45°坐标系上的点(图 1b中黑色的点).
经方程离散,公式(1)可以表示为一组线性方程组:
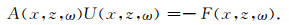
|
(17) |
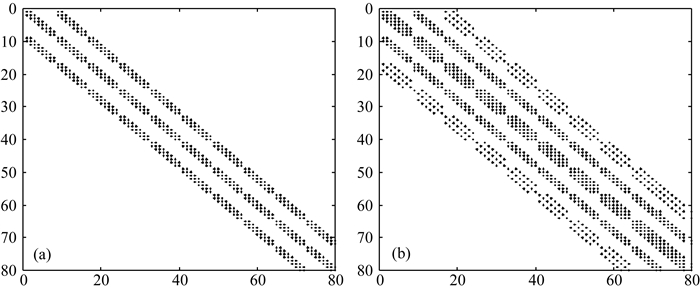
方程组左端的系数矩阵A为一大型稀疏矩阵,称为阻抗矩阵,求解方程(17)需要对矩阵A进行分解,而分解过程需要大量的内存或时间.阻抗矩阵的结构与差分网格有关,不同格式的差分算子对应的阻抗矩阵带宽和非零元素不同(图 2).
|
图 2 10×8网格的阻抗矩阵示意图 (a) 9点差分格式的阻抗矩阵;(b) 17点差分格式的阻抗矩阵. Fig. 2 The impedance matrix of a 10×8 grid (a) The impedance matrix of the 9-point finite-difference scheme; (b) The impedance matrix of the 17-point finite-difference scheme. |
无论频率域还是时间域模拟,数值频散问题都是无法回避的.下面以一维上行波方程为例,从理论上分析数值频散产生的机制:
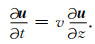
|
(18) |
其一阶中心差分形式为
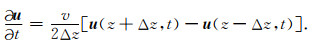
|
(19) |
对上行波有
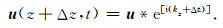
|
(20) |
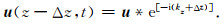
|
(21) |
根据欧拉公式,可将式(19)转换为
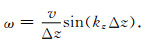
|
(22) |
则地震波相速度为
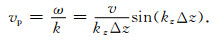
|
(23) |
公式(18)—(23)中,u是时间域波场,Δz是网格间距,v是群速度,vp是相速度,ω是角频率,kz是z方向的波数.
由公式(23)可见,地震波在传播过程中,不同波数的分量具有不同的相速度,且波数越大,相速度滞后群速度越多,此为数值频散产生的理论机制.
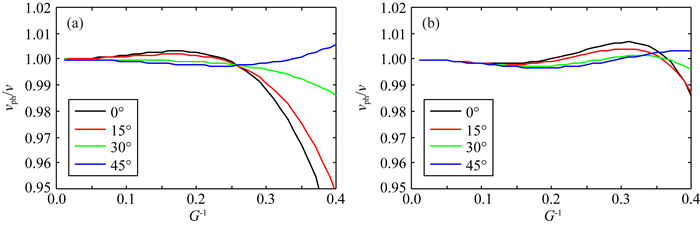
由9点差分和17点差分格式的数值频散曲线(图 3)可以看出:
|
图 3 (a) 9点差分格式的数值频散曲线; (b) 17点差分格式的数值频散曲线 Fig. 3 (a) The numerical dispersion curve of 9-point finite-difference scheme; (b) The numerical dispersion curve of 17-point finite-difference scheme |
(1) 随着一个波长内网格数目增加,模拟误差逐渐减小,数值频散现象得到改善,即增加网格数量可以压制数值频散;
(2) 在相同模拟精度要求下,17点差分格式使用的网格数目更少,即提高网格阶数也可以压制数值频散.
通过以上分析可知,要压制数值频散,应使用间距更小的网格或使用高阶的差分格式.然而,如前文所述,前者会造成阻抗矩阵A变大;后者会造成阻抗矩阵A的带宽和非零元素增加,二者都会造成内存占用量增大和计算效率降低,均不是最优的提高模拟精度的方式.
1.3 优化声波方程压制数值频散 1.3.1 方法推导在不降低效率的前提下,本文研究了一种改进的声波方程来压制数值频散以提高模拟精度.在频率域声波方程的基础上,构建新的声波方程如下:
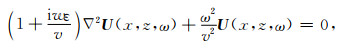
|
(24) |
其中,ε是稳定因子,取小的正值.
下面从波动方程的解出发,分析所构建方程的物理意义.方程(24)对应的时间域形式:
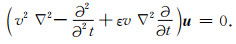
|
(25) |
定义算子:
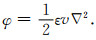
|
(26) |
其空间傅里叶变换是关于波数k的增长函数.
则方程(25)可写成
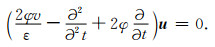
|
(27) |
定义中间波场:
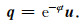
|
(28) |
将式(28)代入(27)并整理得
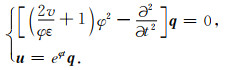
|
(29) |
公式(24)—(29)中,v是声波速度,ω是角频率,U是频率域波场,u是时间域波场,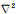
可以看出式(29)具有和常规声波方程相似的形式,若把中间波场q(x, z, t)看作常规声波方程的解,则原波场u(x, z, t)是其关于波数k的指数增长形式,即本文所构建的新的声波方程(24)是在常规声波方程的基础上,对波数k进行补偿的一种形式,且对高波数的补偿比低波数的补偿更强烈.在前文中分析到,数值频散产生的原因是高波数分量滞后较多造成的,而本文构建的新形式可以实现对高波数分量的补偿,进而压制数值频散,提高模拟精度.在计算效率和内存占用量方面,本文构建的新方程在模拟时仅需对Laplace项乘系数即可,没有额外的计算量.
1.3.2 数值模拟为验证改进声波方程(24)的有效性,设计一个两层介质模型进行数值模拟.模型的主要参数如下:模型大小为800 m×800 m,上下两层速度分别为4000 m·s-1和5000 m·s-1,吸收边界厚度为200 m;震源使用主频为30 Hz的雷克子波,位置(x, z)位于(400 m, 200 m)处.进行频率域模拟时使用的最大频率为500 Hz,间隔为0.5 Hz,共计算1000个频率切片,经傅里叶逆变换得到时间域模拟结果.从模拟结果的数值频散压制效果,单炮记录计算用时和分解阻抗矩阵A所需内存三个方面对以下四种格式进行对比分析: 1) Δ=10 m,9点差分格式;2) Δ=10 m,改进的9点差分格式;3) Δ=10 m,17点差分格式;4) Δ=5 m,9点差分格式.
(1) 数值频散压制效果
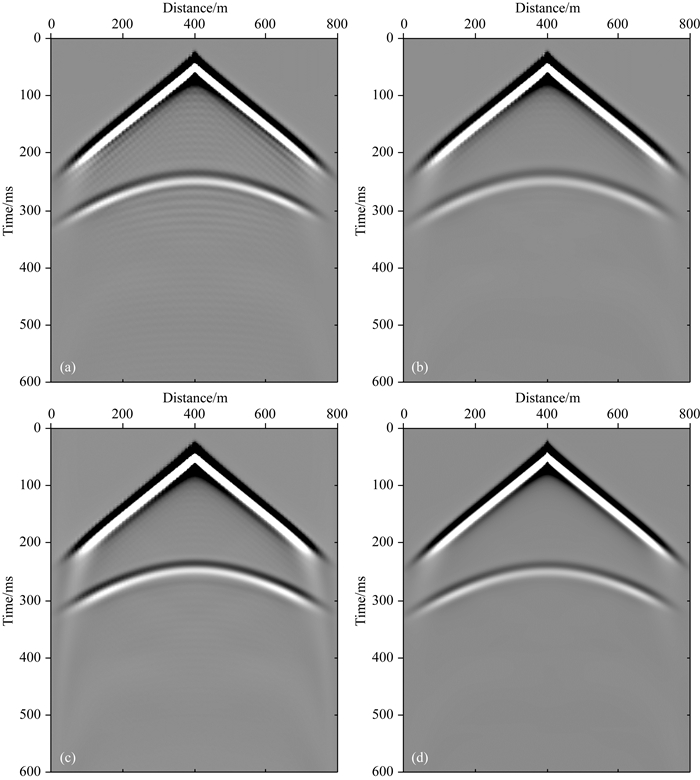
从200 ms处的波场快照(图 4)可以看出,当网格间距为10 m时,9点差分格式出现了比较明显的数值频散现象(图 4a),数值频散造成的干扰波逐渐向有效波场内部扩散,严重时会造成模拟失败;保持网格间距不变,使用本文提出的波数补偿的9点差分格式(图 4b)和17点差分格式(图 4c)时,数值频散现象均得到有效改善;把网格间距减小为5 m,网格数量增加一倍时(图 4d),9点差分格式也能得到较好的模拟结果.单炮记录的模拟结果(图 5)也能得到同样的结论.综合以上分析,补偿波数、增加有限差分算子的长度、减小网格间距都可以有效地压制数值频散.

|
图 4 时间为200ms处的波场快照 (a) Δ=10 m,9点差分;(b) Δ=10 m,改进的9点差分;(c) Δ=10 m,17点差分;(d) Δ=5 m,9点差分. Fig. 4 The wave field snapshots, Time=200 ms (a) Δ=10 m, 9-point difference grid; (b) Δ=10 m, improved 9-point difference grid; (c) Δ=10 m, 17-point difference grid; (d) Δ=5 m, 9-point difference grid. |
|
图 5 单炮记录 (a) Δ=10 m,9点差分;(b) Δ=10 m,改进的9点差分;(c) Δ=10 m,17点差分;(d) Δ=5 m,9点差分. Fig. 5 The single shot records (a) Δ=10 m, 9-point difference grid; (b) Δ=10 m, improved 9-point difference grid; (c) Δ=10 m, 17-point difference grid; (d) Δ=5 m, 9-point difference grid. |
(2) 计算效率和所需内存
在模拟精度得到保证的前提下,计算效率和内存占用量是评价频率域正演方法的两个重要指标.表格1中列出了不同差分格式模拟单炮记录的用时和分解阻抗矩阵所需的内存.
从计算用时来看,改进后的9点差分格式用时最短,略低于常规9差分格式;网格数目增加1倍的9点差分格式,用时随之增加,且增长量高于1倍;17点差分格式用时最长.有研究表明,在时间域模拟时,网格数量增加,会造成计算量呈三次方增长,而有限差分算子长度的增加,会造成计算量线性增长(刘璐等, 2013).本文的模拟结果表明,频率域模拟时,网格数量增加1倍,会造成计算用时呈大于三次方增长(计算时间为原来的10.7倍,27.1398/2.5466≈10.7),而有限差分算子长度的增加,会造成计算用时激增(有限差分算子点数由9点增加到17点,计算用时增长为原来的16.1倍,41.0014/2.5466≈16.1).分析其原因在于,网格数目增加并未改变阻抗矩阵的带宽和非零元素,而有限差分算子长度的增加,使得阻抗矩阵的带宽和非零元素都随之增加,对其进行分解时需要更长的时间,即相比于阻抗矩阵的长宽,带宽和非零元素对计算用时的影响更大.
除计算效率外,分解阻抗矩阵所需的内存也是进行频率域模拟时需考虑的因素.目前的分解方法中,直接分解法计算效率高但内存消耗大;迭代法占用内存少但计算效率低(周聪, 2012).从表 1的统计结果可以看出,相较于常规9点差分,有限差分算子长度和网格数目增加都会造成内存占用量增加.当有限差分算子点数从9点增加到17点,内存占用量约增长为原来的1.72倍,基本呈线性增长;而当网格数量增加1倍时,内存占用量增长为原来的6.97倍.相比于提高有限差分算子阶数和增加剖分网格的数目,改进后的9点差分格式所需内存并未增加,是一种兼顾计算效率和内存消耗的方法.
|
|
表 1 不同方法模拟单炮记录用时和分解阻抗矩阵所需内存 Table 1 Single shot simulation time of different methods and memory required to decompose impedance matrix |
综上所述,虽然改善了数值频散问题,但17点差分格式和小网格间距的9点差分格式都会造成计算时长或所需内存激增.而本文研究的波数补偿差分格式,在保证模拟精度的前提下,无论从计算效率还是所需内存来讲,都是最优方法.
2 MCPML边界条件为消除边界反射,模拟时需在有效区域外增加吸收边界.边界厚度也是影响频率域正演的一个重要因素.边界厚度过小,会造成吸收不完全,产生边界反射;边界厚度过大,会使计算网格数目增大,导致计算效率降低.因此,提高边界的吸收能力是解决问题的关键.本文在常规的PML边界的基础上,将非分裂的多轴卷积完全匹配边界(MCPML)用于频率域正演,测试表明,相同的边界厚度,MCPML的吸收效果更好;在相同吸收效果下,MCPML边界条件所需的边界网格更少,计算效率更高.
2.1 MCPML边界条件推导以x方向为例,传统的PML边界条件可表示为
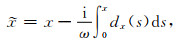
|
(30) |
则有
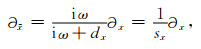
|
(31) |
其中
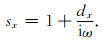
|
(32) |
公式(30)—(32)中x和 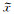
MCPML是指在某一方向的边界内,在x和z两个方向都进行衰减.以二维情况下与x轴垂直的匹配层为例,坐标变换为
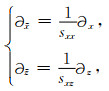
|
(33) |
其中,x方向为主方向,其复拉伸函数为式(32)推广后的形式:
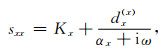
|
(34) |
式中,αx≥0和Kx≥1是辅助吸收因子,dxx是吸收系数.
z方向为辅方向,其复拉伸函数为
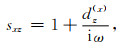
|
(35) |
其中,
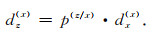
|
(36) |
则在与x轴垂直的匹配层内,复拉伸函数表示为两个方向的叠加作用:
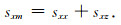
|
(37) |
与z轴垂直方向的匹配层也做同样方式处理.这种多方向衰减的形式,可以使吸收更快,吸收效果更好.
经推导, 带MCPML边界的声波方程仍为(5)式,其差分系数为
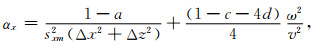
|
(38) |
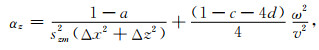
|
(39) |
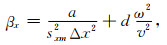
|
(40) |
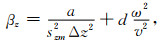
|
(41) |
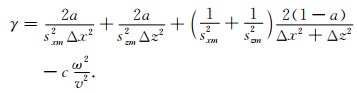
|
(42) |
公式(38)—(42)中,Δx, Δz是网格间距,v是声波速度,w是角频率,sxm和szm分别是x方向和z方向上的叠加后的衰减函数.
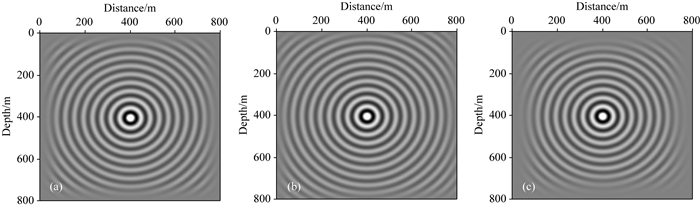
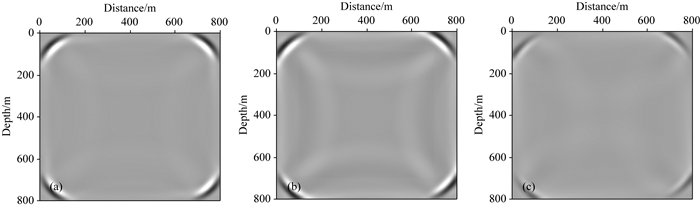
2.2 MCPML边界吸收能力为验证MCPML边界的吸收能力,设计大小为800 m×800 m的单层介质模型,速度为4000 m·s-1,网格间距为:dx=dz=5 m,网格数目为161×161.震源使用主频为30 Hz的雷克子波,位置在模型中心.模拟使用的最大频率为500 Hz,总共计算1000个单频切片(图 6),将频率域模拟结果进行傅里叶逆变换得到时间域波场(图 7).当PML和MCPML边界厚度相同时(20个网格厚度),PML边界(图 7b)内部出现明显的反射能量,说明边界吸收不完全,而MCPML边界(图 7a)吸收效果较好,内部无明显反射;将PML边界的厚度增加到30网格点时(图 7c),PML边界的吸收效果也有了提高.
|
图 6 边界吸收效果, f=50 Hz (a) MCPML边界(20网格厚度);(b) PML边界(20网格厚度);(c) PML边界(30网格厚度). Fig. 6 The boundary absorption effect, f=50 Hz (a) MCPML boundary (20 grids); (b) PML boundary (20 grids); (c) PML boundary (30 grids). |
|
图 7 边界吸收效果, Time=280 ms (a) MCPML边界(20网格厚度);(b) PML边界(20网格厚度);(c) PML边界(30网格厚度). Fig. 7 The boundary absorption effect, Time=280 ms (a) MCPML boundary (20 grids); (b) PML boundary (20 grids); (c) PML boundary (30 grids). |
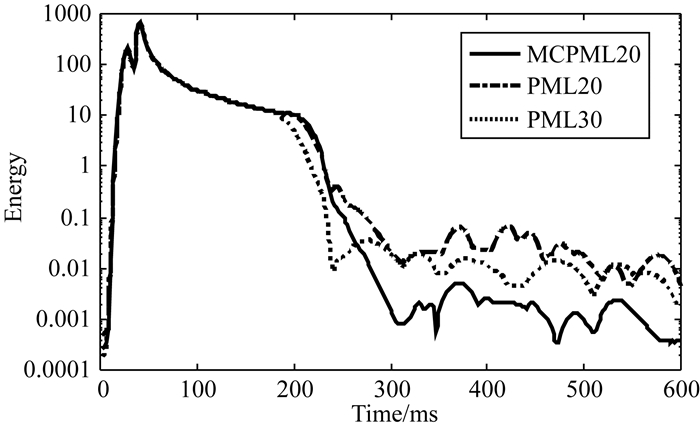
通过物理区域中地震波的能量变化曲线(图 8)可以看出,加载震源后,地震波在内部区域传播时,三者能量保持一致;地震波传播到边界处,能量开始迅速衰减.由于先接触到边界,30个网格厚度的PML边界格式率先出现衰减,但经30网格衰减后,地震波残余能量仅略低于20网格衰减的效果;而经20网格的MCPML衰减后,地震波残余的能量值最低,即吸收效果最好.
|
图 8 地震波能量变化对比图 Fig. 8 The comparison of total energy attenuation with time |
本节模型测试表明,相同的边界厚度,MCPML边界的吸收效果更好;反之,在相同吸收效果下,MCPML边界条件所需的边界网格更少,计算效率更高.
3 MCPML边界条件下的优化声波方程模拟 3.1 方程推导由本文研究的改进声波方程,结合MCPML边界,可以得到在MCPML边界条件下改进的9点差分格式的声波方程:
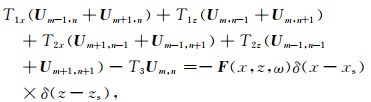
|
(43) |
其中,
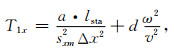
|
(44) |
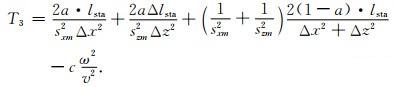
|
(48) |
公式(43)—(48)中,Δx, Δz是网格间距,U是频率域波场,v是速度,ω是角频率,sxm和szm分别是x方向和z方向上的叠加后的衰减函数,a, c, d是最优化差分系数,lsta是Laplace项的修正系数:
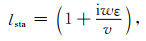
|
(49) |
式中,ε是稳定因子.
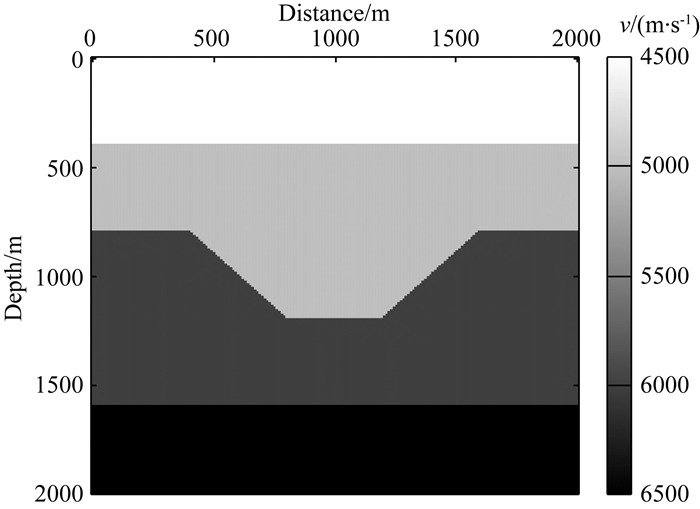
3.2 数值模拟 3.2.1 凹陷模型首先设计一个简单的凹陷模型验证本文提出的改进声波方程(43)的有效性.模型速度场设计如图 9所示,大小为2000 m×2000 m,网格数为201×201,网格间距为:dx=dz=10 m;边界厚度为300 m(30个网格厚度);震源使用主频为30 Hz的雷克子波, 位于(1000 m, 300 m)处;最大模拟频率为500 Hz,总共计算1000个单频切片.
|
图 9 凹陷模型的速度场 Fig. 9 The velocity field of sag model |
分别使用以下4种格式进行频率域模拟,对比分析四种格式得到模拟结果之间的差异:
(1) 9点差分,PML边界;
(2) 9点差分, MCPML边界;
(3) 改进9点差分,PML边界;
(4) 改进9点差分,MCPML边界.
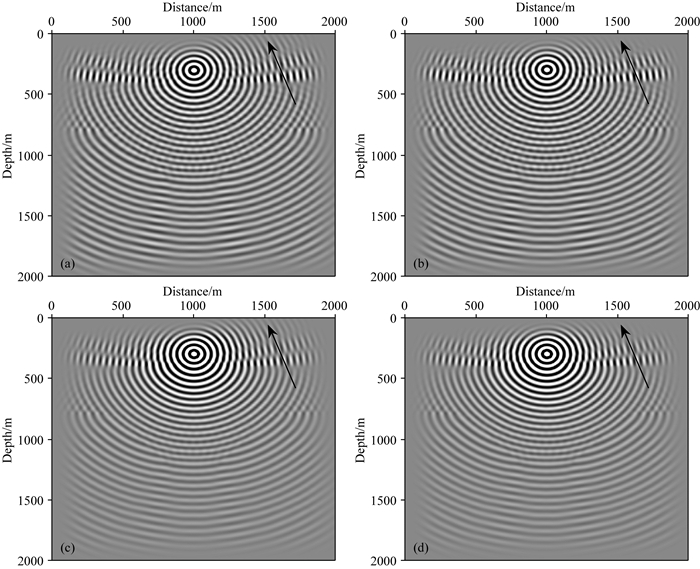
从50 Hz的频率切片(图 10)上可以看出,相同边界厚度的前提下,PML边界的吸收能力相对较差,在模型的上边界处还存在一些残余能量未被吸收(图 10a和10c中箭头标记区域);而经过MCPML边界吸收,模型上边界处残余的能量较弱,不会引起很强的边界反射,证明其吸收效果优于PML边界.
|
图 10 50 Hz单频切片 (a) 9点差分,PML边界; (b) 9点差分, MCPML边界; (c)改进9点差分,PML边界; (d)改进9点差分,MCPML边界. Fig. 10 The single frequency slices of 50 Hz (a) 9 points difference, PML boundary; (b) 9 points difference, MCPML boundary; (c) Improved 9 points difference, PML boundary; (d) Improved 9 points difference, MCPML boundary. |
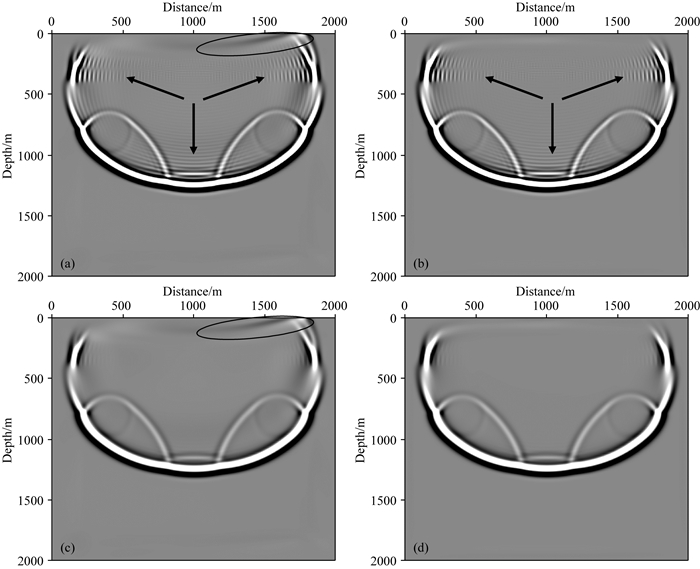
将频率域模拟结果进行傅里叶逆变换,得到时间域的波场快照.取440 ms处的波场快照(图 11)对比分析可以看出:使用9点差分格式和PML边界(图 11a)模拟得到的波场同时存在数值频散(箭头指示区域)和边界反射(椭圆标记区域);使用9点差分格式和MCPML边界(图 11b)进行模拟,边界反射被消除,但波场内部仍存在着数值频散现象(箭头指示区域);而使用改进后带波数补偿的9点差分格式和PML边界时(图 11c),数值频散现象得到明显改善,但由于PML吸收能力有限,边界处的干扰反射并未被消除(椭圆指示区域);而图 11d中同时使用带波数补偿的9点差分和MCPML边界进行模拟,数值频散和边界反射均被消除,得到了高质量的模拟结果.
|
图 11 440 ms波场快照 (a) 9点差分,PML边界; (b) 9点差分, MCPML边界; (c)改进9点差分,PML边界; (d)改进9点差分,MCPML边界. Fig. 11 The wave field snapshots of 440 ms (a) 9 points difference, PML boundary; (b) 9 points difference, MCPML boundary; (c) Improved 9 points difference, PML boundary; (d) Improved 9 points difference, MCPML boundary. |
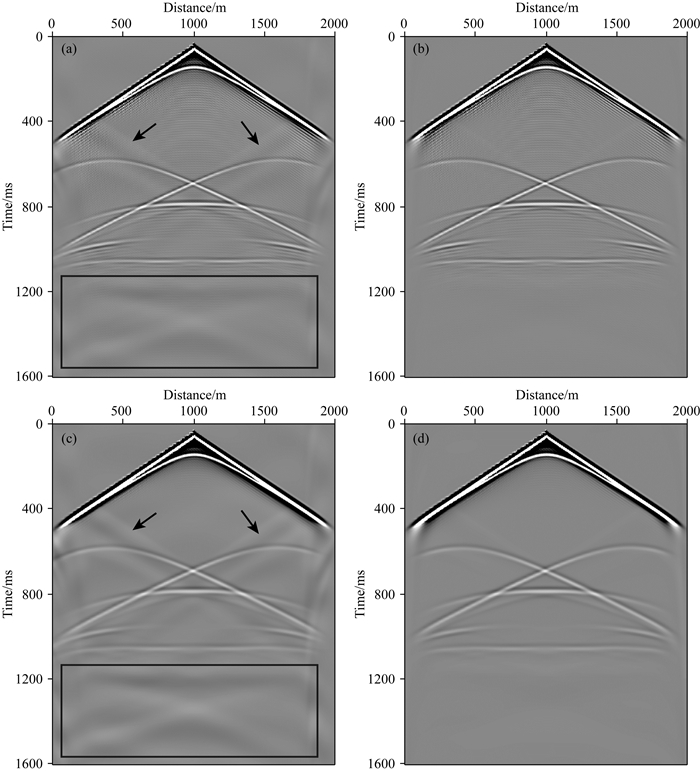
对比分析使用不同格式得到的单炮记录(图 12(a—d))可以看出,图 12a中浅层低速区数值频散较为严重,边界反射也比较明显(箭头和矩形框内区域);与图 12a相比,图 12b和12c分别使用MCPML边界和改进9点差分格式对边界反射和数值频散进行了压制,而图 12d同时使用了改进的9点差分格式和MCPML边界条件,对数值频散和边界反射均有较好的压制效果,由此,验证了公式(43)—(49)的有效性.
|
图 12 单炮记录 (a) 9点差分,PML边界; (b) 9点差分, MCPML边界; (c)改进9点差分,PML边界; (d)改进9点差分,MCPML边界. Fig. 12 The shot records (a) 9 points difference, PML boundary; (b) 9 points difference, MCPML boundary; (c) Improved 9 points difference, PML boundary; (d) Improved 9 points difference, MCPML boundary. |
在计算效率方面,对比公式(5)和公式(43)可见,二者在格式上没有差异,仅对差分系数进行了变换,即阻抗矩阵A的形式没有变化,因此,内存占用量和计算时间不会增加.模拟单炮记录所用时间和分解阻抗矩阵所需内存统计在表 2中.统计结果表明,相比于传统的差分格式,改进后的差分格式阻抗矩阵A的大小并未发生变化,计算时长也未明显增加,是一种准确高效的数值频散压制方法.
|
|
表 2 凹陷模型单炮模拟用时和分解阻抗矩阵所需内存 Table 2 Single shot simulation time and memory required to decompose impedance matrix |
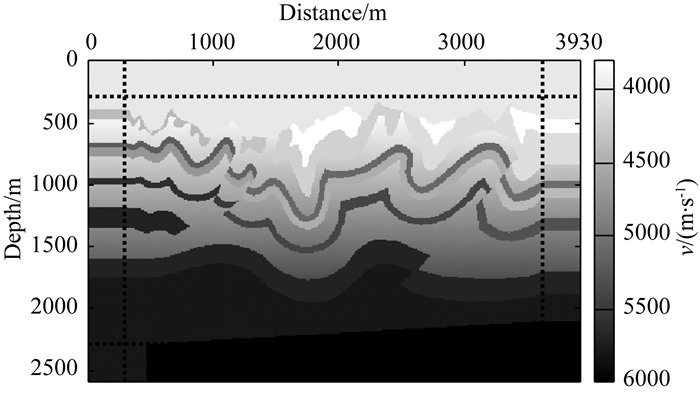
加拿大落基山模型是加拿大落基山的一个横截面模型,其复杂的构造可以为正演提供更丰富的信息(Gray et al., 1995).本文将其速度场设计如图 13所示,虚线外侧是模拟的边界区域.网格数为260×394(含30网格厚度的边界),网格间距为10 m,震源子波主频为30Hz,总共计算1600个频率切片.同样采用改进前9点差分,PML边界;改进前9点差分,MCPML边界;改进后9点差分,PML边界和改进后9点差分,MCPML边界四种模拟方式.
|
图 13 加拿大落基山模型的速度场 Fig. 13 The velocity field of the Canadian Rockies model |
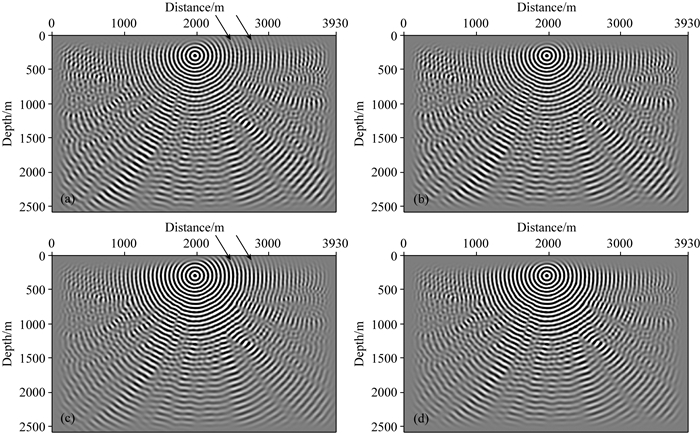
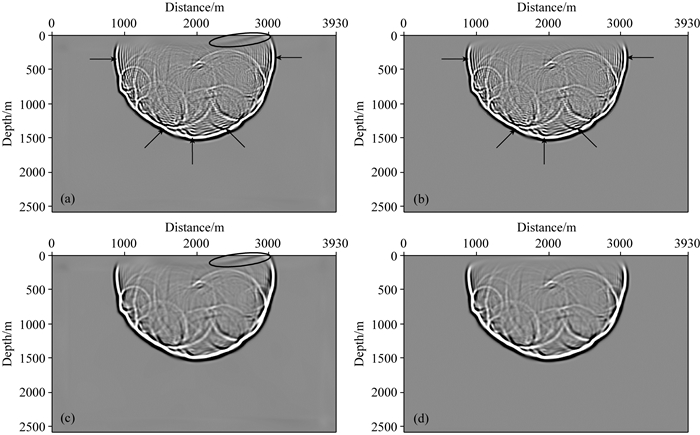
图 14展示的是35Hz单频切片的实部.从图中可以看出,该模型的频率切片上提供了更为丰富的波场信息,但在波场边界处,MCPML边界的吸收效果更好.取600 ms处时间域的波场快照(图 15)对比分析.图 15a中,可同时观察到有效波、数值频散(箭头指示区域)和边界反射(椭圆指示区域);经MCPML吸收,边界反射被消除(图 15b);经波数补偿,数值频散问题得到明显改善(图 15c);而采用优化后的9点差分格式加以MCPML边界,数值频散和边界反射同时被消除,得到清晰可靠的波场模拟结果(图 15d).
|
图 14 35 Hz单频切片 (a) 9点差分,PML边界; (b) 9点差分, MCPML边界; (c)改进9点差分,PML边界; (d)改进9点差分,MCPML边界. Fig. 14 The single frequency slices of 35 Hz (a) 9 points difference, PML boundary; (b) 9 points difference, MCPML boundary; (c) Improved 9 points difference, PML boundary; (d) Improved 9 points difference, MCPML boundary. |
|
图 15 600 ms波场快照 (a) 9点差分,PML边界; (b) 9点差分, MCPML边界; (c)改进9点差分,PML边界; (d)改进9点差分,MCPML边界. Fig. 15 The wave field snapshots of 600 ms |
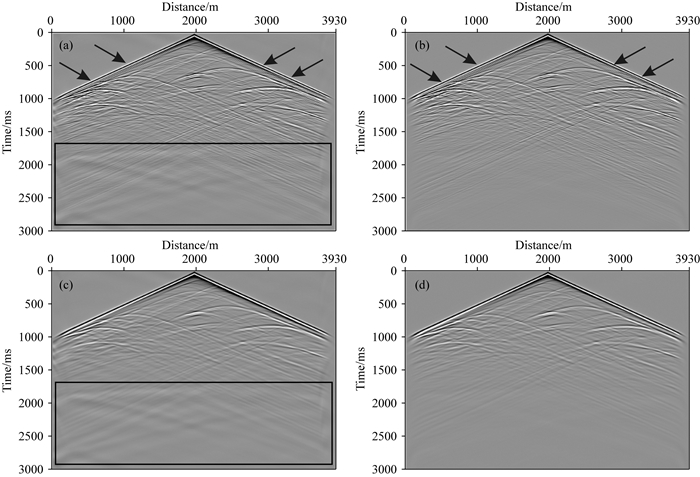
图 16的单炮记录模拟结果表明:数值频散和边界反射都会导致单炮记录上干扰信息增加,数值频散主要表现为高频假象,而边界反射主要表现为低频干扰.比较图 16b和16d可以看出,除箭头标记处之外,图 16b上的高频信息比图 16d多,但均不是有效信息,且会干扰后期的偏移成像;比较图 16c和16d的矩形标记区域可以看出,在改善数值频散的基础上,PML边界对入射到边界内的地震波能量吸收不完全而产生了一些明显的边界反射,相比之下,使用MCPML边界的炮记录上无明显的边界反射,模拟效果更好.
|
图 16 单炮记录 (a) 9点差分,PML边界; (b) 9点差分, MCPML边界; (c)改进9点差分,PML边界; (d)改进9点差分,MCPML边界. Fig. 16 The shot records (a) 9 points difference, PML boundary; (b) 9 points difference, MCPML boundary; (c) Improved 9 points difference, PML boundary; (d) Improved 9 points difference, MCPML boundary. |
同样地,经本模型测试,改进前后的差分方法,并未增加计算用时和占用内存,统计结果不再赘述.
本模型表明,即使在构造复杂的区域,本文研究的方法仍能有效地压制数值频散和边界反射,得到较好的有效波场模拟结果,是一种精确可靠的模拟方法.
4 结论本文研究了频率域模拟中数值频散和边界反射两个重要问题.受计算效率和内存占用量的制约,提高有限差分算子长度或增加有限差分网格数目均不是提高频率域模拟精度的最优解决方案.本文从波动方程出发,分析数值频散产生的理论机制,在此基础上推导了一种改进的声波方程表达式,并给出其波数补偿的物理意义.经验证,改进后的声波方程能够有效地改善数值频散问题,提高模拟精度,且并未增加计算量和内存占用量.在边界问题上,本文采用MCPML边界对边界内的地震波进行吸收衰减,相比PML边界,MCPML边界的吸收能力更强,是一种适用于频率域模拟的边界吸收方法.结合改进的声波方程和MCPML边界条件,给出了一种频率域高精度正演模拟方法,相比于改进前,本文研究的方法模拟精度高,边界吸收干净,波场正演结果清晰可靠.最后的数值模拟结果验证了本方法的准确性、有效性以及对结构复杂区域的适用性.
Bécache E, Fauqueux S, Joly P. 2003. Stability of perfectly matched layers, group velocities and anisotropic waves. Journal of Computational Physics, 188(2): 399-433. DOI:10.1016/s0021-9991(03)00184-0 |
Berenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics, 114(2): 185-200. |
Cao S H, Chen J B. 2012. A 17-point scheme and its numerical implementation for high-accuracy modeling of frequency-domain acoustic equation. Chinese Journal of Geophysics (in Chinese), 55(10): 3440-3449. DOI:10.6038/j.issn.0001-5733.2012.10.027 |
Chen J B. 2014. A 27-point scheme for a 3D frequency-domain scalar wave equation based on an average-derivative method. Geophysical Prospecting, 62(2): 258-277. DOI:10.1111/1365-2478.12090 |
Chew W C, Weedon W H. 1994. A 3D perfectly matched medium from modified maxwell's equations with stretched coordinates. Microwave and Optical Technology Letters, 7(13): 599-604. |
Dong S Q, Han L G, Hu Y, et al. 2018. Acoustic equation high-accuracy modeling in the frequency domain based on MCPML absorbing boundary. Oil Geophysical Prospecting (in Chinese), 53(1): 47-54. |
Gray S H, Marfurt K J. 1995. Migration from topography:Improving the near-surface image. Canadian Journal of Exploration Geophysics, 31(1-2): 18-24. |
Higdon R L. 1991. Absorbing boundary conditions for elastic waves. Geophysics, 56(2): 231-241. DOI:10.1190/1.1443035 |
Hustedt B, Operto S, Virieux J. 2004. Mixed-grid and staggered-grid finite-difference methods for frequency-domain acoustic wave modelling. Geophysical Journal International, 157(3): 1269-1296. DOI:10.1111/j.1365-246x.2004.02289.x |
Jo C H, Shin C, Suh J H. 1996. An optimal 9-point, finite-difference, frequency-space, 2-D Scalar wave extrapolator. Geophysics, 61(2): 529-537. |
Kim Y, Min D J, Shin C. 2011. Frequency-domain reverse-time migration with source estimation. Geophysics, 76(2): S41-S49. DOI:10.1190/1.3534831 |
Komatitsch D, Martin R. 2007. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics, 72(5): SM155-SM167. DOI:10.1190/1.2757586 |
Kuzuoglu M, Mittra R. 1996. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers. IEEE Microwave and Guided Wave Letters, 6(12): 447-449. |
Liang H. 2016. 2-D frequency acoustic wave equation modeling and full wave inversion[Master's thesis] (in Chinese). Beijing: China University of Geosciences (Beijing).
|
Liang K, Wu G C, Yin X Y. 2007. Weighted mean finite-difference operator of qP wave equation in frequency-space domain for TTI medium. Oil Geophysical Prospecting (in Chinese), 42(5): 516-525. |
Liu L, Liu H, Liu H W. 2013. Optimal 15-point finite difference forward modeling in frequency-space domain. Chinese Journal of Geophysics (in Chinese), 56(2): 644-652. DOI:10.6038/cjg20130228 |
Liu X, Liu Y, Ren Z M, et al. 2019. Perfectly matched layer boundary conditions for frequency-domain acoustic wave simulation in the mesh-free discretization. Geophysical Prospecting, 67(7): 1732-1744. DOI:10.1111/1365-2478.12788 |
Liu Y. 2013. The study of dispersion attenuation based on finite difference forward and pre-stack reverse time migration[Master's thesis] (in Chinese). Chendu: Chengdu University of Technology.
|
Lysmer J, Drake L A. 1972. A finite element method for seismology. Methods in Computational Physics:Advances in Research and Applications, 11: 181-216. |
Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics, 49(5): 533-549. DOI:10.1190/1.1441689 |
Meza-Fajardo K C, Papageorgiou A S. 2008. A nonconvolutional, split-field, perfectly matched layer for wave propagation in isotropic and anisotropic elastic media:stability analysis. Bulletin of the Seismological Society of America, 98(5): 1811-1836. DOI:10.1785/0120070223 |
Moreira R M, Santos M A C, Martins J L, et al. 2014. Frequency-domain acoustic-wave modeling with hybrid absorbing boundary conditions. Geophysics, 79(5): A39-A44. DOI:10.1190/geo2014-0085.1 |
Pratt R G. 1990. Inverse theory applied to multi-source cross-hole tomography. Part 2:elastic wave-equation method. Geophysical Prospecting, 38(3): 311-329. |
Pratt R G, Worthington M H. 1990. Inverse theory applied to multi-source cross-hole tomography. Part 1:acoustic wave-equation method:Geophysical Prospecting, 38(3): 287-310. |
Qin Z, Lu M H, Zheng X D, et al. 2009. The implementation of an improved NPML absorbing boundary condition in elastic wave modeling. Applied Geophysics, 6(2): 113-121. |
Qu Y M, Li J L. 2019. Q-compensated reverse time migration in viscoacoustic media including surface topography. Geophysics, 84(4): S201-S217. DOI:10.1190/geo2018-0313.1 |
Qu Y M, Guan Z, Li J L, et al. 2020a. Fluid-solid coupled full-waveform inversion in the curvilinear coordinates for ocean-bottom cable data. Geophysics, 85(3): R113-R133. DOI:10.1190/geo2018-0743.1 |
Qu Y M, Li J L, Guan Z, et al. 2020b. Viscoacoustic reverse time migration of joint primaries and different-order multiples. Geophysics, 85(2): S71-S87. DOI:10.1190/geo2019-0237.1 |
Ren H R, Wang H Z, Gong T. 2009. Seismic modeling of scalar seismic wave propagation with finite-difference scheme in frequency-space domain. Geophysical Prospecting for Petroleum (in Chinese), 48(1): 20-26. |
Shin C. 1995. Sponge boundary condition for frequency-domain modeling. Geophysics, 60(6): 1870-1874. |
Shin C, Yoon K, Marfurt K J, et al. 2001. Efficient calculation of a partial-derivative wavefield using reciprocity for seismic imaging and inversion. Geophysics, 66(6): 1856-1863. |
Shin J, Jun H, Min D J, et al. 2017. Frequency-domain waveform modelling and inversion for coupled media using a symmetric impedance matrix. Geophysical Prospecting, 65(1): 170-183. DOI:10.1111/1365-2478.12423 |
Sourbier F, Haidar A, Giraud L, et al. 2011. Three-dimensional parallel frequency-domain visco-acoustic wave modelling based on a hybrid direct/iterative solver. Geophysical Prospecting, 59(5): 834-856. DOI:10.1111/j.1365-2478.2011.00966.x |
Takekawa J, Mikada H. 2019. Free-surface implementation in a mesh-free finite-difference method for elastic wave propagation in the frequency domain. Geophysical Prospecting, 67(8): 2104-2114. DOI:10.1111/1365-2478.12825 |
Tian K, Huang J P, Li Z C, et al. 2013. Recursive convolution method for implementing complex frequency-shifted PML absorbing boundary condition. Journal of Jilin University (Earth Science Edition) (in Chinese), 43(3): 1022-1032. |
Tian K, Huang J P, Li Z C, et al. 2014. Multi-axial convolution perfectly matched layer absorption boundary condition. Oil Geophysical Prospecting (in Chinese), 49(1): 143-152. |
Tian K. 2014. Study on method of forward modeling and reverse time migration in viscous media[Ph. D. thesis] (in Chinese). Qingdao: China University of Petroleum (East China).
|
Wu G C, Luo C M, Liang K. 2007. Frequency-space domain finite difference numerical simulation of elastic wave in TTI media. Journal of Jilin University (Earth Science Edition) (in Chinese), 37(5): 1023-1033. |
Wu J L, Wu G C. 2018. Finite difference method for acoustic-elastic coupled equations of seismic waves in the frequency domain. Chinese Journal of Geophysics (in Chinese), 61(6): 2396-2408. DOI:10.6038/cjg2018l0340 |
Yin W, Yin X Y, Wu G C, et al. 2006. The method of finite difference of high precision elastic wave equations in the frequency domain and wave-field simulation. Chinese Journal of Geophysics (in Chinese), 49(2): 561-568. |
Yin W. 2008. Forward modeling and parallel algorithm based on high-order finite-difference method in frequency domain. Journal of Jilin University (Earth Science Edition) (in Chinese), 38(1): 144-151. |
Zhang X W, Han L G, Huang L, et al. 2009. A staggered-grid high-order difference method of complex frequency-shifted PML based on recursive integration for elastic wave equation. Chinese Journal of Geophysics (in Chinese), 52(7): 1800-1807. DOI:10.3969/j.issn.0001-5733.2009.07.014 |
Zhao Z Y, Sen M K. 2019. Frequency-domain double-plane-wave least-squares reverse time migration. Geophysical Prospecting, 67(8): 2061-2084. DOI:10.1111/1365-2478.12803 |
Zhou C. 2012. Theory and analysis of full-wavefield modeling in frequency domain using finite-difference method[Master's thesis] (in Chinese). Wuhan: China University of Geosciences.
|
曹书红, 陈景波. 2012. 声波方程频率域高精度正演的17点格式及数值实现. 地球物理学报, 55(10): 3440-3449. DOI:10.6038/j.issn.0001-5733.2012.10.027 |
董士琦, 韩立国, 胡勇, 等. 2018. 基于MCPML边界条件的频率域声波方程高精度模拟. 石油地球物理勘探, 53(1): 47-54. |
梁昊. 2016.二维频率域声波方程正演模拟及其全波形反演研究[硕士论文].北京: 中国地质大学(北京).
|
梁锴, 吴国忱, 印兴耀. 2007. TTI介质qP波方程频率-空间域加权平均有限差分算子. 石油地球物理勘探, 42(5): 516-525. |
刘璐, 刘洪, 刘红伟. 2013. 优化15点频率-空间域有限差分正演模拟. 地球物理学报, 56(2): 644-652. DOI:10.6038/cjg20130228 |
刘洋. 2013.有限差分法正演频散衰减及叠前逆时偏移的研究[硕士论文].成都: 成都理工大学.
|
任浩然, 王华忠, 龚婷. 2009. 标量地震波频率-空间域有限差分法数值模拟. 石油物探, 48(1): 20-26. |
田坤, 黄建平, 李振春, 等. 2013. 实现复频移完全匹配层吸收边界条件的递推卷积方法. 吉林大学学报(地球科学版), 43(3): 1022-1032. |
田坤. 2014.黏性介质正演及逆时偏移成像方法研究[博士论文].青岛: 中国石油大学(华东).
|
田坤, 黄建平, 李振春, 等. 2014. 多轴卷积完全匹配层吸收边界条件. 石油地球物理勘探, 49(01): 143-152. |
吴国忱, 罗彩明, 梁楷. 2007. TTI介质弹性波频率-空间域有限差分数值模拟. 吉林大学学报(地球科学版), 37(5): 1023-1033. |
吴建鲁, 吴国忱. 2018. 频率域声-弹耦合地震波波动方程有限差分方法. 地球物理学报, 61(6): 2396-2408. DOI:10.6038/cjg2018L0340 |
殷文, 印兴耀, 吴国忱, 等. 2006. 高精度频率域弹性波方程有限差分方法及波场模拟. 地球物理学报, 49(2): 561-568. |
殷文. 2008. 基于频率域高阶有限差分法的正演模拟及并行算法. 吉林大学学报(地球科学版), 38(1): 144-151. |
张显文, 韩立国, 黄玲, 等. 2009. 基于递归积分的复频移PML弹性波方程交错网格高阶差分法. 地球物理学报, 52(7): 1800-1807. DOI:10.3969/j.issn.0001-5733.2009.07.014 |
周聪. 2012.频率域全波场有限差分数值模拟及特征分析[硕士论文].武汉: 中国地质大学.
|
 2021, Vol. 64
2021, Vol. 64


