2. 中国石油大学(华东)深层油气重点实验室, 青岛 266580;
3. 中海油田服务股份有限公司油田技术事业部, 北京 101149
2. Key Laboratory of Deep Oil and Gas, China University of Petroleum, Qingdao 266580, China;
3. China Oilfield Services Limited, Beijing 101149, China
适用于固井质量评价的声波测井类的测量方法均是利用套管中传播的某种模式波的幅度或衰减评价水泥的胶结情况.例如, 贴井壁的扇区水泥胶结测井SBT(Segmented Bond Tool)(魏涛, 2010; 陈雪莲等, 2015)在套管中激发了类似薄板中的零阶对称兰姆波, 即准S0模式, 以下简称拉伸波, 通过补偿式的衰减测量方式得到拉伸波的衰减; 超声反射成像测井时声源辐射的声束垂直入射到套管内壁, 主要激发套管共振波, 类似薄板中的高阶对称兰姆波, 共振波幅度的大小反映了套管与水泥之间的耦合程度; 水泥封隔成像测井(斯伦贝谢推出的IBC, Imaging Behind the Casing)中除了垂直入射方式激发共振波外, 还利用斜入射的方式在套管中激发了类似薄板中的零阶反对称兰姆波, 准A0模式, 也称为弯曲型兰姆波(Froelich, 2008; He et al., 2014; 陈雪莲等, 2016; Xu and Hu, 2017); 现在除了应用套管中准兰姆波评价固井质量, 也开始研究利用套管中的准SH波评价套管与水泥间的胶结状况(Tang et al., 2009; Patterson et al., 2015).不同测井方法应用套管中不同的模式波评价套管与水泥间的胶结状况, 各传播模式对套后介质的声学性质以及胶结状况的响应特征也不同, 研究这些模式波的响应特征可以分辨套管和套后介质之间是哪种耦合方式(剪切耦合或法向耦合), 可为在固井质量综合解释或水泥封隔评价时综合多种测井方法测量的结果, 也即套管的多个模式波的幅度或衰减响应, 区分水泥的各种胶结状况提供了可能.比如, 小间隙环空固井(微环)和尾管固井(容易出现水泥沟槽)的质量评价存在较大的不确定性(张宏兵等, 2009; 魏涛, 2010).
套管井中兰姆波的传播问题涉及到层状介质弹性波传播问题, 在某一薄层的厚度远小于波长时, 比如在套管和水泥环之间的微环等, 可用线性滑移界面理论(Schoenberg, 1980)描述该薄层对波传播的影响(唐晓明等, 2018).采用Kelvin-Voigt黏弹体(Fehler, 1982), 在滑移界面理论中引入了切向耦合刚度和法向耦合刚度的概念, 可以很方便和直观地揭示了兰姆波的拉伸和弯曲运动特点及其与水泥间的耦合特征, 不同模态的兰姆波对这两种耦合刚度的敏感性还可以反映其对评价水泥封隔效果的适用性.本文以上述测井方法在套管中激发的模式波的频散、衰减以及全波的响应特征为基础, 将黏弹滑移界面理论应用到套管和水泥之间的耦合界面, 重点分析了拉伸波(SBT仪器在套管中激发的准S0模式)和弯曲型兰姆波(IBC仪器斜入射方式在套管中激发的准A0模式)传播时与套后介质的耦合方式, 对比了两种模式的响应差异, 为综合利用套管中多种模式波的幅度或衰减特征开展固井质量评价以及水泥封隔性评价提供理论基础.
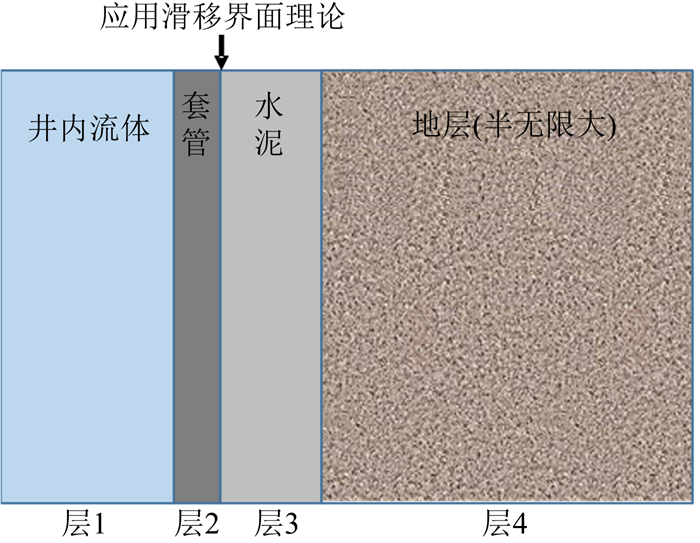
1 理论计算模型 1.1 模式波频散和衰减的计算方法SBT、IBC以及超声成像等测井仪器的工作频率均高于70 kHz, 声源发射的超声脉冲仅能作用于套管很小的区域, 此时柱状径向分层的套管模型可近似为二维的平面多层介质模型(图 1所示), 使得套管中模式波的频散和衰减计算变得更加简便.在图 1所示的二维多层介质模型中, 任一层固体中的纵波和横波势函数可表示为(势函数表达式省略了公共因子exp[j(kzz-ωt)]):
|
图 1 套管井多层介质模型 Fig. 1 Multi-layer medium model with ultra-sonic logging |
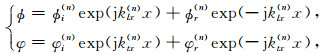
|
(1) |
式(1)中ϕi、ϕr、φi、φr依次表示入射纵波、反射纵波、入射横波、反射横波的振幅系数, 最后一层为半无限大介质, ϕr和φr为零, 上标n为层序号, ω为圆频率, kz为模式波在z方向上的波数, 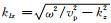
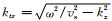
经典的层状介质理论中, 相邻层之间的固-固界面边界条件为法向位移、切向位移、正应力和切向应力连续, 液固或固液界面为法向位移和正应力连续, 切向应力为零.定义位移-应力向量S为
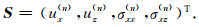
|
(2) |
在套管和水泥环之间的界面, 若存在微环等薄层(厚度远远小于波长), 可应用滑移界面理论模拟微环的响应特征, 滑移边界描述了穿过该界面时应力保持连续, 而位移却发生了“滑移”跃变, 滑移的大小由薄层介质的耦合刚度η确定, 公式为
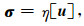
|
(3) |
式中, η=M/d, d为薄层的厚度, σ是应力张量, u是位移, M为薄层介质的弹性模量, 在M为复数时可以描述非弹性耦合效应(唐晓明等, 2018).在图 1的二维模型中套管与水泥环之间的黏弹滑移边界条件可表示为
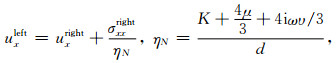
|
(4) |
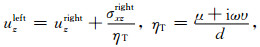
|
(5) |
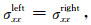
|
(6) |
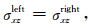
|
(7) |
式(4)—(7)中, 上标为“left”的位移或应力表示套管外壁上的物理量, 上标为“right”的位移或应力表示水泥环内壁上的物理量, ηN和ηT分别称为法向耦合刚度和切向耦合刚度, 法向耦合刚度趋于无穷大时, 说明界面两侧(套管与水泥之间的界面)的法向位移是连续的, 切向耦合刚度趋于无穷大时说明界面两侧的切向位移(与界面平行)是连续的, K和μ分别是薄层介质的体积模量和剪切模量, υ是黏滞系数, 当μ为零时, 剪切刚度ηT描述的是滑移界面为牛顿流体时的黏滞耦合(唐晓明等, 2018).
井内流体、套管、水泥以及地层之间通过边界条件连接起来, 每一层内的左界面与右界面则通过传递矩阵g连接起来(李建赛, 2015), 即:
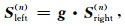
|
(8) |
反复利用各层介质上的边界条件以及层内左右界面的传递关系式(8), 可将流体-套管界面的应力-位移向量Sright(1)与水泥环-地层界面的应力-位移向量Sleft(N)相联系, 公式为
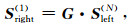
|
(9) |
其中矩阵G是图 1中最左界面和最右界面所有夹层的传递矩阵点乘.
将(9)式中的常数项移到方程的右边可得到:
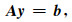
|
(10) |
式中y为图 1模型中由井内流体的ϕr、地层的ϕi和φi等未知的势函数振幅系数构成的向量, b与井内流体中的入射波有关, 是常数项.由方程(10)可以求解获得反射系数Rp(kz, ω), 由于井内流体中只有纵波传播, 所以此处只给出纵波反射系数:
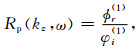
|
(11) |
令式(10)中系数矩阵A的行列式为零, 即:
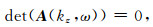
|
(12) |
求解此方程即可得到套管中兰姆波的频散和衰减曲线(Rose, 2004).相速度和衰减(单位为dB/m)的具体表达式为
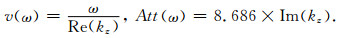
|
(13) |
声源的二维谱Ai(张海澜, 2012)和反射系数Rp的二维谱相乘, 利用实轴积分法可得到模式波的响应波形, 即:
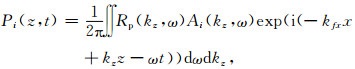
|
(14) |
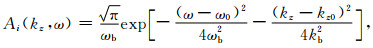
|
(15) |
其中ω0是中心频率, kz0=(ω/vf)*sin(θ)决定了声源辐射声波的传播方向(θ为入射角), ωb为频带宽度, kb为角谱宽度, 他们分别决定脉冲在时间和空间上的宽度.
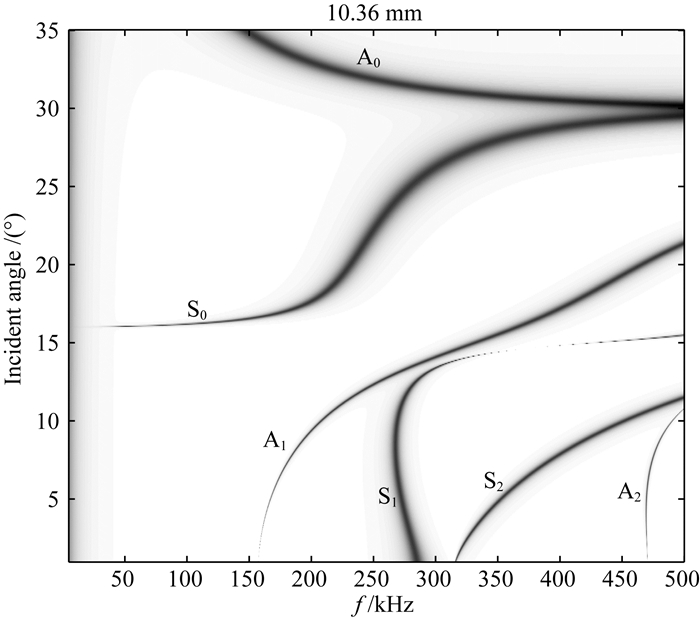
目前常用的套管模式波是拉伸波和弯曲型兰姆波, 本文中的拉伸波特指准零阶对称兰姆波(准S0), 弯曲型兰姆波是指准零阶反对称兰姆波(准A0).Zeroug和Froelich(2003)给出了薄板中兰姆波的有效激发方式, 通过工作频段和声源辐射声束入射到套管内壁的角度选择可在套管中有效的激发某类兰姆波.图 2是10.36 mm厚度的浸水钢板在不同入射角不同频率下的激发效果图, 在较高工作频率下, 垂直入射时主要激发高阶的对称兰姆波S1、S2等模式, 在入射角大于钢板的第二临界角后主要激发弯曲型兰姆波(图 2中标注的A0), 介于两者之间的入射角可激发零阶对称兰姆波(图 2中标注的S0).通过调节式(15)中kz0的大小, 可模拟测井仪器声源辐射声束的不同入射角度, 实现仿真弯曲型兰姆波、拉伸波等模式的测井响应波形.
|
图 2 兰姆波的有效激发方式 Fig. 2 Effective excitation pattern of Lamb waves |
为了探讨滑移边界中法向耦合刚度和切向耦合刚度对两种模式波的影响, 建立了套管-轻质水泥-地层的套管井模型, 这里以轻质水泥为例, 主要是考虑到弯曲型兰姆波的衰减对轻质水泥声阻抗响应的单调性.计算模型的参数见表 1所示.
|
|
表 1 套管井模型各层的参数 Table 1 Parameters of materials in cased well model |
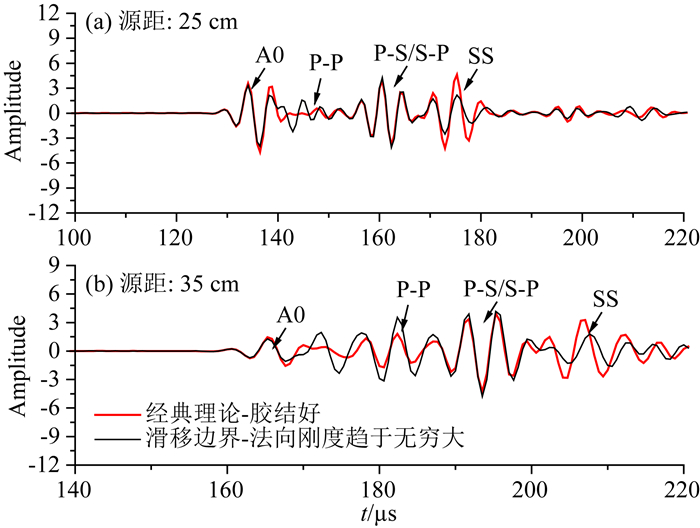
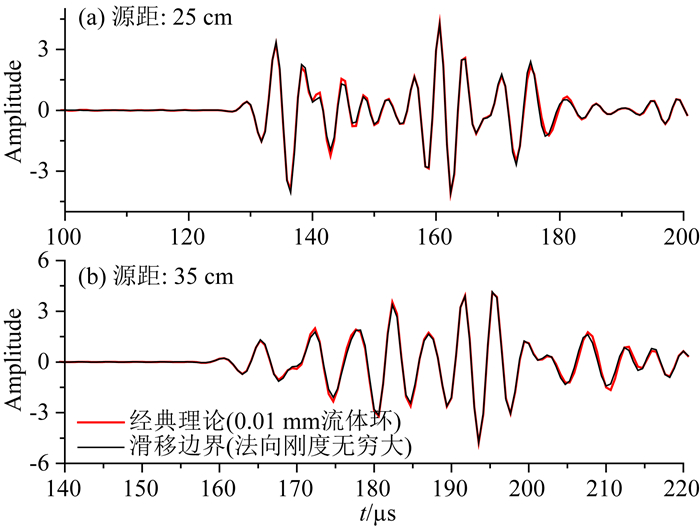
建立套管-轻质水泥-地层的套管井模型, 参考IBC水泥封隔成像测井仪的工作方式, 定向声源辐射声束传播到套管内壁的入射角度设为33°, 声源的中心频率为250 kHz, 两个接收源距分别是25 cm和35 cm.利用式(14)可模拟套管中弯曲型兰姆波的响应特征.在套管和水泥界面应用滑移边界, 设定法向耦合刚度ηN趋于无穷大, 剪切模量μ=0, 通过黏滞系数υ调节剪切刚度的大小, 由图 3可见两个测量源距下的弯曲型兰姆波的波形幅度不变, 此波形与经典理论下(套管和水泥界面固固耦合)胶结良好的波形相比(图 3中红色波形), 首先到达的套管中传播的弯曲型兰姆波基本一致, 水泥和地层界面的反射波P-S/S-P基本一致, 但S-S反射波稍弱, P-P波稍强.可见弯曲型兰姆波的衰减主要由法向耦合刚度控制, 在法向耦合刚度趋于无穷时, 其对黏滞系数不敏感, 但切向耦合刚度的缺失, 使得S-S反射波的幅度降低, 也即泄漏到水泥环中的横波能量降低了.通过进一步的对比发现, 法向耦合刚度趋于无穷大、剪切耦合刚度趋于零时的计算波形与经典理论(套管-流体环-水泥之间按照固液-液固边界计算波形)中套管和水泥环之间加入0.01 mm的微环时的响应特征一致(图 4), 套管和水泥之间的微环存在也即缺失了此界面的剪切耦合.
|
图 3 法向耦合刚度趋于无穷时A0模式波的计算波形 Fig. 3 Calculated flexural Lamb waves with infinite normal stiffness |
|
图 4 法向耦合刚度趋于无穷和经典理论下的微环响应对比 Fig. 4 Response comparison between infinite normal stiffness and classical fluid-solid interface theory |
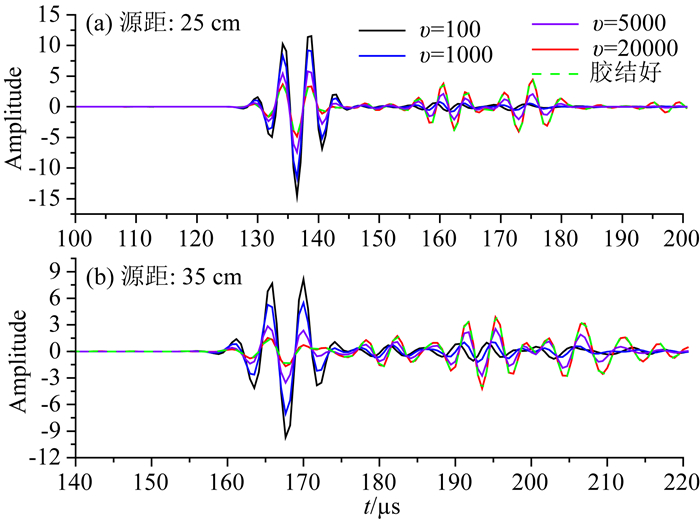
在法向刚度有限(较小, K=0.00225 GPa, μ=0), 黏滞系数υ从100 Pa·s时变化到2×104Pa·s时可完全模拟胶结状况从无胶结到胶结好的波形, 在υ>2×104Pa·s波形与胶结良好时完全一致(图 5).这种黏滞耦合方式可有效的模拟现场声波衰减逐渐变化的趋势, 也即胶结强度从弱到强的变化过程.在经典理论中固固是完全胶结, 固液是完全不胶结, 实际套管外壁与水泥之间的耦合方式很多情况是水泥黏附到套管外壁, 这种弱连接的接触方式可通过调节滑移界面理论中的黏滞耦合系数的大小模拟, 黏滞系数的大小反映了套管和水泥间的胶结程度.
|
图 5 黏滞系数改变模拟胶结由强到弱的变化 Fig. 5 Modeling weak bonding to good bonding situations by different viscous coefficient values |
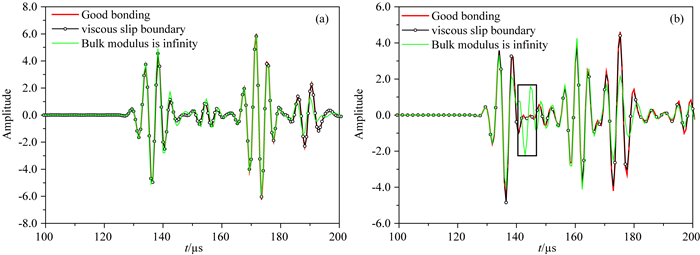
对弯曲型兰姆波, 黏滞系数较大或法向刚度较大均可得到与经典模型下胶结好时弯曲波的响应波形; 差异仅是法向刚度趋于无穷(切向刚度趋于零)时, 来自水泥环外侧的反射S-S波幅度稍弱, P-P波较强, 但黏滞系数较大时, 可更好地模拟胶结好时的整个波列(图 6).图 6a和图 6b设置的滑移边界参数值均是一致的, 图 6a模型中水泥的纵横波速度分别是2600 m·s-1和1390 m·s-1, 图 6b模型中水泥的纵横波速度稍有提高, 增加到2755 m·s-1和1473 m·s-1, 两种水泥参数下, 黏滞系数较大时模拟的全波波列均与胶结良好时完全吻合, 但只保留法向刚度耦合时(图中绿色曲线), 由于图 6b模型中水泥的纵波速度更接近工作频段弯曲型兰姆波的相速度, 此水泥参数下弯曲型Lamb波低频分支的衰减稍小(李建赛, 2015), 使得低频成分的响应幅度增大(图 6b中的矩形框内).
|
图 6 黏滞系数和体积模量趋于无穷大时的全波波形对比 Fig. 6 Waveform contrast between infinite bulk modulus and viscous coefficient |
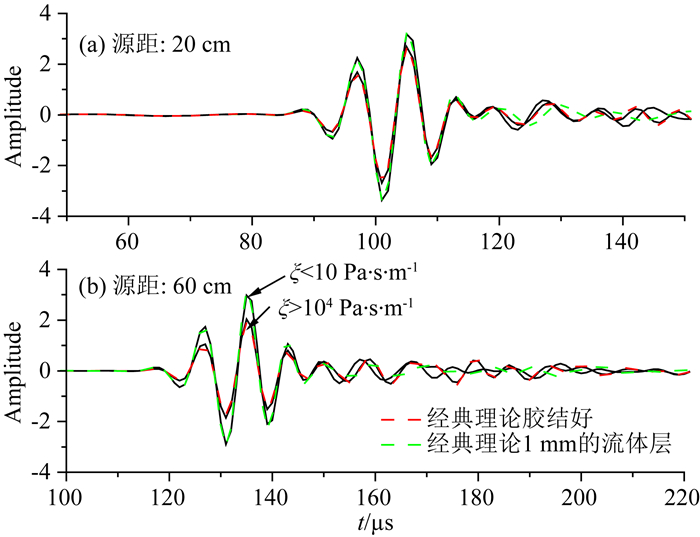
SBT测井仪是在套管中激发拉伸波(准S0), 通过拉伸波的衰减评价套管与水泥间的胶结质量.参照SBT测井仪的工作方式, 设置声源中心频率100 kHz, 源距分别为20 cm和60 cm, 图 7是应用黏弹滑移理论模拟的套管后胶结轻质水泥时拉伸波的响应特征, 法向耦合刚度ηN设置为无穷大, 剪切模量μ=0, 通过黏滞系数υ调节剪切刚度的大小, 在υ < 10时(图中标注的黑色曲线), 与经典流体环的响应一致; 在υ>104时(图中标注的黑色曲线), 与经典理论中胶结好的响应一致.此响应特征明显与弯曲型兰姆波不同, 弯曲型兰姆波在法向耦合刚度趋于无穷大时, 基本不再受黏滞系数变化的影响; 而拉伸波的响应幅度在法向刚度趋于无穷大时, 仍可利用黏滞系数模拟未胶结到完全胶结的各种胶结程度.
|
图 7 法向耦合刚度趋于无穷时拉伸波随黏滞系数变化的响应特征 Fig. 7 Simulated extensional waves with infinite normal stiffness |
通过在套管与水泥界面应用滑移边界模拟弯曲型Lamb波和拉伸波的响应特征, 可知拉伸波与套管后介质的耦合主要通过剪切刚度耦合, 对界面的法向刚度不敏感, 而弯曲型兰姆波主要通过法向刚度与套后物质耦合, 也即弯曲型兰姆波与套后介质的声能量交换主要通过与套后介质的法向形变耦合.由于黏滞系数在法向刚度和切向刚度中均存在, 拉伸波和弯曲型兰姆波的套管井测井响应均可通过调节黏滞系数的大小实现模拟套管与水泥之间由不胶结到完全胶结的过渡状态.
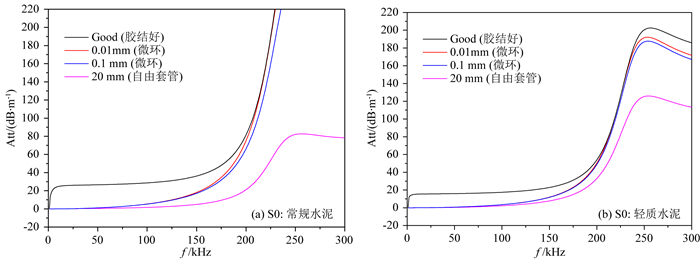
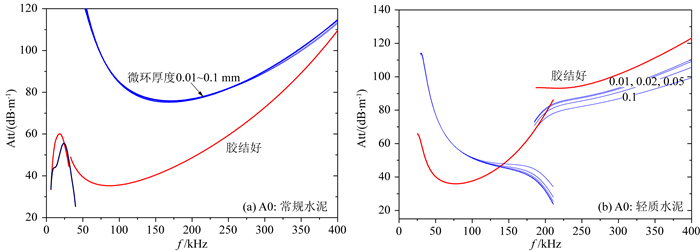
2.2 经典理论下对比拉伸波和弯曲型兰姆波对微环的响应通过拉伸波和弯曲型兰姆波对微环响应的对比, 进一步体现了两种兰姆波在与套管后介质耦合(或泄露声波能量)时不同的响应特征.图 8是不同胶结状况下拉伸波的衰减曲线, 可见在频率小于100 kHz的范围内只要套管后微环存在, 即便是0.01 mm的微环, 其衰减明显降低, 与自由套管时的衰减值(4 dB/m)接近, 微环的存在使得拉伸波依赖的套管和水泥环之间的剪切耦合缺失, 导致其衰减降低.图 9是弯曲型兰姆波的衰减曲线, 在IBC仪器工作频段200~250 kHz, 若套后是轻质水泥时, 微环出现后衰减稍降低, 但远大于自由套管时的衰减(约50 dB/m), 可认为其衰减对微环不敏感; 若套后是常规水泥时, 微环的出现使得弯曲型兰姆波的衰减明显增强, 对于声阻抗相对大的常规水泥, 微环的出现相当于降低了套后介质的等效声阻抗, 使得其等效泊松比增加, 更容易产生体形变, 这充分说明弯曲型兰姆波主要靠法向位移与套后介质耦合.综上分析也说明了弯曲型兰姆波在套管中主要以横向位移为主, 拉伸波以沿着套管轴向振动位移为主.这与2.1节中得出的弯曲型兰姆波在套管中传播时更多的依赖滑移界面理论中的法向耦合刚度与套外介质相互作用、拉伸波主要依赖切向刚度耦合的结论是一致的.
|
图 8 拉伸波的衰减曲线 Fig. 8 Attenuation curves of extensional waves |
|
图 9 弯曲型兰姆波的衰减曲线 Fig. 9 Attenuation curves of flexural Lamb waves |
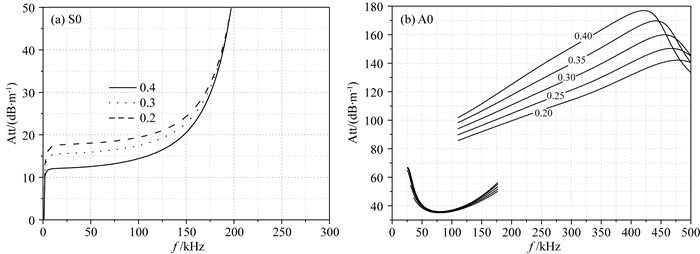
图 10对比了套管后轻质水泥泊松比变化时拉伸波和弯曲型兰姆波衰减的变化, 衰减大说明其沿着套管传播时与套后水泥声耦合好, 能量可更多的泄漏到水泥环中.拉伸波的衰减随着水泥泊松比的增大逐渐降低, 而弯曲型兰姆波的衰减随着泊松比的增大逐渐增加.水泥的纵波阻抗不变, 随泊松比的增大水泥相对变软, 在水泥纵波阻抗不变的情况下其剪切模量降低, 拉伸波主要依靠剪切模量与套后水泥耦合, 因此水泥剪切模量的降低减弱了套管和水泥之间的声耦合程度, 使得其衰减减小; 弯曲型兰姆波与套后介质的耦合主要依赖于界面的法向刚度耦合, 水泥泊松比降低, 水泥变软使得声耦合更好, 衰减增大.
|
图 10 水泥的泊松比对拉伸波和弯曲型兰姆波衰减的影响 Fig. 10 Effect of Poisson ratio on attenuation of extensional and flexural Lamb waves |
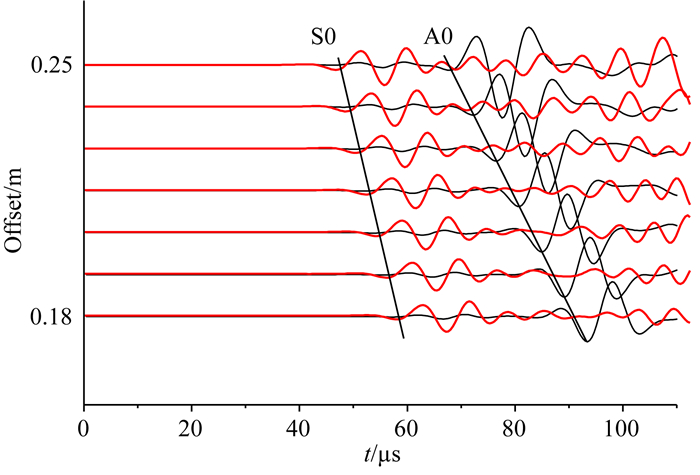
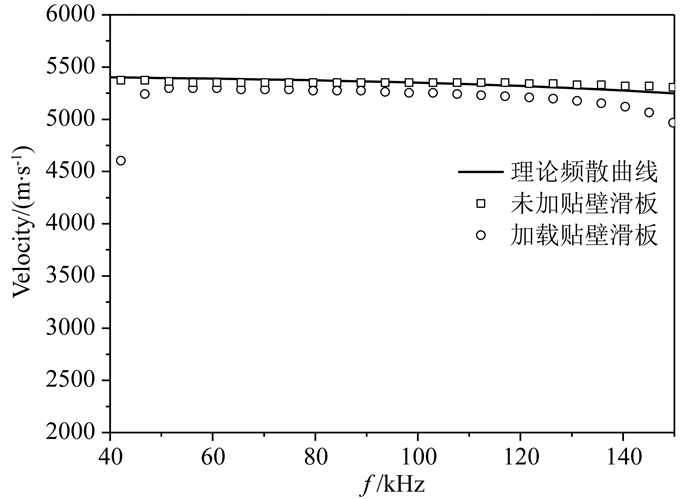
与图 2中描述的定向声源辐射方法不同, 图 11显示的波列是在套管中用非定向声源激发的例子.建立一个自由套管模型, 将一个点声源和接收阵列直接放置于充满泥浆的套管内壁, 声源直接与套管和泥浆耦合, 接收阵列接收的全波波形见图 11中的黑色波形, 可见全波中的弯曲型兰姆波幅度很强, 套管中传播的主要是准A0模式; 仿照贴井壁测量的SBT测井仪, 利用贴壁滑板将声源和接收器放置于套管内壁, 贴壁滑板具有一定的宽度和长度(陈雪莲等, 2015), 声源在贴壁滑板与套管之间激发时, 接收的波列如图 11中的红色波形, 可明显发现套管中的拉伸波幅度明显增强, 弯曲型兰姆波的幅度减弱明显.两种激发方式的对比也体现了两个模式波不同的传播特征, 弯曲型兰姆波主要是套管的弯曲振动, 其与套后介质主要是通过法向位移相互耦合, 这与应用滑移边界理论时得到的结论也是一致的, 即弯曲型兰姆波对套后介质的耦合主要依赖法向刚度耦合, 因此加载了贴壁滑板以后, 贴壁滑板的存在压制了套管的弯曲振动, 使得其响应幅度明显减弱; 相反拉伸波在套管中的振动主要沿着套管的轴向, 其与套后介质的耦合是剪切刚度的耦合, 在应用滑移边界理论时, 也可发现法向刚度耦合对拉伸波的影响很小, 因此与套管轴向平行的贴壁滑板的存在反而相对增强了拉伸波的幅度, 但贴壁滑板的附重会使得拉伸波的相速度稍有降低(图 12).
|
图 11 贴壁滑板对套管中模式波激发的影响 Fig. 11 Influence of the sidewall pad on excitation intensity of Lamb waves |
|
图 12 拉伸波的频散曲线 Fig. 12 Dispersion curves of extensional waves |
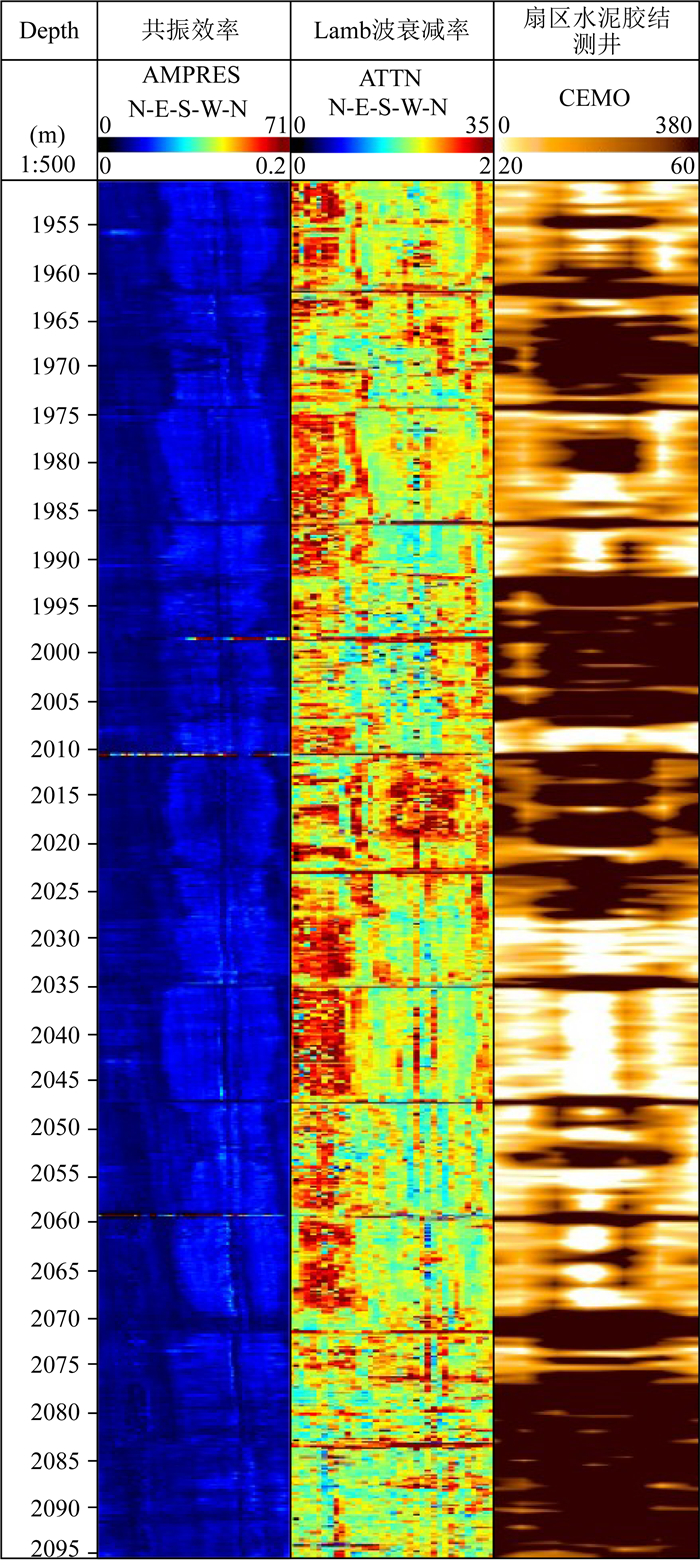
CBL或SBT测井时套管波幅度升高或衰减降低可能是存在微环或者某扇区胶结差的响应特征, 微环一般认为不会造成流体窜槽, 但胶结差的情况需要再次注入水泥才能进行油气开采.如何区分微环还是水泥与套管之间胶结差一直是固井质量评价的难点, 目前常用的方法是在套管内加压, 再次测井, 对比加压前后的测井响应, 判断是否有微环, 这种方式需要重复测井, 测井成本很高.根据图 8和图 9给出的拉伸波和弯曲型兰姆波的微环响应特征, 可以联合IBC和SBT或CBL等测井数据识别微环, 图 13是某井的固井质量测井成果图, 水泥密度是1.9 g·cm-3, 套管稍有偏心.第4道给出的SBT测井结果显示在2030~2068 m拉伸波(准S0)的衰减率在0°~360°都很低, 接近自由套管的衰减值(约4 dB/m), 这可能是套后水泥胶结差或存在微环造成的, 结合第3道IBC测量的弯曲型兰姆波(准A0)的衰减率可知0~100度扇区的衰减值很高, 达到120 dB/m, 这对常规水泥胶结好时的衰减率(约60 dB/m)相比增加很多, 通过图 9a可知造成这一现象与套后有微环的响应特征一致, 通过第二道IBC仪器垂直入射方式测量的共振效率在此扇区比较低, 也可佐证是微环的响应特征; 另一半扇区弯曲型兰姆波的衰减值在50 dB/m附近, 结合SBT的测井结果可确认此扇区水泥胶结差或套管和水泥之间的流体环厚度较大.
|
图 13 水泥胶结测井成果图 Fig. 13 Images showing logging results with cement bonding |
本文应用黏弹滑移界面理论模拟了套管和水泥界面的耦合状态, 并结合拉伸波和弯曲型兰姆波对微环响应以及不同激发方式对兰姆波幅度的影响, 探讨了套管中两种振动模式与套后介质的不同耦合方式, 得到以下结论:
(1) 黏弹滑移界面理论中的黏滞刚度可作为主要耦合参数模拟拉伸波和弯曲型兰姆波在套管和水泥界面由无胶结到完全胶结的响应特征; 对拉伸波而言, 可设定法向耦合刚度趋于无穷大, 弯曲型兰姆波需要设定法向耦合刚度趋于零.
(2) 拉伸波和弯曲型兰姆波的衰减值高体现了套管与套管后物质之间的声耦合好, 也即声波能量更多的泄漏到套后物质中, 套管中的拉伸波与套后介质之间的声耦合更多的是体现滑移边界中的切向耦合刚度, 法向耦合刚度的影响很小; 弯曲型兰姆波则相反, 其更多是依赖法向刚度耦合.这也充分体现了拉伸波在套管中传播时以轴向位移为主, 弯曲型兰姆波在套管中传播时以法向位移为主.这一物理现象在套管和水泥环之间存在微环时也得以体现, 微环中流体的存在明显减弱了套管与水泥之间的剪切耦合, 使得拉伸波的衰减明显降低, 接近自由套管的衰减特征.对套后是轻质水泥时弯曲型兰姆波的衰减与胶结好时仍很接近, 对套后是常规水泥时衰减可由60 dB/m增加到100 dB/m以上, 也即微环的存在增强了套管与水泥之间的法向刚度耦合.
(3) 在固井质量评价时, 可综合拉伸波和弯曲型兰姆波的测量数据, 判定套管和水泥之间的胶结状况, 降低固井质量解释的多解性.在水泥封隔性能的评价时, 还需要进一步研究不同兰姆波的测井响应与水泥抗压强度、水力胶结强度以及剪切胶结强度之间的定量关系, 为水泥环的完整性评价提供支持.
Chen X L, Li J S, Tang X M, et al. 2016. The propagation characteristics of leaky flexural-Lamb waves in casing. Acta Acustica (in Chinese), 41(3): 296-304. |
Chen X L, Tang X M, Zhang C H, et al. 2015. Finite-difference numerical simulation and analysis on nonaxisymmetric acoustic fields in cased borehole. Chinese J. Geophys., 58(1): 318-326. DOI:10.6038/cjg20150129 |
Fehler M. 1982. Interaction of seismic waves with a viscous liquid layer. Bulletin of the Seismological Society of America, 72(1): 55-72. |
Froelich B. 2008. Multimode evaluation of cement behind steel pipe. The Journal of the Acoustical Society of America, 123(5): 3648. |
He X, Chen H, Wang X M. 2014. Ultrasonic leaky flexural waves in multilayered media:Cement bond detection for cased wellbores. Geophysics, 79(2): A7-A11. DOI:10.1190/geo2013-0361.1 |
Li J S. 2015. A fundamental research on the application of flexural Lamb waves in primary cement evaluation[Master's thesis] (in Chinese). Qingdao: China University of Petroleum (East China).
|
Patterson D, Bolshakov A, Matuszyk P J. 2015. Utilization of electromagnetic acoustic transducers in downhole cement evaluation.//SPWLA 56th Annual Logging Symposium. Long Beach, California, USA: Society of Petrophysicists and Well-Log Analysts.
|
Rose J L. 2004. Ultrasonic Waves in Solid Media (in Chinese). He C F, et al. Trans. Beijing: Science Press.
|
Schoenberg M. 1980. Elastic wave behavior across linear slip interfaces. The Journal of the Acoustical Society of America, 68(5): 1516-1521. DOI:10.1121/1.385077 |
Tang X M, Bolshakov A, Wang T, et al. 2009. Method and apparatus for cement bond evaluation using transversely polarized shear waves: US, 7525872 B2.
|
Tang X M, Jiang C, Su Y D, et al. 2018. An acoustic-wave theory for casing bond evaluation using viscoelastic slip boundary modeling. Science China:Earth Sciences, 61(8): 1057-1064. DOI:10.1007/s11430-017-9203-8 |
Wei T. 2010. Logging Evaluation of Cement Bonding in Cased Boreholes (in Chinese). Beijing: Petroleum Industry Press.
|
Xu F L, Hu H S. 2017. Inversion of the shear velocity of the cement in cased borehole through ultrasonic flexural waves. Geophysics, 82(2): D57-D68. DOI:10.1190/geo2016-0314.1 |
Zeroug S, Froelich B. 2003. Ultrasonic leaky-Lamb wave imaging through a highly contrasting layer.//IEEE Symposium on Ultrasonics, 2003. Honolulu, HI, USA: IEEE, 794-798.
|
Zhang H L. 2012. Theoretical Acoustics (in Chinese). 2nd ed. Beijing: Higher Education Press.
|
Zhang H B, Qin Z G, Sang Z P, et al. 2009. Amplitude features of formation wave in acoustic full waveform of casing wells. Progress in Geophysics (in Chinese), 24(3): 1006-1012. DOI:10.3969/j.issn.1004-2903.2009.03.026 |
陈雪莲, 李建赛, 唐晓明, 等. 2016. 套管中泄漏弯曲型Lamb波的传播特征. 声学学报, 41(3): 296-304. |
陈雪莲, 唐晓明, 张聪慧, 等. 2015. 套管井贴壁声源激发的非轴对称声场的有限差分模拟及结果分析. 地球物理学报, 58(1): 318-326. DOI:10.6038/cjg20150129 |
罗斯J L. 2004.固体中的超声波.何存福等译.北京: 科学出版社.
|
李建赛. 2015.弯曲型Lamb波在固井质量评价中的应用基础研究[硕士论文].青岛: 中国石油大学(华东).
|
唐晓明, 江灿, 苏远大, 等. 2018. 用黏弹滑移界面表征的固井声波测井理论. 中国科学:地球科学, 48(8): 1045-1052. |
魏涛. 2010. 油气井固井质量测井评价. 北京: 石油工业出版社.
|
张海澜. 2012. 理论声学. 2版. 北京: 高等教育出版社.
|
张宏兵, 秦正贵, 尚作萍, 等. 2009. 套管井声波全波列中地层波的幅度特性. 地球物理学进展, 24(3): 1006-1012. DOI:10.3969/j.issn.1004-2903.2009.03.026 |
 2020, Vol. 63
2020, Vol. 63


