2020, Vol. 63
表 1
(Table 1)
声波远探测中偏心声源的辐射以及接收波场研究
引用本文
许家旗, 胡恒山. 2020. 声波远探测中偏心声源的辐射以及接收波场研究. 地球物理学报, 63(9): 3545-3561,
doi: 10.6038/cjg2020N0015.
Xu J Q, Hu H S.
2020. Study on the radiation and reception of the wave field in a single-well imaging system with an eccentric source. Chinese J. Geophys. (in Chinese), 63(9): 3545-3561,
doi: 10.6038/cjg2020N0015.
声波远探测中偏心声源的辐射以及接收波场研究
哈尔滨工业大学力学系, 哈尔滨 150001
摘要：通过最速下降积分法获得了充液井孔中偏心点声源激发的井外波场的远场渐近解；利用互易性获得井外存在反射体时井内偏心接收的波场渐近解，渐近解结果与有限差分的结果吻合；分析了声源频率、偏心距离以及方位角对波场辐射与接收的影响.计算发现：声源频率是影响井外波场的主导因素，声源频率较低时，偏心点声源激发的远场波场与偏心距离无关，可以将偏心点声源视为中心声源；声源频率较高时，偏心点声源激发的远场波场与中心声源之间存在不可忽略的差异，且频率越高、偏心距离越大，差异越大.计算还发现：采用偏心声源与偏心接收时，辐射波场与接收波场的幅度都具有方位角依赖性.最后我们给出利用反射波幅度变化来消除反射体方位角180°不确定性的算例.
关键词:
偏心声源
渐近解
声波远探测
方位角
Study on the radiation and reception of the wave field in a single-well imaging system with an eccentric source
Department of Mechanics, Harbin Institute of Technology, Harbin 150001, China
Abstract: The far-field asymptotic solutions to the wave field excited by an eccentric point source in a fluid-filled borehole are derived by the steepest descent integration method. When there is a reflector outside the borehole, the asymptotic solution to the reflected wave field received by eccentric receivers in the borehole is obtained using reciprocity. The asymptotic results are in good agreement with those from the finite difference method. The effects of frequency and eccentric distance on the wave field are analyzed. Simulations show that frequency is the dominant factor affecting the wave field outside the borehole. When the frequency is low, the far-field wave field excited by the eccentric source is independent of eccentric distance, and the eccentric source can be regarded as a central source. When the frequency is high, the difference between the far-field wave field excited by the eccentric point source and the central source cannot be neglected. The higher the frequency and the greater the eccentric distance, the greater the difference is. Simulations also show that the amplitude of the radiated wave field and the received wave field are both azimuth-dependent when using the eccentric source and eccentric receivers. Finally, an example is given to show the elimination of the 180° uncertainty of azimuth angle of the reflector by using the variation of reflected wave amplitude.
Keywords:
Eccentric source Asymptotic solution Single-well imaging Azimuth
0 引言
5 声源和接收器偏心时远探测波场特征的分析
6 结论
声波远探测技术是近年来发展较快的技术, 可以对井外范围数十米的裂缝、断层、地质界面进行探测, 具有巨大的应用前景.多年来, 国内外对声波远探测方法开展了一系列研究(董经利等, 2020; 古希浩等, 2020; 郝仲田等, 2014; 张义德和胡恒山, 2014), Hornby在1989年从阵列波数据中提取处反射波, 并利用偏移的方法得到了井旁地层结构变化的图像(Hornby, 1989).1998年, Schlumberger公司推出了反射波成像测井仪(Geoquest, 1998).国内, 薛梅(2002)、乔文孝等(2004)、何峰江(2005)针对单极源条件下的反射波成像问题展开了一系列研究.但是, 单极子声波远探测无法识别反射体的方位, 且单极子源较高的声源频率造成其探测范围有限.针对单极子声源存在的不足与问题, Tang(2004)首次提出了用偶极子声源来进行声波远探测.Tang和Patterson(2009)利用四分量偶极数据对井旁裂缝和盐丘内部的精细构造进行了成像.Wei和Tang(2012)采用有限差分模拟了偶极源远探测中波弹性波的辐射、反射以及接收系数, 发现：SH波有较大的辐射范围以及较强的接收敏感度, 适合反射波成像; 在慢速地层中, P波也有较强的接收敏感度, 也可用来反射波成像.Tang等(2014)给出了偶极源声波远探测中反射波位移的渐近解可以快速模拟声波远探测问题.尽管偶极源声波远探测与单极源声波远探测相比, 声源具有一定的方向指向性, 但是仍然存在反射体方位角180°不确定性的问题.为了唯一确定反射体的方位角, 在单极源声波远探测中, Zhang和Hu(2014)提出同时接收位移和声压信号来消除方位角的不确定性.针对偶极源声波远探测, Gong等(2015)提出利用三分量位移传感器接收反射波场, 以达到消除方位角不确定的目的.另外一种消除方位角不确定性的技术是环向布置4个(Yamamoto et al., 2000; Borl and et al., 2005; Haldorsen et al., 2005)或者8个接收器(Haldorsen et al., 2006; Hirabayashi et al., 2017)全方位接收反射波的信号来确定反射体的方位角.
为了消除方位角的不确定性, 我们提出在井中放置偏心点声源来唯一确定反射体的方位角.前人对偏心声源激发的井内声场开展了大量研究(Zhang et al., 1996; 沈建国和张海澜, 2000; Byun and Nafi, 2006; Pardo et al., 2013), 发现利用偏心点声源可以用来测量快速地层各向异性(Chen et al., 2010; Nwosu et al., 2015; Sakiyama et al., 2016).Wang等(2011)研究了偏心点声源在慢地层井孔中激发的声场, 并将其与偶极子和四极子仪器的模拟结果比较, 认为偏心点声源可以近似为单极子声源、偶极子声源的叠加或者单极子声源、偶极子声源和四极子声源的叠加.以上的研究集中在偏心点声源激发的井内场, 对于偏心点声源激发的井外波场还未见研究.
本文中, 我们首先通过最速下降积分法获得井内偏心点声源的远场辐射场, 在此基础上分析声源频率、偏心距离对辐射场的影响, 并研究井外辐射波场随方位角变化特征, 提出利用偏心和接收器同时偏心来识别反射体方位角的方法, 并通过互易关系获得该条件下的井内接收反射波场的渐近解, 并与有限差分数值解进行比较, 分析接收波场随方位角的变化特征.最后给出算例模拟当声源与接收器都发生偏心时, 利用反射波幅度变化来消除反射体方位角180°不确定性.值得注意的是：通常偏心是希望减少却又常常发生的, 一般认为是引起误差的因素.故测井仪一般带有扶正器.但本文恰恰利用偏心效应来反映方位.那么, 就必须实时实场确定发射器、接收器在井中的位置(偏心多少).
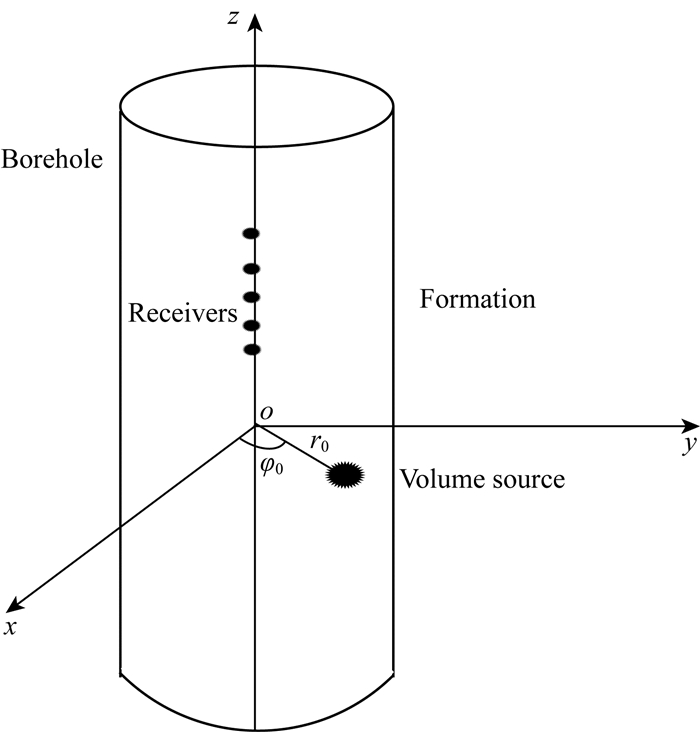
1 井中偏心声源激发的井外位移的远场渐进解将一个膨胀点声源偏心放置在充液井孔中, 声源的坐标为(r0, φ0, 0), 如图 1所示.点声源由体积改变V0G(t)来描述, 其中V0是体积变化量, G(t)是声源的时间函数.在本研究里, 傅里叶变换表达式为
|
图 1 充液井孔中偏心声源模型图 Fig. 1 Model of an eccentric source in a fluid filled borehole |
|
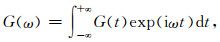
(1) |
根据Kurkjian和Chang (1986)中式(3), 并利用第二类贝塞尔函数与汉克函数的关系, 流体势函数表达为
|
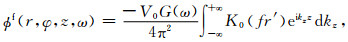
(2) |
其中,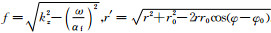 
|
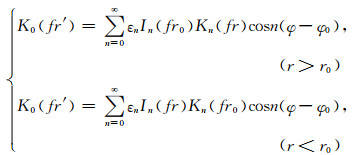
(3) |
其中εn是纽曼因子, 当n=0时为1, 其余的情况值为2.In和Kn分别是第一类, 第二类n阶变型贝塞尔函数.
将方程(3)代入(2)中得：
|
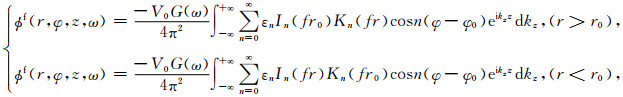
(4) |
流体中反射波的位移势为
|
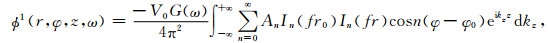
(5) |
其中An为反射波位移势的待定系数.则流体中的总位移为
|
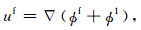
(6) |
其中, 
|
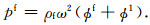
(7) |
由偏心单极源激发的井外位移的通解为(Zhang et al., 1996)：
|
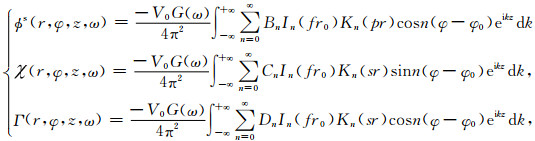
(8) |
其中,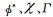 
|
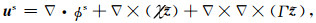
(9) |
其中, 
|
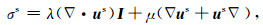
(10) |
其中, λ=ρ(α2－2β2), μ=ρβ2.ρ、α、β分别是井外地层的密度, 纵波、横波速度.系数An、Bn、Cn、Dn通过井壁处的边界条件来确定：在井壁处径向位移和正应力连续：
|
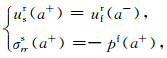
(11) |
以及切应力为零：
|
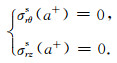
(12) |
将方程(4)—(7)和(8)—(10)代入边界条件(11)—(12)得到(Tang and Cheng, 2004)：
|
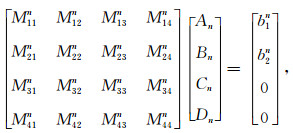
(13) |
其中Mijn(i, j≤4)和b1n, b2n的具体表达式在附录A里给出.对于任意的n值, 系数An、Bn、Cn、Dn由与n值相对应的方程(13)给出.
获得系数后, 方程(8)中的井外势函数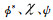
|
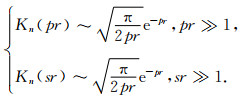
(14) |
将(14)代入(8)中, 采用最速下降积分法来计算波数域积分(Aki and Richards, 1980), 最终得到：
|
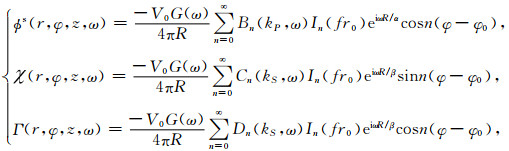
(15) |
其中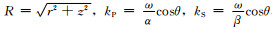
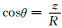
从(15)中看出, 偏心点源激发的井外场可以等效为不同阶声源的激发声场的叠加.在本文中, 井外位移场的时间-空间表达为
|
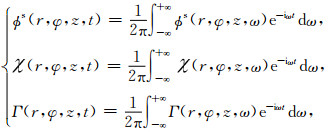
(16) |
(16) 式通过快速傅里叶变换(FFT)计算.
接下来我们模拟分析不同频率和偏心距离下井外远场波场的变化规律.
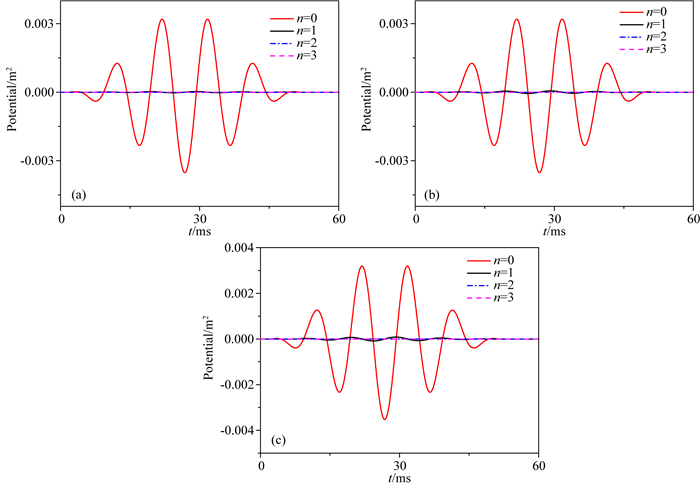
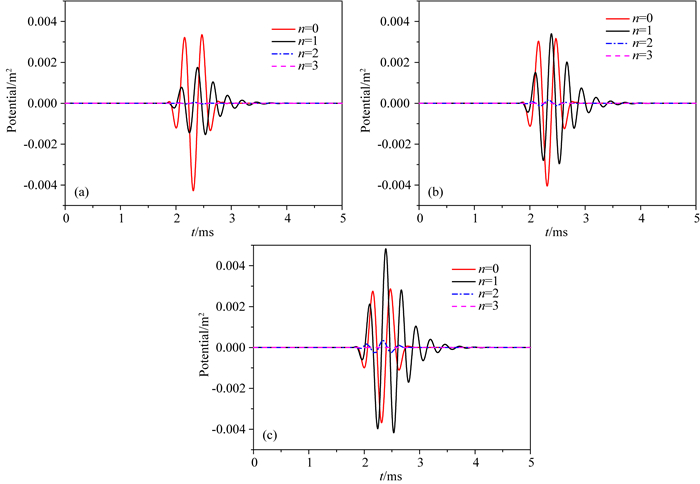
2 井外远场位移的数值模拟和分析在本章节中, 我们将计算模拟偏心点源的井外波场.井孔半径a为0.1 m, 井内流体和地层参数由表 1给出, 地层采用表 1中的快速地层1, 声源信号采用余弦包络脉冲.为了研究频率对井外波场的影响规律, 余弦包络脉冲的中心频率分别采用0.1 kHz和3 kHz, 偏心距离分别取0.02 m、0.04 m、0.06 m.不失一般性, 将单极源的偏心方位角φ0设为0°.当声源频率为100 Hz, 声源偏心距离分别为0.02 m、0.04 m和0.06 m时, 图 2给出了在井外远场一点(z=2 m, r=5 m, φ=30°)接收到的P波波场前四阶分量的波形图.从图 2看出, 声源中心频率取0.1 kHz时, 无论偏心距离取何值, 波形的主要贡献来自零阶分量(n=0)而高阶分量的值几乎为零.这是因为声源频率较低, 波长远大于井孔的几何尺寸, 因此井孔对偏心单极源的辐射场的影响可以忽略.在远场位置, 由于偏心距离远小于坐标原点与观测点之间的距离(r0/R≈0.005~0.02), 进而偏心对波场的影响可以忽略.当声源中心频率为3 kHz, 声源偏心距离分别为0.02 m、0.04 m和0.06 m时, 图 3给出了井外一点(z=2 m, r=5 m, φ=30°)的P波场前四阶分量的波形图.从图 3中我们发现：除了零阶分量波, 高阶分量波对于井外P波也有贡献, 并且当偏心距离增大时, 高阶分量波所占的比例也随之增加.从图 3c中看出, 当偏心距离为0.06 m时, 一阶分量波(n=1)的幅值甚至大于零阶分量波(n=0).增加井中偏心单极源的频率, 井孔的几何尺寸变得与波长相当, 在这种条件下, 由于井孔带来的偏心效果对井外远场波场辐射有较大的影响.因此当声源频率增加时, 为了获得精确的井外远场波场, 需要考虑高阶分量波的贡献, 并且偏心距离越大, 高阶分量的贡献越大, 需要考虑的高阶分量越多.
|
表 1 井外流体和地层参数 Table 1 Parameters of borehole fluid and formations |
|
图 2 低频声源辐射的井外远处P波的前4阶分量 (a) r0=0.02 m; (b) r0=0.04 m; (c) r0=0.06 m.偏心声源中心频率为0.1 kHz. Fig. 2 The first four components of far-filed P wave waveforms outside the borehole with low-frequency source (a) r0=0.02 m; (b) r0=0.04 m; (c) r0=0.06 m.The central frequency of eccentric source is 0.1 kHz. |
|
图 3 中频声源辐射的井外远场P波波场的前4阶分量 (a) r0=0.02 m; (b) r0=0.04 m; (c) r0=0.06 m.偏心声源中心频率为3 kHz. Fig. 3 First four order components of far-filed P wave waveforms outside the borehole with moderate-frequency source (a) r0=0.02 m; (b) r0=0.04 m; (c) r0=0.06 m. The central frequency of eccentric source is 3 kHz. |
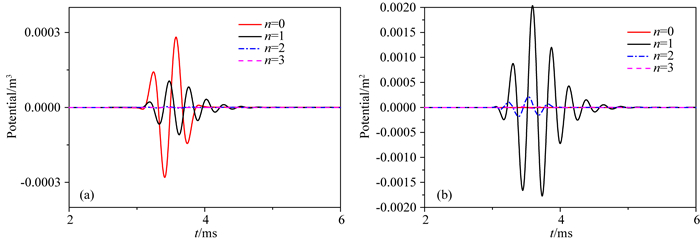
以上是对井外远场纵波的分析, 下面我们研究声源偏心时井外远场横波的各阶分量的贡献.当单极源的频率为3 kHz, 偏心距离为0.02 m时, 图 4给出了井外一点(z=2 m, r=5 m, φ=30°)的SV波与SH波的前四阶分量.当单极源发生偏心时, 高阶分量对井外横波也有贡献.除了P波和SV波外, 偏心单极源也激发出了SH波, SH波的零阶波分量(n=0)为零, 一阶波分量(n=1)幅度最大.从图 3a和图 4c中可以看出偏心声源激发出SH波的量级与P波相当.
|
图 4 中频声源辐射的井外远场S波波场的前4阶分量 (a) SV波; (b) SH波.偏心声源中心频率为3 kHz, 偏心距离为0.02 m. Fig. 4 First four order components of far-filed S wave waveforms outside the borehole with moderate-frequency source (a) SV wave; (b) SH wave. The central frequency of eccentric source is 3 kHz and r0=0.02 m. |
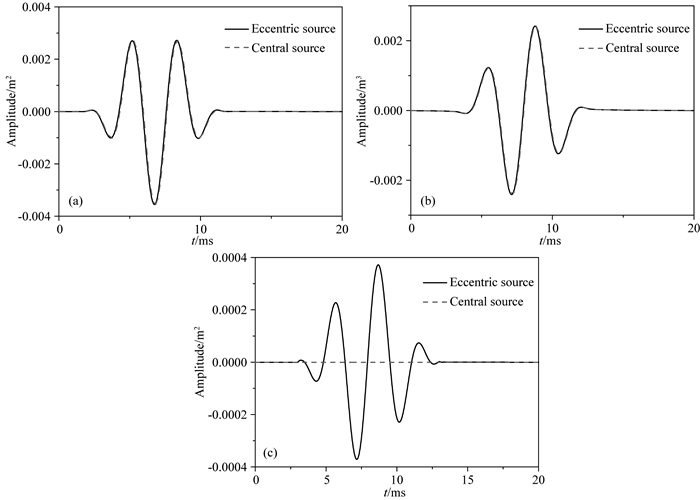
根据以上的分析, 计算偏心声源激发的井外波场时采用前四阶分量已经足够精确, 因此在接下的波场模拟中我们只取波场的前四阶分量的贡献.为了进一步阐明声源频率和偏心距离对波场的影响, 我们比较不同频率下偏心声源与中心声源激发波场之间的差异.当声源中心频率为0.3 kHz时, 声源位于井轴和发生偏心时(偏心距离r0=0.08 m), 井外地层为表 1中的快速地层1, 图 5给出了井外一点(z=2 m, r=5 m, φ=30°)接收到波场.从图中看出：偏心声源激发的P波和SV波波形与中心声源相同.虽然偏心点声源激发出了SH波而中心点声源的SH波为零, 但从图 5中看出偏心声源激发出的SH波幅值与P波以及SV波相比较小可以忽略.当声源频率在几百赫兹甚至更低时, 即使声源发生较大的偏心, 我们仍可以将偏心点声源视为居中声源.例如在井间勘探时(声源频率在几百赫兹)声源发生不可避免或者未知偏心时, 我们仍可以认为声源是居中放置的来进行波场的正演模拟而不至于产生误差.
|
图 5 低频时偏心源与居中源激发的井外波场比较 (a) P波; (b) SV波; (c) SH波.声源中心频率为0.3 kHz, r0=0.08 m. Fig. 5 Comparison between wave fields outside borehole generated by eccentric source and central source with low frequency (a) Pwave; (b) SVwave; (c) SHwave. The central frequency of source is 0.3 kHz and r0=0.08 m. |
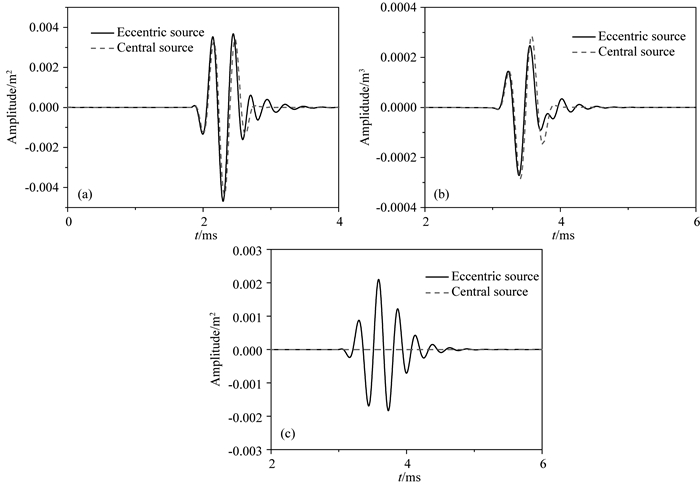
当声源频率为3 kHz时, 偏心声源(偏心距离为0.02 m)与中心声源激发的井外远场一点(z=2 m, r=5 m, φ=30°)处波场对比由图 6所示.从图中可以看出, 二者激发出的井外P波与SV波有所差异, 且偏心声源激发出了SH波, SH波的幅度与P波量级相当.声源频率提高时, 即使发生较小的偏心, 偏心声源与中心声源激发的井外远场波场之间的差异不可忽略.当进一步提高声源频率, 其余参数不变, 图 7给出了声源中心频率为5 kHz时偏心声源与中心声源激发的井外波场.比较图 7与图 6中看出, 提高声源的中心频率, 偏心声源与居中声源辐射波场之间的差异也增大.
|
图 6 中频时偏心源与居中源激发的井外波场比较 (a) P波; (b) SV波; (c) SH波.声源中心频率为3 kHz, r0=0.02 m. Fig. 6 Comparison between wave fields outside borehole generated by eccentric source and central source with moderate frequency (a) P wave; (b) SV wave; (c) SHwave. The central frequency of source is 3 kHz and r0=0.02 m. |
|
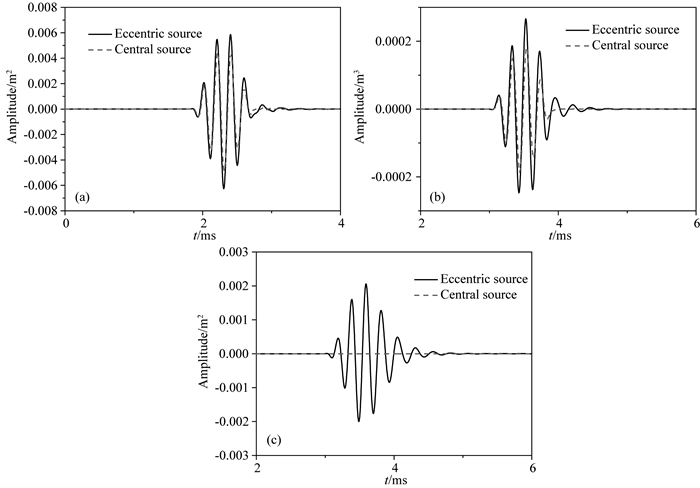
图 7 高频时偏心源与居中源激发的井外波场比较 (a) P波; (b) SV波; (c) SH波.声源中心频率为5 kHz, r0=0.02 m. Fig. 7 Comparison between wave fields outside borehole generated by eccentric source and central source with high frequency (a) P wave; (b) SV wave; (c) SHwave. The central frequency of source is 5 kHz and r0=0.02 m. |
由上述分析, 我们发现：声源频率和偏心距离影响偏心声源的远场辐射波场.其中, 声源频率是主导因素, 当声源频率较低时, 井孔效应可以忽略, 在这种情况下偏心距离对远场辐射场没有影响, 偏心声源可以视为中心声源; 当声源频率较高时, 井孔对声源辐射有影响, 偏心声源与中心声源产生的井外远场波场之间有所差异, 且偏心距离越大差异越大.
3 偏心点声源远场辐射波场的方位特征
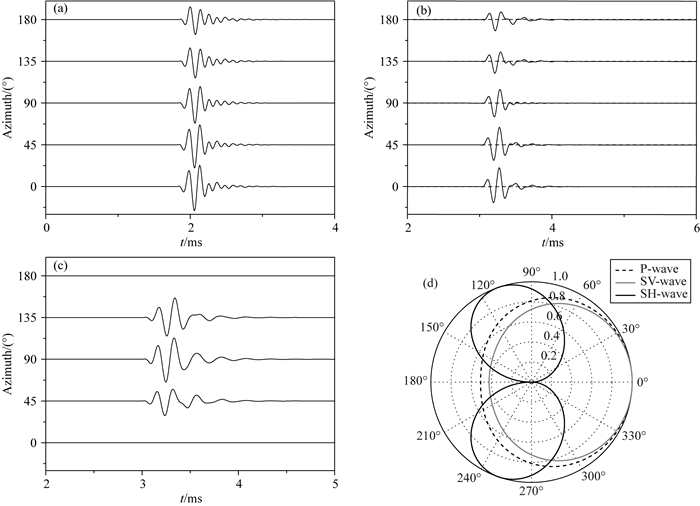
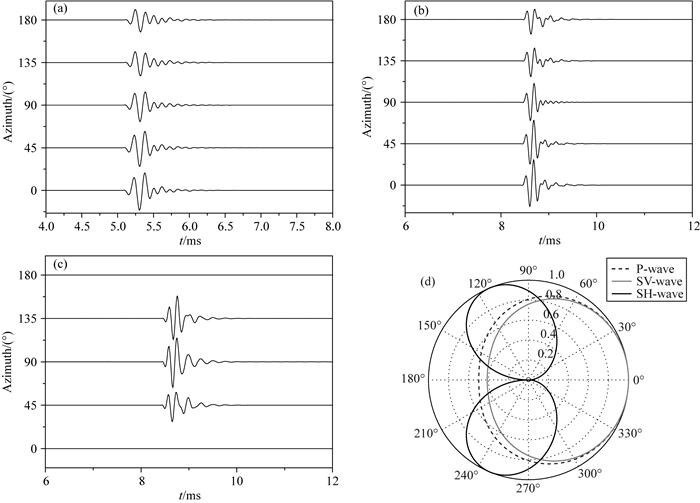
当点声源位于井轴上时, 由于声源与井孔的轴对称性, 辐射波场不依赖于方位角.因此在单井声波远探测时, 采用居中点声源无法获知井外反射界面的方位角(Hornby, 1989; Tang and Patterson, 2009).在本章节中, 我们研究方位角对偏心点声源远场辐射波场影响, 声源频率为6 kHz, 偏心距离为0.02 m, 声源的方位角φ0=0°.在本模型中偏心点声源位于x轴上, 整个波场关于x轴对称, 因此方位角φ取180°~360°时的波场与方位角φ为0°~180°时关于x轴对称, 为了方便只给出方位角在0°~180°范围内的波场计算结果.为了清晰地显示偏心点声源的远场辐射特征, 同时根据(15)式给出相应的归一化的波场指向图.图 8给出了快速地层1中5个沿环向均匀分布的接收器的接收波形图以及指向图, 接收器的轴向坐标z=2 m, 径向坐标r=5 m, 方位角φ分别为0°~360°.从图 8中可以看出, 在0°~180°范围内井外远场P波幅度随着方位角增大而减小：当方位角为0°, P波幅度达到最大; 方位角为180°时, P波幅度达到最小.SV波幅度随方位角的变化规律与P波相同.而SH波幅度在方位角为90°~120°之间时达到最大, 在方位角为0°和180°时幅度为零.当井中声源存在偏心时, 即使偏心距离r0与辐射距离
|
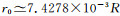
图 8 快速地层中不同方位角下的接收器接收到的波场和归一化波场辐射图 (a) P波; (b) SV波; (c) SH波; (d)远场辐射图.接收器的坐标位置为z=2 m, r=5 m, φ=0~360°. Fig. 8 Waveforms received by receivers with different azimuths in the fast formation and normalized radiation patterns (a) P wave; (b) SV wave; (c) SH wave; (d) Far-field radiation pattern.The positions of receivers are z=2 m, r=5 m, φ=0~360°. |
|
图 9 快速地层中不同方位角下的接收器接收到的波场和归一化波场辐射图 (a) P波; (b) SV波; (c) SH波; (d)远场辐射图.接收器的坐标位置为z=2 m, r=15 m, φ=0~360°. Fig. 9 Waveforms received by receivers with different azimuths in the fast formation and normalized radiation patterns (a) P wave; (b) SV wave; (c) SH wave; (d) Far-field radiation pattern. The positions of receivers are z=2 m, r=15 m, φ=0~360°. |
|
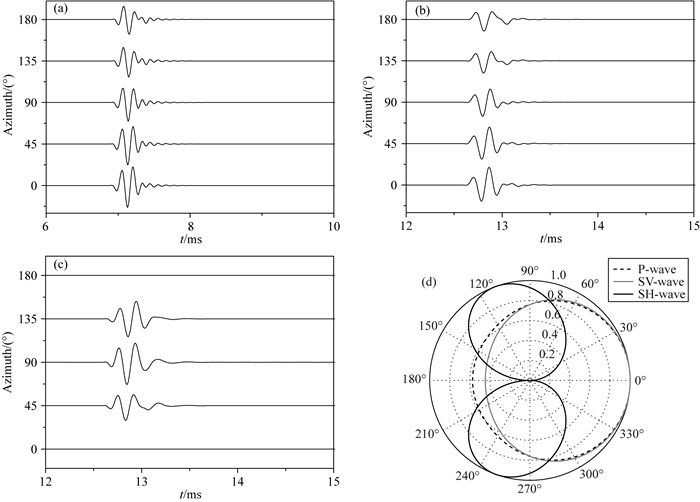
图 10 慢速地层中不同方位角下的接收器接收到的波场和归一化波场辐射波 (a) P波; (b) SV波; (c) SH波; (d)远场辐射图.接收器的坐标位置为z=2 m, r=15 m, φ=0~360°. Fig. 10 Waveforms received by receivers with different azimuths in the slow formation and normalized radiation patterns (a) P wave; (b) SV wave; (c) SHwave; (d) Far-field radiation patterns.The positions of receivers are z=2 m, r=15 m, φ=0~360°. |
经过上述分析, 当频率较高时, 偏心点声源的远场辐射波具有如下方位特性：沿偏心声源的偏心方向, 远场辐射P波与SV波的幅度最大, 而SH波幅度为零; 沿偏心声源的偏心反方向, 远场辐射P波与SV波的幅度最小, SH波幅度为零; 沿垂直偏心点声源的偏心方向附近, 远场辐射SH波的幅度较大.单极源的辐射波方位性质可以应用在声波远探测中来识别反射界面方位, 目前偶极源声波远探测仍然存在方位角存在180°不确定性的问题(Tang, 2004; Tang and Patterson, 2009).而采用偏心点声源时, 当方位角发生180°改变时, 辐射P波和SV波的幅度会发生改变, 对于同一个反射界面, 对应反射波的幅度也会发生改变.井内声源为偏心声源并在井中放置单极接收器记录反射波激发的声压信号, 当反射体方位角为零时, 反射信号的幅度达到最大值, 当反射界面方位角为180°时, 反射信号的幅度达到最小值.这样就能通过比较反射信号的幅度来解决远探测中反射体方位角180°不确定性的问题.
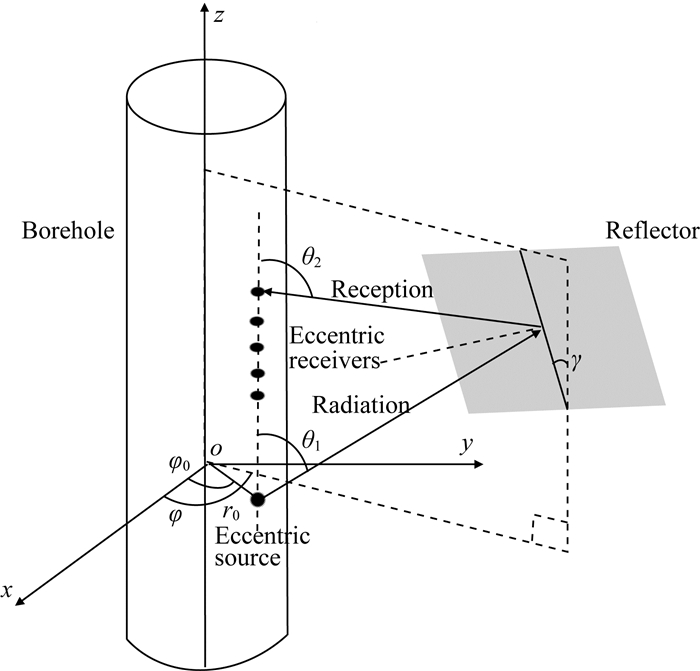
4 远探测时反射回波声场解析解在上文中, 我们已经分析了偏心点声源的远场辐射特征, 发现了：偏心点声源激发的井外波具有方位角依赖性.当方位角发生180°变化时, 辐射波的幅度发生明显的变化, 可用来识别井外反射体的方位角.根据弹性波辐射与接收的互易性, 偏心放置的接收器接收的反射波应该也具有方位角依赖性.如图 11所示, 井内的声源与接收器都偏心放置, 且接收器与声源的偏心距离以及偏心方向相同, 井外存在一个反射体, 反射体的倾角为γ, 方位角为φ.由于结构与声源的非轴对称性, 很难获得反射波场的解析解, 采用有限差分计算耗费大量的时间.为了快速计算反射波场, 我们利用互易原理在已知偏心声源激发井外波场的基础上求解反射波场的渐近解.将远场的位移势函数(15)代入式(9)并省略高阶项得到：
|
图 11 含偏心声源和偏心接收器的声波远探测模型图 Fig. 11 Single-well imaging model with eccentric source and eccentric receivers |
|
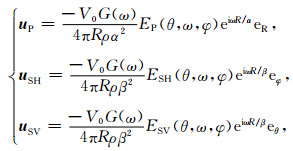
(17) |
其中uP、uSH和uSV分别是球坐标系下的P波、SH波和SV波的位移.EP(θ, ω, φ), ESH(θ, ω, φ)和ESV(θ, ω, φ)是辐射系数:
|
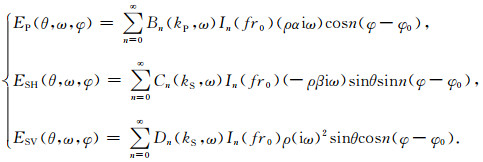
(18) |
当井外反射体的尺寸远大于波长时, 可以将其近似为一个无限大平面.偏心声源辐射的球面波在反射体处发生反射, 当反射平面距离声源较远时, 反射波为(Aki and Richards, 1980)：
|
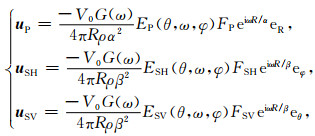
(19) |
其中FP、FSH和FSV是与入射角相关的平面波反射系数, 可由Zoeppritz方程计算(Aki and Richards, 1980).如图 11所示, 反射回来的弹性波被井中偏心放置的单极接收器接收, 在声波远探测的频率内, 井孔对弹性波的作用不可忽略, 直接求解反射波激发的井内声压比较困难(Schoenberg, 1986; Peng, 1994).在本文中可以利用互易关系(Xu et al., 2019)获得井内偏心放置的接收器接收的井内声压：
|
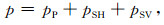
(20) |
其中：
|
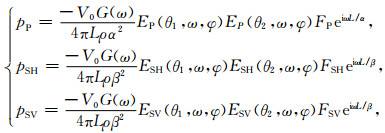
(21) |
式(20)中θ1是辐射波与井轴的夹角, θ2是反射波与井轴的夹角.从上式可以看出, 采用偏心声源激发, 偏心单极接收器接收的声压信号由三部分构成, 分别是反射P波, 反射SV波以及反射SH波.指的注意的是, 式(20)是声源和接收器都偏心情况下的渐近解, 如果令声源或者接收器的偏心距离r0=0, 便可求解声源居中, 接收器偏心时的反射波或者声源偏心, 接收器居中的反射波.更为特殊的情况时仪器与声源的偏心距离都为零, 此时式(20)对应单极源声源, 单极接收器接收到的反射波.
为了验证渐近解的正确性, 我们在(20)中取r0=0 m, 此时渐近解对应声源与接收器都位于井轴上的特殊情况.我们通过三维时域有限差分方法(Wang and Tang, 2003; 王治, 2016; 杨玉峰等, 2016)模拟井外存在反射界面时井内接收的波场, 并与渐近解获得的结果进行比较.如图 12所示, 井孔半径为0.1 m, 声源中心频率为5 kHz, 声源与接收器都位于井轴上, 接收器与发射器之间的距离为0.4~1.8 m, 接收器之间的距离为0.2 m, 反射界面与坐标原点之间的距离为1.5 m, 反射界面的倾角γ=0°, 方位角φ=0°.把反射界面与声源的距离取的较小的目的一是为了减少有限差分所需要的时间, 二是为了说明远场渐近解在界面离井孔近时是否可靠.模型中慢速地层, 快速地层2以及井中流体参数见表 1.
|
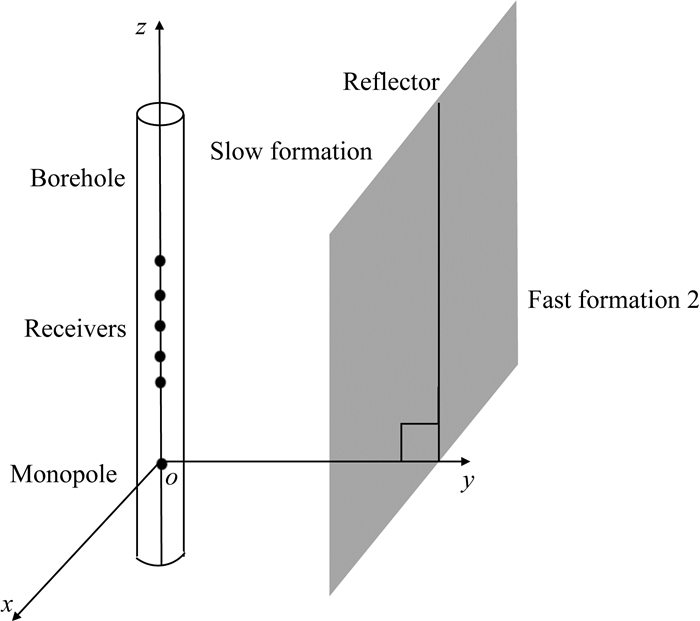
图 12 声源与接收器都位于井轴时的远探测示意图 Fig. 12 Sketch of remote detection with source and receivers located at the borehole axis |
图 13给出了有限差分模拟的井外存在反射界面井内声压全波图.通常界面距离井轴较远(10 m或者数十米), 因此源距要比界面距离井轴的距离小很多.而在本算例中为了节省计算时间并验证渐近解在界面距离井轴近时的准确性, 界面距离设为1.5 m, 因此为了与实际的情况一致, 源距不宜取得过大, 源距最大取1.8 m.从图 13中可以看出, 全波信号中幅度最大的波群是井孔导波波群.从图中也可以看出, 来自井外界面的反射波幅度相对于井孔斯通利波幅度较小, 随着源距增大会淹没在斯通利波群中.为了与渐近解比较, 我们将反射波从全波信号中分离出来, 可以通过将全波信号减去井孔直达波信号得到反射波信号.图 14同时给出了分别由渐近解与数值解得到的反射波形.从图 14中可以看出, 渐近解的计算的反射P-P、SV-SV波与数值解吻合较好, 这说明了在反射界面离井孔较近时远场渐近解计算的反射P-P与SV-SV也是正确的.
|
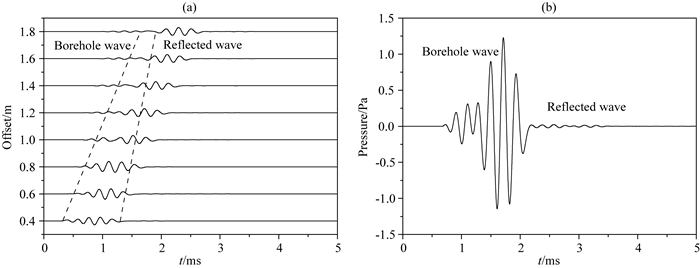
图 13 井轴处接收到的声压全波波形 (a)归一化的全波阵列图; (b)源距1.2 m处接收的声压全波波形.声源中心频率为5 kHz. Fig. 13 Full waveforms of the acoustic pressure at the borehole axis (a) Normalized full waveforms of acoustic pressure; (b) Full waveform of the acoustic pressure at 1.2 m. The central frequency of eccentric source is 5 kHz. |
|
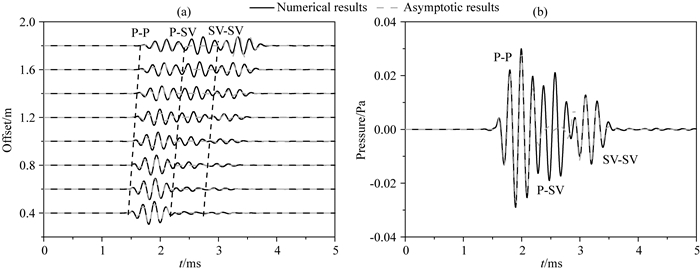
图 14 反射波渐近解与数值解的对比 (a)归一化声压反射波阵列图; (b)源距1.2 m时声压反射波波形.声源中心频率为5 kHz. Fig. 14 Comparison between asymptotic solutions and numerical solutions to reflected waves (a) Normalized waveforms of reflected wave; (b) Waveform of reflected wave at 1.2 m. The central frequency of eccentric source is 5 kHz. |
渐近解与数值解之间的差异来自与反射P-SV的贡献, 因为在渐近解中没有计算转换波, 随着源距的增大, 转换波的幅度逐渐增大.但是在源距较小时, 转换波幅度较小可以忽略, 这从全波阵列中可以看出.值得注意的是：实际的声波远探测条件下, 界面通常距离声源较远, 此时波的传播距离远大于源距, 转换波的幅度很小, 因此采用渐近解计算而忽略转换波的贡献是可行的.
接下来我们利用渐近解来模拟井外存在距离较远的反射体井内接收的反射信号.首先我们研究反射体方位角对接收信号的影响, 反射体的倾角为15°, 反射体距离坐标原点15 m, 反射体的方位角分别为0°~180°, 声源频率为6 kHz, 声源与接收器的偏心距离r0=0.03 m, 接收器与发射器的距离为4 m.计算采用的模型参数见表 1.图 15是不同方位角时, 井内偏心单极接收器接收到的声压信号.从图中可以看出, 井内接收器接收的反射波信号有两个波群, 分别是P波波群和S波波群.从图 15a中可以看出：接收的P波信号幅值随方位角的增大而减小, 这与偏心声源辐射P波随方位角的变化规律相同; 接收的S波信号幅值随方位角的增大先增大后减小, 这是因为接收的S波信号由SH波信号与SV波信号共同构成.图 15b、c分别给出了不同方位角时的SH波信号和SV波信号.接收的SH波信号的幅度随方位角增大先增大后减小, 在方位角为90°时达到最大, 在方位角为0°和180°时为零.接收的SV波信号的幅度随方位角增大而减小.综上所述, 接收的P、SH以及SV波信号随方位角变化的规律与辐射声波的变化规律一致, 且由于声源和接收器都是偏心放置, 接收的反射波信号对方位角的敏感度相比于偏心声源的辐射波增加.
|
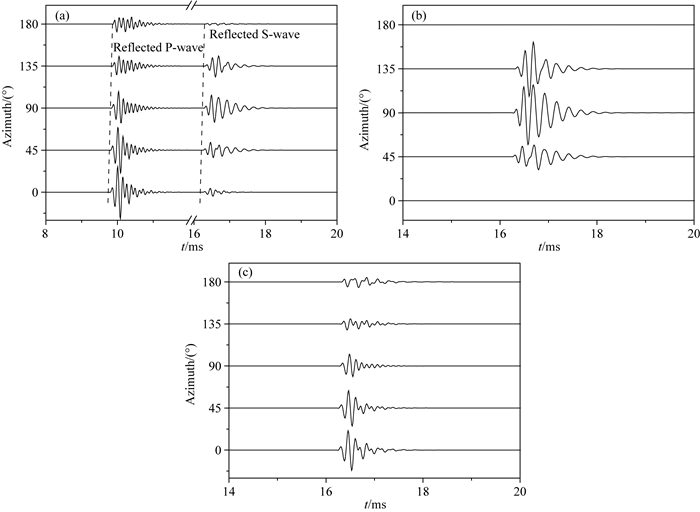
图 15 不同方位角反射体时井内接收器接收到反射波波形 (a)反射全波; (b)反射SH波; (c)反射SV波.偏心声源中心频率为6 kHz. Fig. 15 Reflected waveforms from the reflectors with different azimuths (a) Reflected full wave; (b) Reflected SH wave; (c) Reflected SV wave. The central frequency of eccentric source is 6 kHz. |
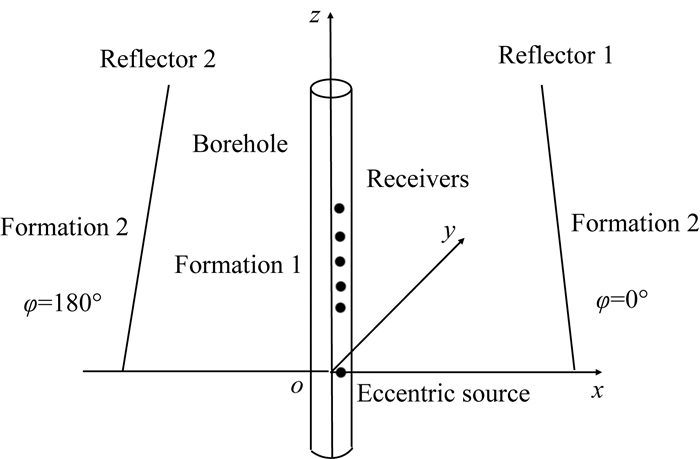
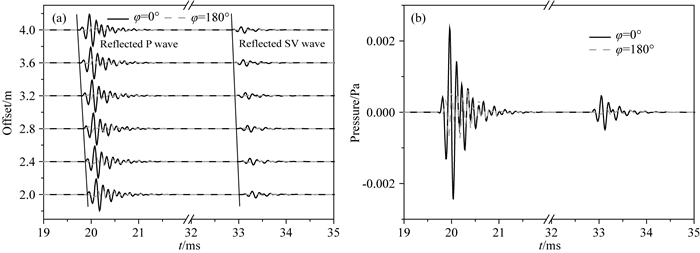
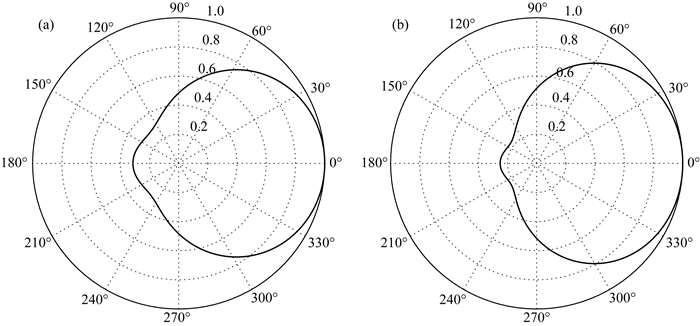
在本节中, 我们利用获得渐近解模拟井外存在反射界面时偏心声源激发偏心接收器接收到的反射全波阵列信号, 并阐明如何通过反射波来消除反射体方位角180°的不确定性.如图 16所示, 井孔半径为0.1 m, 声源与接收器的偏心距离为0.03 m, 偏心方位角为φ0=0°, 中心频率为6 kHz.接收器与发射器之间的距离为2~4 m, 接收器之间的距离为0.4 m.为了阐明方位角变化对反射波场的影响, 井外两个反射界面1、2的方位角分别0°和180°, 反射界面的倾角都为15°.反射界面与坐标原点之间的距离为30 m.模型中地层1, 地层2以及井中流体参数见表 1.图 17给出了分别来自井外两个反射界面的反射全波波形图, 其中灰色虚线是来自方位角为0°的反射界面的反射波, 黑色实线是来自方位角为180°的反射界面的反射波.从图中可以看出, 来自偏心点声源同侧的地层界面(方位角为0°)的反射波幅度显著大于来自偏心点声源异侧的地层界面(方位角为180°)的反射波幅度.值得注意的是, 当反射体方位角为0°或者180°时, 反射波信号里没有SH波信号, 所以井内声压信号只与P波以及SV波有关.图 18给出了反射界面距离声源30 m时, 接收波场的归一化指向图, 从图中可以看出, 采用偏心声源与偏心接收器时反射体方位角为180°时的幅度远小于方位角为0°时的幅度.在本次模型计算中反射体与井轴的距离为30 m, 接收到的声压信号仍然具有方位角依赖性.实际上从式(20)中就可以看出接收声压的方位角依赖性与距离无关.因此采用偏心声源和偏心接收器的收发方式可以用来消除声波远探测中反射界面方位角180°不确定性来唯一确定地层界面的方位.
|
图 16 井旁界面反射体模型图 Fig. 16 Interface reflection model outside a borehole |
|
图 17 方位角相差180°时井内接收器接收到反射全波 (a)归一化的反射全波阵列图; (b)收发距离为4m时反射全波. Fig. 17 Reflected waveforms with azimuth difference between the reflectors as 180° (a) Normalized reflected waveforms; (b) Waveforms of reflected wave at 4 m. |
|
图 18 声源与接收器时发生偏心时接收到的归一化反射波指向图 (a)反射P波的指向图; (b)反射SV波的指向图. Fig. 18 Normalized reception patterns of reflected waves when source and receiver are eccentric (a) Reception pattern of reflected P-waves; (b) Reception pattern of reflected SV-wave. |
本研究首先通过最速积分法获得了充液井孔中偏心点声源激发的井外远场声场的渐近解, 并分析了声源频率与偏心距离对辐射声场的影响, 然后通过互易关系获得了井内偏心接收的反射波场的渐近解.研究发现：声源频率是影响偏心点声源的主导因素.当声源频率较低时(300 Hz或者更低), 偏心点声源激发的高阶分量波的贡献可以忽略.在低频时, 偏心点声源激发的井外远场波场与偏心距离无关, 我们可以将其视为位于井轴上的声源; 当声源频率较高时(3 kHz或者更高), 即使偏心距离很小, 偏心点声源激发的井外波场高阶分量波的贡献也不可忽略, 且高阶分量波的贡献随偏心距离与声源频率的增加而变大.在声源频率较高时, 对于井外P波以及SV波, 偏心点声源与居中声源之间的差异不可忽略, 且偏心点声源激发出了SH波.
频率较高时, 偏心点声源激发的井外远场波场随方位角变化.激发P波和SV波在沿偏心点源的偏心方向幅度最大, 在沿偏心点声源的偏心反方向上幅度较小; 激发的SH波在与声源偏心方向垂直的方向附近处幅度最大, 在沿声源的偏心方向上幅度为零.偏心点声源激发波场随方位角变化的特征可以用来识别井外反射体方位角.
根据偏心点声源辐射波场的随方位角变化特征, 提出了在声波远探测中采用偏心声源发射, 偏心接收器接收的方法.通过互易性获得了该条件下的渐近解, 并将渐近解退化到居中声源, 居中接收的特殊情况与有限差分的结果进行了比较, 渐近解与数值解吻合较好.值得注意的是, 当声源偏心接收器位于井轴或者声源位于井轴接收器偏心时也可用该方法求解.渐近解与数值解之间的误差来自于转换波的贡献, 当反射界面距离声源的距离相对于源距较大时, 转换波的贡献是可以忽略的.分析了当反射体距离界面较远时(十几米或者数十米)接收波场随方位角的变化, 发现：接收的反射P波和S波信号幅值随方位角的增大而减小, 接收的反射SH波信号随方位角的增大先增大后减小.接收波场随方位角的变化规律与偏心声源辐射波场随方位角变化规律相同, 且由于声源与接收器都是偏心放置, 波场对方位角的敏感度较高.值得注意的是, 接收波场对方位角的敏感度不依赖于反射体距声源的距离.
最后我们利用渐近解模拟了井外30 m处反射体方位角发生180°变化时, 井内接收的波场响应.结果发现：即使在较远的距离, 反射体方位角发生180°, 井内接收的反射波幅度仍发生明显的变化, 说明同时利用声源和接收器的偏心接收可以消除反射体方位角的180°不确定性来唯一确定声波远探测时的方位角在理论上可行的.实际地层的黏性耗散会影响接收到的反射波幅度和波形, 因此, 计算和分析耗散介质中的反射波是有待开展的研究.
附录AMijn(i, j≤4)和b1n、b2n的具体表达式为
|
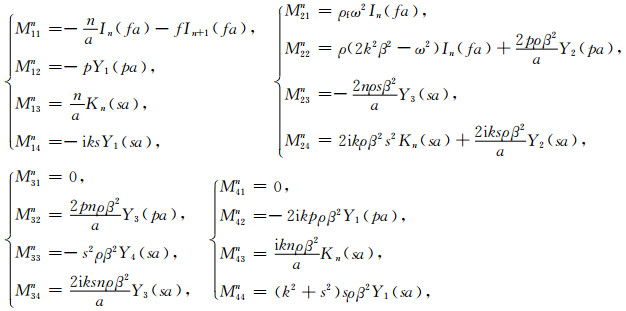
(A1) |
其中Yn(n=1, 2, 3, 4)是下面贝塞尔函数的组合：
|
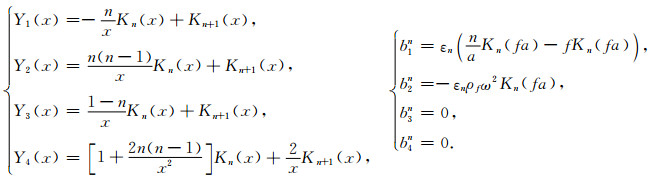
(A2) |
References
Aki K, Richards P G. 1980. Quantitative Seismology:Theory and Methods. New York: W. H. Freeman & Co.
|
Borland W H, Holderson J, Al Rougha H A B, et al. 2005. Integration of microelectrical and sonic reflection imaging around the borehole-offshore UAE.//75th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Byun J, Nafi T M. 2006. Effects of an off-centered tool on dipole and quadrupole logging. Geophysics, 71(4): F91-F100. |
Chen T, Wang B, Zhu Z Y, et al. 2010. Asymmetric source acoustic LWD for improved formation shear velocity estimation.//80th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 548-552.
|
Dong J L, Xu X K, Zhang J Y, et al. 2020. Overview and development of acoustic far detection technology. Progress in Geophysics (in Chinese), 35(2): 566-572. DOI:10.6038/pg2020CC0180 |
Geoquest S. 1998. Geoframe BARS user' Guide. Version 1.0. Kanagawa: Schlumberger K K, 1-6.
|
Gong H, Chen H, He X, et al. 2015. Eliminating the azimuth ambiguity in single-well imaging using 3C sonic data. Geophysics, 80(1): A13-A17. |
Gu X H, Tang X M, Zhuang C X, et al. 2020. Simulation of dipole shear-wave reflection survey for multi-fracture system using liner slip interface theory. Progress in Geophysics (in Chinese), 35(3): 955-962. DOI:10.6038/pg2020DD0053 |
Haldorsen J, Voskamp A, Thorsen R, et al. 2006. Borehole acoustic reflection survey for high resolution imaging.//76th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 314-318.
|
Haldorsen J B U, Borland W, Al Rougha H A B, et al. 2005. Azimuthal sonic imaging.//67th Annual International Conference and Exhibition, EAGE, Extended Abstracts, I017.
|
Hao Z T, Sun X F, Liu X E, et al. 2014. The application research of dipole acoustic reflection imaging technology. Progress in Geophysics (in Chinese), 29(5): 2172-2177. DOI:10.6038/pg20140527 |
He F J. 2005. The study on the simulation of the borehole acoustic reflection imaging logging tool and its waveform processing method[Ph.D. thesis]. Beijing: China University of Petroleum (Beijing).
|
Hirabayashi N, Sakiyama N, Ikegami T. 2017. Characteristics of waveforms recorded by azimuthally spaced hydrophones of sonic logging tool for incident plane waves. Geophysics, 82(6): D353-D368. DOI:10.1190/geo2017-0201.1 |
Hornby B E. 1989. Imaging of near-borehole structure using full-waveform sonic data. Geophysics, 54(6): 747-757. DOI:10.1190/1.1442702 |
Kurkjian A L, Chang S K. 1986. Acoustic multipole sources in fluid-filled boreholes. Geophysics, 51(1): 148-163. |
Nwosu N, Alford J, Kadir H, et al. 2015. Enhancing shale reservoir completion design using oriented unipole logging while drilling sonic measurements in horizontal well.//85th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Pardo D, Matuszyk P J, Torres-Verdin C, et al. 2013. Influence of borehole-eccentered tools on wireline and logging-while-drilling sonic logging measurements. Geophysical Prospecting, 61(S1): 268-283. |
Peng C B. 1994. Borehole effects on downhole seismic measurements[Ph. D. thesis]. Cambridge, MA: Massachusetts Institute of Technology.
|
Qiao W X, Che X H, Li G, et al. 2004. The physical modelling of acoustic reflection image logging. Geophysical Prospecting For Petroleum (in Chinese), 43(3): 294-297. |
Sakiyama N, Syresin D, Iritani R, et al. 2016. LWD unipole for probing azimuthally heterogeneous formation properties: Characterization through numerical modeling and field data.//2016th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 612-616.
|
Schoenberg M. 1986. Fluid and solid motion in the neighborhood of a fluid-filled borehole due to the passage of a low-frequency elastic plane wave. Geophysics, 51(6): 1191-1205. DOI:10.1190/1.1442174 |
Shen J G, Zhang H L. 2000. Numerical study on 3D acoustic field generated by eccentric sources in borehole. Chinese Journal of Geophysics (in Chinese), 43(2): 279-286. |
Tang X M. 2004. Imaging near borehole structure using directional acoustic wave measurement. Geophysics, 69(6): 1378-1386. DOI:10.1190/1.1836812 |
Tang X M, Cao J J, Wei Z T. 2014. Shear-wave radiation, reception, and reciprocity of a borehole dipole source:With application to modeling of shear-wave reflection survey. Geophysics, 79(2): T43-T50. |
Tang X M, Cheng C H. 2004. Quantitative Borehole Acoustic Methods. San Diego: Elsevier Science Publishing Co. Inc.
|
Tang X M, Patterson D J. 2009. Single-well S-wave imaging using multicomponent dipole acoustic log date. Geophysics, 74(6): WCA211-WCA223. DOI:10.1190/1.3227150 |
Tsang L, Rader D. 1979. Numerical evaluation of the transient acoustic waveform due to a point source in a fluid-filled borehole. Geophysics, 44(10): 1706-1720. DOI:10.1190/1.1440932 |
Wang T, Dawber M, Boonen P M. 2011. Theory of unipole acoustic logging tools and their relevance to dipole and quadrupole tools for slow formations.//81st Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Wang T, Tang X M. 2003. LWD Finite-difference Modeling of elastic wave propagation:A nonsplitting perfectly matched layer approach. Geophysics, 68(5): 1749-1755. DOI:10.1190/1.1620648 |
Wang Z. 2016. Reciprocity relations of the elastic wavefields in layered elastic and porous media[Ph.D. thesis]. Harbin: Harbin Institute of Technology.
|
Wei Z T, Tang X M. 2012. Numerical simulation of radiation, reflection, and reception of elastic waves from a borehole dipole source. Geophysics, 77(6): D253-D261. DOI:10.1190/geo2012-0061.1 |
Xu J Q, Hu H S, Wang Z. 2019. Asymptotic solution to a 3D dipole single-well imaging system with combined monopole and dipole receivers with an application in elimination of azimuth ambiguity. Geophysics, 84(5): D191-D207. DOI:10.1190/geo2018-0658.1 |
Xue M. 2002. Study on remote exploration acoustic reflection well logging & its acoustic sonde design[Ph.D. thesis]. Beijing: China University of Petroleum (Beijing).
|
Yamamoto H, Watanable S, Koelman J M V, et al. 2000. Borehole acoustic reflection survey experiments in horizontal wells for accurate well positioning.//70th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Yang Y F, Guan W, Cui N G, et al. 2016. FDTD simulation and analysis of the collar wave propagation in acoustic logging while drilling. Chinese Journal of Geophysics (in Chinese), 59(1): 368-380. DOI:10.6038/cjg20160131 |
Zhang B X, Wang K X, Dong Q D. 1996. Nonaxisymmetric acoustic field excited by a cylindrical tool placed off a borehole axis and extraction of shear wave. The Journal of the Acoustical Society of America, 99(2): 682-690. DOI:10.1121/1.414645 |
Zhang Y D, Hu H S. 2014. Position determination of the interface out of a borehole based on the phase feature of reflected waves. Progress in Geophysics (in Chinese), 29(2): 870-878. DOI:10.6038/pg20140253 |
Zhang Y D, Hu H S. 2014. A technique to eliminate the azimuth ambiguity in single-well imaging. Geophysics, 79(6): D409-D416. DOI:10.1190/geo2013-0310.1 |
董经利, 许孝凯, 张晋言, 等. 2020. 声波远探测技术概述及发展. 地球物理学进展, 35(2): 566-572. DOI:10.6038/pg2020CC0180 |
古希浩, 唐晓明, 庄春喜, 等. 2020. 用滑移界面理论模拟多裂缝体系的偶极横波远探测声场. 地球物理学进展, 35(3): 955-962. DOI:10.6038/pg2020DD0053 |
郝仲田, 孙小芳, 刘西恩, 等. 2014. 偶极横波远探测测井技术应用研究. 地球物理学进展, 29(5): 2172-2177. DOI:10.6038/pg20140527 |
何峰江. 2005.声反射成像测井仪器仿真及波形处理技术研究[博士论文].北京: 中国石油大学(北京).
|
乔文孝, 车小花, 李刚, 等. 2004. 反射声波成像测井的物理模拟. 石油物探, 43(3): 294-297. |
沈建国, 张海澜. 2000. 井内偏心声源激发的三维声场的数值研究. 地球物理学报, 43(2): 279-286. |
王治. 2016.分层弹性与孔隙介质中弹性波场的互易关系[博士论文].哈尔滨: 哈尔滨工业大学.
|
薛梅. 2002.远探测声波反射波测井研究[博士论文].北京: 中国石油大学(北京).
|
杨玉峰, 关威, 崔乃刚, 等. 2016. 随钻声波测井FDTD模拟及钻铤波传播特性研究. 地球物理学报, 59(1): 368-380. DOI:10.6038/cjg20160131 |
张义德, 胡恒山. 2014. 基于反射波相位特征的井外界面方位判别法. 地球物理学进展, 29(02): 870-878. DOI:10.6038/pg20140253 |