随着中国经济的快速发展, 能源需求逐渐增大, 油气资源短缺问题越发突出, 环境污染严重, 天然气水合物等非常规清洁能源因储量巨大、分布集中、开发技术日趋进步等优势, 成为油气资源接替的重要新领域(吴超, 2019).天然气水合物是自1960年以来发现可保持稳定数百万年的天然气资源, 广泛分布于海洋沉积物和多年冻土区, 其数量远超传统和其他非常规资源的总和(Makogon, 2010; Collett et al., 2011; Lu et al., 2011; Wu et al., 2018; Liu et al., 2019), 具有储量大、能量密度高、清洁度高等特点(Zhang et al., 2012), 被广泛认为是一种极具潜力的能源替代形式(Yang et al., 2019).考虑到全球能源危机, 天然气水合物已引起国际密切关注.作为一种非常规清洁能源, 如何在前期勘探中确定天然气水合物的赋存位置是后续开发的重要前提.
在地壳动力作用下, 赋存于海底的天然气水合物处在动态平衡中, 不断分解并释放出甲烷气体, 这些气体通过泥火山、断层、裂隙等运移通道进入海水后, 以气泡的形式上升运移, 形成气泡羽流, 或称甲烷羽流(席世川等, 2017).而海底冷泉是指在压力梯度的影响下, 从海底(或更深)沉积地层中运移和排放出的以水、碳氢化合物(天然气和石油)、硫化氢、细粒沉积物为主要成分的低温流体以喷涌或渗漏的方式溢出海底, 产生一系列的物理、化学和生物作用的一种海洋地质现象(栾锡武, 2008).气泡羽流发育于海底活动冷泉区域上方, 而海底冷泉区域通常与天然气水合物的分解密切相关, 冷泉羽状流下部往往能发现富含天然气水合物的沉积储层(邸鹏飞等, 2008; 刘善琪等, 2015).目前研究的冷泉羽状流多以天然气为主要成分, 其气体主要来源于天然气水合物的分解, 作为指示天然气水合物的重要标志, 潜在的能源因素和环境效应使海底冷泉及相关研究备受关注, 在海洋工程安全、天然气水合物勘查、常规及深部油气勘探、全球气候变化、碳循环和极端生物群落等研究方面都具有重要意义(Kowsmann and De Carvalho, 2002; 栾锡武等, 2010; 刘伯然等, 2015).因此研究海底冷泉羽状流的地震响应特征, 对确定天然气水合物的储集区域, 了解天然气水合物成藏和成藏环境等均有重要意义.
海底冷泉羽状流的溢出能够改变海底沉积层的物理性质(如声学特性), 因此可采用海底探测、声呐及地震等方法来探测海底冷泉羽状流(陈林和宋海斌, 2005; 李灿苹等, 2016; 韩同刚等, 2018).海底可视技术(Sauter et al., 2006)及声呐系统(Westbrook et al., 2009; 栾锡武等, 2010; Klaucke et al., 2010; 梅赛等, 2013; 刘斌和刘胜旋, 2017)可一定程度地观测并识别海底冷泉羽状流, 但海底可视技术不适合大范围普查式勘查, 声呐系统虽可大面积探测, 却难以对小气泡羽流有效成像, 且探测深度有限.与之相比, 地震方法以气泡散射成像理论为基础, 通过浅地层剖面探测、高分辨率地震探测和常规多道反射地震探测识别海底冷泉羽状流, 是观测冷泉活动羽状流的最为经济而有效的手段.逸散于海水的气泡羽流可产生声学羽流、云状扰动、串珠状扰动、“火焰”状反射、斑点状反射、点划线反射等地震反射特征(Kruglyakova et al., 2002; Luan et al., 2008; 顾兆峰等, 2008; 刘伯然等, 2015), 根据地震记录中的散射特征可以识别各类海底冷泉羽状流, 从而确定海底天然气水合物发育的可能性.然而需要注意的是, 上述地震反射特征还未经过实际观测到的海底羽状流活动验证, 后续的地震波数值模拟和实际验证仍然需要对这些地震反射特征进一步核实.
通过上述分析可知, 羽状流地震响应(波动现象)是后续海底冷泉羽状流研究及分析的基础, 并且可以通过地震方法观测羽状流产生的地震响应特征来进一步探寻与天然气水合物相关的一些问题, 如根据地震响应反演水合物的气含量及探寻水合物的分解和运移规律(李灿苹等, 2013a).但是对于究竟如何处理海洋地震资料从而识别海底冷泉羽状流, 并没有形成完善的理论及方法体系; 地震波在海底冷泉羽状流内部的传播机制也并不明确.因此, 要实现对海底冷泉地震响应的精确识别及分析, 确定海底冷泉以及其下赋存的天然气水合物, 仍然存在着极大的挑战.
在目前海底冷泉研究的基础上, 为进一步探讨海底冷泉羽状流的地震响应特征, 逐步完善其内部响应理论, 对海底冷泉进行精确、完整地描述并建立模型, 进而对地震波在其内部的传播机制及海底冷泉对地震波的反射特征进行精准的数值模拟, 与实际地震探测资料相结合, 形成完善的海底冷泉识别体系是极为关键的.海底冷泉羽状流的地震数值模拟技术可以经济有效地模拟海底冷泉散射地震波场, 分析散射波场的响应特征, 确定羽状流的位置、形态及气体运移量, 具有广阔的应用前景.为探讨羽状流的地震响应特征, 李灿苹等(2013b)结合实际海底冷泉羽状流赋存状态及含气泡水体特征, 建立了符合实际赋存特征的海底冷泉羽状流模型, 对其进行地震波数值模拟获得炮集记录, 单炮记录上显示出明显的散射波场特征; You等(2015)通过叠前逆时偏移处理得到较好的成像结果, 与实际赋存的羽状流地震剖面具有相似的地震响应特征, 即都表现为随机分布的羽状流气泡产生的短同相轴; Li等(2016)探讨了羽状流气含量与地震属性之间的相关性, 研究发现气含量与地震振幅属性之间存在较好的线性相关性.这为进一步研究羽状流的地震响应奠定了基础, 也为寻找天然气水合物提供了一条新思路.但在地震响应数值模拟方面, 海底冷泉羽状流内部的地震波响应机理及传播特征究竟如何, 目前在国际上尚无定论.在海底冷泉的模型建立方面, 还没有能够适用于高频地震响应的建模理论及体系, 因此, 如何实现海底冷泉的高频建模及数值模拟仍然存在着极大的难点及挑战.
为了解决海底冷泉羽状流高频数值模拟的问题, 本文建立了完整的适用于高频的海底冷泉羽状流模型, 提出利用含气泡液体声波方程进行海底冷泉地震波数值模拟.本文利用Keller-Miksis气泡振动模型来描述海底冷泉气泡在地震波作用下的运动状态, 同时考虑气泡间的声相互作用, 建立海底冷泉气泡模型, 使用含气泡液体声波方程来描述声波在含气泡液体即海底冷泉中的传播, 与气泡振动方程联立求解, 推导得出能够描述含气泡液体对声波传播的衰减系数和传播速度, 从而实现海底冷泉羽状流的精确数值模拟.在频率域使用有限差分法分别对声波方程和含气泡液体声波方程进行数值模拟, 得到了不同震源子波主频下的地震波场响应并进行对比分析, 从而得出海底冷泉羽状流数值模拟的频谱特征.通过模型试算, 验证了含气泡液体声波方程描述海底冷泉地震响应的有效性.含气泡液体声波方程数值模拟的地震响应与海底冷泉羽状流的频谱特征能够为天然气水合物羽状流地震散射成像提供理论依据.
1 海底冷泉气泡的声学传播理论 1.1 声波方程的基本理论当一列自由行进的声波在传播路径上遇到气泡, 气泡对声波的影响表现为气泡对声波的散射效应.在散射问题中, 该气泡可视为一个极易压缩的弹性球, 这时在介质中除了原来的声波外, 还会出现一列从气泡向四周散射的散射波, 这两种声波在空间中叠加而产生干涉.由于散射波的发散方向是由气泡向外, 因此气泡对散射波来说是一种辐射声源, 而对于入射波则变成了次级声源, 所以介质中存在气泡时的实际声场可以看成是初级声源和次级声源辐射声场的叠加.
现设有一列可以认为是从很远传来的平面波在液体介质中沿轴(竖直方向)方向传播, 其地震波场表示为

|
(1) |
式(1)中, P0表示初始波场, Pi表示波场, ω表示声波的圆频率, k表示波数, z表示空间坐标, t表示时间.
当此列声波在它的传播路径上遇到气泡时, 由于气泡的存在, 这时在液体介质中除了原来的声波外, 还会出现一列从圆球向四周散射的散射波, 使得介质中存在着散射声场.此时, 将气泡视为速度异常体, 声波在液体介质中的传播可表示为
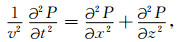
|
(2) |
式(2)中, x、z分别表示笛卡尔坐标系的水平和竖直方向坐标, P表示地震波场, v表示传播速度.在频率域, 方程(2)可表示为

|
(3) |
式(3)中, P表示频率域的地震波场, 
海底冷泉由于含大量气泡, 其性质与普通海水有本质区别.传统的海底冷泉地震波数值模拟均将其看作一种气-液混合的平稳随机介质进行研究, 通过引入声学理论(黄景泉和李福新, 1994), 由气泡的半径大小和体积分数估计气泡对声波的等效弹性参数和等效密度, 进而求得混合介质中的等效声波速度, 使用纯液体声波方程理论来描述海底冷泉的地震响应及散射特征.但在模拟过程中, 并未充分考虑气泡在声波作用下的运动以及气泡之间的相互作用.如果水中传播的声波能量足够大, 将产生空化现象, 使得液体介质在宏观上转变为含有气泡的混合介质(姚文苇和鲜晓军, 2014).此时, 传统的纯液体中的声波方程将不再适用于声波在海底冷泉中的传播.因此, 需要运用新的理论和方法来进行较高频率下的海底冷泉数值模拟.
1.2 声波在含气泡液体中的传播特性当使用高频声波对海底冷泉进行数值模拟时, 海底冷泉由于空化作用在宏观上转变为含有气泡的混合介质, 对此混合体, 如果忽略声传播过程中混合体与周围空气之间的物质交换, 有下面的关系成立:
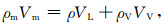
|
(4) |
式(4)中, ρm、ρ、ρV分别表示混合体、原液体及气泡内气体的密度; Vm、VL、VV分别表示混合体、原液体及气泡的总体积, 它们之间满足关系式

|
(5) |
令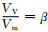

|
(6) |
式(6)中, β表示混合体中所含气泡的总体积占混合体体积的百分比, 即气体所占的体积分数, 表示如下:

|
(7) |
式(7)中, R表示气泡的瞬态半径, N表示单位体积液体中气泡的个数, 根据文章中设立的假设前提, N必须保持常数, 并且有
通常情况下, 混合体的主要成分是液体, 因而β为一小量, 同时, ρV相对于ρm、ρ而言, 也是一小量, 故可忽略(6)式中的二阶小量:

|
(8) |
声波在混合体中传播时, 其连续性方程可写成如下形式:

|
(9) |
式(9)中, u表示质点振动速度场, t表示时间.
将(8)式代入(9)式, 忽略二阶以上的小量, 且有β≪1时, 可得到以下的式子:

|
(10) |

|
(11) |
当液体的黏滞系数不可忽略时, 声波在其中传播的动量方程用广义的纳维-斯托克斯方程表示为

|
(12) |
式(12)中, P表示波场, η称为切变(或第一)黏滞系数, η′称为膨胀(或第二)黏滞系数.如果液体在声波的扰动下做无旋运动, 则有

|
(13) |
从而(12)式变为
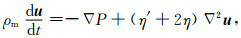
|
(14) |
而对于黏热介质, 其修正的物态方程为

|
(15) |
式(15)中, ρ′=ρ-ρ0, 表示由于声扰动引起的介质的密度变化, ρ0表示无声扰动时介质的密度, v表示绝热声速, κ表示介质常数, CV表示定容比热, CP表示恒压比热.如果式(15)中后两项对压强变化的影响可以忽略时, 可以近似认为

|
(16) |
对式(14)变形得到

|
(17) |
而由式(15)知

|
(18) |
考虑到动量方程的表示
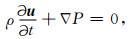
|
(19) |
通过式(18)和(19)可以得到声波在含气泡液体中的传播方程

|
(20) |
我们用方程(20)来描述声波在含气泡液体中的声传播.当声波在纯液体中传播时上式右边等于零, 则上式还原到纯液体中的声传播方程.
气泡在声波的作用下做径向振动, 在线性响应情况下, 气泡半径的径向变化可以表示为
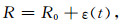
|
(21) |
式(21)中, R0表示气泡的初始半径, 即没有声压驱动情况下气泡的半径, 它是一个常数; ε(t)是气泡在声波作用下半径的变化量, 是时间的函数.
根据Keller-Miksis方程, 考虑液体压缩性时气泡的径向振动(Plesset and Calif, 1949)可以描述为

|
(22) |
式(22)中, 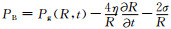
考虑式(21), 则式(20)变为(Zabolotskaya and Soluyan, 1973)
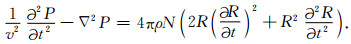
|
(23) |
考虑到声波在液体中传播时, 液体对声波的吸收效应之后, 式(23)变为

|
(24) |
式(24)中, 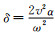

|
(25) |
设入射平面波为

|
(26) |
式(26)中, P0表示初始波场, Pa表示地震波场, ω表示声波的圆频率.
将式(21)和(26)代入式(22)中得到气泡线性振动的表达式:

|
(27) |
式(27)中,

|
(28) |

|
(29) |
ω0表示气泡的共振角频率.设

|
(30) |
由此气泡半径R的表达式已知, 将其代入式(24), 得到关于地震波场的表达式

|
(31) |
k的实部Re(k)即代表声波传播, 而k的虚部Im(k)代表含气泡液体对声波的吸收系数.含气泡液体中的声速由
根据以上理论, 本文提出利用含气泡液体声波方程来描述海底冷泉在声波作用下的传播特性及其地震响应特征, 声波在海底冷泉内的传播速度由vm=ω/k给出, 此时, 海底冷泉气泡群在声波的作用下发生径向运动, 其运动状态使用Keller-Miksis方程来描述, 在此运动过程中, 气泡的半径会发生变化, 同时引起周围海水物理性质的变化.因此, 在进行海底冷泉地震波数值模拟时, 需要对海底冷泉的气泡含量、速度、密度、黏滞系数、表面张力系数等参数进行描述, 以确保模拟结果的准确性.
2 冷泉模型的建立现阶段国内外对于海底冷泉的研究大多依赖于摄影及声呐声学记录仪, 海水中的地震响应研究较少, 海底冷泉的地震响应与气泡半径、气泡含量以及海底水合物甲烷气通量等因素有关, 可通过研究冷泉羽状流的地震响应来探讨与天然气水合物相关的问题.如何定量描述冷泉的气泡半径、气泡含量以及海底水合物甲烷气通量等因素至关重要.因此, 对海底冷泉进行合理建模成为研究其地震响应的必要步骤.当冷泉从海底溢出后, 会释放出甲烷、硫化氢等气体, 在海水中形成气泡, 而这些气泡的存在会改变海水的声学特性, 尤其是声波在海水中的传播速度.姚文苇(2008)基于声压的贝塞尔函数研究了气泡对液体中声速的影响, 李灿苹等(2010, 2013b, 2017)探讨了气泡对海水中声波传播速度的影响, 之后根据含气泡介质声速模型及随机介质理论建立了羽状流水体模型, 其建模理论如下:

|
(32) |
式(32)中,

|
(33) |
其中, K、Kb、ρ、ρb、σ为固定值参量, ω、a、φ和R为给定可变参量.由此, 给定参量, 通过此公式可以计算出随气泡半径和含量变化的含气泡海水声波速度.公式(32)内各参数的详细说明可见表 1.
|
|
表 1 声速表达式(32)中各参数说明 Table 1 Explanation of parameters in Equation (32) of acoustic velocity |
海底冷泉羽状流的建模流程分为以下几步:
(1) 确定羽状流速度体规模:横向距离, 纵向深度, 及横纵向网格步长;
(2) 依据网格步长将模型网格化;
(3) 羽状流区域, 依据随机介质理论给定每个网格点赋予背景气泡半径和含量;
(4) 依据含气泡介质声速模型(32)式及表 1, 给定羽状流速度, 得到海底冷泉气泡散射模型.
当冷泉从海底溢出形成气泡后会改变海水的性质, 比如海水的密度、速度、黏滞系数、表面张力系数等, 进而影响海水在地震记录上的响应特征.气泡的参数变化也会引起海水参数的变化, 气泡的半径变化、单位体积内气泡的个数以及气泡在声波作用下的运动情况等都是会引起海水参数变化的主要因素.因此, 在建立海底冷泉羽状流模型时, 为了能够全面、完整地描述气泡引起的海底冷泉在密度、速度、黏滞系数、表面张力系数等物理参数方面的变化, 应该将气泡的半径、单位体积内气泡的个数以及气泡在声波作用下的运动等影响因素都考虑在内.
李灿苹等(2013b)的海底冷泉羽状流建模理论主要依据姚文苇(2008)推导出的含气泡介质声速模型来确定羽状流区域的声波速度, 但只建立了海底冷泉羽状流的速度模型, 并未给出含气泡区域的其它物理参数; 另外, 姚文苇(2008)在计算含气泡介质声速的过程中假设气泡为球形, 泡内为分布均匀的理想气体, 并假定声波传播过程中气泡不破裂不合并, 且中心不动, 这与声波作用在气泡时气泡的运动不符, 也并未考虑到气泡在声波作用下产生的相互之间的运动.在建立海底冷泉羽状流模型时, 若不考虑上述问题, 一方面会导致海底冷泉羽状流的建模不准确, 另一方面不能准确描述海底冷泉气泡群在声波作用下的运动及响应, 会在其后的地震响应数值模拟中产生误差.
针对这些问题, 本文利用Keller-Miksis方程来描述气泡在声波作用下的运动状态, 以含气泡液体声波方程为基础, 使用公式表示海底冷泉的速度, 同时对海底冷泉区域的气泡含量、密度、黏滞系数、表面张力系数等参数进行描述, 建立了完整的海底冷泉散射模型.所建立的海底冷泉羽状流模型要能够直观、准确、全面地表现出海底冷泉羽状流气泡群区域的物理特性, 包括海底冷泉的气泡含量、密度、黏滞系数、表面张力系数、速度等参数, 以及海底冷泉羽状流区域与周围海水区域物理性质的差异.除此之外, 建立海底冷泉羽状流模型的目的是重点研究海底冷泉羽状流产生的地震响应, 所以海底冷泉羽状流模型的设计既要具有实际意义又要对实际羽状流作适当的简化, 在此前提下, 建立的海底冷泉羽状流模型的形态要有一定的实际参考性.因此, 在建立海底冷泉羽状流模型时, 首先根据随机介质理论绘制出海底冷泉羽状流的基本形状, 并根据公式及实际情况赋予海底冷泉羽状流区域的物理参数(气泡含量、密度、黏滞系数、表面张力系数、速度)值; 再将海底冷泉羽状流放到海水背景场中, 形成完整的海底冷泉羽状流模型.
根据以上理论基础, 本文建立了海底冷泉羽状流模型.图 1、图 4即为建立的海底冷泉羽状流模型, 图 1为简单宝石体模型, 图 4为5个不同形态的海底冷泉组合形成的复杂模型.
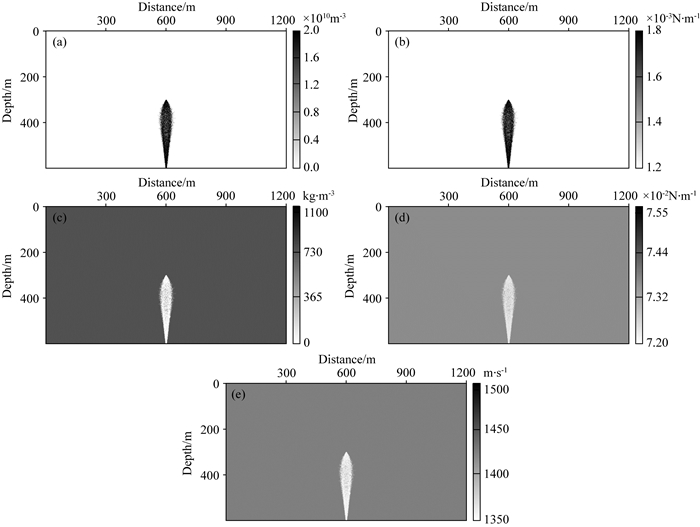
|
图 1 宝石体海底冷泉参数模型. (a)单位体积内气泡个数; (b)切变黏滞系数; (c)液体密度; (d)表面张力系数; (e)液体速度 Fig. 1 Parameter model of gemstone submarine cold seepage. (a) Number of bubbles per unit volume; (b) Shear viscosity coefficient; (c) Liquid density; (d) Surface tension coefficient; (e) Liquid velocity |

|
图 2 海底冷泉模型1地震波场快照.声波方程模拟:(a) 0.3 s; (b) 0.4 s; (c) 0.5 s; 含气泡液体声波方程模拟:(d) 0.3 s; (e) 0.4 s; (f) 0.5 s Fig. 2 Snapshots of submarine cold seepage model 1. Acoustic equation simulation: (a) 0.3 s; (b) 0.4 s; (c) 0.5 s; Acoustic equation of bubbly liquid simulation: (d) 0.3 s; (e) 0.4 s; (f) 0.5 s |

|
图 3 海底冷泉散射模型1不同子波主频地震记录.声波方程模拟:(a) 80 Hz; (b) 160 Hz; (c) 240 Hz; 含气泡液体声波方程模拟:(d) 80 Hz; (e) 160 Hz; (f) 240 Hz Fig. 3 Records of submarine cold seepage model 1. Acoustic equation simulation: (a) 80 Hz; (b) 160 Hz; (c) 240 Hz; Acoustic equation of bubbly liquid simulation: (d) 80 Hz; (e) 160 Hz; (f) 240 Hz |

|
图 4 复杂海底冷泉参数模型. (a)单位体积内气泡个数; (b)切变黏滞系数; (c)液体密度; (d)表面张力系数; (e)液体速度 Fig. 4 Parameter model of complex submarine cold seepage. (a) Number of Bubbles per Unit Volume; (b) Shear Viscosity Coefficient; (c) Liquid density; (d) Surface tension coefficient; (e) Liquid velocity |
图 1是文中建立的宝石体海底冷泉参数模型, 速度模型整体大小为:横向1200 m, 纵向深600 m, 网格大小为1 m×1 m.图中中间位置异常区域为海底冷泉羽状流, 周围为速度均为1500 m·s-1的均匀海水.从图中可以看出, 气泡的存在使冷泉区域的密度与海水的密度差异最为显著, 但冷泉区域的密度与海水密度的差异不会对整体的密度造成太大影响, 一定程度上可以忽略.其次, 冷泉区域及海水中切变黏滞系数以及表面张力系数也存在差异, 而这些变化都会导致海水中声速的变化, 最终体现在冷泉的地震响应上.
3 地震波数值模拟及特征分析 3.1 地震波数值模拟能够在液体中传播的弹性波只有纵波(无旋波), 其可用流体中的声波近似代替, 两者具有同样的性质.由于液体中的弹性波传播不存在转换波问题, 故液体中地震波的传播问题可以直接用声波方程即标量地震波动方程来研究.本文所研究的内容为海底冷泉羽状流中的地震波传播问题, 因而采用含气泡液体声波方程来描述海底冷泉的声传播特性.为了研究所建立的海底冷泉羽状流模型以及含气泡液体声波方程对海底冷泉羽状流模型的模拟效果, 本文在频率域分别使用声波方程和含气泡液体声波方程进行数值模拟, 对比不同子波主频下地震响应的波场特性, 分析地震波在海底冷泉羽状流中的衰减特性, 并对模拟地震波场进行成像.
根据建立的海底冷泉羽状流模型, 使用传统声波方程及本文推导的含气泡液体声波方程对其进行正演模拟, 震源子波选用雷克子波, 其子波主频分别取80 Hz、160 Hz、240 Hz进行低-中-高频的数值模拟, 得到相应的波场快照和地震记录.通过对比不同时刻下的波场快照和不同子波主频下的单炮地震记录, 分析冷泉羽状流位置及形态对模拟海底冷泉羽状流地震波场特征的影响.
图 2给出了模型1分别使用声波方程模拟和含气泡液体声波方程模拟在不同时刻的波场快照, 从图中可以看出, 声波在遇到海底冷泉气泡后地震波场出现了紊乱, 呈现出散射特征.随着声波继续向下传播, 波场的紊乱区域增加, 散射特征逐渐增强, 在冷泉气泡所在位置的散射波场呈现出明显的指向性, 气泡部位的地震波表现为以气泡所在部位为顶点的散射波序列, 散射序列顶点构成区域与海底冷泉羽状流形态相似, 能够明显区别于周围海水区域.将使用声波方程模拟的波场快照与使用含气泡液体声波方程模拟的波场快照进行对比, 在相同的模拟条件下, 后者在冷泉区域的散射特征比前者更加清晰, 能够更加细致地刻画海底冷泉气泡在声波作用下的散射效应.
图 3为模型1分别使用声波方程和含气泡液体声波方程在80 Hz、160 Hz和240 Hz子波主频下的模拟地震响应对比图, 从图中可以看出, 海底冷泉羽状流所在位置处, 地震波场具有明显的散射特征, 该区域散射能量最强, 向两侧散射能量逐渐减弱, 向下能量很快衰减, 能够分辨出海底冷泉的边界, 且与速度模型中冷泉区域的位置相吻合.对比不同子波主频下的地震响应, 随着子波主频的增大, 地震记录的分辨率提高, 海底冷泉区域的散射响应愈加清晰; 可以看出子波主频为240 Hz时的模拟结果效果最好, 此时冷泉区域最清晰可辨, 可以确切分辨出冷泉的上顶点界面及左右边界.在较低频率时, 虽然冷泉区域存在一定的散射波场紊乱, 但特征并不明显, 分辨率也较低.这说明, 在使用含气泡液体声波方程对海底气泡冷泉进行模拟时, 子波主频越高, 冷泉的散射特征越明显, 分辨率越高, 模拟结果越好, 对海底冷泉气泡区域的散射特征刻画效果越细致.
将声波方程模拟的地震记录与含气泡液体声波方程模拟的地震记录进行对比, 可以看出两个方程的模拟结果均能体现出气泡区域的散射特征, 但含气泡液体声波方程的模拟结果更加细致、准确.从波场快照和模拟记录当中可以看出, 随着子波主频的增加, 数值频散随之增强.两相对比, 在相同的模拟条件下, 含气泡液体声波方程模拟的优势更加突出.
图 4为复杂海底冷泉气泡散射模型, 其大小为1200 m×600 m, 海水区域速度均为1500 m·s-1, 包含5个位置、形态、大小各不相同的冷泉羽状流.
图 5给出了复杂海底冷泉气泡散射模型在不同时刻的波场快照.图 6给出了复杂海底冷泉气泡散射模型相应的单炮地震记录.在图 5、6中, 可以看出海底冷泉区域明显的散射特征, 地震波形表现为以气泡所在位置为顶点的散射波系列, 多散射进行相干, 形成与冷泉羽状流形态吻合的散射区域, 海底冷泉的形态清晰可辨; 随着子波主频的增大, 海底冷泉区域的散射越加清晰, 地震记录在240 Hz时的分辨率最高; 图 5及图 6中海底冷泉模拟结果呈现出与模型1模拟结果相似的散射特征, 证明了文中的含气泡液体声波方程的模拟结果是有效的.
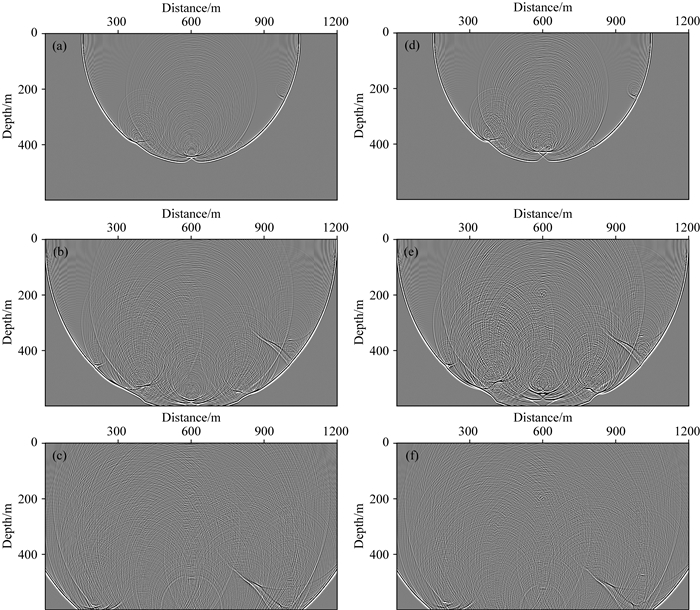
|
图 5 海底冷泉模型2地震波场快照.声波方程模拟:(a) 0.3 s; (b) 0.4 s; (c) 0.5 s; 含气泡液体声波方程模拟:(d) 0.3 s; (e) 0.4 s; (f) 0.5 s Fig. 5 Snapshots of submarine cold seepage model 2. Acoustic equation simulation: (a) 0.3 s; (b) 0.4 s; (c) 0.5 s; Acoustic equation of bubbly liquid simulation: (d) 0.3 s; (e) 0.4 s; (f) 0.5 s |

|
图 6 海底冷泉散射模型2不同子波主频地震记录.声波方程模拟:(a) 80 Hz; (b) 160 Hz; (c) 240 Hz; 含气泡液体声波方程模拟:(d) 80 Hz; (e) 160 Hz; (f) 240 Hz. Fig. 6 Records of submarine cold seepage model 2. Acoustic equation simulation: (a) 80 Hz; (b) 160 Hz; (c) 240 Hz; Acoustic equation of bubbly liquid simulation: (d) 80 Hz; (e) 160 Hz; (f) 240 Hz |
为了能够更加全面地了解海底冷泉地震响应的波场特征, 首先对海底冷泉数值模拟结果进行频谱分析, 分别抽取震源附近(600 m)和远离震源(1100 m)的一道数据, 进行快速傅里叶变换, 得到振幅谱, 分析不同子波主频下海底冷泉模拟结果的频谱特性以及含气泡液体声波方程和声波方程模拟结果在频谱特性之间的区别.
图 7中是海底冷泉数值模拟地震波场的频谱分析结果, 其中, 图 7(a, b)分别是模型1在不同子波主频下模拟结果的近、远道数据振幅谱, 图 7(c, d)是模型1在240 Hz子波主频下分别使用含气泡液体声波方程和声波方程模拟结果的近、远道数据振幅谱, 图 7(e, f)分别是模型2在不同子波主频下模拟结果的近、远道数据振幅谱, 图 7(g, h)是模型2在240 Hz子波主频下分别使用含气泡液体声波方程和声波方程模拟结果的近、远道数据振幅谱.在振幅对比图中可以看出, 随着子波主频的增高, 地震记录主频及振幅逐渐降低, 说明随着子波主频的增大, 声波在海底冷泉中传播时的能量衰减逐渐增强; 每条振幅曲线的变化趋势相同, 说明声波在海底冷泉中的传播遵循相同的衰减规律; 复合海底冷泉模型模拟结果的振幅曲线比简单模型模拟结果的振幅曲线更加复杂, 呈现出更加细致的起伏, 说明海底冷泉羽状流的形态会影响其地震响应; 分别对比图 7(a, b)、(e, f), 可以看到远道数据的振幅曲线比近道数据的振幅曲线杂乱, 远道数据远离海底冷泉羽状流, 信息杂乱, 但整体呈现出的变化趋势与近震源道近似, 特征与近震源道数据相同.对比图 7(c, d, g, h), 可以看出含气泡液体声波方程的模拟结果与声波方程的模拟结果整体相同, 说明两种方法的模拟结果具有相似性, 证明了含气泡液体声波方程模拟结果的有效性; 在细节处, 含气泡液体声波方程模拟结果的振幅曲线更加复杂, 在相同的频率成分下展现了更加复杂的波场信息, 这说明使用含气泡声波方程能够更加细致地描述出海底冷泉气泡在声波作用下的运动, 相对声波方程的模拟结果来说, 含气泡液体声波方程的模拟更加切合实际.

|
图 7 海底冷泉模拟地震波场频谱图 Fig. 7 Spectrum of seismic field records of submarine cold seepage model |
在气-液两相介质中, 水体中的气泡对声波传播的衰减(聂邦胜等, 2007)主要因为以下两点:
(1) 散射衰减现象.当声波在气-液两相介质中传播时, 一部分声波在经过水体中的气泡时将被散射开来, 气泡则作为新的散射声源, 一部分入射波经过气泡散射会改变传播方向, 其余入射声波不改变传播方向, 这部分散射声波所消耗的能量就是所发生的散射衰减.气泡对声波能量散射衰减强弱, 与气泡的平均直径D和波长λ有关, 按平均直径D和波长λ的关系大致可分为三种情况(Ts为散射衰减系数):
(a) 在λ≫D的情况下, 即在瑞雷范围内, Ts∝D3f4;
(b) 在λ≈D的情况下, 即在散射范围内Ts∝Df2;
(c) 在λ≪D的情况下, 即在扩散范围内Ts∝1/D.
(2) 吸收衰减现象.该现象原因有二:一是声波穿过气泡的过程中, 气泡会发生形变, 该过程存在热传导损耗; 二是声波穿过气泡的过程中, 小气泡会发生振动, 会将部分入射波的能量转化为液体分子的无规则热运动.当声波入射频率足以达到气泡的共振频率时, 气泡由于共振现象吸收声波的能力最强, 衰减系数也最强.
理想海水中声速约为1531 m·s-1, 甲烷气体中声速约为465 m·s-1, 正演模拟中所用高频震源为240 Hz左右, 而气泡半径在10-2~10-5m左右, 由上可知海底冷泉气泡流对地震波的散射作用属于瑞雷散射范围, 海水中气泡共振频率(气泡半径为10-3m时约几kHz)与海洋地震频率相差较大, 故海底冷泉气泡对地震波的衰减作用主要为散射衰减, 频率越接近共振频率其吸收现象越明显, 则衰减越强, 即地震频率与气泡的衰减作用呈正相关性.
3.3 地震波场偏移成像为了更加全面地分析海底冷泉气泡在含气泡液体声波方程下的特征, 现对模拟得到的海底冷泉羽状流模型的炮集记录(240 Hz)进行常规偏移成像处理, 得到的偏移剖面如下图 8所示.

|
图 8 海底冷泉模拟地震记录偏移剖面 Fig. 8 Migration profile of seismic field record of submarine cold seepage model |
从偏移剖面中可以观察到, 利用海底冷泉的散射波可以对其进行清晰成像, 成像结果对于模型中的冷泉形态有清晰的刻画, 且对冷泉顶部的成像效果明显好于底部, 冷泉底部的成像精度不高, 在羽状流水体两侧存在画弧现象.对于规模较小的羽状流来说, 成像剖面对其形态有清晰刻画, 但相对大规模的水体来说分辨率较低.
4 结果分析与讨论本文提出利用含气泡液体声波方程来描述声波在海底冷泉中的传播, 在频率域使用有限差分法对海底冷泉进行数值模拟, 得到了不同子波主频下的海底冷泉地震响应, 对比分析其地震响应声学散射特征及频谱特征, 得出以下结论:
与传统声波方程相比, 含气泡液体声波方程能够更准确地描述海底冷泉的散射特征:冷泉羽状流气泡区地震波场散射特征清晰, 随着子波主频的增大, 波场的散射紊乱越加明显; 子波主频越高, 地震响应分辨率越高, 对海底冷泉形态、位置的刻画越清晰; 散射特征在冷泉气泡柱区域最明显, 能量最强, 地震波形表现为以气泡所在位置为顶点的散射波序列, 多散射进行相干, 散射区域的形态与冷泉羽状流形态相似.在对地震响应进行频谱分析之后, 发现含气泡液体声波方程对海底冷泉羽状流中气泡在声波作用下的运动刻画得更加细致, 随着子波主频的增大, 声波在海底冷泉中的衰减增强, 声波在海底冷泉气泡中的衰减比在水中的衰减严重得多, 且主要为散射衰减.海底冷泉的地震记录偏移剖面显示可以利用散射波进行清晰成像, 顶底成像精度高于两侧, 大规模冷泉的成像精度高于小规模冷泉.
本文在建立海底冷泉羽状流模型时, 为了简化模型便于计算, 并未考虑单位体积内气泡个数及气泡半径的随机变化及其在不同深度的变化, 为了进一步贴合实际, 在今后的研究中可以进一步探讨以上因素对海底冷泉羽状流地震响应的影响.
Chen L, Song H B. 2005. Geophysical features and identification of natural gas seepage in marine environment. Progress in Geophysics (in Chinese), 20(4): 1067-1073. |
Collett T S, Lee M W, Agena W F, et al. 2011. Permafrost-associated natural gas hydrate occurrences on the Alaska North Slope. Marine and Petroleum Geology, 28(2): 279-294. DOI:10.1016/j.marpetgeo.2009.12.001 |
Di P F, Feng D, Gao L B, et al. 2008. In situ measurement of fluid flow and signatures of seep activity at marine seep sites. Progress in Geophysics, 2008(05): 1592-1602. |
Gu Z F, Liu H S, Zhang Z X. 2008. Acoustic detecting method for bubbles from shallow gas to sea water. Marine Geology & Quaternary Geology (in Chinese), 28(2): 129-135. |
Han T G, Tong S Y, Chen J X, et al. 2018. Analysis of detection methods for submarine plume. Progress in Geophysics (in Chinese), 33(5): 2113-2125. DOI:10.6038/pg2018CC0154 |
Huang J Q, Li F X. 1994. Dissipative effects of an isolated bubble in water on the sound wave. Applied Mathematics and Mechanics (in Chinese), 15(6): 549-554. |
Klaucke I, Weinrebe W, Petersen C J, et al. 2010. Temporal variability of gas seeps offshore New Zealand:Multi-frequency geoacoustic imaging of the Wairarapa area, Hikurangi margin. Marine Geology, 272(1-4): 49-58. DOI:10.1016/j.margeo.2009.02.009 |
Kowsmann R O, De Carvalho M D. 2002. Erosional event causing gas-venting on the upper continental slope, Campos Basin, Brazil. Continental Shelf Research, 22(16): 2345-2354. DOI:10.1016/S0278-4343(02)00060-2 |
Kruglyakova R, Gubanov Y, Kruglyakov V, et al. 2002. Assessment of technogenic and natural hydrocarbon supply into the Black Sea and seabed sediments. Continental Shelf Research, 22(16): 2395-2407. DOI:10.1016/S0278-4343(02)00064-X |
Li C P, Liu X W, Yang L, et al. 2010. Study on the bubble radius and content effect on the acoustic velocity of seawater with bubbles. Geoscience (in Chinese), 24(3): 528-533. |
Li C P, Liu X W, Zhao L C. 2013a. Progress on cold seeps and bubble plumes produced by gas hydrate. Progress in Geophysics (in Chinese), 28(2): 1048-1056. |
Li C P, Liu X W, Gou L M, et al. 2013b. Numerical simulation of bubble plumes in overlying water of gas hydrate in the cold seepage active region. Science China:Earth Sciences, 56(4): 579-587. DOI:10.1007/s11430-012-4508-y |
Li C P, Gou L M, You J C, et al. 2016. Further studies on the numerical simulation of bubble plumes in the cold seepage active region. Acta Oceanologica Sinica, 35(1): 118-124. DOI:10.1007/s13131-016-0803-3 |
Li C P, You J C, Zhu W J. 2016. Identification of bubble plumes and analysis of its correlation with resource environment. Progress in Geophysics (in Chinese), 31(6): 2747-2755. DOI:10.6038/pg20160653 |
Li C P, Gou L M, You J C, et al. 2017. Study on numerical models about bubble plumes in the cold seepage active region. Marine Geology & Quaternary Geology (in Chinese), 37(5): 141-150. |
Liu B, Liu S X. 2017. Gas bubble plumes observed at north slope of South China Sea from multi-beam water column data. Acta Oceanologica Sinica (in Chinese), 39(9): 83-89. |
Liu B R, Song H B, Guan Y X, et al. 2015. Characteristics and formation mechanism of cold seep system in the northeastern continental slope of South China Sea from sub-bottom profiler data. Chinese Journal of Geophysics (in Chinese), 58(1): 247-256. DOI:10.6038/cjg20150122 |
Liu S Q, Yin F L, Zhu B J, et al. 2015. Numerical simulation on the formation of cold seepage. Chinese Journal of Geophysics (in Chinese), 58(5): 1731-1741. |
Liu W G, Li Y H, Xu X H. 2019. Influence factors of methane hydrate formation from ice:Temperature, pressure and SDS surfactant. Chinese Journal of Chemical Engineering, 27(2): 405-410. DOI:10.1016/j.cjche.2018.03.033 |
Lu H L, Lorenson T D, Moudrakovski I L, et al. 2011. The characteristics of gas hydrates recovered from the Mount Elbert Gas Hydrate Stratigraphic Test Well, Alaska North Slope. Marine and Petroleum Geology, 28(2): 411-418. DOI:10.1016/j.marpetgeo.2010.01.002 |
Luan X W, Jin Y, Obzhirov A, et al. 2008. Characteristics of shallow gas hydrate in Okhotsk Sea. Science in China Series D:Earth Sciences, 51(3): 415-421. DOI:10.1007/s11430-008-0018-3 |
Luan X W, Liu H, Yue B J, et al. 2010. Characteristics of cold seepage on side scan sonar sonogram. Geoscience (in Chinese), 24(3): 474-480. |
Makogon Y F. 2010. Natural gas hydrates-A promising source of energy. Journal of Natural Gas Science and Engineering, 2(1): 49-59. DOI:10.1016/j.jngse.2009.12.004 |
Mei S, Zhao T H, Yang Y, et al. 2013. The water column acoustical detection of methane plume and gas migration flux calculation. Marine Geology Frontiers (in Chinese), 29(3): 53-59. |
Nie B S, Qiu R G. 2007. Research on method of detecting submarine to acoustics feature of air bubble. Ocean Technology (in Chinese), 26(4): 51-53. |
Plesset M S, Calif P. 1949. The dynamics of cavitation bubbles. Journal of Applied Mechanics, 16(3): 277-282. |
Sauter E J, Muyakshin S I, Charlou J L, et al. 2006. Methane discharge from a deep-sea submarine mud volcano into the upper water column by gas hydrate-coated methane bubbles. Earth and Planetary Science Letters, 243(3-4): 354-365. DOI:10.1016/j.epsl.2006.01.041 |
Westbrook G K, Thatcher K E, Rohling E J, et al. 2009. Escape of methane gas from the seabed along the West Spitsbergen continental margin. Geophysical Research Letters, 36(15): L15608. DOI:10.1029/2009GL039191 |
Wu Z R, Li Y H, Sun X, et al. 2018. Experimental study on the effect of methane hydrate decomposition on gas phase permeability of clayey sediments. Applied Energy, 230: 1304-1310. DOI:10.1016/j.apenergy.2018.09.053 |
Xi S C, Zhang X, Wang B, et al. 2017. The indicators of seabed cold seep and comparison among main distribution areas. Marine Geology Frontiers (in Chinese), 33(2): 7-18. |
Yang L, Liu Y L, Zhang H Q, et al. 2019. The status of exploitation techniques of natural gas hydrate. Chinese Journal of Chemical Engineering, 27(9): 2133-2147. DOI:10.1016/j.cjche.2019.02.028 |
Yao W W. 2008. Effect of bubble on propagation of acoustic wave. Journal of Shaanxi Institute of Education (in Chinese), 24(1): 107-109. |
Yao W W, Xian X J. 2014. Study on acoustic parameter in bubble-liquid medium. Piezoelectrics & Acoustooptic (in Chinese), 36(4): 548-551, 554. |
You J C, Li C P, Cheng L F, et al. 2015. Numerical simulation of methane plumes based on effective medium theory. Arabian Journal of Geosciences, 8(11): 9089-9100. DOI:10.1007/s12517-015-1916-2 |
Yuan Y, Miao B Y, An Y. 2018. Investigation on sound transmission and heat production in bubbly liquid. Journal of Applied Acoustics (in Chinese), 37(5): 717-721. |
Zabolotskaya E A, Soluyan S I. 1973. Emission of harmonic and combination-frequency waves by air bubbles. Sov Physics Acoustic, 18: 396-398. |
Zhang Z G, Wang Y, Gao L F, et al. 2012. Marine gas hydrates:future energy or environmental killer?. Energy Procedia, 16: 933-938. DOI:10.1016/j.egypro.2012.01.149 |
陈林, 宋海斌. 2005. 海底天然气渗漏的地球物理特征及识别方法. 地球物理学进展, 20(4): 1067-1073. |
邸鹏飞, 冯东, 高立宝, 陈多福. 2008. 海底冷泉流体渗漏的原位观测技术及冷泉活动特征. 地球物理学进展, (05): 1592-1602. |
杜功焕, 朱哲民, 龚秀芬. 2001. 声学基础. 2版. 南京: 南京大学出版社.
|
顾兆峰, 刘怀山, 张志珣. 2008. 浅层气逸出到海水中的气泡声学探测方法. 海洋地质与第四纪地质, 28(2): 129-135. |
韩同刚, 童思友, 陈江欣, 等. 2018. 海底羽状流探测方法分析. 地球物理学进展, 33(5): 2113-2125. DOI:10.6038/pg2018CC0154 |
黄景泉, 李福新. 1994. 水中孤立气泡对声波的耗散作用. 应用数学和力学, 15(6): 549-554. |
李灿苹, 刘学伟, 杨丽, 等. 2010. 气泡半径和含量对含气泡海水声波速度的影响. 现代地质, 24(3): 528-533. |
李灿苹, 刘学伟, 赵罗臣. 2013a. 天然气水合物冷泉和气泡羽状流研究进展. 地球物理学进展, 28(2): 1048-1056. |
李灿苹, 刘学伟, 勾丽敏, 等. 2013b. 冷泉活动区天然气水合物上覆水体中气泡羽状流的数值模拟. 中国科学:地球科学, 43(3): 391-399. |
李灿苹, 尤加春, 朱文娟. 2016. 气泡羽状流的识别及其与资源环境相关性分析. 地球物理学进展, 31(6): 2747-2755. DOI:10.6038/pg20160653 |
李灿苹, 勾丽敏, 尤加春, 等. 2017. 冷泉活动区气泡羽状流数值模型研究. 海洋地质与第四纪地质, 37(5): 141-150. |
刘斌, 刘胜旋. 2017. 南海北部陆坡气泡羽状流的发现:多波束水体数据. 海洋学报, 39(9): 83-89. |
刘伯然, 宋海斌, 关永贤, 等. 2015. 南海东北部陆坡冷泉系统的浅地层剖面特征与分析. 地球物理学报, 58(1): 247-256. DOI:10.6038/cjg20150122 |
刘善琪, 尹凤玲, 朱伯靖, 等. 2015. 冷泉形成的数值模拟研究. 地球物理学报, 58(5): 1731-1741. |
栾锡武. 2008.海底冷泉的成因机制.//中国地球物理学会第二十四届年会论文集.北京: 中国大地出版社, 1.
|
栾锡武, 刘鸿, 岳保静, 等. 2010. 海底冷泉在旁扫声纳图像上的识别. 现代地质, 24(3): 474-480. |
梅赛, 赵铁虎, 杨源, 等. 2013. 甲烷羽状流水体声学探测及气体运移通量测算. 海洋地质前沿, 29(3): 53-59. |
聂邦胜, 邱仁贵. 2007. 气泡声学特性探潜方法研究. 海洋技术学报, 26(4): 51-53. |
吴超. 2019. 探析新疆非常规能源的发展. 冶金管理, (3): 78-79. |
席世川, 张鑫, 王冰, 等. 2017. 海底冷泉标志与主要冷泉区的分布和比较. 海洋地质前沿, 33(2): 7-18. |
姚文苇. 2008. 气泡对声传播影响的研究. 陕西教育学院学报, 24(1): 107-109. |
姚文苇, 鲜晓军. 2014. 含气泡液体内的声学参数研究. 压电与声光, 36(4): 548-551, 554. |
袁月, 苗博雅, 安宇. 2018. 声波在含气泡液体中传播特性及产热效应. 应用声学, 37(5): 717-721. |
 2020, Vol. 63
2020, Vol. 63


