2. 海底科学与探测技术教育部重点实验室, 青岛 266100;
3. 青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室, 青岛 266100
2. Key Lab of Submarine Geosciences and Prospecting Techniques. MOE. China, Qingdao 266100, China;
3. Laboratory for Marine Mineral Resources, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266100, China
传统油气资源勘探为了获得探区内的精确地下构造, 需进行高密度的数据采集, 勘探成本较高.由于目标区域和野外环境的限制, 地震勘探数据会出现坏道、缺道等不规则和不完整现象, 进而影响对地震资料的后续处理和解释.野外勘探数据量的日益增长也对数据的存储和远距离传输造成了一定的挑战.基于以上三点, 对于非完整地震数据重建的研究具有一定的理论和实际意义(Cao et al., 2011).
传统地震数据重建方法大致可以归纳为三类.第一类是基于预测滤波器的重建方法, 如F-X域预测滤波方法(Spitz,1991), F-K域预测滤波方法(Gülünay,2003)等.此类方法通常将非均匀采样数据当作规则数据来处理, 并通过高斯窗进行插值, 这容易造成较大误差, 插值结果的不确定性较大.第二类是基于波动方程的方法, 其利用波传播的物理性质重构地震波场(Ronen,1987; Stolt,2002), 这类方法可以处理非均匀采样数据, 但需要地下结构的先验信息, 计算量较大, 对采样率要求也较高, 对于粗网格采样的数据重构效果不佳.第三类是基于变换域的方法, 这类方法先对地震数据进行某种变换编码, 常用的有傅里叶变换(Sacchi et al., 1996; Sacchi et al., 1998)、Radon变换(Kabir et al., 1995; Wang et al., 2010)、Curvelet变换(Herrmann and Hennenfent, 2008; Hennenfent et al., 2010)等, 根据数据在变换域内的特征对其做插值等处理后再进行逆变换解码, 从而完成对数据的重构.与前两类方法相比, 这类方法计算效率高, 效果较理想.
非完整信号重建是一个不适定的反问题, 正则化方法可以有效缓解反问题不适定性.目前研究最多的主要是稀疏正则化方法, 压缩感知技术(Candès et al., 2006a)基于信号的稀疏性或可压缩性, 打破了Nyquist采样定理的要求, 为随机缺失的非完整信号重建问题提供了稀疏先验信息.曹静杰等(2012)在压缩感知框架下, 利用地震数据在Curvelet(Candès et al., 2006b)域内的稀疏性, 将地震数据重建转化为一个稀疏优化问题, 然后构造L0范数的逼近函数作为目标函数, 并用梯度投影法求解, 在jittered采样方法(Hennenfent and Herrmann, 2008)的基础上, 进一步提出了分段随机采样方法, 数值实验也显示了文中所提方法的有效性.白兰淑等(2014)在Curvelet域综合利用CRSI方法(Herrmann and Hennenfent, 2008)和Bregman迭代阈值算法(Yin, 2010; Ma, 2011), 提出了一种新的联合迭代算法, 加快了算法收敛速度.相比Curvelet变换, Shearlet变换(Häuser and Steidl, 2012; Kutyniok et al., 2012)具有更敏感的方向性, 可对地震信号进行更稀疏的表示.Häuser和Ma(2012)首次将Shearlet变换引入地震数据重建, 采用ADMM求解, 取得了良好的重建效果.张良等(2017)也将Shearlet变换引入地震数据重建, 在欠采样的情况下, 根据地震数据缺失情况设计采样矩阵, 用正交匹配追踪法求解稀疏系数, 最后通过反变换实现地震数据重建.除稀疏正则化方法之外, TV正则化也可被用于地震数据处理.Anagaw和Sacchi(2012)提出基于TV正则化的地震成像方法, 此方法利用了TV正则化方法的保边界性质.此后, Gholami和Sacchi (2013)又利用TV正则化改善了盲反卷积的效果.Zhang等(2014)将TV正则化引入波阻抗反演.
上述两种正则化方法仅利用了一种先验假设, 如压缩感知仅利用了信号的稀疏性质, TV正则化则仅利用了信号的分块结构.目前, 对于稀疏和TV正则化联合的双正则化方法的研究主要集中在地震信号去噪方面.Tang和Ma(2011)利用地震信号在Curvelet域内稀疏性和TV正则化的保边界性质, 提出了基于Curvelet变换的L1和TV双正则化的地震信号去噪方法, TV正则化的引入缓解了信号处理中出现的吉布斯效应.由于一阶TV正则化易引起伪影, 造成重建不准确(Vese, 2001; Lysaker et al., 2003; Hinterberger and Scherzer, 2006), 研究者开始将高阶TV或TGV(Bredies et al., 2010)作为正则化约束, Lari和Gholami(2014)同样利用地震信号在Curvelet域内的稀疏性, 引入二阶TV正则化, 提出L1和二阶TV正则化方法用于压制随机噪声.Kong和Peng(2015)利用地震信号在Shearlet变换域内的稀疏性, 提出L1和TGV双正则化的方法用于压制地震数据的随机噪声.
受到上述研究的启发, 本文将基于Shearlet变换的L1和TGV双正则化方法应用于地震图像重建.在压缩感知框架下, 首先通过Shearlet变换得到稀疏系数, Shearlet变换具有多尺度、多方向性,基于此可构建L1正则化模型, L1正则化项用于促进变换系数的稀疏性.考虑到复杂地下介质的轮廓信息, 仅利用信号的稀疏性一项先验信息是不合适的, 因此我们对传统压缩感知的L1正则化模型进行改进, 引入TGV正则化项, 构建L1和TGV双正则化模型, TGV正则化用于保持地下介质图像的边界信息.根据模型的分块性质, 采用ADMM求解此模型, 每个子问题均可得到显式解.最后, 与传统的单一正则化方法对比, 包括基于Shearlet变换的L1正则化方法, 基于Wavelet变换的L1正则化方法和TGV正则化方法, 通过数值实验验证本文所提方法的有效性.进一步的, 通过数值实验将所提方法推广到连续采样的情况, 验证其对于连续缺失数据重建的有效性.
1 基本原理 1.1 基于压缩感知的地震数据重建方法
令



|
(1) |
地震数据重构问题即由部分波场数据b求解完整波场数据f, 显然这是一个病态的反问题.在无先验信息情况下, 求解一个病态反问题是困难的.压缩感知理论正是给出了一个用于求解上述病态反问题的先验信息, 即原始波场数据是可压缩的或在某一变换域内满足数据的稀疏性.若存在某个变换D使得x=Df是稀疏的, 令A=RD-1, 则(1)式可化为

|
(2) |
由压缩感知理论知, (2)式可由如下的约束极小化问题求解:
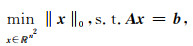
|
(3) |
其中零范数‖·‖0表示向量的非零元素的个数.由于L0范数的存在, (3)式是NP困难的.在实际求解过程中, 通常基于一定的松弛策略用L1范数代替L0范数:

|
(4) |
(4) 式即为基追踪模型(Donoho,2006).进一步的, (4)式可转化为无约束优化问题, 即

|
(5) |
其中λ>0为正则化参数.(5)式又称为L1正则化模型.多种凸优化算法均可用于求解(4)或(5)式, 如正交匹配追踪法(Tropp and Gilbert, 2007), Bregman迭代法(Yin, et al., 2008), ISTA(Blumensath and Davies, 2009), FISTA(Beck and Teboulle, 2009), ADMM(Yang and Zhang, 2011).
1.2 Shearlet变换
相比小波变换, Shearlet变换可以提供更多的方向信息.Shearlet变换通过剪切算子和平移算子检测奇异性的方向和位置.令

|
(6) |
其中Bs为剪切矩阵, Aa为各向异性尺度矩阵, s∈R为剪切参数, a∈R+为膨胀系数.Shearlet变换的基函数为

|
(7) |
其中


|
(8) |
带权重参数α=(α0, …, αk-1)的k阶TGV定义如下(Bredies and Holler, 2015a; 2015b):

|
其中


|
(9) |
其中, 

本文对(5)式引入TGV正则化项, 建立如下模型:
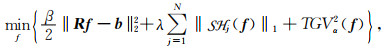
|
(10) |
其中, β>0, λ>0为权重参数, 
为有效求解(10)式, 需对TGV范数进行改写.引入新变量p, 则
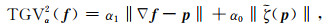
|
(11) |
其中,

|
在数值计算中用有限差分算子代替求导计算, 令▽1f=D1f, ▽2f=D2f, 其中D1, D2分别为x、y轴的前向有限差分算子, 则
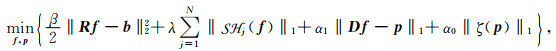
|
(12) |
其中α1, α0>0, (10)到(12)式详细推导过程可参考相关文献(Bredies et al., 2010).
2.2 算法
考虑到(12)式的分块形式, (12)式可由ADMM求解.引入辅助变量
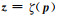

|
(13) |
应用ADMM求解(13)式可得如下的迭代格式:
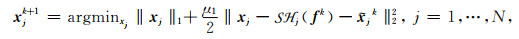
|
(14) |
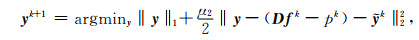
|
(15) |

|
(16) |

|
(17) |

|
(18) |
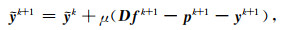
|
(19) |

|
(20) |
(14), (15)和(16)式结构相似, 显式解可由一个收缩算子给出.(14)式可由下式求解

|
(21) |
其中Shrink为收缩算子, Shrink(a, b)=max|a|-b, 0·sgn(a).(15)式显式解如下

|
(22) |
其中Ω为地震数据区域.类似的(16)式显式解如下

|
(23) |
(17) 式中三项均为二次函数, 故可通过令其导数为零的方式得到显式解, 具体如下

|
(24) |

|
(25) |

|
(26) |
基于(21)—(26)式可给出用于求解(10)式的算法如下:
给定参数α0>0, α1>0, β>0, λ>0, μj>0, j=1, 2, 3, 初始点

步骤1:由(21)式求解xk+1, 由(22)式求解yk+1, 由(23)式求解zk+1;
步骤2:由(24)式求解fk+1;
步骤3:由(25), (26)式求解pk+1;
步骤4:由(18)式求解


步骤5:若算法收敛或达到最大迭代次数则跳出循环, 否则转步1.
3 数值实验本节首先通过两组数值实验对比验证模型(10)对于随机采样的非完整地震图像重建的有效性, 然后将此方法推广到连续采样的情况.
3.1 随机采样针对每组实验分别设置三个对比方法, 第一是基于小波变换的L1正则化方法, 如(5)式所示, 算法采用ISTA; 第二是基于Shearlet变换的L1正则化方法, 即在(12)式中令α1=α2=0;第三是TGV正则化方法, 在(12)式中令λ=0即可.采样方式选择高斯随机采样.关于参数设置, β为保真项权重参数, 令β=1e+3, λ为稀疏项参数, 其大小需根据数据中所含噪声水平设置, 对于不含噪声数据设λ=0.08, α0=0.01, α1=0.001.衡量图像重建质量的相对误差公式为

|
(27) |
其中ftrue为原始完整数据, f为算法重建数据.
图 1a为截取的部分水平层状介质图像, 图 1b为随机抽取50%道所得图像, 由此进行重建, 对比验证本文所提方法的重建效果.图 2a为本文所提方法所得结果, 重点对比图中两个局部细节, 如图 2a中两个红色方框所示, 局部放大图像分别由图 2b和图 2c给出.由图 2a可知, 本文所提方法可以在低采样率的情况下较好地重建地下介质图像, 由图 2b和图 2c可知, 本文所提方法不仅可以重建浅层较强反射图像, 深部微弱反射图像也得到较好地重建, 由(27)式可得图 2的相对误差为4.1610×10-4.由图 3—5可知, 基于小波变换的L1正则化方法可以较好的重建浅层反射较强的层状图像, 但细节的保持欠佳, 深层较弱反射图像未能得到有效重建, 其相对误差为0.0015;相比之下, 基于Shearlet变换的L1正则化方法可以有效提升重建质量, 其相对误差为8.9836×10-4; 最后, 基于TGV正则化的方法无法对空缺较多的位置进行有效重建, 其相对误差为9.1343×10-4.为进一步对比四者的重建效果, 取第256道信号单独对比, 其结果分别如图 6、图 7所示.通过对比图中曲线可知, 本文所提方法和基于TGV正则化方法所得结果与原始信号拟合度最高, 然而从图 5可知TGV正则化方法不能完成重建任务, 基于Wavelet变换的L1正则化方法所得信号曲线与原始信号拟合度较差, 尤其对于200 ms以下振幅较小的信号, 基于Shearlet变换的L1正则化方法所得结果虽然在在总体上有较大提升, 但其所得结果的振幅有一定的损失.图 8为不同采样率下四种方法的相对误差曲线, 相对误差曲线从整体上反映了对不同采样率的情况四种方法重建结果的好坏.从图中可知, 对于不同采样率, 本文所提基于Shearlet变换的双正则化方法所得结果的相对误差最小.

|
图 1 (a) 原始图像; (b)随机采样50%所得图像 Fig. 1 (a) Original image; (b) Image with 50% sampling rate |

|
图 2 (a) Shearlet+TGV+L1重建结果; (b)方框1的局部放大图像; (c)方框2的局部放大图像 Fig. 2 (a) Result via Shearlet+TGV+L1; (b) Partially enlarged image in box 1; (c) Partially enlarged image in box 2 |

|
图 3 (a) Wavelet+L1重建结果;(b)方框1的局部放大图像;(c)方框2的局部放大图像 Fig. 3 (a) Result via Wavelet+L1; (b) Partially enlarged image in box 1; (c) Partially enlarged image in box 2 |

|
图 4 (a) Shearlet+L1重建结果;(b)方框1的局部放大图像;(c)方框2的局部放大图像 Fig. 4 (a) Result via Sheralet+L1; (b) Partially enlarged image in box 1; (c) Partially enlarged image in box 2 |

|
图 5 (a) TGV重建结果; (b)方框1的局部放大图像; (c)方框2的局部放大图像 Fig. 5 (a) Result via TGV; (b) Partially enlarged image in box 1; (c) Partially enlarged image in box 2 |

|
图 6 (a) Shearlet+TGV+L1单道结果; (b) Wavelet+L1单道结果 Fig. 6 (a) Single trace result via Shearlet+TGV+L1; (b) Single trace result via Wavelet+L1 |

|
图 7 (a) Shearlet+L1单道结果; (b) TGV单道结果 Fig. 7 (a) Single trace result via Shearlet +L1; (b) Single trace result via TGV+L1 |

|
图 8 不同采样率的相对误差曲线 Fig. 8 Relative error curves for different sampling rates |
第二组数值实验的原始图像及50%采样结果如图 9所示, 该数据体较上一组数据具有较复杂的结构.采样方法, 稀疏变换及参数设置保持不变.图 10展示了本文所提方法的重建结果及局部放大图, 相对误差为8.1904×10-4, 由图可看出, 重建效果较好, 细节恢复较真实.图 11为基于Wavelet变换下的L1正则化方法重建结果及局部放大图, 相对误差为0.0024, 此结果相对误差较大, 图中出现了纵向伪影.图 12为基于Shearlet变换的L1正则化方法的重建结果及局部放大图, 相对误差为0.0012.图 13为TGV正则化方法的重建结果及局部放大图, 相对误差为7.7479×10-4.综合对比图 10—13可知, 本文所提方法相比另外三种方法可以较好的重建复杂地下介质图像, 细节也得到了较好的保持.图 14和图 15为四种方法的单道对比图, 由图可知本文所提方法所得信号与原信号的拟合度更高.图 16为四种方法在不同采样率情况下的相对误差曲线, 由此可知对于不同采样率的情况, 本文所提基于Shearlet变换的双正则化方法所得结果的相对误差最小.

|
图 9 (a) 原始图像; (b) 50%采样结果 Fig. 9 (a) Original wavefield image; (b) Image with 50% sampling rate |

|
图 10 (a) Shearlet+TGV+L1所得结果; (b)方框1的局部放大图像; (c)方框2的局部放大图像 Fig. 10 (a) Result via Shearlet+TGV+L1; (b) Partially enlarged image in box 1; (c) Partially enlarged image in box 2 |

|
图 11 (a) Wavelet+L1所得结果; (b)方框1的局部放大图像; (c)方框2的局部放大图像 Fig. 11 (a) Result via Wavelet+L1; (b) Partially enlarged image in box 1; (c) Partially enlarged image in box 2 |

|
图 12 (a) Shearlet+L1重建所得结果; (b)方框1的局部放大图像; (c)方框2的局部放大图像 Fig. 12 (a) Result via Shearlet+L1; (b) Partially enlarged image in box 1; (c) Partially enlarged image in box 2 |

|
图 13 (a) TGV重建所得结果; (b)方框1的局部放大图像; (c)方框2的局部放大图像 Fig. 13 (a) Result via TGV; (b) Partially enlarged image in box 1; (c) Partially enlarged image in box 2 |

|
图 14 (a) Shearlet+TGV+L1单道结果; (b) Wavelet+L1单道结果 Fig. 14 (a) Single trace result via Shearlet+TGV+L1; (b) Single trace result via Wavelet+L1 |

|
图 15 (a) Shearlet +L1单道结果; (b) TGV单道结果 Fig. 15 (a) Single trace result via Shearlet +L1; (b)Single trace result via TGV |

|
图 16 不同采样率的相对误差曲线 Fig. 16 Relative error curves for different sampling rates |
综合两组数值实验可知, 第一, 基于压缩感知的L1正则化可以在较低采样率的情况下完成重建任务, TGV正则化方法则难以完成, 这是因为在空缺较大的位置, TGV正则化方法会将其识别为边界, 且TGV正则化方法具有良好的保护边界的性质, 故其难以完成重建任务.第二, 稀疏变换是L1正则化方法的关键, 经变换后得到系数越稀疏, 重建效果越好, 两组实验均显示基于Shearlet变换的L1正则化方法的重建结果较基于小波变换的L1正则化方法有较大提高, 这得益于Shearlet变换的多方向, 多尺度性质, 其可以对信号进行更稀疏的表示.第三, 本文所提的基于Shearlet变换的L1和TGV双正则化方法可以较好的重建地下介质图像, 从整体上, 对于不同采样率, 相对误差都是最小的, 从局部细节上, 底部弱反射图像亦得到了较好的重建效果.
3.2 非随机采样上述两组随机采样的实验是基于压缩感知技术的, 而压缩感知理论的基础是随机采样, 然而实际中常出现连续缺道的情况, 难以满足随机采样的假设, 故本节将模型10推广至连续采样的情况.本节不设置对比实验, 仅验证本文所提方法对于连续采样的非完整地震数据重建的有效性.不失一般性, 分别对原始图像连续抽取10道、15道、20道, 由此采用本文所提方法进行重建, 所得结果和绝对误差分别如图 17、图 18和图 19所示.由图可知, 三种情况均可得到良好的重建结果, 这表明本文所提方法具有一定的空间表示能力, 可以对有限范围的连续缺失道进行重建, 然而随着缺失道数的增加, 重建结果将会变差, 绝对误差也将明显增大.

|
图 17 (a) 连续缺失10道; (b)重建结果; (c)绝对误差 Fig. 17 (a) The case of 10 missing traces; (b) Reconstruction result; (c) Absolute error |

|
图 18 (a) 连续缺失15道; (b)重建结果; (c)绝对误差 Fig. 18 (a) The case of 15 missing traces; (b) Reconstruction result; (c) Absolute error |

|
图 19 (a) 连续缺失20道; (b)重建结果; (c)绝对误差 Fig. 19 (a) The case of 20 missing traces; (b) Reconstruction result; (c) Absolute error |
由于缺道, 坏道等问题, 地震数据常出现不完整现象, 从反演的角度看, 非完整图像重建是一个不适定的反问题.压缩感知技术可以利用较少的随机采样数据重建完整信号, 其主要思想是利用信号在某一变换域内的稀疏性, 为反问题的求解提供了稀疏先验信息, 基于此, 可将信号重建问题转换为L1正则化问题, L1正则化项用于促进解的稀疏性, 然而其未考虑地下图像的结构特性.本文将TGV正则化引入L1正则化模型, 构建基于L1和TGV的双正则化模型, 用于地下介质图像的重建.相比小波变换, Shearlet变换具有多尺度, 多方向性, 通过该变换得到的系数更稀疏, 故本文通过Shearlet变换获得信号的稀疏性.基于所建模型的分块形式, 本文采用交替方向乘子法计算所提基于Shearlet变换的双正则化模型.最后, 通过数值实验对比了三种方法, 包括了基于小波变换和Shearlet变换的L1正则化方法以及TGV正则化方法, 结果显示基于小波变换和Shearlet变换的L1正则化方法及本文所提的双正则化方法均可在随机采样50%的情况下重建地下介质图像, 但基于小波变换的L1正则化方法难以较好的重建图中细节, 基于Shearlet变换的L1正则化虽然可使重建质量大幅提高, 但其重建结果的振幅会有一定的损失, 相比之下, 本文所提基于Shearlet变换的L1和TGV的双正则化方法可以较好地重建图像, 重建结果的相对误差较小, 局部细节及深层弱反射信号均可得到较好的重建.
压缩感知的理论基础是随机采样, 然而实际中也常出现地震道大范围连续缺失的情况, 这难以满足随机采样的假设.对于有限的连续缺失的情况, 本文所提重建方法亦具有一定的有效性, 然而对于大面积连续缺失的情况, 如连续缺失25道以上, 则重建结果较差.因此, 如何对大范围连续缺失信号进行更好的空间表示, 利用有限的信息进行重建, 发展更好的重建方法将是我们下一步的研究重点, 如由数据驱动的机器学习重建方法等.
致谢 感谢评审人提出的宝贵意见, 使得本文的研究内容有了很大的充实.
Anagaw A Y, Sacchi M D. 2012. Edge-preserving seismic imaging using the total variation method. Journal of Geophysics and Engineering, 9(2): 138-146. DOI:10.1088/1742-2132/9/2/138 |
Bai L S, Liu Y K, Lu H Y, et al. 2014. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing. Chinese Journal of Geophysics (in Chinese), 57(9): 2937-2945. |
Beck A, Teboulle M. 2009. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences, 2(1): 183-202. DOI:10.1137/080716542 |
Bredies K, Holler M. 2015a. A TGV-based framework for variational image decompression, zooming, and reconstruction. Part Ⅰ:Analytics. SIAM Journal on Imaging Sciences, 8(4): 2814-2850. DOI:10.1137/15M1023865 |
Bredies K, Holler M. 2015b. A TGV-based framework for variational image decompression, zooming, and reconstruction. Part Ⅱ:Numerics. SIAM Journal on Imaging Sciences, 8(4): 2851-2886. DOI:10.1137/15M1023877 |
Bredies K, Kunisch K, Pock T. 2010. Total generalized variation. SIAM Journal on Imaging Sciences, 3(3): 492-526. DOI:10.1137/090769521 |
Blumensath T, Davies M E. 2009. Iterative hard thresholding for compressed sensing. Applied and Computational Harmonic Analysis, 27(3): 265-274. |
Candès E J, Romberg J, Tao T. 2006a. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on information theory, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
Candès E, Demanet L, Donoho D, et al. 2006b. Fast discrete curvelet transforms. Multiscale Modeling and Simulation, 5(3): 861-899. DOI:10.1137/05064182X |
Cao J J, Wang Y F, Yang C C. 2012. Seismic data restoration based on compressive sensing using the regularization and zero-norm sparse optimization. Chinese Journal of Geophysics (in Chinese), 55(2): 596-607. |
Cao J, Wang Y, Zhao J, et al. 2011. A review on restoration of seismic wavefields based on regularization and compressive sensing. Inverse Problems in Science and Engineering, 19(5): 679-704. DOI:10.1080/17415977.2011.576342 |
Donoho D L. 2006. Compressed sensing. IEEE Transactions on information theory, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
Gülünay N. 2003. Seismic trace interpolation in the Fourier transform domain. Geophysics, 68(1): 355-369. |
Gholami A, Sacchi M D. 2013. Fast 3D blind seismic deconvolution via constrained total variation and GCV. SIAM Journal on Imaging Sciences, 6(4): 2350-2369. DOI:10.1137/130905009 |
Häuser S, Ma J. 2012. Seismic data reconstruction via shearlet-regularized directional inpainting. Preprint, May.
|
Häuser S, Steidl G. 2012. Fast finite shearlet transform. arXiv preprint arXiv: 1202.1773.
|
Hennenfent G, Fenelon L, Herrmann F J. 2010. Nonequispaced curvelet transform for seismic data reconstruction:A sparsity-promoting approach. Geophysics, 75(6): WB203-WB210. DOI:10.1190/1.3494032 |
Hennenfent G, Herrmann F J. 2008. Simply denoise:Wavefield reconstruction via jittered undersampling. Geophysics, 73(3): V19-V28. DOI:10.1190/1.2841038 |
Herrmann F J, Hennenfent G. 2008. Non-parametric seismic data recovery with curvelet frames. Geophysical Journal International, 173(1): 233-248. DOI:10.1111/j.1365-246X.2007.03698.x |
Hinterberger W, Scherzer O. 2006. Variational methods on the space of functions of bounded Hessian for convexification and denoising. Computing, 76(1): 109-133. |
Kabir M M N, Verschuur D J. 1995. Restoration of missing offsets by parabolic Radon transform. Geophysical Prospecting, 43(3): 347-368. DOI:10.1111/j.1365-2478.1995.tb00257.x |
Kong D, Peng Z. 2015. Seismic random noise attenuation using shearlet and total generalized variation. Journal of Geophysics and Engineering, 12(6): 1024-1035. DOI:10.1088/1742-2132/12/6/1024 |
Kutyniok G, Shahram M, Zhuang X. 2012. Shearlab:A rational design of a digital parabolic scaling algorithm. SIAM Journal on Imaging Sciences, 5(4): 1291-1332. DOI:10.1137/110854497 |
Lari H H, Gholami A. 2014. Curvelet-TV regularized Bregman iteration for seismic random noise attenuation. Journal of Applied Geophysics, 109: 233-241. DOI:10.1016/j.jappgeo.2014.08.005 |
Lysaker M, Lundervold A, Tai X C. 2003. Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time. IEEE Transactions on image processing, 12(12): 1579-1590. DOI:10.1109/TIP.2003.819229 |
Ma J. 2011. Improved iterative curvelet thresholding for compressed sensing and measurement. IEEE Transactions on Instrumentation and Measurement, 60(1): 126-136. DOI:10.1109/TIM.2010.2049221 |
Ronen J. 1987. Wave-equation trace interpolation. Geophysics, 52(7): 973-984. DOI:10.1190/1.1442366 |
Sacchi M D, Ulrych T J. 1996. Estimation of the discrete Fourier transform, a linear inversion approach. Geophysics, 61(4): 1128-1136. DOI:10.1190/1.1444033 |
Sacchi M D, Ulrych T J, Walker C J. 1998. Interpolation and extrapolation using a high-resolution discrete Fourier transform. IEEE Transactions on Signal Processing, 46(1): 31-38. DOI:10.1109/78.651165 |
Spitz S. 1991. Seismic trace interpolation in the FX domain. Geophysics, 56(6): 785-794. DOI:10.1190/1.1443096 |
Stolt R H. 2002. Seismic data mapping and reconstruction. Geophysics, 67(3): 890-908. DOI:10.1190/1.1484532 |
Tang G, Ma J. 2011. Application of total-variation-based curvelet shrinkage for three-dimensional seismic data denoisin. IEEE geoscience and remote sensing letters, 8(1): 103-107. DOI:10.1109/LGRS.2010.2052345 |
Tropp J A, Gilbert A C. 2007. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Transactions on information theory, 53(12): 4655-4666. DOI:10.1109/TIT.2007.909108 |
Vese L. 2001. A Study in the BV Space of a Denoising-Deblurring Variational Problem. Applied Mathematics and optimization, 44(2): 131-161. |
Wang J, Ng M, Perz M. 2010. Seismic data interpolation by greedy local Radon transform. Geophysics, 75(6): WB225-WB234. DOI:10.1190/1.3484195 |
Yang J, Zhang Y. 2011. Alternating direction algorithms for L1-problems in compressive sensing. SIAM Journal on Scientific Computing, 33(1): 250-278. |
Yin W. 2010. Analysis and generalizations of the linearized Bregman method. SIAM Journal on Imaging Sciences, 3(4): 856-877. DOI:10.1137/090760350 |
Yin W, Osher S, Goldfarb D, et al. 2008. Bregman iterative algorithms for L1-minimization with applications to compressed sensing. SIAM Journal on Imaging Sciences, 1(1): 143-168. DOI:10.1137/070703983 |
Zhang F, Dai R, Liu H. 2014. Seismic inversion based on L1-norm misfit function and total variation regularization. Journal of Applied Geophysics, 109: 111-118. DOI:10.1016/j.jappgeo.2014.07.024 |
Zhang L, Han L G, Xu D X, et al. 2017. Seismic data reconstruction with Shearlet transform based on compressed sensing technology. Oil Geophysical Prospecting, 52(2): 220-225. |
白兰淑, 刘伊克, 卢回忆, 等. 2014. 基于压缩感知的Curvelet域联合迭代地震数据重建. 地球物理学报, 57(9): 2937-2945. |
曹静杰, 王彦飞, 杨长春. 2012. 地震数据压缩重构的正则化与零范数稀疏最优化方法. 地球物理学报, 55(2): 596-607. |
张良, 韩立国, 许德鑫, 等. 2017. 基于压缩感知技术的Shearlet变换重建地震数据. 石油地球物理勘探, 52(2): 220-225. |
 2020, Vol. 63
2020, Vol. 63


