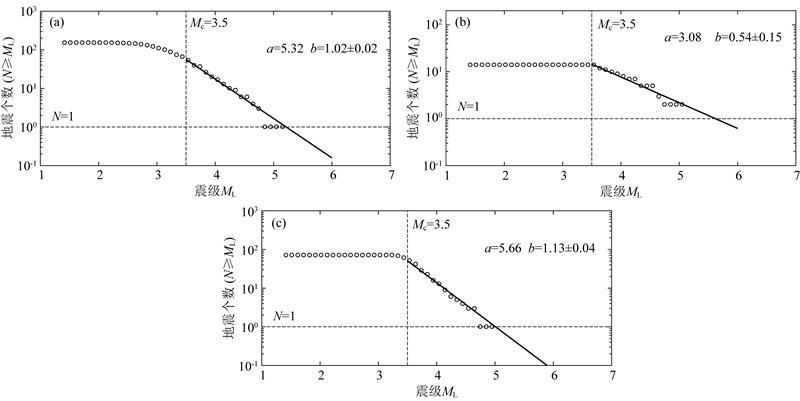
地震研究的终极目标是对地震事件的发生时间、位置和震级进行准确的预测.目前,地震短期预测仍是具有高复杂度的世界性科学难题,现有的预测方法仍存在很大的可创新空间(周硕愚等,2019).对于地壳内部的构造地震而言,地震事件的发生是整体断层系统长期演化的结果.因此,地震预测方法的发展离不开对发震断层内部的摩擦过程及触发机制的研究.随着观测技术和岩石物理学实验的深入开展,人们对断层演化物理机制的研究取得了深入的认识,表明地震的演化过程就是断层在不同时空状态下克服摩擦的过程.基于近三十年实验结果所得到的摩擦本构关系,即速率-状态摩擦定律(Rate- and State-Dependent Friction Law,以下简称RSF)为定量化描述断层内部的复杂属性提供了一个基本框架(Dieterich, 1972, 1978, 1979a, 1979b; Ruina, 1980, 1983; Rice, 1983).前人应用RSF的数值分析成功地解释和重现了地震演化周期的各个阶段(Dieterich, 1992, 1994; Rubin and Ampuero, 2005; 张龙等,2013),因此,RSF已成为了解地震成因机制和断层时空演化的重要依据.
前震泛指主震之前较短时间内,在主震附近发生的中小地震.而主震发生之前所出现的一系列前震活动则构成了整个的前震序列(周少辉和蒋海昆,2016).本文所讨论的前震是与主震发生时间、空间位置接近,和主震发生有着直接关系的“前震”(foreshock).在所有的地震所出现的短临前兆中,前震是公认最有效的强震预测指标之一(周少辉和蒋海昆,2016).例如1975年海城MS7.3地震的成功预报主要依靠于前震序列所提供的时间、空间和地震频次信息(Wang et al., 2006).因此,对前震成因机制的研究可为地震短临预测提供重要的参考.利用统计学方法,前人对前震活动进行了系统性的总结,其中释放加速的小震活动和古登堡-里克特定律中b值变小是前震序列最典型的两个特征(周少辉和蒋海昆,2016).从力学成因机制上考虑,统计规律中得到的这两个特征是否拥有共性仍需要进一步分析探讨,因此,了解其力学成因机制是尤为重要的.描述前震序列加速发生的经验模型可表示为Ṅ=αt-ω,其中,Ṅ为前震发生率,α为常数,ω为接近于1的常数,t为距主震发生的时间(Scholz, 2002).经验模型明确地表达出了前震发生的加速特征,但未能解释前震的力学机制.Popov(2010)则认为前震是整个地震成核和快速蠕动过程中的一部分.基于RSF,Popov(2010)给出了前震发生率Ṅ可近似于A/(Hlt),其中,t为距主震发生时间,H=B/Dc-k/σ,σ为断层上有效正应力,A和B为RSF中的摩擦参数,Dc为临界滑动位移,k=Gη/l,G为剪切模量,l为断层的特征尺度,η为描述裂纹几何状态的参数,一般近似于1.上述近似表达式虽然从地震成核的角度量化了时间与前震发生率的关系,表达出前震发生率随着主震的临近而逐渐升高,但仍不能完整地描述前震序列的基本活动性特征和包括“前震-主震-余震”在内的整个地震序列时空变化的特征.例如,无法反映出类似1975年海城MS7.3地震前震序列中大震前所出现暂时“平静”的现象(王琳等,2013).
基于RSF,本文将进一步探讨前震产生的力学成因机制,利用Dieterich(1992, 1994)所提出的断层滑移函数研究前震序列中地震活动性增加,以及一些前震序列在大震前出现短暂“平静”现象的可能的原因,并探讨前震序列中古登堡-里克特定律中b值变小与前震序列加速发生所存在的可能的共性.
1 方法 1.1 基于速率-状态摩擦定律分析前震发生的力学机制
基于RSF,对断层采用单自由度弹簧-滑块模型近似,当断层处于成核阶段并进入自加速过程时,断层上的滑移δ和滑移速率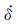
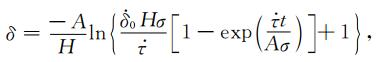
|
(1) |

|
(2) |
其中,H=B/Dc-k/σ,k=Gη/l,σ为作用于断层上的有效正应力,A和B为RSF中的摩擦参数,Dc为临界滑动位移,G为剪切模量,l为断层的特征尺度,η为描述裂纹几何状态的参数,远场剪应力加载速率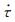

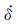
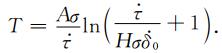
|
(3) |
在描述前震成因机制的模型中,最具有代表性的是Dieterich基于RSF所提出的前震模型-Ⅰ与前震模型-Ⅱ(Dieterich and Kilgore, 1996).前震模型-Ⅰ表示先前地震所产生的应力扰动改变了包括主震在内所有后续地震发生的可能性,即应力扰动影响断层的后续成核和失稳.在这种情况下每一个前震的发生都受先前地震产生的应力变化的影响,而这个地震发生后所产生的新应力扰动又继续影响着后续的地震发生.前震模型-Ⅱ则表示了主震成核区域的断层自加速滑移触发了前震,即主震成核过程中的主震断层自加速滑移驱动了前震加速成核(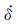
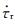


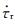
|
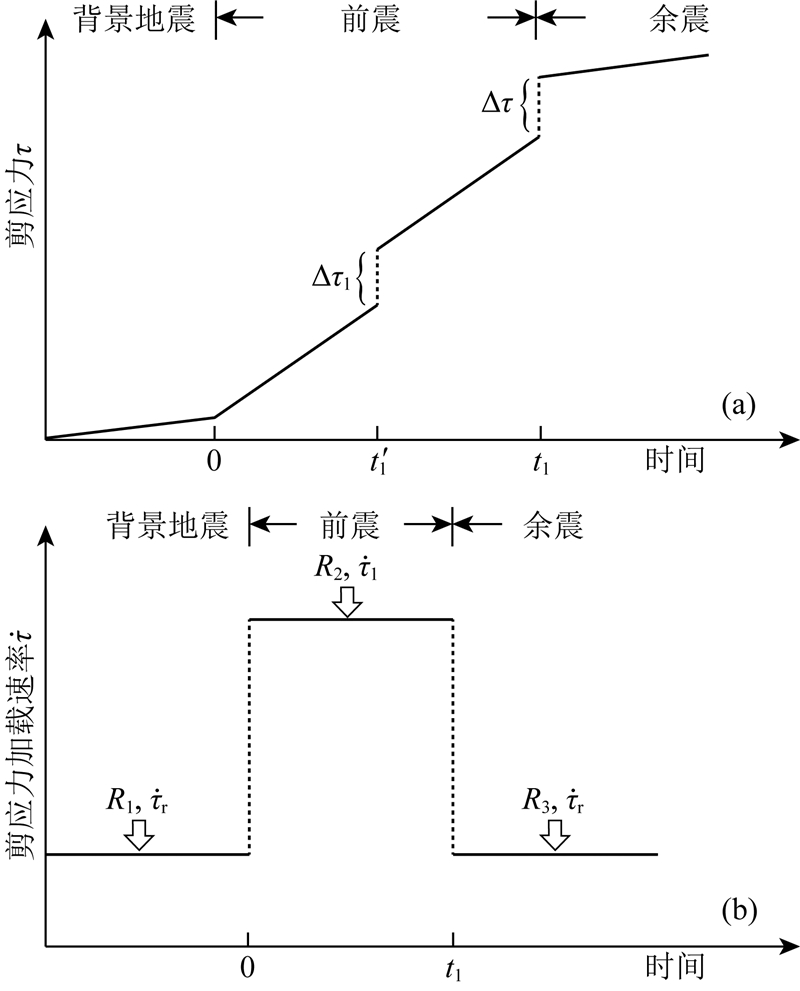
图 1 (a) 剪应力随时间变化示意图;(b)剪应力加载速率随时间变化示意图 Fig. 1 (a) Schematics diagram showing how the shear stress vary with time; (b) Schematics diagram showing how the shear stressing rate vary with time |
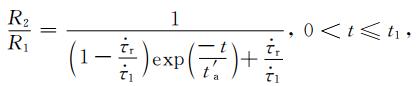
|
(4) |
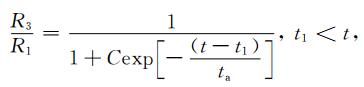
|
(5) |

|
(6) |
在公式(4),(5)和(6)中,R1表示剪应力加载速率为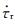


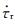
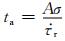
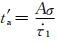

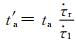
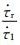
若t1持续时间非常短,即t1 < t′a,且由主震成核引起的前震成核区剪应力上升率远大于由远场加载引起的剪应力上升率,即
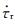
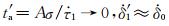
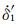
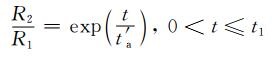
|
(7) |
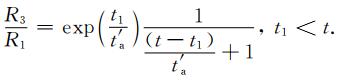
|
(8) |
主震的出现代表前震序列的结束,震源区的剪应力加载速率恢复到背景水平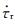
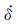
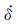
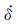
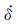
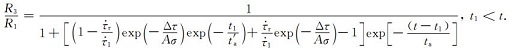
|
(9) |
若前震序列中小震发生时对震源区产生的应力扰动相对于主震成核对前震震源区造成的应力升高可以忽略,则利用前震模型-Ⅱ得到的公式(4)便可以描述前震序列发生率.但若前震序列中出现中强震时,比如1975年海城MS7.3地震前震序列中出现的MS5.0地震,此时MS5.0地震的发生对震源区造成的应力扰动不应该被忽略.假设前震序列中中强震的发生对震源区产生应力扰动Δτ1,如图 1所示,则由附录公式(A28)可知受此应力扰动后前震发生率变为
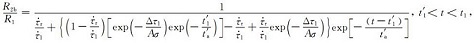
|
(10) |
其中R2b为应力扰动Δτ1产生后前震序列的地震发生率,t′1为Δτ1产生时刻.在这种情况下,主震发生并对震源区产生应力扰动Δτ后,由附录公式(A31)、(A32)和(A33)可知余震发生率可表示为
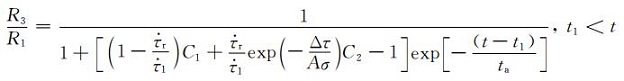
|
(11a) |
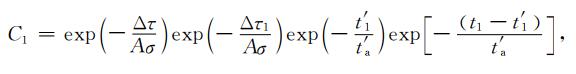
|
(11b) |
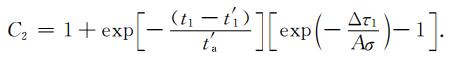
|
(11c) |
从公式(10)中可以看出,受应力扰动后的前震发生率主要取决于
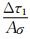
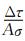
古登堡-里克特震级-频度关系(Gutenberg and Richter, 1944)可以表示为lgN(≥m)=a-bm,其中,N(≥m)表示震级大于等于m的地震总个数,a值代表所选研究区的地震活动总体水平,b值同区域介质特性、应力状态和不均匀性等有关,能反映所研究区域地震的震源特性(Rundle, 1989; Marzocchi and Sandri, 2003).地震数量的增量表示成震级的函数为
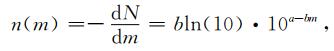
|
(12) |
其中n表示对于无穷小的震级增量所对应的地震个数增量,此时N的单位为个数/年.累积的地震矩率可以表示为
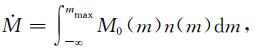
|
(13) |
其中,M0(m)表示震级为m的地震的地震矩,mmax表示所研究序列的最大矩震级.地震矩与震级的关系可近似为M0(m)=10p+q·m(Kanamori and Anderson, 1975),其中p与q为常数,q一般取值为1.5,m代表矩震级.根据Kostrov模型(Scholz, 2002),形变率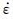
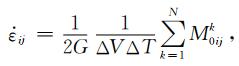
|
(14) |
其中ΔV为研究区体积,ΔT为时间,G为剪切模量.若区域内发震断层的类型基本近似,则剪应力加载率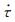
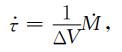
|
(15) |
其中,
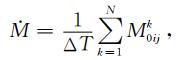
|
(16) |
将公式(15)与(12)和(13)联立可得:
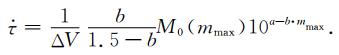
|
(17) |
若在
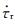

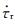
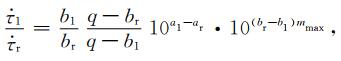
|
(18) |
其中a1与b1表示在
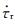
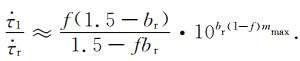
|
(19) |
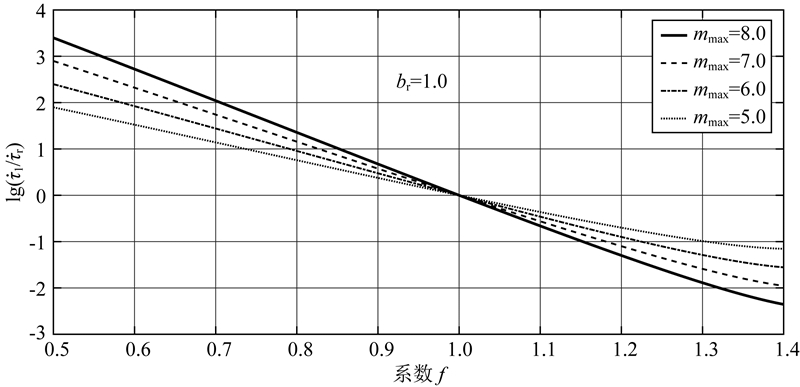
公式(19)建立了研究区内剪应力加载速率的变化与其同时域内b值的变化之间的关系.如图 2所示,当系数f小于1,即b1 < br时,f的取值越小

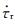
|
图 2
  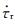 |
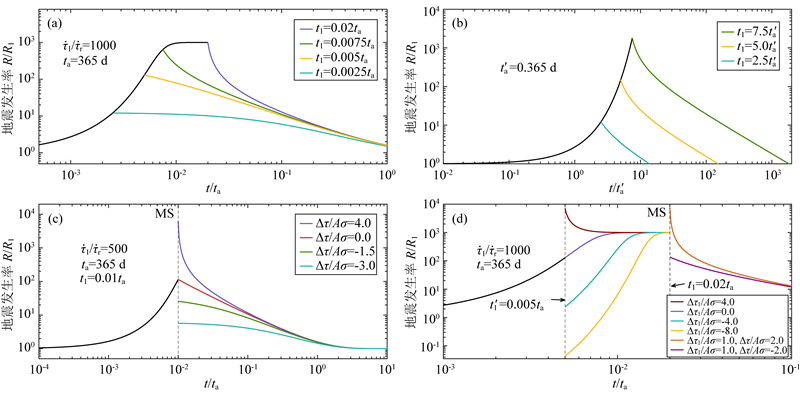
利用前震模型-Ⅱ得到的前震发生率公式(4)与余震发生率公式(5),本文得到如图 3a所示的在不同持续时间t1下地震发生率特征.当t1≪t′a时,前震发生率R2随时间的增加而快速上升;当t1>t′a时,前震发生率R2便维持在一稳定值,此时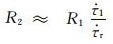
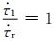
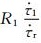
|
图 3
地震发生率随时间演化特征示意图
(a),(b),(c)中黑色实线代表前震,彩色实线代表余震,(d)中主震(MS)发生之前的曲线均代表前震. (a)利用本文公式(4)和(5)拟合前震与余震的地震发生率示意图( =1000,ta=365 d);(b)利用本文公式(7)和(8)拟合前震与余震的地震发生率示意图;(c)利用本文公式(4)和(9)拟合前震与受应力扰动后的余震的地震发生率示意图;(d)利用本文公式(4),(10)和(11)拟合前震,受应力扰动的前震和受应力扰动的余震的地震发生率示意图.
Fig. 3
Schematic diagram of the seismicity rate with time
The black solid curves and the color solid curves in (a), (b), (c) represents the foreshocks and the aftershocks, the curves before the mainshock (MS) in (d) represents the foreshocks.(a) Schematic diagram of foreshocks and aftershocks sequence by Eqs. (4) and (5) ( =1000,ta=365 d);(b)利用本文公式(7)和(8)拟合前震与余震的地震发生率示意图;(c)利用本文公式(4)和(9)拟合前震与受应力扰动后的余震的地震发生率示意图;(d)利用本文公式(4),(10)和(11)拟合前震,受应力扰动的前震和受应力扰动的余震的地震发生率示意图.
Fig. 3
Schematic diagram of the seismicity rate with time
The black solid curves and the color solid curves in (a), (b), (c) represents the foreshocks and the aftershocks, the curves before the mainshock (MS) in (d) represents the foreshocks.(a) Schematic diagram of foreshocks and aftershocks sequence by Eqs. (4) and (5) ( =1000, ta=365 d). (b) Schematic diagram of foreshocks and aftershocks sequence by Eqs. (7) and (8). (c) Schematic diagram of foreshocks and disturbed aftershocks sequence by Eqs. (4) and (9). (d) Schematic diagram of foreshocks, foreshocks affected by stress perturbation and aftershocks affected by stress perturbation by Eqs. (4), (10) and (11). =1000, ta=365 d). (b) Schematic diagram of foreshocks and aftershocks sequence by Eqs. (7) and (8). (c) Schematic diagram of foreshocks and disturbed aftershocks sequence by Eqs. (4) and (9). (d) Schematic diagram of foreshocks, foreshocks affected by stress perturbation and aftershocks affected by stress perturbation by Eqs. (4), (10) and (11).
|
从近似公式(7)和(8)中可以看出,前震发生率的近似解同解析解(4)和(5)所展现的不同之处在于,近似解所表现出的前震发生率R2在主震发生之前是一直以e指数上升的趋势升高,并且主震发生后余震发生率R3最终会趋于0(图 3b),这是因为近似解中忽略了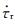
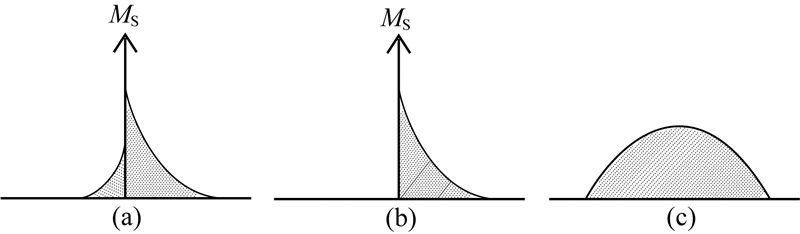
结合公式(4)和(9)可以得到如图 3c所示的前震-主震-余震型序列地震发生率随时间演化特征,当主震对震源区所产生应力扰动Δτ>0时,余震发生率如图 3c中紫色线所示,即在t1时刻地震发生率陡增,随后余震发生率R3逐渐下降,这种地震发生率分布与Scholz(2002)书中所描述的前震-主震-余震型地震序列示意图(图 4a)完全相似.当Δτ=0时,公式(4)与(9)所表现出的地震发生率特征同图 3a完全相同,即在t1时刻地震发生率是连续的.而当应力加载Δτ < 0时,t1时刻的地震发生率会出现较大的下降,但如图 3c中所示,余震发生率R3仍高于背景地震发生率R1且回归到背景地震发生率所需要的时间尺度为ta,与应力扰动Δτ>0时余震发生率回归到背景场水平所需的时间尺度相同.与前人研究结果不同的是,Dieterich(1994)地震发生率模型给出,当应力加载Δτ < 0时便会有地震影区的出现,即t1时刻地震发生率R3便小于背景地震发生率R1,随后R3逐渐上升并经历ta的时间尺度恢复到R1水平.而本文的结果表明应力加载Δτ < 0时并非一定会出现地震影区,也有可能出现地震发生率逐渐下降的余震序列(图 3c).只有当负向应力扰动Δτ足够大时,本文的结果才会出现地震影区.
|
图 4 地震序列类型的示意图(引自Scholz,2002.图 4.22) (a)前震-主震(MS)-余震型序列;(b)主震-余震型序列;(c)群震型序列. Fig. 4 Schematic diagram illustrating the various types of earthquake sequences (from Scholz, 2002. Fig. 4.22) (a) Mainshock (MS) with foreshocks and aftershocks sequence; (b) Mainshock-aftershock sequence; (c) Swarm sequence. |
在前人的研究中,前震模型-Ⅰ与前震模型-Ⅱ是相互独立的两个模型(Dieterich and Kilgore, 1996),而本文将这两个模型结合并进行了定量化研究进而得出公式(4)、(10)与(11).当Δτ1=0时,这组公式所表现出的就是前震模型-Ⅱ,而当Δτ1≠0时,即在前震模型-Ⅱ所蕴含的力学机制基础上,考虑了前震模型-Ⅰ所蕴含的应力变化对前震序列演化特征的影响.如图 3d所示,前震序列在t′1时刻前地震发生率特征同图 3a中R1相同,当Δτ1>0时,t′1时刻地震发生率陡增到一定值后,后续的前震发生率R2b开始下降,在这种情况下整个前震序列演化特征类似于图 4a所示的完整的前震-主震-余震型地震序列,但这段序列其实全部是由后面t1时刻发生的主震的成核所引起.当Δτ1 < 0时前震序列在t′1时刻地震发生率陡降,随后后续的前震序列地震发生率R2b再次逐渐上升.若∣Δτ1∣相对较大,如图 3d中Δτ1/Aσ=-8这条曲线所示,此时t′1时刻的前震发生率R2与背景地震发生率R1之比小于0.1,即表明前震在此时“静止”,随后后续的前震序列R2b逐渐升高.若主震发生在“静止”期之间,则整个地震序列演化特征表现为:逐渐加速的前震→地震发生率平静→主震→余震,这与1975年海城MS7.3地震前震序列的演化特征十分相似(吴开统等,1976;王琳等,2013).若主震发生在前震“静止”期之后,则整个序列演化特征表现为:加速发生的前震→平静→加速发生的前震→主震→余震.图 3d中Δτ1/Aσ=1,Δτ/Aσ=2这条曲线表示t′1时刻前震序列中产生的应力扰动Δτ1>0,且t1时刻主震发生并产生应力扰动Δτ>0时对余震发生率R3的影响,表明在这种情况下R3在t1时刻出现了陡增后,后续的余震发生率逐渐降低,并最终趋于背景地震发生率R1的水平.当Δτ < 0时,本文例举Δτ1/Aσ=1,Δτ/Aσ=-2情况下余震的发生率,在这种条件下R3在t1时刻陡降后,后续的余震发生率逐渐降低并最终趋于R1的水平,若∣Δτ∣足够大,则R3可能在t1时刻下降到R1之下,并经过ta的时间尺度回归到R1的水平,即出现主震后余震的影区.
3 讨论
慢地震是指以几个小时到几个月的时间尺度缓慢地发生了有限的断层位错,但没有高频地震波辐射的断层慢滑动事件(吴忠良和许忠淮, 2013).前人已将RSF应用于慢地震的研究中(Segall et al., 2010; Ikari et al., 2013),其中Segall等(2006)在研究夏威夷Kilauea火山地区慢滑移触发地震时,证明了慢滑移所引起的应力变化的增加(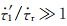
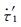
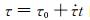
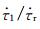
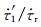
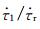
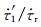
公式(4)是按照Dieterich和Kilgore(1996)前震模型-Ⅱ的力学机制进行的推导,但实际上如前震模型-Ⅰ所述,每一个地震的发生都会对后续的地震产生影响,只不过当这种影响相对于主震成核所造成的影响太小时可忽略,而当前震中出现相对较大震级地震时,就不应该忽略这次地震产生的应力扰动对后续地震的影响,也就表明此时需要将前震模型-Ⅰ的物理过程与前震模型-Ⅱ进行结合,由此本文推出前震公式(10).该公式表明若前震序列中出现的地震对整个震源区产生较大的应力扰动Δτ为负值,则有可能出现前震序列先密集后平静再主震的现象,这也是Scholz(2002)和Popov(2009)所给出Ṅ~t-1前震模型所无法表达的.实际上,前震序列中出现不可忽略的应力扰动Δτ也许不止一次,当考虑多次应力扰动对前震区的影响时,前震发生率在时间空间分布上呈现出的形式可能更为多样.因此,看似完整的一个地震序列(“前震-主震-余震”)也有可能是后续更大地震的一段前震序列,而如何识别不同触发机制的前震仍需要更为深入研究.若前震中出现的中强震产生的应力扰动Δτ足够大,那么其对整个的地震循环将会产生扰动并可影响主震发生的时间,当Δτ为正值时会缩短此次主震成核周期,导致主震提前发生,反之当Δτ为负值时则会导致主震发生时间推迟(解孟雨和史保平,2016).而Δτ的临界值与主震发生时间提前或推后量Δt的大小的确定及与地震预报融合,目前仍是一个难以解决的问题.另外,在给出地震发生所需时间T时(Dieterich, 1992, 1994),本文采用了Dieterich(1994)解中的近似假设,即地震发生时断层的滑移量和滑移速率趋于无穷大,但在实际地震中地震发生时断层滑移量和滑移速率应为一有限值,当滑移量和滑移速率为有限值的断层失稳时间T的解由Beeler和Lockner(2003)给出,但其对于现象的分析则更为复杂.
前人通过元分析(meta-analysis)方法对前震研究的结果表明,很多前震活动可能并未被检测到( Mignan,2014 ).最近,最新的高分辨率地震目录显示,在2008年至2017年间,南加利福尼亚州发生的大部分中强地震都伴有较高地震活动性的前震,而这些前震大多震级非常小,因此之前并未被地震网络探测到,这表明了自然界中的前震活动可能比以往认为的更普遍(Trugman and Ross, 2019).基于本文的方法,若区域内被观测到的背景地震发生率R1为0或者非常接近于0,则观测到的前震发生率R2同样为0或者接近于0,所以在实际应用中,本文的方法更适用于具有检测微小震级地震能力且背景地震活动丰富的地区.理论上,前震分布在主震成核所能够影响到的区域内,但这一区域的边界范围的计算方法暂时仍是一个未被解决的问题.
在Dieterich模型中,单自由度的弹簧滑块模型类比了远场对断层加载速率为Vpl的摩擦过程,即断层的黏滑机制.弹簧的有效刚度k表示为k=Gη/l,其中G为剪切模量,η为描述裂纹几何状态的参数,l为断层的特征尺度,剪切应力加载速率可以写为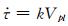
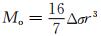
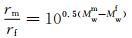
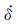
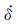

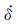
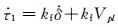

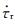

|
图 5 断层滑移速率示意图 Fig. 5 Schematic of fault slip speed |
古登堡-里克特定律中的a值为地震产生率,公式(19)更适用于背景地震和余震与前震a值相近的情况,即满足t1≪t′a.从公式(19)中可以明显看出b值的变化同剪应力加载速率变化的关系,与前震发生率公式相比较可以得出前震b值变小与发生率逐渐增加的共性可能是区域内剪应力加载速率的升高.Gulia和Wiemer(2019)的近期研究表明,震级大于MW6.0的主震的余震的b值通常比背景地震的b值大20%左右,而若MW6.0或更大震级的地震发生后伴随的“余震”序列的b值相对背景场b值变小或者不变,则可能发生更大震级的地震,并依此提出了FTLS (Foreshock Traffic Light System),以用于对地震风险的评估.Gulia和Wiemer (2019)认为前震序列b值减小也许是因为前震区域内应力的升高,而我们的成果可能会对前震序列中b值的减小的原因提供新的认识.
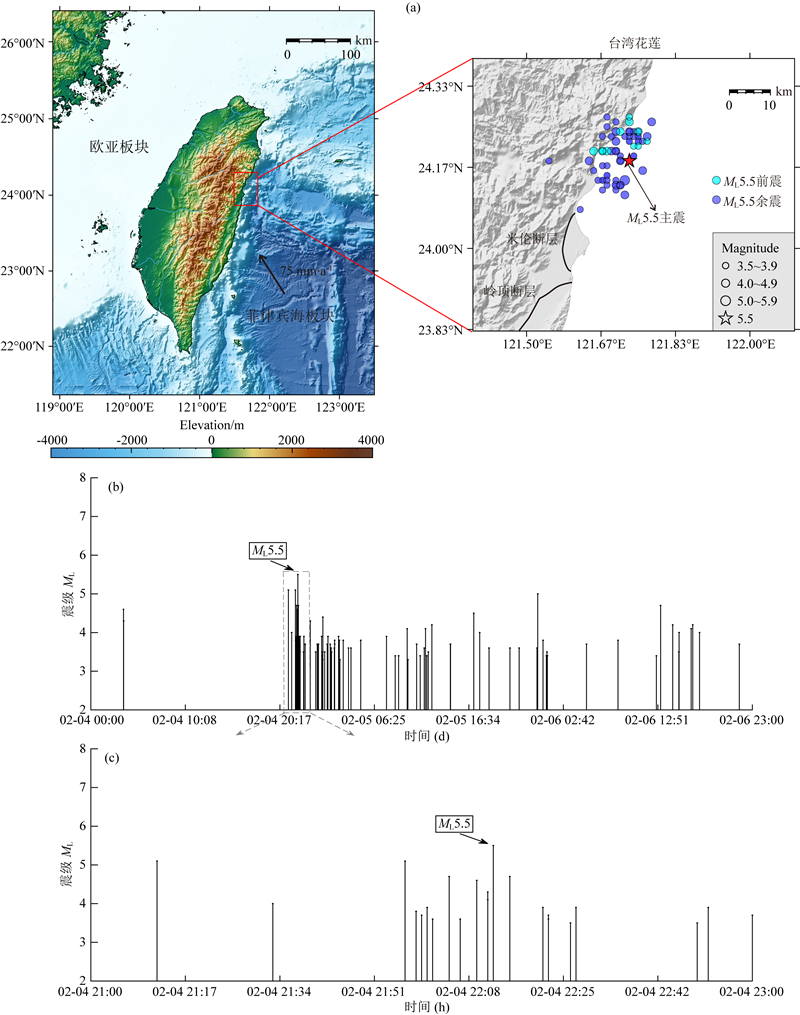
4 实例分析2018年2月4日在我国台湾花莲东海岸米伦断层附近(23.83°N—24.39°N,121.38°E—122.1°E)发生了主震震级为ML5.5的前震-主震-余震型地震,ML5.5主震震中位置为24.18°N,121.73°E,震源深度为10 km.在ML5.5主震发生2天后,即2018年2月6日该区域又发生主震震级为ML6.0的主震-余震型地震,ML6.0主震震中位置为24.14°N,121.69°E,震源深度为10 km.自2月4日地震开始后至2月10日,该区域地震共造成17人死亡,295人受伤,4幢建筑坍塌和至少175幢建筑受损.台湾地处环太平洋地震带的西部,该地震带是菲律宾海板块与欧亚板块的边界构造带,菲律宾海板块以大约75 mm·a-1的速度向西北方向俯冲到欧亚板块之下,产生强烈的逆冲和左旋剪切作用,形成海岸山脉和纵谷断裂(邓起东等,2002;USGS,2018),造成该地区地震活动极为频繁.而此次花莲地震序列是由菲律宾海板块和欧亚大陆板块之间的米伦断层左旋走滑所致(Kuo et al., 2018).本文的重点是研究2018年2月4日ML5.5地震序列,ML5.5地震前震、ML5.5地震及其余震的空间与时间分布如图 6所示.从图 6b与图 6c中可以看出ML5.5地震前震发生率逐渐升高,ML5.5地震发生后地震频率开始降低.从图 6a中可以看出ML5.5前震集中在ML5.5地震北方且处于ML5.5余震空间分布范围之内,ML5.5余震分布围绕在ML5.5地震10 km内,其东北至西南走向展布约20 km,西北至东南走向展布约10 km.
|
图 6 台湾地形图及花莲ML5.5地震序列时空分布图 (a)台湾地形图与花莲ML5.5地震序列空间分布图;(b)花莲ML5.5地震序列M-T图;(c)花莲ML5.5地震前2 h与地震后1 h M-T图(图 6b中虚线框内的放大图). Fig. 6 Time and space distribution of the Hualian ML5.5 earthquake sequence and topography map of Taiwan (a) Map showing topography of Taiwan, and locations of the Hualian ML5.5 earthquake sequence; (b) M-T diagram of Hualian ML5.5 earthquake sequence; (c) M-T diagram of 2 hours before the Hualian ML5.5 earthquake and 1 hour after the earthquake (Enlarged figure of the dashed box in Fig. 6b). |
图 7表示了花莲ML5.5地震发生前2 h的前震及其震后2 h的余震地震发生率与时间的关系,单位为个数/小时.黑色圆圈代表其x轴对应的时间点前后半小时中研究区内发生地震的总个数,即实际地震发生率,单位为个数/小时.黑色实线代表利用本文地震发生率公式(4)与(5)拟合情况,黑色虚线表示利用发生率近似公式(7)与(8)的拟合情况.花莲地区背景地震平均每4天发生一个,即背景地震发生率R1约为0.0104个/小时.将t1设置为2 h,则从公式(4)、(5)可知待拟合参数为
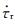

|
图 7 ML5.5前震与余震发生率图 实际地震发生率由时窗推移法求得,其中时窗取0.8 h,每间隔0.25 h计算一次,MS表示主震发生的时刻. Fig. 7 Schematic of ML5.5 foreshock seismicity rate and aftershock seismicity rate The seismicity rate is obtained by migration time window methods, the time window takes 0.8 hours and calculated every 0.25 hours.MS represents the moment when the mainshock occurred. |
拟合结果表明,当ta取值730 h,
利用古登堡-里克特震级-频度关系对花莲地震分析,取完备震级Mc=3.5后利用最大似然法计算得到研究区内a值与b值的变化如表 1和图 8所示.从中可以看出,背景地震和ML5.5余震序列的b值皆接近于1.0,ML5.5前震序列的b值近似为0.5.利用本文公式(19),br取1.0,f取0.5.根据台湾气象局(2018)给出的“1901—2000的灾害性地震列表”及“2001迄今的灾害性地震列表”,自1901年以来台湾花莲地区地震的最大震级为1920年6月5日发生的震源深度为20 km的ML8.3地震.所以研究区内最大震级取ML8.3,则可计算得到
|
|
表 1 通过G-R定律拟合而得到的研究区内不同时间尺度下的a值与b值 Table 1 The calculated a-value and b-value by G-R law with different time spans |
|
图 8 花莲地震序列发生后不同时间段内地震目录的震级-频度(M-F)图 (a)背景地震序列M-F图;(b) ML5.5前震序列M-F图;(c) ML5.5余震序列M-F图. Fig. 8 The Magnitude-Frequency plot for the catalog of Hualian earthquakes with different time spans (a) M-F plot for background earthquake sequence; (b) M-F plot for ML5.5 foreshock sequence; (c) M-F plot for ML5.5 aftershock sequence. |
前震的发生可能由主震成核过程中断层自加速滑移所驱动,当前震成核区受到较大的应力扰动时,后续的前震序列受主震和这次扰动共同影响.本文由Dieterich(1992, 1994)地震发生率模型给出了受主震成核影响下前震发生率的解析表达式与近似公式及受应力扰动影响时的前震发生率公式.解析表达式表明前震发生率由区域应力加载速率
将RSF定律与单自由度弹簧-滑块模型相结合(Dieterich, 1992, 1994)可得到如公式(2)所示的断层滑移速率函数.当单个断层处于成核-自加速过程时,不同时域内断层的滑移速率为
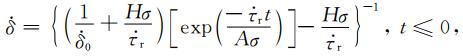
|
(A1) |
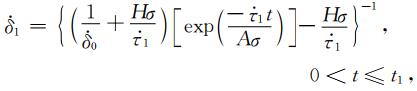
|
(A2) |
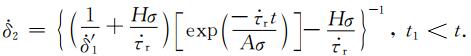
|
(A3) |
假定t=0为前震开始时刻,t1为前震结束主震发生时刻,
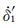
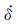
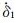
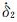
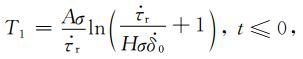
|
(A4) |

|
(A5) |
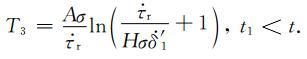
|
(A6) |
在公式(A4),(A5)和(A6)中,T1表示以初始速度
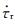

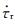

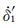

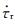
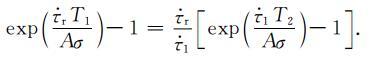
|
(A7) |
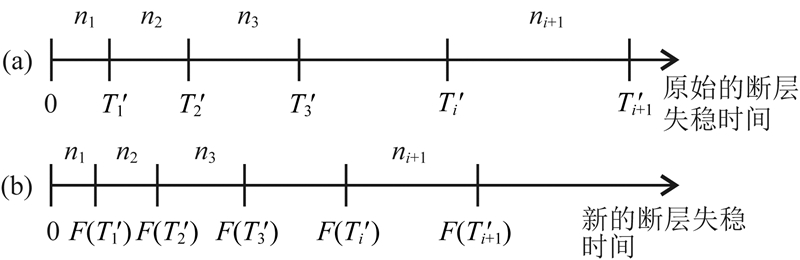
根据Dieterich模型所述的地震群体化模型(Dieterich, 1994; Kaneko and Lapusta, 2008),如附图A1所示,设定任一时间段Δti=ΔT′i+1-ΔT′i内地震发生的个数只同Δti的长短相关,即地震发生频率始终为一常数值,则可将这种状态定义为背景场,由R1来表示.当研究区域内未受到应力扰动时,该区域的背景地震发生率R1保持不变,于是有:
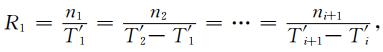
|
(A8) |
|
附图 A1 应力扰动前后断层失稳时间轴变化示意图(引自Kaneko and Lapusta, 2008) (a)受应力扰动前断层的失稳时间;(b)受应力扰动后断层的失稳时间. Fig. A1 Schematics showing how the time to instability for each nucleation site in the population changes due to a stress step (from Kaneko and Lapusta, 2008) (a) The original time to instability for the nucleation site in the absence of perturbation; (b) The time to instability after the static stress perturbation. |
其中ni+1为T′i到T′i+1时间段内地震发生的个数,T′i为背景场下断层失稳的时间(附图A1a).而当研究区域内不同尺度的断层受到应力扰动影响后,每个断层的失稳时间均发生变化,这一现象类似于Coulomb应力加载模型中的时钟提前或推后(ΔCFF/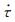
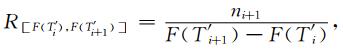
|
(A9) |
将公式(A9)代入公式(A8)中,可得到与背景地震发生率相关的受应力扰动影响后的地震发生率为:
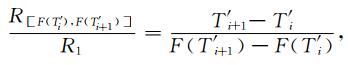
|
(A10) |
而当T'i+1-T'i趋近于无穷小时,其微分解可表示为:

|
(A11) |
则:
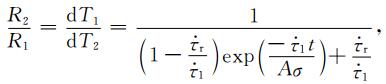
|
(A12) |
公式(A3)可写为
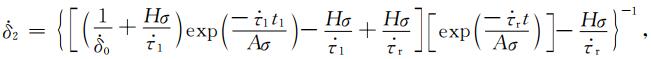
|
(A13) |
当地震发生时,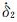

|
(A14) |
由公式(A4)得:

|
(A15) |
进而有:
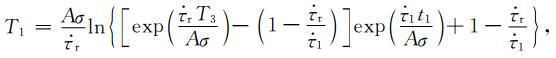
|
(A16) |
则:

|
(A17) |
其中R2表示前震发生率,R3表示主震后的余震发生率.若t1持续时间非常短,即t1≈Δt,且主震成核远大于由板块构造运动对前震成核区的影响,即
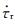
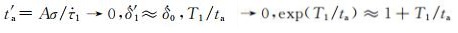
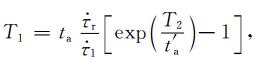
|
(A18) |
进而可得:

|
(A19) |
同理,T3/Aσ≈1/Hσ

|
(A20) |
进而可得:
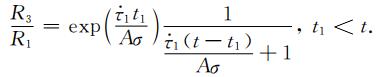
|
(A21) |
若t1时刻主震发生后对研究区域产生的应力扰动为Δτ,并且研究区域内剪应力加载速率恢复到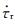
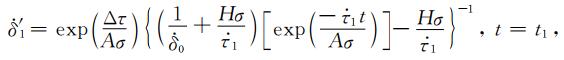
|
(A22) |
将公式(A22)代入公式(A3)中,可得断层失稳时有:

|
(A23) |
将公式(A4)代入公式(A23)中并整理可得施加应力扰动Δτ后余震发生率R3为

|
(A24) |
若前震序列中产生中等强度地震,比如1975年海城MS7.3地震前震序列中的MS5.0地震,并对前震成核区造成的应力扰动为Δτ1,而前震成核仍受主震成核影响时,断层滑移速率可表示为

|
(A25) |
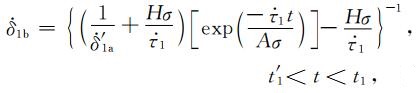
|
(A26) |
其中t′1为前震序列中应力扰动Δτ1产生时刻,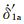
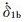

|
(A27) |
将公式(A4)代入公式(A27)中并整理可得:
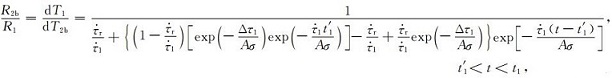
|
(A28) |
其中T2b为应力扰动Δτ1产生后前震序列中地震发生尚需时间,R2b为应力扰动Δτ1产生后后续前震序列的地震发生率.进一步考虑主震发生后产生的应力扰动Δτ对后续余震序列的影响,则断层滑移速率可表示为
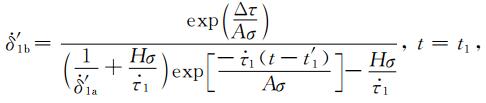
|
(A29) |
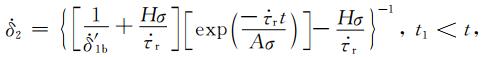
|
(A30) |
其中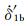
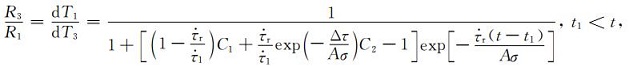
|
(A31) |
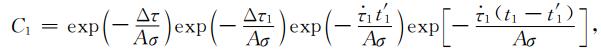
|
(A32) |
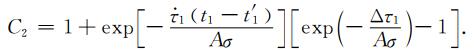
|
(A33) |
Beeler N M, Lockner D A. 2003. Why earthquakes correlate weakly with the solid Earth tides:Effects of periodic stress on the rate and probability of earthquake occurrence. Journal of Geophysical Research:Solid Earth, 108(B8): 2391. DOI:10.1029/2001JB001518 |
Brune J N. 1970. Tectonic stress and the spectra of seismic shear waves from earthquakes. Journal of Geophysical Research, 75(26): 4997-5099. DOI:10.1029/JB075i026p04997 |
Brune J N. 1971. Correction[to "tectonic stress and the spectra, of seismic shear waves from earthquakes"]. Journal of Geophysical Research, 76(20): 5022. |
Deng Q D, Zhang P Z, Ran Y K, et al. 2002. Basic characteristics of active tectonics of China. Science in China Series D:Earth Sciences, 46(4): 356-372. DOI:10.1360/03yd9032 |
Dieterich J H. 1972. Time-dependent friction in rocks. Journal of Geophysical Research, 77(20): 3690-3697. DOI:10.1029/JB077i020p03690 |
Dieterich J H. 1978. Time-dependent friction and the mechanics of stick slip. Pure and Applied Geophysics, 116(4-5): 790-806. DOI:10.1007/BF00876539 |
Dieterich J H. 1979a. Modeling of rock friction:1. Experimental results and constitutive equation. Journal of Geophysical Research:Solid Earth, 84(B5): 2161-2168. DOI:10.1029/JB084iB05p02161 |
Dieterich J H. 1979b. Modeling of rock friction:2. Simulation of preseismic slip.. Journal of Geophysical Research:Solid Earth, 84(B5): 2169-2175. DOI:10.1029/JB084iB05p02169 |
Dieterich J H. 1992. Earthquake nucleation on faults with rate-and state-dependent strength. Tectonophysics, 211(1-4): 115-134. DOI:10.1016/0040-1951(92)90055-B |
Dieterich J H. 1994. A constitutive law for rate of earthquake production and its application to earthquake clustering. Journal of Geophysical Research:Solid Earth, 99(B2): 2601-2618. DOI:10.1029/93JB02581 |
Dieterich J H, Kilgore B. 1996. Implications of fault constitutive properties for earthquake prediction. Proceedings of the National Academy of Sciences of the United States of America, 93(9): 3787-3794. DOI:10.1073/pnas.93.9.3787 |
Gulia L, Wiemer S. 2019. Real-time discrimination of earthquake foreshocks and aftershocks. Nature, 574(7777): 193-199. DOI:10.1038/s41586-019-1606-4 |
Gutenberg B, Richter C F. 1944. Frequency of earthquakes in California. Bulletin of the Seismological Society of America, 34(4): 185-188. |
Hanks T C, Kanamori H. 1979. A moment magnitude scale. Journal of Geophysical Research:Solid Earth, 84(B5): 2348-2350. DOI:10.1029/JB084iB05p02348 |
Ikari M J, Marone C, Saffer D M, et al. 2013. Slip weakening as a mechanism for slow earthquakes. Nature Geoscience, 6(6): 468-472. DOI:10.1038/NGEO1818 |
Jie M Y, Shi B P. 2016. Numerical simulation of fault instability due to an arbitrary static stress perturbation:A comparison with the Dieterich model and Coulomb failure model. Chinese Journal of Geophysics (in Chinese), 59(2): 593-605. DOI:10.6038/cjg20160217 |
Jie M Y. 2018. Study on earthquake triggering mechanism and aftershock activity based on rare-and state-dependent friction law. Beijing:University of Chinese Academy of Sciences.
|
Kanamori H, Anderson D L. 1975. Theoretical basis of some empirical relations in seismology. Bulletin of the Seismological Society of America, 65(5): 1073-1095. |
Kanamori H. 1977. The energy release in great earthquakes. Journal of Geophysical Research, 82(20): 2981-2987. DOI:10.1029/JB082i020p02981 |
Kaneko Y, Lapusta N. 2008. Variability of earthquake nucleation in continuum models of rate-and-state faults and implications for aftershock rates. Journal of Geophysical Research:Solid Earth, 113(B12). DOI:10.1029/2007JB005154 |
Kuo Y T, Wang Y, Hollingsworth J, et al. 2018. Shallow fault rupture of the M1lun fault in the 2018 MW6.4 Hualien earthquake:a high-resolution approach from optical correlation of Pléiades satellite imagery. Seismological Research Letters, 90(1): 97-107. DOI:10.1785/0220180227 |
Marzocchi W, Sandri L. 2003. A review and new insights on the estimation of the b-value and its uncertainty. Annals of Geophysics, 46(6): 1271-1282. |
M1gnan A. 2014. The debate on the prognostic value of earthquake foreshocks:A meta-analysis. Scientific Reports, 4: 4099. |
Narteau C, Byrdina S, Shebalin P, et al. 2009. Common dependence on stress for the two fundamental laws of statistical seismology. Nature, 462(7273): 642-645. DOI:10.1038/nature08553 |
Popov V L. 2010. Contact Mechanics and Friction. Berlin: Springer.
|
Rice J R. 1983. Constitutive relations for fault slip and earthquake instabilities. Pure and Applied Geophysics, 121(3): 443-475. |
Rubin A M, Ampuero J P. 2005. Earthquake nucleation on (aging) rate and state faults. Journal of Geophysical Research:Solid Earth, 110(B11). DOI:10.1029/2005JB003686 |
Ruina A L. 1980. Friction laws and instabilities: A quasistatic analysis of some dry friction behavior[Ph. D. thesis]. Brown University.
|
Ruina A. 1983. Slip instability and state variable friction laws. Journal of Geophysical Research:Solid Earth, 88(B12): 10359-10370. DOI:10.1029/JB088iB12p10359 |
Rundle J B. 1989. Derivation of the complete Gutenberg-Richter magnitude-frequency relation using the principle of scale invariance. Journal of Geophysical Research:Solid Earth, 94(B9): 12337-12342. DOI:10.1029/JB094iB09p12337 |
Scholz C H. 2002. The Mechanics of Earthquakes and Faulting. 2nd ed. New York: Cambridge University Press.
|
Schorlemmer D, Wiemer S, Wyss M. 2005. Variations in earthquake-size distribution across different stress regimes. Nature, 437(7058): 539-542. DOI:10.1038/nature04094 |
Segall P, Desmarais E K, Shelly D, et al. 2006. Earthquakes triggered by silent slip events on Kilauea volcano, Hawaii. Nature, 442(7098): 71-74. DOI:10.1038/nature04938 |
Segall P, Rubin A M, Bradley A M, et al. 2010. Dilatant strengthening as a mechanism for slow slip events. Journal of Geophysical Research:Solid Earth, 115(B12). DOI:10.1029/2010JB007449 |
Taiwan Weather Bureau. 2018. Record of disastrous earthquakes during 1901-2018. https://www.cwb.gov.tw/V8/C/.[2018-04-03].
|
Taiwan Weather Bureau. 2018. Disastrous earthquakes from 2001 to now.https://www.cwb.gov.tw/V8/C/.[2018-04-03].
|
Trugman D T, Ross Z E. 2019. Pervasive foreshock activity across southern California. Geophysical Research Letters, 46(15): 8772-8781. DOI:10.1029/2019GL083725 |
USGS. 2018. Earthquake Hazards Program.https://earthquake.usgs.gov/.[2018-04-03].
|
Wang K L, Chen Q F, Sun S H, et al. 2006. Predicting the 1975 Haicheng earthquake. Bulletin of the Seismological Society of America, 96(3): 757-795. DOI:10.1785/0120050191 |
Wang L, Han M H, Wang P, et al. 2013. Data collection and analysis of Yingkou-Haicheng M7.3 seismic sequence. Journal of Disaster Prevention and Reduction. |
Wu K T, Yue M S, Wu H Y, et al. 1976. Certain characteristics of Haicheng earthquake (M=7.3) sequence. Chinese Journal of Geophysics (Acta Geophysica Sinica) (in Chinese), 19(2): 95-109. |
Wu Z L, Xu H Z. 2013. Seismological Encyclopedia (fourth)-slow earthquake. Recent Developments in World Seismology (in Chinese), (5): 39-42. DOI:10.3969/j.issn.0235-4975.2013.05.009 |
Zhang L, Jiang Z S, Wu Y Q. 2013. Review of rate-and state-dependent friction laws and their applications to seismic faulting. Progress in Geophysics (in Chinese), 28(5): 2352-2362. DOI:10.6038/pg20130517 |
Zhou S H, Jiang H K. 2016. A review of foreshock research. Earthquake (in Chinese), 36(3): 1-13. DOI:10.3969/j.issn.1000-3274.2016.03.001 |
Zhou S Y, Jiang Z S, Shen C Y, et al. 2019. Research into philosophy of science and methodology on earthquake prediction:looking back over 50 years and looking forward. Journal of Geodesy and Geodynamics (in Chinese), 39(7): 661-676. |
邓起东, 张培震, 冉勇康, 等. 2002. 中国活动构造基本特征. 中国科学(D辑), 32(12): 1020-1030. DOI:10.3969/j.issn.1674-7240.2002.12.007 |
台湾气象局. 2018. 1901-2000的灾害性地震列表. https://www.cwb.gov.tw/V8/C/.[2018-04-03].
|
台湾气象局. 2018. 2001迄今的灾害性地震列表. https://www.cwb.gov.tw/V8/C/.[2018-04-03].
|
王琳, 韩敏红, 王鹏, 等. 2013. 营口海城7.3级地震序列资料整理与分析. 防灾减灾学报, (3): 68-70. |
吴开统, 岳明生, 武宦英, 等. 1976. 海城地震序列的特征. 地球物理学报, 19(2): 95-109. |
吴忠良, 许忠淮. 2013. 地震学百科知识(四)——慢地震. 国际地震动态, (5): 39-42. DOI:10.3969/j.issn.0235-4975.2013.05.009 |
解孟雨, 史保平. 2016. 数值模拟静态应力扰动下的断层失稳:结果分析兼与Dieterich模型和Coulomb模型的对比. 地球物理学报, 59(2): 593-605. DOI:10.6038/cjg20160217 |
张龙, 江在森, 武艳强. 2013. 速度-状态摩擦本构定律及其在地震断层中的应用研究进展. 地球物理学进展, 28(5): 2352-2362. DOI:10.6038/pg20130517 |
周少辉, 蒋海昆. 2016. 前震研究进展综述. 地震, 36(3): 1-13. DOI:10.3969/j.issn.1000-3274.2016.03.001 |
周硕愚, 江在森, 申重阳, 等. 2019. 地震预报的科学哲学与方法论探索——50年回眸与前瞻. 大地测量与地球动力学, 39(7): 661-676. |
 2020, Vol. 63
2020, Vol. 63

