2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 青岛 266071;
3. 中国石油西南油气田公司勘探开发研究院, 成都 610041
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China;
3. Research Institute of Exploration and Development, PetroChina Southwest Oil and Gas Field Company, Chengdu 610041, China
与叠后地震反演相比,叠前反演能获得多种储层弹性参数反演结果,可以针对不同的地质状况选择不同的参数反演结果来实现储层识别(Sun et al., 2014).随着油气勘探逐步深入,具有复杂地质构造的油气藏逐渐成为开发的重点,常规的线性反演方法受地震数据频带跟子波影响,很难有效地进行储层预测.而以地质统计学反演为代表的随机反演方法充分利用了测井数据在分辨率上的优势,可以有效地识别地下薄储层(Francis, 2005, 2006a, b;Sams and Saussus, 2008;Grana et al., 2012;王保丽等,2015;孙瑞莹等,2016;沈洪涛等,2017).
叠前地质统计学反演属于多参数反演方法,因此需要考虑反演参数之间的相关性.常规的地质统计学反演方法主要运用了序贯高斯模拟方法(Sequential Gaussian Simulation,SGS)(Deutsch and Journel, 1992)来实现数据的模拟(姜晓宇等,2014).序贯高斯模拟属于条件模拟方法,其首先对硬数据进行高斯变换,之后依次获取各个节点的条件累计分布函数并对其进行抽样,最后对样本值进行高斯反变换,得到模拟结果.由于对模拟数据进行高斯变换的影响,当进行多参数模拟时,序贯高斯模拟就难以再现模拟参数之间的统计分布特征(Soares,2001).针对该问题,Soares(2001)提出了直接序贯模拟(Direct Sequential Simulation,DSS)和直接序贯协模拟(Direct Sequential Co-Simulation,Co-DSS)方法.该模拟方法可以直接在原始数据域对数据进行模拟,不需要进行高斯变换,其利用克里金估计得到的局部均值和方差直接对全局条件分布函数进行采样,因此模拟参数之间的相关特性可以得到很好地体现.之后,基于联合分布的直接序贯协模拟方法(Horta and Soares, 2010;Nunes et al., 2016)的提出更进一步解决了再现非线性相关变量之间统计特点的问题.
传统地质统计学反演的基础是逐道反演方法(Haas and Dubrule, 1994),其受地震信噪比影响,反演结果往往存在着误差累计.而基于全局随机反演策略(Azevedo et al., 2013, 2015)的地质统计学反演方法将模拟及协模拟方法作为模型扰动技术,将模拟结果正演得到的合成地震记录与实际地震记录之间的相关系数作为模拟结果的优选标准以及模型扰动的约束条件,经过不断迭代,可以得到与实际地震记录最为匹配的模拟结果.然而基于直接序贯模拟及协模拟的全局迭代地质统计学反演方法仅通过比较不同模拟结果所合成的地震记录与观测地震记录之间的局部相关系数大小来实现对模拟结果的优选,存在一定的不稳定性(Pereira et al., 2016).针对该问题,本文引入Metropolis优化算法(Metropolis et al., 1953;Hasting,1970)以及考虑先验模型约束及横向约束的目标函数来对模拟结果进行优选,其不仅可以有效避免非线性问题中的局部极值问题,还添加了先验模型约束项与横向约束项(Hamid and Pidlisecky, 2015)来提高反演结果的稳定性及横向连续性.同时,我们根据目标函数的表达形式,重新构建了基于目标函数的优化局部相关系数表达形式,提高了反演的稳定性.
本文将基于联合分布的直接序贯协模拟方法与Metropolis优化算法相结合,在贝叶斯框架下构建目标函数,并构建新的优化局部相关系数,提出了基于Metropolis优化算法和优化局部相关系数的全局迭代地质统计学反演方法.首先利用直接序贯模拟及基于联合分布的直接序贯协模拟得到纵横波阻抗及密度的多个模拟结果,并通过正演关系得到合成地震记录;之后计算对应的目标函数值,利用Metropolis准则对模拟结果进行优选;最后根据目标函数计算当前状态下的优化局部相关系数,并将其与当前反演结果作为条件数据,利用直接序贯协模拟及基于联合分布的直接序贯协模拟重新模拟得到新的模拟结果,并再次利用Metropolis准则对模拟结果进行优选;经过一系列迭代,直到得到最终的反演结果.
1 理论与方法 1.1 直接序贯模拟直接序贯模拟算法可以利用由克里金估计得到的局部均值和方差,直接对模拟参数的全局条件概率分布函数进行抽样.其基础是简单克里金估计(Goovaerts,1997),克里金均值Z(x0)*及克里金方差σE2(x0)可写作:
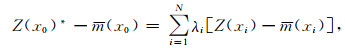
|
(1) |
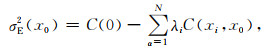
|
(2) |
式中,m(x0)表示模拟数据在待估计点x0的均值,m(xi)为模拟数据在临近点xi的均值,λi为临近点xi的权重系数,Z(xi)表示模拟数据在临近点xi的变量值,C(0)为模拟数据在待估计点x0的方差,C(xi, x0)为模拟数据在待估计点x0与临近点xi的协方差,N表示参与简单克里金计算的临近点个数.其中,权重系数可通过式(3)计算:
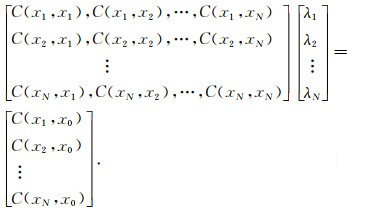
|
(3) |
根据待估计点x0的克里金均值Z(x0)*和克里金方差σE2(x0),可以得到以Z(x0)*为中心值,以σE2(x0)为方差的局部采样区间N(Z(x0)*, σE2(x0)),即:
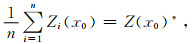
|
(4) |
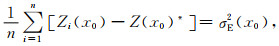
|
(5) |
式中,Zi(x0)为局部采样空间N(Z(x0)*, σE2(x0))的采样值,n为采样值的个数.
根据硬数据的分布特征,定义一个全局累计高斯分布函数G(y(x0)*, σE2(x0)),其中y(x0)*为克里金均值Z(x0)*所对应的高斯值.在高斯分布函数G(y(x0)*, σE2(x0))中产生一个随机的高斯数yG,其所对应的反演参数值即为模拟值Zs(x0)(Azevedo and Soares, 2017).
相比传统的序贯高斯模拟,直接序贯模拟不需要原始数据进行任何非线性变换,通过对变量之间的联合概率分布进行抽样,可以有效地再现变量之间的统计关系.
1.2 基于联合分布的直接序贯协模拟对于叠前地质统计学反演来说,需要模拟得到多个变量(如纵波阻抗、密度、横波阻抗)的模拟结果,这需要考虑变量之间的相关性.传统的协模拟方法只适用于变量之间满足线性相关的情况,当变量之间并不满足完全线性关系时,协模拟方法就难以表征变量之间的统计分布特征(肖亚楠,2018).
针对该问题,Horta和Soares(2010)提出了基于联合分布的直接序贯协模拟方法.在已知其中一个变量的模拟结果的情况下,根据变量之间的联合概率密度分布可以计算其他变量的条件概率分布,通过对条件概率分布进行抽样来再现变量之间的统计关系.
其基础是同位简单协克里金(Xu et al., 1992;Almeida and Journel, 1994),假设Z2为待模拟变量,Z1为已知变量,则待模拟变量Z2在待估计点x0处的克里金均值Z2(x0)*与克里金方差σE2(x0)可用式(6)和(7)进行表征:
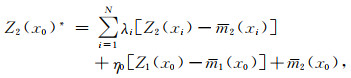
|
(6) |
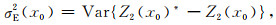
|
(7) |
其中,m2(x0)和m2(xi)分别表征待模拟变量Z2在待估计点x0与临近点xi处的均值,λi是待模拟变量Z2在临近点xi处的权重系数,Z2(xi)为待模拟变量Z2的在临近点xi的变量值,m1(x0)表征已知变量Z1在待估计点处x0的均值,η0是指已知变量Z1在待估计点x0处的协克里金权重,Z1(x0)为已知变量Z1在x0处的变量值.
同位简单协克里金的权重值可用式(8)计算:
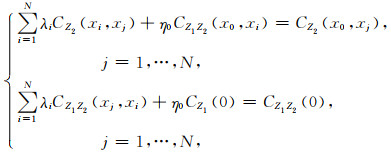
|
(8) |
式中,CZ2(xi, xj)是待模拟变量Z2在临近点xi与xj之间的协方差,CZ1(0)为已知变量Z1在待估计点x0处的方差,CZ1Z2(x0, xi)为待模拟变量Z2与已知变量Z1在临近点xi处与待估计点x0处之间的协方差,CZ1Z2(xj, xi)为待模拟变量Z2与已知变量Z1在临近点xi与xj处之间的协方差,CZ1Z2(0)为已知变量Z1与待模拟变量Z2在待估计点x0处之间的协方差.由于相关系数实际上是未考虑量纲的协方差,待模拟变量Z2与已知变量Z1的协方差CZ1Z2(xi, xj)、CZ1Z2(x0, xi)及CZ1Z2(0)可以利用两者的局部相关系数进行转化,因此局部相关系数可以通过计算克里金权重,应用到随机模拟之中.
基于联合分布的直接序贯模拟方法通过对变量之间的全局联合概率分布函数抽样,不仅可以保证模拟结果满足变量之间的联合概率分布特性,还可以提高模拟的精度.
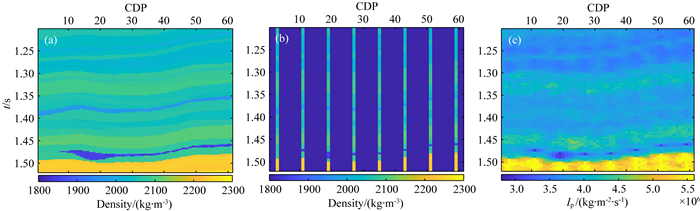
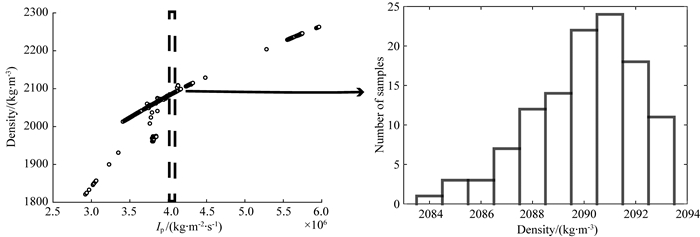
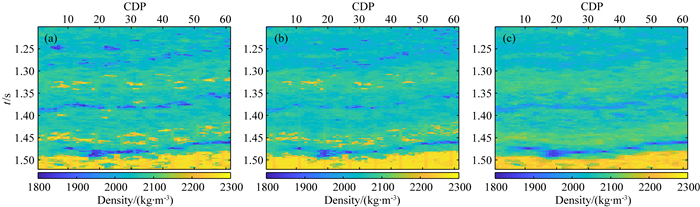
利用Marmous2模型的一部分进行模拟测试.图 1为密度模型(a)、密度伪井数据(b)及已知的纵波阻抗模拟结果(c).图 2为纵波阻抗与密度的联合概率分布及某模拟点的条件概率分布.图 3为直接序贯模拟、直接序贯协模拟及基于联合概率分布的直接序贯协模拟的一次模拟结果.可以发现,基于联合分布的直接序贯协模拟方法的模拟结果更加精确.
|
图 1 密度模型及已知的纵波阻抗模拟结果 (a)密度模型数据;(b)提取的伪井数据;(c)纵波阻抗模拟结果. Fig. 1 Density model and known P-wave impedance simulation result (a) Density model; (b) Pseudo-well data; (c) Known P-wave impedance simulation results. |
|
图 2 纵波阻抗与密度的联合分布及密度条件概率分布直方图 Fig. 2 The joint distribution between P-wave impedance and density, and the histogram of conditional probability distribution of density |
|
图 3 不同模拟结果的对比 (a)直接序贯模拟;(b)直接序贯协模拟;(c)基于联合概率分布的直接序贯协模拟. Fig. 3 Comparison of simulation results (a) Direct sequential simulation; (b) Direct sequential co-simulation; (c) Direct sequential co-simulation based on joint probability distribution. |
本文提出的叠前地质统计学反演方法是在贝叶斯理论的框架下,将直接序贯模拟及基于联合分布的直接序贯协模拟作为模型扰动技术,将考虑先验模型约束项及横向约束项的目标函数及Metropolis准则作为模拟结果的优选手段,并将基于目标函数的优化局部相关系数作为条件约束的全局迭代随机反演方法.
(1) Zoeppritz近似方程及正演关系
叠前地震反演的理论基础是Zoeppritz方程,然而精确的Zoeppritz方程极其复杂,不利于反演(李建华等,2016).因此,许多学者(Aki and Richards, 1980;Shuey,1985;Gidlow et al., 1992)对其进行了简化,提出了Zoeppritz近似方程.
本文主要根据Fatti近似方程(Fatti et al., 1994)来进行叠前反演.该近似公式具体形式为
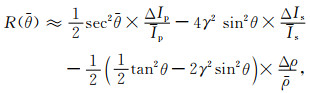
|
(9) |
式中,R(θ)表示PP波反射系数;Ip、Is和ρ分别代表地下纵波阻抗Ip、横波阻抗Is和密度ρ的平均值;ΔIp、ΔIs和Δρ分别代表地层分界面两侧的纵波速度、横波速度和密度的变化量;θ表示入射角;γ为横纵波速比.
给定子波序列W(t),则合成地震记录S(t, θ)可表示为(Sen and Biswas, 2017):
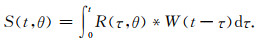
|
(10) |
(2) Metropolis优化算法
传统全局迭代反演方法通过比较局部相关系数的大小来对模拟结果进行优选,当新解的局部相关系数大于旧解的局部相关系数时,进行模型更新,反之保留原有结果.因此其忽略了非线性问题中局部极值的影响,因此本文考虑引入Metropolis优化算法对模拟结果进行优选.
Metropolis优化算法的基础是Metropolis接受准则(Yin et al., 2014),可表示为
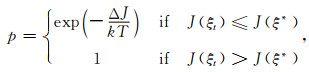
|
(11) |
式中,J表示所构建的目标函数,k和T是可调参数,ξt是当前模型,ξ*为扰动后产生的新模型.可以借鉴模拟退火算法的收敛策略,使接受概率p逐渐衰减,最终得到较为可靠的反演结果.
(3) 基于贝叶斯定理的目标函数构建方法及优化局部相关系数的构建
利用Metropolis优化算法对模型进行优选,需要建立似然函数.本文在贝叶斯理论的框架下,构建了反演的似然函数,并引入了由测井数据构建的平滑模型约束信息及横向约束项,来提高反演的稳定性和横向连续性.
一般来说,地震背景噪声满足均值为0、方差为σn2的正态分布(Pan et al., 2017;Chen et al., 2017),因此似然函数p(d|Ip, Is, ρ)可表示为
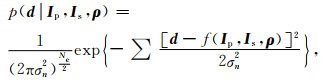
|
(12) |
式中:d为观测地震数据;f代表正演算子;Ne为采样点的个数.
为提高反演的稳定性,我们考虑在似然函数中引入平滑模型约束信息,那么似然函数可表示为
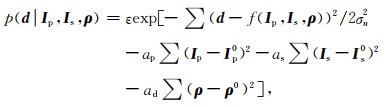
|
(13) |
式中,Ip0、Is0和ρ0为根据测井数据或者确定性反演结果所构建的纵横波阻抗及密度的平滑约束;ap、as与ad为可调因子;ε为一常数.
考虑随机反演的横向连续性问题,我们引入了横向二阶差分约束(Hamid and Pidlisecky, 2015;刘婵娟,2017),因此目标函数可写为
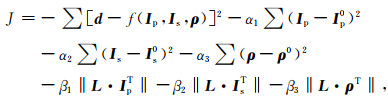
|
(14) |
式中,
传统的局部相关系数是指反演结果所合成的地震记录与实际地震记录之间的互相关,其具体计算公式为(Soares,2001):
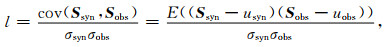
|
(15) |
式中,Ssyn表示模拟结果所合成的地震道集,Sobs表示实际地震道集,σsyn与σobs表示两者的标准差,usyn与uobs为合成地震记录及观测地震记录的振幅均值.
为了使模型更新所利用的相关系数与目标函数保持一致性,并提高反演的稳定性,我们根据目标函数的表达形式,重新构建了基于目标函数的优化局部相关系数表达形式.令z=1+α1+α2+α3+β1+β2+β3,则优化局部相关系数表达式可写为
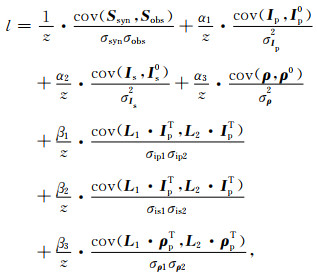
|
(16) |
式中,

本文根据全局随机反演策略,提出了基于Metropolis优化算法的全局迭代反演方法.考虑到纵波阻抗反射系数在AVO近似方程中的权重问题,将纵波阻抗作为横波阻抗及密度模拟的条件数据.因此,其具体步骤如下:
(1) 将已知的测井数据为硬数据,运用直接序贯模拟方法模拟得到纵波阻抗的NS个实现,并利用纵波阻抗模拟结果计算每个模拟点横波阻抗及密度的条件概率分布函数.
(2) 利用同位简单协克里金方法计算每个模拟点横波阻抗与密度的局部均值与方差,并利用局部均值和方差对条件概率分布函数进行抽样,得到横波阻抗及密度的NS个实现.
(3) 利用模拟得到的纵波阻抗、横波阻抗和密度,运用Fatti近似方程,正演得到叠前合成地震记录.
(4) 利用贝叶斯定理建立目标函数,分区块计算每一区域的目标函数值,利用Metropolis准则判断是否进行状态更新,并利用当前状态下的纵横波阻抗及密度值计算每一区域的优化局部相关系数.
(5) 将当前纵横波阻抗、密度模拟结果及优化局部相关系数作为软数据,利用直接序贯协模拟及考虑联合分布的直接序贯协模拟得到新的模拟结果,重复步骤3~5,直到达到最大迭代次数.
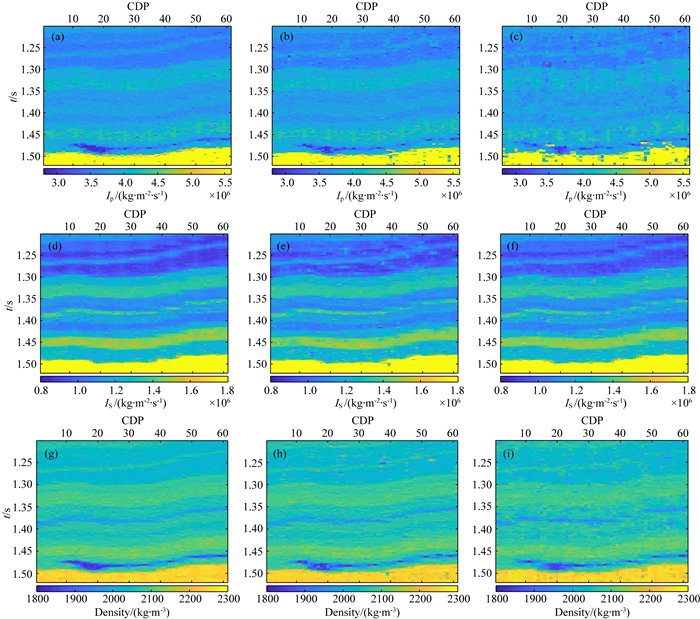
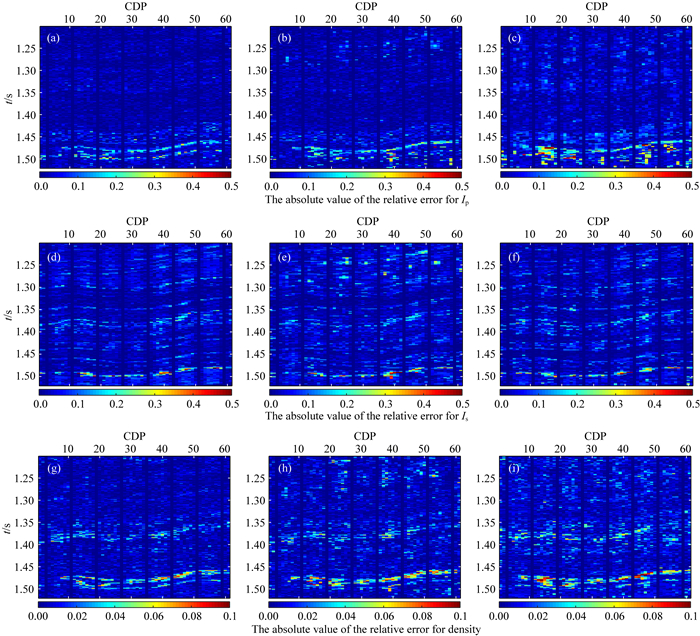
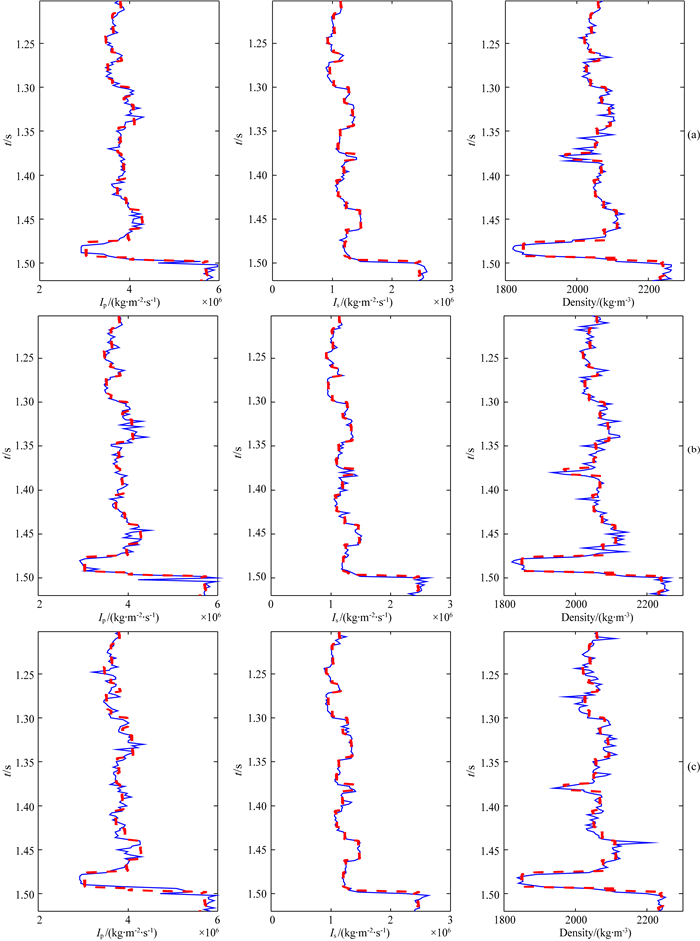
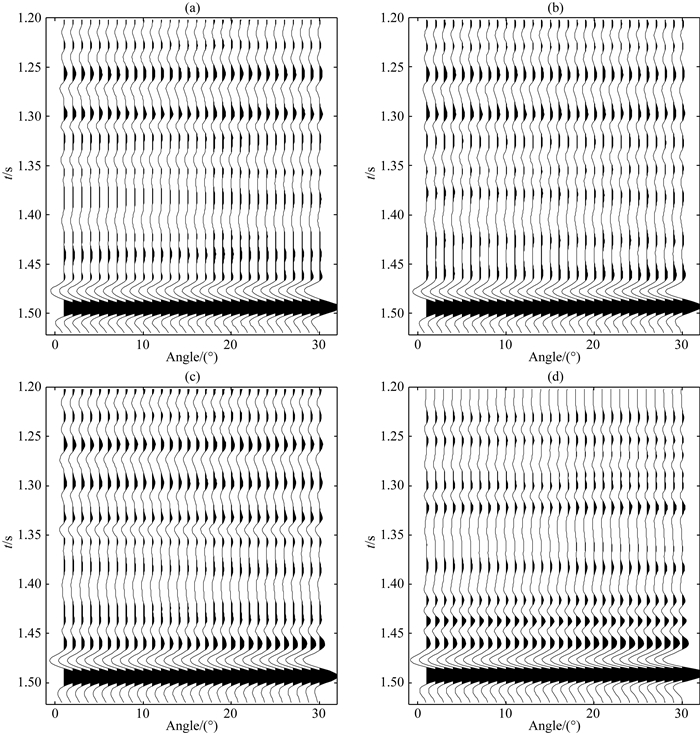
2 模型试算为了验证反演的可行性,利用Marmous2模型的一部分,进行了叠前反演试算.设置最高迭代次数为10000次,每次迭代利用协模拟方法分别模拟得到纵横波阻抗及密度的10次模拟结果,利用Metropolis准则选取其中的最优结果,并将其作为下次迭代的条件数据.为提高算法的计算效率,本文利用了并行策略.图 4为纵波阻抗、横波阻抗和密度模型及其纵向横向变差函数.为了分别测试Metropolis优化算法及优化局部相关系数对反演结果的影响,分别利用基于Metropolis优化算法和优化局部相关系数的反演方法、基于Metropolis优化算法和原局部相关系数的反演方法以及只考虑原局部相关系数大小变化的反演方法,前2种反演方法目标函数一致(均为式(14)),仅局部相关系数的计算公式不同(分别为式(16)、式(15)),反演结果分别如图 5所示,图 6为反演结果与真实模型的相对误差绝对值.图 7为模型第18道真实模型与不同方法反演结果的对比,图 8为所对应的合成角道集与真实角道集的对比,可以发现在相同迭代次数的情况下,三种反演方法的反演结果均能获得较好的反演结果,但基于优化相关系数与Metropolis优化算法的反演结果相较于其他反演结果稳定性更高,总体误差更小.

|
图 4 纵波阻抗、横波阻抗和密度模型数据及纵向横向变差函数 (a)(b)(c)纵波阻抗模型及其对应的纵向横向变差函数;(d)(e)(f)横波阻抗模型及其对应的纵向横向变差函数;(g)(h)(i)密度模型及其对应的纵向横向变差函数. Fig. 4 Model data of P-wave impedance, S-wave impedance and density, and the longitudinal and the transverse variation function (a) (b) (c) P-wave impedance model and its corresponding longitudinal and transverse variation function; (d) (e) (f) S-wave impedance model and its corresponding longitudinal and transverse variation function; (g) (h) (i) Density model and its corresponding longitudinal and transverse variation function. |
|
图 5 不同反演方法的反演结果对比 (a)(d)(g)基于Metropolis优化算法及优化局部相关系数的反演结果;(b)(e)(h)基于Metropolis优化算法及原局部相关系数的反演结果;(c)(f)(i)仅考虑原局部相关系数的反演结果. Fig. 5 Comparison of inversion results for different inversion methods (a) (d) (g) The inversion results based on Metropolis optimization algorithm and optimized local correlation coefficient; (b) (e) (h) The inversion results based on Metropolis optimization algorithm and original local correlation coefficients; (c) (f) (i) The inversion results using original local correlation coefficients. |
|
图 6 不同反演方法反演结果的相对误差绝对值 (a)(d)(g)基于Metropolis优化算法及优化局部相关系数的反演方法;(b)(e)(h)基于Metropolis优化算法及原局部相关系数的反演方法;(c)(f)(i)仅考虑原局部相关系数的反演方法. Fig. 6 Comparison of the relative error absolute values of inversion results for different inversion methods (a) (d) (g) The inversion method based on Metropolis optimization algorithm and optimized local correlation coefficient; (b) (e) (h) The inversion method based on Metropolis optimization algorithm and original local correlation coefficients; (c) (f) (i) The inversion method using original local correlation coefficients. |
|
图 7 模型第18道真实模型与三种反演结果的对比 (a)基于优化局部相关系数与Metropolis优化算法的反演方法;(b)基于原局部相关系数与Metropolis优化算法的反演方法;(c)仅考虑原局部相关系数的反演方法.红色虚线:真实模型,蓝色实线:反演结果. Fig. 7 Comparison of model and the inversion results of three inversion method at the 18th trace (a) The inversion method based on optimized local correlation coefficient and Metropolis optimization algorithm; (b) The inversion method based on the original local correlation coefficient and Metropolis optimization algorithm; (c) The inversion method using the original local correlation coefficient. Red dotted line: real models; blue solid line: inversion results. |
|
图 8 模型第18道的真实角道集与三种反演结果所合成的角道集对比 (a)真实角道集;(b)基于Metropolis优化及优化局部相关系数反演结果所合成角道集;(c)基于Metropolis优化及原局部相关系数反演结果所合成角道集;(d)仅考虑原局部相关系数反演结果所合成角道集. Fig. 8 Comparison between the real angle gather and the synthetic angular trace at the 18th trace (a) True angle gather; (b) Synthetic angle gather computed by the inversion results based on the Metropolis optimization algorithm and the optimized local correlation coefficient; (c) Synthetic angle gather computed by the inversion results based on the Metropolis optimization algorithm the original local correlation coefficient; (d) Synthetic angle gather computed by the inversion results based on the original local correlation coefficients. |
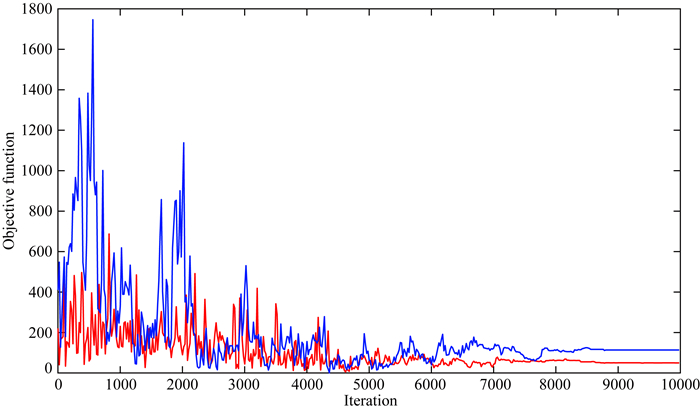
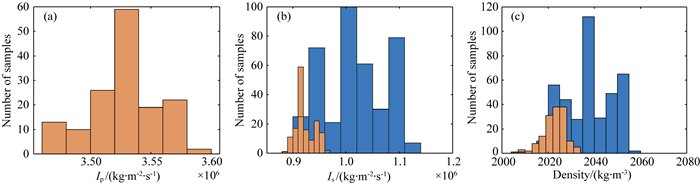
图 9为基于Metropolis优化算法分别利用原相关系数与优化局部相关系数两种反演方法的目标函数值随迭代次数的变化,可以发现利用优化局部相关系数的反演方法目标函数能更加稳定地收敛,且最终结果的目标函数值更小,在并行计算的情况下,共耗时12 min 17 s.而基于原局部相关系数的反演方法在8000次迭代左右,才基本达到平稳状态,且收敛过程具有较大的起伏.图 10为某采样点达到平稳状态下纵横波阻抗及密度的后验分布直方图及此时纵波阻抗模拟结果所对应的横波阻抗与密度的条件分布直方图,可以发现横波阻抗和密度的后验概率分布均位于其条件概率分布之中且满足正态分布,因此可以选取达到平稳状态下多个反演结果的均值作为反演结果.
|
图 9 基于Metropolis优化算法的地质统计学反演目标函数值随迭代次数变化 蓝线:原局部相关系数;红线:优化局部相关系数. Fig. 9 Objective function value based on Metropolis optimization algorithm versus iterations Blue line: original local correlation coefficient. Red line: optimize local correlation coefficient. |
|
图 10 某采样点纵横波阻抗及密度的后验分布直方图及横波阻抗与密度的条件分布直方图 橙色:后验概率直方图;蓝色:条件概率直方图. Fig. 10 The posterior probability histogram of P and S-wave impedance and density and the conditional distribution histogram of S-wave impedance and density Orange: posterior probability histogram. Blue: conditional distribution histogram. |
从模型测试中可以看出,基于Metropolis优化算法及优化局部相关系数的叠前地质统计学反演是可以适用于叠前反演的,且稳定性与收敛性相比传统的考虑相关系数变化的迭代反演方法有了一定程度的提高.
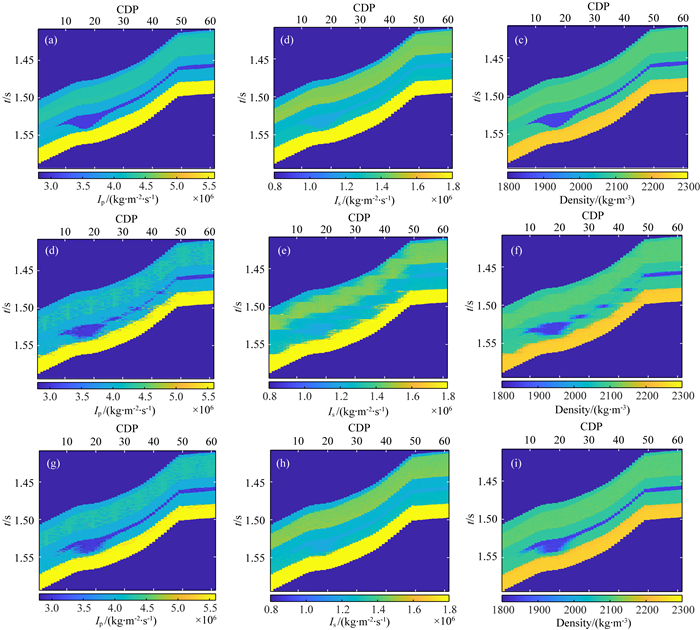
当构造起伏较大时,等时求取横向变差函数及定义横向约束项具有较大误差,此时可利用层位数据求取沿层横向变差函数,并定义对应的横向约束项,消除地层起伏因素的影响.因此,我们根据模型数据,选取底部1.45~1.5 s之间的部分数据,对其进行一定程度的旋转,以此为模型进行大倾角测试.图 11为模型数据及反演的结果,可以发现利用沿层横向变差函数及对应横向约束项的反演结果在大倾角状况下具有更好的反演效果,因此在大倾角状况下沿层位求取变差函数及定义横向约束项是较为必要的.
|
图 11 大倾角测试模型及反演结果 (a)(b)(c)大倾角模型;(d)(e)(f)利用等时横向变差函数及对应横向约束项的反演结果;(g)(h)(i)利用沿层横向变差函数及对应横向约束项的反演结果. Fig. 11 High-dip test models and inversion results (a) (b) (c) High-dip model; (d) (e) (f) Inversion results based on isochronous transversal variation function and corresponding transversal constraints; (j) (k) (l) Inversion results based on transversal variation function along the horizon and corresponding transversal constraints. |
为了验证基于Metropolis抽样及优化局部相关系数的全局迭代叠前地质统计学反演在实际数据中的应用效果,利用实际数据进行反演测试.该数据来自东部某工区,属于致密砂岩储层,储层内部“甜点”表征低孔低渗背景下局部高孔渗的区域,是勘探开发中最为关注的地质目标.经过岩石物理分析得知,纵波阻抗可以很好地表征“甜点”的分布.利用井数据求取纵向变差函数,利用确定性反演结果求取横向变差函数.为了提高反演的稳定性,将叠前角度道集叠加为三个部分角度叠加数据,其中心角度分别为7°、15°、24°.利用部分叠加地震数据进行AVA反演测试.
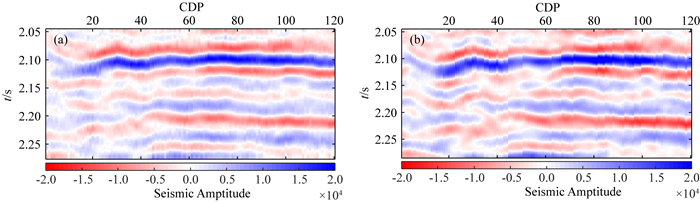
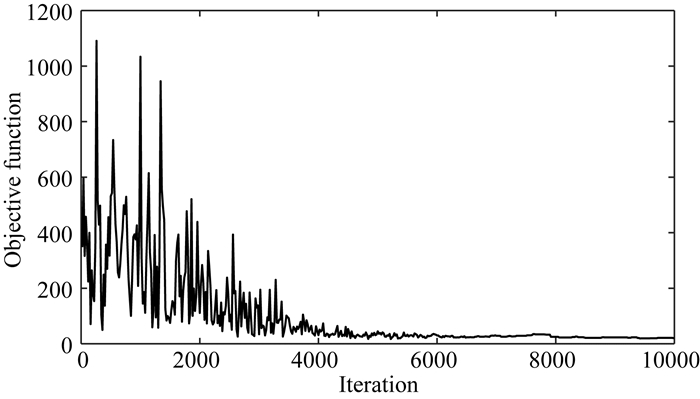
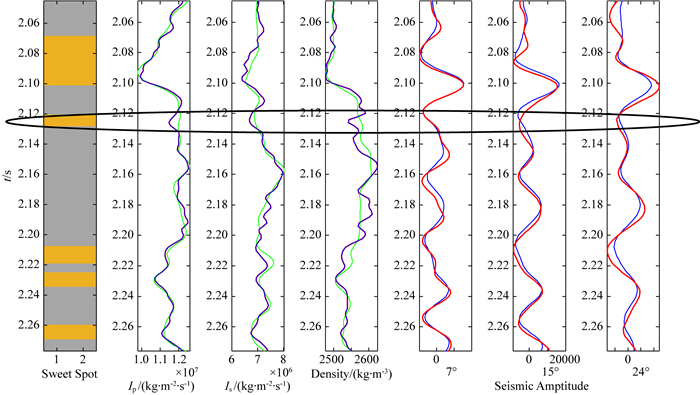
纵横波阻抗及密度的反演结果以及确定性反演纵波阻抗的反演剖面如图 12所示,可以发现,井曲线(井位置位于CDP=64)与反演剖面是相吻合的.图 13为反演结果所合成的中角度地震记录与实际中角度地震记录的对比,可以发现两者较为接近,说明反演结果所合成的地震记录与实际地震记录具有较好的相关性.图 14是目标函数随迭代次数的变化,我们可以发现迭代5000次以后,反演基本收敛,因此我们可以选取收敛后一系列反演结果的均值作为最终反演结果,即为图 12所示的剖面.图 15展示了全局迭代叠前地质统计学反演及确定性反演在井位置处(CDP=64)的反演结果,可以发现地质统计学反演结果在井位置处反演结果与真实井数据完全吻合,这是由于地质统计学反演利用井数据作为硬数据进行反演,因此相比确定性反演具有更高的分辨率,可以很好反映确定性反演没能表征出的2.13 s左右的薄层.因此,基于Metropolis优化算法及优化局部相关系数的全局迭代地质统计学反演可以较好地应用于叠前实际数据反演.

|
图 12 纵波阻抗、横波阻抗、密度反演剖面 (a)纵波阻抗反演剖面;(b)横波阻抗反演剖面;(c)密度反演剖面;(d)确定性反演纵波阻抗反演剖面. Fig. 12 Inverted P- and S-wave impedance and density profile (a) Inverted P-wave impedance profile; (b) Inverted S-wave impedance profile; (c) Inverted density profile; (d) Inverted P-wave impedance profile based on deterministic inversion. |
|
图 13 反演结果所合成地震记录与实际地震记录的对比 (a)反演结果合成中角度地震记录;(b)中角度实际地震记录. Fig. 13 Comparison between the synthetic seismic record obtained by inversion results and the real seismic record (a) Synthetic seismic record at middle angle; (b) Real seismic record at middle angle. |
|
图 14 目标函数随迭代次数变化 Fig. 14 Objective function versus iteration times |
|
图 15 井位置处(CDP=64)反演结果与井数据对比 灰色区域:非甜点;黄色区域:甜点;蓝线:地质统计学反演结果及其合成地震记录;绿线:确定性反演结果;红线:实际井数据及井旁道观测地震记录. Fig. 15 Comparison between the inversion results at near-well location (CDP=64) and the well data Gray area: Non-sweet spot; Yellow area: Sweet spot; Blue line: Geostatistics inversion results and synthetic seismic data; Green line: Deterministic inversion results; Red line:Actual well data and the observed seismic data at well trace. |
本文将Metropolis优化算法与全局迭代地质统计学反演方法相结合,提出了基于Metropolis优化算法的全局迭代地质统计学反演方法,该方法的优势主要存在以下几点:
(1) 在贝叶斯理论的框架下,建立目标函数,并引入横向约束,通过Metropolis优化算法对模拟结果进行优选,可以克服原有全局迭代地质统计学方法仅利用地震记录局部相关系数进行优化所带来的不确定性,提高反演的稳定性.
(2) 根据目标函数构建了新的优化局部相关系数,将新的基于目标函数的局部相关系数应用于协模拟之中,提高了叠前地质统计学反演的收敛性与稳定性.
(3) 模型测试与实际数据应用表明,基于Metropolis抽样算法与优化局部相关系数的全局迭代地质统计学反演方法可以有效地应用于叠前反演,且能较好地反演较薄储层.
Aki K, Richards P G. 1980. Quantitative seismology: Theory and methods. New York: W. H. Freeman & Co.
|
Almeida A S, Journel A G. 1994. Joint simulation of multiple variables with a Markov-type coregionalization model. Math Geology, 26(5): 565-588. |
Azevedo L, Nunes R, Soares A, et al. 2013. Stochastic seismic AVO inversion.//83rd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Azevedo L, Nunes R, Soares A, et al. 2015. Geostatistical seismic AVO inversion directly for facies-real case application.//85th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Azevedo L, Soares A. 2017. Geostatistical Methods for Reservoir Geophysics. Berlin: Springer International Publishing.
|
Chen H Z, Pan X P, Li Y X, et al. 2017. Bayesian Markov Chain Monte Carlo inversion for weak anisotropy parameters and fracture weaknesses using azimuthal elastic impedance. Geophysical Journal International, 210(2): 801-818. |
Deutsch C V, Journel A G. 1992. GSLIB:Geostatistical Software Library and User's Guide. Oxford: Oxford University Press.
|
Fatti J L, Smith G C, Vail P J, et al. 1994. Detection of gas in sandstone reservoirs using AVO analysis; A 3-D seismic case history using the Geostack technique. Geophysics, 59(9): 1362-1376. |
Francis A. 2005. Limitations of deterministic and advantages of stochastic seismic inversion. Canadian Soc. Expi Geophys. Record, 30(2): 5-11. |
Francis A. 2006a. Understanding stochastic inversion:Part 1. First Break, 24(11): 69-77. |
Francis A. 2006b. Understanding stochastic inversion:Part 2. First Break, 24(12): 79-84. |
Gidlow P M, Smith G C, Vail P. 1993. Vail P. Hydrocarbon detection using fluid factor traces: A case study.//63rd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Goovaerts P. 1997. Geostatistics for Natural Resources Evaluation. New York: Oxford University Press.
|
Grana D, Mukerji T, Dvorkin J, et al. 2012. Stochastic inversion of facies from seismic data based on sequential simulations and probability perturbation method. Geophysics, 77(4): M53-M72. |
Haas A, Dubrule O. 1994. Geostatistical inversion-a sequential method of stochastic reservoir modelling constrained by seismic data. First Break, 12(11): 561-569. |
Hamid H, Pidlisecky A. 2015. Multitrace impedance inversion with lateral constraints. Geophysics, 80(6): M101-M111. |
Hastings W K. 1970. Monte Carlo sampling methods using Markov chains and their applications. Biometrika, 57(1): 97-109. |
Horta A, Soares A. 2010. Direct sequential co-simulation with joint probability distributions. Mathematical Geosciences, 42(3): 269-292. |
Jiang X Y, Ji Z F, Mao F J, et al. 2014. Application of random simulation method in the study of physical property of reservoir. Progress in Geophysics (in Chinese), 29(6): 2665-2668. DOI:10.6038/pg20140629 |
Li J H, Liu B H, Zhang Y Q, et al. 2016. Oil-bearing reservoir prediction with prestack AVO inversion. Oil Geophysical Prospecting (in Chinese), 51(6): 1180-1186. DOI:10.13810/j.cnki.issn.1000-7210.2016.06.018 |
Liu C J. 2017. Study of the fast stochastic inversion method based on the lateral constraint[Master's thesis] (in Chinese). Qingdao: China University of petroleum (East China).
|
Metropolis N, Rosenbluth A W, Rosenbluth M N, et al. 1953. Equation of state calculations by fast computing machines. The Journal of Chemical Physics, 21(6): 1087-1092. |
Nunes R, Soares A, Azevedo L, et al. 2016. Geostatistical seismic inversion with direct sequential simulation and co-simulationwith multi-local distribution functions. Mathematical Geosciences, 49(5): 583-601. DOI:10.1007/s11004-016-9651-0 |
Pan X P, Zhang G Z, Chen H Z, et al. 2017. McMC-based AVAZ direct inversion for fracture weaknesses. Journal of applied Geophysics, 138: 50-61. |
Pereira P, Azevedo L, Nunes R, et al. 2016. Integrating of initial guess models into geostatistical seismic inversion methodologies.//86th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Sams M, Saussus D. 2008. Comparison of uncertainty estimates from deterministic and geostatistical inversion.//78th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 27(1): 3713.
|
Sen M K, Biswas R. 2017. Transdimensional seismic inversion using the reversible jump Hamiltonian Monte Carlo algorithm. Geophysics, 82(3): R119-R134. |
Shen H T, Guo N C, Qin T, et al. 2017. Application of geostatistical inversion for super thin reservoir prediction. Progress in Geophysics (in Chinese), 32(1): 248-253. DOI:10.6038/pg20170135 |
Shuey R T. 1985. A simplification of the Zoeppritz equations. Geophysics, 50(4): 609-614. |
Soares A. 2001. Direct sequential simulation and cosimulation. Mathematical Geology, 33(8): 911-926. |
Sun R Y, Yin X Y, Tan X D, et al. 2014. Stochastic inversion of elastic impedance based on Metropolis sampling algorithm.//84th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Sun R Y, Yin X Y, Wang B L, et al. 2016. A direct estimation method for the Russell fluid factor based on stochastic seismic inversion. Chinese Journal of Geophysics (in Chinese), 59(3): 1143-1150. DOI:10.6038/cjg20160334 |
Wang B L, Yin X Y, Ding L X, et al. 2015. Study of fast stochastic inversion based on FFT-MA spectrum simulation. Chinese Journal of Geophysics (in Chinese), 58(2): 664-673. DOI:10.6038/cjg20150227 |
Xiao Y N. 2018. Study of seismic stochastic inversion method based on sequential co-simulation[Master's thesis] (in Chinese). Qingdao: China University of petroleum (East China).
|
Xu W, Tran T, Srivastava M, et al. 1992. Integrating seismic data in reservoir modelling: The collocated co-kriging alternative.//The 67th Annual Technical Conference and Exhibition of the Society of Petroleum Engineers.
|
Yin X Y, Sun R Y, Wang B L, et al. 2014. Simultaneous inversion of petrophysical parameters based on geostatistical a priori information. Applied Geophysics, 11(3): 311-320. |
姜晓宇, 计智锋, 毛凤军, 等. 2014. 随机模拟技术在储层物性研究中的应用. 地球物理学进展, 29(6): 2665-2668. DOI:10.6038/pg20140629 |
李建华, 刘百红, 张延庆, 等. 2016. 叠前AVO反演在储层含油气性预测中的应用. 石油地球物理勘探, 51(6): 1180-1186. |
刘婵娟. 2017.基于横向约束的快速随机反演方法研究[硕士论文].青岛: 中国石油大学(华东).
|
沈洪涛, 郭乃川, 秦童, 等. 2017. 地质统计学反演技术在超薄储层预测中的应用. 地球物理学进展, 32(1): 248-253. DOI:10.6038/pg20170135 |
孙瑞莹, 印兴耀, 王保丽, 等. 2016. 基于随机地震反演的Russell流体因子直接估算方法. 地球物理学报, 59(3): 1143-1150. DOI:10.6038/cjg20160334 |
王保丽, 印兴耀, 丁龙翔, 等. 2015. 基于FFT-MA谱模拟的快速随机反演方法研究. 地球物理学报, 58(2): 664-673. DOI:10.6038/cjg20150227 |
肖亚楠. 2018.基于序贯协模拟的地震随机反演方法研究[硕士论文].青岛: 中国石油大学(华东).
|
 2020, Vol. 63
2020, Vol. 63


