2. 北京应用大气研究所, 北京 100029
2. Beijing Institute of Applied Meteorology, Beijing 100029, China
本研究的第一部分讨论了非静态大气静力适应过程中的波动对风垂直切变的响应,第二部分从气块运动的角度出发讨论了两类波动在非静态大气静力适应过程中的具体作用,进一步揭示了风垂直切变的影响.为了更加直观地描述风切变在适应过程中的作用,本文从能量转换的角度出发,讨论非静态大气静力适应过程中的能量转换情况.
能量的转换和守恒定律是大气运动遵循的普遍规律,从本质上讲,大气静力适应过程可以看作是大气能量传播、转换的过程,其中不同形式能量的转换以及不同尺度能量的传播表征着不同的物理机制和物理阶段;因此,从能量的角度研究风垂直切变对静力适应过程的影响能更加清楚地揭示其中的物理本质.Bannon(1995)研究了一维静态大气静力适应过程中的能量转换情形,揭示了适应过程的基本物理机制;Bannon(1996)探讨了非线性静力适应过程中能量分配的情形,指出采用一维线性模型来描述静力适应过程中能量转换的情形,存在不足;Sotack和Bannon(1999)研究了由热强迫引起的非静力扰动能量在一维线性模型中的转换情况,论证了声波在静力适应过程中的重要作用;Chagnon和Bannon(2001)基于位势涡度守恒给出了三维系统中非静力能量的转换机制,从能量的角度比较了几种可压缩近似方案的差异;Duffy(2002)研究了一维非等温大气中的静力适应过程,假设初始扰动由热力强迫引起,则拉格朗日形式的扰动能量在有效能量和动能之间转换,并随着时间增加,有效势能保持常数,扰动能量主要在有效弹性势能和动能之间转换;Chagnon和Bannon(2004)研究了在不同时空结构的热力强迫下静力适应过程中能量的分配和转换机制;Fanelli和Bannon(2005)利用非线性数值模式分别研究了在热力强迫和动力强迫下静力适应过程中能量的转换机制;崔新东等(2016)根据三维静态大气静力适应过程中能量转换机制给出适应终态时能量的一般分配特征.
时至今日,对于非静态大气静力适应中能量转换机制的研究仍处于空白状态,解决这一问题的关键是研究风垂直切变对静力适应过程中能量转换的影响,依赖前两部分的研究成果,本文的结构安排如下:第二部分基于线性扰动方程组,导出可压缩大气静力适应过程中扰动能量的转换机制;第三部分导出在频域中扰动能量谱的收支方程;第四部分讨论在四种不同的水平基流垂直切变模型中能量谱的变化特征,并分析存在水平基流垂直切变时对可压缩大气静力适应过程中能量转换的影响;第五部分为结论部分.注意,文中从第一部分引用的公式标注为(*_Ⅰ),从第二部分引用的公式标注为(*_Ⅱ).
1 静力适应过程中的能量转换在忽略地球旋转效应、黏性力作用和摩擦力作用的绝热线性系统中,大气的能量可表征为基本气流能量与扰动能量的叠加(Van Delden,2015).静力适应过程中扰动能量总是以扰动动能EK、扰动有效势能EAP和扰动弹性势能EAE(Andrews,1981;Bannon, 2005, 2012, 2013)的形式存在,各种形式能量的相互转换是基本气流和扰动发展与否的能源机制.从本研究第一部分描述静力适应过程的扰动线性方程组出发(郭海龙等,2020),对式(8_Ⅰ)、式(9_Ⅰ)和式(10_Ⅰ)分别乘以u′、v′和w′得到:
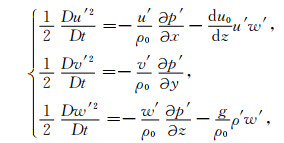
|
(1) |
其中D/Dt≡∂/∂t+u0(z)∂/∂x,单位质量的扰动动能密度可由扰动水平动能密度Ekh和扰动垂直动能密度Ekv组成:
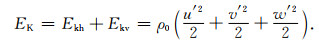
|
(2) |
由式(1)和式(2)得到单位质量的扰动动能密度收支方程为
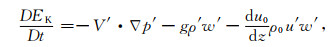
|
(3) |
其中V′=u′i+v′j+w′k,▽为三维梯度算子,得到单位质量的扰动有效位能密度收支方程为

|
(4) |
得到单位质量的扰动弹性势能密度收支方程为
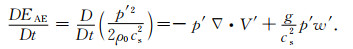
|
(5) |
对式(3)、式(4)和式(5)在整个空间区域求积分,可得到研究体积内空气的扰动总动能、扰动总有效位能和扰动总弹性势能的收支方程分别为

|
(6) |

|
(7) |
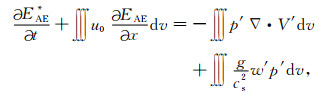
|
(8) |
其中:
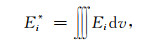
|
(9) |
由式(6)、(7)和(8)可得扰动总能量的收支方程为

|
(10) |
式(10)第一项为扰动总能量的局地变化项,第二项为水平基流引起的平流变化项,第三项为水平基流垂直切变引起扰动能量与基本气流能量间的转换项,第四项为系统与外界的能量交换项.
若假设在研究区域的边界Ω上无净的扰动速度,即:

|
(11) |
利用边界条件式(11)和高斯公式,则式(10)表明,扰动总能量与基本气流能量的交换依赖于水平基流的垂直切变及垂直动量通量的贡献.比较式(6)、(7)和(8)可以得到扰动总动能、扰动总弹性势能、扰动总有效位能和基本气流能量这四种能量之间的相互转化:

|
(12) |
式(12)为EK*与EAE*的转换项,表征气压梯度力对空气运动的做功情况,当在正变压区域存在辐散运动,在负变压区域存在辐合运动时,有〈EK* EAE*〉>0,表示EAE*转换为EK*,相反,当在正变压区域存在辐合运动,而在负变压区域存在辐散运动时,有〈EK* EAE*〉 < 0,表示EK*转换为EAE*:
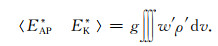
|
(13) |
式(13)为EAP*与EK*之间的转换项,表征重力对空气运动的做功情况,当暖气团上升或冷气团下沉时,有〈EAP* EK*〉 < 0,表示EAP*转化为EK*,相反,当冷气团上升或暖气团下沉时,有〈EAP* EK*〉>0,EK*转化为EAP*:

|
(14) |
式(14)为EAE*与EAP*之间的转换项,表征净浮力对空气运动的做功情况,当高压区存在垂直上升运动或低压区对应垂直下沉运动时,有〈EAE* EAP*〉>0,表示EAP*向EAE*转换,当高压区存在垂直下沉运动或低压区对应垂直上升运动时,有〈EAE* EAP*〉 < 0,表示EAE*向EAP*转换:

|
(15) |
式(15)为扰动总能量与基本气流能量Ebase*的转换项,而扰动能量与基本气流能量的转换是通过扰动动能的形式实现的,由VWS引起的垂直动量通量输送是诱发扰动动能和基本气流能量交换的机制,当正的VWS对应向上输送的垂直动量通量或负的VWS对应向下输送的垂直动量通量时,有〈Ebase* EK*〉>0,表示EK*的衰减用以维持基本气流;当正的VWS对应向下输送的垂直动量通量或负的VWS对应向上输送的垂直动量通量时,有〈Ebase* EK*〉 < 0,表示Ebase*向EK*转换,使得扰动能够发展而基本气流衰减.由此得到非静态大气静力适应过程中各种能量之间的相互转换关系如图 1所示.

|
图 1 静力适应过程中能量转换关系示意图 双箭头虚线表示系统与外界的能量交换,实线表示系统内部能量之间的转换 Fig. 1 Schematic diagram of the energies conversion in the process of hydrostatic adjustment The double arrows indicate the energies exchange between the system and the outside world. The solid lines represent the energy conversion between the internals of the system. |
根据式(12)、(13)、(14)和(15)可以将式(6)、(7)和(8)写为
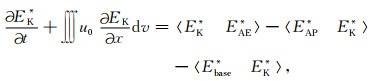
|
(16) |
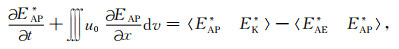
|
(17) |
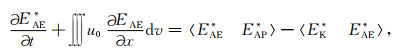
|
(18) |
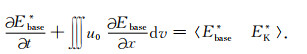
|
(19) |
由图 1可知,静力适应过程也是扰动能量之间或扰动能量同基本气流能量之间的转换过程,当有热力因素或动力因素破坏了大气静力平衡关系时,立刻激发出声重力波,使得扰动能量发生转换并向整个空间传播,而VWS使得扰动能量与基本气流能量之间发生转换,在波动结构和水平基流的共同作用下,使大气重新达到静力平衡状态或使扰动继续发展.
2 静力适应过程中的能量谱 2.1 动能谱及收支方程由傅里叶变换可将三维空间中的能量转换到频域空间,由式(2)可定义单位质量扰动动能为
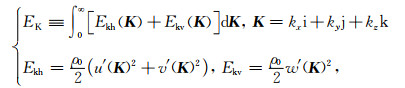
|
(20) |
其中Ekh(K)和Ekv(K)分别表示波数矢量为K的扰动水平动能和扰动垂直动能,即水平动能谱和垂直动能谱.将式(1)代入式(20)可知水平动能谱的收支方程为
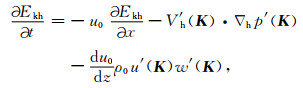
|
(21) |
其中Vh′=u′h+v′j,▽h=∂/∂x+∂/∂y,等式右端第一项为水平平流项,第二项为气压梯度力引起的能量变化,表征了声重力波的贡献,第三项为垂直动量通量和水平基流的垂直切变引起的扰动水平动能与基本气流能量的交换项.垂直动能谱的收支方程为
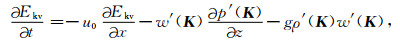
|
(22) |
其中等式右端第一项为平流项,第二项为气压梯度力作用项和第三项为重力作用项分别表征声重力波中性质各异的两类波动的作用.
2.2 有效位能谱及收支方程由式(4)可定义单位质量扰动有效位能为

|
(23) |
其中Eap为有效位能谱,则有效位能谱的收支方程为
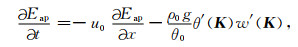
|
(24) |
等式(24)右端第一项为平流项,第二项为热量的垂直输送项.
2.3 有效弹性势能谱及收支方程由式(5)可定义单位质量扰动有效弹性势能为
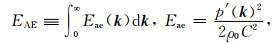
|
(25) |
其中Eae为有效位能谱,则有效位能谱的收支方程为
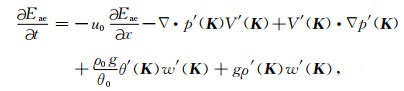
|
(26) |
等式(26)右端第一项为平流项,第二项为速度散度项,第三项为气压梯度力作用项,第四项为热量的垂直输送项,相比式(24)此项为有效弹性势能与有效位能的转化项,第五项为重力作用下的质量通量项,相比式(21)和式(22)此项为有效弹性势能与动能之间的交换项;则非静态大气适应过程中能量转换关系可表示为图 2.

|
图 2 静力适应过程中能量收支关系结构图 实线表示系统内部的能量转换机制,虚线表示系统与外界的能量转换机制,虚箭头表征系统扰动能量与系统基态能量间的转换机制. Fig. 2 Schematic diagram of the energy spectrum in the process of hydrostatic adjustment The energy conversion mechanism within the system, between the system and the outside world, and between the perturbed state and steady state are represented by the solid line arrows, dotted line arrows, and hollow arrows, respectively. |
当系统与外界无能量交换时,在整个静力适应过程中系统内部能量谱的收支满足守恒定律,扰动有效弹性势能作为能量中转站,使得非静力扰动能量在扰动有效位能、扰动动能和扰动弹性势能间进行转换,而扰动水平动能则为基本气流能量与扰动能量进行转换的媒介;当静力适应过程得以实现时扰动弹性势能与扰动垂直动能间的转换被终止,由此可知静力适应过程是大气可压缩性和重力共同作用的复杂物理过程,缺一不可, 同时也可看出,地转偏差是引起扰动水平动能与扰动有效弹性势能转换的机制,而静力平衡的破坏是引起扰动垂直动能与扰动有效弹性势能转换的机制.
3 VWS对能量谱的影响基于第二部分的理论,当扰动变量写为波动形式时,则扰动能量可写为

|
(27) |
其中f*T=(u* v* w* ρ* p*),M矩阵为

|
(28) |
进一步可将式(27)写为

|
(29) |
其中diag(eλjt)表示以eλjt为元素的对角矩阵,λj为特征向量,E为特征向量矩阵.由式(29)可知,扰动总能量与初始扰动、波动结构、基本气流及其垂直切变等要素相关.假设初始时刻非静力扰动能量由扰动弹性势能和扰动有效位能组成,取FAT(0)=(0 0 0 0 1 hPa),水平波数kx=ky,垂直水平比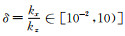
当水平基流在整层大气中为常数分布时,扰动能量谱随时空和垂直水平比的分布如图 3所示.图 3显示,在由热力学扰动破坏静力平衡的第1 min内(图 3a、d、g),对流层低层(图 3g),由浮力做功引起的感热垂直输送使Eap在各尺度上迅速减小,转换为Eae,与此同时,由扰动气压梯度力做功和重力做功引起部分Eae转换为EK,当δ < 0.1时,Ekv远大于Ekh,随着δ的增加,Ekv所占比例减小而Ekh所占比例增加,当δ>1时,Ekh、Ekv和Eae所占比例近似相同.对流层高层和平流层低层(图 3 a、d),扰动能量之间的转换情形同对流层低层相似,随着垂直高度的增加,Eae所占比例增加,其余三种形式的能量比例均减小,当δ>1时,扰动能量具有Eae>Ekh>Ekv>Eap的分布特征.在静力平衡被破坏的第21(图 3b、e、h)和第41 min内(图 3c、f、i),扰动能量主要为Eae与EK之间的转换,系统中Eae所占比例最小,随着δ的增加,各种形式的扰动能量所占比例均呈振荡型分布,当δ < 0.1时,Eae曲线与Ekh曲线呈反相关,而与Ekv曲线呈正相关,表明Eae与Ekh的转换占据主导地位;当δ>1时,Eae与Ekv的转换占据主导地位;表明在相同热力学扰动下,δ越大,静力平衡被破坏的程度越高;随着垂直高度的增加,Eae所占比例增加,EK所占比例减小,随着时间的增加,各形式扰动能量的比例曲线振荡剧烈程度增加,所占扰动总能量的比例基本保持不变.

|
图 3 mod_a模型中扰动能量谱分布 横坐标为垂直水平比,纵坐标为各类扰动能量与扰动总能量的比值,沿横坐标方向为同一水平高度,沿纵坐标方向为同一时间段;蓝色表征Eae,绿色表征Eap,红色表征Ekh,灰色表征Ekv,虚线表征初始时刻扰动能量份额. Fig. 3 The distribution of energy spectra in the constant model The abscissa is the aspect ratio, the ordinate is the ratio of each kind of perturbation energies to the total energies, the height is same along the abscissa, the time is same along the ordinate, the blue lines indicate Eae, the green lines is Eap, the red lines is Ekh, the gray lines is Ekv, and the dotted lines indicate the ratio of initial perturbation energies. |
当水平基流随垂直高度呈线性增长分布时,扰动能量谱随时空和垂直水平比的分布如图 4所示,在扰动1 min内(图 4a、d、g),初始Eap迅速减小,在浮力作用下使Eap转换为Ek,当δ < 0.1时,mod_b中扰动能量谱的分布同mod_a的情形较一致;由于水平基流在垂直方向的剪切作用,使得当δ>1时,mod_b中扰动能量谱的分布与mod_a中出现较大的差异;以mod_a中各扰动能量谱分布曲线作为基准,则在静力平衡被破坏的第21(图 4b、e、h)和第41 min内(图 4c、f、i),mod_b各层中Eae所占比例均呈减小趋势,Ekh所占比例呈增加趋势,在0.1 < δ < 1的区间内变化幅度最显著;而Ekv所占比例随δ的增加呈先减小后增加的趋势,在δ=1附近达到最大值,由此可知,水平基流的垂直切变,使得不同形式的扰动能量所占比例发生了变化,且随垂直水平比的不同产生差异.

|
图 4 mod_b模型中扰动能量谱分布(图中标识同图 3) Fig. 4 The distribution of energy spectra in the linear model(Explanations are same as in Fig. 3) |
比较图 4b、e、h可知,在不同高度上,各扰动能量随δ的分布均呈震荡型,变化特征基本一致,在δ < 0.1的条件下,由水平气压梯度力做功引起的Eae与Ekh的转换占据主导,随着δ的增加,垂直气压梯度力与重力做功引起的Eae与Ekv的转换逐渐加强占据主导地位,当δ接近10时,各类扰动能量所占比例趋于稳定.比较图 4b、c、e、f、h、i可知,随着时间的增加,各种形式的能量振荡幅度变大,表明各能量之间的转换作用呈增强趋势,水平基流的垂直切变使得扰动能量的分布随时间发生变化.
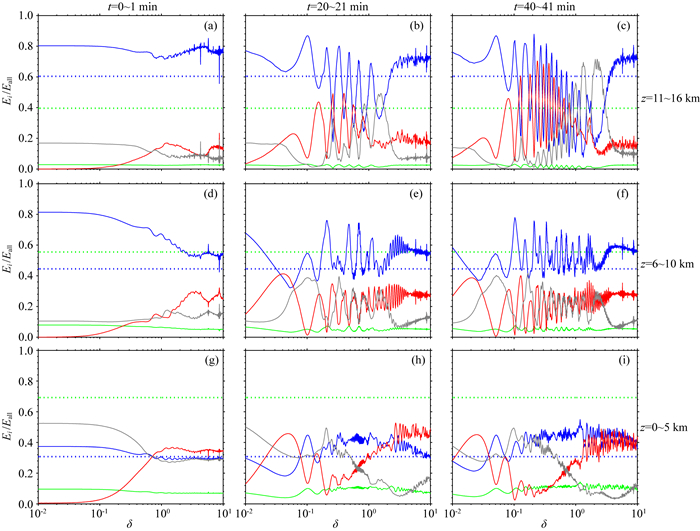
3.3 mod_c水平基流呈反气旋式切变当水平基流分布呈东风急流分布时,在对流层低层有负的风切变,在平流层低层有正的风切变,在对流层高层为急流轴区域,伴随有负的风切变向正的风切变的过渡带.此种情形下,扰动能量谱随时空和垂直水平比的分布如图 5所示.
|
图 5 mod_c模型中扰动能量谱分布(图中标识同图 3) Fig. 5 The distribution of energy spectra in the anticyclone model(Explanations are same in Fig. 3) |
在扰动初始1 min内(图 5a、d、g),初始热力学扰动能量在浮力、气压梯度力和重力的作用下,使得扰动能量以Eae、Eap、Ekh、Ekv的形式重新分配,相比图 3和图 4可知,在δ < 0.1的范围内,三类模型中各曲线的分布特征较一致,而在δ>1的范围内,各曲线的分布出现明显差异,说明在扰动初始1 min内,水平基流的垂直切变对能量分配的影响在小尺度和微尺度系统中较显著.在静力平衡被破坏的第21 min内(图 5b、e、h),对流层低层(图 5h),各类扰动能量谱的分布曲线呈波动状,负的风切变应力使得各类扰动能量谱曲线振荡幅度减小,Eae谱和Eap谱的变化曲线较mod_b中同一条件下增大,Ekh谱的变化曲线在0.1 < δ < 1范围内明显减小,Ekv谱的变化曲线在δ=0.1附近显著增大,而在δ=1附近显著减小;说明水平基流垂直切变的方向影响扰动能量的重新分配,对扰动动能分配的影响在中小尺度尤为显著,正的风切变使得扰动能量谱振荡趋于剧烈,而负的风切变使得扰动能量谱振荡趋于平稳.比较对流层高层(图 5e)显示,在东风急流的急流轴区,各类扰动能量谱的分布曲线类似于mod_a中的情形,但曲线振荡幅度较小;比较平流层低层(图 5b),扰动能量谱的分布曲线同mod_b中情形类似,但曲线振荡幅度较大;说明,水平基流的垂直切变方向决定扰动能量谱分布曲线的基本特征,其大小决定扰动能量谱分布的振荡幅度.
比较图 5b、c、e、f、h、i可知,随着时间的增加,对流层低层(图 5h、i),在δ=0.1附近的范围内,Ekh在总能量中的比例趋于零,扰动能量主要以Eae和Ekv的形式存在,而在δ=5附近的范围内,Ekv在总能量中的比例趋于零,扰动能量主要以Eae和Ekh的形式存在;平流层低层(图 5b、c)的情形则同对流层低层情形完全相反.说明,负的风切变使得微尺度和小尺度(中尺度)系统中Ekv(Ekh)的比例随时间减小,正的风切变作用相反.
3.4 mod_d水平基流呈气旋式切变当水平基流分布类似西风急流特征时,对流层低层有正的风切变,在平流层低层有负的风切变,在对流层高层为急流轴区伴随有正的风切变向负的风切变的过渡带.此结构中,扰动能量谱随时空和垂直水平比的分布如图 6所示.比较图 5和图 6可知,在对流层高层(图 6d、e、f),两种模型下扰动能量谱的分布特征基本一致,都同mod_a的情形类似,在对流层低层(图 6g、h、i),扰动能量谱的分布特征同图 5中平流层低层中的情形类似,都有正的风切变存在时的特征,随时间的增加由扰动动能发展的趋势;在平流层低层(图 6a、b、c),扰动能量主要为Eae,在δ < 1的范围内,Ekv大于Ekh,而在δ>1的范围内,Ekh大于Ekv;此分布特征与mod_a中情形较类似.
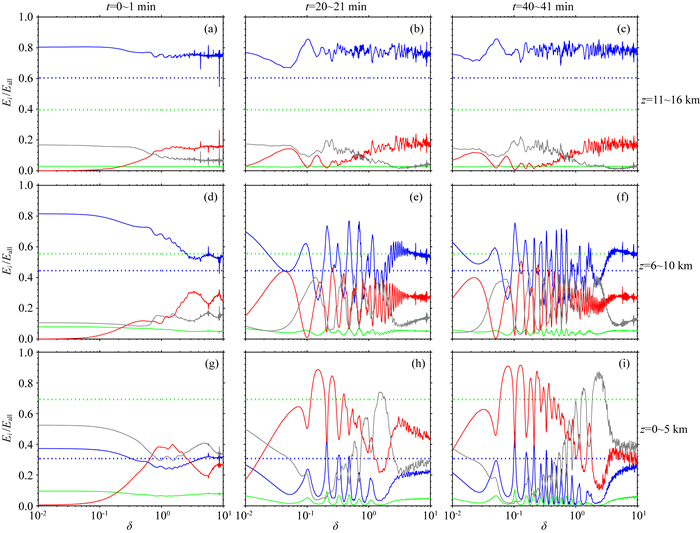
|
图 6 mod_d模型中扰动能量谱分布(图中标识同图 3) Fig. 6 The distribution of energy spectra in the cyclone model(Explanations are same as in Fig. 3) |
除了以上的结论外,由图 2可知,风垂直切变对能量转换的影响,还作用于基本气流与扰动水平动能之间的相互转换,风切变应力对空气团做功,使得扰动动量在垂直方向发生传输,从而使得扰动能量发生改变,对于四种风切变模型,风垂直切变应力在受扰1 min内对基本气流能量的影响情况如图 7所示.在对流层低层(图 7c),mod_b中VWS引起的水平基流能量与扰动水平动能的转换量在δ < 3的范围内,mod_c仅在δ=2的附近的三小段区域内,mod_d中,在δ < 0.5的范围内有〈Ebase* EK*〉>0,风垂直切变应力使得气团的扰动水平动能向基本气流转换,起到维持基本气流,削弱扰动能量的作用.而在其余的尺度范围内,均有〈Ebase* EK*〉 < 0,风垂直切变作用使得基本气流能量向扰动水平动能转换,增强扰动能量.

|
图 7 风垂直切变对基本气流能量的影响 蓝色代表mod_b模型,绿色代表mod_c模型,红色代表mod_d模型,实线表示〈Ebase* EK*〉>0,虚线表示〈Ebase* EK*〉 < 0. Fig. 7 The effects of Vertical Wind Shear (VWS) on basic flow The mod_b in blue line, the mod_c in green line, the mod_d in red line. The solid lines indicate 〈Ebase* EK*〉>0, the dotted lines indicate 〈Ebase* EK*〉 < 0. |
此外,图 7显示,在对流层高层(图 7b),mod_b在δ < 0.2的取值范围、mod_c在δ < 3、6 < δ < 8和δ接近10的取值范围、mod_d在0.1 < δ < 0.4、0.8 < δ < 3的取值范围内均有〈Ebase* EK*〉>0,有扰动动能向基本态转换;在其余尺度范围内有〈Ebase* EK*〉 < 0,有基本态能量向扰动动能转换.在平流层低层(图 7a),mod_b在δ < 3的范围内,mod_c在δ < 0.5的范围内,mod_d在1 < δ < 4的范围内,均有〈Ebase* EK*〉>0,其余部分有〈Ebase* EK*〉 < 0.
比较图 7a、b、c可知,正的风垂直切变在中尺度和大尺度系统中使能量从扰动态转移到基本态中,从而维持基本气流并削弱扰动,有利于静力适应过程的实现;而在小尺度和微尺度系统中使能量从基本态转移到扰动态中,促使扰动得以发展;而负的风垂直切变作用则正好相反.
4 结论本文为了研究VWS对静力适应过程中能量转换的影响,基于线性模型下的波动假设,讨论了四种风垂直切变模型中能量谱的转换情况,从能量转换的视角对VWS在静力适应过程中的作用给出了一个清晰的物理描述.
研究发现,对于绝热无摩擦的闭合系统,在整个静力适应过程中,系统的总能量满足守恒定律,破坏静力平衡的扰动能量以动能,有效势能和有效弹性势能的形式存在并相互转换,其中有效弹性势能扮演能量中转站的角色,这也表征由大气可压缩性引起的波动对大气静力适应过程作用重大,浮力对气块做功是有效势能转换为有效弹性势能的物理机制,垂直动能与有效弹性势能的转换可用于表征静力平衡被破坏的程度;当水平基流无垂直切变时,扰动能量与基本气流能量之间的交换被抑制,其物理实质为风切变应力引起的动量通量输送被切断.
在等温大气中,当大气初始扰动为有效势能和有效弹性势能时,水平基流的垂直切变改变了扰动能量在各能量形式中的分配比例,这种作用随扰动尺度和时间的变化有显著差异,系统尺度越小基流垂直切变的影响越显著;通过比较mod_c和mod_d中的情形,得到结论,负的风切变应力使得四类扰动能量谱随系统尺度的变化趋于平缓,使得微尺度和小尺度(中尺度)系统中Ekv(Ekh)的比例随时间减小,正的风切变使得扰动能量谱随系统尺度的变化显现跳跃的特征,使得中尺度(微尺度和小尺度)系统中Ekv(Ekh)的比例随时间减小.
从基态和扰动相互作用的角度来说,在mod_a模型中,基态能量与扰动态能量无转换,在mod_b中,大尺度和中尺度系统中风切变应力作用使得扰动能量被削弱,微尺度系统中使得扰动能量被加强;在mod_c中,对流层低层除部分微尺度系统外,风切变应力使得扰动能量被加强,而在对流层高层及平流层低层的大尺度和中尺度系统中,风切变应力使得扰动能量均被削弱;mod_d的情形同mod_c相反.
本文从能量视角揭示了风垂直切变对大气静力适应过程的影响,基于构造的风切变模型和初始的热力学扰动做了具体讨论,但破坏大气静力平衡的外界强迫不仅限于热力强迫,大气垂直廓线参数也并非定常,未来的研究将对非等温湿大气下,初始扰动性质对静力适应过程的影响进行探讨.
Andrews D G. 1981. A note on potential energy density in a stratified compressible fluid. Journal of Fluid Mechanics, 107: 227-236. |
Bannon P R. 1995. Hydrostatic Adjustment:Lamb's problem. Journal of the Atmospheric Sciences, 52(10): 1743-1752. |
Bannon P R. 1996. On the anelastic approximation for a compressible atmosphere. Journal of the Atmospheric Sciences, 53(23): 3618-3628. |
Bannon P R. 2005. Eulerian available energetics in moist atmosphere. Journal of the Atmospheric Sciences, 62(12): 4238-4252. |
Bannon P R. 2012. Atmospheric available energy. Journal of the Atmospheric Sciences, 69(12): 3745-3762. |
Bannon P R. 2013. Available energy of geophysical systems. Journal of the Atmospheric Sciences, 70(8): 2650-2654. |
Chagnon J M, Bannon P R. 2001. Hydrostatic and Geostrophic adjustment in a compressible atmosphere:Initial response and final equilibrium to an Instantaneous localized heating. Journal of the Atmospheric Sciences, 58(24): 3776-3792. |
Chagnon J M, Bannon P R. 2004. Wave response during hydrostatic and Geostrophic adjustment. Part Ⅰ:transient dynamics. Journal of the Atmospheric Sciences, 62(5): 1311-1329. |
Cui X D, Liu Y D, Zhao Z L, et al. 2016. Study of characteristics of the acoustic gravity wave and energy conversion in the three-dimensional hydrostatic adjustment process. Acta Meteorologica Sinica, 74(1): 127-132. |
Duffy D G. 2002. Hydrostatic Adjustment in Nonisothermal atmospheres. Journal of the Atmospheric Sciences, 60(2): 339-353. |
Fanelli P F, Bannon P R. 2005. Nonlinear atmospheric adjustment to thermal forcing. Journal of the Atmospheric Sciences, 62(12): 4253-4272. |
Guo H L, Liu Y D, Cui X D. 2020. Effects of Vertical Wind Shear (VWS) on hydrostatic adjustment-part Ⅰ:wave response. Chinese Journal of Geophysics (in Chinese), 63(6): 2170-2183. DOI:10.6038/cjg2020M0213 |
Sotack T, Bannon P R. 1999. Lamb's hydrostatic adjustment for heating of finite duration. Journal of the Atmospheric Sciences, 56(1): 71-81. |
Van Delden A. 2015. Chapter 3 of Atmospheric Dynamics. IMAU, Utrecht University, Netherlands, http://www.staff.science.uu.nl/~delde102/AtmosphericDynamics.htm.
|
崔新东, 刘宇迪, 赵增亮, 等. 2016. 三维静力适应过程中声重力波的特性和能量转换研究. 气象学报, 74(1): 127-132. |
郭海龙, 刘宇迪, 崔新东. 2020. 风垂直切变对大气静力适应过程的影响——第一部分:波动响应. 地球物理学报, 63(6): 2170-2183. DOI:10.6038/cjg2020M0213 |
 2020, Vol. 63
2020, Vol. 63


