2. 中国石油大学(华东)地球科学与技术学院, 青岛 266580;
3. 中国科学院油气资源研究重点实验室, 中国科学院地质与地球物理研究所, 北京 100029
2. School of Geosciences, China University of Petroleum(East China), Qingdao 266580, China;
3. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
龙马溪组页岩是我国页岩气勘探的主力产层,其弹性性质的研究对页岩气甜点预测和水力压裂设计具有重要的指导作用.目前基于数字岩心的弹性等效建模方法主要基于常规岩石物理解析表征和静态模量数值模拟,属于间接类方法,适用于组分单一、较为均匀的岩石样本(例如Berea砂岩、Fontainebleau砂岩等).对于矿物构成和微结构复杂的强非均质页岩,这些方法因假设前提条件或等效算法的局限性而计算精度有限.动态模量数值模拟属于直接类方法,适用于复杂岩石样本的弹性性质研究,但目前关于该方法的研究和应用相对较少.
数字岩心是利用X射线微CT技术以非破坏性方式获取岩石样品矿物颗粒和微孔结构的三维高分辨率图像,可用于求取岩石物理性质(如弹性模量、渗透率等)和模拟流体在孔、缝空间的运移和流动.常见的岩石物理弹性等效解析模型主要有(Mavko et al., 2009):微分等效介质模型(DEM)、自相容近似模型(SCA)、Xu&White模型、Nur模型、Kuster-Toksz模型等.邓继新等(2015)基于龙马溪组页岩数字岩心,详细对比研究了DEM、SCA、Backus平均模型的弹性等效建模精度.Zhao等(2016)综合利用Xu&White、SCA、DEM等模型,提出了表征不同成熟度有机页岩的弹性等效模型.Yang等(2017)联合应用DEM、SCA和Gassmann方程,研究了不同孔隙纵横比对等效速度建模的影响.这些岩石物理解析等效模型因假设前提条件的理论局限性,极大限制了其使用范围.近十年发展起来的静态模量数值模拟方法极大地拓展了岩石弹性等效建模的适应性,例如Arns等(2002)采用有限元法模拟计算了不同孔隙度下Fontainebleau砂岩数字岩心的弹性参数,并与实验测量结果进行对比验证.Knackstedt等(2009)讨论了复杂碎屑岩和碳酸盐岩数字岩心的弹性等效数值建模计算问题.孙建孟等(2014)利用扩展有限元法求取了低渗透砂岩数字岩心的弹性模量.Zhang等(2016)基于龙马溪组页岩数字岩心实现弹性等效有限元数值模拟,详细讨论了不同孔隙度和干酪根对岩石弹性模量的影响.胡洋铭等(2018)基于CT成像的微观结构图像,开展线弹性有限元方法弹性参数计算研究.静态法适用性广,但由于线性等效计算模型的局限性,对于复杂介质弹性等效的计算精度有限,很难精确模拟矿物组分、流体性质、饱和状况及复杂颗粒接触关系的影响,特别是对岩石微结构随压力的变化和声波小应变引起的动/静态模量差异缺乏有效表征手段.另外,静态法对数字岩心分辨率有很高要求,且岩心模型一般较大导致其计算效率低.
动态模量等效数值模拟方法是基于数字岩心中波传播响应特征,求取弹性参数的直接方法,与实验测量结果的可比性更强.Saenger等(2004)给出利用波动方程旋转交错网格计算随机裂缝介质的弹性参数.Saenger(2008)基于Fontainebleau砂岩数字岩心数据,详细比较了动、静态两种方法弹性等效数值建模结果,分析了流体黏度对砂岩弹性性质的影响.Saenger等(2011)指出了相对于静态法而言,动态方法能考虑波传播时引起的流动效应及其对有效弹性参数的影响.Madonna等(2012)基于Berea砂岩数字岩心和实验测量数据,对比分析了实验测量速度随压力的变化特征,据此进行数值模拟结果的校准.针对岩心超声实验测量波传播环境,张鲁新等(2010)应用不分裂卷积完全匹配层吸收边界和旋转交错网格有限差分方法,高精度模拟波在孔弹模型中的传播行为.有研究人员采用该方法研究了数字岩心多孔介质中弹性波的传播和散射特性(Zhang et al., 2014; 王志伟等,2018).印兴耀等(2016)利用声波方程有限差分法求取了Fontainebleau和Berea砂岩数字岩心的岩石弹性模量,并与静态法计算结果进行了比较.Zhu等(2017)提出采用不同吸收边界条件进行宽频带的数字岩心弹性等效数值建模方法,计算分析了纵波速度随孔隙度的变化情况.
动态模量等效数值模拟技术面临的挑战主要包括:(1)与砂岩数字岩心不同,页岩数字岩心(龙马溪组)拥有更细的微观结构(范围从微米至纳米),研究波与微结构(矿物与孔隙)相互作用对弹性模量的影响需要超高频超声探测频率(MHz),介质的强非均质特征要求数值模拟算法具有更高的稳定性与计算精度;(2)针对页岩数字岩心复杂的矿物组分和孔隙结构以及流体多样性,为保证和超声实验波形的可对比性,动态弹性等效模拟对孔弹参数估计和双相介质孔弹方程的精度要求高,确保构建的非均质双相介质数字岩心模型大致体现实验岩心的岩石物理特性和波传播行为;(3)精确模拟施加压力对岩心微结构变形的影响是动态弹性等效建模的关键,特别是基质中的软孔和有机质中的微孔随有效压力的变形,需要有效的表征手段.目前应用动态法求取页岩弹性参数的研究相对较少,数字岩心内部各点设定的模量参数基本不随压力改变,上述挑战问题表现不太突出.本文利用第三代(上海光源)高性能同步辐射纳米CT(Shanghai Synchrotron Radiation Facility, SSRF)进行计算机断层扫描,得到龙马溪组页岩高分辨数字岩心图像(分辨率为1 μm).首先利用多阈值Otsu分割方法将数字岩心分解为黏土、石英、孔隙、TOC、长石类、黄铁矿类等六种类型.采用晶体学中的取向分布函数(ODF)来分析数字岩心中矿物颗粒取向分布方位特征,并结合矿物组分等效模量法给出各类矿物组分的弹性模量.采用二元函数分水岭算法构建不同压力下的数字岩心模型,最后基于Biot孔弹方程,应用不分裂卷积完全匹配层(CPML)吸收边界条件及旋转交错网格有限差分法实现不同压力下的数字岩心模型等效速度建模.与该岩心样品超声实验测量结果进行交叉验证和算法校准,有效改善动态法弹性等效数值建模精度.
1 页岩数字岩心特征 1.1 页岩数字岩心本文使用直径为1 mm、长约5 mm的龙马溪组页岩岩石样本,通过上海光源第三代高性能同步辐射纳米CT进行计算机断层扫描,基于不同物质对光束吸收能力的不同,得到高分辨率(1 μm)的三维图像.图 1所示为该页岩数字岩心图像水平切片,可清晰地分辨出裂纹(绿圈所示)、粒间小孔、黄铁矿、石英、黏土等矿物组分及其结构形态分布、尺寸大小、几何形状等.黄铁矿(白色亮点,红圈所示)、石英(灰白色)、黏土(灰色)、孔隙及TOC(最暗部分,蓝圈所示)等矿物组分在空间平面的结构形态分布.可见,龙马溪组页岩的岩性构成、矿物组分和孔隙/矿物颗粒结构形态变化导致其表现出较强的非均质性,对页岩的静、动态弹性模量及力学参数均产生重要作用.

|
图 1 龙马溪组页岩数字岩心图像水平切片 (a)第16张切片;(b)第266张切片. Fig. 1 Horizon slices of Longmaxi Formation shale digital core images (a) 16th horizon slice; (b) 266th horizon slice. |
整个数字岩心数据体由1604张切片组成,为便于方法研究和降低孔弹方程正演模拟耗时,本文选取如图 3a所示的部分数据,其分辨率为400×400×400像素,大小为400 μm×400 μm×400 μm.根据不同矿物的X射线吸收率,来确定各组矿物相应的灰度值范围,实现阈值分割.阈值分割方法很多(Andrä et al., 2013),本文采用Ostu方法进行阈值提取,多阈值Ostu分割法是图像处理中非常重要的一类方法(申铉京等,2017).假设图像有M个像素点,总灰度级为S,图像中灰度级为i的像素点有mi(i=0, 1, 2, …, S)个,呈现的灰度概率为Pi=mi/M,总像素可表示为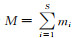

|
图 3 龙马溪组页岩三维数字岩心 (a)原始数据; (b)阈值分割结果. Fig. 3 3D digital cores of Longmaxi Formation shale (a) Raw data; (b) Result of threshold segmentation. |
|
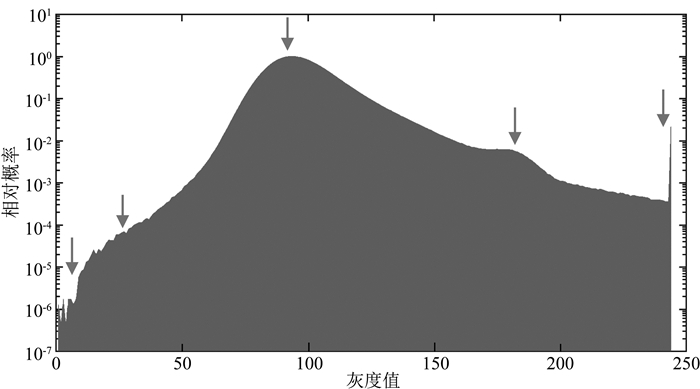
图 2 龙马溪组页岩三维数字岩心灰度直方图 Fig. 2 Histograms of the grayscale values of Longmaxi Formation shale 3D digital cores |
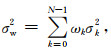
|
(1) |
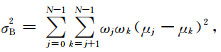
|
(2) |
其中ωk、σk2、μk代表第k类的概率、方差和均值,分别定义为: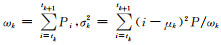
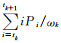
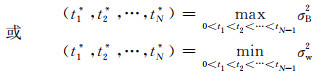
|
(3) |
式中t1*, t2*, …, tN*表示最优的分割阈值,等式右边0 < t1 < t2 < … < tN-1则表示初始阈值.
根据图 2中箭头示意的峰值及拐点,同时考虑某些矿物对X射线的吸收率相近,以及页岩孔隙及主要骨架(石英、长石)的差异性,将原始的数字岩心图像分割为六组矿物类型:①孔隙,②TOC,③黏土,④石英,⑤方解石、长石、重晶石等,⑥黄铁矿、菱铁矿等.根据各类的灰度分布概率,利用公式(3)计算得到最优的分割阈值,结果如图 3所示.
2 孔弹参数估计 2.1 矿物组分等效弹性模量根据岩石物理手册(Mavko et al., 2009)可知各种矿物的基本弹性参数(如弹性模量、速度、密度等),通过数字岩心阈值分割数据体的矿物含量分析,该样本各矿物组分的百分含量及其基本弹性参数如表 1所示.基于超声实验的有限压力,假定这些矿物基本弹性参数在数值模拟过程中不随压力变化而改变.
|
|
表 1 各种矿物百分含量及弹性参数 Table 1 Percentage of minerals and their elastic parameters |
利用Hill平均法计算阈值分割后六种矿物组分类型的等效弹性模量(Zhang et al., 2014),以黄铁矿(第六组)为例,其计算过程如下:
设定黄铁矿、菱铁矿和辉石的体积百分含量总和为1,则其百分比含量分别为:η1=72.34%、η2=12.77%、η3=14.89%.首先采用Voigt和Reuss公式分别计算等效体积模量:
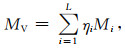
|
(4) |
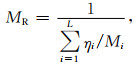
|
(5) |
其中ηi是每种组分百分含量,L为矿物组分数量,Mi是每种组分的体积模量.参考表 1中的弹性模量值,代入公式(4)、(5),得到等效体积模量为MV=136.44 GPa和MR=132.93 GPa, 此为上下两个界限值,利用Hill平均公式:
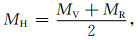
|
(6) |
求取MH=134.685 GPa.同理,可以求取各组分的等效弹性模量,结果如表 2所示.
|
|
表 2 各组矿物等效弹性参数 Table 2 Equivalent elastic parameters of each group minerals |
根据物源和沉积过程的方向特性以及后期改造的局部构造应力方向特性,一般认为岩石颗粒和孔缝分布存在一定的方向特性.另外,依据晶体学基本原理,不同的矿物具有不同的优势排列方向.特别是富含黏土矿物的页岩(Dabat et al., 2019),矿物颗粒、层理及微裂缝存在明显的分布方向特征,导致计算的等效弹性参数的各向异性分布.利用取向分布函数(Orientation Distribution Function, ODF)可对之定量分析(Bachmann et al., 2010;Hielscher et al., 2010),具体计算方法见附录A.
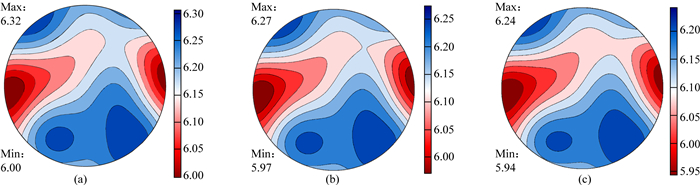
本文使用Bachmann等(2010)提供的开源软件工具箱MTEX,利用表 1所示各矿物基本弹性参数,来计算页岩样本矿物颗粒的取向分布函数,即矿物颗粒弹性刚度张量,据此计算等效速度的上界值(Voigt值)、下界值(Reuss值)和平均值(Hill值).本文以样本主要构成组分——石英颗粒为例,计算样本中石英颗粒的取向分布,结果如图 4所示(极射赤平投影极图).可见,三种张量计算得到的石英速度各向异性都小于5.3%(各自最大速度与最小速度之间差值的相对比值),由于样本石英含量达49%,基本可以认为整个模型的骨架弹性参数分布是各向同性的.
|
图 4 纵波速度分布的上半球极图 (a) Voigt分布;(b) Hill分布;(c) Reuss分布. Fig. 4 Upper hemispheric polar graph of the calculated aggregate P-wave velocities distribution (a) Voigt distribution; (b) Hill distribution; (c) Reuss distribution. |
模拟波在数字岩心中的传播过程,拾取初至时间来求取纵波速度,据此建立该岩心的等效弹性模型.
3.1 不同压力条件下岩石颗粒接触关系分析研究不同压力下纵波速度的变化情况,首先需要构建表征不同压力的页岩数字岩心模型.在岩石物理学中,颗粒介质模型理论是专门描述岩石内部颗粒的接触关系(例如Hertz-Mindlin模型).不同有效压力条件下岩石颗粒接触关系会发生变化,不同大小和形状的孔隙可以作为一种特殊颗粒来处理.对于有限压力的超声实验,颗粒间接触关系与压力之间可以用如下线性公式来表示(Madonna et al., 2012):
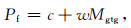
|
(7) |
其中Mgtg∈[0, 1]表征颗粒的接触关系,Pf为有效压力,c和w是拟合系数.Madonna等(2012)研究了Berea砂岩数字岩心在50 MPa有效压力范围内岩石颗粒的接触关系,确定c=0.9743 MPa和w=200.86 MPa.
本文参照Madonna等(2012)给出的二元函数来近似描述龙马溪组页岩数字岩心在不同压力条件下颗粒间的接触关系,其本质是采用分水岭算法建立每个压力条件下数字岩心中的岩石颗粒(含孔隙)之间的接触关系图,据此确定Mgtg的取值.假定Pf =0 MPa对应的Mgtg=0,而最大Pf对应的Mgtg=1.以此为基准,通过图像差异比较算法,比较各压力条件下的接触关系图来确定该压力点的Mgtg值,从而建立Pf-Mgtg之间的关系曲线.在图像分析中广泛采用分水岭算法来识别图像中的各种边缘结构(Alam and Haque, 2017),其计算过程是一个迭代标注过程,分两个步骤,一个是排序过程:对原始灰度图像进行梯度计算,按照每个像素的灰度级进行从低到高排序;一个是淹没过程:对每个局部极小值的影响域慢慢向外扩展至边缘进行标注.分水岭算法优势在于对微弱边缘具有良好的响应,是识别封闭连续边缘的有效方法.由于数字岩心中的噪声干扰较弱,微弱边界过度识别的问题不突出.
本文以龙马溪组页岩数字岩心为例进行说明,图 5a为数字岩心阈值分割图像,图中不同颜色表示的是不同的矿物组分,蓝色区域表示孔隙,绿色和淡蓝色区域分别是石英和黏土组分,其二值化灰度图如图 5b所示.对二值化灰度图像进行分水岭变换,得到如图 5c所示的岩石颗粒边缘结构图.

|
图 5 数字岩心颗粒接触表征过程 (a)阈值分割图;(b)二值化图;(c)岩石颗粒边缘结构图. Fig. 5 Digital core grain-to-grain contact characterization (a) Threshold segmentation image; (b) Binary image; (c) Rock grain edge structure map. |
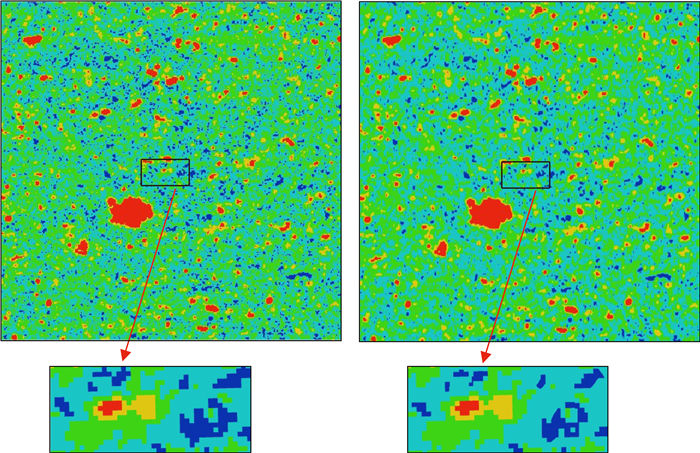
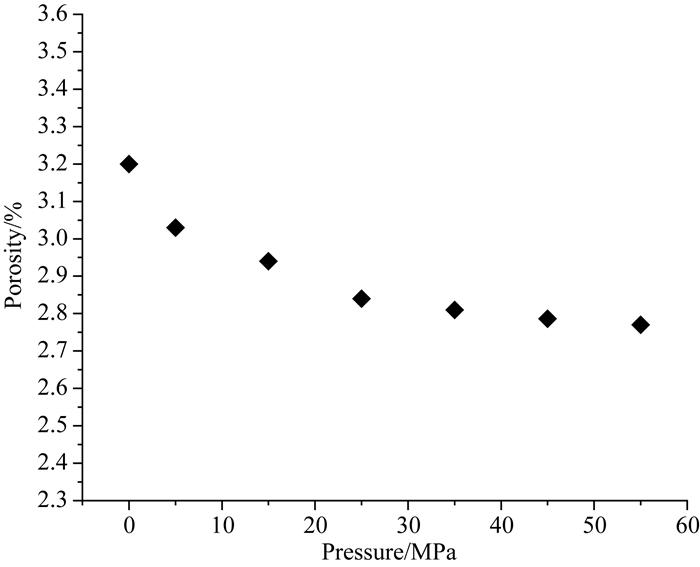
不同压力条件下岩石颗粒的接触关系会有所变化,图 6左右两边分别为有效压力0 MPa和55 MPa对应的数字岩心阈值分割模型.图中黑框放大所示可以看出压力的变化对孔隙结构及孔隙与颗粒接触关系产生较大影响,特别是对软孔隙形状和尺寸以及TOC等“软物质”的作用较强,引起“软物质”相关孔隙度的明显变化,如图 7所示为孔隙度随压力增大而渐渐变小.
|
图 6 不同压力下数字岩心结构变化(左边0 MPa,右边55 MPa) Fig. 6 Structure changes of digital core under different pressures (left 0 MPa, right 55 MPa) |
|
图 7 不同压力的数字岩心模型的孔隙度变化 Fig. 7 Porosity of digital core model under different pressures |
构建不同压力的数字岩心孔弹参数模型,据此开展超声数值模拟进行动态法等效弹性建模.考虑到页岩较强的非均质性,本文利用高精度的旋转交错网格有限差分法求解Biot方程来模拟超声波在数字岩心中的传播,吸收边界条件则采用消除边界效应俱佳的不分裂卷积完全匹配层(CPML),具体算法介绍见附录B,模型具体孔弹参数和模拟计算参数参考表 2和表 3.拾取模拟的直达波初至走时来计算纵波速度.图 8是采用不同主频子波数值模拟0 MPa的数字岩心模型得到的波场快照.可见,不同频率模拟的散射强度有所不同.为了质控不同压力下的数字岩心模拟的条件,采用相同的初始参数、相同的震源位置和接收条件进行模拟.在模型顶部激发震源,底部放置检波器,模拟过程中不同于常规的利用均匀介质作为背景参考计算岩石等效速度,本文采用0 MPa时的数字岩心作为背景参考来计算压力对等效速度的影响.
|
|
表 3 动态模拟参数 Table 3 Dynamic simulation parameters |

|
图 8 页岩数字岩心模型(0 MPa)中传播的波场动态模拟快照 Fig. 8 Wave field snapshots of dynamic simulation propagating in shale digital cores model (0 MPa) |
计算等效速度的基本公式为
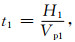
|
(8) |
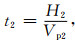
|
(9) |
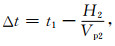
|
(10) |
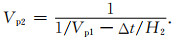
|
(11) |
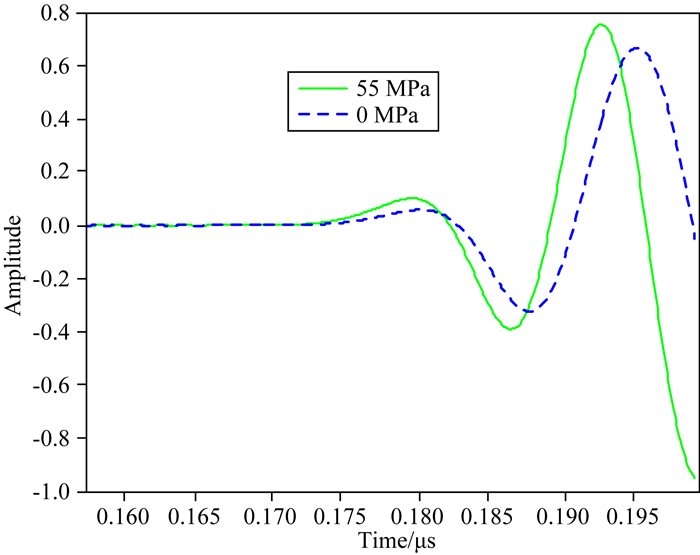
假设公式(11)中Vp2为待求结果,H1=H2为激发点到接收点的距离.先求出参考模型时间t1,再利用不同压力与0 MPa数字岩心振幅峰值时间差来计算Vp2.图 9所示为0 MPa和55 MPa数字岩心模型底部第12个检波器的接收结果,计算每道结果Vp2n,取22个检波器计算结果的平均值Vave作为最后结果.计算公式:
|
图 9 0 MPa和55 MPa时间延迟结果 Fig. 9 Time delay results of 0 MPa and 55 MPa |
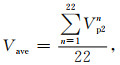
|
(12) |
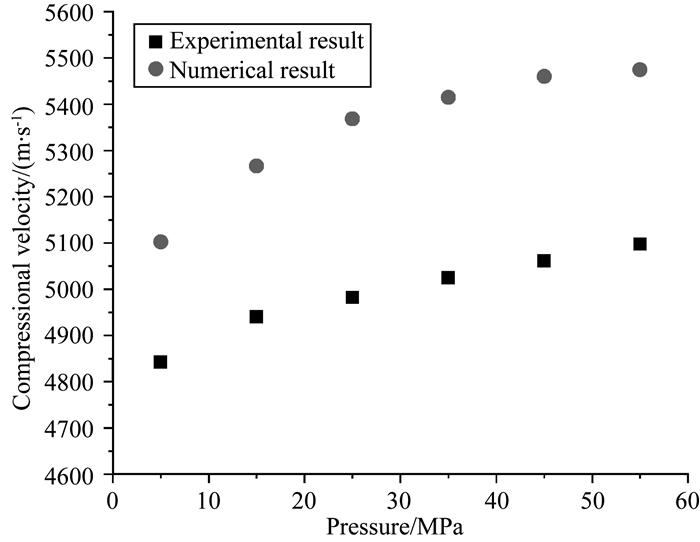
选取300 MHz主频进行动态模拟多组压力下的数字岩心模型,计算不同压力模拟记录与0 MPa参考模型记录之间的初至最大振幅峰值的平均走时差,来确定等效速度,得到如图 10(灰色实心圆圈)所示的结果.可见,随着压力的增加,纵波速度是逐步增大;速度增长率逐渐变缓,这与图 10(黑色实心方框)所示超声实验测量结果变化趋势一致,说明数值模拟结果是有效的.
|
图 10 速度随压力变化的实验与数值结果 Fig. 10 Experimental and numerical results of pressure-dependent compressional velocity |
图 10中速度与压力变化曲线展示了数值模拟与超声实验二者保持较好的相对变化关系,但绝对值有较大差别.实验所用超声主频为1 MHz,但该页岩岩心在兆赫兹范畴的速度频散较弱.一般而言,数字岩心超声模拟得到的速度普遍高于岩心实测速度(Knackstedt et al., 2009;Zhang et al., 2012),原因可能是数字岩心的分辨能力有限,大量的微孔、裂纹、节理和颗粒接触特征等细节未能刻画并参与模拟计算.另外,页岩矿物组分复杂,以六类矿物分类较粗,没有考虑到所有的矿物.模拟计算得到的岩石等效弹性性质与实测有一定的偏差,可以将实验室测量作为标准对数值结果进行校正(Madonna et al., 2012),校正公式如下:
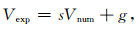
|
(13) |
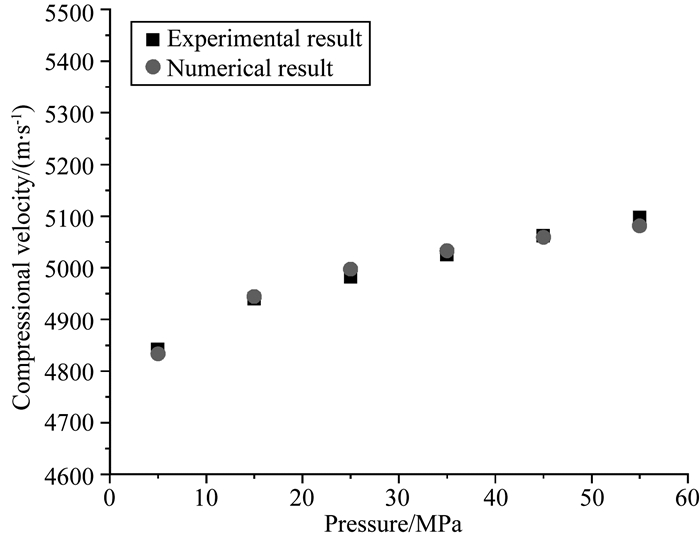
其中Vexp是实验室测量的速度;Vnum是数值模拟获取的速度;s和g是关系因子.利用最小二乘法拟合得到:s=0.4486,g =2385.3.校正结果如图 11,能够看出数值计算的结果获得较佳的校准,与实验室所测结果基本一致.
|
图 11 基于实验校正数值结果 Fig. 11 Numerical results calibration based on experimental results |
弹性参数的确定对页岩储层表征起关键作用.龙马溪组页岩具有矿物组成种类多、微结构复杂和强非均质等特征,采用常规岩石物理解析方法和目前流行的静态数值等效建模方法进行弹性建模存在一定的局限性.因此本文基于高分辨率的页岩数字岩心数据,进行多阈值分割,利用矿物组分等效模量法计算各类矿物的弹性模量;在此基础上采用分水岭算法建立每个压力条件下数字岩心中的岩石颗粒(含孔隙)之间的接触关系,从而构建不同压力下的页岩数字岩心模型;利用Biot孔弹方程,采取不分裂卷积完全匹配层(CPML)有限差分法对页岩数字岩心模型进行模拟研究.通过不同模型的走时差来计算平均等效速度,并结合超声实验结果对数值结果进行验证和校准.主要获得以下结论和认识:
(1) 利用上海光源第三代高性能同步辐射纳米CT进行计算机断层扫描,获取高分辨率的龙马溪组页岩数字岩心数据.以此为基础,选用多阈值Otsu分割方法将数字岩心分解为黏土、石英、孔隙、TOC、长石类、黄铁矿类等六种矿物类型;采用晶体学中的取向分布函数(ODF)来分析数字岩心中矿物颗粒取向分布方位特征,并结合矿物组分等效模量法给出各类矿物组分的弹性模量.
(2) 采用二元函数分水岭方法描述不同压力下的岩石孔隙变形和颗粒接触关系变化,建立表征不同压力的数字岩心模型.然后基于Biot孔弹方程,选择不分裂卷积完全匹配层(CPML)旋转交错网格有限差分法模拟波在模型中的传播,以未加压的数字岩心模型为标准,先计算不同压力下弹性波初至走时的平均时间差,进而估算各压力点的数字岩心模型等效速度.
(3) 与该岩心样品的超声实验测量速度相比,动态法数值模拟与其保持较好的相对变化关系,但数值计算结果略偏高,据此校正数值计算过程中表征岩石微结构及颗粒接触关系随压力变化的二元函数,从而有效地提高动态法弹性等效数值建模的精度,为页岩储层的“甜点”分析提供更准确的参考.
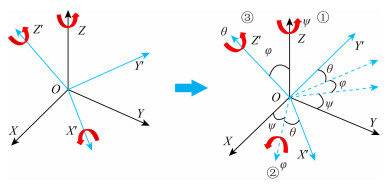
附录A 取向分布函数(ODF)取向分布函数是一种能详细描述样品晶粒分布状态的确切的表示方法,通过引入“Euler角”和“Euler空间”的概念,来描述空间中任意晶粒取向,其原理是首先确定“Euler角”和“Euler空间”,每一个晶粒在Euler空间中都能用一个取向点来表达.首先定义一个坐标系O-XYZ(图A1黑色坐标),然后定义一个与样品的微观方向相关的坐标系O-X′Y′Z′(图A1浅蓝色坐标),后者相对于前者的某一方向可以通过图中①、②、③任意三次旋转来完成,这样就建立了一个以(ψ, φ, θ)为坐标系的Euler空间.Euler空间中的任意晶粒都能用某个取向点来表达,将样品中全部晶粒的取向都标注于Euler空间里,就可以得到样品中全部晶粒的三维取向分布图.
|
图 A1 “Euler角”和“Euler空间”变换示意图 Fig. A1 Transformation of "Euler angle" and "Euler space" |
当样品中晶粒非常多且取向分布情况复杂时,常选择取向密度函数D(ψ, φ, θ)来表达多晶集合体的取向分布情况.定义处于取向(ψ, φ, θ)周围的取向单元dΩ=sinθdψdφdθ中的晶粒的体积百分比(聂冠军等,2012)如下:
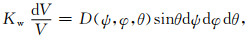
|
(A1) |
式中dV为取向落在该取向元的晶粒体积;V为样品的体积;Kw为比例系数,常取值为1.由于ODF无法直接测量,只得根据几个实测的极图数据(苑蕾等,2017),通过傅里叶分析中的级数展开原理,用调和函数分析法,利用下列公式进行计算:
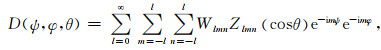
|
(A2) |
式中Wlmn为级数的第lmn项系数,l是级数展开项.可以根据以下公式求取Wlmn之后,反代入公式(A2),从而计算出D(ψ, φ, θ).
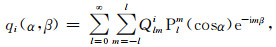
|
(A3) |
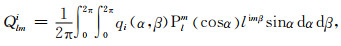
|
(A4) |
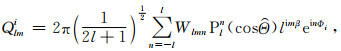
|
(A5) |
式中qi(α, β)为晶面i的极图函数,α是晶面法线的倾角,β是晶面法线的旋转角;ei和e-i是单独一项自然对数函数,此处的i2=-1;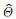
(1) Biot方程
令ui和wi分别为固体骨架位移和流相相对位移,uif为流相位移, wi=ϕ(uif-ui),忽略震源项的各向同性流体饱和孔隙介质Biot方程为
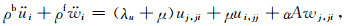
|
(B1) |
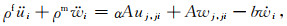
|
(B2) |
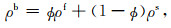
|
(B3) |
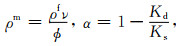
|
(B4) |
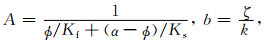
|
(B5) |
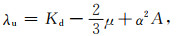
|
(B6) |
其中“··”表示二阶导数,字母下标逗号右边“ji”表示对其求偏导,用流体密度ρf与固体颗粒密度ρs定义ρb和ρm.ν是表征孔隙结构特征的弯曲度因子,干岩石骨架体积模量为Kd,各向同性孔隙介质中液相体积模量为Kf,固体体积模量为Ks,μ为剪切模量,α是Biot系数,A为耦合模量,k为渗透率,λu为饱和岩石的拉梅系数,b为黏滞系数,ζ为孔隙中流体的黏滞系数.
联立方程(B1)与(B2),令液相相对速度qi=ẇi和固体速度vi= 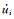
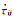
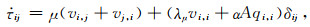
|
(B7) |
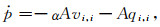
|
(B8) |
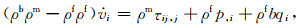
|
(B9) |
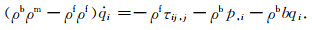
|
(B10) |
(2) 不分裂卷积完全匹配层(CPML)
引入复数因子定义复数坐标:
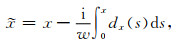
|
(B11) |
式中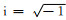
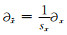
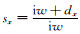
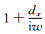
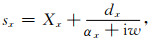
|
(B12) |
式中αx≥0,Xx≥1.此后采用微分方程法或迭代卷积法推导迭代格式CPML吸收边界的流程,最终说明CPML中参数设置的普遍规则.
将(B12)代入(B11),并做逆Fourier变换:
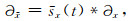
|
(B13) |
式中sx(t)是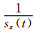
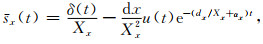
|
(B14) |
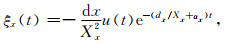
|
(B15) |
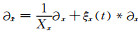
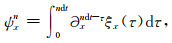
|
(B16) |
式(B16)进一步可写成:
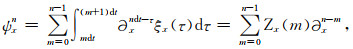
|
(B17) |
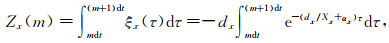
|
(B18) |
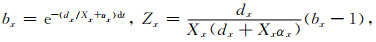
|
(B19) |
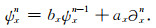
|
(B20) |
采取迭代格式的CPML实现时只需要一个额外的辅助变量ψx,即能够较佳地提高计算效率,不仅避开场分解下产生的诸多方程,而且不从时间域完成卷积计算,使波动方程转换到PML区域需要将空间导数做如下的变换:
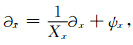
|
(B21) |
设定参数dx:
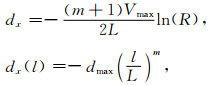
|
(B22) |
其中,m是多项式的阶数,一般取为2或3;l(0≤l≤L)是PML里的运算点至PML区域内边界的距离;L是该PML区域的厚度;R是理论反射系数,常取10-6.令:
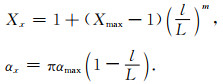
|
(B23) |
当αx=0,Xx=1时,sx和常规PML一致.αx在PML区域内在0~αmax间线性变化,常令αmax=f0,式中f0为子波频率.
(3) 旋转交错网格有限差分
旋转交错网格(RSG)方法沿着空间网格的对角线方位求取空间导数,使所得结果沿着正常坐标轴方向线性内插获得直角坐标轴方位的空间导数.使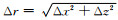
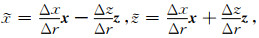
|
(B24) |
因此,直角坐标下沿坐标轴方向的一阶空间导数可表示为
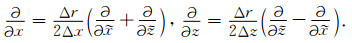
|
(B25) |
下面给出2N阶旋转交错网格有限差分中每个物理量的离散格式(2D):
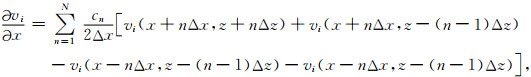
|
(B26) |
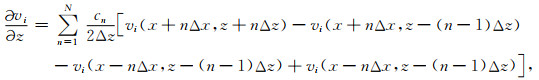
|
(B27) |
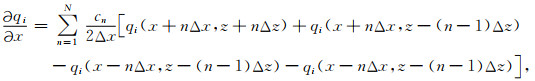
|
(B28) |
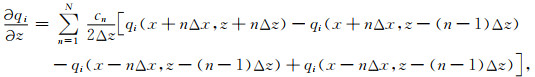
|
(B29) |
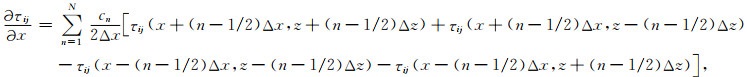
|
(B30) |
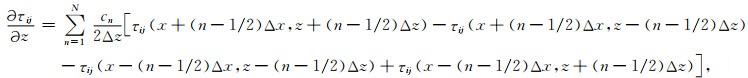
|
(B31) |
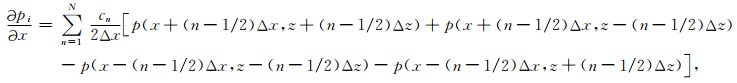
|
(B32) |
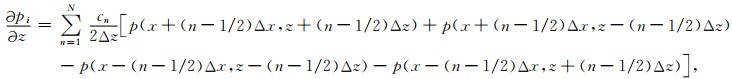
|
(B33) |
其中N表示此差分近似阶数的1/2,cn为差分系数,然后对式(B26)—(B33)求取各参数的辅助变量,便能求出复数坐标下的空间导数(即施加CPML),再代入公式(B7)—(B10),合并整理得到:
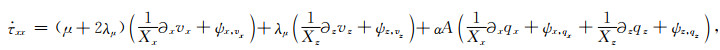
|
(B34) |
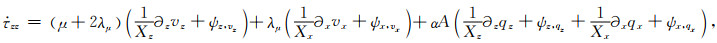
|
(B35) |
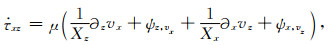
|
(B36) |
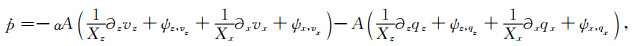
|
(B37) |
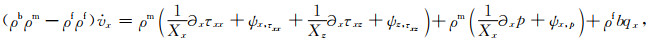
|
(B38) |
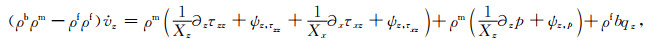
|
(B39) |
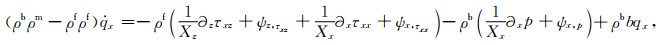
|
(B40) |
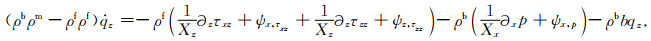
|
(B41) |
Alam M F, Haque A. 2017. A new cluster analysis-marker-controlled watershed method for separating particles of granular soils. Materials, 10(10): 1195.
|
Andrä H, Combaret N, Dvorkin J, et al. 2013. Digital rock physics benchmarks-Part Ⅰ:Imaging and segmentation. Computers & Geosciences, 50(1): 25-32. |
Arns C H, Knackstedt M A, Pinczewski W V, et al. 2002. Computation of linear elastic properties from microtomographic images:Methodology and agreement between theory and experiment. Geophysics, 67(5): 1396-1405. DOI:10.1190/1.1512785 |
Bachmann F, Hielscher R, Jupp P E, et al. 2010. Inferential statistics of electron backscatter diffraction data from within individual crystalline grains. Journal of Applied Crystallography, 43(6): 1338-1355. DOI:10.1107/S002188981003027X |
Dabat T, Hubert F, Paineau E, et al. 2019. A general orientation distribution function for clay-rich media. Nature Communications, 10: 5456. DOI:10.1038/s41467-019-13401-0 |
Deng J X, Wang H, Zhou H, et al. 2015. Microtexture, seismic rock physical properties and modeling of Longmaxi Formation shale. Chinese Journal of Geophysics (in Chinese), 58(6): 2123-2136. DOI:10.6038/cjg20150626 |
Hielscher R, Mainprice D, Schaeben H. 2010. Material behavior: texture and anisotropy.//Freeden W, Nashed M, Sonar T eds. Handbook of Geomathematics. Berlin Heidelberg: Springer.
|
Hu Y M, Zhao J G, Sun L Q, et al. 2018. A study on effect of pore structure on acoustic properties of carbonate rocks using micro-CT imaging.//CPS/SEG 2018 International Geophysical Conference and Exhibition (in Chinese). Beijing: China Academic Journal (CD-ROM Edition) e-Magazine.
|
Knackstedt M A, Latham S, Madadi M, et al. 2009. Digital rock physics:3D imaging of core material and correlations to acoustic and flow properties. The Leading Edge, 28(1): 28-33. DOI:10.1190/1.3064143 |
Madonna C, Almqvist B S G, Saenger E H. 2012. Digital rock physics:numerical prediction of pressure-dependent ultrasonic velocities using micro-CT imaging. Geophysical Journal International, 189(3): 1475-1482. DOI:10.1111/j.1365-246X.2012.05437.x |
Mavko G, Mukerji T, Dvorkin J. 2009. The Rock Physics Handbook (Tools for Seismic Analysis of Porous Media). Cambridge: Cambridge University Press.
|
Nie G J, Shan Y H, Tian Y, et al. 2012. Numerical modeling of textures in polycrystals:theory and applications in geosciences. Geotectonica et Metallogenia (in Chinese), 36(1): 56-68. DOI:10.1007/s11783-011-0280-z |
Saenger E H, Krüger O S, Shapiro S A. 2004. Effective elastic properties of randomly fractured soils:3D numerical experiments. Geophysical Prospecting, 52(3): 183-195. DOI:10.1111/j.1365-2478.2004.00407.x |
Saenger E H. 2008. Numerical methods to determine effective elastic properties. International Journal of Engineering Science, 46(6): 598-605. DOI:10.1016/j.ijengsci.2008.01.005 |
Saenger E H, Enzmann F, Keehm Y, et al. 2011. Digital rock physics:Effect of fluid viscosity on effective elastic properties. Journal of Applied Geophysics, 74(4): 236-241. DOI:10.1016/j.jappgeo.2011.06.001 |
Shen X J, Liu X, Chen H P. 2017. Fast computation of threshold based on multi-threshold Otsu criterion. Journal of Electronics and Information (in Chinese), 39(1): 144-149. |
Sun J M, Yan G L, Jiang L M, et al. 2014. Research of influence laws of fluid properties on elastic parameters of fractured low permeability reservoir rocks based on digital core. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese), 38(3): 39-44. |
Wang Z W, Fu L Y, Zhang Y, et al. 2016. The ultrasonic response of numerical simulation and analysis of scattering characteristics in digital core for shale reservoir. Chinese Journal of Geophysics (in Chinese), 61(3): 1069-1082. DOI:10.6038/cjg2018K0563 |
Yang Z Q, He T, Zou C C. 2017. Shales in the Qiongzhusi and Wufeng-Longmaxi Formations:a rock-physics model and analysis of the effective pore aspect ratio. Applied Geophysics, 14(3): 325-336. DOI:10.1007/s11770-017-0628-7 |
Yin X Y, Qin Q P, Zong Z Y. 2016. Simulation of elastic parameters based on the finite difference method in digital rock physics. Chinese Journal of Geophysics (in Chinese), 59(10): 3883-3890. DOI:10.6038/cjg20161031 |
Yuan L, Wang H J, An J L, et al. 2017. Crystallographic characteristics of hydroxylapatite in hard tissues of seawater Lateolabrax japonicus. Acta Geologica Sinica (in Chinese), 91(10): 2231-2239. |
Zhang W H, Fu L Y, Zhang Y, et al. 2016. Computation of elastic properties of 3D digital cores from the Longmaxi shale. Applied Geophysics, 13(2): 364-374. DOI:10.1007/s11770-016-0542-4 |
Zhang Y, Toksöz M N. 2012. Impact of the cracks lost in the imaging process on computing linear elastic properties from 3D microtomographic images of Berea sandstone. Geophysics, 77(2): R95-R104. |
Zhang Y, Fu L Y, Zhang L X, et al. 2014. Finite difference modeling of ultrasonic propagation (coda waves) in digital porous cores with un-split convolutional PML and rotated staggered grid. Journal of Applied Geophysics, 104: 75-89. DOI:10.1016/j.jappgeo.2014.02.012 |
Zhao L X, Xuan Q, Han D H, et al. 2016. Rock-physics modeling for the elastic properties of organic shale at different maturity stages. Geophysics, 81(5): D527-D541. DOI:10.1190/geo2015-0713.1 |
Zhang L X, Fu L Y, Pei Z L. 2010. Finite difference modeling of Biot't poroelastic equations with unsplit convolutional PML and rotated staggered grid. Chinese Journal of Geophysics (in Chinese), 53(10): 2470-2483. DOI:10.3969/j.issn.0001-5733.2010.10.021 |
Zhu W, Zhao L X, Shan R. 2017. Modeling effective elastic propertiesof digital rocks using a new dynamic stress-strain simulation method. Geophysics, 82(6): MR163-MR174. DOI:10.1190/geo2016-0556.1 |
邓继新, 王欢, 周浩. 2015. 龙马溪组页岩微观结构、地震岩石物理特征与建模. 地球物理学报, 58(6): 2123-2136. DOI:10.6038/cjg20150626 |
胡洋铭, 赵建国, 孙朗秋等. 2018.使用微米CT成像的孔隙结构对碳酸盐岩声学性质的影响研究.//CPS/SEG北京2018国际地球物理会议暨展览电子论文集.北京: 《中国学术期刊(光盘版)》电子杂志社.
|
聂冠军, 单业华, 田野, 等. 2012. 组构数值模拟的原理及其在地学中的应用. 大地构造与成学, 36(1): 58-68. |
申铉京, 刘翔, 陈海鹏. 2017. 基于多阈值Otsu准则的阈值分割快速计算. 电子与信息学报, 39(1): 144-149. |
孙建孟, 闫国亮, 姜黎明, 等. 2014. 基于数字岩心研究流体性质对裂缝性低渗透储层弹性参数的影响规律. 中国石油大学学报(自然科学版), 38(3): 39-44. DOI:10.3969/j.issn.1673-5005.2014.03.006 |
王志伟, 符力耘, 张艳, 等. 2018. 龙马溪组页岩数字岩芯超声响应数值模拟及散射特征分析. 地球物理学报, 61(3): 1069-1082. DOI:10.6038/cjg2018K0563 |
印兴耀, 秦秋萍, 宗兆云. 2016. 数字岩石物理中弹性参数的有限差分计算方法. 地球物理学报, 59(10): 3883-3890. DOI:10.6038/cjg20161031 |
苑蕾, 王河锦, 安佳丽. 2017. 海水鲈鱼硬体组织中羟基磷灰石的结晶特性. 地质学报, 91(10): 2231-2239. DOI:10.3969/j.issn.0001-5717.2017.10.006 |
张鲁新, 符力耘, 裴正林. 2010. 不分裂卷积完全匹配层与旋转交错网格有限差分在孔隙弹性介质模拟中的应用. 地球物理学报, 53(10): 2470-2483. DOI:10.3969/j.issn.0001-5733.2010.10.021 |
 2020, Vol. 63
2020, Vol. 63


