地球物理学报  2020, Vol. 63 Issue (5): 2107-2119   PDF    
引用本文
戴世坤, 陈轻蕊, 李昆, 等. 2020. 重力异常场空间-波数混合域三维数值模拟. 地球物理学报, 63(5): 2107-2119, doi: 10.6038/cjg2020M0584.  
Dai S K, Chen Q R, Li K, et al. 2020. Three-dimensional numerical simulation of the gravity anomaly field in the space-wave number mixed domain. Chinese J. Geophys. (in Chinese), 63(5): 2107-2119, doi: 10.6038/cjg2020M0584.  
重力异常场空间-波数混合域三维数值模拟
戴世坤1,2, 陈轻蕊1,2, 李昆1,2, 凌嘉宣1,2     
1. 中南大学地球科学与信息物理学院, 长沙 410083;
2. 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083
收稿日期 2018-10-08, 2019-05-10 收修定稿
基金项目: 国家自然科学基金项目（41574127），国家科技重大专项（2018YFC0603602）和中南大学研究生自主创新项目（2018zzts200，2018zzts203）联合赞助
第一作者简介: 戴世坤, 男, 1963年生, 教授, 博士生导师, 研究方向为重、磁、电、震三维正反演理论与方法及其实用化软件开发.E-mail:dskgmes@csu.edu.cn
通讯作者: 陈轻蕊, 女, 1992年生, 在读博士研究生, 研究方向为重、磁、电数值模拟与反演成像方法及并行化算法研究.E-mail:1532550316@qq.com
摘要：重力勘探中复杂条件下的三维正演计算量大存储要求高，使得这种条件下重力勘探高效、精细正反演变得困难.针对这一问题，提出一种空间-波数混合域数值模拟方法，该方法将空间域引力位积分进行水平方向二维傅里叶变换，将三维空间域卷积问题转换为多个不同波数之间相互独立的空间垂向一维积分问题，一维积分垂向可离散为多个单元积分之和，每个单元采用二次形函数表征密度变化，可得出单元积分的解析表达式.该方法计算量和存储需求少，算法高度并行；保留垂向为空间域，优势之一在于可根据实际情况合理调整单元疏密程度，准确模拟任意复杂地形和密度异常体的重力异常，兼顾计算精度与计算效率；优势之二在于用形函数拟合求得积分的解析解，计算精度和效率高；充分利用一维形函数积分的高效和高精度，不同波数之间一维积分高度并行性及快速傅里叶变换的高效性，实现重力异常场三维数值模拟.设计棱柱体模型，通过数值解和解析解对比验证了该方法的正确性、适用性和高效性.针对任意复杂地形条件下的重力场及其张量的模拟问题，提出一种快速算法，对其有效性进行了验证.探究标准FFT法的截断效应对计算精度的影响，对比分析Gauss-FFT法和标准FFT扩边法两种方法的计算精度和效率，总结了二者的选取策略，结果表明选用标准FFT扩边法计算效率更高.实际地形的数值模拟表明本文算法适用于任意复杂地形的高效计算.
关键词: 重力数值模拟      空间-波数混合域      傅里叶变换      形函数积分     
Three-dimensional numerical simulation of the gravity anomaly field in the space-wave number mixed domain
DAI ShiKun1,2, CHEN QingRui1,2, LI Kun1,2, LING JiaXuan1,2     
1. School of Geosciences and Info-Physics of Central South University, Changsha 410083, China;
2. key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring of Ministry of Education, Central South University, Changsha 410083, China
Abstract: In gravity exploration, the three-dimensional forward calculation under complex conditions requires a large amount of storage, which makes it difficult to conduct highly efficient and fine forward modeling and inversion of gravity exploration under such conditions. To solve this problem, a numerical simulation method of the space-wave number mixed domain is proposed. This method transforms the convolution problem of gravitational potential integral in the three-dimensional space domain into several non-convolution problems by using two-dimensional Fourier transforms in the horizontal direction. For the problem of spatial vertical one-dimensional integration with independent wavenumber, the vertical integration of one-dimensional integration is discretized into the sum of multiple unit integrals. Quadratic function is used to characterize the density change of each unit, and the analytical expression of unit integral is derived. This method has less computation and storage requirements, and its algorithm is highly parallel, and the vertical integration is preserved in the spatial domain. One of its advantages is that it can be adjusted reasonably according to the actual situation. Integral element density can accurately simulate gravity anomalies of arbitrary complex terrain and density anomalies, taking into account both calculation accuracy and calculation efficiency. The other advantage is that the analytical solution of integration can be obtained by fitting shape function, with high calculation accuracy and efficiency. The high efficiency and accuracy of integration of one-dimensional shape function can be fully utilized, and the high parallelism of one-dimensional integration between different wavenumbers and the high efficiency of fast Fourier transform can be fully utilized. The correctness, applicability and efficiency of this method are verified by comparing numerical and analytical solutions. A fast algorithm is proposed to simulate the gravity field and its tensors under arbitrary complex terrain conditions. The validity of the algorithm is verified. The truncation effect of the standard FFT method is explored. The calculation accuracy and efficiency of Gauss-FFT method and standard FFT method are compared and analyzed. The selection strategies of the two methods are summarized. The results show that the standard FFT method is more efficient. The numerical simulation of real terrain shows that the proposed method is suitable for the efficient calculation of arbitrary complex terrain.
Keywords: Gravity anomaly field numerical simulation    Space-wave number mixing domain    Fourier transform    Shape function integral    
0 引言

重力勘探中，复杂条件(指规模面积大、地形复杂和异常体形体复杂)其重力异常场高效、高精度数值模拟在重力异常反演成像及人机交互解释中有着重要作用，国内外很多学者都进行了比较全面的研究(陈涛和张贵宾，2019；李红雨等，2019).以引力位满足泊松方程为依据，求解引力位的本质是求解泊松方程.对于该方程的解法，从不同求解域分，主要有空间域法和频率域法.

空间域方法的求解，大致可分为解析法、微分法和积分法三种.解析法是通过规则形体的解析表达式直接计算，仅适用于简单形体，计算精度高.微分法是直接从泊松方程出发，在重力勘探中，目前发展的主要方法是求解该方程的变分问题，用有限单元法求解区域节点上的场，蔡永恩和王其允(2004)用有限单元法加载一种新的边界条件计算了重力场，获得了较好的效果，但在大规模区域计算时，计算量大.积分法是从引力位满足的积分解出发，将复杂形体用一些规则几何体剖分，利用这些规则几何体的解析解叠加近似计算复杂异常体的引力位、重力场及其重力张量，常用的规则几何体模型有长方体(Nagy，1966)、直立棱柱体(Li and Chouteau, 1998；Nagy et al., 2000；Chakravarthi et al., 2002)和多面体(Talwani and Ewing, 1960)等；还有学者利用奥-高公式和格林公式将体积分转化为面积分，常用的面元模型有三角形为面元的多面体模型(徐世浙，1984；Paul，1974；Barnett，1976)和多边形为面元的多面体模型(Kwok，2010；García-Abdeslem，1992)等；骆遥和姚长利(2007)改进了均匀密度多面体重力正演公式，金钢燮等(2009)利用在等参有限元中高斯数值积分直接计算积分，为计算任意复杂形体的重磁异常提供了一种新途径；在并行计算方面，陈召曦等(2012)利用长方体组合模型实现了基于GPU并行的重力、重力梯度三维快速正演；Wang等(2017)将模型剖分成很多个立方体，采用MPI并行算法，有效的提高了三维重力正演的计算效率；Ren等(2017)提出一种基于非结构化网格的自适应快速多极子方法，借助并行计算，实现了三维重磁场及其梯度张量正演.积分法并行性好，特别适合多核多节点计算机并行运算，用于复杂条件重力异常场数值模拟有很大的发展潜力.

频率域方法是利用傅里叶变换，将引力位场在空间域的褶积转化为频率域简单的乘积，计算频谱通过反傅里叶变换求得空间域重力异常场值.二维傅氏变换的谱域法可以分为点元谱域法(Bhattacharyya and Navolio, 1976)、线元谱域法(吴志宣，1981；吴志宣，1983)和面元谱域法(梅岩辉，2007；李焓等，2008)三种.熊光楚(1984)利用三维傅氏变换计算重磁异常；Parker提出Parker公式(Parker，1973；冯锐，1986)，应用于常密度模型和起伏地形下的变密度模型；张凤旭等(2006)用离散余弦变换计算重力场值；柴玉璞等(1988, 2009)利用偏移采样技术极大的提高了傅里叶变换的计算精度，吴乐园(2014)、Wu和Tian(2014)、Wu(2016)在此基础上提出Gauss-FFT法，该方法避免了零波数计算，降低了边界效应影响，提高了计算精度.谱方法由于其并行度好，计算量小，对计算机存储要求低，如果能压制或有效消除傅里叶变换造成的截断效应影响，则是一种较为理想的数值模拟方法.

重力勘探中复杂条件下三维重力异常场数值模拟计算量大存储要求高，使得这种条件下重力勘探高效、精细正反演变得困难.针对这一问题，利用空间域引力位积分为三重卷积的特点，本文提出一种空间-波数混合域数值模拟方法，该方法借助水平方向二维傅里叶变换，将三维空间域卷积问题转换为多个不同波数之间相互独立的空间垂向一维积分问题，由此大大减少了计算量和对存储的需求，同时算法高度并行.设计棱柱体模型，通过数值解和解析解对比验证该方法的正确性、适用性和高效性.针对任意复杂地形条件下的重力场及其张量的模拟问题，提出一种快速算法，对其有效性进行验证.探究标准FFT法的截断效应对计算精度的影响，对比分析Gauss-FFT法和标准FFT扩边法两种方法的计算精度和效率，总结二者的选取策略.最后利用一个实际地形数据表明了本文算法适用于任意复杂地形的高效计算.

1 方法原理

引力位u满足积分(长春地质学院物探系重力组，1975)：

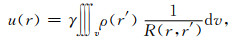
(1)

式中，为测点到异常体的距离，(x, y, z)为观测点坐标，(x′, y′, z′)为异常体内任意一点坐标，v为异常体体积，ρ(r′)为剩余密度，单位为kg·m-3，γ=6.67×10－11N·m2·kg-2为万有引力常量.

重力场g、梯度张量g与引力位u之间的关系为

(2)

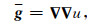
(3)

式中, 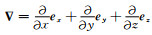为梯度算符，g的单位是毫伽(mGal)，g的单位是厄缶(E).

利用式(2)和(3)，可通过引力位求重力场和梯度张量.对式(1)进行二维傅氏变换，可得：

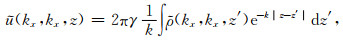
(4)

式中，kx、ky分别为x、y方向对应的波数(柴玉璞，1997)，为空间-波数域密度，为空间-波数域引力位.

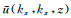
利用傅里叶变换的微分性质，重力场与重力张量在空间-波数域的表达式为

(5)

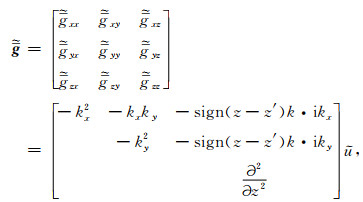
(6)

其中，符号函数为

(7)

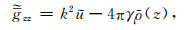
(8)

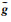
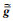
和分别为空间-波数域的重力场和重力张量，重力张量矩阵对称，独立分量6个.综合式(4)—(8)可得到空间-波数域引力位、重力场及其梯度张量的表达式.

利用水平方向二维傅里叶变换，将引力位的三重卷积转化为多个空间域垂向的一维积分，不同波数之间的积分相互独立，并行性好；垂向一维积分可离散为多个单元积分之和，每个单元采用二次形函数表征密度，求得单元积分的解析表达式，垂向网格剖分灵活，能兼顾计算精度和计算效率.

2 算法

为了实现(4)式的高效、高精度计算，这里主要研究3个问题：用形函数计算一维空间域积分、起伏地形条件下的快速算法和几个关键环节的处理.

2.1 一维空间域积分

采用基于二次插值的形函数法(徐世浙，1994)计算空间域垂向一维积分.将一维积分沿深度方向剖分为多个单元，每个单元内用二次形函数描述密度变化.

将(4)式沿z方向离散为N个单元，可得：

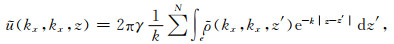
(9)

每个单元内，将密度表示为节点密度的二次插值函数：

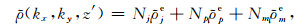
(10)

式中Nje、Npe、Nme为二次形函数；为单元3个节点的空间-波数域密度值.

式(9)中单元积分为

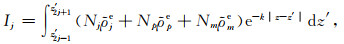
(11)

式中z′2j－1、z′2j+1为第j个单元积分的上下限，可根据密度变化，灵活选择垂向单元采样间隔.离散后的一维单元积分可推导出解析表达式，其推导过程详见附录A.

2.2 起伏地形条件下快速算法

水平地形条件下，测点在同一平面上，式(9)中每个垂向单元的一维积分只需计算一次.在起伏地形条件下，当地形起伏区间内无异常体时，可通过延拓直接求得起伏地形上的场，当地形起伏区间存在异常体时，需要计算地形最高点和最低点之间M个单元2M+1个深度节点所在平面的场，再插值求得起伏地形上的场.在地形起伏区间包含异常体时，若按普通做法，反复调用式(9)，计算量是水平地形条件下的2M+1倍，算法效率低.针对这一问题，本文提出一种起伏地形条件下的重力异常场快速算法.

如图 1所示，起伏地形最高点zmin和最低点zmax之间剖分M个单元2M+1个深度节点，起伏地形最低点以下剖分N个单元2N+1个节点.在计算起伏地形上2M+1个深度节点所在平面的场时，地形起伏最低点以下的异常体产生的场可通过延拓求得，能减少单元积分的重复计算，提高算法效率.下面具体介绍快速算法的内容.

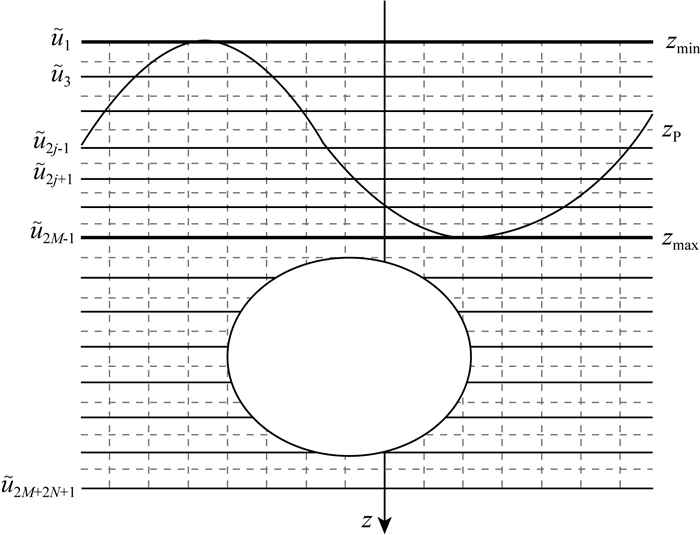
图 1 起伏地形模型示意图 Fig. 1 Undulating terrain model

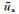
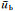
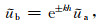
延拓是根据观测平面上的场计算高于(或低于)它的平面的场，计算公式为

(12)

式中k是波数，h是延拓的高度，下部异常体的异常场向上延拓时指数项符号为-，h取正值，上部异常体的异常场向下延拓时指数项符号为+，h取负值.

地形起伏区间任意深度点zp所在平面上的场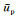的计算分为3个步骤：

(1) 计算地形起伏最低点以下N个单元在平面zmax产生场，将该场延拓至起伏地形区间2M+1个深度点所在平面，得到起伏地形最低点以下所有异常体在这些平面的重力异常.

(2) 计算起伏地形区间单元积分对其本身3个节点所在平面的重力异常，向外延拓，可得该单元对其他起伏地形深度点所在平面的重力异常，以此类推，可求得起伏地形区间每个单元对起伏地形区间2M+1个深度点所在平面的重力异常.

(3) 将步骤(1)和(2)求得在同一深度点产生的重力异常相加，可求得地形起伏区间任意深度点所在平面上的重力异常场.

综上，用快速算法计算地形起伏区间2M+1个深度节点所在平面的场，起伏地形区间单元积分的计算次数为3×M次，普通算法的计算次数为M×(2M+1)次，随着地形起伏上网格数量的增多，快速算法减少的计算量更大，算法优势越明显.

2.3 关键环节处理

为了准确实施上述算法，需处理如下几个关键环节：

(1) 当波数kx=ky=k=0时，式(11)的单元积分改写为

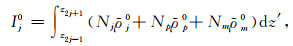
(13)

式中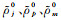为单元节点的零波数密度的傅里叶变换，式(13)推导详见附录A.

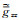
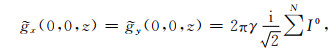
计算零波数的重力场和重力张量时，仅重力场3个分量和数值不为0，写为

(14)

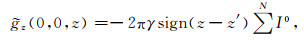
(15)

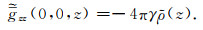
(16)

(2) 在计算突变模型的z方向积分时，突变节点在相邻单元剩余密度值不同，在用形函数积分时要分别赋值.若不处理，计算模型比实际模型偏大.连续密度模型则不用处理.

(3) 本文对节点进行傅里叶变换，由离散傅里叶变换的内涵可知，以节点进行傅里叶变换本质是以节点为中心的小单元的傅里叶变换(陈龙伟等，2016)，解析解对应的模型在水平方向左右前后4个界面向外各加半个网格距离，使得数值解和解析解两者使用的模型大小相同.

3 算法测试

设计棱柱体模型，将数值解与解析解对比，验证算法的正确性和适用性.验证起伏地形条件下重力场及其张量快速算法的有效性.探究标准FFT法的截断效应对计算精度的影响，对比Gauss-FFT法和FFT扩边法两种方法的计算精度和计算效率，总结二者的选取策略.测试的计算机为CPU-Inter Core i3-4150, 主频为3.5 GHz, 内存为8 GB.

用相对均方根误差(relative root mean square error, rrms)衡量计算精度，并认为当rrms < 1%时，达到计算精度要求，该误差统计方式能突出大异常值所占的比重，避免小异常和零值点造成的误差失真.计算公式为

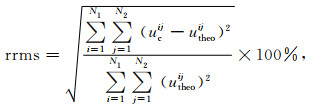
(17)

式中，ucij表示数值解，utheoij表示解析解，N1、N2分别表示计算平面两个方向节点个数.

3.1 常密度模型

设计一个棱柱体模型，模型如图 2所示，计算范围x方向-500~500 m，y方向-500~500 m，z方向0~500 m，剖分网格节点个数201×201×101，3个方向均匀剖分，网格间距均为5 m.异常体范围x方向-250~250 m，y方向-250~250 m，z方向100~200 m，异常密度为ρc=1000 kg·m-3.傅里叶变换采用标准FFT法实现，由于标准FFT存在截断效应，水平方向左右两边同时扩边2 km，将计算结果和解析解进行对比.

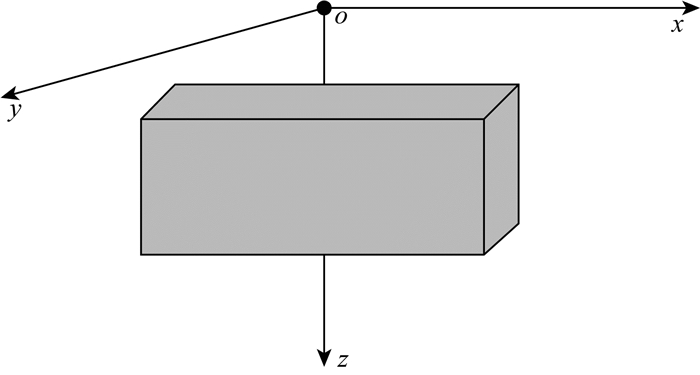
图 2 模型示意图 Fig. 2 Model schematic

图 3是y=-10 m重力场数值解与解析解的剖面等值线图，图 4是y=-10 m重力张量数值解与解析解的剖面等值线图.该剖面穿过异常体，从图中可看出，数值解和解析解等值线吻合程度高，在这个剖面上重力场gx、gy、gz 3个分量的相对均方根误差分别为0.05、0.51、0.04，重力张量gxx、gxy、gxz、gyy、gyz、gzz的相对均方根误差分别为0.36、0.52、0.35、0.27、0.72、0.28.各分量相对均方根误差均小于1%，表明算法正确.

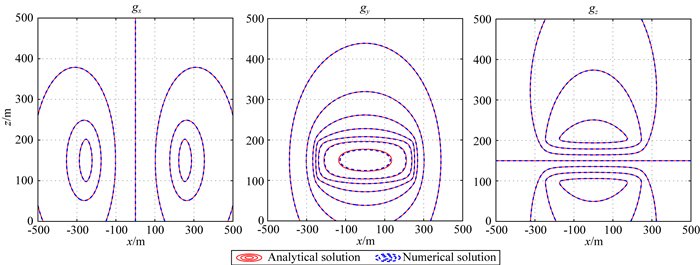
图 3 y=-10 m重力场数值解与解析解剖面等值线图 Fig. 3 The profile contour map of the numerical and analytical solutions of the gravity field when y=-10 m
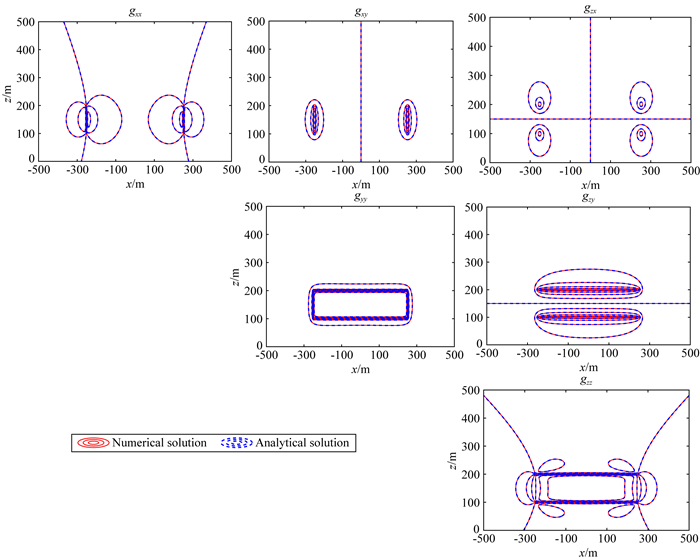
图 4 y=-10 m重力梯度张量数值解与解析解剖面等值线图 Fig. 4 The profile contour map of the numerical and analytical solutions of the gravity tensor when y=-10 m
3.2 变密度模型

设计变密度模型，该模型的计算范围和异常体大小与常密度模型相同，如图 2所示，异常体剩余密度呈二次函数变化，异常密度ρb变化范围是0~2500 kg·m-3，函数表达式为

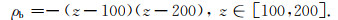
(18)

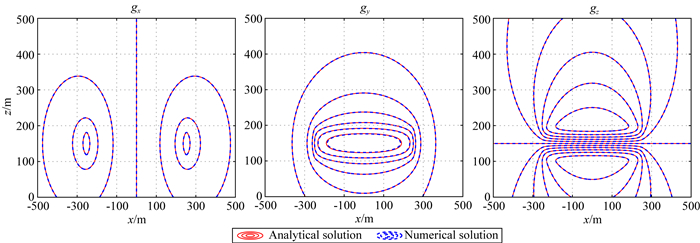
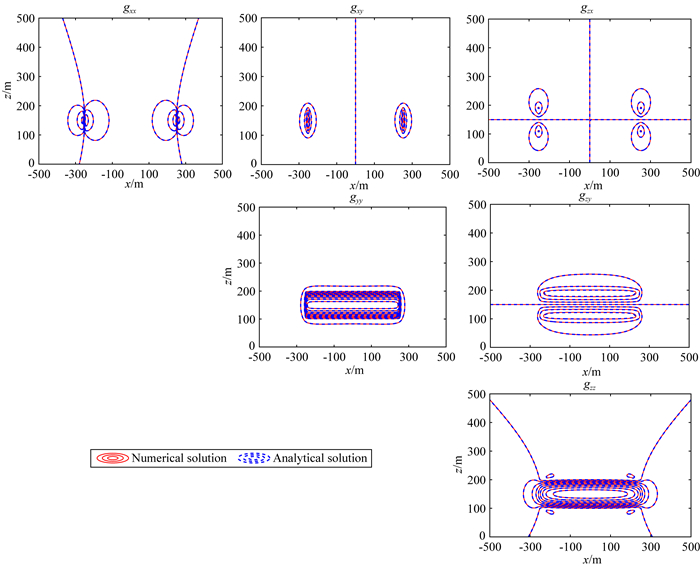
傅里叶变换采用采用标准FFT法实现，水平方向左右两边同时扩边2 km，将计算结果和解析解进行对比.图 5是y=-10 m重力场数值解与解析解的剖面等值线图，图 6是y=-10 m重力张量数值解与解析解的剖面等值线图.从图中可看出，重力场与张量数值解和解析解平面等值线图吻合度高，剖面重力场gx、gy、gz 3个分量的相对均方根误差分别为0.05、0.62、0.04，重力张量gxx、gxy、gxz、gyy、gyz、gzz的相对均方根误差分别为0.39、0.56、0.20、0.14、0.42、0.08.相对均方根误差均小于1%，验证了算法适用于连续介质的计算.

图 5 y=-10 m重力场数值解和解析解剖面等值线图 Fig. 5 Contours of numerical and analytical solutions of the gravity field with y=-10 m
图 6 y=-10 m重力张量数值解和解析解剖面等值线图 Fig. 6 Contours of numerical and analytical solutions of the gravity tensor with y=-10 m
3.3 起伏地形条件下数值算例

设定模型如图 2所示，计算区域x方向-500~500 m，y方向-500~500 m，水平方向剖分节点个数201×201，x、y方向的网格间距均为5 m，z方向网格间距为10 m.异常体范围x方向-250~250 m，y方向-250~250 m，z方向100~200 m，异常密度为ρc=1000 kg·m-3，在上方加上起伏地形，设地形起伏最低点z=0 m，地形起伏最低点以下网格节点个数为101，改变起伏地形最高点与最低点之间深度节点个数，分别用本文提出的快速算法和普通算法计算这些节点所在平面的重力异常场，比较两种算法计算的时间.这里傅里叶变换采用标准FFT法实现.

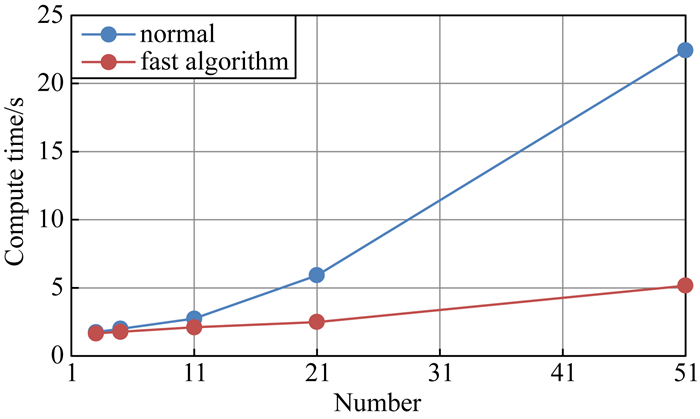
图 7为用快速算法和普通算法的时间对比图.由图可知，当地形起伏区节点个数为3时，普通算法的计算时间为1.74 s，快速算法1.65 s，二者速度相近；当该节点数为51时，普通算法的计算时间为22.44 s，快速算法是5.16 s，快速算法仅约为普通算法耗时的1/4.随着计算节点个数增多，快速算法的优势越来越明显.计算结果表明在起伏地形条件下重力异常场数值模拟中，快速算法具有更高的计算效率.

图 7 普通算法与快速算法的计算时间对比图 Fig. 7 Comparison of calculation time between common algorithm and fast algorithm
3.4 计算精度与效率

采用标准FFT法进行重力场数值模拟存在截断效应影响，当计算区域一定时，其截断效应的大小与异常体埋深有关，埋深浅，截断效应小，埋深越深，截断效应越大.基于4个高斯点的Gauss-FFT法截断效应影响小，计算精度高，但是其计算量是标准FFT的16倍.通过扩大计算区域标准FFT法可以减少截断效应影响，达到较高的计算精度.这里设计不同埋深棱柱体模型，测试标准FFT法扩边距离对截断效应的影响，同时与4个高斯点Gauss-FFT法计算结果比较，分析算法的计算精度与效率.

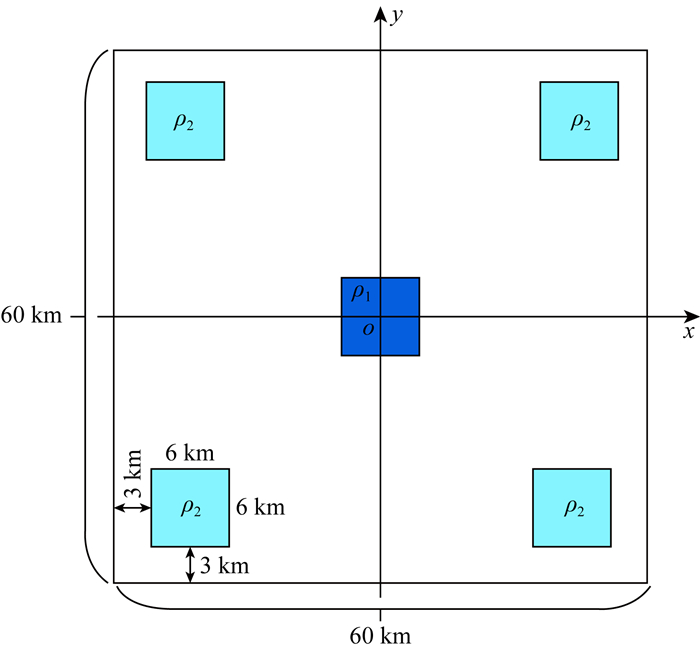
模型如图 8所示，计算区域x方向-30~30 km，y方向-30~30 km，z方向0~10 km，计算区域有5个大小相同的棱柱异常体，平面位置如图 8所示，4个角上的异常体位置对称，将5个异常体放在同一深度，异常体大小为6 km×6 km×3 km，正中间异常体的剩余密度为ρ1=1000 kg·m-3，另外4个异常体剩余密度均为ρ2=500 kg·m-3.剖分节点个数201×201×101，网格均匀剖分，x、y方向网格间距均为300 m，z方向网格间距100 m.

图 8 平面模型示意图 Fig. 8 Schematic of planar model

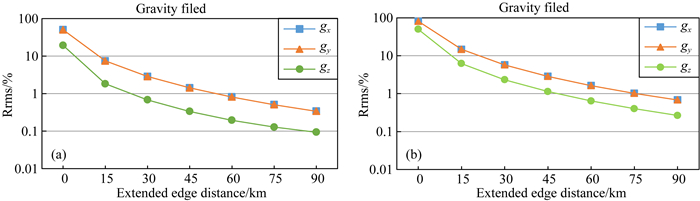
采用标准FFT扩边法分别计算异常体质心埋深为3.1 km和6.1 km重力异常，观测平面为z=0 m.图 9和图 10中横轴表示单边扩边距离.

图 9 不同埋深异常体的重力场的计算精度与标准FFT法扩边距离的曲线图 (a)质心埋深3.1 km；(b)质心埋深6.1 km. Fig. 9 Curves of the rrms of the gravity field of abnormal bodies at different depths and extention distance of standard FFT method (a) Centroid depth 3.1 km; (b) Centroid depth 6.1 km.
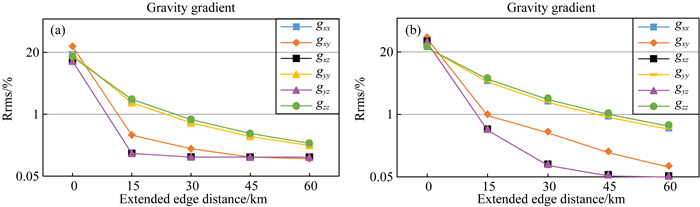
图 10 不同埋深异常体的重力张量的计算精度与标准FFT法扩边距离的曲线图 (a)质心埋深3.1 km；(b)质心埋深6.1 km. Fig. 10 Curves of rrms of gravity tensors of abnormal bodies at different depths and extention distance of standard FFT method (a) Centroid depth 3.1 km; (b) Centroid depth 6.1 km.

图 9表示重力场计算精度与标准FFT扩边距离的关系.从图 9可以看出，随着扩边距离的增加，重力场的截断效应影响减小，计算精度提高.当扩边距离大于异常体深度10倍时gz分量的相对均方根误差小于1%.

图 10表示重力张量的计算精度与标准FFT扩边距离的关系.图 10中，随着扩边距离的增加，重力张量截断效应影响迅速减小，计算精度提高.扩边距离大于异常体埋深5倍，gxz、gyz和gxy的相对均方根误差小于1%；扩边距离大于异常体埋深10倍，主对角张量gxx、gyy和gzz的相对均方根误差小于1%.

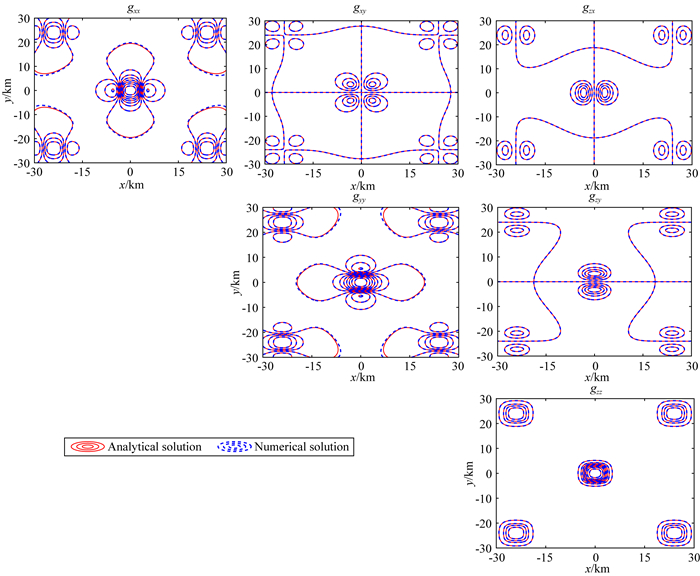
图 11是重力场数值解与解析解的平面等值线图.图 12为重力张量数值解与解析解的平面等值线图，这里模型异常体质心埋深3.1 km，扩边30 km，采用标准FFT法计算地面重力场及其张量.由图中可以看出，数值解与解析解吻合程度好.若要提高计算精度，需要进一步扩边.

图 11 扩边30 km重力场数值解与解析解 Fig. 11 Numerical and analytical solutions of the gravity field with 30km extension
图 12 扩边30 km重力张量的数值解与解析解 Fig. 12 Numerical and analytical solutions of the gravity tensors with extension 30 km

上述模型异常体质心埋深3.1 km，采用标准FFT法计算地面重力异常gz，扩边30 km，剖分节点个数401×401×101，计算时间为4.05 s，均方根误差为0.68%；采用不扩边的4个高斯点Gauss-FFT法计算地面重力异常gz，剖分节点个数201×201×101，计算时间为20.06 s，均方根误差为0.05%. Gauss-FFT法能获得更高的计算精度，但其计算时间约是FFT扩边法的5倍.

综合考虑计算精度和计算时间两个因素，标准FFT扩边法比Gauss-FFT法更有利于实现大规模、高效高精度重力场及其张量数值模拟，特别在面向实际问题时，标准FFT扩边法可根据需要选择不同的扩边距离，选择灵活，兼顾计算精度与计算效率.

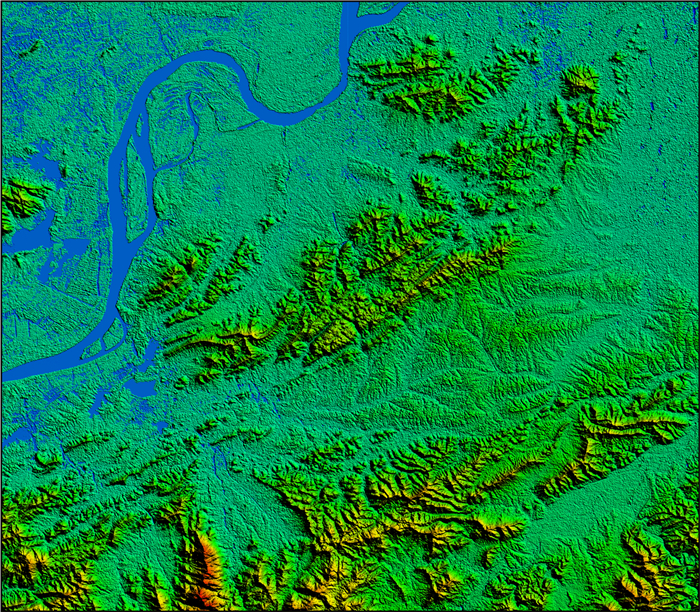
3.5 实际地形数据模拟

采用安徽省的DEM数字高程数据(经度为117.6°E至118.4°E，纬度为30.5°N至31.2°N)进行数值模拟，数据由“地理空间数据云”平台提供，得到地形如图 13所示，境内南部山峰、丘陵纵横交结，呈北东向展布；中部丘陵、岗地起伏，也呈北东向展布，发育了一系列冲、坳谷地；西北部平原，地势低下坦荡，由长江及其支流的冲积作用发育而成，水网密度高.在该区域内，起伏地形的最大海拔为1009 m，海拔最低点为-37 m.参照文献(Ren et al., 2017)中选择的模型区域，设垂直坐标向下为正，计算范围如下：x方向-35~35 km，y方向-35~35 km，z方向-1.01~5 km，密度设为2670 kg·m-3.为了将大部分主要地形描述清楚，将网格剖分为141×141×263，水平方向网格间距均为500 m，垂直方向前262个网格采样间隔均为4 m，最后一个网格间距为4962 m，设观测平面为-2000 m.

图 13 DEM数字高程数据图 Fig. 13 Map of DEM digital elevation data

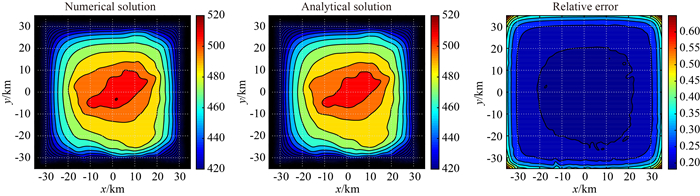
利用本文算法进行数值模拟，傅里叶变换采用标准FFT，水平方向单边扩边距离为100 km，计算网格为541×541×263，取中间141×141个网格区域作为计算结果.以重力异常gz的计算结果为例，图 14为观测平面-2000 m重力异常gz数值解与解析解及二者的相对误差图，解析解用141×141个高度不同的常密度棱柱体组合求得，计算区域相对误差最大为0.7%；非并行运算解析解耗时约150.3 s，数值解耗时约32.1 s，计算速度提高了四倍，若采用并行计算，计算时间将大大减少.当地形起伏密度分布不均匀，数值解只需改变单元密度的值，无需增加网格数，计算时间不变；而解析解需剖分更精细，计算时间更长，此时数值计算优势更明显，文献(Ren et al., 2017)中用了同样的模型，用16线程并行计算，耗时为453.6 s，表明本文算法适用于任意复杂地形的高效计算.

图 14 数值解与解析解及其相对误差图 Fig. 14 Numerical and analytical solutions and their relative errors
4 结论

利用空间域引力位积分为三重卷积的特点，本文提出一种空间-波数混合域数值模拟方法，该方法借助水平方向二维傅里叶变换，将三维空间域卷积问题转换为多个不同波数之间相互独立的空间垂向一维积分问题，由此大大减少了计算量和对存储的需求.保留垂向为空间域，优势之一在于便于浅层单元剖分可适当加密，随着深度增加，单元剖分适当稀疏，可以准确模拟任意复杂地形和密度异常体的重力异常，兼顾了计算精度与计算效率；优势之二在于一维积分垂向可离散为多个单元积分之和，每个单元采用二次形函数表征密度变化，可得出单元积分的解析表达式，计算精度高、效率高.该方法充分利用一维形函数积分的高效和高精度、不同波数之间一维积分高度并行性及快速傅里叶变换的高效性, 实现了重力场及其张量的高效高精度的数值模拟.本文研究得出以下结论：

(1) 解析解与本文算法的数值解对比表明，本文提出的重力异常场空间-波数混合域三维数值模拟方法正确，计算精度高.

(2) 地形起伏条件下本文提出的重力场及其张量数值模拟快速算法正确有效，地形起伏越大，快速算法计算效率越高.

(3) 标准FFT法存在截断效应，当扩边距离大于异常体埋深十倍时，数值解预解析解均方根误差小于1%，综合计算精度和时间考虑，标准FFT扩边法比Gauss-FFT法更有利于实现大规模、高效、高精度的重力场及其张量的数值模拟.

(4) 使用台式机(CPU-Inter Core i3-4150, 主频为3.5 GHz, 内存为8 GB)计算，三维数值模拟网格剖分为201×201×101，串行计算地面上201×201个节点的重力场及其张量梯度，耗时仅1.97 s，占用内存约为53 M，与目前主流方法相比，计算时间和内存需求至少减少两个数量级，规模越大，优势越明显.本文提出的空间-波数混合域重力三维积分解数值模拟算法具有高度并行性，若采用并行算法，计算效率能大大提高.

附录A

单元积分的一般表达式为

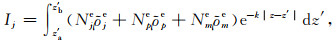
(A1)

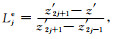
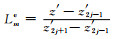
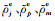
式中Ij表示第j个单元积分，[z′a, z′b]为积分区间，Nj、Np、Nm为二次形函数，Nje=(2Lje－1)Lje，Npe=4LjeLme，Nme=(2Lme－1)Lme，式中为单元内自然坐标，式中z′2j－1、z′2j+1为第j个单元积分的上下限，为单元节点上的空间-波数域剩余密度值.

定义符号函数：

(A2)

不失一般性，设θ=sign(z－z′)·k.当k≠0时，若观测平面z不在单元内，积分区间[z′a, z′b]即为[z′2j－1, z′2j+1]，式(A1)写为

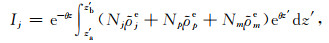
(A3)

解析解为

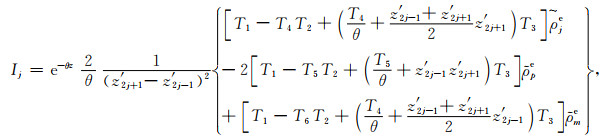
(A4)

式中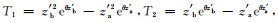

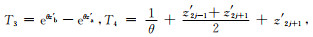
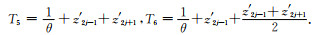
当z在单元内，式(A1)写为

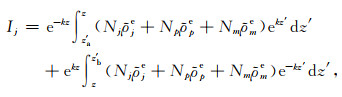
(A5)

同理可计算得解析解.

当k=0时，零波数单元积分写为

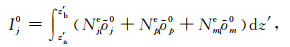
(A6)

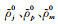
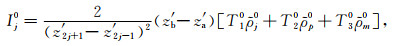
式中为单元3个节点零波数剩余密度值，当观测平面z不在单元内时：

(A7)

式中：

当z在单元内时：

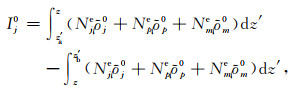
(A8)

同理可求得解析解.

References
Barnett C T. 1976. Theoretical modeling of the magnetic and gravitational fields of an arbitrarily shaped three-dimensional body. Geophysics, 41(6): 1353-1364. DOI:10.1190/1.1440685
Bhattacharyya B K, Navolio M E. 1976. A fast fourier transform method for rapid computation of gravity and magnetic anomalies due to arbitrary bodies. Geophysical Prospecting, 24(4): 633-649. DOI:10.1111/j.1365-2478.1976.tb01562.x
Cai Y E. Wang Q Y.2004. New bounday conditions for calculating gravity anomalies by finite element method.//2004 Academic Symposium on Gravity and Solid Tide and Proceedings of the Symposium on Academician Xu Houze's 70th Birthday. Wuhan: Chinese Geophysical Society, Chinese Society for Geodesy, Photogrammetry and Cartography.
Chai Y P. 1988. Algorithm investigation of dft of potential field. Acta Geophysica Sinica (in Chinese), 31(2): 211-224.
Chai Y P. 1997. Offset sampling theory and its application. Beijing: Petroleum Industry Press.
Chakravarthi V, Raghuram H M, Singh S B. 2002. 3-D forward gravity modeling of basement interfaces above which the density contrast varies continuously with depth. Computers & Geosciences, 28(1): 53-57.
Chen L W, Dai S K, Wu M P. 2016. Computation of discrete frequency when using FFT algorithm with random sampling points. Progress in Geophysics (in Chinese), 31(1): 164-169. DOI:10.6038/pg20160118
Chen T, Zhang G B. 2019. Deriving the full gravitational gradient tensor from gravity anomaly:an equivalent source technique. Progress in Geophysics (in Chinese), 34(4): 1398-1410. DOI:10.6038/pg2019CC0194
Chen Z X, Meng X H, Guo L H, et al. 2012. Three-dimensional fast forward modeling and the inversion strategy for large scale gravity and gravimetry data based on GPU. Chinese Journal of Geophysics (in Chinese), 55(12): 4069-4077. DOI:10.6038/j.issn.0001-5733.2012.12.019
Feng R. 1986. A computation method of potential field with three-dimensional density and magnetization distributions. Acta Geophysica Sinica (in Chinese), 29(4): 399-406.
García-Abdeslem J. 1992. Gravitational attraction of a rectangular prism with depth-dependent density. Geophysics, 57(3): 470-473. DOI:10.1190/1.1443261
Gravity Group, Department of Geophysical Prospecting, Changchun Institute of Geology. 1975. Second-order vertical derivative of gravity potential-improvement and fabrication of topographic correction measuring plate. Journal of Jilin University:Geoscience Edition, (1): 94-98.
Kwok Y K. 2010. Gravity gradient tensors due to a polyhedron with polygonal facets. Geophysical Prospecting, 39(3): 435-443.
Li H, Qiu Z Y, Wang W Y. 2008. A review of the forward calculation of gravity and magnetic anomalies caused by irregular models. Geophysical & Geochemical Exploration, 32(1): 36-43.
Li H Y, Cao C, Li F T, et al. 2019. Development of airborne and marine gravity exploration and gravity gradient strategic exploration for the ocean and unknown land. Progress in Geophysics (in Chinese), 34(1): 316-325. DOI:10.6038/pg2019BB0367
Li X, Chouteau M. 1998. Three-dimensional gravity modeling in all space. Surveys in Geophysics, 19(4): 339-368.
Luo Y, Yao C L. 2007. Forward method for gravity, gravity gradient and magnetic anomalies of complex body. Earth Science-Journal of China University of Geosciences, 32(4): 517-522.
Mei Y H. 2007. The consistency of forward calculation formula of magnetic and gravity anomalies for homogene. Computing techniques for geophysical and geochemical exploration, 29(SI): 32-34.
Nagy D. 1966. The gravitational attraction of a right rectangular prism. Geophysics, 31(2): 362-371.
Nagy D, Papp G, Benedek J. 2000. The gravitational potential and its derivatives for the prism. Journal of Geodesy, 74(7-8): 552-560.
Parker R L. 1973. The rapid calculation of potential anomalies. Geophysical Journal International, 31(4): 447-455. DOI:10.1111/j.1365-246X.1973.tb06513.x
Paul M K. 1974. The gravity effect of a homogeneous polyhedron for three-dimensional interpretation. Pure and Applied Geophysics, 112(3): 553-561. DOI:10.1007/BF00877292
Ren Z Y, Tang J T, Kalscheuer T, et al. 2017. Fast 3-D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multilevel fast multipole method. Journal of Geophysical Research:Solid Earth, 122(1): 79-109. DOI:10.1002/2016JB012987
Talwani M, Ewing W M. 1960. Rapid computation of gravitational attraction of three-dimensional bodies of arbitrary shape. Geophysics, 25(1): 203-225.
Wang M, Zheng Y M, Yao C L. 2017. A study on parallel computation based on 3D forward algorithm of gravity. International Journal of Geosciences, 8(9): 1073-1079. DOI:10.4236/ijg.2017.89060
Wu L Y. 2004. High-precision Fourier-domain modeling of potential fields: Gauss-FFT method[Ph.D. thesis]. Hangzhou: Zhejiang University.
Wu L Y. 2016. Efficient modelling of gravity effects due to topographic masses using the Gauss-FFT method. Geophysical Journal International, 205(1): 160-178.
Wu L Y, Tian G. 2014. High-precision Fourier forward modeling of potential fields. Geophysics, 79(5): G59-G68. DOI:10.1190/geo2014-0039.1
Wu X Z. 1981. Computation of spectrum of potential field due to 3-dimensional bodies (homogeneous models). Acta Geophysica Sinica (in Chinese), 24(3): 336-348.
Wu X Z. 1983. The computation of spectrum of potential field due to 3-d arbitrary bodies with physical parameters varying with depth. Acta Geophysica Sinica (in Chinese), 26(2): 177-187.
Xiong G C. 1984. Some problems about the 3-D fourier transforms of the gravity and magnetic fields. Acta Geophysica Sinica (in Chinese), 27(1): 103-109.
Xu S Z. 1984. The calculation of the gravitational anomaly and its derivative of the geologic body with arbitrary configuration by boundary-elements method. Geophysical Prospecting for Petroleum, 23(2): 22-37.
Xu S Z. 1994. Finite element method in geophysics. Beijing: Science Press.
Zhang F X, Meng L S, Zhang F Q, et al. 2006. A new method for spectral analysis of the potential field and conversion of derivative of gravity-anomalies:cosine transform. Chinese Journal of Geophysics (in Chinese), 49(1): 244-248.
蔡永恩, 王其允. 2004.有限元方法计算重力异常的新边界条件.//2004年重力学与固体潮学术研讨会暨祝贺许厚泽院士70寿辰研讨会会议论文集.武汉: 中国地球物理学会, 中国测绘学会. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-HBKJ200400004062.htm
柴玉璞. 1988. 位场DFT算法研究. 地球物理学报, 31(2): 211-224. DOI:10.3321/j.issn:0001-5733.1988.02.010
柴玉璞. 1997. 偏移抽样理论及其应用. 北京: 石油工业出版社.
柴玉璞. 2009. 位场波数域转换算法误差方程及其应用(英文). 应用地球物理, 6(3): 205-216.
长春地质学院物探系重力组. 1975. 重力位二阶垂向导数——地形改正量板的改进与制做. 吉林大学学报:地球科学版, (1): 94-98.
陈龙伟, 戴世坤, 吴美平. 2016. 应用任意采样点数FFT算法时离散频率计算. 地球物理学进展, 31(1): 164-169. DOI:10.6038/pg20160118
陈涛, 张贵宾. 2019. 利用重力异常计算重力梯度的等效源技术. 地球物理学进展, 34(4): 1398-1410. DOI:10.6038/pg2019CC0194
陈召曦, 孟小红, 郭良辉, 等. 2012. 基于GPU并行的重力、重力梯度三维正演快速计算及反演策略. 地球物理学报, 55(12): 4069-4077. DOI:10.6038/j.issn.0001-5733.2012.12.019
冯锐. 1986. 三维物性分布的位场计算. 地球物理学报, 29(4): 399-406. DOI:10.3321/j.issn:0001-5733.1986.04.010
金钢燮, 胡祥云, 超敬来, 等. 2009. 复杂形体重磁异常的等参数有限元积分算法研究. 石油地球物理勘探, 44(2): 231-239. DOI:10.3321/j.issn:1000-7210.2009.02.019
李焓, 邱之云, 王万银. 2008. 复杂形体重、磁异常正演问题综述. 物探与化探, 32(1): 36-43.
李红雨, 曹诚, 李凤婷, 等. 2019. 航空、航海重力和重力梯度在海洋、未知陆地战略勘探的发展. 地球物理学进展, 34(1): 316-325. DOI:10.6038/pg2019BB0367
骆遥, 姚长利. 2007. 复杂形体重力场、梯度及磁场计算方法. 地球科学-中国地质大学学报, 32(4): 517-522. DOI:10.3321/j.issn:1000-2383.2007.04.012
梅岩辉. 2007. 均质多面体重磁异常正演计算表达式的一致性. 物探化探计算技术, 29(S1): 32-34.
吴乐园. 2014.重磁位场频率域高精度正演方法: Gauss-FFT法[博士论文].杭州: 浙江大学. http://cdmd.cnki.com.cn/Article/CDMD-10335-1014359316.htm
吴宣志. 1981. 三度体(均质模型)位场波谱的正演计算. 地球物理学报, 24(3): 336-348. DOI:10.3321/j.issn:0001-5733.1981.03.012
吴宣志. 1983. 三度体(物性随深度变化模型)位场波谱的正演计算. 地球物理学报, 26(2): 177-187. DOI:10.3321/j.issn:0001-5733.1983.02.009
熊光楚. 1984. 重、磁场三维傅里叶变换的若干问题. 地球物理学报, 27(1): 103-109. DOI:10.3321/j.issn:0001-5733.1984.01.011
徐世浙. 1984. 用边界单元法计算任意形体的重力异常及其导数. 石油物探, 23(2): 22-37.
徐世浙. 1994. 地球物理中的有限单元法. 北京: 科学出版社.
张凤旭, 孟令顺, 张凤琴, 等. 2006. 重力位谱分析及重力异常导数换算新方法——余弦变换. 地球物理学报, 49(1): 244-248. DOI:10.3321/j.issn:0001-5733.2006.01.031