随着油、气田资源开发程度提高，对于复杂油气储层的开发需求进一步加大，要求随钻电磁波测井仪器具有更大的探测深度与更精确的地质导向能力(Zhou, 2009; Rabinovich et al., 2012, 杨震等，2016).关于不同空间分布对电测井测量信号相对贡献的研究，是仪器探测特性分析和响应规律研究的基础(Barber, 1988; Clark et al., 1990; Bittar et al., 2003; Li and Wang, 2016; 王磊等, 2015)，而邓少贵等(2017)基于井周界面电磁散射研究随钻电磁波探测特性，根据不同分量信号组合探测井旁界面，并对其前探和侧探能力做了适用性分析.在感应测井中，Doll几何因子(Doll，1949)将响应与地层电阻率视为线性关系，可描述高阻地层中互不干扰的独立单元环对测井响应的贡献率几何分布，在此基础上，Gianzero和Anderson(1981)、Moran(1982)、Howard等(1990)、张庚骥(1982)通过近似、等效等方法考虑了涡流间的相互影响，将几何因子理论成功地应用到低阻地层，分别给出了Gianzero、Moran、Born、高阶几何因子定义，校正了感应测井工作频率下电磁波传播的趋肤效应影响.随钻电磁波测井工作频率一般在100 kHz以上，通过幅度比与相位差刻度电阻率.Zhou等(1992)基于几何因子理论研究了EPRL仪器的相位差响应函数，邢光龙等(Xing and Yang, 2006; 邢光龙等，2008)利用电磁场Born近似理论进一步导出了幅度比与相位差对介电常数与电导率的响应函数，显示响应信号与电阻率是更为复杂的非线性关系.利用几何因子理论对电磁波测井响应的研究：(1)大多基于等效偶极子源，没有考虑线圈结构及井眼影响；(2)在描述井周介质贡献率的空间分布中，对其地质属性的敏感性描述不足，更适用于低频和高阻地层，而在高频、低阻及异常体与背景地层对比度高等条件下精度有所欠缺；(3)给出的幅度比与相位差和视电阻率是非线性关系，幅度比与相位差贡献分布难以表征视电阻率的贡献分布.Clark等(1988)通过伪几何因子对双发双收补偿测井仪的径向探测特性进行了分析，但伪几何因子通过模拟侵入主要用于得到径向探测深度，对纵向及微观敏感性描述不足.目前国内外对于由幅度比、相位差刻度且对井周介质属性敏感的纵、横向微观及宏观几何贡献分布的精确描述研究较少.

本文从测井响应对地质属性求偏导出发，构造电性异常体地层模型，提出一种新的敏感性函数定义用以定量表征井周介质对响应信号的贡献率几何分布，据此分析不同井眼、频率、背景地层电阻率、电阻率对比度等条件下的贡献分布规律.井周全空间敏感性分布计算量大，为此引入模式匹配法(张庚骥, 1982)，对该2D旋转对称问题降维处理，纵向上采用广义反射理论模拟多层层状介响应，径向上选取合适的网格剖分参数以满足小尺度异常体的响应精确模拟，精细模拟幅度比和相位差对井周介质敏感的纵、横向微观与宏观敏感性分布，进而分析随钻电磁波电阻率测井纵、横向探测特性，为随钻电磁波测井探测深度与分辨率的研究提供了理论基础.

目前主流补偿型阵列随钻电磁波测井仪器如Schlumberger ARC、Baker Hughes MPR等都是基于单发双收同轴线圈系，通过增加工作频率与源距，采用对称或加权补偿等方式发展而来.图 1a为仪器设计的基本线圈结构，电磁波测井通过提取两个同轴接收线圈感应电动势的相位差(PD)和幅度比(AR)刻度电阻率(Hue et al., 2006)：

图 1

Fig. 1

图 1 线圈系结构 Fig. 1 Coil array configuration

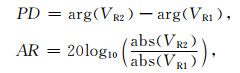
(1)

式中，V_R1、V_R2分别为两个接收线圈的感应电动势.

图 1b为对称型补偿线圈系，T₁、T₂对称放置，两者交替发射信号，PD=(PD₁+PD₂)/2、AR=(AR₁+AR₂)/2, PD₁、AR₁为发射线圈T₁工作时提取的相位差与幅度比，PD₂、AR₂为发射线圈T₂工作时提取的相位差与幅度比.

建立含井眼的二维旋转对称地层模型，如图 2，背景地层电阻率为R_b，为求得图示区域内每一个点的敏感度，在点(r, z)处取截面积ΔS=drdz、电阻率为R_abnormal的异常体，响应值对电阻率的偏导可视为响应信号对电阻率的敏感性(Wang et al., 2008；Wang et al., 2018)，敏感性大小可表征对测井响应的相对贡献，考虑异常部分与地层电阻率对比度的影响，将敏感性定义进行推广，定义敏感性函数|S|，其中

图 2

Fig. 2

图 2 异常体地层模型 Fig. 2 Formation model with abnormal body

(2)

式中，f(R_b)表示地层电阻率为R_b时的响应值，f(r, z, R_b; ΔS, R_abnormal)表示存在异常体时的响应值，f(R_abnormal)表示地层电阻率全为异常值时的响应.分子用差分代替偏导，分母对其归一化处理.响应信号f是井眼、侵入、各向异性、电阻率等多种地层参数的函数，在此仅讨论背景地层与异常体的影响.

对敏感性函数进行径向或纵向积分，定义：

(3)

纵向微分敏感性函数S_V表示响应信号对坐标z处厚度为dz的薄层电阻率异常体的敏感性，径向微分敏感性函数S_H表示响应信号对半径为r、壁厚为dr的圆筒状介质电阻率异常体的敏感性.

将纵向微分敏感性函数对z积分，得到厚度为2z的无限延伸的层状介质敏感性函数，定义为纵向积分敏感性函数，表示为

(4)

将径向微分敏感性函数对r积分，得到半径为r的纵向无限延伸圆柱状介质敏感性函数，定义为径向积分敏感性函数，表示为

(5)

根据麦克斯韦方程组，纵、横向非均匀旋转对称介质下电场满足：

(6)

式中，层数μ为磁导率，ω为角频率，ε为介电常数，σ_m(r)是第m层坐标r处的电导率；E_m表示第m层的电场强度；(r_T, z_T)表示源的坐标.当m层为非源所在层时，式(2)右端为零，此时令rE_m=R_m(r)Z_m(z)，得

(7)

在径向上，运用一维有限元素法，首先将r轴剖分成N个区间，结点设为r₀, r₁, …, r_N，其中r₀=极小值, r_N→∞，[r_i－1, r_i]为区间i，用σ_mⁱ表示m层第i个区间的电导率值.然后在区间i取插值基函数并逐区间安装，得到R_m≈g^Tc_m.将式(3)转化成泛函极值问题求解，通过极值条件得到广义本征方程：

(8)

式中，C_m是由特征向量c_m组成的矩阵，Λ_m²由特征值(λ_m)²组成的对角阵.且

图 3

Fig. 3

图 3 模式匹配法计算模型 Fig. 3 Computing model of numerical mode matching method

(9)

纵向上易求得波在介质中的层内衰减公式，用广义反射阵描述波在多层介质的反射与折射.场强表示为rE_m=g^TC_m[u_m⁺(z)+u_m^－(z)]，令u_m^－(z)=Q_m⁺(z)u_m⁺(z)，上标“+、-”表示上、下行波，Q_m⁺(z)为第m层内对上行波的广义反射阵.根据电场与磁场在层界面的连续性，变换推导得到广义透射阵的递推表达式，考虑无穷远处界面反射系数趋于零，可递推出各个层反射与透射矩阵(张庚骥和汪涵明，1996).

当dr=dz=1 cm，求解区域为3 m×3 m时，需计算90000个点的敏感性函数，而敏感性函数需进行多次电磁波响应正演，求解区域内敏感性分布计算量大，对正演算法的运算速度要求高.模式匹配法是二维旋转对称地层模型响应模拟最快速的正演方法(Chew, 1999; 范业活等, 2016; 林蔺等, 2017)，可将其运用于小尺度异常体对响应贡献的全空间几何分布快速精细模拟中.

令频率f分别为400 kHz和2 MHz，线圈距为[24, 30]in，在区域r∈[0, 3]m, z∈[－1.5, 1.5]m内等间距取异常电阻率地层环.取背景地层R_b=5 Ωm，R_abnormal趋近于R_b.计算结果如图 4、5，对于图中的两部分高敏感区，幅度比分布向右下延伸，敏感范围较广较深，相位差集中于接收线圈附近，向发射线圈方向扩散，这说明幅度比具有较强的径向探测能力，同时大范围的敏感区域表明受到较多的围岩贡献；频率增加到2MHz时，幅度比敏感区域大幅缩小，且径向缩减幅度大于纵向方向，表明径向探测深度减小，而相位差敏感区主要分布于发射与接收线圈之间，这表明其纵向分层能力与线圈距密切相关.

图 4

Fig. 4

图 4 单发双收线圈(f=400 kHz)相位差与幅度比敏感性分布 Fig. 4 Phase difference and amplitude ratio sensitivity distribution of single transmitter double receiver coil array (f=400 kHz)

图 5

Fig. 5

图 5 单发双收线圈(f=2 MHz)相位差与幅度比敏感性分布 Fig. 5 Phase difference and amplitude ratio sensitivity distribution of single transmitter double receiver coil array (f=2 MHz)

通过对敏感性函数进行径向或纵向积分，计算得到幅度比与相位差的纵向与径向微分敏感性曲线S_V, S_H：图 6为纵向微分敏感性曲线，图中发射线圈与近接收线圈之间有小段曲线敏感度不变，在接收线圈附近敏感度高；频率较大时，敏感范围集中，分辨率高；相位差比幅度比敏感范围更集中，分辨率高，对区分薄层、获取近井区域电阻率更有利.图 7为径向微分敏感性，曲线在井轴附近出现小段负敏感区域，频率高时的幅度比信号尤为明显，负敏感区将导致井轴附近区对响应贡献率降低，井眼部分对响应信号的影响减少.

图 6

Fig. 6

图 6 幅度比与相位差纵向微分敏感性 Fig. 6 Vertical differential sensitivity of amplitude ratio and phase difference

图 7

Fig. 7

图 7 幅度比与相位差径向微分敏感性 Fig. 7 Horizontal differential sensitivity of amplitude ratio and phase difference

三线圈系难以达到实际探测需求，对此合理布局线圈系方案可达到更好的探测效果，以双发双收对称补偿型线圈系为例，线圈结构如图 1b所示，取目标区域为r∈[0, 4]m, z∈[－2, 2]m，令频率f=2 MHz，线圈距为[－35.625, －4, 4, 35.625]in.对比图 8与图 9，幅度比与相位差上下对称，分布规则，与三线圈系相比敏感区域集中在测量点附近而不是分散于两个接收线圈处，幅度比敏感区主要分布于两个发射线圈之间，相位差敏感区分布于接收线圈之间，在测量点敏感度达最高值，纵向分层能力相比三线圈系有所提高，在径向上对称线圈系井轴附近的敏感性部分抵消，减小了井眼的影响.敏感性分布可以直观地表示双发双收线圈系合成信号的全空间及纵、横向敏感范围，该方法同样可应用于更为复杂的线圈系，通过优化组合能够实现对不同空间范围敏感，从而实现对目标区域介质的探测需求.

图 8

Fig. 8

图 8 双发双收线圈系幅度比敏感性图 Fig. 8 Amplitude ratio sensitivity of double transmitters and double receivers

图 9

Fig. 9

图 9 双发双收线圈系相位差敏感性图 Fig. 9 Phase difference sensitivity of double transmitters and double receivers

随钻电磁波测井一般利用伪几何因子探测深度表征径向探测特性.建立阶跃侵入模型，侵入深度为r，伪径向积分几何因子G(r)可表示为

(10)

其中，r为侵入深度，R_a为侵入后响应信号刻度的视电阻率，R_xo为侵入带电阻率，R_t为原状地层电阻率.

构造含井眼、阶跃侵入地层模型，令R_abnormal=R_xo，R_b=R_t，采用对称补偿线圈结构，线圈距为[-28.0, -3.0, 3.0, 28.0] in，计算幅度比与相位差径向积分敏感性函数在该模型下随侵入直径的变化趋势，如图 10所示，与文献中伪几何因子对比(Clark et al., 1988)，曲线趋势大致相同.定义G=S_HI=50%时对应的半径为探测深度，由相位差与幅度比敏感性函数得到的探测深度分别为36 in、54 in，而伪几何因子探测深度分别为36 in、52 in，两种方法达到了同样的效果.另外，由图中可看出伪几何因子与敏感性函数并不是严格分布在0~1之间的，随侵入加深会有小段异常，这是由于波在界面处的反射造成的.

图 10

Fig. 10

图 10 伪几何因子与径向积分敏感性函数对比 Fig. 10 Comparison of pseudo geometric factor and horizontal integration sensitivity function

通过构造含井眼模型研究径向精细结构对敏感性的影响，令地层电阻率为1 Ωm，异常体电阻率趋近地层电阻率，分别建立不同井径下盐水泥浆(电阻率为0.1 Ωm)与淡水泥浆(电阻率为10 Ωm)地层模型，得到径向积分敏感性函数曲线如图 11，在井径为9 in、淡水泥浆条件下曲线与无井眼几乎重合，其他有井眼条件下曲线会发生一定程度的偏移，井径为12 in时偏离较大，在泥浆电阻率为10 Ωm时得到的幅度比50%敏感度与无井眼时相差约5 cm，这表明在井径较大、地层与泥浆电阻率对比度较大等情况对探测特性的影响大，此时井眼影响不可忽略.

图 11

Fig. 11

图 11 不同井眼条件径向积分敏感性函数对比 Fig. 11 Horizontal integration sensitivity function in different borehole conditions

以下均采用径向积分敏感性函数S_HI研究电磁波测井的径向探测特性.建立半径为r的柱状体模型，线圈距为[24, 30] in，令R_b=10 Ωm，电阻率对比度为1.1.如图 12，频率降低时，幅度比50%敏感性探测深度从1 m增大到5 m，变化明显，相位差从0.3 m增大到1 m.

图 12

Fig. 12

图 12 频率对探测深度影响 Fig. 12 Depth of investigation in different frequency

令频率为2 MHz，R_b=1 Ωm，选取不同的R_abnormal值，如图 13所示，幅度比50%敏感性深度在0.5~0.7 m之间变化，相位差深度在0.3~0.4 m之间变化，可知对比度的影响较小.选取不同的地层电阻率值，令电阻率对比度为1.1，如图 14，可知电阻率对探测深度影响较大，低阻时探测深度较浅，高阻较深，高阻时幅度比50%敏感性深度可达2.3 m；曲线左段有部分敏感性函数接近甚至低于零，此时该段对响应贡献率低，范围随地层电阻率增加而扩大，电阻率为1 Ωm时，幅度比不敏感深度约0.1 m，电阻率为100 Ωm时，幅度比达到0.5 m，由此可知幅度比的刻度方式减弱了部分井眼影响.考虑电磁波传播效应影响，趋肤深度，可知，电阻率R越小，频率f越大，趋肤深度越小，电磁波衰减越快，故探测范围越小，趋势与图示结果相符.

图 13

Fig. 13

图 13 电阻率对比度对探测深度影响 Fig. 13 Depth of investigation in different resistivity contrast

图 14

Fig. 14

图 14 背景地层电阻率对探测深度影响 Fig. 14 Depth of investigation in different background formation resistivity

令线圈距为[24, 30] in，令R_b=10 Ωm，电阻率对比度为1.1.用纵向积分敏感性函数S_VI研究电磁波测井的纵向分辨能力影响因素，分别比较S_VI为50%与90%时的对应层厚，S_VI为90%可认为不受围岩影响.如图 15，横坐标为层界面位置，层厚H= 2z.频率高时分辨能力高，相位差分辨率比幅度比高；频率为2 MHz时，幅度比50%敏感性层厚为0.4 m，而相位差为0.2 m，接近接收线圈距；层厚达到1.6 m时，相位差可忽略围岩影响，达到2 m时幅度比可忽略围岩影响.

图 15

Fig. 15

图 15 频率对纵向分辨率影响 Fig. 15 Vertical resolution in different frequency

选取频率为2 MHz，R_b=1 Ωm，取不同R_abnormal值，图 16为不同电阻率对比度下的纵向积分敏感性函数曲线，在对比度从1.1~50变化时，幅度比50%敏感性层厚变化范围约为0.4~0.6 m，相位差约为0.2~0.3 m；幅度比90%敏感性函数层厚在1.2~1.8 m变化，相位差在0.4~1.4 m变化.图示曲线出现比较明显的两个拐点，这是由于在两个接收线圈之间，敏感度较高，积分敏感性函数变化快，而在接收线圈以外，敏感性函数增加逐渐变缓.

图 16

Fig. 16

图 16 电阻率对比度对纵向分辨率影响 Fig. 16 Vertical resolution in different resistivity contrast

选取不同的地层电阻率值，令电阻率对比度为1.1.由图 17可知，纵向探测能力受电阻率影响较大，当电阻率为1时，幅度比50%敏感性层厚为0.3 m，相位差为0.2 m；电阻率为100时，幅度比分辨率约为1.6 m，相位差约为0.6 m；对低阻分辨率高，高阻分辨率低.

图 17

Fig. 17

图 17 地层电阻率对分辨率影响 Fig. 17 Vertical resolution in different background formation resistivity

(1) 敏感性函数能够定量表征电磁波测井响应对地层微观与宏观敏感性，单发双收线圈系幅度比与相位差敏感分布形态类似，以发射、接收线圈为基点呈弧形分布，幅度比高敏感点向径向、下方延伸，分布区域较广较深，探测深度较深，受围岩影响较大；相位差敏感区域分布较集中，具有较高的纵向分辨率；对称补偿线圈系敏感区域呈上下对称分布，向径向延伸.

(2) 井周介质的空间敏感性研究是仪器探测特性、实现精确地质导向的理论基础，利用径向积分敏感性函数可对仪器探测范围定性分析，利用纵向积分敏感性函数可分析纵向分层能力的影响因素.模拟得知，地层电阻率增大时探测深度显著加深，纵向分层能力减弱，目的层与背景地层电阻率对比度增大时探测深度增大，分层能力降低；地层电阻率对敏感性影响远大于对比度影响.

(3) 敏感性函数是测井响应值与异常体电性、尺寸等的函数，与几何因子及响应函数等方法相比可研究线圈、井眼等对探测特性的影响，能够应用于井径较大、泥浆电阻率较小等条件下复杂线圈系空间探测敏感性研究，对于仪器的探测特性研究及线圈系设计有着重要作用.