2. 吉林大学地球探测科学与技术学院, 长春 130026;
3. 中国石油吉林油田公司乾安采油厂, 吉林松原 138000
2. College of Geo-exploration Science and Technology, Jilin University, Changchun 130026, China;
3. Qian An Oil Factory, Jilin Oilfield, CNPC, Songyuan Jilin 138000, China
人工地震是地球物理勘探中重要的方法之一,在保证精度和分辨率的情况下,探测深度甚至能够达到莫霍面(刘洋等,2018).受到复杂地表和地下条件的影响,地震数据中随机噪声会引起低信噪比问题,地震数据的质量决定了能否获取地下介质的准确图像,而地震数据处理能力的好坏是能否获取高质量地下成像结果的关键.地震数据具有不同于常规图像数据的时-空变特性,是时变确定性信号与时变非平稳随机信号的叠加(钟铁等,2017),这在一定程度上增加了地震数据信噪分离问题的复杂性.常规噪声压制方法在处理非平稳随机噪声导致的低信噪比数据时效果有限,最终往往导致不准确的构造解释,甚至反演失败.因此,开展有效的信噪分离方法研究具有重要的实际意义.目前有效的地震数据信噪分离滤波方法可以分为数据域滤波和变换域滤波.
基于数据域滤波的方法主要利用有效信号和随机噪声在数据域的分选性进行信噪分离.如Wiener线性滤波(鲁志波等,2007)等低通滤波方法依据随机噪声和有效信号的能量分布差异进行信噪分离.针对零均值高斯噪声的均值滤波(李腾飞等,2018)方法容易破坏图像中的细节信息,导致图像数据模糊.Tukey首次提出了中值滤波(陈宏希,2016)的概念,可以保护细节信息的同时滤除随机干扰,得到了很好的发展.但是地震数据的时-空变特性,使得常规中值滤波的处理效果有限,Liu等(2009)和刘洋等(2011)提出了改进的中值滤波方法,扩展了中值滤波在地震数据处理中的应用.伪吉布斯效应的最小化全变差(Rudin et al., 1992)算法在数据处理领域得到了较好的发展,但也存在破坏数据平滑性的缺点,容易产生“阶梯效应”(Durand and Froment, 2003).一些学者提出如全变差的迭代算法(Gholami,2015)、小波阈值算法和全变差算法的联合算法(Chan and Zhou, 2000)等的改进算法,都取得了一定的改善效果.另外,在函数中使用二阶导数的二阶TV算法(Lysaker et al., 2003;Esedolu and Osher, 2004;Chan et al., 2005;Guo and Wang, 2018)虽然在一定程度上提高了其信噪分离水平,但是也有学者(Lari and Gholami, 2014)指出其存在提高信噪比能力不足的缺陷.
基于变换域滤波的方法利用稀疏变换将地震数据投影到变换域,利用地震数据和随机噪声在变换域内具有不同的分布特征实现分离噪声的目的.如利用傅里叶变换(Zhang,2018)压制随机干扰,但该算法不能够很好地处理地震非平面波,同时也容易引入吉布斯效应.τ-p变换(王旭谦等,2017)可以对线性面波进行表征,但该算法处理时-空变信号能力有限,对弯曲同相轴压缩性不够理想,限制了该算法的发展.Radon变换(巩向博等,2014;王亮亮等,2017)只能较好地描述直线和特定的曲线,如双曲线、抛物线,这在一定程度上限制了该算法的发展.最近,许多学者用研究图像数据方向性特征的类小波变换方法处理地震数据.曲波变换(Liu et al., 2016;Zhang H et al., 2017;南方舟等,2018)的实现过程中考虑了方向性参数,对曲线形状的地震信号具有较好的表征能力,但也存在产生伪影现象和同相轴边缘不光滑现象的不足(唐刚,2010).
压缩感知(Compressive sensing,CS)是由Donoho(2006)在信号处理领域正式提出的概念,目前在地震数据处理领域也有较好的应用.Liu等(2016)利用压缩感知理论压制地震数据的随机噪声,宋维琪和吴彩端(2017)利用压缩感知方法提高地震资料分辨率,张良等(2017)利用压缩感知技术重建地震数据,这些方法都取得了较好的效果.压缩感知理论的根本条件是信号本身具有可压缩性,许多学者都对利用稀疏变换的信噪分离方法进行了研究,如:结合傅里叶变换、曲波变换等方法在处理消噪问题时都有较好的效果.但是,这些稀疏变换方法都不是特殊针对地震数据而设计的,因此在处理地震数据时容易表现出不适应性.Fomel(2006)和Fomel和Liu(2010)研究了针对地震数据属性的类小波变换,在小波提升算法的基础上,通过结合地震局部倾角属性,构造一种特殊针对地震同相轴方向性特征的数学变换方法,并将其命名为“seislet变换”.刘洋等(2009)将低阶seislet变换扩展到高阶seislet变换.Liu和Fomel(2010)结合seislet变换和波动方程炮检距连续算子,构建了“OC-seislet变换”.Liu和Liu(2013)依据时距曲线方程,构建地震数据依赖速度的VD倾角,首次提出了VD-seislet变换的概念,在强随机噪声环境下依然有理想的数据表征能力.Liu等(2017)提出广义VD-seislet变换的概念,面对复杂地质条件下的地震数据也有理想的数据稀疏表征能力.
本文将地震数据信噪分离问题归纳为数学基追踪问题,利用VD-seislet变换在压缩感知理论框架下约束模型稀疏度,TV范数约束数据边界,构建seislet-TV双正则化约束条件,并通过权系数平衡二者的权重,利用分裂Bregman迭代算法(Goldstein and Osher, 2009;Gholami and Siahkoohi, 2010;Gholami and Sacchi, 2012;Gholami,2015;Li and Li, 2016)对信噪分离问题进行求解.通过理论模型和实际数据测试,并与工业标准随机噪声压制方法(如:FXdecon算法)进行比较,为有效解决地震随机噪声压制问题提供一种迭代策略.
1 理论基础 1.1 地震数据信噪分离数学反问题人工地震数据d可以看作有效信号m和随机噪声n的线性叠加形式:
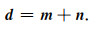
|
(1) |
当n为高斯白噪声时,满足‖m-d‖22=0.但由于野外勘探环境等的影响,随机噪声并不完全满足理想正态分布,对于公式(1)所示的信噪分离问题,常常引入一个正的误差参数γ满足‖m-d‖22≤γ.由于公式(1)对应的信噪分离问题为数学欠定问题,需要引入额外的约束条件来求取期望解,此时问题变为
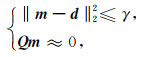
|
(2) |
其中,Q为约束算子,本文利用数据在变换域中的稀疏性作为约束条件,γ>0为误差范围.
压缩感知理论(Donoho,2006;Candès,2006;Zhang R et al., 2017)突破了传统香农采样定理的局限性,假设有效信号m是稀疏的(只有少数元素不为零),可以在压缩感知理论框架下对反演问题进行求解,公式(1)对应的信噪分离问题转变为如下约束最优化问题:
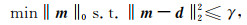
|
(3) |
其中,‖‖0表示L0范数,也就是数据中非零元素的个数.对于数学非凸优化问题,并且是NP-hard问题(Candès and Recht, 2009;Kreimer et al., 2013)的公式(3),通常很难得到它的全局最优解.为求解该问题,可以根据基追踪方法(Basis Pursuit,BP),将公式(3)转化为
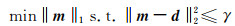
|
(4) |
所示的凸优化问题,其中,‖‖1表示L1范数.Elad和Bruckstein(2002)证明这一转化过程的等效条件.
公式(4)所示的凸优化约束问题在数学上依然难以求解,可以进一步转化为非约束问题:
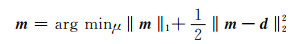
|
(5) |
进行求解,式中,μ为惩罚算子.公式(5)就为描述信噪分离的数学模型.但是地震数据的特殊性决定了消噪后的地震数据m很难是稀疏的.根据压缩感知理论,可以对m进行变量替换,借助稀疏变换,使m表现出稀疏性,也就是:
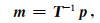
|
(6) |
式中,T-1表示稀疏逆变换,p为变换域系数,并且满足p的非零元素个数远小于m的非零元素个数.利用公式(6)对公式(4)进行修改,可以得到式(1)所示问题在压缩感知理论框架下的解:
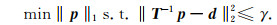
|
(7) |
根据公式(5),可以得到在压缩感知框架下,随机噪声压制反问题的近似解:
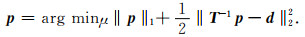
|
(8) |
最终,计算的p通过公式(6)就可以获得所需的有效信号m.Montefusco和Papi(2003)以小波变换为例,论述了公式(5)和(8)为等价问题,并且对应的解即为经典的软阈值消噪结果.进一步分析可以看到,公式(5)需要满足随机噪声在数据域内为高斯分布,而公式(8)需要满足随机噪声在稀疏变换域内高斯分布的假设.
1.2 Seislet-TV双正则化随机噪声压制方法Seislet变换是通过地震数据模式(例如,地震同相轴局部倾角属性,地震信号频率等)和离散小波变换(DWT)相结合构建的.Seislet变换的核心是设计基于地震数据模式的预测算子P和更新算子U,具体定义见于附录.在CMP道集中应用VD-seislet变换时,大幅值的有效信号系数分布在小尺度范围内,而随机噪声会以小幅值分布在整个变换域内,此时应用阈值算法就可以去除随机噪声.但常规阈值算法容易导致去噪结果过于平滑.
Rudin等(1992)提出了一种最小化全变差去噪模型,广泛应用于图像数据处理领域,用于保持强不连续性.全变差的定义为:
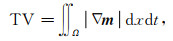
|
(9) |
式中,Ω表示数据域,▽m表示数据m的梯度.那么,最小化全变差的模型为
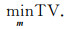
|
(10) |
但值得注意的是,该方法不能很好地重建数据的平滑部分,并可能在信噪分离结果中带入不期望出现的阶梯效应,即:TV算法可以保证数据的边缘信号,但会在一定程度上损失信号的平滑程度.
为避免TV算法与常规阈值算法的缺点,本次研究将式(8)所示的seislet变换稀疏约束条件与TV约束条件相结合,构建新的双正则化条件:(1-β)‖Tm‖1+β‖m‖TV,得到如下约束问题:
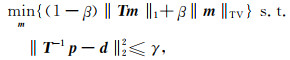
|
(11) |
其中,β∈[0, 1],为权系数.当β∈(0, 1)时,兼顾L1范数正则化项和TV范数正则化项.公式(11)所示的约束问题可以利用分裂Bregman(Split Bregman)迭代算法进行求解.
Osher等(2005)提出解决公式(8)对应约束最优化问题的线性Bregman迭代(Yin et al., 2008)方法,该方法通过计算一系列凸优化问题(Yin et al., 2008)进行约束问题求解,线性Bregman迭代框架为
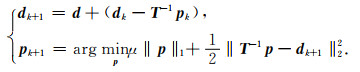
|
(12) |
线性Bregman迭代框架只能针对单一正则化约束问题,无法直接对(11)式进行求解.Goldstein和Osher(2009)在式(12)的基础上,提出
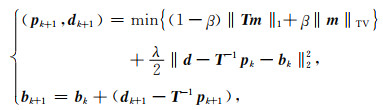
|
(13) |
求解公式(11)所示的双正则化约束问题,其中b0=0.公式(13)即为分裂Bregman迭代框架(Goldstein and Osher, 2009;Gholami and Sacchi, 2012;Lari and Gholami, 2014;Li and Li, 2016;Aghamiry et al., 2018).对于(13)式所示的约束最优化问题可以结合公式(8)和(12),将其转换为
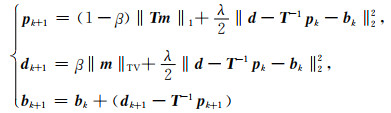
|
(14) |
的形式进行求解.
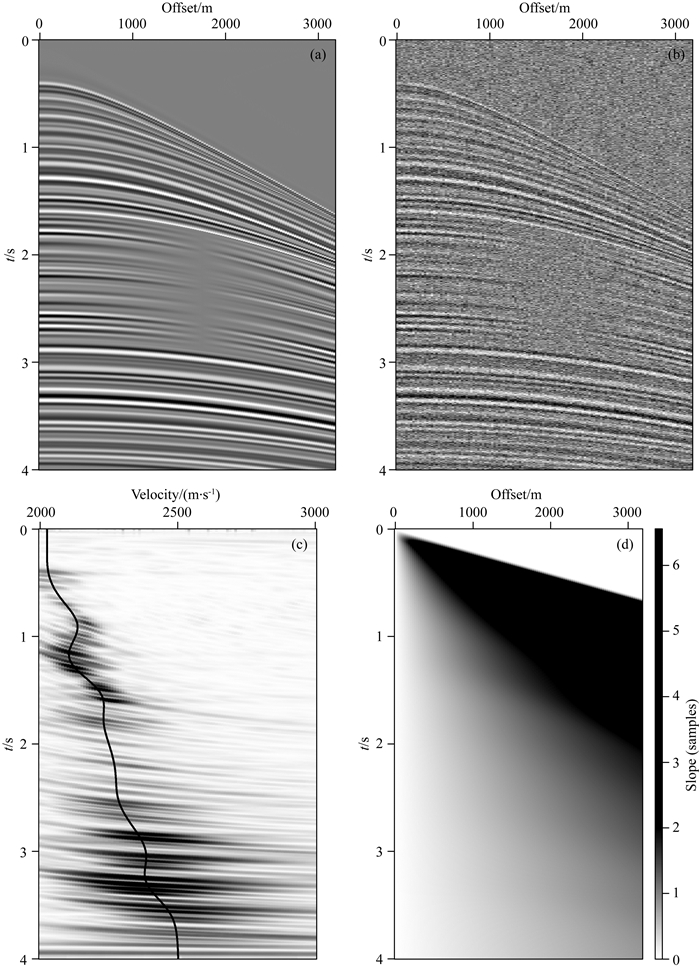
2 理论模型分析为测试本文算法的有效性,首先建立一个包含多条双曲型同相轴的叠前CMP道集(图 1a)进行算法测试.该模型(Fomel,2009)通过反动校正求得,为了增加模型的复杂性,在1.8 s~2.8 s处加入了AVO效应对同相轴振幅分布的影响,图中可以看出数据在该位置存在强不连续性.接下来,在该模型中加入高斯白噪声,满足正态分布,如图 1b所示,利用信噪比公式(刘洋等,2017):
|
图 1 叠前共中心点道集模型 (a)存在AVO现象的理论模型;(b)随机噪声模型;(c)速度谱及拾取的速度参数;(d)局部倾角. Fig. 1 Prestack CMP model (a) Syntetic data with AVO; (b) Synthetic data with random noise; (c) Velocity spectrum and picked velocity parameters; (d) Local slope. |
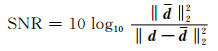
|
(15) |
来衡量噪声强度以及评价信噪分离的效果,其中d表示原始数据(含有随机噪声),d表示无噪声信号或者消噪后的结果,求得含噪声数据的信噪比为SNR=-1.976.从噪声模型中可以看到,许多弱同相轴信号已经被随机噪声淹没.为了构建VD-seislet变换,利用经典NMO方程对含噪声数据进行速度分析,并拾取速度参数(图 1c).从速度拾取结果可以看出,尽管AVO现象在一定程度上影响了同相轴的振幅信息,使得同相轴具有强不连续性,但是通过选取有效的速度分析方法(Fomel,2009)依然可以获得比较准确的速度参数,根据公式(A8)计算局部倾角信息(图 1d),该倾角信息能够反映同相轴的局部倾向,利用该信息可以设计压缩地震同相轴的VD-seislet稀疏变换.
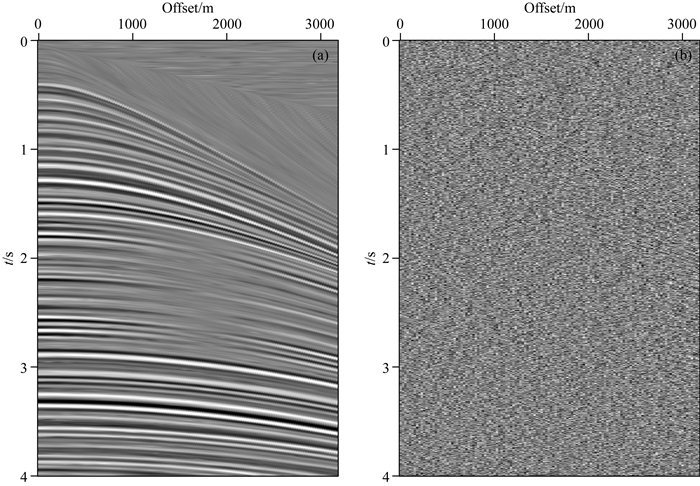
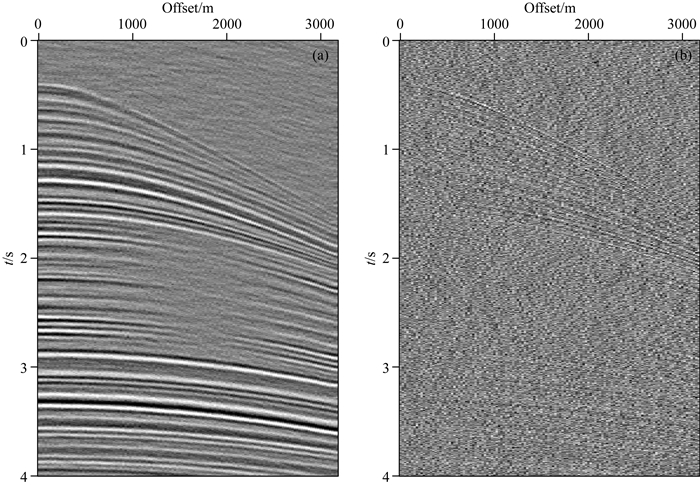
利用本文算法对含噪声数据进行去噪处理.为保证同时满足L1范数稀疏约束和TV范数约束条件,选取权系数β∈(0, 1).根据参数测试结果,选取权系数β=0.17,百分数阈值参数为7%,迭代次数8次,利用分裂Bregman迭代算法求解式(14)对应的最优化问题,得到去噪结果如图 2a所示.根据信噪比公式(15)计算信噪比SNR=11.55,从处理结果可以看出,本文算法可以在有效压制数据中随机噪声同时保护信号的强不连续性,提高地震资料的信噪比,同时差剖面(图 2b)表明本文算法只在浅层位置有较少有效信号损失,这是因为该位置振幅信息较弱,已经被强随机噪声淹没导致的.为了对比本文算法的有效性,选取工业标准的FXdecon方法(Gülünay, 2017)对噪声数据(图 1b)进行处理,得到随机噪声压制结果(图 3a),并根据信噪比公式计算信噪比SNR=7.714.从处理结果可以看到,FXdecon方法虽然可以滤除一部分随机噪声,在一定程度上提高地震资料的信噪比,但去噪结果与原始数据之间的差剖面(图 3b)显示该算法损失了较多的有效信号,尤其是中、远炮检距位置.
|
图 2 Seislet-TV双正则化方法随机噪声压制结果 (a)本文方法处理结果;(b)处理结果与原始数据之间的差异. Fig. 2 Denoising result using seislet-TV dual regularization (a) Denoising result using the proposed method; (b) Difference profile. |
|
图 3 FXdecon方法随机噪声压制结果 (a) FXdecon方法处理结果;(b)处理结果与原始数据之间的差异. Fig. 3 Denoising result using FXdecon method (a) Denoising result using the FXdecon method; (b) Difference profile. |
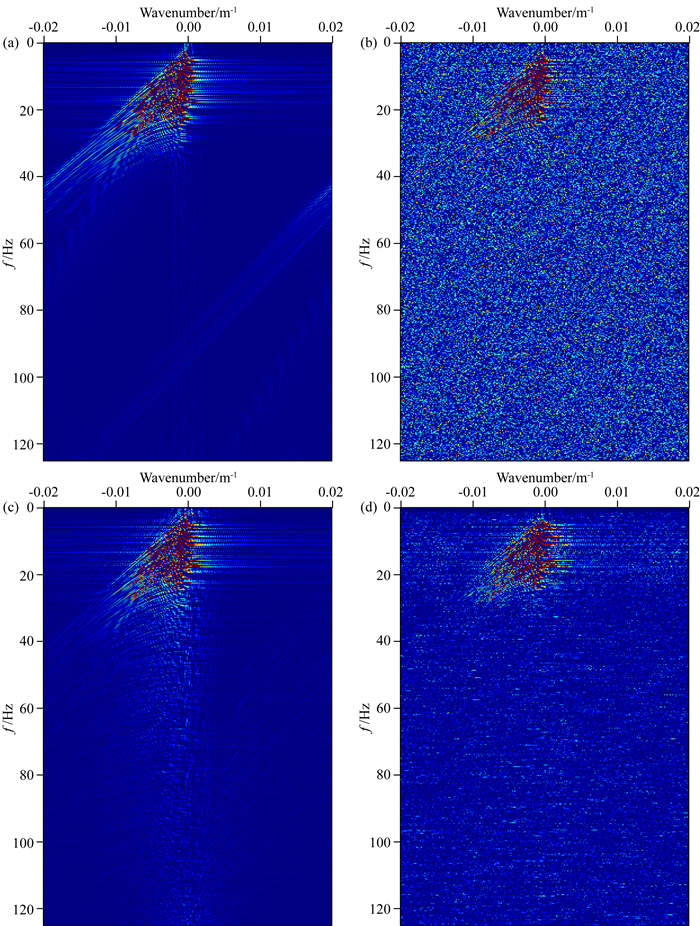
接下来,本文分别计算各数据的频谱对各方法的信噪分离能力进行比较.图 4a为理论模型的频谱,可以看到能量团比较集中.图 4b为含随机噪声模型的频谱,由于强随机噪声的影响,能量比较分散,噪声能量也导致大部分有效信号能量被淹没.图 4c为本文所提seislet-TV双正则化算法信噪分离结果的频谱,从图中可以看出该算法信噪分离结果比较理想,有效信号能量变得连续,几乎无噪声能量存在.图 4d为FXdecon信噪分离方法消噪结果的频谱,从图中可以看出,尽管该方法去除了一部分随机噪声,但从其频谱中依然可以看出有许多随机噪声的存在,有效信号能量在一定程度上被剩余噪声淹没.综合对比消噪结果、差剖面、信噪比和频谱,本文所提联合算法信噪分离能力要优于工业标准的FXdecon方法.
|
图 4 各数据的频谱 (a)原始信号;(b)含噪声数据;(c)本文方法处理结果;(d) FXdecon方法处理结果. Fig. 4 Spectrums of different data (a) Synthetic data; (b) Synthetic data with random noise; (c) Denoising result using the proposed method; (d) Denoising result using the FXdecon method. |
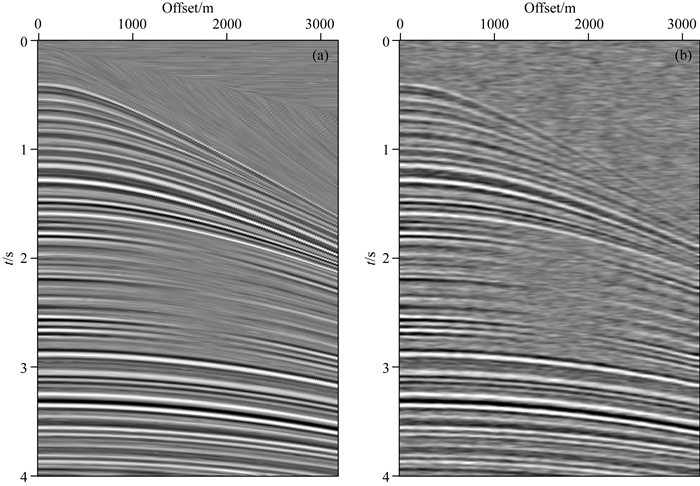
同时,为了进一步证明本文算法的有效性,本文首先选取单一VD-seislet变换阈值消噪算法进行对比,选取与联合算法相同的阈值参数,得到信噪分离结果如图 5a所示,求得信噪比SNR=10.83,从图中可以看出,尽管VD-seislet变换阈值消噪算法可以去除大部分的随机噪声,提高很多信噪比,但也破坏了一部分数据,使得不连续位置的信息变得近似连续.接下来利用单一TV范数算法进行消噪处理(图 5b),求得信噪比SNR=8.237,从图中可以看出,尽管该算法提高了一定的信噪比,但效果有限,分辨率依然较低.同时对比消噪结果、信噪比,依然可以看出本文所提联合算法要优于单一VD-seislet变换阈值消噪算法和单一TV范数算法.
|
图 5 VD-seislet变换及TV范数随机噪声压制结果 (a) VD-seislet变换阈值处理结果;(b) TV范数处理结果. Fig. 5 Denoising result using VD-seislet transform and TV norm method (a) Denoising result using the VD-seislet tranform method; (b) Denoising result using TV norm method. |
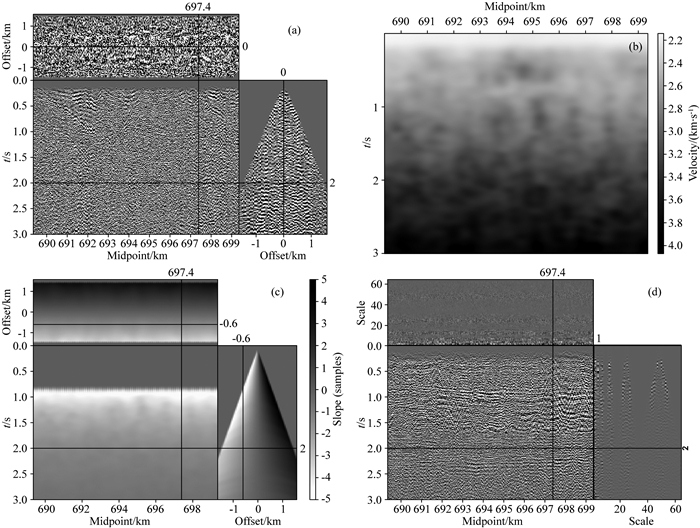
在实际资料处理中,选取波兰某地区的陆上地震数据进行测试.图 6a为经过去面波处理后的实际数据的CMP道集,由于该数据体覆盖次数较低,从图中可以看出该数据体信噪比偏低,强随机噪声的存在影响了有效信号的识别,反射同相轴并不清晰.尽管如此,利用NMO方程(A7)依然可以拾取到比较准确的速度信息(图 6b),速度信息将用于构建局部倾角(A8).从速度谱可以看到速度扫描方法对随机噪声有较好的免疫性.利用该速度信息构建的局部倾角场(图 6c)能够准确反映同相轴的走向及时-空变特征.利用倾角信息可以构建基于该倾角信息的Rk算子进而得到VD-seislet变换,沿着炮检距方向能够实现地震数据的稀疏表征.该数据体中部分有效信号能量较弱,导致变换域(图 6d)内有效信号与随机噪声分选性较差;同时还存在无法被速度扫描方法获取地低速噪声,它们的振幅较高,并存在于较大级数范围内.
|
图 6 实际数据测试 (a)实际数据;(b)速度谱;(c)局部倾角;(d) VD-seislet变换系数. Fig. 6 Field data test (a) Field dataset; (b) Velocity spectrum; (c) Local slope; (d) VD-seislet transform coefficients. |
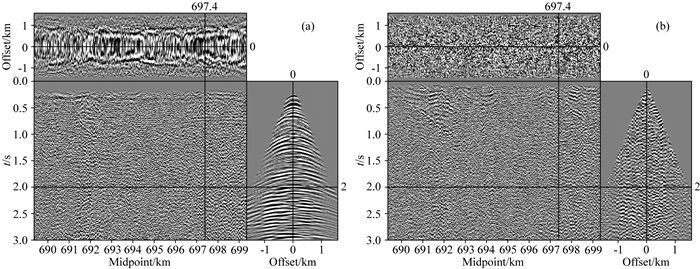
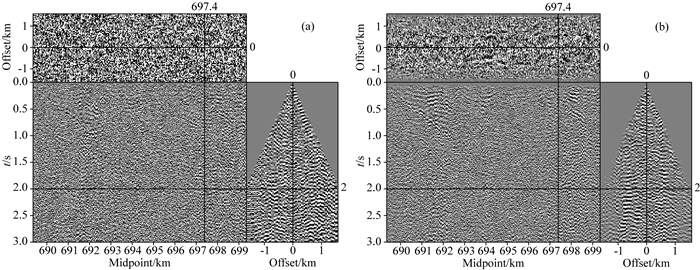
接下来利用本文算法对该数据进行处理.选取权系数β=0.17,该权系数可以保证结合L1范数正则化条件和TV范数正则化条件的有效组合特征.由于该数据的特殊性,单一的软阈值算法并不能去除低速噪声,本文在处理该数据时在级数方向上采用线性窗函数与非线性软阈值相结合的算法,选取合适的级数阈值(将级数大于8的系数置零)和百分数阈值(8%)进行组合,迭代5次,利用分裂Bregman迭代算法进行计算,得到信噪分离结果(图 7a),计算去噪结果与原始数据之间的差异如图 7b所示.从图中可以看到,本文算法可以有效去除不相干随机噪声,很好地恢复反射同相轴形态,能够有效保护同相轴的振幅空间变化关系,提高数据体信噪比,为了突出显示,差剖面和去噪结果使用不同的绘图参数.为了验证本文算法的有效性,选取工业标准FXdecon方法进行对比.去噪结果如图 8a所示,从图中可以看出FXdecon方法对低信噪比数据的数据处理能力有限,只能压制近炮检距范围内的少量随机干扰,同时还引入了一些弱能量的假频同相轴信息,差剖面(图 8b)也表明该方法难以处理低信噪比数据.
|
图 7 seislet-TV双正则化方法处理结果 (a)去噪结果; (b)去噪结果与原始数据的差异. Fig. 7 Denoising result using seislet-TV dual regularization (a) Denoising result using the proposed method; (b) Difference between Fig. 4a and Fig. 5a |
|
图 8 FXdecon方法处理结果 (a)去噪结果; (b)去噪结果与原始数据的差异. Fig. 8 Denoising result using FXdecon method (a) Denoising result; (b) Difference between Fig. 4a and Fig. 6a. |
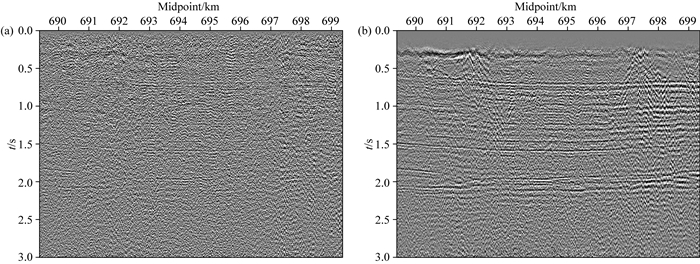
接下来,对两种处理结果的叠加剖面进行对比.图 9a和9b为两种方法的叠加剖面,从图中可以看出:FXdecon方法得到的叠加剖面信噪比较低,同相轴连续性较差,分辨率也较低;而本文算法的叠加剖面中,整体质量有较大的提升,地层连续性增强,分辨率也较高,验证了本文算法的有效性.
|
图 9 不同处理方法的叠加剖面 (a) FXdecon方法;(b)本文算法. Fig. 9 The stacking results using different methods (a) FXdecon method; (b) The proposed method. |
本文在压缩感知理论框架下,利用L1范数约束模型稀疏度,并结合TV范数构建新的seiselt-TV双正则化条件,获得新的迭代信噪分离模型,并利用分裂Bregman迭代算法进行求解.该迭代模型可以将TV去噪方法边界保持的优点和阈值消噪方法的优点相结合,克服TV消噪方法容易产生阶梯效应和阈值消噪过度平滑的不足.对理论模型和实际地震数据进行处理和分析,并且对比工业FXdecon方法、单一阈值消噪方法和TV算法,结果表明本文迭代方法能够提供更合理的随机噪声压制结果,保护时-空变地震有效信号和数据边界信息.
附录Seislet变换的实现类似于小波提升算法(Sweldens,1995),利用预测算子和更新算子实现地震数据的预测和更新,完成不同尺度下的变换结果(Fomel and Liu, 2010).
Seislet变换分解算法的实现流程如下:
(1) 将数据整理成一个记录序列,对于seislet变换而言,输入数据为地震数据,变换方向仅为空间方向,将地震道序号分成奇数列o和偶数列e.
(2) 根据地震道信息之间的相关性,偶数部分通过预测算子P来预测奇数列o,求取奇数列与预测值之间的差值序列r,该差值序列可以反映原信号的高频成分:
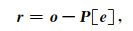
|
(A1) |
r也就是seislet变换系数.
(3) 利用更新算子U对差值序列进行更新得到偶数列的近似序列c,也就是seislet变换的尺度系数:
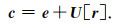
|
(A2) |
(4) 重复步骤(1),(2),(3)可以实现不同尺度下seislet变换结果.
Seislet变换重构算法实现流程如下:
(5) 首先寻找最后一级的seislet变换系数r和尺度系数c;
(6) 利用更新算子U实现seislet变换系数r的更新,获得尺度系数c的更新值,得到重构偶数序列:
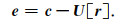
|
(A3) |
(7) 利用预测算子P对重构的偶数列e进行更新,得到seislet变换系数的预测值,重构得到seislet变换域系数:
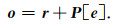
|
(A4) |
(8) 重复步骤(5),(6),(7)可以实现不同尺度下seislet变换的重构.
以CDF5/3双正交小波(Cohen et al., 1992)为例,通过两个相邻采样点之间的线性插值定义预测算子和更新算子(Fomel and Liu, 2010;Liu et al., 2015)为:
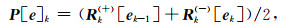
|
(A5) |
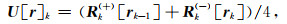
|
(A6) |
其中,ek是第k个空间变换尺度上地震数据的偶数部分,rk表示在第k个空间变换尺度上奇数部分与偶数部分预测值的残差.Rk(+)和Rk(-)表示根据地震数据模式对左右相邻地震道同相轴进行时移(局部倾角的走向)来预测数据的算子.由于预测需要在不同空间尺度上运算,这也就意味着地震道之间要能够在不同的空间距离之间进行预测计算.
对于基于不同倾角模式的seislet变换,只需定义与倾角相关的算子Rk即可,基于平面波分解滤波器(PWD)(Fomel,2002)的倾角估算方法,对噪声比较敏感,因此需要一种新的稳健倾角估算方法.
地震数据同相轴的运动学关系是地震数据处理的重要理论基础之一.局部倾角是时空域地震数据的一个关键运动学模式.对于叠前CMP道集数据,Liu等(2015)利用经典双曲型反射波模型
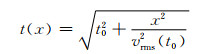
|
(A7) |
来定义地震同相轴局部倾角.其中,t(x)表示炮检距x的反射波走时,t0表示零炮检距的反射波走时,vrms(t0)表示叠加或均方根(RMS)速度,可以通过速度扫描求得.对于一系列常速度,CMP道集中的反射波走时与倾角之间有σ=dt/dx的关系,可以得到:
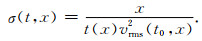
|
(A8) |
可以看出,通过在每一点(t0, x)处进行速度扫描,就能得到对应的扫描时间和均方根或叠加速度vrms(t0, 0),利用双曲线的时距关系,能够计算得到vrms(t, x),根据公式(A8)即可得到(t, x)对应的地震局部倾角.当计算出地震数据的VD倾角模式后,就可以设计基于预测算子和更新算子模式的Rk,据此设计的倾角算子可以构建VD-seislet变换来表征双曲反射波数据.
Aghamiry H, Gholami A, Operto S. 2018. Imaging contrasted media with total variation constrained full waveform inversion and split Bregman iterations.//80th Annual International Meeting, EAGE Conference & Exhibition. EAGE. https://www.researchgate.net/publication/323656456_Imaging_Contrasted_Media_with_Total_Variation_Constrained_Full_Waveform_Inversion_and_Split_Bregman_Iterations
|
Candès E J. 2006. Compressive sampling.//Proceedings of the International Congress of Mathematicians. Madrid: European Mathematical Society Publishing House, 1433-1452.
|
Candès E J, Recnt B. 2009. Exact matrix completion via convex optimization. Foundations of Computational Mathematics, 9(6): 717-772. DOI:10.1007/s10208-009-9045-5 |
Chan T, Esedoglu S, Park F, et al. 2005. Recent developments in total variation image restoration.//Mathematical Models of Computer Vision. New York: Springer Verlag.
|
Chan T F, Zhou H M. 2000. Total variation improved wavelet thresholding in image compression.//Proceedings 2000 International Conference on Image Processing. Vancouver, BC, Canada: IEEE, 391-394. https://www.researchgate.net/publication/3886321_Total_variation_improved_wavelet_thresholding_in_image_compression
|
Chen H X. 2016. A layered median filter algorithm based on noised pixels connected component. Computer Applications and Software (in Chinese), 33(10): 321-324. |
Cohen A, Daubechies I, Feauveau J C. 1992. Biorthogonal bases of compactly supported wavelets. Communications on Pure and Applied Mathematics, 45(5): 485-560. DOI:10.1002/cpa.3160450502 |
Donoho D L. 2006. Compressed sensing. IEEE Transactions on Information Theory, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
Durand S, Froment J. 2003. Reconstruction of wavelet coefficients using total variation minimization. SIAM Journal on Scientific computing, 24(5): 1754-1767. DOI:10.1137/S1064827501397792 |
Elad M, Bruckstein A M. 2002. A generalized uncertainty principle and sparse representation in pairs of bases. IEEE Transactions on Information Theory, 48(9): 2558-2567. DOI:10.1109/TIT.2002.801410 |
Esedolu S, Osher S J. 2004. Decomposition of images by the anisotropic Rudin-Osher-Fatemi model. Communications on Pure & Applied Mathematics, 57(12): 1609-1626. |
Fomel S. 2002. Applications of plane-wave destruction filters. Geophysics, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
Fomel S. 2006. Towards the seislet transform.//76th Annual International Meeting, SEG Extended Abstracts. SEG, 2847-2850.
|
Fomel S. 2009. Adaptive multiple subtraction using regularized nonstationary regression. Geophysics, 74(1): V25-V33. |
Fomel S, Liu Y. 2010. Seislet transform and seislet frame. Geophysics, 75(3): V25-V38. DOI:10.1190/1.3380591 |
Gholami A, Siahkoohi H R. 2010. Regularization of linear and non-linear geophysical ill-posed problems with joint sparsity constraints. Geophysical Journal International, 180(2): 871-882. DOI:10.1111/j.1365-246X.2009.04453.x |
Gholami A, Sacchi M D. 2012. A fast and automatic sparse deconvolution in the presence of outliers. IEEE Transactions on Geoscience & Remote Sensing, 50(10): 4105-4116. |
Gholami A. 2015. Nonlinear multichannel impedance inversion by total-variation regularization. Geophysics, 80(5): R217-R224. DOI:10.1190/geo2015-0004.1 |
Goldstein T, Osher S. 2009. The split Bregman method for L1-Regularized problems. SIAM Journal on Imaging Sciences, 2(2): 323-343. DOI:10.1137/080725891 |
Gong X B, Han L G, Li H J. 2014. Anisotropic Radon transform and its application to demultiple. Chinese Journal of Geophysics (in Chinese), 57(9): 2928-2936. DOI:10.6038/cjg20140918 |
Guo S, Wang H Z. 2018. Absolute acoustic-impedance estimation with L1 norm constraint and combined first and second order TV regularizations.//88th Annual International Meeting, SEG Extended Abstracts. Anaheim, California, USA: SEG, 501-505. https://www.researchgate.net/publication/327607709_Absolute_acoustic-impedance_estimation_with_L1_norm_constraint_and_combined_first_and_second_order_TV_regularizations
|
Gülünay N. 2017. Signal leakage in f-x deconvolution algorithms. Geophysics, 82(5): W31-W45. |
Kreimer N, Stanton A, Sacchi M D. 2013. Tensor completion based on nuclear norm minimization for 5D seismic data reconstruction. Geophysics, 78(6): V273-V284. DOI:10.1190/geo2013-0022.1 |
Lari H H, Gholami A. 2014. Curvelet-TV regularized Bregman iteration for seismic random noise attenuation. Journal of Applied Geophysics, 109: 233-241. DOI:10.1016/j.jappgeo.2014.08.005 |
Li T F, Liu J M, Duan Y. 2018. A depth image real-time image inpainting algorithm based on window filtering and mean filtering. Software Engineering (in Chinese), 21(11): 17-20. |
Li Z X, Li Z C. 2016. Accelerated and automatic sparse parabolic Radon transform in the mixed frequency-time domain with alternating split Bregman algorithm.//86th Annual International Meeting, SEG Extended Abstracts. Dallas, Texas: SEG, 4524-4528. https://www.researchgate.net/publication/307879893_Accelerated_and_automatic_sparse_parabolic_radon_transform_in_the_mixed_frequency-time_domain_with_alternating_split_Bregman_algorithm
|
Liu W, Cao S Y, Chen Y K, et al. 2016. An effective approach to attenuate random noise based on compressive sensing and curvelet transform. Journal of Geophysics and Engineering, 13(2): 135-145. |
Liu Y, Fomel S, Liu C, et al. 2009. High-order seislet transform and its application of random noise attenuation. Chinese Journal of Geophysics (in Chinese), 52(8): 2142-2151. DOI:10.3969/j.issn.0001-5733.2009.08.024 |
Liu Y, Liu C, Wang D. 2009. A 1D time-varying median filter for seismic random, spike-like noise elimination. Geophysics, 74(1): V17-V24. |
Liu Y, Fomel S. 2010. OC-seislet:seislet transform construction with differential offset continuation. Geophysics, 75(6): WB235-WB245. DOI:10.1190/1.3479554 |
Liu Y, Wang D, Liu C, et al. 2011. Weighted median filter based on local correlation and its application to poststack random noise attenuation. Chinese Journal of Geophysics (in Chinese), 54(2): 358-367. DOI:10.3969/j.issn.0001-5733.2011.02.012 |
Liu Y, Liu C. 2013. Velocity-dependent seislet transform and its applications. 83th Annual International Meeting, SEG, Expanded Abstracts. SEG, 3661-3666.
|
Liu Y, Fomel S, Liu C. 2015. Signal and noise separation in prestack seismic data using velocity-dependent seislet transform. Geophysics, 80(6): WD117-WD128. DOI:10.1190/geo2014-0234.1 |
Liu Y, Li B X, Wang D, et al. 2017. Local SNR estimation method based on regularization for seismic data. Chinese Journal of Geophysics (in Chinese), 60(5): 1979-1987. DOI:10.6038/cjg20170529 |
Liu Y, Zhang P, Liu C. 2017. Seismic data interpolation using generalised velocity-dependent seislet transform. Geophysical Prospecting, 65: 82-93. DOI:10.1111/1365-2478.12578 |
Liu Y, Zhang P, Liu C, et al. 2018. Seismic data interpolation based on Bregman shaping iteration. Chinese Journal of Geophysics (in Chinese), 61(4): 1400-1412. DOI:10.6038/cjg2018L0422 |
Lu Z B, Wang X, Hu G E. 2007. An anisotropic Wiener denoising algorithm based on structure tensor. Computer Science (in Chinese), 34(7): 229-231. |
Lysaker M, Lundervold A, Tai X C. 2003. Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time. IEEE Transactions on Image Processing, 12(12): 1579-1590. DOI:10.1109/TIP.2003.819229 |
Montefusco L B, Papi S. 2003. A parameter selection method for wavelet shrinkage denoising. BIT Numerical Mathematics, 43(3): 611-626. DOI:10.1023/B:BITN.0000007055.60934.b7 |
Nan F Z, Xu Y, Liu W, et al. 2018. Denoising methods of OBS data based on sparse representation. Chinese Journal of Geophysics (in Chinese), 61(4): 1519-1528. DOI:10.6038/cjg2018L0130 |
Osher S, Burger M, Goldfarb D, et al. 2005. An iterative regularization method for total variation-based image restoration. Multiscale Modeling & Simulation, 4(2): 460-489. |
Rudin L I, Osher S, Fatemi E. 1992. Nonlinear total variation based noise removal algorithms. Physica D-Nonlinear Phenomena, 60(1-4): 259-268. DOI:10.1016/0167-2789(92)90242-F |
Song W Q, Wu C D. 2017. Seismic data resolution improvement based on compressed sensing. Oil Geophysical Prospecting (in Chinese), 52(2): 214-219. |
Sweldens W. 1995. Lifting scheme: A new philosophy in biorthogonal wavelet constructions.//Proceedings of SPIE 2569, Wavelet Applications in Signal and Image Processing III. San Diego, CA, United States: SPIE, 68-79. https://www.researchgate.net/publication/2783093_The_Lifting_Scheme_A_New_Philosophy_in_Biorthogonal_Wavelet_Constructions
|
Tang G. 2010. Seismic data reconstruction and denoising based on compressive sensing and sparse representation[Ph. D. thesis] (in Chinese). Beijing: Tsinghua University. http://cdmd.cnki.com.cn/Article/CDMD-10003-1011280421.htm
|
Wang L L, Mao W J, Tang H H, et al. 2017. Amplitude preserved seismic data reconstruction by fast 3D parabolic Radon transform. Chinese Journal of Geophysics (in Chinese), 60(7): 2801-2812. DOI:10.6038/cjg20170725 |
Wang X Q, Yang J D, Huang J P, et al. 2017. Fast Gaussian beam migration method based on matching-pursuit decomposition and events-picking in tau-p domain. Progress in Geophysics (in Chinese), 32(2): 745-752. DOI:10.6038/pg20170240 |
Yin W T, Osher S, Goldfarb D, et al. 2008. Bregman iterative algorithms for L1 minimization with applications to compressed sensing. SIAM Journal on Imaging Sciences, 1(1): 143-168. DOI:10.1137/070703983 |
Zhang G L. 2018. Time-phase amplitude spectra based on a modified short-time Fourier transform. Geophysical Prospecting, 66(1): 34-46. DOI:10.1111/1365-2478.12528 |
Zhang H, Chen X H, Zhang L Y. 2017. 3D simultaneous seismic data reconstruction and noise suppression based on the curvelet transform. Applied Geophysics, 14(1): 87-95. |
Zhang L, Han L G, Xu D X, et al. 2017. Seismic data reconstruction with Shearlet transform based on compressed sensing technology. Oil Geophysical Prospecting (in Chinese), 52(2): 220-225. |
Zhang R, Zhang K, Alekhue J E. 2017. Depth-domain seismic reflectivity inversion with compressed sensing technique. Interpretation, 5(1): T1-T9. |
Zhong T, Li Y, Yang B J, et al. 2017. Statistical features of the random noise in land seismic prospecting. Chinese Journal of Geophysics (in Chinese), 60(2): 655-664. DOI:10.6038/cjg20170219 |
陈宏希. 2016. 一种基于噪声连接分量的层次中值滤波算法. 计算机应用与软件, 33(10): 321-324. DOI:10.3969/j.issn.1000-386x.2016.10.071 |
巩向博, 韩立国, 李洪建. 2014. 各向异性Radon变换及其在多次波压制中的应用. 地求物理学报, 57(9): 2928-2936. DOI:10.6038/cjg20140918 |
李腾飞, 刘嘉敏, 段勇. 2018. 基于窗口滤波与均值滤波的深度图像实时修复算法. 软件工程, 21(11): 17-20. |
刘洋, Fomel S, 刘财, 等. 2009. 高阶seislet变换及其在随机噪声消除中的应用. 地球物理学报, 52(8): 2142-2151. DOI:10.3969/j.issn.0001-5733.2009.08.024 |
刘洋, 王典, 刘财, 等. 2011. 局部相关加权中值滤波技术及其在叠后随机噪声衰减中的应用. 地球物理学报, 54(2): 358-367. DOI:10.3969/j.issn.0001-5733.2011.02.012 |
刘洋, 李炳秀, 王典, 等. 2017. 基于正则化条件的地震数据局部信噪比估计方法. 地球物理学报, 60(5): 1979-1987. DOI:10.6038/cjg20170529 |
刘洋, 张鹏, 刘财, 等. 2018. 地震数据Bregman整形迭代插值方法. 地球物理学报, 61(4): 1400-1412. DOI:10.6038/cjg2018L0422 |
鲁志波, 王鑫, 胡国恩. 2007. 结合结构张量和Wiener滤波的图像去噪算法. 计算机科学, 34(7): 229-231. DOI:10.3969/j.issn.1002-137X.2007.07.062 |
南方舟, 徐亚, 刘伟, 等. 2018. 基于稀疏表达的OBS去噪方法. 地球物理学报, 61(4): 1519-1528. DOI:10.6038/cjg2018L0130 |
宋维琪, 吴彩端. 2017. 利用压缩感知方法提高地震资料分辨率. 石油地球物理勘探, 52(2): 214-219. |
唐刚. 2010.基于压缩感知和稀疏表示的地震数据重建与去噪[博士论文].北京: 清华大学. http://cdmd.cnki.com.cn/Article/CDMD-10003-1011280421.htm
|
王亮亮, 毛伟建, 唐欢欢, 等. 2017. 快速3D抛物Radon变换地震数据保幅重建. 地球物理学报, 60(7): 2801-2812. DOI:10.6038/cjg20170725 |
王旭谦, 杨继东, 黄建平, 等. 2017. 基于匹配追踪分解和tau-p域拾取的快速高斯束偏移方法. 地球物理学进展, 32(2): 745-752. DOI:10.6038/pg20170240 |
张良, 韩立国, 许德鑫, 等. 2017. 基于压缩感知技术的Shearlet变换重建地震数据. 石油地球物理勘探, 52(2): 220-225. |
钟铁, 李月, 杨宝俊, 等. 2017. 陆地地震勘探随机噪声统计特性. 地球物理学报, 60(2): 655-664. DOI:10.6038/cjg20170219 |
 2020, Vol. 63
2020, Vol. 63


