0 引言

页岩气是天然气的非常规来源之一，它赋存于非连通的小页岩裂缝中，很难提取。近十年来，随着能源危机的出现和水力压裂技术的不断发展，以水力压裂为核心技术的页岩气勘探逐渐成为当今最热门的研究领域之一(Loucks et al., 2009; Ambrose et al., 2010; 邹才能等, 2011；Curtis et al., 2012).为了成功地估计页岩气的分布，必须获得页岩微观结构，这对于天然气勘探和生产具有重要意义(崔景伟等, 2012; 王玉丹等, 2015).传统的表面观察方法，如光学和扫描电子显微镜，都不足以获得页岩样品的三维信息，反而会破坏页岩样品(Milner et al., 2010; Yang et al., 2013).并且由于页岩样品难以开发并且极其珍贵，这些方法并不理想.

X射线计算机断层扫描(X-ray CT)技术是20世纪70年代以来在医学、生物学、工业和科学领域得到成功应用的一种无创性的内部结构可视化方法(Herman, 2009)，因此我们尝试用X射线CT技术重建页岩微结构，并且该技术对于页岩具有非破坏性.

本文利用同步辐射(SR)源产生的平行X射线束获取投影数据(Wang et al., 2016).利用NI LabVIEW的数据录入和监控模块(DSC)EPICS(实验物理和工业控制系统)进行通信，在上海同步辐射装置(SSRF)的BL13W1 XAFS波束线上生成了同步辐射源，该光源是能量可调的、单色的和自然准直的X射线束.使用单色光束的好处是它可以避免多色光束引起的X射线硬化；同时由于能量可调，因而频谱宽；并且空间分辨率高(Mayo et al., 2012).

从层析成像的角度来看，滤波反投影(FBP)是X射线CT图像重建的常规算法(Natterer and Wubbeling, 2001).FBP有几种变化形式，它们都依赖于CT成像的Fourier中心切片定理，并且它们都结合了(线性)滤波操作和反投影操作.相比之下，正则化建模和优化方法利用非线性运算，并且通常是迭代的(Jiang and Wang, 2002; 王彦飞, 2007; 王彦飞等, 2011).与FBP算法相比，优化重建算法的主要优点是它们对噪声不敏感，并且灵活.例如，数据可以在任何一组直线上收集，投影不必在角度上均匀分布；此外由于正则化技术的应用，不完整的数据也可以用来重建页岩内部结构(Wang et al., 2017).

本文提出用非光滑正则化建模并结合一种快速的优化计算方法来解决利用同步辐射(SR)源产生的X射线束的页岩稀疏恢复问题.利用稀疏L1范数+全变差(TV)项，既考虑了页岩组份(比如孔隙)的稀疏性，同时又考虑了成像的保边结构，利用该方法可以成功地去除噪声和重构伪影.实验数据表明所提出的非光滑正则化及优化方法比传统的滤波反投影法有更好的成像结果.

1 方法理论 1.1 正演建模

由于三维(3D)信息可以逐层获得，因此我们只考虑二维(2D)X射线CT图像重建问题.从分析的角度来看，二维X射线CT问题是反演被检测材料的X射线衰减图像f(x)的Radon变换(Herman, 2009; Natterer and Wubbeling, 2001; Nashed and Scherzer, 2001)：

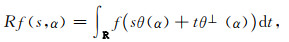
(1)

其中，可以通过常规的滤波反投影(FBP)公式由180°投影数据重建：

(2)

其中，Rf(s, θ(α))的导数是关于第一个变量s的.

在离散情况下，f(x, y)表示离散图像矩阵(f∈ )，R(f)表示有限采样点(s_i, α_j)处的观测值.我们将使用符号m表示要恢复的图像，d表示正弦图域中的测量或投影，L表示有限样本的离散Radon变换.则离散形式的Radon变换可以公式化为(Wang et al., 2017)：

(3)

其中，称为成像矩阵，是观察到的投影数据，η是未知噪声图像.

1.2 反问题的不适定性

页岩X射线CT成像是典型的不适定反问题，体现在以下几个方面：

(1) 线积分算子是一个紧算子，因此，不适定问题中的3个限定条件有可能全部满足；

(2) 数值实现上，仅给出(s_i, α_j)处的有限个投影，方程(3)将是一个欠定线性系统，因此它是一个离散的不适定问题；

(3) 公式(2)的实际应用中，需要选择合适的Riesz势函数；该函数的选择不当将加剧解的振荡；

(4) 噪声的放大效应将使得反问题的解偏离真实解；

(5) 尺度问题.页岩气赋存于微纳米孔隙中，观测到的X射线成像数据的每一个组份是周围其他物质成分的线性组合.

解决不适定反问题的基本思路是正则化技巧，并辅之以快速实现算法(王彦飞, 2007; 王彦飞等, 2011).由于页岩气勘探开发中一个重要的问题是微纳米孔隙结构成像，很明显，孔隙结构具有稀疏性特征，因此本文考虑孔隙成像的非光滑正则化方法.

1.3 L1+TV稀疏非光滑正则化

正则化方法是处理不适定问题的常用技术，并逐渐成为X射线CT领域的研究热点.正则化方法通常被建模为最小化问题，公式为

(4)

其中，ψ是一个凸函数(称为正则化项)，而C是一个凸集，代表了m的先验知识，D(·, ·)是一个距离函数(称为保真项)，用于度量Lm如何逼近投影数据d.这里α>0被称为正则化参数.

正则化项和保真项是正则化方法的核心，得到了广泛的研究.正则化项有很多选择，如基于全变差的选取，基于小波的稀疏表示方法，基于紧帧和字典的X射线CT图像重建方法(Chambolle, 2004; Luo and Wang, 2018).在本文中，我们使用全变差(TV)函数和待求函数(图像)的L1范数作为正则化项.这是因为一方面，页岩通常由不相容的组分组成，如孔隙、黏土矿物和石英颗粒等，因此，我们可以假设衰减函数(对应着图像m)是分段常数函数，具有个体的稀疏性.另一方面，众所周知，全变差极小化方法迫使图像(或函数)是分段常数近似.对于保真度项，我们使用l₂范数作为距离函数D，即D(Lm, d)=‖Lm－d‖_l2²，因为我们假定X射线CT投影数据中的噪声服从高斯分布.

因此，本文建立的正则化模型表达式为

(5)

其中我们对解施加了一个非负约束，即S={m:m≥0}，因为衰减系数在物理上总是非负的.公式(5)中的α和β为两个正则参数.

有关正则化参数选取策略的讨论一直伴随着不适定问题的研究过程，为了得到迭代正则化算法的收敛性结果，需要对正则化参数加上很强的限制条件.目前正则化参数的选择有先验和后验两种取法.先验法需要预先对原始数据的误差水平δ做出估计，后验法可以直接应用带噪声的原始数据做估计, 但需要求解相应的偏差方程和多次解线性方程组(王彦飞，2007).由于X射线层析成像计算量很大，解偏差方程和多次解线性方程组会导致很大的CPU时间.因此本文采用先验的正则参数选取方法.

1.3.1 非光滑逼近与梯度计算

公式(5)的L1范数，我们采用Huber函数逼近，定义为

(6)

显然，当δ→0时，m_δ(x)趋近于L1范数逼近.

为了逼近公式(5)中的TV函数，我们定义一个光滑函数(王彦飞, 2007)：

(7)

其中，M_ζ(x)的离散化可以通过设置h_t=1/N来实现，于是参数m可以离散为于所有的i形成一个N×(N+1)矩阵.M_ζ(m)的梯度可以通过对任意的获得，即：

(8)

因此：

(9)

其中diag(ф′(m))表示N×N的对角矩阵，其第i对角元为ф′((T_im)²), T是一个N×(N+1)的矩阵，其第i行为T_i，并且：

(10)

由公式(5)可以看出，目标函数J(m)的梯度g(m)，由三部分组成，即：

(11)

其中，和J₃(m)=TV(m)的梯度分别为

(12)

其中，是公式(6)函数p(m)的导数.因此目标函数J(m)的梯度可以显式地表示为

(13)

1.3.2 最速下降法

有效的算法是正则化X射线CT图像重建问题(3)的另一个关键问题.针对X射线CT成像的大规模问题，本文采用梯度下降法求解该模型.最速下降法是最简单的梯度下降法，在第k次迭代中，将m_k表示为更新的页岩结构图像，则下一个更新值将通过迭代格式实现，公式为

(14)

其中，s_k=－g_k=－g(m_k)是搜索方向，τ_k是步长.

当我们进行迭代求解时，沿着负梯度方向进行搜索，并执行回溯线性搜索来确保迭代点的可行性，其基本思想是从一列步长点列中选择满足非精确线搜索条件的一个最优步长.通常，τ_k通过求解非线性优化问题得到，公式为

(15)

其中，符号argmin表示用特定参数最小化函数.可以证明，最速下降法是一种正则化方法(Nashed, 1970).然而，最速下降法在多次迭代后收敛较慢，且迭代方向呈锯齿形(袁亚湘, 1993).因此，接下来我们将考虑加速技巧.

1.3.3 快速梯度下降法

我们采用梯度投影方法对(5)式进行求解(Dai and Fletcher, 2005; Wang and Ma, 2007).由于(5)的解集合为S，则梯度投影公式可以定义为

(16)

其中，P_S(·)为投影算子，定义作：P_S(·)=(·)₊=max{0, ·}.

利用最速下降法进行迭代求解时，沿着负梯度方向进行搜索，且要求每次迭代目标函数都下降，这种做法有些过于保守.本文考虑非单调梯度下降方法，该方法形式上与最速下降法相同，只是在步长选择上，采用迭代公式为

(17)

其中，y_k=g_k+1－g_k，s_k=m_k+1－m_k.实际计算中，我们采用的迭代形式为

(18)

其中，γ∈(0, 1)且逼近1/2，r_k=τ_k¹/τ_k².当目标函数逼近二次函数时，r_k反映了梯度下降方向与梯度变换方向的余弦变化.

注1：上述迭代算法是为二次规划问题设定的.由于我们的目标函数(5)中，L1正则化项和TV正则化项目的是为了对解施加先验约束，使模拟数据与观测数据作最佳逼近，因此，我们的问题是逼近二次规划问题的，所以可以用上述的非单调梯度下降方法求解.

注2：合适的初始点m₀的选择对于梯度下降法的收敛性也非常重要.对于我们的页岩微纳米孔隙结构成像问题，初始点m₀通过FBP算法(即公式(2))获得.

总结上面的推导过程，可以得到该极小化问题的梯度投影算法步骤如下：

步骤1：初始化：

(1) 选择最大迭代步数k_max，α, β∈(0, 1), 令k=0;

(2) 利用FBP公式(2)获得问题的初始解m₀.

步骤2：取定初始步长τ₀ (求解公式(15)), 利用公式(16)得到迭代点m₁；根据已知的迭代点m₀和m₁，利用公式(18)计算步长τ_k.

步骤3：执行迭代算法：m_k+1=(m_k－τ_kΔJ(m_k))₊，其中：(·)₊=max{0, ·}.

步骤4：进行终止条件判断：达到停机要求则输出，否则令k←k+1，返回第2步继续进行迭代计算.

注3：在该算法中，要求初始值必须满足非负约束条件.为了保证每一步迭代过程中迭代点列的可行性，引入了投影技巧(由公式(·)₊=max{0, ·}保证)，这样算法的收敛性就有了保障.停机准则我们采用的是：‖min(m, g(m))‖≤ε，其中ε>0是一个小的正数.‖min(m, g(m))‖≤ε意味着dist(m, S)足够小，这里dist(·, ·)为距离算子.为了加快收敛速度，需要为方程Lm=d提供一个合适的初始解m₀.不同于常规的梯度下降算法，初始解为给定的常数，本文指出可以利用FBP算法获得解作为初始值m₀.

2 实验结果 2.1 页岩实验

我们考虑一个使用平行X射线束的计算机断层成像问题的实验装置.多能X射线显微层析成像实验是在上海同步辐射装置(SSRF)的BL13W1波束线上进行的.采用16极摆动器装置，在磁场为1.9 T以及磁周期长度为14 cm的条件下，导出了X射线源.其中，储能环在3.5 GeV下工作，电流为230 mA，采用加电方式.X射线源是同步加速器，即在储能环中加速的电子束通过弯曲磁铁系统时发出高频X射线辐射.

在实验过程中，将圆柱形页岩样品安装在旋转台上，在连续旋转过程中以0.167°增量步长旋转，总计180°.X射线能量从10 keV到24 keV之间选取.样品到探测器的距离为10 cm，曝光时间为4 s，透射的X射线被薄闪烁屏吸收，该屏将X射线转换成一定波长的可见光.采用本征像素尺寸为3.3 μm×3.3 μm的光学Peter CCD探测器，通过10倍物镜进行图像采集.实验过程如图 1所示.

2.2 页岩微米CT成像

本研究中，页岩样品取自于2017年中科院在贵州习科1井的页岩取样.它由石英(43%)、长石(12%)、黄铁矿(5%)、白云石(5%)和含伊利石-蒙皂石-绿泥石(35%)的黏土组成.为了进行实验，首先借助切割机将样品切割成小矩形棱镜.然后用砂纸将小棱镜抛光成直径1 mm长度5 mm的小圆柱体，用于多能X射线计算机断层成像实验.在本实验中，我们使用了多个能谱.能量太低时，X射线几乎被页岩样品吸收，不能正确成像，比如能量为10 keV时，一个切片的投影数据如图 3a所示，所有数据经反演计算的成像结果如图 2所示.本文选取能量为18 keV时的投影数据用于反演计算.一个切片的投影数据如图 3b所示.我们对比了常规方法(FBP)和本文提出的正则化方法的计算结果，分别如图 4a、b.很明显，本文提出的方法显著去除了伪影，成像效果更佳清晰.

3 结论与认识

页岩微纳米孔隙结构探测已成为当今非常规油气生产中的热点问题.本文提出了一种非光滑正则化方法来重建页岩微观结构；在实际计算中，发展了一种快速投影梯度下降法.我们的实际数据是在上海同步辐射装置的BL13W1波束线下获得的.

实验数据测试表明，本文提出的方法能够稳定地恢复页岩微观结构，并能提供一系列高质量的CT图像.因此，除了通常使用FBP的商业软件外，本文提出的方法是页岩微纳米孔隙结构X射线CT图像重建的另一种适当选择.在下一步的研究中，我们将基于成像数据进行进一步的处理，比如围绕数据约束的建模方法以及机器学习等智能分析方法对矿物组份百分率、图像分割等展开研究.