0 引言

滑坡作为世界上最具破坏性的地质灾害之一(Petley，2012；Uhlemann et al., 2016)，通常会造成巨大的人员伤亡、财产损失和基础设施破坏(Bird and Bommer, 2004；Huang，2009；Dijkstra et al., 2014；Glendinning et al., 2014；Hearn et al., 2018).例如，由1920年的海原地震引发的黄土滑坡造成了超过10万的人员伤亡(Close and McCormick, 1922)；1963年的意大利Vainot滑坡导致250 m高巨浪穿过了Vajont大坝，最终导致超过2500人丧生，并造成大坝设施的废弃(Voight and Faust, 1992).因此，滑坡的风险防范与灾害防治受到了社会的广泛关注.

滑坡体三维结构是滑坡治理的重要参数，它反映了滑坡滑动面上下介质的物理性质差异，同时这些差异也为沉积层的物理性质、滑动面的三维空间展布提供了重要信息(Heincke et al., 2006；Donohue et al., 2012；Yamakawa et al., 2012)，这些信息有助于我们更好地理解滑坡体的动力学过程，并且采取合适的防灾减灾措施.

迄今为止，滑坡体三维结构的探测工作中应用了许多地球物理学方法，如原位地球物理测量、电阻率层析成像(ERT)以及地震层析成像等.其中，原位地球物理测量包括压力计、倾斜仪、实验室测量等，可准确提供滑坡体的物理参数信息(Petley，2012)，这些原位观测可以直接确定滑坡的基底界面和边坡稳定性分析所需的参数.但是，滑坡体的不稳定性对于钻孔的限制较大，同时降低了测量点的横向分辨率(Jongmans and Garambois, 2007).ERT方法通过测量风化和蚀变的滑坡体介质的电阻率差异(包括颗粒的矿物性质、地下水含量、电解质的性质、孔隙度等)，从而得到滑坡体的二维或者三维电阻率结构(Xu et al., 2016a).然而由于长时间连续观测的难度较大，ERT对滑坡结构的时间变化的研究较少.使用P波和S波的主动震源地震成像通过炸药和布设密集的地震检波器来获得滑坡体高分辨率地震波速度结构以描述滑坡内部特征(Ferrucci et al., 2000).主动震源方法在不稳定滑坡上实施炸药等观测比较危险，另外，该方法获取滑坡结构随时间的变化成本昂贵，使得相关工作并没有大规模展开.

近年来，被动震源成像方法(例如背景噪声成像技术)被广泛应用于探测不同尺度(包括局部、区域、大陆和全球尺度)的地球内部结构(Shapiro et al., 2005；Yao et al., 2006；Yang et al., 2007；Bensen et al., 2008；Zheng et al., 2008；Stehly et al., 2009；Wang et al., 2017；Xie et al., 2018).背景噪声成像方法通过计算两个台站长时间地震噪声记录的互相关来获取它们之间的经验格林函数，再通过层析成像以得到地球内部的速度结构(Trampert and Woodhouse, 1996；Ekström et al., 1997；Ritzwoller and Levshin, 1998；Yoshizawa and Kennett, 2002；Lin et al., 2009).与传统面波成像方法对比，背景噪声成像并不依赖地震的发生，并且更容易得到高频面波信息(Bensen et al., 2007；Prieto et al., 2011).此外，密集分布的台阵有利于提高噪声成像的分辨率(Shapiro et al., 2005).

随着地震流动台站布设越来越便利，利用背景噪声成像技术研究滑坡体结构的工作也开始零星出现，例如Renalier等(2010)利用从噪声互相关函数中提取的1.7~7 Hz面波信号反演了法国Avigononet滑坡浅层100 m的三维剪切波速度结构.然而，由于滑坡体的结构复杂、横向非均匀性大以及高频面波的快速衰减，从互相关函数中提取高频面波存在一定难度，因此在滑坡上的噪声成像工作较少.

在本文中，我们对四川理县西山村滑坡上布设的38个流动地震台站记录的三分量地震噪声进行互相关计算，提取了滑坡上的高频面波经验格林函数.同时我们还测试了不同旋转方式对互相关函数计算的影响，并通过聚束分析方法获得了滑坡上1~5 Hz的噪声源的位置，我们得到的高频面波经验格林函数为滑坡上Rayleigh波和Love波频散曲线的提取以及横波速度反演提供了基础.

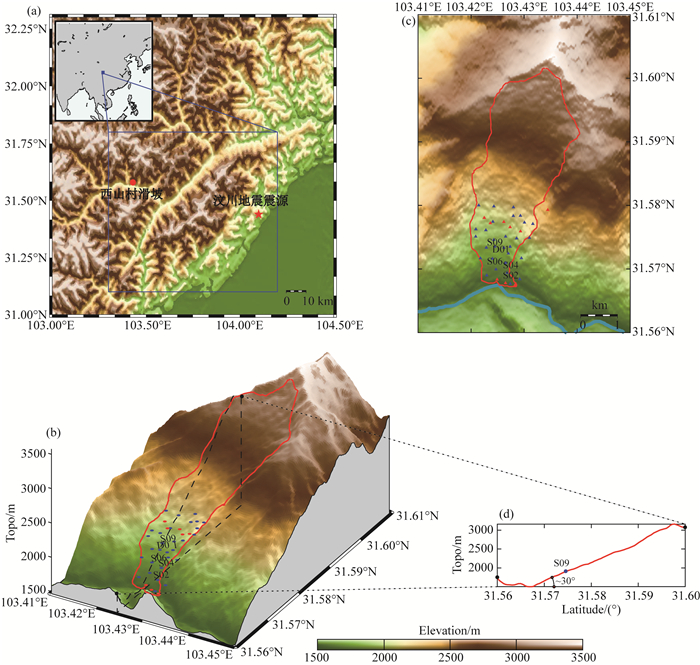
1 数据与预处理

西山村滑坡位于地震活动性强的龙门山脉断裂带(邓起东等，1994)，离512汶川地震震中约为60 km.该滑坡是一个大型堆积层滑坡，底部和顶部的海拔高度差约为2 km，东西向跨度约1 km.野外地质调查发现滑坡体的厚度在30~70 m之间，其体积超过了8千万方(盛敏汉等，2018).滑坡大体朝南北向延伸，滑动方向约为201°，滑坡倾角约为25° ~ 40°，平均倾角约30°(图 1).

为了研究滑坡体的三维速度结构以及监测滑坡体上由于变形等原因造成的微震，我们从2016年12月到2017年3月在西山村滑坡上布设了38个地震流动台站(图 1b)，平均台间距约为200 m，最小的台间距约为100 m，最大的台间距约为3 km.其中蓝色三角形为30个Guralp 40TD型的短周期仪器，频带范围为0.5~100 Hz；红色三角形为8个Guralp 3ESPCDE型的宽频带仪器，频带范为0.03~100 Hz.采样率均为100 Hz.

由于连续波形中的噪声信号对于互相关计算比较重要，因此我们首先分析了滑坡体上记录到的地震背景噪声特征.图 2a中的红色波形展示了2016年12月1日S09台站的原始波形记录，其中振幅较大的事件为周边的天然地震信号以及滑坡上动物以及人类活动等产生的人文地震信号.通常，10 Hz以上的高频信号为道路上的交通噪音以及滑坡上高频事件信号(Lak et al., 2011；盛敏汉等，2018).另外，由于滑坡体沉积层的厚度约为50 m，其横波速度约为400 m·s^-1，10 Hz以上的信号很难约束滑坡沉积层与基岩的分界面(Haney and Tsai, 2017).因此，本文主要研究频率10 Hz以下的地震背景噪声信号.图 2a中的蓝色波形展示了原始波形低通滤波10 Hz后的结果，可以发现大部分的事件信号被压制了.图 2b为2a原始波形对应的频谱图，我们能清楚地看到频率在1~10 Hz以及10~50 Hz两个能量较大的信号.我们从原始波形中截取了持续时间2500 s比较平静的波形(图 2c)，并且对该段信号进行了傅里叶变换到频率域(图 2d)，发现在该段信号的主频为1~10 Hz，这说明滑坡体上的地震背景噪声主要集中在1~10 Hz.

此外，one-bit时间域归一化方法能够在一定程度上消除连续波形里的事件信号的影响(Bensen et al., 2007)，图 3中的蓝色和红色波形分别展示了S09的原始波形进行one-bit归一化前后对应的频谱图，我们可以清楚地看到one-bit归一化对于10 Hz以上的信号有较强的压制作用，也从另一方面说明10 Hz以上的信号主要为事件信号.这些结果都表明原始波形的频谱在1~10 Hz的峰值对应的信号主要为某一持续的噪声信号而非事件信号，适合我们在该频带内通过噪声互相关提取面波信号.

2 高频面波信号的提取

互相关计算前的数据处理流程对于互相关结果有较大的影响.我们的数据处理流程与Bensen(2007)文章提到的数据处理方法几乎一致，包括对各个台站每天的数据进行重采样、去仪器响应、去均值、去趋势以及带通滤波处理，随后进行时间域和频率域的归一化处理，最后通过计算波形间的互相关并且叠加得到互相关函数.而为了在滑坡上得到可靠的互相关函数，首先我们需要选取合适的数据处理方式.

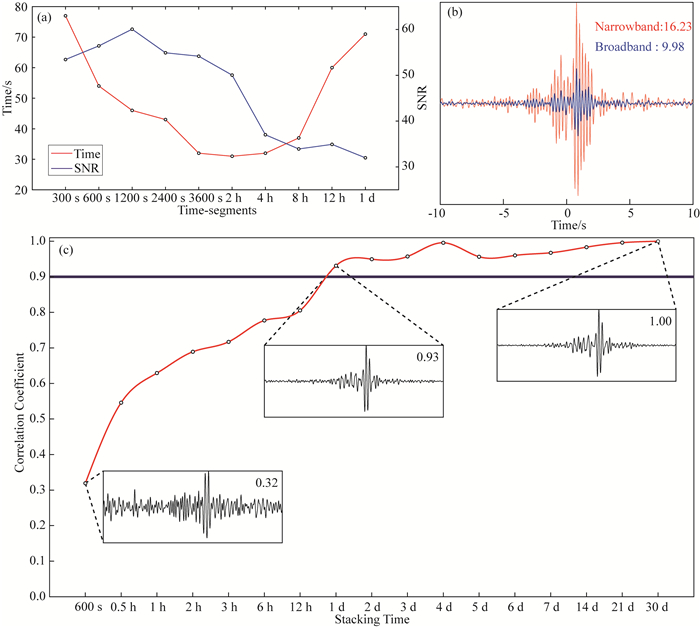
首先是互相关函数计算所需数据的裁剪时间长度的影响，不同的裁剪时间长度决定了计算的互相关函数不同的叠加次数以及运算时间.由于密集台站的互相关计算量较大，选择合适的裁剪时间长度可以有效地减少互相关计算时间并且提高互相关函数的信噪比.此前的一些背景噪声成像工作采用的裁剪时间长度为1天或者1小时(Xu et al., 2016b；Wang et al., 2017).这里我们测试了裁剪时间长度对于信噪比以及运算时间的影响.针对时间长度相同的地震背景噪声数据，图 4a中的红色以及蓝色折线分别表示采用不同的裁剪时间长度得到的互相关函数所需的运算时间以及信噪比.我们可以看出随着裁减时间的减小，得到的互相关函数信噪比有着增加的趋势，这可能是由于随着裁减时间的减小对应的叠加次数增加；而互相关函数的计算时间随着裁减时间的减小先减小后增加，这是由于裁剪时间的减小一方面导致了互相关的总计算量减小而使得计算时间减小，另一方面导致了程序的重复计算次数增加而使得程序运行时间增加，因此总体上的运算时间有先减小后增大的趋势.我们综合考虑互相关的运算时间以及信噪比，认为1200~3600 s是计算互相关合适的裁减时间长度.

其次是互相关函数处理过程中的滤波处理方式.互相关计算时的滤波处理总的来讲可以分为两个部分：(1)去除原始波形的仪器响应；(2)带通滤波处理.其中去仪器响应是用来压制极低和极高频信号以及消除仪器的不规则响应.此前研究中的带通滤波处理通常则是计算互相关之前首先滤波到一个比较宽的频带，互相关计算之后再滤波到研究所需的多个比较窄的频带(Shapiro et al., 2005；Yao et al., 2006；Yang et al., 2007；Bensen et al., 2008；Lin et al., 2008).这样做虽然比起多次滤波后再进行互相关计算能够减少互相关计算量，但是对于频带内较高频的信号的信噪比却有一定的影响.如图 4b蓝色和红色波形分别为台站S02和S06先进行0.1~10 Hz的带通滤波后进行互相关计算再对互相关函数滤波到1~5 Hz以及直接窄带滤波到1~5 Hz进行互相关计算得到的互相关结果，先带通滤波再窄带滤波对应的信噪比小于直接窄带滤波的信噪比，因此直接进行窄带滤波再进行互相关计算能够在一定程度上提高互相关函数的波形质量.

此外，叠加的时间长度对于互相关函数质量影响也比较大，一般情况下通过长时间的互相关函数的叠加能够有效地增加信噪比，然而实际上在叠加时间长度达到一定时间后互相关函数的信噪比增加的幅度会变得很小从而达到收敛.为了研究滑坡上互相关函数的收敛情况，我们选取了S04和S09台站对计算了他们之间一个月的互相关函数并且得到了一个月的叠加结果，随后分别计算了不同叠加时间长度的互相关函数与一个月的叠加结果间的互相关系数(图 4c).从图中我们可以发现叠加时间为600 s的互相关函数与一个月的结果间的互相关系数较小(0.32)，而随着叠加时间的增加互相关系数不断增大，在叠加时间约为1天时超过了0.9(0.93)，超过1天后互相关函数接近收敛；从波形结果的对比我们也能发现600 s的叠加结果信噪比较低，而1天的叠加结果与1个月的叠加结果几乎一致，并且有很明显的面波信号.这些结果说明在滑坡上1天的叠加时间就能够得到比较可靠的互相关函数，而叠加更长时间对互相关函数的信噪比没有明显的提升.

最后我们需要考虑的是滑坡的地形因素.由于研究区域的滑坡存在约为30°的倾角，而面波在滑坡上沿着滑坡面传播时地形的影响不能被忽略(Ping et al., 2018)，因此我们在计算互相关时需要将他们旋转到同一平面上.为此我们重新定义了在滑坡面上的三个分量R、T、V，其中R为台站对在滑坡面上的径向分量，T为台站对在滑坡面上的切向分量，V为垂直于滑坡面的分量.为了减少互相关计算量，我们首先对台站间的E、N、Z三个分量进行两两互相关计算得到了九个不同分量的互相关函数(EE，EN，EZ，NE，NN，NZ，ZE，ZN，ZZ)，然后类比Lin等(2008)的方法，采用以下公式将他们旋转到滑坡面上的RR，RT，RV，TR，TT，TV，VR，VT，VV分量：

其中α和θ分别为台站间的水平方位角以及滑坡倾角.对于台站间的水平方位角，我们可以通过台站的经纬度计算获得.而滑坡倾角的确定方式主要有两种，一种是简单的将滑坡体看成一个倾斜30°的斜面(图 1d)；另一种则是通过三维地形数据获取台间真实的高程差Δh，并且利用台站间的经纬度获得台站间的水平距离d，然后使用公式

如果对滑坡上的坐标进行旋转，会涉及到真实的台间距与它们在旋转后的平面上的台间距存在误差的问题.在进行频散提取的时候，对视速度造成直接影响的就是台间距，因此我们需要对旋转的方式进行测试以保证旋转之后的误差不会过大，这里我们计算了直接将滑坡看作一个30°的斜面以及使用三维地形数据进行旋转前后台站间距的误差值，如图 5所示，直接把滑坡当成一个平面进行旋转得到的台间距误差相对较大(图 5a)，而使用三维地形数据进行旋转得到的台间距误差主要在5%以内(图 5b)，因此我们在对台站位置进行旋转时采取使用三维地形数据进行旋转的方式.

进行了以上这些测试后我们确定了合适的数据处理方式，并且得到了九个不同分量的互相关函数.图 6展示了D01与S09台站九个不同分量的互相关函数结果，其中RR、TT、VV分量都有很明显的面波信号，VV以及TT分量分别包含了Rayleigh波以及Love波信息，RR分量既包含Rayleigh波也包含Love波信息(Lin et al., 2008).

图 7展示了VV和TT分量的互相关函数剖面图，从图中我们能发现以下三个特点.第一，VV和TT的互相关函数正负半轴不对称，体现了研究区域较强的噪声源方向性；第二，两者的视速度不同，VV主要对应Rayleigh波能量，TT分量主要对应Love波能量，相较之下VV对应的面波视速度约为700 m·s^-1，TT约为400 m·s^-1，造成VV分量信号速度更高的原因可能是由于滑坡浅层比较复杂的速度结构(Moro and Ferigo, 2011)；第三，Love波信号相对于Rayleigh波信号信噪比更高，如图 7a, b，VV分量的互相关函数除了Rayleigh波信号之外部分台站还会出现一些多余的噪声信号产生(图中红色虚线框所示)，TT分量则没有相对应的噪声信号，另外Love波信号相对于Rayleigh波信号振幅更大(图 7c).

由于前人的研究很少涉及到对垂直分量的旋转，而一般仪器的垂直分量比水平分量信噪比更高，因此前人的研究中主要是利用垂直分量的互相关函数研究Rayleigh面波信号，利用背景噪声研究Love波的研究也就相对较少.而在本文的研究中，TT分量有着比VV分量更高的信噪比，因此利用TT分量包含的Love波信息对SH波速进行约束能够在一定程度上提高反演的准确性(Li et al., 2010).

最后，我们从38个台站间共703条互相关函数中提取了129条信噪比高于30的Love波格林函数，以及108条信噪比高于15的Rayleigh波格林函数.其中，Love波的视速度约为400 m·s^-1，而Rayleigh波的视速度约为700 m·s^-1.并且，互相关函数的信噪比随着台间距的增加而降低，如图 8中，大于1 km的台站对互相关函数中仅有3条信噪比较高.

3 噪声源分析

通常情况下，均匀分布的噪声源的互相关函数正负半轴能量对称(Xu et al., 2016b)，而正负半轴能量不对称的互相关函数可能是由于背景噪声分布不均.图 8中互相关函数负半轴的能量表示从滑坡底部传向滑坡顶部，正半轴则相反(Lin et al., 2013).滑坡上的互相关函数负半轴能量较大，表明该区域1~5 Hz的背景噪声大部分可能来自滑坡底部，这种不均匀分布的噪声对面波信号的速度影响较大(Tsai，2009).

噪声成像的理论基础是基于弥散波长以及均匀分布的噪声源(Weaver and Lobkis, 2001；Snieder，2004；Roux et al., 2005)，具有较强方向性的噪声源会在一定程度上造成频散曲线提取的误差(Yao and Van Der Hilst，2009).噪声源的分布信息是对速度进行校正获取精确的面波频散的重要基础(Wang et al., 2016)，因此对于滑坡上噪声源进行定位对以后在滑坡体三维速度结构成像非常重要.

首先我们使用聚束分析(beamforming)(Gerstoft et al., 2006)计算了信噪比高于10的互相关函数1~5 Hz的噪声源分布(图 9a)，发现噪声源主要集中在慢度约2.8 s·km^-1(速度约360 m·s^-1)、方位角约为170°附近，聚束分析的结果说明滑坡上1~5 Hz的主要噪声来源来自滑坡体的南部.此外，该噪声源能量密集，说明该噪声源可能是一个比较集中的源.由于高频面波衰减较快而且交通噪声主要在10 Hz以上(Lak et al., 2011)，因此滑坡上1~5 Hz的噪声可能是来自于距离滑坡体南部约为50 m的杂谷脑河(如图 9b).

此前的研究表明，对于河流噪声的频谱与沉积层的Q值相关(Tsai et al., 2012).这里我们基于Tsai等(2012)文章中的方程(7)对杂谷脑河产生的噪声频谱进行了计算，结果表明河流噪声的频谱与观察到的真实噪声数据的频谱(图 9c)比较一致.虽然在滑坡体上1~5 Hz的背景噪声存在许多其他来源(例如人类动物活动等)，但是主要的噪声能量很有可能来自于杂谷脑河.在以后的工作中，我们将利用该噪声源信息对频散曲线进行校正以提高速度成像的准确度.

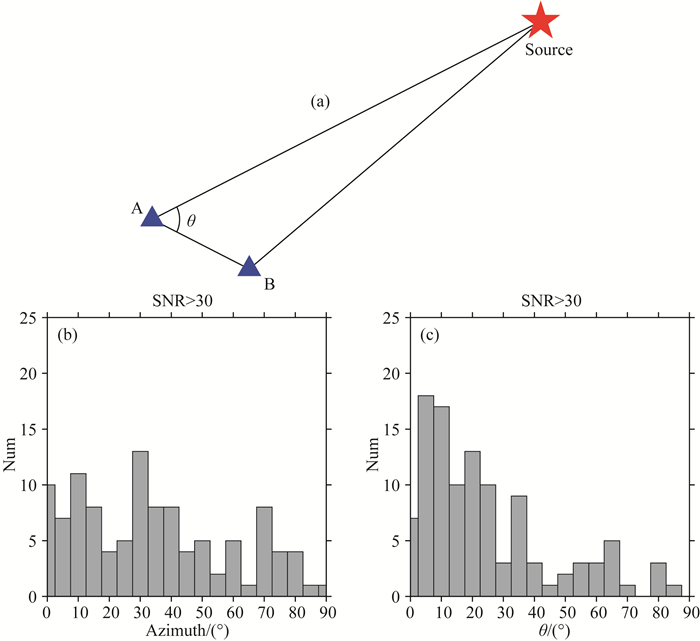
4 讨论 4.1 噪声源对面波信号的影响

对于区域存在的持续噪声，台站对与噪声源的相对位置在一定程度上影响着互相关函数的信噪比(Wang et al., 2018).如果噪声源在台站对的连线(或延长线)上，一般会比较容易得到较高信噪比的互相关函数(如图 10a中θ=0的情况)；如果噪声源距离两个台距离比较接近，那么很难得到较好的互相关函数.因此我们可以通过观察如图 10a所示的θ角大小来大致估计噪声源的分布.

图 10b展示了信噪比大于30的互相关函数的台站对间相对正北向的方位角的分布直方图，可以发现直方图分布比较分散，只有少数的方位角小于45°.而如果我们考虑用上一节得到的噪声源信息对图 10a中的θ角进行计算，得到的直方图结果如图 10c所示，可以发现对于重新计算的角度大部分互相关函数分布在小于25°的范围内.这一分布特点与区域存在的持续噪声对应较好，也从侧面证实了噪声源定位的可靠性.

此外，噪声源对互相关函数中的面波视速度也有较大影响，在得到的TT分量的互相关函数中，Love波视速度主要集中在300~700 m·s^-1，然而部分互相关函数的速度较大，甚至达到了2 km·s^-1.为了研究Love波速度存在较大差异的原因，我们选取了两个方位不同的测线k1与k2，其中k1位于滑坡体内部，而k2位于滑坡体边缘(图 11).k1与k2两个测线各自的台站间互相关函数速度比较一致，其中k1测线均为约400 m·s^-1，k2测线约2000 m·s^-1，这可能是由于k1测线内的台站对与噪声源的连线对应的θ较小而k2测线内的台站对与噪声源的连线对应的θ较大.这种速度随θ的变化规律与图 9b所示的噪声源对应的传播路径对应较好，同时也证实了对互相关函数进行速度校正的重要性.

4.2信号提取频带分析

不同频率的面波信号对应不同的敏感深度(Lin et al., 2008)，因此信号的提取频带也影响着速度结构反演的深度.通过噪声互相关提取面波信号的频带不仅与地震仪器的响应相关，而且也受到台站的分布与噪声源信息的影响.此前我们已经证明了地震仪所记录到的持续噪声信号在1~10 Hz，并且主要来自于滑坡体南部的杂谷脑河.然而，我们提取的信噪比较高的互相关函数主要在1~5 Hz内，这一点可能与高频面波衰减较快有关(Johnston and Toksoz, 1981；刘建华等，2004).

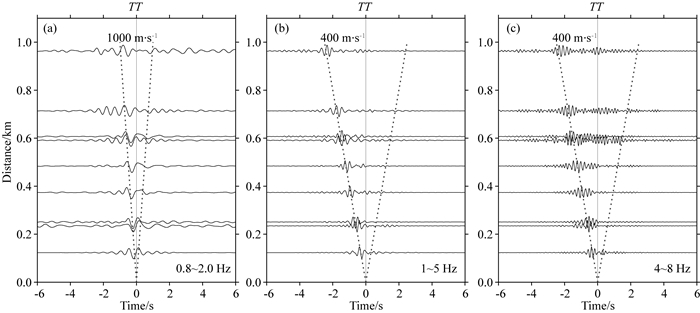
为了研究在滑坡上是否能够提取更宽频带的面波信号，我们在滑坡上选择了一个与噪声源连线一致的南北方向的测线计算互相关函数，使用的初次滤波频带范围为0.5~10 Hz，随后将它们分别滤波到0.8~2 Hz，1~5 Hz以及4~8 Hz.我们发现在这些频带范围内均能得到比较好的Love波信号(如图 12).在得到的三个不同频带互相关函数中，1~5 Hz的信噪比较高，速度约为400 m·s^-1；0.8~2 Hz的信号较弱，速度大小约为1000 m·s^-1，相比与400 m·s^-1有较大幅度的增加，推测可能是由于面波的频散特征，不过这一点还有待在后续的工作中证实；4~8 Hz的信号信噪比较低，但与1~5 Hz的信号速度较为接近，可能是由于在此高频区间频带较窄，导致面波速度变化并不会太大.虽然相比于1~5 Hz其他两个频带的互相关函数信号信噪比较低，但是这也说明部分台站对能够提取到更宽频带的信号.

这里我们讨论了提取0.8~8 Hz信号的可行性，后续的成像工作我们会考虑在更宽的频带中开展，以获得更多深度上的约束.不过由于低于1 Hz以及高于5 Hz互相关函数的信号信噪比较低，在对信号进行处理的时候需要尤为注意.

5 结论

在本文中，我们对布设在西山村滑坡上的38个地震台的ENZ三个分量进行了两两互相关计算，并且通过旋转得到了滑坡上1~5 Hz九个不同分量(RR，RT，RT，TR，TT，TV，VR，VT，以及VV)的互相关函数.在九个分量中，包含Love波信息的TT分量和包含Rayleigh波信号的VV分量的信噪比较高，其中Love波视速度约为400 m·s^-1，而Rayleigh波的视速度约为700 m·s^-1，造成1~5 Hz Rayleigh波速度大于Love波的原因可能是滑坡浅层较为复杂的速度结构.另外，滑坡上互相关函数的收敛测试表明，1天的叠加时间就能够得到较稳定的互相关函数，该短时间收敛的特点有利于对滑坡体结构随时间的变化进行研究.此外，由于1~5 Hz的互相关函数存在一定噪声源方向性的影响，我们首先根据聚束分析得到了在该频带下约400 m·s^-1的能量对应的噪声主要来自于方位角约为170°的方向；同时我们对杂谷脑河产生的噪声频谱进行了理论计算，发现河流噪声与地震仪记录到的持续噪声的频谱比较接近，说明滑坡上1~5 Hz噪声很有可能来自于滑坡体南部的杂谷脑河.

本文的工作证实了通过噪声互相关可以得到滑坡上的高频Love波和Rayleigh波信号，通过合理的数据预处理(旋转、裁剪、直接滤波等)能够较好地提高互相关函数的信噪比，噪声源分析得到的噪声源信息确保了后续在滑坡上进行的噪声成像反演工作的准确性.