2. 中国自然资源航空物探遥感中心, 北京 100083
2. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China
如何有效快速地识别岩体分布及属性特征是重、磁解释的重要研究内容.重磁异常在平面上具有较高的分辨率, 对地下岩性、断裂构造的平面分布有较好的识别能力.重磁异常分别反映了地质体的密度和磁性差异特征, 故可以通过研究重磁异常的相关性来定位地质体以及识别其岩石物性特征.Garland(1951)提出了基于重、磁位泊松定理的对应分析方法, 用于确定单个地质体的泊松比(磁化强度与剩余密度比值), 从而推测地质体的岩性特征.Cordell和Taylor(1971)将该方法应用于北极地区地质体磁化方向的确定.Chandler等(1981)基于重、磁位泊松定理提出采用滑动窗口计算重、磁异常的皮尔逊相关系数(Correlation Coefficient,CC),得到了一组相关系数值,该方法在Michigan and Lake City地区获得了良好的应用效果.之后相继有研究者采用该方法开展了相关应用研究工作(Von Frese et al., 1982, 1997a, b ; Chandler and Malek, 1991;刘沈衡, 1993; Price and Dransfield, 1994; Mendonça, 2004;曾昭发等, 2006; Mendonça and Meguid, 2008;刘彦华等, 2008; De Ritis et al., 2010;范正国等, 2012).
基于重、磁位泊松定理的重、磁相关性分析是采用滑动窗口来计算化极磁力异常(RTP)与重力异常一阶垂向导数之间的皮尔逊相关系数, 其反映了给定窗口重磁异常的线性相关程度和重磁异常的同源程度.如果皮尔逊相关系数绝对值趋于1, 说明重磁异常高相关性, 两者同源或者离场源较远.如果皮尔逊相关系数趋于0, 则说明两者相关性差或不相关, 两者可能不同源.皮尔逊相关系数只是用来衡量两个变量线性相关程度的指标, 必须先确认要研究的两个变量是线性相关的才能使用皮尔逊相关系数, 因此该方法有比较强的约束使用条件.值得说明的是如果两个变量的相关系数很大,严格来讲也不能说明两者线性相关, 很可能是离群点导致相关系数变大.在重磁异常应用方面领域, 其缺点是在场源体外皮尔逊相关系数|CC|趋于1, 这种在场源体外的强相关性极大干扰了重磁异常解释, 且皮尔逊相关系数不能提供重磁场本身的信息.
基于以上分析, 考虑到重、磁异常垂向导数的零值线可以近似圈定场源体的平面范围, 而相关系数能够反映两者的重磁同源特征, 提出了基于相关系数(CC)和垂向导数(Vertical Derivative, VDR)的重磁相关分析方法, 给出了一个新的重磁场源平面位置及属性判别参数.该方法计算的判别参数能反映场源的平面分布范围, 在场源范围内取得极值, 而在场源体外则趋于或等于零, 克服了在场源外相关系数|CC|趋于1的缺点, 有效地减少了解释干扰, 使得重磁同源地质体易于识别.为了验证该方法的正确性和有效性, 本文进行了两组同源和两组不同源模型实验, 以及不同窗口模型实验, 并开展了南海珍贝-黄岩海山链地区的实际重磁资料的处理工作, 进一步说明了该方法具有良好的场源位置-属性判别实际应用效果.
1 方法由重磁位泊松定理可知, 在重磁同源的情况下, 磁位与重力位以及各阶导数之间呈线性关系, 重磁之间具有相似性(Baranov, 1957), 因此可引入线性相关分析方法来刻画两者之间的相似程度.除了皮尔逊相关系数, 余弦相似度也可以衡量两个变量之间相似程度, 则皮尔逊相关系数和余弦相似度均可以被用来进行重磁场源的相关分析研究, 但它们适用于不同的情况, 下文将详细论述.从本质上讲, 皮尔逊相关系数就是数据中心化后的余弦相似度, 它们适用于不同的数据分析模型.但两者均是从方向上考虑两个变量之间的相似性, 而不是它们幅值大小.因此, 本文将皮尔逊相关系数和余弦相似度均称之为相关系数.
重磁异常相关系数可采用滑动矩形窗口进行计算.将窗口内的异常值可以看作是n维向量(n等于窗口内点数), 即可以利用相关系数的理论公式进行计算, 每个窗口计算值代表了重力异常与磁力异常之间的相似程度.相关系数的取值在[-1, 1]之间, 当重磁异常的线性关系增强时, 相关系数趋于1(正相关)或-1(负相关), 如果重磁异常的相关系数等于0,则表明它们之间不存在线性相关关系.相关系数与重磁异常的幅值无关, 不能反映重磁场强的信息.
通过以上分析可得, 相关系数的计算结果均只能反映高磁高密度和低磁低密度(趋于+1)、高磁低密度和低磁高密度(趋于-1), 而且在场源外其绝对值|CC|趋于1, 因此相关系数不能很好地反映场源的位置及其场强的信息.考虑到垂向导数(一阶或二阶)是有效的场源位置识别方法, 在高密度、高磁性的区域形成正值区, 而在低密度、低磁性或无磁性区域形成负值区, 远离场源区域则趋于零值.因此结合相似度和垂向导数各自优势, 提出了一种新的重磁场源位置及属性判别参数GMCP, 主要计算过程如下:
(1) 重力异常垂向导数归一化(NVDRg)计算

|
(1) |
(2) 化极磁力异常归一化(NRTP)计算

|
(2) |
(3) 重磁异常相关系数(CC)计算

|
(3) |
其中, cov为协方差; D为均方差; μVDRg为重力垂向一阶导数均值; μRTP为化极磁力异常均值.
(4) 重磁场源判别参数(GMCP)计算

|
(4) |
其中, max为取极大值;sign为取±号.threshold为重磁同源相似度阈值, 可根据实际情况和研究需要取值.例如threshold取0.5, 即当阈值threshold大于0.5时, 认为重磁异常同源, 当阈值threshold小于0.5时, 认为重磁异常不同源.实际计算判别参数GMCP中, 由于重磁垂向导数在场源体外是快速趋于零值, 因此阈值threshold也可取较小的值.计算中归一化处理是为了消除重磁不同量纲以及幅值的影响.判别参数GMCP参数绝对值大小由重磁异常共同决定, 具有相同的权重.GMCP数值的大小分布反映了重磁异常的强度和场源的分布规模.而GMCP正负号则反映了重磁场源的正负相关性.GMCP>0时为正相关, 代表了该区域存在高磁高密度或低磁低密度的重、磁场源; GMCP<0时为负相关, 代表了该区域存在高磁低密度或低磁高密度的重、磁场源; GMCP等于零值, 则表示无重磁源区.因此GMCP值有效地利用了重磁位场垂向导数所提供的地质体边缘特征, 又融合了重、磁相似度的属性特征, 较之单一的相似系数或相关系数具有更好的识别性能和提供了更多的场源信息.另外, 该方法也适用重力异常垂向二阶导数和化极磁力异常垂向一阶导数之间的计算.
由于重磁异常普遍存在背景场, 则在进行相关分析时, 需要根据重磁异常类型选择.传统的相关系数计算使滑动窗口内的重磁异常均值为零.但是如果重磁数据已经进行了位场分离, 获得了剩余异常, 或者使用重力异常垂向二阶导数与化极磁异常垂向一阶导数, 则取窗口均值则不再适用.由于重力数据已经进行了垂向导数计算, 理论上讲不受背景场的影响, μVDRg均值应取零.但化极磁异常仍然存在背景场.但如果使用重力异常垂向二阶导数和化极磁力异常垂向一阶导数则均不受背景场的影响.因此将相关系数计算中μRTP均值的选择分为三种情况, 即:(1)μRTP取窗口的平均值.适用于化极磁异常存在区域场的情况, 相当于对化极磁异常做了一次滑动平均.(2)μRTP取零.适用于对化极磁力异常进行了场分离或者使用重力异常垂向二阶导数和化极磁力异常垂向一阶导数(垂向导数消除了背景场的影响)的情况.(3)μRTP取全区的平均值.适用化极磁力异常存在背景场影响的情况.
2 理论模型实验设置了四组不同的模型以验证本文提出方法的有效性和稳定性.每组均设置了2~5个直立长方体, 为不同尺寸大小及不同密度-磁化强度组合.分别对四组复杂模型的重力垂向一阶导数和磁力异常进行了正演计算, 前两组模型均进行了无干扰实验、加入5%的随机干扰以及10%的随机干扰实验.后两组实验是为了验证该方法对重磁不同源的效果, 分别为完全不同源和部分同源.另外考虑到滑动窗口对计算结果的影响, 对第三组模型进行相关实验.实验中μVDRg均值取零, 化极磁异常(RTP)由正演计算的垂直磁化磁异常(ΔT⊥)代替, 但为了叙述方便并与前述公式统一, 仍采用RTP一词进行描述.
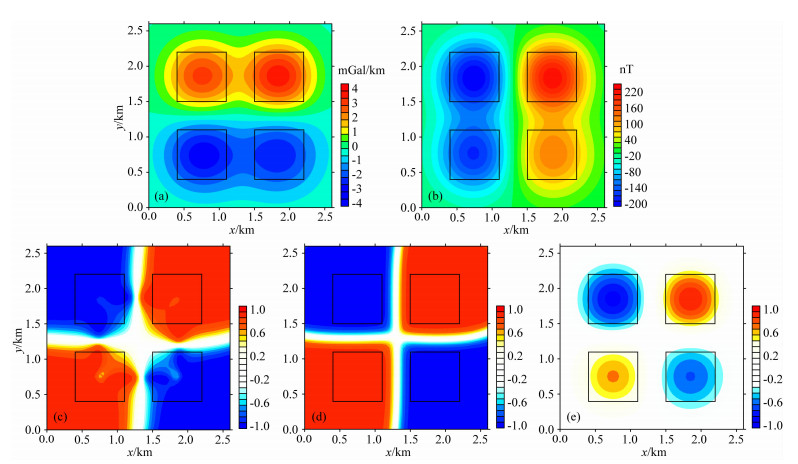
2.1 重磁同源模型1实验该组模型大小相同, 埋深不同、物性参数不同的四个直立长方体(表 1).其中图 1a, 1b分别无随机干扰重磁异常, 图 2a, 2b分别为含5%随机干扰的重磁异常, 图 3a, 3b分别为含10%随机干扰的重磁异常.当重力当重磁数据中不含随机干扰且μRTP取窗口平均值时, 相关系数基本上能够识别模型物性相关程度, 但是有小部分区域出现了畸变(图 1c), 而μRTP取零值时, 相关系数能够准确识别(图 1d).而当数据中代入5%以及10%的干扰且μRTP取窗口平均值时, 相关系数在模型范围内变化较大(图 2c, 2c), 已不能准确识别模型物性的相关程度, 而μRTP取零值时, 相关系数在模型范围内均趋向于1或-1(图 2d, 图 3d), 同样显示结果准确、稳定且受干扰影响小.同时也可以看到, 当μRTP不同的取值, 相关系数在模型区域外重磁均具有很高的相关性, 在实际中不利于解释.但依据本文提出的重磁相关分析方法, 判别参数GMCP能够较好地反映场源分布及其重磁相关性特征(图 1e, 2e, 3e).在场源体的范围内GMCP值为极值区, 而在场源体外为零值区, 能够比较容易地定位场源, 而GMCP值的正负则代表重磁场源的正负相关性.
|
|
表 1 模型1参数 Table 1 The parameters of synthetic model 1 |
|
图 1 模型1无随机干扰实验结果 (a) VDRg; (b) ΔT⊥; (c) CC-μRTP取窗口均值; (d) CC-μRTP取零; (e) GMCP. Fig. 1 Test results of synthetic models 1 without any noise |

|
图 2 模型1含5%随机干扰实验结果 (a) VDRg; (b) ΔT⊥; (c) CC-μRTP取窗口均值; (d) CC-μRTP取零; (e) GMCP. Fig. 2 Test results of synthetic models 1 with 5% random noise |

|
图 3 模型1含10%随机干扰实验结果 (a) VDRg; (b) ΔT⊥; (c) CC-μRTP取窗口均值; (d) CC-μRTP取零; (e) GMCP. Fig. 3 Test results of synthetic models 1 with 10% random noise |
模型2由五个大小不同, 埋深不相同、物性参数不同的直立长方体组成(表 2), 其中图 4a, 4b分别为无随机干扰重磁异常, 图 5a, 5b为含5%随机干扰的重磁异常, 6a, 6b为含10%随机干扰的重磁异常.当重磁数据中不含随机干扰且μRTP取窗口平均值时, 在模型范围内部分区域相关系数值不能正确地识别右侧模型物性相关程度(Fig. 4c), 而μRTP取零值时, 相关系数则能够准确识别(Fig. 4d).而当数据中代入5%以及10%的干扰且μRTP取窗口平均值时, 相关系数值则识别效果较差(Fig. 5c, 6c), 而μRTP取零值时, 相关系数则能较好的反映重磁之间的相关性(Fig. 5d, 6d), 受干扰影响较小.该组与模型1实验的结果基本上类似, 重磁场源位置及属性判别参数GMCP能够较好的反映了场源的分布及其重磁相关性(Fig. 4e, 5e, 6e).
|
|
表 2 模型2参数 Table 2 Parameters of synthetic model 2 |

|
图 4 模型2无随机干扰实验结果 (a) VDRg; (b) ΔT⊥; (c) CC-μRTP取窗口均值; (d) CC-μRTP取零; (e) GMCP. Fig. 4 Test results of synthetic models 2 without any noise |

|
图 5 模型2含5%随机干扰实验结果 (a) VDRg; (b) ΔT⊥; (c) CC-μRTP取窗口均值; (d) CC-μRTP取零; (e) GMCP. Fig. 5 Test results of synthetic models 2 with 5% random noise |

|
图 6 模型2含10%随机干扰实验结果 (a) VDRg; (b) ΔT⊥; (c) CC-μRTP取窗口均值; (d) CC-μRTP取零; (e) GMCP. Fig. 6 Test results of synthetic models 2 with 10% random noise |
以上两组重磁同源模型实验结果表明, 相关系数在场源区外也显示出高的相关性, 其结果很不利于地质解释.而依据本文提出的重磁场源位置及属性判别方法, 当判别参数GMCP>0时, 表示为正相关, 场源为高磁高密度或低磁低密度, 当判别参数GMCP<0, 表示为负相关, 场源为高磁低密度或低磁高密度, 可以看出计算结果与模型一致.该判别参数GMCP值既能表示重磁场源之间的相关性, 又能圈定场源位置, 比传统相关系数均更直观, 易于解释.
2.3 重磁部分同源模型3实验模型3由两个大小相同, 埋深相同的直立长方体组成(表 3), 为部分同源的重磁异常模型.其中图 7a, 7b分别为重磁异常.可以看到μRTP取窗口平均值时, 在模型范围内部分区域相关系数值不能正确地识别模型物性相关程度(Fig. 7c), 而且模型区域外干扰很大.当μRTP取零值时, 相关系数则能够准确识别模型同源部分, 但不同源区域外效果不佳(Fig. 7d).但从GMCP参数却较好的反映了模型同源部分的分布及其重磁相关性, 图面易于解释, 较好地反映了场源的分布范围, 对不同源模型区域也有一定的指示意义(Fig. 7e).
|
|
表 3 模型3参数 Table 3 Parameters of synthetic model 3 |

|
图 7 模型3实验结果 (a) VDRg; (b) ΔT⊥; (c) CC-μRTP取窗口均值; (d) CC-μRTP取零; (e) GMCP. Fig. 7 Test results of synthetic models 3 |
模型4由两个大小相同, 埋深相同的直立长方体组成(表 4), 为完全不同源的重磁异常模型.其中图 8a, 8b分别为重磁异常.可以看到μRTP取窗口平均值时, 相关系数几乎不能提供有关场源的有效信息(Fig. 8c).当μRTP取零值时, 相关系数显示存在两个负相关的区域, 且在模型区域外有较强的相关性, 识别效果不佳(Fig. 8d), 这与基于重磁相似性的前提有关.但GMCP参数却清晰的识别出两个负相关场源的分布范围(Fig. 8e), 这与高磁低密度或低磁高密度的模型参数是相吻合的.
|
|
表 4 模型4参数 Table 4 Parameters of synthetic model 4 |

|
图 8 模型4实验结果 (a) VDRg; (b) ΔT⊥; (c) CC-μRTP取窗口均值; (d) CC-μRTP取零; (e) GMCP. Fig. 8 Test results of synthetic models 4 |
考虑到窗口大小对计算结果的影响, 以部分同源模型3为例, 对不同窗口大小进行了20组实验.从图 9可以得出, 随着计算窗口的增大, GMCP幅值逐渐减小, 但其极值区域仍然较好地指示了场源范围.为了解GMCP的变化特性, 沿对角线方向做了一条剖面(图 10.位置见图 9a中蓝线), 可以看到随着窗口尺寸增大, GMCP幅值逐渐降低, 但不同窗口在GMCP≈0.2值附近比较稳定, 且能较好的指示场源体范围.如果以GMCP>0.5为场源识别强度, 在该模型中认为取0.8 km×0.8 km窗口比较合适(约等于形体长度的一半).结合野外实际测量原则, 即最少要有3个测点控制地质体的范围, 由此推荐选取窗口的大小为不超过拟探测地质体长度的1/2为宜.

|
图 9 模型3不同窗口大小实验结果 Fig. 9 Test results of synthetic models 3 using different window size |

|
图 10 模型3不同窗口大小实验结果剖面图(剖面位置见图 9a) Fig. 10 Profile map of Synthetic models 3 test using different window size (Profile position is shown in Fig. 9a) |
为了验证本文提出方法对实际资料的处理效果, 选取南海中央海盆15°N附近分布呈近东西向展布的珍贝-黄岩海山链进行实验, 识别海山的重磁响应特征, 了解该地区岩石物性分布, 进而推断其岩石类型.珍贝-黄岩海山链被认为是南海残留的扩张中心(Taylor and Hayes, 1980), 其物质属性对研究南海壳幔相互作用和演化历史具有重要的意义.该地区水深大(图 11), 平均水深在3400 m以上, 岩石采样以及地球物理探测难度高, 导致研究难度增大.目前卫星重力数据、航空磁力数据具有较好的覆盖率和分辨率(图 12, 图 13), 对研究较大尺度地壳结构及岩石物质属性具有天然优势.根据拖网资料, 该地区主要分布为玄武岩、粗面岩等, 测年结果显示属于南海扩张期后晚中新世火山活动的产物(詹美珍等, 2015), 具有较强的磁性.前人从定性角度归纳了南海海山的三类重磁响应特征, 并推测了其可能的岩石类型(陈洁等, 2012).因此基于前人的研究结果, 也可以对本文方法实验的可靠性提供了较好的判断依据.

|
图 11 研究区水深(Smith and Sandwell, 1997) Fig. 11 Terrain feature of the study area (Smith and Sandwell, 1997) |
|
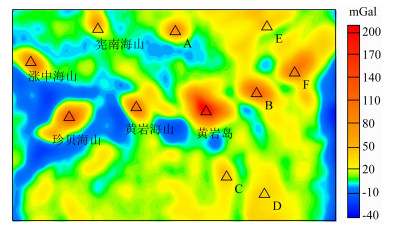
图 12 研究区自由空间重力异常(Sandwell et al., 2014) Fig. 12 Free-air gravity in study area (Sandwell et al., 2014) |
|
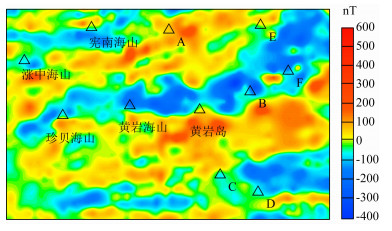
图 13 研究区磁异常(Okubo et al., 1997; CCOP) Fig. 13 Areomagnetic anomalies in study area (Okubo et al., 1997; CCOP) |
由于研究区处于低纬度地区, 为了尽量减小斜磁化的影响, 首先对磁异常数据进行化极处理.可以看到, 化极处理前珍贝、黄岩海山位于负磁异常之上(图 13), 而化极后海山则对应高磁异常峰值(图 14), 与已知的地质认识吻合.

|
图 14 研究区化极磁异常 Fig. 14 RTP magnetic anomalies in study area |
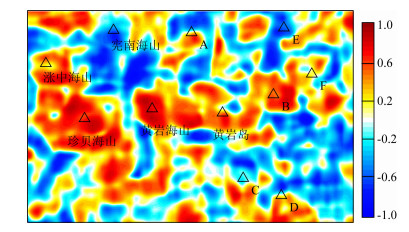
图 15为研究区重磁异常的传统相关系数.图 16为本文方法计算的重磁场源位置及属性判别参数GMCP值.对比两图, 可以看到相关系数识别的结果大面积强相关性, 并与海山的对应关系不够明显, 难以用于解释.而判别参数GMCP融合值较相关系数对海山的识别效果有了明显的改善, 较好的识别出了海山的物性分布特征.
|
图 15 研究区重磁相关系数 Fig. 15 Person correlation coefficient of gravity and magnetic anomalies |
从图 16可以看出, 涨中海山、珍贝海山、黄岩海山、黄岩岛、B海山以及F海山为正相关性, GMCP强度较大, 具有高磁性高密度的特征, 推测为基性火山岩(玄武岩).其中珍贝海山、黄岩海山与地形具有很好的对应关系.而涨中海山、B海山的高磁高重范围与地形部分吻合, 这可能由于磁异常方向的复杂性以及没有完全化到地磁极有关.有关珍贝海山、黄岩海山的推论与陈洁等(2012)的一致.另外, 宪南海山、A海山、E海山、C海山具有负相关性, 其中宪南海山、A海山与地形具有高度的对应关系, 而E海山、C海山负相关区与地形部分吻合, 推测为花岗岩或者变质岩.有关宪南海山的推论与陈洁等(2012)的一致.由于化极磁异常与D海山对应性较差, 因此对D海山识别效果不佳.另外在图 15中也分布了大面积GMCP低值区, 这些区域代表了岩石物性相对均匀, 表现为较弱的重磁场特征.

|
图 16 研究区GMCP值 Fig. 16 GMCP value of gravity and magnetic anomalies |
本文提出了一种基于相关系数和垂向导数的重磁场源位置及属性识别方法.该方法克服了传统相关系数在场源体外高相似性的缺点, 为重、磁解释提供了一个新的判别参数, 比传统相关系数都具有更好的可解释性.该方法有效地利用重磁垂向导数所反映的地质体边缘特征, 融合了重、磁相似度的属性特征, 又可以有效的定位以及缩小重、磁源位置范围, 比传统相关系数具有更好的场源定位识别能力以及场源属性信息.当GMCP>0时为正相关, 代表了该区域存在高磁高密度或低磁低密度的重、磁场源; 当GMCP<0时为负相关, 代表了该区域存在高磁低密度或低磁高密度的重、磁场源; GMCP趋于零值则表示无重磁源区.由于重磁场存在背景场, 讨论了三种背景场不同情况下, 相关系数的不同计算方法以及窗口大小选取的问题.两组同源(含噪声)和两组不同源复杂组合模型实验结果以及南海海盆实际重磁异常计算结果均验证了本文所提出的重磁场源位置及属性识别方法的正确性和有效性.
Baranov V. 1957. A new method for interpretation of aero-magnetic maps:pseudogravimetric anomalies. Geophysics, 22(2): 359-382. DOI:10.1190/1.1438369 |
Chandler V W, Koski J S, Hinze W J, et al. 1981. Analysis of multisource gravity and magnetic anomaly data sets by moving-window application of Poisson's theorem. Geophysics, 46(1): 30-39. |
Chandler V W, Malek K C. 1991. Moving-window Poisson analysis of gravity and magnetic data from the Penokean orogen, east-central Minnesota. Geophysics, 56(1): 123-132. DOI:10.1190/1.1442948 |
Chen J, Zhu B D, Wen N, et al. 2012. Gravity-magnetic response of the islands and seamounts of South China Sea. Chinese Journal of Geophysics (in Chinese), 55(9): 3152-3162. DOI:10.6038/j.issn.0001-5733.2012.09.033 |
Cordell L, Taylor P T. 1971. Investigation of magnetization and density of a north Atlantic seamount using Poisson's theorem. Geophysics, 36(5): 919-937. DOI:10.1190/1.1440224 |
De Ritis R, Ventura G, Chiappini M, et al. 2010. Regional magnetic and gravity anomaly correlations of the Southern Tyrrhenian Sea. Physics of the Earth and Planetary Interiors, 181(1-2): 27-41. DOI:10.1016/j.pepi.2010.04.003 |
Fan Z G, Liu Q K, Huang X Z, et al. 2012. Adaptive correlative analysis between aeromagnetic and gravity anomaly. Journal of Jilin University (Earth Science Edition) (in Chinese), 42(6): 1903-1911. |
Garland G D. 1951. Combined analysis of gravity and magnetic anomalies. Geophysics, 16(1): 51-62. |
Liu S H. 1993. Correspondence analysis of gravitational and magnetic anomalies and it's applications. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 15(3): 232-237. |
Liu Y H, Chen Z G, Ouyang C L. 2008. The application of correspondence analysis of gravity and magnetic anomalies in Xiangshan area. Geophysical and Geochemical Exploration (in Chinese), 32(6): 586-589. |
Mendonça C A. 2004. Automatic determination of the magnetization-density ratio and magnetization inclination from the joint interpretation of 2D gravity and magnetic anomalies. Geophysics, 69(4): 938-948. DOI:10.1190/1.1778237 |
Mendonça C A, Meguid A M A. 2008. Programs to compute magnetization to density ratio and the magnetization inclination from 3-D gravity and magnetic anomalies. Computers & Geosciences, 34(6): 603-610. |
Okubo Y, Ishihara T, Daigo M J N. 1997. Magnetic anomalies of east and southeast Asia andtheir linear features. Journal of Asian Earth Sciences, 15(2-3): 161-163. DOI:10.1016/S0743-9547(97)00004-4 |
Price A D, Dransfield M H. 1994. Lithological mapping by correlation of the magnetic and gravity data from Corsair W.A. Exploration Geophysics, 25(4): 179-187. DOI:10.1071/EG994179 |
Sandwell D T, Müller R D, Smith W H F, et al. 2014. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science, 346(6205): 65-67. DOI:10.1126/science.1258213 |
Smith W H F, Sandwell D T. 1997. Global sea floor topography from satellite altimetry and ship depth soundings. Science, 277(5334): 1957-1962. |
Taylor B, Hayes D E. 1980. The tectonic evolution of the South China Sea basin.//Hay D E ed. The Tectonic and Geologic Evolution of Southeast Asia Seas Islands. Washington DC: American Geophysical Union, 89-104.
|
Von Frese R R B, Hinze W J, Braile L W. 1982. Regional North American gravity and magnetic anomaly correlations. Geophysical Journal of the Royal Astronomical Society, 69(3): 745-761. DOI:10.1111/j.1365-246X.1982.tb02773.x |
Von Frese R R B, Jones M B, Kim J W, et al. 1997a. Spectral correlation of magnetic and gravity anomalies of Ohio. Geophysics, 62(1): 365-380. DOI:10.1190/1.1444139 |
Von Frese R R B, Jones M B, Kim J W, et al. 1997b. Analysis of anomaly correlations. Geophysics, 62(1): 342-351. DOI:10.1190/1.1444136 |
Zeng Z F, Wu Y G, Hao L B, et al. 2006. The Poisson's theorem based analysis method and application of magnetic and gravity anomalies. Journal of Jilin University (Earth Science Edition) (in Chinese), 36(2): 279-283. |
Zhan M Z, Sun W D, Ling M X, et al. 2015. Huangyan ridge subduction and formation of porphyry Cu-Au deposits in Luzon. Acta Petrologica Sinica (in Chinese), 31(7): 2101-2114. |
陈洁, 朱本铎, 温宁, 等. 2012. 南海海岛海山的重磁响应特征. 地球物理学报, 55(9): 3152-3162. DOI:10.6038/j.issn.0001-5733.2012.09.033 |
范正国, 刘前坤, 黄旭钊, 等. 2012. 自适应重磁对应分析. 吉林大学学报(地球科学版), 42(6): 1903-1911. |
刘沈衡. 1993. 重磁异常对应分析及应用. 物探化探计算技术, 15(3): 232-237. |
刘彦华, 陈宗刚, 欧阳长亮. 2008. 重磁异常对应分析在相山地区的应用. 物探与化探, 32(6): 586-589. |
曾昭发, 吴燕冈, 郝立波, 等. 2006. 基于泊松定理的重磁异常分析方法及应用. 吉林大学学报(地球科学版), 36(2): 279-283. |
詹美珍, 孙卫东, 凌明星, 等. 2015. 黄岩海山链俯冲与吕宋岛斑岩铜金成矿. 岩石学报, 31(7): 2101-2114. |
 2020, Vol. 63
2020, Vol. 63


