2. 中国科学院大学, 北京 100049;
3. 中国科学院青藏高原地球科学卓越创新中心, 北京 100101
2. University of the Chinese Academy of Sciences, Beijing 100049, China;
3. Chinese Academy of Sciences Center for Excellence in Tibetan Plateau Earth Sciences, Beijing 100101, China
地震波走时广泛应用于地震数据处理中,如叠前偏移(Zhao et al., 1998;Popovici and Sethian, 2002;刘国峰等,2009)、地震层析成像(Rawlinson and Kennett, 2008;张风雪等,2011;Liang et al., 2016;张明辉等,2019)及地震定位(Nelson and Vidale, 1990;Bai and Greenhalgh, 2006;De Kool and Kennett, 2014;赵爱华等,2015)等.走时计算的方法可以主要分为两大类:即射线追踪类方法(Zhang and Toksöz,1998;Zhao et al., 1992;Bai and Greenhalgh, 2005;Zhang and Thurber, 2005;Bai et al., 2010;Xu et al., 2006)和程函方程求解类方法(Vidale,1988;Podvin and Lecomte, 1991;Sethian and Popovici, 1999;Rawlinson and Sambridge, 2004b;Zhao,2005;Qian et al., 2007;孙章庆等, 2009, 2012;Waheed et al., 2015).射线追踪类方法的原理是沿程函方程的特征方向求解走时,这种方法在复杂速度模型中会出现焦散面和阴影区等问题(Xu et al., 2014, 2010).程函方程求解类方法有效避免了射线类方法的不足,且在计算精度和效率方面具有显著优势(Vidale, 1988, 1990;Rawlinson and Sambridge, 2004b),因此,自提出以来发展迅速,逐渐成为走时计算的主流方法.
然而,起伏地表的处理一直是程函方程类方法的难点所在,需要在满足地震波传播的物理规律前提下,对起伏地形带来的不规则边界做灵活、稳定的处理,从而保证数值计算的精度和效率(侯爵等,2014).传统的程函方程类方法采用模型扩展的策略处理起伏地表(Hole,1992;Taillandier et al., 2009;Huang and Bellefleur, 2012;李勇德等,2016),其核心思想是将起伏地形当作介质内部不连续面,通过填充低速介质将物理空间地形起伏的不规则模型扩展为计算空间的规则模型来处理.然而,该处理过程中采用的起伏地形的阶梯状表示及虚拟填充介质可能导致计算精度的损失(Ma and Zhang, 2015;郭高山等,2019).近年来逐渐提出的非结构化网格方法(Lelièvre et al., 2011;Bouteiller et al., 2018)可有效处理起伏地形,但其建模及走时求解算法颇为复杂、计算量大.Zhang and Chen(2006)在模拟起伏地表模型地震波场模拟时利用贴体网格构建的曲线坐标系方法巧妙地处理了地形起伏的难题,且兼有结构网格求解高效的优点.该方法自提出以来得到迅速发展(Lombard et al., 2007;Appelö and Petersson,2009;Lan and Zhang, 2011;Shragge,2016;Zhang et al., 2012, 2016;Sun et al., 2018). Lan和Zhang(2013a)将该处理方案引入至走时计算领域,为起伏地表下的的走时计算提供了一条新的途径.他们基于贴体网格的建模方式,推导建立了曲线坐标系的程函方程,该方程能够精确无损的刻画复杂地质模型的形态,并可用基于结构化网格的高效数值方法求解.同时,他们也针对性地发展了曲线坐标系程函方程的求解方法,包括Lax-Friedrichs扫描法(刘一峰和兰海强,2012;Lan and Zhang, 2013a,2013b)和迎风扫描法(Lan and Chen, 2018;Lan et al., 2018).然而,上述两种方法都存在震源奇异性问题(Vidale,1988;Fomel et al., 2009;Luo and Qian, 2011;Waheed and Alkhalifah, 2017),如图 1所示,由于使用了平面波近似球面波,C点的数值解与真实解之间存在较大误差,且该误差随着迭代过程传播到整个计算空间.
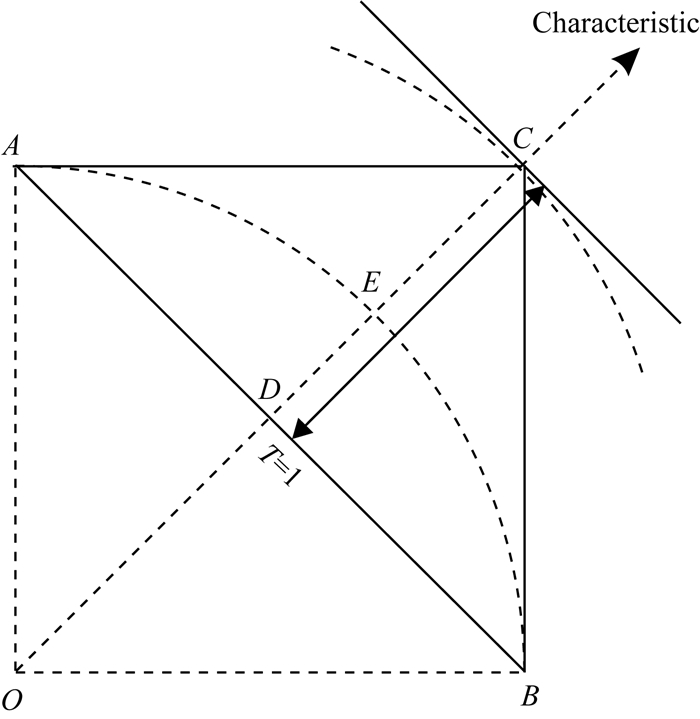
|
图 1
震源奇异性原理图,其中O点为震源点,C点为待求点的走时,A,B点的走时为1,地震波以球面波的形式传播,C点的实际走时为 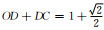 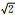 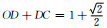 |
震源奇异性的问题一直伴随程函方程的发展,多位学者就该问题进行过深入研究,主要解决方法包括源点网格加密(Rawlinson and Sambridge, 2004a;De Kool et al., 2006),球坐标系程函方程(Alkhalifah and Fomel, 2010)以及因式分解(Fomel et al., 2009;Luo and Qian, 2011,2012;Noble et al., 2014;Treister and Haber, 2016).源点网格加密方法通过细化震源处网格,来减小源点处的截断误差,从而提高计算精度,但这种处理方式导致计算量增加,降低了算法的效率(Rawlinson et al., 2006).球坐标系程函方程的方法通过模拟球面波的传播来降低震源点误差,这种方法算法复杂,实际处理中难以有效应用.近年来,因式分解法受到越来越多的关注,该方法在没有明显增加计算量的情况下可从根源上解决震源奇异性的问题,且在各向同性和各向异性介质中都可应用.
针对曲线坐标系程函方程存在的震源奇异性问题,本文首先借鉴因式分解的思想,推导建立了曲线坐标系因式分解程函方程.然后,结合快速扫描法,发展了求解因式分解曲线坐标系程函方程的数值算法,从根源上解决了起伏地表的走时计算的震源奇异性问题.最后,通过数值实例,并与前人的方法进行详细的对比,全面分析测试新方法的优劣.
1 方法原理曲线坐标系中,各向同性介质的程函方程可表示为
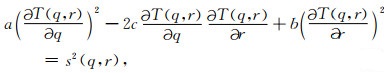
|
(1) |
上述方程可以由笛卡尔坐标系(x, y)中的程函方程变换到曲线坐标系(q, r)得到(详见Lan and Zhang, 2013b).方程中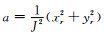
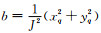
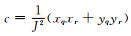
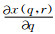
为了解决震源奇异性问题,本研究对方程(1)进行因式分解.
首先,分别将走时T和慢度s分解成两个乘法因子:
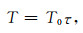
|
(2a) |
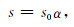
|
(2b) |
其中T0为已知因子,τ为未知因子,s0为震源处的慢度,α为修正因子.这里T0是以球面形式传播的,τ是在T0附近的扰动,所以该方法很好地以球面波近似波前,规避了震源奇异性的问题.
根据链式法则,走时偏导数表示如下:
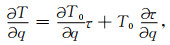
|
(3a) |
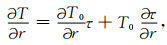
|
(3b) |
将(3)式代入到方程(1)中,可以得到因式分解的曲线坐标系程函方程:
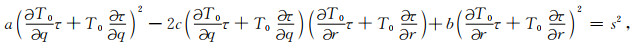
|
(4) |
其中因子T0可以解析求解,通过数值求解因子τ,可以精确计算走时值T,规避震源奇异性的问题,从而提高走时值T的精度.
本研究选择T0为下列曲线坐标系程函方程的解:
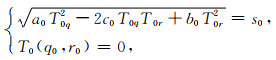
|
(5) |
其中(q0, r0)表示震源点的位置,此时a0=a(q0, r0),b0=b(q0, r0),c0=c(q0, r0).
求解方程(5),可得:
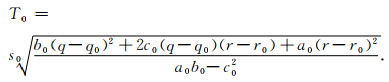
|
(6) |
本研究通过引入数学上用于求解静态Hamilton-Jacobi方程的方法(Luo and Qian, 2012),用于求解曲线坐标系因式分解程函方程(4).该方法的关键在于局部解,即如何从一个点的周围网格点来求得可能的走时值.如图 2所示,在间距为h的矩形网格内部,待求的是C点的τ值,将方程(4)分别在相应的四个三角形上离散.例如,在三角形ΔCWS中,W=(xW, yW),C=(xC, yC),S=(xS, yS),分别使用一阶差分近似τ的偏导数:
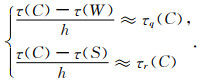
|
(7a) |
|
图 2 差分格式示意图.其中C点待求点的走时,W, E, N, C分别表示待求点周围左、右、上、下四个点的走时 Fig. 2 The finite difference scheme. C represents the point where the traveltime is to be computed. W, E, N and C represent the point of the left, right, upper and lower points around the point C, respectively |
将上式(7)代入方程(4)中,可以得到如下方程:

|
(7b) |
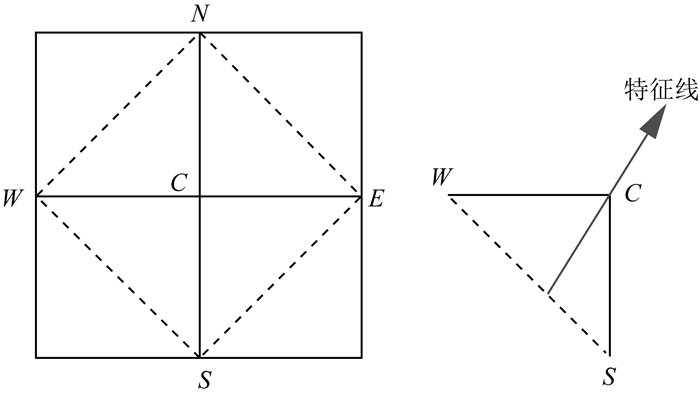
关于τ(C)的一元二次方程(7b),该方程的解有以下三种情况:①只有一个解;②有两个不同的解;③没有解.
如果①和②发生,需要判断得到的解是否满足如下的因果条件:通过C的特征向量T,
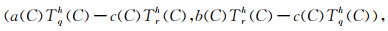
|
(7c) |
在三角形的两边WC和SC之间,如图 2所示.
如果③发生时,利用特征线的方法,令特征向量T沿着三角形两边WC和SC.
例如,当特征向量T沿着WC时,则走时的侯选值为
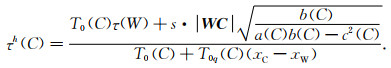
|
(7d) |
然而,对于每一个三角形,τ(C)可能有多个满足因果条件的解,四个三角形中,则有更多可能满足因果条件的解,此时,需要从中选择令T值最小的τ(C)值作为当前τ(C)值的更新值.
基于上述局部算法,结合Gauss-Seidel扫描更新的全部策略,构建完整的快速扫描算法,具体如下:
1.初始化:在震源点上的τ值赋初值为1,即τ(q0, r0)=1.其他网格点上的τ初值设为一个较大的值(远大于所有计算点最终能算出的τ值),这些点上的τ值在后续计算时会被更新.
2.Gauss-Seidel迭代:在交替的4个方向上,使用Gauss-Seidel型迭代法求解离散的非线性方程组,分别按四个方向扫描:
(1) i=1:I, j=1:J;(2) i=1:I, j=J:1,
(3) i=I:1, j=1:J;(4) i=I:1, j=J:1.
1) 每一个网格点处,在4个三角形ΔCEN,ΔCNW,ΔCWS和ΔCSE上离散方程(7b),并在每个三角形上分别求解离散后的方程.例如,在三角形ΔCWS上,求解方程(7b)有两个可能的根,τC, 1和τC, 2.
2) 如果有两个实根,τC, 1和τC, 2
*如果τC, 1和τC, 2都满足因果条件,则
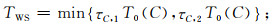
|
*如果只有τC, 1满足因果条件,则TWS=τC, 1T0(C);
*如果只有τC, 2满足因果条件,则TWS=τC, 2T0(C);
*如果τC, 1和τC, 2均不满足因果条件,用特征线方法沿着WC,SC得到τWC和τSC,并判断是否满足因果条件τWCT0(C)≥TW,τSCT0(C)≥TS,此时需要选择TWS=min{τWCT0(C), τSCT0(C)}.
3) 如果方程(7b)没有实根,用特征线方法沿着WC,SC得到τWC和τSC,并判断是否满足因果条件τWCT0(C)≥TW,τSCT0(C)≥TS,此时需要选择TWS=min τWCT0(C), τSCT0(C).
4) 从4个三角形中选择最小值,TC=min{TEN, TNW, TWS, TSE}.
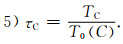
|
3.收敛判断:如果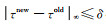
本研究通过3组数值实例测试了新方法计算地震波走时的精度和效率.模型1为水平地表模型,模型2为起伏地表模型,这两组模型中速度均设置为2 km·s-1的均匀介质,将因式分解法与震源网格加密、迎风扫描法进行对比,并测试了不同的震源位置对结果的影响.模型3为相同的复杂地表模型,速度模型为Marmousi模型,测试新方法对复杂速度结构的适用性.
模型1:水平地表均匀介质
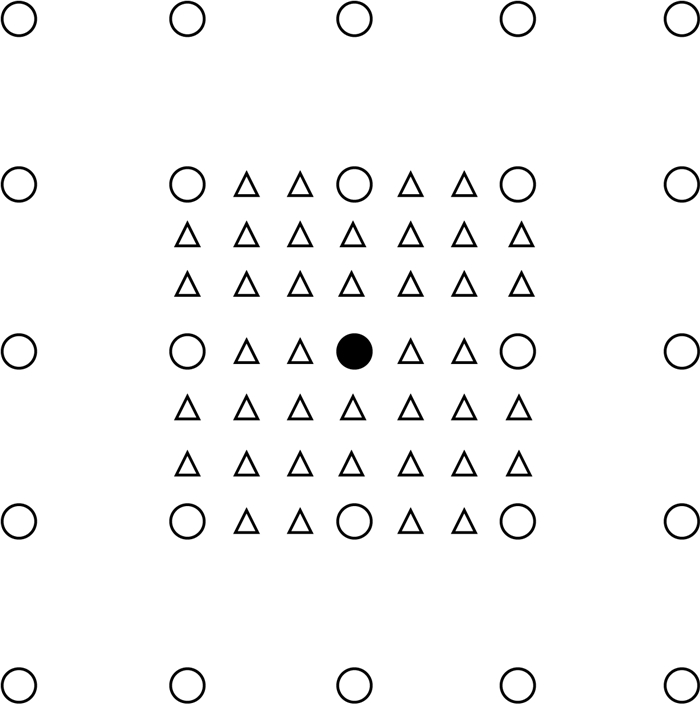
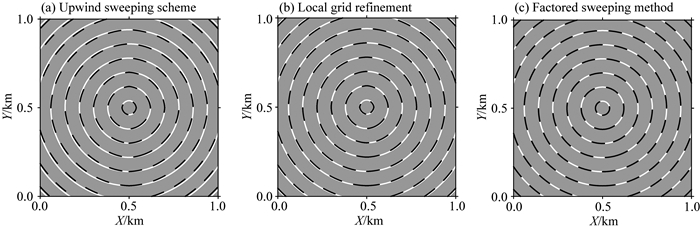
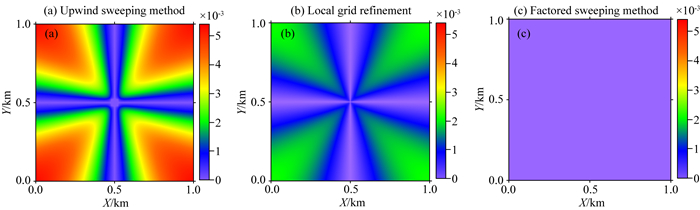
模型大小为1 km×1 km,均匀介质速度为2 km·s-1,震源位于模型中心,模型表面水平.用四种不同精度的网格100×100,200×200,400×400,800×800分别离散该模型.本文将迎风扫描法、震源网格加密方法(如图 3所示)、因式分解法计算的走时结果与解析解的结果进行对比.由于篇幅限制,这里只展示网格精度为100×100的走时计算与对比结果(图 4).通过图 4可以看到,不同的方法都能够较好的吻合解析解,验证了本文方法的正确性,震源网格加密一定程度上能够降低震源奇异性的影响,但是,因式分解法表现出更高的计算精度.图 6进一步给出了这三种方法计算走时的绝对误差图,可以得出因式分解法具有更好的计算精度.
|
图 3 震源网格加密示意图 圆点代表震源点,圆圈代表未进行细化的网格点,三角形代表细化的网格点. Fig. 3 Local grid refinement The dot represents the source, the circle represents the grid point that has not been refined, and the triangle represents grid point that has been refined. |
|
图 4 模型1的走时数值解和解析解对比图 (a)迎风扫描法;(b)震源网格加密方法;(c)因式分解法.黑色点线代表数值解,白色实线代表解析解.其中网格密度为100×100,震源位于(0.5 km, 0.5 km). Fig. 4 Traveltime contours (in seconds) on the 100×100 mesh for Model 1 with the source at the center (a) Upwind sweeping method; (b) Local grid refinement; (c) Factored sweeping method. The black dashed lines and white continuous lines represent the numerical and analytical solutions, respectively. |
|
图 6 模型1的走时误差图 (a)迎风扫描法; (b)震源网格加密法; (c)因式分解法.网格密度为100×100,震源位于(0.5 km, 0.5 km). Fig. 6 Absolute errors of traveltime calculated by (a) upwind sweeping method, (b) local grid refinement; (c) factored sweeping method, respectively, on the 100×100 mesh for Model 1 |
表 1对比了因式分解法与迎风扫描法两种方法不同网格精度下的L1误差、迭代次数以及CPU时间.因式分解法计算走时的L1误差比迎风扫描法计算走时的L1误差明显较小,相差4~6个数量级.从迭代次数和CPU时间来看,两者的迭代次数都不随着网格精度的增加而增加,这对于高精度的走时计算至关重要.同时,因式分解法的迭代次数、所用的CPU时间更少,效率更高.主要原因在于,因式分解法的求解过程同样遵守了走时从已知到未知传播的物理规律,保持了迎风格式的优势,算法结构更为简洁,因此计算效率相对于Legendre形式的迎风快速扫描法计算效率更高;因式分解的过程本质上是对走时场的球面近似,因此能够更好的模拟震源点附近的高曲率的波前面,提高走时的计算精度.
|
|
表 1 因式分解法和迎风扫描法计算走时的L1误差、迭代次数和CPU时间 Table 1 L1 error, iteration numbers, and statistics for CPU time consuming for the upwind sweeping method and factored sweeping method for the flat surface model (Model 1) |
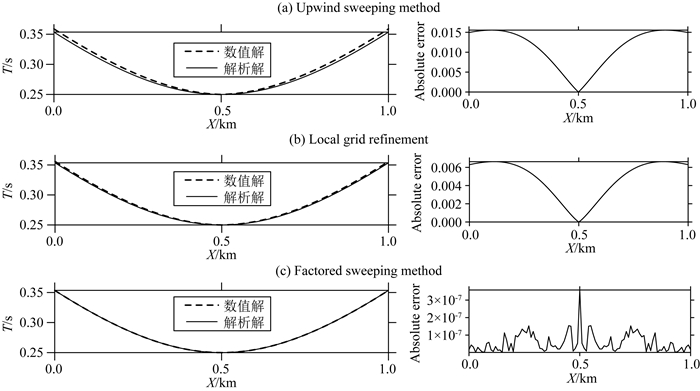
为了进一步对比迎风扫描法、震源网格加密和因式分解法三者的精度.本文选取了地表处的走时曲线作为参考,对比三种方法的数值解和解析解之间的相对误差.从图 5再次证明了因式分解法的数值解与解析解更吻合,精度更高.网格加密的方法虽能够一定程度的提高精度,但是相对因式分解,其提高幅度有限.
|
图 5 模型1地表处的走时数值解与解析解的对比 (a)左图:迎风扫描法计算的走时,右图:对应的绝对误差.(b)左图:震源网格加密方法计算的走时,右图:对应的绝对误差.(c)左图:因式分解法计算的走时,右图:对应的绝对误差.其中,虚线为数值解,实线为解析解.网格密度为100×100,震源位于(0.5 km, 0.5 km). Fig. 5 Comparison of numerical and analytical traveltimes counted at the flat surface on the 100×100 mesh for Model 1 (a) Upwind sweeping method; (b) Local grid refinement; (c) Factored sweeping method. The left panels show the traveltimes at the surface, whereas the right panels show the corresponding absolute error (in seconds). The continuous and dashed lines in the left panels represent the analytical and numerical solutions, respectively. |
模型2:起伏地表均匀介质
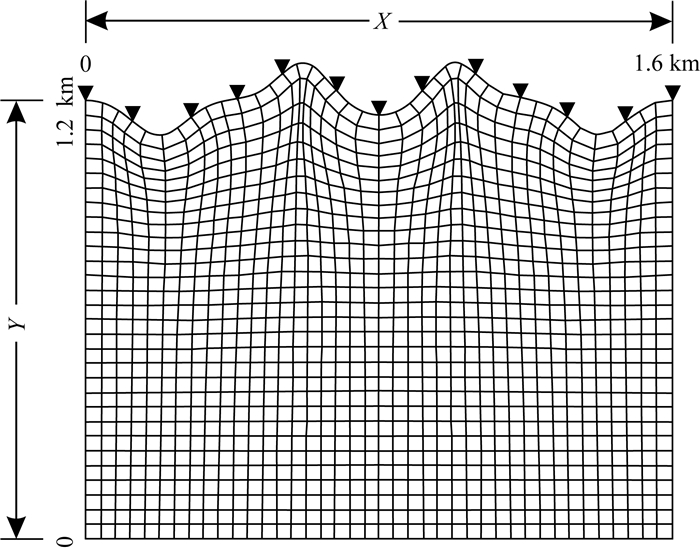
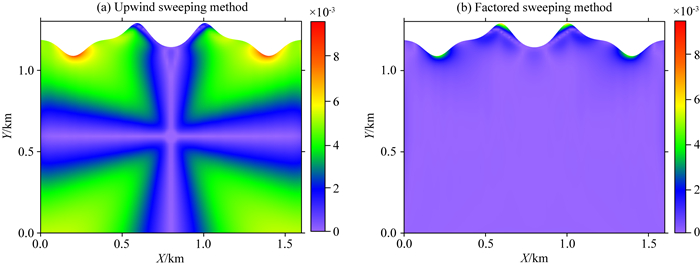
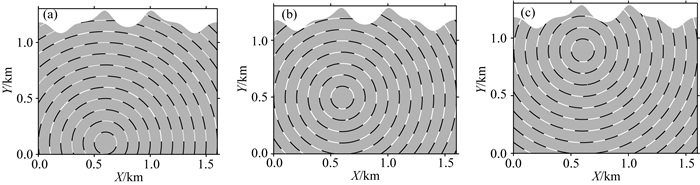
为了进一步测试因式分解法计算起伏地表走时的优势,选取Lan等文章中采用的数值模型(Lan and Zhang, 2013a, b).模型大小1.6 km×1.32 km,震源位于模型中央,地表由两个山峰和三个山谷组成,地形起伏较大,幅度从1.1 km到1.32 km,如图 7所示.本文使用4种不同精度的网格160×120,320×240,640×480,1280×960分别离散该模型.由于篇幅限制,这里只展示网格精度为160×120的走时场(图 8).从图 8中可以看出,起伏地表情况下,因式分解法的计算精度高.从表格2可以看出,因式分解法计算走时的L1误差比迎风扫描法计算走时的L1误差小,迭代次数和CPU时间也更小,说明因式分解法计算走时的精度和效率更高.图 10给出了两种方法计算走时的绝对误差图,可以看出迎风扫描法计算走时在源点处的误差较大,并且源点处的误差随着迭代过程逐渐传播到整个计算域,导致计算误差较大.这种现象的发生,主要是因为波是以球形方式传播到整个波场中,越靠近源点位置,波形曲率越大,以平面波的形式近似波前误差越大.而因式分解法很好地以球面波近似波前,规避了震源奇异性的问题,相对误差较小.相比于迎风扫描法的走时计算误差在坐标轴方向误差小而在对角线方向误差大,因式分解法计算的走时误差在各个方向都很均匀.这主要是由于迎风扫描法计算走时忽略了对角线上节点的信息,如图 1所示,基于平面波假设的迎风扫描法在对角线上(C点)会产生较大的误差,而轴线上的走时(A,B两点)误差小(Hassouna and Farag, 2007;卢回忆等,2013).从图 9和10也可以看到,地表处的走时误差相对较大,并且地形起伏越大,误差越大,这是由于贴体网格在地表处各向异性更强导致的走时误差增大(兰海强等,2012).此外,进一步测试不同震源深度对因式分解法计算走时的影响,图 11给出了不同震源位置处因式分解法计算走时的数值解与解析解的对比走时等值线图,可以看出不同震源位置处,因式分解法计算走时的精度都很高.
|
图 7 离散模型2的贴体网格,网格大小为160×120 倒黑色三角形表示均匀分布在起伏地表上的检波器.为清楚起见,网格密度显示为原来的1/4. Fig. 7 The boundary conforming grid (160×120) for Model 2 The inverted black triangles mark the evenly located receivers at the irregular free surface. For clarify, the grids are shown with a reducing density factor of 4. |
|
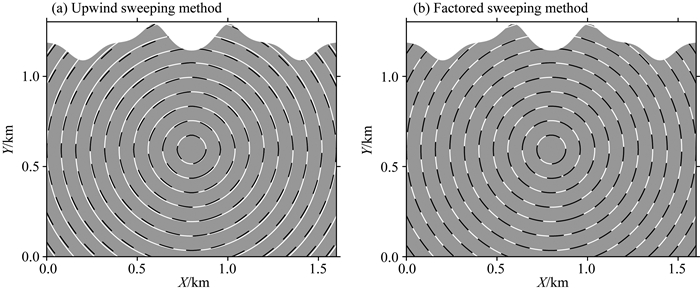
图 8 模型2的走时数值解和解析解对比图 (a)迎风扫描法;(b)因式分解法.黑色点线代表数值解,白色实线代表解析解.其中网格密度为160×120,震源位于(0.8 km, 0.6 km). Fig. 8 Traveltime contours (in seconds) on the 160×120 mesh for Model 2 with the source at the point (0.8 km, 0.6 km) (a) Upwind sweeping method; (b) Factored sweeping method. The black dashed lines and white continuous lines represent the numerical and analytical solutions, respectively |
|
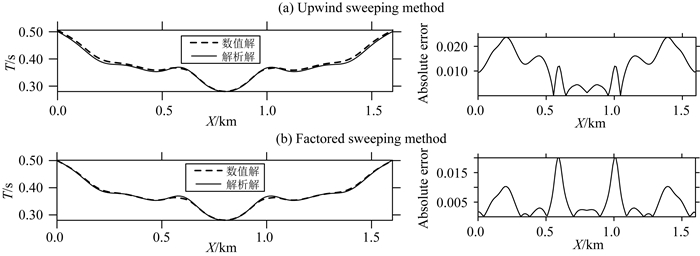
图 9 模型2地表处的走时数值解与解析解的对比 (a)左图:迎风扫描法计算的走时,右图:对应的绝对误差; (b)左图:因式分解法计算的走时,右图:对应的绝对误差.其中,虚线为数值解,实线为解析解.网格密度为160×120,震源位于(0.8 km, 0.6 km). Fig. 9 Comparison of numerical and analytical traveltimes counted at the non-flat surface on the 160×120 mesh for Model 2 (a) Upwind sweeping method; (b) Factored sweeping method. The left panels show the traveltimes at the surface, whereas the right panels show the corresponding absolute error (in seconds). The continuous and dashed lines in the left panels represent the analytical and numerical solutions, respectively. |
|
图 10 模型2的走时误差图 (a)迎风扫描法; (b)因式分解法.网格密度为160×120,震源位于(0.8 km, 0.6 km). Fig. 10 Absolute errors of traveltime calculated by (a) upwind sweeping method and (b) factored sweeping method, respectively, on the 160×120 mesh for Model 2 |
|
图 11 模型2不同震源深度时因式分解法的数值解与解析解的对比图 (a) (0.6 km, 0.1 km);(b) (0.6 km, 0.5 km);(c) (0.6 km, 0.9 km).白色实线代表解析解,黑色虚线代表数值解. Fig. 11 Traveltime contours (in seconds) on the 160×120 mesh with different source depths for Model 2 (a) (0.6 km, 0.1 km); (b) (0.6 km, 0.5 km); (c) (0.6 km, 0.9 km). The continuous and dashed lines represent the numerical and analytical solutions, respectively. |
模型3:起伏地表复杂速度模型
为了测试新方法对复杂地表条件下复杂速度结构的适用性,在水平地表Marmousi模型的基础上修改为起伏地表模型,同时对模型进行一定的高斯光滑,其速度结构如图 12所示.同样,使用不同网格精度分别离散该模型:160×120,320×240,640×480,1280×960.限于篇幅,这里只展示网格精度为160×120的走时计算与对比结果(图 13).图 14为地表处的数值解和解析解的对比图,图 15进一步给出了两种方法在全局域的数值解和解析解的对比图.可以看出,因式分解法相比于迎风扫描法精度更高,这里使用的高阶Lax格式作为真实解,结果显示,因式分解法与真实解吻合更好,验证了新方法对复杂速度模型的有效性.图 16给出了未进行光滑的Marmousi模型对应的误差图,同样可以看出,因式分解法相比于迎风扫描法,精度仍然较高,但提高较为有限.此外,从表 3中可以看出,因式分解法计算走时的L1误差比迎风扫描法计算走时的L1误差小,迭代次数和CPU时间都较小.该模型充分证明了因式分解法计算复杂地表和复杂速度模型的走时方面具有显著的优势.
|
|
表 2 因式分解法、迎风扫描法计算走时的L1误差、迭代次数和CPU时间 Table 2 L1 error, iteration numbers, and statistics for CPU time consuming for the upwind sweeping method and factored sweeping method for the non-flat surface model (Model 2) |
|
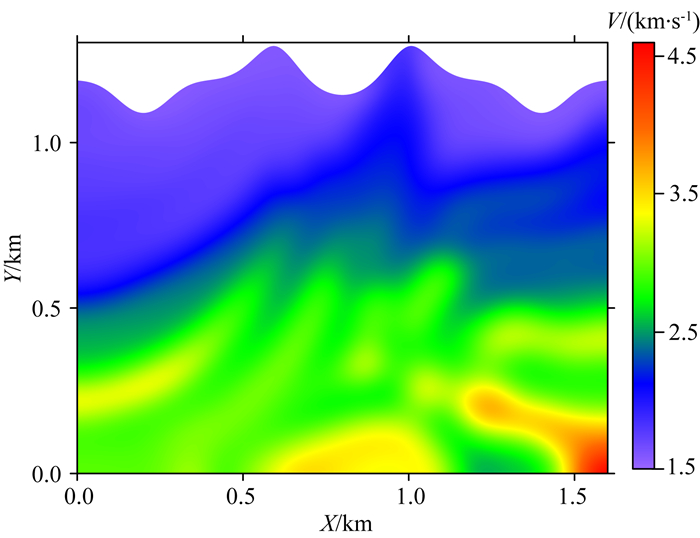
图 12 模型3的速度结构 Fig. 12 P-wave velocity structure for Model 3 |
|
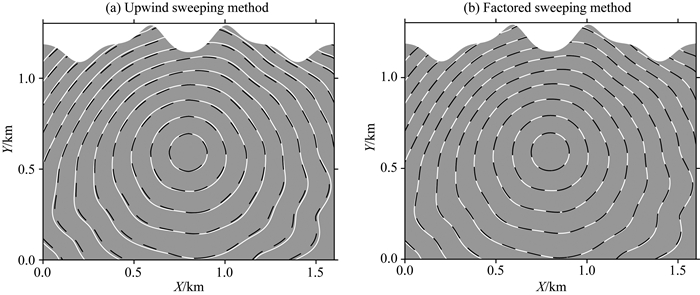
图 13 模型3的走时数值解和解析解对比图 (a)迎风扫描法;(b)因式分解法.黑色点线代表数值解,白色实线代表解析解.其中网格密度为160×120,震源位于(0.8 km, 0.6 km). Fig. 13 Traveltime contours (in seconds) on the 160×120 mesh for Model 3 with the source at the point (0.8 km, 0.6 km) (a) Upwind sweeping method; (b) Factored sweeping method. The black dashed lines and white continuous lines represent the numerical and analytical solutions, respectively. |
|
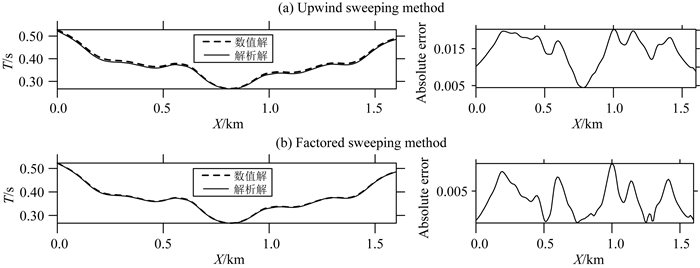
图 14 模型3地表处的走时数值解与解析解的对比 (a)左图:迎风扫描法计算的走时,右图:对应的绝对误差.(b)左图:因式分解法计算的走时,右图:对应的绝对误差.其中,虚线为数值解,实线为解析解.网格密度为160×120,震源位于(0.8 km, 0.6 km). Fig. 14 Comparison of numerical and analytical traveltimes counted at the non-flat surface on the 160×120 mesh for Model 3 (a) Upwind sweeping method; (b) Factored sweeping method. The left panels show the traveltimes at the surface, whereas the right panels show the corresponding absolute error (in seconds). The continuous and dashed lines in the left panels represent the analytical and numerical solutions, respectively. |
|
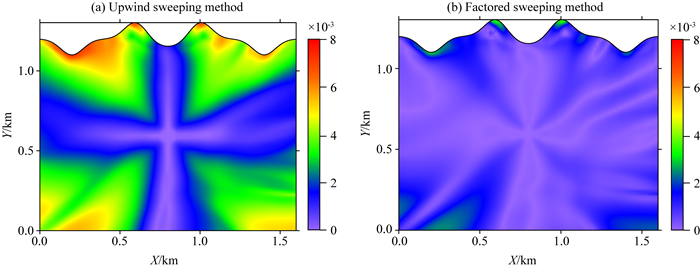
图 15 模型3的走时误差图 (a)迎风扫描法; (b)因式分解法.网格密度为160×120,震源位于(0.8 km, 0.6 km). Fig. 15 Absolute errors of traveltime calculated by (a) upwind sweeping method and (b) factored sweeping method, respectively, on the 160×120 mesh for Model 3 |
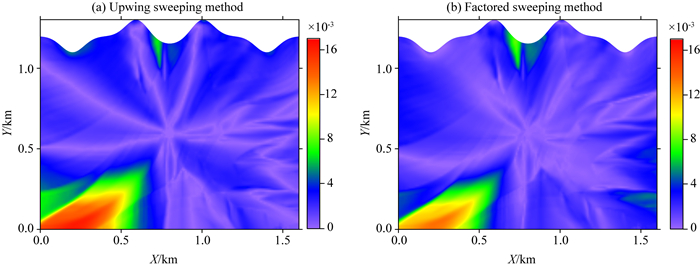
|
图 16 未光滑的Marmousi模型对应的走时误差图 (a)迎风扫描法; (b)因式分解法.网格密度为160×120,震源位于(0.8 km, 0.6 km). Fig. 16 Absolute errors of traveltime calculated by (a) upwind sweeping method and (b) factored sweeping method, respectively, on the 160×120 mesh for original Marmousi model |
|
|
表 3 因式分解法和迎风扫描法计算走时的L1误差、迭代次数和CPU时间 Table 3 L1 error, iteration numbers, and statistics for CPU time consuming for the upwind sweeping method and factored sweeping method for the non-flat surface model (Model 3) |
本文借鉴因式分解的思想,推导建立了因式分解的曲线坐标系程函方程,并结合快速扫描法,发展了相应的数值求解算法,极大地降低了走时计算的误差,从而提高算法的精度.通过数值模型,将因式分解法与迎风扫描方法、震源网格加密方法做了详细对比(计算精度和效率).论证了因式分解法求解曲线坐标系程函方程的优越性.结果表明:
(1) 因式分解的曲线坐标系程函方程有效规避了震源奇异性问题,提高了震源处走时的计算精度,从而显著提高整个模型空间的求解精度.
(2) 相较于迎风扫描法,因式分解法的震源计算精度明显提高,且计算效率不会随着网格精度增加而降低.
然而,因式分解法在处理强速度间断面时对精度的提高较为有限,这可能是由于因式分解基于的扰动理论在强速度间断面情况下效果不够显著,有待进一步研究.
目前,本文中的因式分解法只应用到求解二维曲线坐标系程函方程.但随着三维地震勘探的广泛应用,对三维复杂地表模型的走时计算精度提出了更高的要求.下一步拟将因式分解快速扫描法拓展到三维曲线坐标系程函方程的计算,为三维复杂地表条件下地震走时数据的高精度成像提供方法基础.
致谢 感谢美国爱荷华州立大学的Songting Luo博士提供程序和建设性意见.感谢英国剑桥大学Rawlinson Nicholas教授提供2D-FMM程序.特别感谢两位评审专家为本文完善提出的宝贵意见.
Alkhalifah T, Fomel S. 2010. Implementing the fast marching eikonal solver:Spherical versus Cartesian coordinates. Geophysical Prospecting, 49(2): 165-178. DOI:10.1046/j.1365-2478.2001.00245.x |
Appelö D, Petersson N. 2009. A stable finite difference method for the elastic wave equation on complex geometries with free surfaces. Communications in Computational Physics, 5(1): 84-107. DOI:10.2140/camcos.2009.4.217 |
Bai C Y, Greenhalgh S. 2005. 3-D non-linear travel-time tomography:imaging high contrast velocity anomalies. Pure and Applied Geophysics, 162(11): 2029-2049. |
Bai C Y, Greenhalgh S. 2006. 3D Local earthquake hypocenter determination with an irregular shortest-path method. Bulletin of the Seismological Society of America, 96(6): 2257-2268. |
Bai C Y, Huang G J, Zhao R. 2010. 2-D/3-D irregular shortest-path ray tracing for multiple arrivals and its applications. Geophysical Journal International, 183(3): 1596-1612. |
Bouteiller P L, Benjemaa M, Métivier L, et al. 2018. An accurate discontinuous Galerkin method for solving point-source Eikonal equation in 2-D heterogeneous anisotropic media. Geophysical Journal International, 212(3): 1498-1522. |
De Kool M, Rawlinson N, Sambridge M. 2006. A practical grid-based method for tracking multiple refraction and reflection phases in three-dimensional heterogeneous media. Geophysical Journal International, 167(1): 253-270. |
De Kool M, Kennett B. 2014. Practical earthquake location on a continental scale in Australia using the AuSREM 3D velocity Model. Bulletin of the Seismological Society of America, 104(6): 2755-2767. |
Fomel S, Luo S T, Zhao H K. 2009. Fast sweeping method for the factored eikonal equation. Journal of Computational Physics, 228(17): 6440-6455. |
Guo G S, Lan H Q, Chen L. 2019. A comparative study of both model expansion and topography flatten in topography handling in seismic traveltime tomography. Chinese Journal of Geophysics (in Chinese), 62(5): 1704-1715. |
Hassouna M S, Farag A A. 2007. Multistencils fast marching methods:A highly accurate solution to the eikonal equation on Cartesian domains. IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(9): 1563-1574. |
Hole J A. 1992. Nonlinear high-resolution three-dimensional seismic travel time tomography. Journal of Geophysical Research:Solid Earth, 97(B5): 6553-6562. |
Hou J, Zhang Z J, Lan H Q, et al. 2014. Progress in numerical simulation of seismic wave propagation under an undulating surface. Progress in Geophysics (in Chinese), 29(2): 488-497. |
Huang J W, Bellefleur G. 2012. Joint transmission and reflection traveltime tomography using the fast sweeping method and the adjoint-state technique. Geophysical Journal International, 188(2): 570-582. |
Lan H Q, Zhang Z J. 2011. Three-dimensional wave-field simulation in heterogeneous transversely isotropic medium with irregular free surface. Bulletin of the Seismological Society of America, 101(3): 1354-1370. |
Lan H Q, Zhang Z, Xu T, et al. 2012. Effects due to the anisotropic stretching of the surface-fitting grid on the traveltime computation for irregular surface by the coordinate transforming method. Chinese Journal of Geophysics (in Chinese), 55(10): 3355-3369. |
Lan H Q, Zhang Z J. 2013a. A High-order fast-sweeping scheme for calculating first-arrival travel times with an irregular surface. Bulletin of the Seismological Society of America, 103(3): 2070-2082. |
Lan H Q, Zhang Z J. 2013b. Topography-dependent eikonal equation and its solver for calculating first-arrival traveltimes with an irregular surface. Geophysical Journal International, 193(2): 1010-1026. |
Lan H Q, Chen L. 2018. An upwind fast sweeping scheme for calculating seismic wave first-arrival travel times for models with an irregular free surface. Geophysical Prospecting, 66(4): 327-341. |
Lan H Q, Chen L, Badal J. 2018. A hybrid method for calculating seismic wave first-arrival traveltimes in two-dimensional models with an irregular surface. Journal of Applied Geophysics, 155: 70-77. |
Lelièvre P G, Farquharson C G, Hurich C A. 2011. Computing first-arrival seismic traveltimes on unstructured 3-D tetrahedral grids using the fast marching method. Geophysical Journal International, 184(2): 885-896. |
Li Y D, Dong L G, Liu Y Z. 2016. First arrival traveltime tomography based on an improved scattering-integral algorithm. Chinese Journal of Geophysics (in Chinese), 59(10): 3820-3828. |
Liang X F, Chen Y, Tian X B, et al. 2016. 3D imaging of subducting and fragmenting Indian continental lithosphere beneath southern and central Tibet using body-wave finite-frequency tomography. Earth and Planetary Science Letters, 443: 162-175. |
Liu G F, Liu H, Li B, et al. 2009. Method of prestack time migration of seismic data of mountainous regions and its GPU implementation. Chinese Journal of Geophysics (in Chinese), 52(12): 3101-3108. |
Liu Y F, Lan H Q. 2012. Study on the numerical solutions of the eikonal equation in curvilinear coordinate system. Chinese Journal of Geophysics (in Chinese), 55(6): 2014-2026. |
Lombard B, Piraux J, Gélis C, et al. 2007. Free and smooth boundaries in 2-D finite-difference schemes for transient elastic waves. Geophysical Journal International, 172(1): 252-261. |
Lu H Y, Liu Y K, Chang X. 2013. MSFM-based travel-times calculation in complex near-surface model. Chinese Journal of Geophysics (in Chinese), 56(9): 3100-3108. |
Luo S T, Qian J L. 2011. Factored singularities and high-order Lax-Friedrichs sweeping schemes for point-source traveltimes and amplitudes. Journal of Computational Physics, 230(12): 4742-4755. |
Luo S T, Qian J L. 2012. Fast sweeping methods for factored anisotropic eikonal equations:Multiplicative and additive factors. Journal of Scientific Computing, 52(2): 360-382. |
Ma T, Zhang Z J. 2015. Topography-dependent eikonal traveltime tomography for upper crustal structure beneath an irregular surface. Pure and Applied Geophysics, 172(6): 1511-1529. |
Nelson G D, Vidale J E. 1990. Earthquake locations by 3-D finite-difference travel times. Bulletin of the Seismological Society of America, 80(2): 395-410. |
Noble M, Gesret A, Belayouni N. 2014. Accurate 3-D finite difference computation of traveltimes in strongly heterogeneous media. Geophysical Journal International, 199(3): 1572-1585. |
Podvin P, Lecomte I. 1991. Finite difference computation of traveltimes in very contrasted velocity models:a massively parallel approach and its associated tools. Geophysical Journal International, 105(1): 271-284. |
Popovici A M, Sethian J A. 2002. 3-D imaging using higher order fast marching traveltimes. Geophysics, 67(10): 604-609. |
Qian J L, Zhang Y T, Zhao H K. 2007. A fast sweeping method for static convex Hamilton-Jacobi equations. Journal of Scientific Computing, 31(1-2): 237-271. |
Rawlinson N, Sambridge M. 2004a. Multiple reflection and transmission phases in complex layered media using a multistage fast marching method. Geophysics, 69(5): 1338-1350. |
Rawlinson N, Sambridge M. 2004b. Wave front evolution in strongly heterogeneous layered media using the fast marching method. Geophysical Journal International, 156(3): 631-647. |
Rawlinson N, De Kool M, Sambridge M. 2006. Seismic wavefront tracking in 3D heterogeneous media:applications with multiple data classes. Exploration Geophysics, 37(4): 322-330. |
Rawlinson N, Kennett B L N. 2008. Teleseismic tomography of the upper mantle beneath the southern Lachlan Orogen, Australia. Physics of the Earth and Planetary Interiors, 167(1-2): 84-97. |
Sethian J A, Popovici M A. 1999. Three dimensional traveltime computation using the Fast Marching Method. Geophysics, 64(2): 516-523. DOI:10.1117/12.323280 |
Shragge J. 2016. Acoustic wave propagation in tilted transversely isotropic media:Incorporating topography. Geophysics, 81(5): C265-C278. |
Sun Y C, Zhang W, Chen X F. 2018. 3D seismic wavefield modeling in generally anisotropic media with a topographic free surface by the curvilinear grid finite-difference method. Bulletin of the Seismological Society of America, 108(3A): 1287-1301. |
Sun Z Q, Sun J G, Han F X. 2009. Traveltimes computation using linear interpolation and narrow band technique under complex topographical conditions. Chinese Journal of Geophysics (in Chinese), 52(11): 2846-2853. DOI:10.3969/j.issn.0001-5733.2009.11.019 |
Sun Z Q, Sun J G, Han F X. 2012. Traveltime computation using the upwind finite difference method with nonuniform grid spacing in a 3D undulating surface condition. Chinese Journal of Geophysics (in Chinese), 55(7): 2441-2449. |
Taillandier C, Noble M, Chauris H, et al. 2009. First-arrival traveltime tomography based on the adjoint-state method. Geophysics, 74(6): WCB1-WCB10. |
Treister E, Haber E. 2016. A fast marching algorithm for the factored eikonal equation. Journal of Computational Physics, 324: 210-225. |
Vidale J E. 1988. Finite-difference calculation of travel times. Bulletin of the Seismological Society of America, 78(6): 2062-2076. |
Vidale J E. 1990. Finite-difference calculation of traveltimes in three dimensions. Geophysics, 55(5): 521-526. |
Waheed U B, Yarman C E, Flagg G. 2015. An iterative, fast-sweeping-based eikonal solver for 3D tilted anisotropic media. Geophysics, 80(3): C49-C58. |
Waheed U B, Alkhalifah T. 2017. A fast sweeping algorithm for accurate solution of the tilted transversely isotropic eikonal equation using factorization. Geophysics, 82(6): WB1-WB8. |
Xu T, Xu G M, Gao E G, et al. 2006. Block modeling and segmentally iterative ray tracing in complex 3D media. Geophysics, 71(3): T41-T51. |
Xu T, Zhang Z J, Gao E G, et al. 2010. Segmentally iterative ray tracing in complex 2D and 3D heterogeneous block models. Bulletin of the Seismological Society of America, 100(2): 841-850. |
Xu T, Li F, Wu Z B, et al. 2014. A successive three-point perturbation method for fast ray tracing in complex 2D and 3D geological models. Tectonophysics, 627: 72-81. |
Zhang F X, Li Y H, Wu Q J, et al. 2011. The P wave velocity structure of upper mantle beneath the North China and surrounding regions from FMTT. Chinese Journal of Geophysics (in Chinese), 54(5): 1233-1242. |
Zhang H J, Thurber C. 2005. Adaptive mesh seismic tomography based on tetrahedral and Voronoi diagrams:Application to Parkfield, California. Journal of Geophysical Research:Solid Earth, 110(B4): B04303. |
Zhang J, Toksöz M N. 1998. Nonlinear refraction traveltime tomography. Geophysics, 63(5): 1726-1737. |
Zhang M H, Liu Y S, Hou J, et al. 2019. Review of seismic tomography methods in near-surface structures reconstruction. Progress in Geophysics (in Chinese), 34(1): 48-63. |
Zhang W, Chen X F. 2006. Traction image method for irregular free surface boundaries in finite difference seismic wave simulation. Geophysical Journal International, 167(1): 337-353. |
Zhang W, Zhang Z G, Chen X F. 2012. Three-dimensional elastic wave numerical modelling in the presence of surface topography by a collocated-grid finite-difference method on curvilinear grids. Geophysical Journal International, 190(1): 358-378. |
Zhang Z G, Xu J K, Chen X F. 2016. The supershear effect of topography on rupture dynamics. Geophysical Research Letters, 43(4): 1457-1463. |
Zhao A H, Ding Z F, Bai Z M. 2015. Improvement of the ray-tracing based method calculating hypocentral loci for earthquake location. Chinese Journal of Geophysics (in Chinese), 58(9): 3272-3285. |
Zhao D P, Hasegawa A, Horiuchi S. 1992. Tomographic imaging of P and S wave velocity structure beneath northeastern Japan. Journal of Geophysical Research:Solid Earth, 97(B13): 19909-19928. |
Zhao H K. 2005. A fast sweeping method for Eikonal equations. Mathematics of Computation, 74(250): 603-627. DOI:10.1090/S0025-5718-04-01678-3 |
Zhao P, Uren N F, Wenzel F, et al. 1998. Kirchhoff diffraction mapping in media with large velocity contrasts. Geophysics, 63(6): 2072-2081. |
郭高山, 兰海强, 陈凌. 2019. 模型扩展和地形平化起伏地形处理方案在地震走时层析成像中的对比研究. 地球物理学报, 62(5): 1704-1715. DOI:10.6038/cjg2019M0102 |
侯爵, 张忠杰, 兰海强, 等. 2014. 起伏地表下地震波传播数值模拟方法研究进展. 地球物理学进展, 29(2): 488-497. DOI:10.6038/pg20140203 |
兰海强, 张智, 徐涛, 等. 2012. 贴体网格各向异性对坐标变换法求解起伏地表下地震初至波走时的影响. 地球物理学报, 55(10): 3355-3369. DOI:10.6038/j.issn.0001-5733.2012.10.018 |
李勇德, 董良国, 刘玉柱. 2016. 基于改进的散射积分算法的初至波走时层析. 地球物理学报, 59(10): 3820-3828. DOI:10.6038/cjg20161026 |
刘国峰, 刘洪, 李博, 等. 2009. 山地地震资料叠前时间偏移方法及其GPU实现. 地球物理学报, 52(12): 3101-3108. DOI:10.3969/j.issn.0001-5733.2009.12.019 |
刘一峰, 兰海强. 2012. 曲线坐标系程函方程的求解方法研究. 地球物理学报, 55(6): 2014-2026. DOI:10.6038/j.issn.0001-5733.2012.06.023 |
卢回忆, 刘伊克, 常旭. 2013. 基于MSFM的复杂近地表模型走时计算. 地球物理学报, 56(9): 3100-3108. DOI:10.6038/cjg20130922 |
孙章庆, 孙建国, 韩复兴. 2009. 复杂地表条件下基于线性插值和窄带技术的地震波走时计算. 地球物理学报, 52(11): 2846-2853. DOI:10.3969/j.issn.0001-5733.2009.11.019 |
孙章庆, 孙建国, 韩复兴. 2012. 三维起伏地表条件下地震波走时计算的不等距迎风差分法. 地球物理学报, 55(7): 2441-2449. DOI:10.6038/j.issn.0001-5733.2012.07.028 |
张风雪, 李永华, 吴庆举, 等. 2011. FMTT方法研究华北及邻区上地幔P波速度结构. 地球物理学报, 54(5): 1233-1242. DOI:10.3969/j.issn.0001-5733.2011.05.012 |
张明辉, 刘有山, 侯爵, 等. 2019. 近地表地震层析成像方法综述. 地球物理学进展, 34(1): 48-63. DOI:10.6038/pg2019CC0534 |
赵爱华, 丁志峰, 白志明. 2015. 基于射线追踪技术计算地震定位中震源轨迹的改进方法. 地球物理学报, 58(9): 3272-3285. DOI:10.6038/cjg20150922 |
 2020, Vol. 63
2020, Vol. 63


