2. 地球探测信息仪器教育部重点实验室, 长春 130026
2. Key Laboratory of Geo-Exploration Instrumentation, Ministry of Education, Changchun 130026, China
地面磁共振(Magnetic Resonance Sounding, MRS)是一种直接对地下水进行定量探测,并对孔隙分布定性评估的非侵入性地球物理方法(肖立志等, 2013; Behroozmand et al., 2015).该方法利用地磁场B0作为背景场,地下水中的氢质子在B0中自旋,频率称为Larmor频率fL=γ|B0|/(2π),其中γ为旋磁比(Trushkin et al., 1995; 林君等, 2013; Legchenko et al., 2016a).通过人工产生的交变磁场B1,激发氢质子产生能级跃迁(林君等, 2017).当撤去B1后,氢质子从高能级回迁至低能级,释放能量产生自由感应信号(free induction decay, FID),实现对地下水的直接探测(Behroozmand et al., 2016; 王琦等,2018).基于上述原理,发生磁共振的基本条件是,激发场B1的发射频率fT等于氢质子的自旋频率(Larmor频率fL),即fT=fL(Behroozmand et al., 2013; 林君等, 2018).然而,由于B0受到自身时变性、不均匀性以及外界磁性介质和电磁噪声的影响,导致实际中难以获得准确的Larmor频率(Hürlimann et al., 1998; Chen et al., 2005; Girard et al., 2005;Grunewald and Knight, 2012; Legchenko et al., 2010; Legchenko et al., 2016b).当fT≠fL时,氢质子发生偏共振现象.
针对偏共振现象,Walbrecker等(2011)首先推导了共振激发和偏共振激发对地面磁共振信号幅度和相位的影响.利用偏共振激发能够提高信号幅度的优点,Grombacher等(2014)提出了一种复合脉冲激发方式,增强了信号的正交分量幅度,从而改进了地面磁共振反演的分辨率.Grombacher和Knight(2015)还从多种B0不均匀情况以及脉冲时间的角度,讨论了偏共振对于含水量估计的影响.蒋川东等(2018)提出同时利用磁共振信号实部和虚部的复包络反演方法,通过自动搜索方案估计未知的系统相位,实现了偏共振探测中含水量和弛豫时间T2*的准确反演.但是,以上研究均要求已知Larmor频率,才能获得准确的频率偏量.如果使用错误偏共振或共振核函数进行反演,会导致含水量和T2*估计存在严重偏差(Jiang et al., 2018).
针对未知Larmor频率的情况,Grombacher等(2016)提出了一种频率环测量方案.首先在估计的Larmor频率两侧,分别按照设定的频率偏量进行两次偏共振激发,最后利用设定频率偏量的核函数进行反演.该方案能够在一定范围内降低未知Larmor频率的影响,但是仍然要求估计的Larmor频率不能远离真实值.Grombacher等(2018)还将频率环与最新开发的绝热脉冲(Grunewald et al., 2016;Grombacher,2018)相结合,将最小的未知频率偏量扩大到3 Hz.
本文针对未知Larmor频率导致的偏共振激发,在频率环的基础上提出双频磁共振探测方法(Dual-Frequency Magnetic Resonance Sounding, DF-MRS).该方法只需知道Larmor频率的范围区间,在此区间外设定两个发射频率进行偏共振激发,利用发射频率差值的一半作为频率偏量计算核函数,从而获得准确的反演结果.首先,从磁共振和偏共振的基本原理出发,推导出双频磁共振下的磁化矢量和灵敏度核函数的表达式.其次,建立双层含水层模型,通过改变设定频率偏量和电阻率,分析双频磁共振与偏共振核函数和信号的差异.然后,通过仿真实验,讨论假设磁共振、假设偏共振和双频磁共振情况下得到的反演结果的准确性.最后,通过野外实测数据反演结果,验证双频磁共振探测方法的有效性和优势.
1 双频磁共振探测原理 1.1 磁共振和偏共振在地磁场B0和激发磁场B1的作用下,氢质子自旋产生的宏观磁化矢量M可以用布洛赫方程(Bloch, 1946)描述,在旋转参考系中(Levitt, 2008):
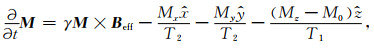
|
(1) |
其中,γ是氢质子磁旋比;Mx、My和Mz是M在单位矢量方向
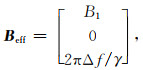
|
(2) |
其中,Δf=fT-fL是发射频率和Larmor频率之间的频率偏量.
对于磁共振情况,即Δf=0 Hz,Beff只在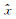
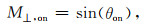
|
(3) |
其中,θon= |γB1|τ是发射期间的有效扳倒角,τ是发射时间.
对于磁偏共振(即Δf≠0 Hz),Beff还存在ẑ方向与Δf相关的分量2πΔf/γ.M⊥表示为
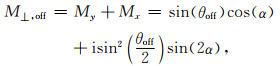
|
(4) |
其中,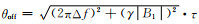
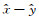
由上述表达式可知,在磁共振情况时,M⊥, on只在ŷ方向上存在分量.而对于偏共振情况时,M⊥, off在
对于一维层状大地模型,当发射线圈和接收线圈共线时,接收磁场与激发磁场B1相等,地面磁共振正演模型用下式表示(Weichman et al., 2000; Legchenko and Valla, 2002):
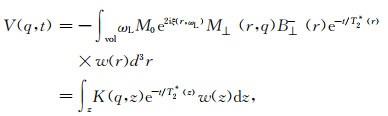
|
(5) |
其中,V(q, t)表示在t时刻对应脉冲矩q的信号,q=Iτ,I是发射电流幅度;M0是净磁化矢量;ξ是发射和接收磁场由于椭圆极化产生的相位分量;B⊥- (r)描述了接收线圈的空间灵敏度(Hoult, 2000);w(r)和T2*(r)分别表示地下水含水量和横向弛豫时间的空间分布;K(q, z)称为灵敏度核函数,即当脉冲矩为q时,在深度z处,厚度为1 m,含水量为100%的含水层产生的FID信号大小.
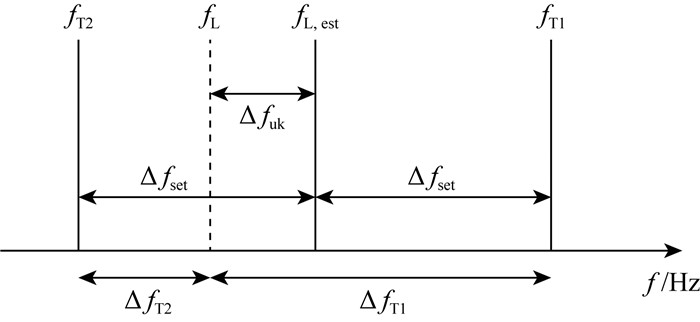
1.2 双频磁共振探测原理双频磁共振探测方法是在频率环方法的基础上进行的改进,见图 1所示.假设真实的Larmor频率fL未知,采用磁力仪在多个位置进行测量取平均值得到Larmor频率的估计值fL, est.由于B0空间不均匀性或磁性干扰,真实fL和fL, est之间存在未知的频率偏量Δfuk.显然,如果使用fL, est作为发射频率fT进行探测,然后利用磁共振核函数进行反演,Δfuk的存在必然引起反演结果存在较大误差.如果设定一个频率偏量Δfset,使用fT=fL, est+Δfset进行偏共振激发,利用Δfset偏共振核函数进行反演,反演结果也会存在较大误差.
|
图 1 双频磁共振探测原理图 fL是真实Larmor频率;fL, est是估计的Larmor频率;Δfuk是未知频率偏量;Δfset是设定频率偏量;fT1和fT2是双频共振发射频率;ΔfT1和ΔfT2是真实频率偏量. Fig. 1 Schematic diagram of DF-MRS method. fL is the true Larmor frequency fL, est is the estimated Larmor frequency; Δfuk is the unknown frequency offset; Δfset is the set frequency offset; fT1 and fT2 are the DF-MRS transmitting frequencies; ΔfT1 and ΔfT2 are the true frequency offsets. |
双频磁共振探测方法使用两次偏共振激发,频率分别为fT1=fL, est+Δfset和fT2=fL, est-Δfset.如果fL, est的不确定度较大,可选择较大的频率偏移范围Δfset(~10 Hz),即只需保证fL, est在fT1和fT2之间.当使用fT1和fT2进行偏共振激发后,对两次探测数据的实部(d1R和d2R)和虚部(d1I和d2I)分别进行处理:
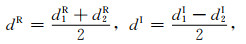
|
(6) |
再利用Δfset=(fT1+fT2)/2计算偏共振核函数,进行反演计算,从而消除Δfuk的影响.
根据表达式(4)对于两个发射频率fT1和fT2,产生的横向磁化矢量M⊥, T1和M⊥, T2分别为
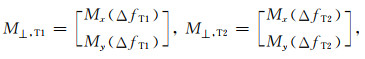
|
(7) |
其中,ΔfT1=Δfuk+Δfset和ΔfT2=Δfuk-Δfset.对两个磁化矢量的实部进行相加除以2,虚部进行相减除以2,得到:
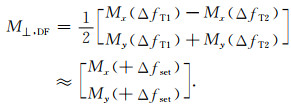
|
(8) |
从公式(8)可见,此时双频磁共振的M⊥, DF与频率偏量为Δfset偏共振的M⊥, off近似相等,进而得到双频磁共振的核函数与偏共振的核函数近似相等.因此,利用表达式(6)得到的双频磁共振探测数据和根据Δfset计算的偏共振核函数,即可实现含水量和T2*的准确反演.
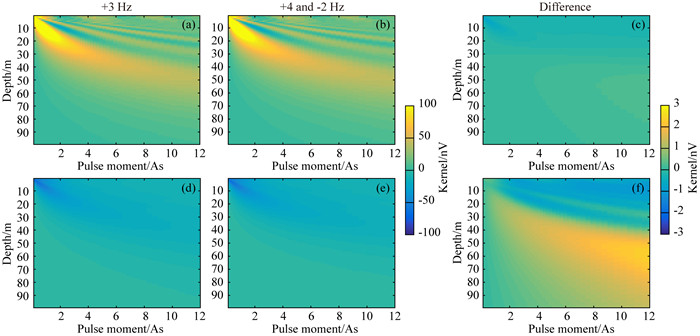
2 双频核磁共振仿真实验 2.1 灵敏度核函数为了证明双频磁共振方法在未知Larmor频率时,仍然能够实现对地下水进行准确探测,首先对双频磁共振和偏共振的灵敏度核函数进行对比和分析,如图 2所示.仿真的正演模型参数如下:B0为54721 nT,fL为2330 Hz,地磁倾角I为60°,地磁偏角D为0°,电阻率ρ为500 Ωm均匀分布.发射和接收线圈为正方形,边长为50 m.q的范围为0.1~12 As,数量为100,按对数分布,τ为20 ms.假设估计的Larmor频率为2331 Hz,即与fL存在+1 Hz的未知偏量Δfuk.双频磁共振的激发频率分别为2334 Hz和2328 Hz,即设定频率偏量Δfset为+3 Hz,而真实频率偏量分别为+4 Hz和-2 Hz.因此需要对比+3 Hz偏共振和(+4, -2)Hz双频磁共振的核函数之间的差值.
|
图 2 双频磁共振与偏共振核函数的对比 (a)和(d)是+3 Hz偏共振核函数的实部和虚部;(b)和(e)是+4 Hz和-2 Hz双频磁共振核函数实部和虚部;(c)和(f)是两者核函数实部和虚部的差值. Fig. 2 Comparison of DF-MRS and off-MRS kernel functions (a) and (d) are the real and imaginary parts of the +3 Hz off-MRS kernel function; (b) and (e) are the real and imaginary parts of the +4 Hz and -2 Hz DF-MRS kernel functions; (c) and (f) are the differences respectively correspond to the real and imaginary parts of the kernel functions. |
由图 2可以得到,双频磁共振和偏共振核函数的实部和虚部均近似相等.在图 2(c, f)中,两个核函数的差值很小,且实部的差异明显小于虚部的差异,实部的绝对误差最大为0.87 nV,虚部的绝对误差最大为2.43 nV.因此可以证明,即使存在+1 Hz的未知频率偏量,也可以使用+3 Hz的偏共振核函数代替(+4, -2)Hz的双频磁共振核函数.
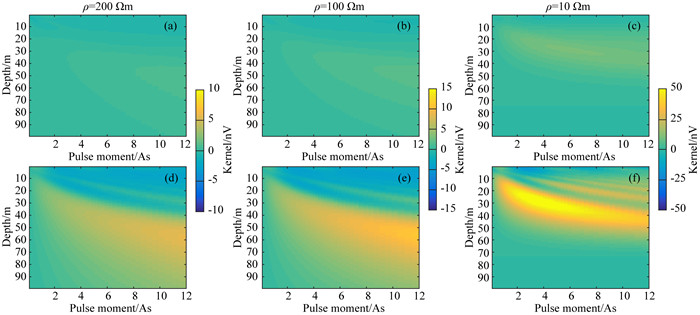
进一步研究表明,电阻率参数是影响核函数实部和虚部差异的主要原因之一.当地下电阻率逐渐减小时,偏共振和双频磁共振核函数的虚部差值逐渐增大,见图 3所示.当ρ=200 Ωm和ρ=100 Ωm时,核函数的实部和虚部差值与图 2中ρ=500 Ωm时基本一致,但虚部差值的幅度逐渐增大.当ρ=10 Ωm时,虚部差值的分布发生较大变化,且幅度达到50 nV.说明在这种情况下,双频磁共振与偏共振的核函数差异较大,无法再使用偏共振核函数代替双频磁共振核函数进行反演计算.
|
图 3 不同电阻率时,双频磁共振与偏共振的核函数差值 (a)和(d)电阻率为200 Ωm时核函数实部和虚部的差值;(b)和(e)电阻率为100 Ωm时核函数实部和虚部的差值;(c)和(f)电阻率为10 Ωm时核函数实部和虚部的差值. Fig. 3 Difference in kernel function between DF-MRS and off-MRS at different resistivities (a) and (d) are the real and imaginary parts of the kernel function deviation at a resistivity of 200 Ωm; (b) and (e) are the real and imaginary parts of the kernel function deviation at a resistivity of 100 Ωm; (c) and (f) are the real and imaginary parts of the kernel function deviation at a resistivity of 10 Ωm. |
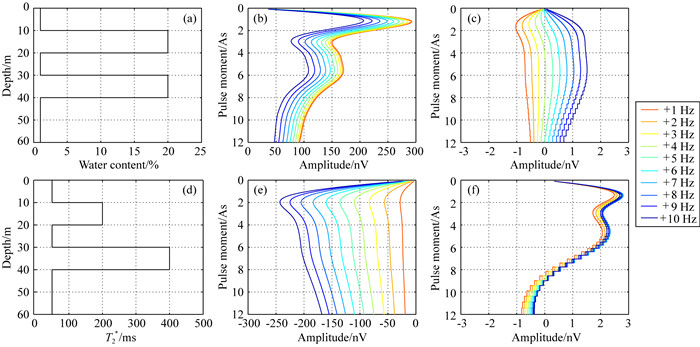
为了分析设定频率偏量Δfset对双频磁共振信号的影响,本文建立包含两个含水层的仿真模型,厚度均为10 m,如图 4(a和d)所示.第一层深度为10~20 m,含水量为20%,T2*为200 ms,对应粗砂层.第二层深度为30~40 m,含水量为20%,T2*为400 ms,对应砾石层.其余深度处的含水量均为1%,T2*为50 ms,对应为隔水层.仿真模型的正演参数与图 2中计算核函数的参数保持一致.
|
图 4 双含水层仿真模型及双频磁共振信号与偏共振信号的对比 (a)和(d)分别是仿真模型的含水量和T2*;(b)和(e)是Δfset=1~10 Hz时不同脉冲矩下双频磁共振信号初始振幅的实部和虚部;(c)和(f)是Δfset=1~10 Hz时不同脉冲矩下双频磁共振与偏共振信号初始振幅实部和虚部的差值 Fig. 4 Double aquifer simulation model and comparison of DF-MRS signal and off-MRS signal (a) and (d) are the water content and T2* of the simulation model respectively; (b) and (e) are the real and imaginary parts of the initial amplitude of the DF-MRS signal when Δfset=1~10 Hz; (c) and (f) is the real and imaginary parts of the initial amplitude deviation between the DF-MRS and the off-MRS signal when Δfset=1~10 Hz. |
根据表达式(5)和(6)分别计算Δfset= 1~10 Hz范围内的双频磁共振信号初始幅度V0的实部和虚部, 如图 4(b和e)所示.当Δfset由1 Hz变化到10 Hz时,V0的实部逐渐减小,而V0的虚部逐渐增大.图 4 (c, f)给出了双频磁共振信号与其分别对应的偏共振信号的差值曲线,说明两个信号之间的差异非常小,实部差值在-1~1.5 nV,虚部差值在-1~3 nV,这与图 2中核函数得到的结果相吻合.
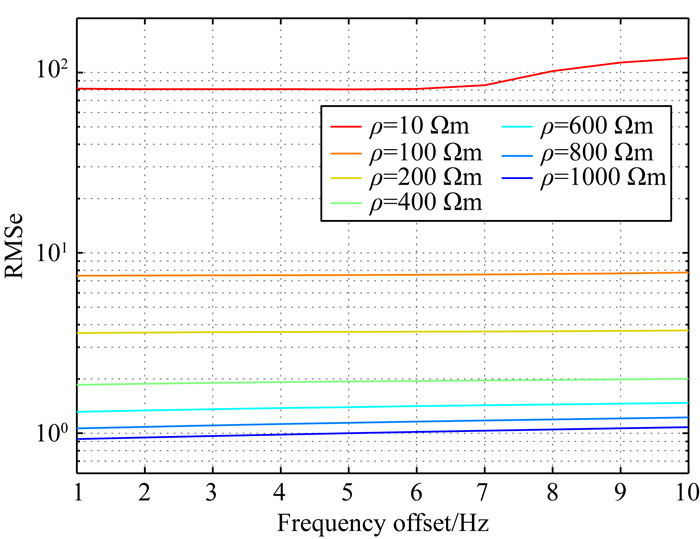
为了更全面地讨论电阻率变化时双频磁共振方法的适用性,图 5给出了当ρ分别等于10, 100, 200, 400, 600, 800, 1000 Ωm时,双频磁共振信号与偏共振信号的均方误差(RMSe)随Δfset= 1~10 Hz的变化情况.对于相同电阻率的情况下,当Δfset增加时,RMSe曲线也随之增加,但增加幅度较小,说明Δfset对双频磁共振方法的影响较小.当ρ处于100~1000 Ωm范围内,对于所有频率的RMSe均在10 nV以内.而当ρ=10 Ωm时,RMSe达到约100 nV以上.这与图 3中双频磁共振与偏共振核函数差值得到的结论一致,说明此时双频磁共振方法的误差较大,会导致错误的反演结果.
|
图 5 双频磁共振信号均方根误差随电阻率和设定频率偏移变化曲线 Fig. 5 The root mean square error of the DF-MRS signal as a function of resistivity and set frequency offset |
对于图 4中的仿真模型和双频磁共振信号(模型参数见2.2小节),使用复数QT反演方法(Müller-Petke et al., 2016),获取地下含水量和弛豫时间T2*的分布结果.为了在仿真实验中模拟野外环境,在双频磁共振信号中加入了水平为20 nV高斯噪声,并进行了抽道处理,抽道数为30.在反演过程中,假设初始模型为同一含水层,含水量和T2*分别为1%和50 ms.根据L曲线方法选择正则化参数为10000,经过50次迭代后,所有的反演数据与仿真数据的误差统计χ2值约等于1.
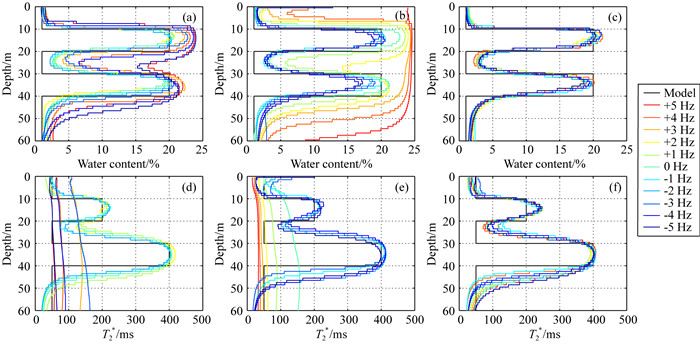
假设无法获得真实的Larmor频率fL,本文分别对比假设磁共振、假设偏共振和双频磁共振三种情况下的反演结果,见图 6所示.其中假设磁共振时,反演过程使用发射频率fT计算共振核函数,存在未知频率偏量Δfuk.假设偏共振时,根据接收信号估计的频率偏量Δf计算偏共振核函数,此时也可能存在Δfuk.当双频磁共振时,只需根据设定频率偏量Δfset计算偏共振核函数,无需考虑Δfuk的影响.
|
图 6 Larmor频率未知时假设磁共振、假设偏共振和双频磁共振情况下反演结果的对比 (a)和(d)是当Δfuk=-5~+5 Hz时假设磁共振情况反演得到的含水量和T2*;(b)和(e)是当Δfuk= -5~+5 Hz时假设偏共振情况反演得到的含水量和T2*;(c)和(f)是当Δfuk= -5 ~+5 Hz时使用双频磁共振方法反演得到的含水量和T2*. Fig. 6 Comparison of the inversion results for assuming on-MRS, assuming off-MRS and DF-MRS when the Larmor frequency is unknown (a) and (d) are the water content and T2* obtained by assuming on-MRS when Δfuk= -5~+5 Hz; (b) and (e) the water content and T2* obtained by assuming off-MRS when Δfuk=-5~+5 Hz; (c) and (f) are the water content and T2* obtained by inversion using DF-MRS when Δfuk=-5~+5 Hz. |
由图 6(a,d)中含水量和T2*的反演结果可知,假设磁共振情况,Δfuk为-2~+2 Hz时,反演结果均与仿真模型基本相似.当Δfuk为-5~-3 Hz和+3~+5 Hz,Δfuk的变化使得两个含水层和隔水层的含水量估计偏高(最大误差为19.9%),而T2*分布严重偏离了仿真模型,无法区分含水层和隔水层.显然,当fL未知时,假设共振的反演结果会显著降低含水量和T2*的估计精度.
当假设偏共振情况时,根据图 6(b, e)可知,当Δfuk为负偏移时,反演的含水量和T2*分布曲线基本能反映仿真模型.但当Δfuk≥0 Hz时,随着Δfuk增加,对两个水层的含水量估计误差逐渐变大,最高约4.6%.对隔水层的分辨能力越来越差,甚至出现假含水层.而T2*分布曲线在所有深度下基本无变化,即无法分辨含水层和隔水层.
对于双频磁共振情况,见图 6(c, f).当Δfuk从-5 Hz变化到+5 Hz时,对于两个含水层的含水量反演结果与仿真模型基本一致, 含水量最大误差为1.4%.T2*的反演结果只在第一层含水层与仿真模型稍有不同,T2*最大偏差为49.4 ms.对比这三种情况的反演结果,当无法获得Larmor频率时均存在未知频率偏量Δfuk,但双频磁共振方法将设定频率偏量Δfset的偏共振核函数应用到反演过程中,可以抵消Δfuk对含水量和T2*反演结果的影响,实现了对地下水文参数的准确解释.
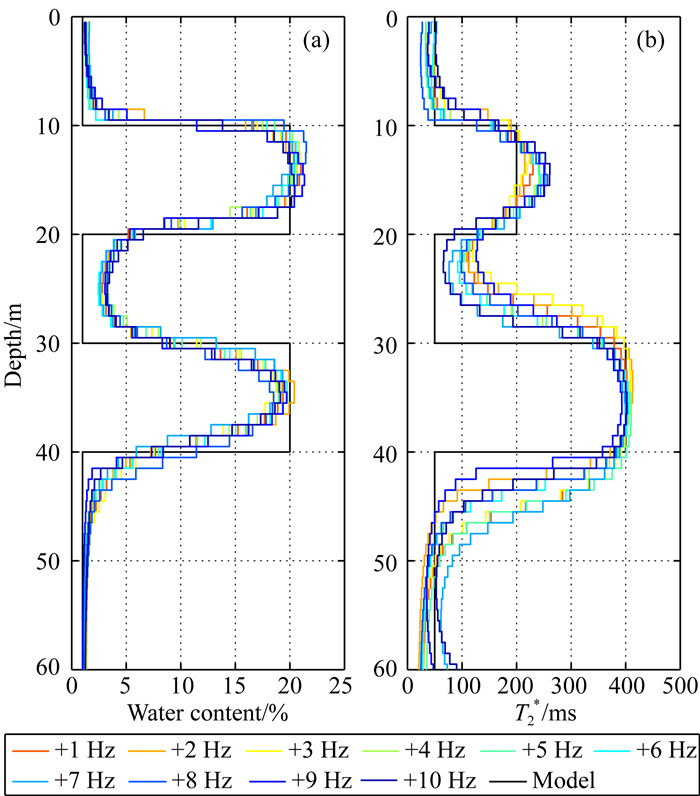
为了讨论Δfset变化对反演结果的影响,在图 7中给出了Δfuk为1 Hz和Δfset= 1~10 Hz时,双频磁共振反演得到的含水量和T2*随深度变化曲线.可以得到,含水量分布曲线与仿真模型基本相同,T2*分布曲线在第二层含水层与仿真模型拟合较好,在第一层含水层与仿真模型稍有差别(在15.3 ~61.1 ms之间),且Δfset越小,T2*偏差越小.
|
图 7 不同设定频率偏量Δfset情况下双频磁共振反演结果对比 (a)当Δfset= 1~10 Hz时反演得到的含水量;(b)当Δfset= 1~10 Hz时反演得到的T2*. Fig. 7 Comparison of DF-MRS inversion results with different set frequency offsets (a) The water content obtained by inversion when Δfset= 1~10 Hz; (b) T2* obtained by inversion when Δfset= 1~10 Hz. |
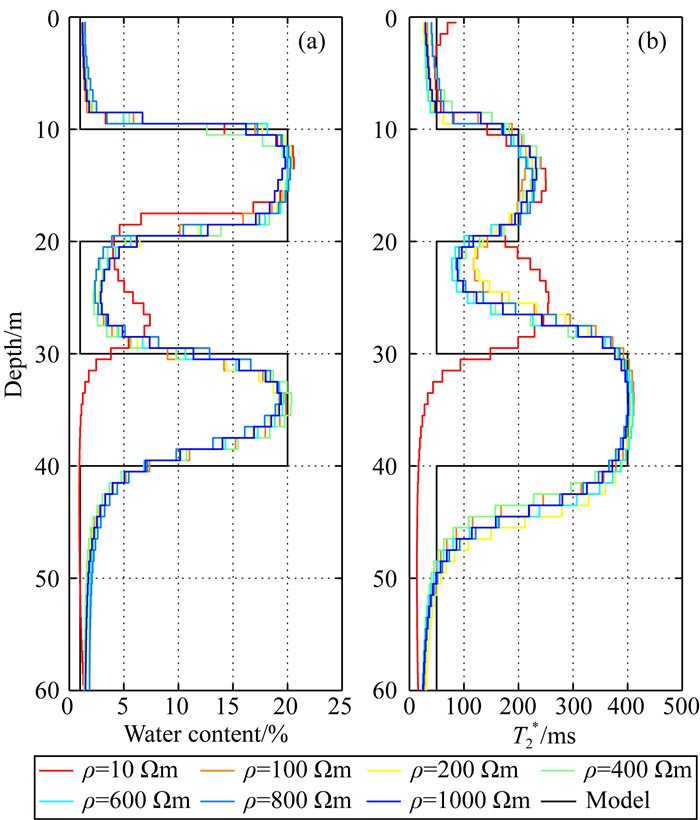
图 8给出了当电阻率ρ分别等于10, 100 Ωm, 200, 400, 600, 800, 1000 Ωm时,使用双频磁共振反演得到的含水量和T2*随深度变化曲线.当ρ在100~1000 Ωm范围内,对于两个含水层的含水量分布均能准确反映仿真模型.T2*分布曲线只在第二层含水层的边界未达到较好的反映,其他结果与仿真模型基本吻合.当ρ=10 Ωm时,只有浅层的含水量和T2*得到正确估计,而从反演结果无法准确反映深层含水层.原因有两方面:第一,电阻率低时,电磁波的穿透能力下降,导致无法获取深层含水层的信号;第二,由图 3f可知,当电阻率低时,双频共振的核函数与偏共振核函数的差异大,因此导致较大误差.这与图 5中ρ=10 Ωm时对应曲线反映的结果是一致的,说明低电阻率会影响双频共振方法解释的可靠性.
|
图 8 不同电阻率情况下双频磁共振反演结果对比 (a)当ρ=10, 100, 200, 400, 600, 800, 1000 Ωm时反演得到的含水量;(b)反演得到的T2*. Fig. 8 Comparison of DF-MRS inversion results for different resistivities (a) The water content obtained by inversion when ρ=10, 100, 200, 400, 600, 800, 1000 Ωm; (b) T2* obtained by inversion. |
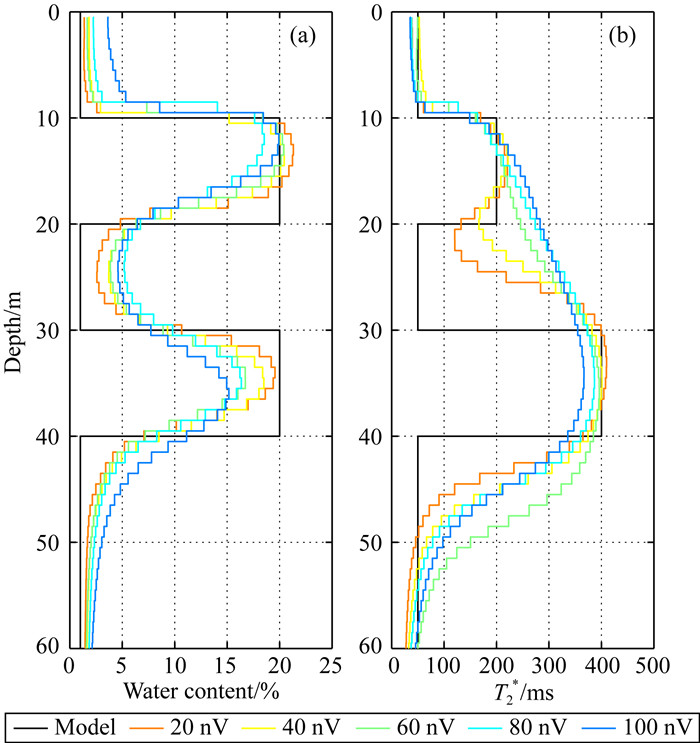
利用图 4中的仿真模型和当Δfset= 3 Hz和Δfuk=1 Hz时的双频磁共振信号,分别加入水平为20~100 nV的高斯噪声,反演结果如图 9所示.对于含水量曲线,随着噪声水平增加,第一层含水层反演结果稍有偏差.而在第二层含水层的偏差较大,在噪声水平为100 nV时达到4.9%.对于T2*曲线,当噪声较大(>60 nV)时,已无法区分含水层和隔水层边界,但是含水层内的T2*估计较好.说明虽然噪声水平对反演结果影响较大,但是在较高噪声水平时,双频磁共振方法仍然能够获得可靠的反演结果.
|
图 9 不同噪声水平情况下双频磁共振反演结果对比 (a)当噪声水平分别为20, 40, 60, 80, 100 nV时反演得到的含水量;(b)反演得到的T2*. Fig. 9 Comparison of DF-MRS inversion results for different noise levels (a) The water content obtained by inversion when the noise levels are 20, 40, 60, 80, 100 nV, respectively; (b)T2* obtained by inversion. |
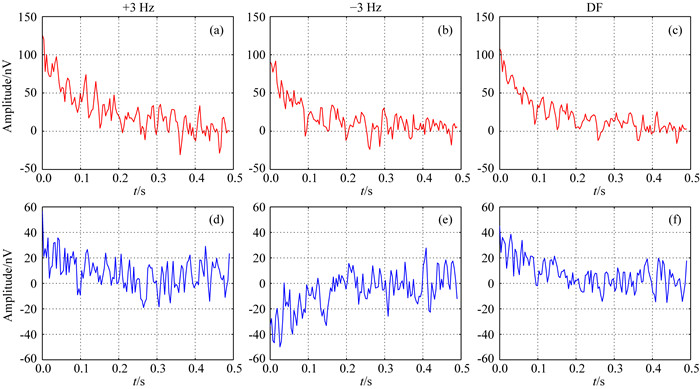
为了验证双频磁共振方法的有效性,利用吉林大学JLMRS地下水探测仪器进行了野外实验.测试地点选择在长春市郊烧锅镇的太平池水库附近,原因在于在该地进行过多次磁共振实验,环境噪声水平不高,并且有先验的钻探结果可供对比.结合资料得到该地含水层构造为:(1)地下0~13 m,黏土质砂层,平均含水量为2%;(2) 13~25 m,细砂和中砂层,平均含水量12%;(3) 25~45 m,黏土质砂层,平均含水量为4%;(4) 45~62 m,细砂层,平均含水量为7%.测量地点的平均B0为54720 nT,在一天内变化小于12 nT,对应fT为2333±0.5 Hz,I为62.11°,测量地下电阻率约为100~300 Ωm.采用单匝正方形发射和接收线圈,边长均为50 m;脉冲矩q在0.5~10 As之间按照对数间隔,数量为20个,每组q下重复测量32次.测量噪声水平平均为11 nV.图 10给出了在q= 1.2 As时,实测双频(2330 Hz和2336 Hz)磁共振信号的实部和虚部曲线.
|
图 10 野外实测双频磁共振信号 (a)和(d) q=1.2 As时实测2336 Hz(+3 Hz)信号实部和虚部曲线;(b)和(e) q=1.2 As时实测2330 Hz(-3 Hz)信号实部和虚部曲线;(c)和(f)计算得到的双频磁共振信号的实部和虚部曲线. Fig. 10 Field measured DF-MRS signals (a) and (d) are the real and imaginary curves of the 2336 Hz (+3 Hz) signal when q=1.2 As; (b) and (e) are the real and imaginary curves of the 2330 Hz (-3 Hz) signal are measured when q=1.2 As; (c) and (f) are the real and imaginary curves of the calculated DF-MRS signals. |
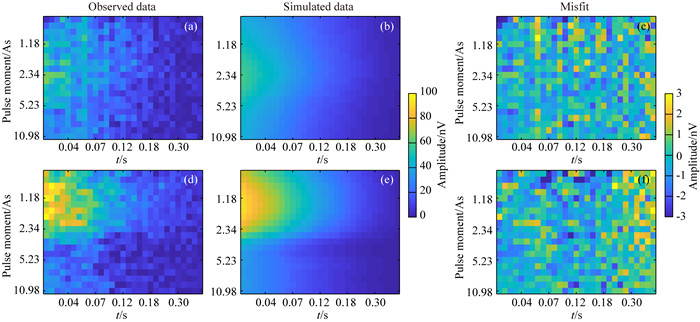
为了说明实测数据与反演数据的吻合情况,图 11(a, d)分别显示了实测2336 Hz(+3 Hz)和2330 Hz (-3 Hz)信号经双频磁共振方法处理后得到观测数据的实部和虚部.图 11(b, e)分别示出了对应的反演数据,可以看到反演数据准确地吻合观测数据.为了更好地验证双频磁共振数据质量,图 11(c, f)分别给出了观测数据和反演数据的实部、虚部误差的χ2估计值.总体而言,数据吻合较好,误差随机出现,χ2=1.06.
|
图 11 双频磁共振观测数据、反演数据和二者误差 (a)和(d)经双频磁共振方法处理后得到观测数据的实部和虚部;(b)和(e)对应反演数据的实部和虚部;(c)和(f)观测数据和反演数据的实部和虚部误差. Fig. 11 DF-MRS observation data, inversion data, and misfit (a) and (d) are the real and imaginary parts of the observed data processed by the DF-MRS method; (b) and (e) correspond to the real and imaginary parts of the inversion data; (c) and (f) are the real and imaginary misfits of the observed and inverted data. |
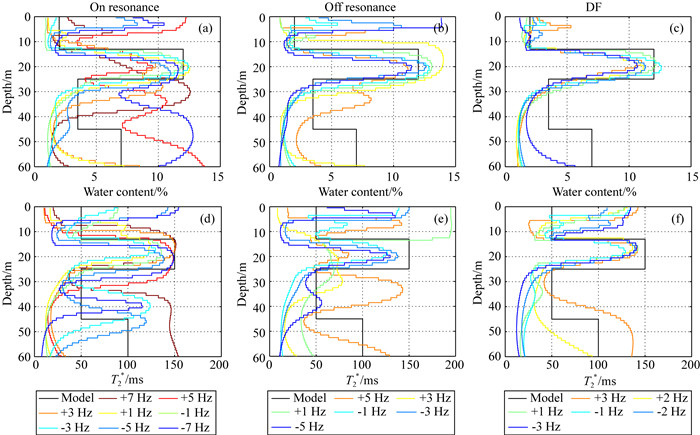
图 12给出了对于假设磁共振、假设偏共振和双频磁共振方法得到的反演结果对比.在反演过程中,假设初始模型为同一含水层,含水量为5%,T2*为50 ms.根据L曲线选择正则化参数为20000,经过70次迭代,根据分布得到数据误差统计χ2≈1.
|
图 12 实测数据假设磁共振、假设偏共振和双频磁共振的反演结果对比 (a)和(d)当Δfuk= -7~+7 Hz时假设磁共振情况反演的含水量和T2*;(b)和(e)是当Δfuk= -5~+5 Hz时假设偏共振情况反演的含水量和T2*;(c)和(f)是当Δfuk= -3~+3 Hz时使用双频磁共振方法反演的含水量和T2*. Fig. 12 Comparison of inversion results of the measured data correspond to assuming on-MRS, assuming off-MRS and DF-MRS (a) and (d) water content and T2* of the assumed on-MRS when Δfuk= -7~+7 Hz; (b) and (e) are the water content and T2* of the assumed off-MRS when Δfuk= -5~+5 Hz; (c) and (f) are the water content and T2* using the DF-MRS method when Δfuk= -3~+3 Hz. |
图 12 (a, d)是忽略Δfuk的情况下,假设均采用共振核函数时的反演结果.可以得到只有当fT和fL接近时(±1 Hz),反演结果的含水量和T2*与已知资料相近.当Δfuk较大时,反演误差较大,如在浅层(<5 m)处出现假含水层,第二层的含水量偏低,第三层的含水量偏高等.随着Δfuk增大,反演结果的误差也随之增大,当Δfuk=±7 Hz时已经不能反映地下含水层的真实分布情况.图 12 (b, e)是采用+2 Hz偏共振核函数的反演结果,与对应的仿真结果类似,Δfuk为正偏移时除了在浅层出现假含水层,反演结果与钻探结果相近,而在负偏移时反演结果误差较大.
图 12 (c, f)是经双频磁共振方法采用Δfset偏共振核函数得到的反演结果,反演结果与假设磁共振和偏共振情况相比,含水量和T2*分布能够正确反演地下含水层分布情况.只是对于深层(大于45 m)含水层,由于发射电流有限,且电阻率较低,未能获得有效的反演结果.因此, 通过实测数据反演结果可以证明,当Larmor频率未知时,相比于假设磁共振和偏共振情况需要准确获得Δfuk,本文提出的双频磁共振方法能在忽略Δfuk影响的基础上获得更准确的地下含水层分布.
4 结论由于地磁场在空间上分布不均匀,以及存在外界磁性干扰等问题,产生磁共振现象的Larmor频率难以准确确定,导致存在未知频率偏量的偏共振激发.本文针对未知Larmor频率情况下难以准确探测地下水的问题,提出地面双频磁共振探测方法.在估计的Larmor频率两侧,根据设定频率偏量进行两次偏共振激发并计算偏共振核函数,对双频磁共振探测数据进行反演,从而消除未知频率偏量对含水量和T2*反演结果的影响.
仿真实验从灵敏度核函数、信号虚实部特性,以及不同频率偏差、电阻率大小、噪声水平对双频磁共振的信号以及反演结果影响等方面展开.结果表明,当地下电阻率大于100 Ωm时,双频磁共振的核函数与设定频率的偏共振核函数基本相当,虚部最大误差小于10 nV.当电阻率小于100 Ωm时,两者的偏差较大.双层含水模型的仿真结果指出,设定频率偏量在1~10 Hz范围内,双频磁共振信号与偏共振信号的差值曲线较小,最大值小于3 nV,因此可以利用偏共振核函数度对双频磁共振信号进行反演.通过假设磁共振、假设偏共振和双频磁共振的反演结果得到,未知频率偏量在-5~+5 Hz范围内,双频磁共振均能获得准确的反演结果,而假设共振只能在-2~+2 Hz范围内,假设偏共振只能在部分范围内获得较准确的反演结果.通过改变设定频率偏量得到,双频磁共振均能得到较好的反演结果.但是当环境噪声增大时,或电阻率减小时,反演结果逐渐变差,尤其是深层含水层的结果严重偏离仿真模型.
最后,本文通过野外实测数据证明了双频磁共振探测方法的有效性.双频磁共振数据反演得到的含水量和T2*与钻探结果基本相符,而假设磁共振和假设偏共振时,反演结果均存在较大的偏差.本文提出的双频磁共振探测方法是在最新的频率环的基础上进行的改进和提升,解决了频率环要求未知频率偏量尽量小的限制.双频磁共振方法只需知道Larmor频率的范围区间即可消除未知频率偏量的影响.但是电阻率是影响双频磁共振的重要因素,因此在下一步的研究中将解决低电阻率情况下的双频磁共振准确反演问题.
Behroozmand A A, Dalgaard E, Christiansen A V, et al. 2013. A comprehensive study of parameter determination in a joint MRS and TEM data analysis scheme. Near Surface Geophysics, 11(5): 557-567. DOI:10.3997/1873-0604.2013040 |
Behroozmand A A, Keating K, Auken E. 2015. A review of the principles and applications of the NMR technique for near-surface characterization. Surveys in Geophysics, 36(1): 27-85. DOI:10.1007/s10712-014-9304-0 |
Behroozmand A A, Esben A, Fiandaca G, et al. 2016. Increasing the resolution and the signal-to-noise ratio of magnetic resonance sounding data using a central loop configuration. Geophysical Journal International, 205(1): 243-256. DOI:10.1093/gji/ggw004 |
Bloch F. 1946. Nuclear induction. Physical Review, 70(7-8): 460-474. DOI:10.1103/PhysRev.70.460 |
Chen Q, Marble A E, Colpitts B G, et al. 2005. The internal magnetic field distribution, and single exponential magnetic resonance free induction decay, in rocks. Journal of Magnetic Resonance, 175(2): 300-308. |
Girard J F, Legchenko A, Boucher M. 2005. Stability of MRS signal and estimation of data quality. Near Surface Geophysics, 3(3): 187-194. DOI:10.3997/1873-0604.2005013 |
Grombacher D, Walbrecker J O, Knight R. 2014. Imparting a phase during excitation for improved resolution in surface nuclear magnetic resonance. Geophysics, 79(6): E329-E339. DOI:10.1190/geo2013-0452.1 |
Grombacher D, Knight R. 2015. The impact of off-resonance effects on water content estimates in surface nuclear magnetic resonance. Geophysics, 80(6): E329-E342. DOI:10.1190/geo2014-0402.1 |
Grombacher D. 2018. Numerically optimized modulations for adiabatic pulses in surface nuclear magnetic resonance. Geophysics, 83(2): JM1-JM14. |
Grombacher D, Dlugosch R, Grunewald E, et al. 2018. Frequency cycling to alleviate unknown frequency offsets for adiabatic half-passage pulses in surface nuclear magnetic resonance. Geophysics, 83(5): JM29-JM38. DOI:10.1190/geo2017-0701.1 |
Grombacher D, Müller-Petke M, Knight R. 2016. Frequency cycling for compensation of undesired off-resonance effects in surface nuclear magnetic resonance. Geophysics, 81(2): WB33-WB48. |
Grunewald E, Knight R. 2012. Nonexponential decay of the surface-NMR signal and implications for water content estimation. Geophysics, 77(1): EN1-EN9. |
Grunewald E, Grombacher D, Walsh D. 2016. Adiabatic pulses enhance surface nuclear magnetic resonance measurement and survey speed for groundwater investigations. Geophysics, 81(4): WB85-WB96. |
Hürlimann M D, Helmer K G, Sotak C H. 1998. Dephasing of Hahn echo in rocks by diffusion in susceptibility-induced field inhomogeneities. Magnetic Resonance Imaging, 16(5-6): 535-539. DOI:10.1016/S0730-725X(98)00059-9 |
Hoult D I. 2000. The principle of reciprocity in signal strength calculations-A mathematical guide. Concepts in Magnetic Resonance, 12(4): 173-187. DOI:10.1002/1099-0534(2000)12:4<173::AID-CMR1>3.0.CO;2-Q |
Jiang C D, Wang Q, Du G F, et al. 2018. Characteristics of surface nuclear magnetic off-resonance signal and complex envelope inversion. Acta Physica Sinica (in Chinese), 67(1): 013302. |
Jiang C D, Müller-Petke M, Wang Q, et al. 2018. Two-dimensional QT inversion of complex magnetic resonance tomography data. Geophysics, 83(6): JM65-JM75. DOI:10.1190/geo2017-0756.1 |
Legchenko A, Valla P. 2002. A review of the basic principles for proton magnetic resonance sounding measurements. Journal of Applied Geophysics, 50(1-2): 3-19. DOI:10.1016/S0926-9851(02)00127-1 |
Legchenko A, Vouillamoz J M, Roy J. 2010. Application of the magnetic resonance sounding method to the investigation of aquifers in the presence of magnetic materials. Geophysics, 75(6): L91-L100. DOI:10.1190/1.3494596 |
Legchenko A, Vouillamoz J M, Lawson F M A, et al. 2016a. Interpretation of magnetic resonance measurements in the varying earth's magnetic field. Geophysics, 81(4): WB23-WB31. |
Legchenko A, Vouillamoz J M, Lawson F M A, et al. 2016b. Interpretation of magnetic resonance measurements in the varying earth's magnetic field. Geophysics, 81(4): WB23-WB31. DOI:10.1190/geo2015-0474.1 |
Levitt M H. 2008. Spin dynamics:Basics of nuclear magnetic resonance. 2nd ed. New Jersey: John Wiley and Sons Ltd.
|
Lin J, Jiang C D, Lin T T, et al. 2013. Underground magnetic resonance sounding (UMRS) for detection of disastrous water in mining and tunneling. Chinese Journal of Geophysics (in Chinese), 56(11): 3619-3628. DOI:10.6038/cjg20131103 |
Lin J, Zhang J, Yi X F. 2017. Design and experiment of small antenna for magnetic resonance sounding in underground applications. Chinese Journal of Geophysics (in Chinese), 60(11): 4184-4193. DOI:10.6038/cjg20171106 |
Lin J, Zhao Y, Yi X F, et al. 2018. Characteristics of underground magnetic resonance and advanced detection of hazardous water. Chinese Journal of Geophysics (in Chinese), 61(4): 1615-1627. DOI:10.6038/cjg2018L0444 |
Müller-Petke M, Braun M, Hertrich M, et al. 2016. MRSmatlab-A software tool for processing, modeling, and inversion of magnetic resonance sounding data. Geophysics, 81(4): WB9-WB21. DOI:10.1190/geo2015-0461.1 |
Trushkin D V, Shushakov O A, Legchenko A V. 1995. Surface NMR applied to an electroconductive medium. Geophysical Prospecting, 43(5): 623-633. DOI:10.1111/j.1365-2478.1995.tb00271.x |
Walbrecker J O, Hertrich M, Green A G. 2011. Off-resonance effects in surface nuclear magnetic resonance. Geophysics, 76(2): G1-G12. |
Wang Q, Tian B F, Zhang J, et al. 2018. Surface nuclear magnetic resonance signal extraction based on the sparse representation. Chinese Journal of Geophysics (in Chinese), 61(8): 3446-3456. DOI:10.6038/cjg2018L0608 |
Weichman P B, Lavely E M, Ritzwoller M H. 2000. Theory of surface nuclear magnetic resonance with applications to geophysical imaging problems. Physical Review E, 62(1): 1290-1312. DOI:10.1103/PhysRevE.62.1290 |
Xiao L Z, Xie Q M, Xie R H, et al. 2013. Noise reduction for NMR logging with regularization-heursure algorithm. Chinese Journal of Geophysics (in Chinese), 56(11): 3943-3952. DOI:10.6038/cjg20131136 |
蒋川东, 王琦, 杜官峰, 等. 2018. 地面核磁偏共振响应特征与复包络反演方法. 物理学报, 67(1): 013302. |
林君, 蒋川东, 林婷婷, 等. 2013. 地下工程灾害水源的磁共振探测研究. 地球物理学报, 56(11): 3619-3628. DOI:10.6038/cjg20131103 |
林君, 张健, 易晓峰. 2017. 地下核磁共振小尺寸线圈设计和实验. 地球物理学报, 60(11): 4184-4193. DOI:10.6038/cjg20171106 |
林君, 赵越, 易晓峰, 等. 2018. 地下磁共振响应特征与超前探测. 地球物理学报, 61(4): 1615-1627. DOI:10.6038/cjg2018L0444 |
王琦, 田宝凤, 张健, 等. 2018. 基于稀疏表示的地面磁共振信号提取方法. 地球物理学报, 61(8): 3446-3456. DOI:10.6038/cjg2018L0608 |
肖立志, 谢庆明, 谢然红, 等. 2013. 核磁共振测井的正则化-启发式阈值降噪研究. 地球物理学报, 56(11): 3943-3952. DOI:10.6038/cjg20131136 |
 2020, Vol. 63
2020, Vol. 63


