断层崖广泛地分布于正断层或正断层分量明显的断层下盘,是识别断层的重要构造地貌特征,如温泉盆地西缘盆地断层崖、华山北麓断层崖、阿克斯希尔断层崖、南斯巴达断层崖(吴中海等, 2005; Tsimi et al., 2015; Topal et al., 2016).断层错动形成的断层崖,在地表过程的作用下,开始了剥蚀和堆积的过程,因此在不同发育阶段具有不同的几何形态(邓起东等, 1985).野外观测到的断层崖呈现不同的形态特征,如断层陡坎、断层三角面、断层梯形面等(程谦恭, 1988; Topal et al., 2016).
构造地貌分析可以快速有效地定量或半定量判断新构造期间的断裂活动性(黄小巾等, 2018).根据断层陡坎的演变规律,断层陡坎的演化被分为了自由面阶段和碎屑坡阶段(Wallace, 1978).Kokkalas等人(2005)基于扩散方程的解析解,将断层陡坎碎屑坡阶段的演化简化为一维扩散问题,建立了断层陡坎高度、坡度角与时间和扩散系数的关系,推算了希腊中部已知年代的断层陡坎的扩散系数.观测和数值模拟结果表明北贝加尔湖的断层崖高度与断层垂直滑动速率间存在线性关系(Petit et al., 2009a, 2009b).基于DEM数据的统计研究表明,断层三角面坡度角与断层滑动速率存在线性关系(Tsimi et al., 2015).
断层崖的形成是断层和地表过程共同作用的结果,但是这些不同的过程是如何影响断层崖的形态和几何特征的?如何通过断层崖的形态和几何特征,反推断层特征活动性质和地表过程环境?为了回答这些问题,本文建立了二维地表演化数值模型,对断层崖形态和几何特征的主要影响因素进行了系统的数值模拟研究.
1 模型与数值方法 1.1 控制方程断层陡崖是正断层活动和地表演化耦合作用的结果,因此模拟正断层陡崖演化的动力学过程,包括模拟正断层滑动和地表演化过程两部分.断层滑动过程相对地表过程来说,时间尺度很短.因此,在模型中可以通过沿断层面移动节点来简化断层的滑动过程.进而,控制方程只涉及地表演化过程:
(1) 河流下切过程
模型中河流下切过程对地表的侵蚀作用采用了河流水力侵蚀模型(Howard, 1994; Lague, 2014),即假设河流下切对地表的改造作用与汇流面积以及局部的地形梯度呈正相关关系:
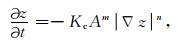
|
(1) |
式中z为高程,t为时间,Kc为河流下切系数,A为汇流面积,▽z为地形局部坡度.其中,汇流面积A用于替代水流量以便对计算进行简化(Istanbulluoglu et al., 2003).通常取指数参数m=1/2,n=1(Stock et al., 1999).
(2) 山坡蠕移过程
山坡上的物质搬运主要受重力控制,由于冻融、干湿、冷热交替和生物活动,导致山坡上形成了可以通过蠕移、滑坡等物理过程向坡下方向移动的物质.这里,我们仅考虑长时间山坡蠕移过程产生的物质搬运的平均作用,不考虑滑坡过程,因此采用线性扩散过程来进行模拟(Culling, 1960, 1963):
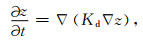
|
(2) |
式中Kd为山坡蠕移系数.
1.2 数值方法(1) 水流流向和汇流面积
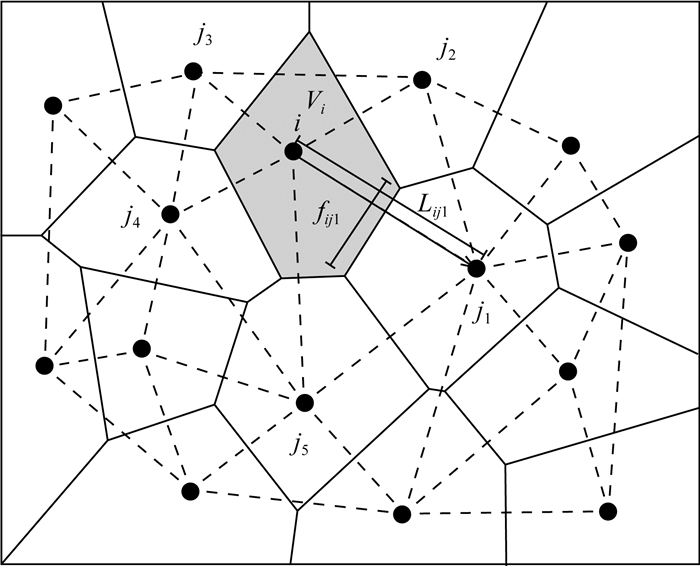
在二维空间上,构建德洛内三角剖分(Delaunay triangulation)和其对应的泰森多边形(Voronoi diagram)(Aurenhammer, 1991).选择德洛内三角形的顶点作为控制节点(图 1中的黑色实心圆),泰森多边形作为控制体积(图 1中黑色多边形).选择单向流模型,即水流和水流携带的物质从控制节点流向高程小于节点高程且坡度最大的相邻控制节点(图 1中箭头).节点的汇流面积是节点上游所有节点对应控制体积(图 1中灰色区域)的面积之和.采取CASCADE算法,对水流流向和节点的汇流面积进行计算(Braun et al., 1997).
|
图 1 节点与控制体积 节点与控制体积示意图.模型区域被分为有限个控制体积,用黑色多边形表示.虚线表示相邻节点(黑色圆点)的间距.灰色区域表示控制体积.箭头表示流向. Fig. 1 Node and control volume Schematic diagram of node and control volume. The study zone is divided into several control volumes (black polygons). Dash lines are spacings between adjacent nodes (solid black circle). Grey area is the control volume. The arrow is the flow direction. |
(2) 有限体积格式
扩散项的处理,对节点i,在控制体积Vi内积分(图 1),根据散度定理可得
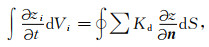
|
(3) |
其中,n是控制体积表面外法线方向单位矢量,S是控制体积的外边界.
假设时间积分步长足够小,控制体积内的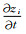
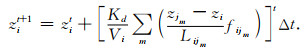
|
(4) |
CFL条件(Courant-Friedrichs-Lewy condition)作为计算流体力学中判断格式的稳定性和收敛性的必要条件,其原理是差分方程的依赖域必须包含相应微分方程的依赖域.在我们本文采用的时间显式格式中,根据CFL条件,时间步长需要满足(Refice et al., 2012)
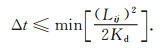
|
(5) |
河流下切项的处理,对节点i,在控制体积Vi内积分,空间上采用中心差分,时间上采用向前差分,整理后可得
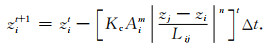
|
(6) |
根据CFL条件,时间步长需满足(Refice et al., 2012):
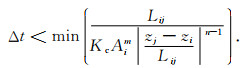
|
(7) |
(3) 正断层活动
我们根据给定的断层滑动速率和滑动周期,在每次正断层活动时,沿断层面移动断层下盘(x≥100 m)的节点,上盘节点位置保持不变.随着断层的不断活动,断层面附近的节点距离和控制体积逐渐加大时,我们进行网格重划分并将节点高程插值到新的网格上.
1.3 模型与初边值条件
我们采用1500 m×1500 m模型区域来研究正断层陡崖的演化,模型的平均节点间距为5 m,断层位置是x=100 m.模型的底边(x=0)为开放边界,即边界处节点高程一直为零(z≡0),开放边界处节点的物质均运出,用来模拟侵蚀基准面.模型的其他边界为封闭边界,即在垂直于边界方向不允许物质流入流出(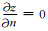
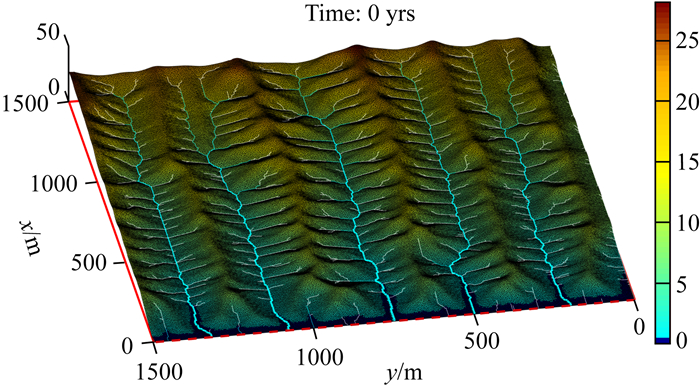
图 2展示了模型的初始地形:一组准垂直于底边界,地形平缓的山脊山谷(绘图时,高程被放大了4倍).初始地形是保持边界条件不变,给定随机高程(0≤z≤1),对该区域施加均匀的隆升速率(u=1×10-3m·yr-1)、河流下切系数(Kc=5×10-4yr-1)和山坡蠕移系数(Kd=1×10-2m2·yr-1)情况下演化得到的.
|
图 2 模型的初始与边界条件 高程方向放大了4倍显示的初始地形.蓝绿色和白色线条是初始河网(汇流面积A>1×103m2),其中蓝绿色线条是主河道(汇流面积A>1×104m2).边界条件用红色线表示,其中虚线表示开放边界,实线表示封闭边界. Fig. 2 Initial and boundary conditions Initial topography with elevation magnified 4 times. Cyan and white lines are the initial river network (Contributing area A > 1×103m2), where cyan lines are main channel (Contributing area A > 1×104m2). Red lines indicate the boundary conditions, dash line: open boundary; solid line: closed boundary. |
我们的模拟旨在通过对比不同参数演化得到的正断层陡崖的形态与几何特征,归纳不同形态的正断层陡崖的形成机制及其控制因素,并建立正断层陡崖几何特征与正断层活动性质的关系.
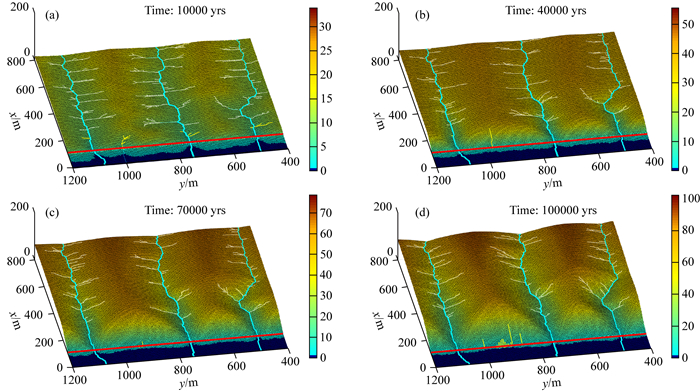
2.1 断层三角面的演化过程在算例1中,我们探讨断层三角面形态的正断层陡崖的演化过程.图 3展示了河流下切系数Kc=1×10-4yr-1,扩散系数Kd=3×10-2m2·yr-1,断层平均滑动速率vf=1×10-3m·yr-1,断层倾角dip=60°,断层滑动周期T=1×103yrs情况下的正断层陡崖演化过程.结果显示,断层(图中红色线)开始活动后,断层上盘的物质被剥离并输运到开放边界后流出,因此该区域(x < 100 m)的高程逐渐减小到侵蚀基准面;断层的活动导致上下盘形成高差,促使断层崖上游的次级河道(图中白色线)不断切割山脊的侧翼,主河道不断切割山谷,断层崖上游地形逐渐从平缓(图 3a)变得起伏(图 3d);除此之外,断层活动形成的高差也促使断层面上形成沟壑(图中黄色线).断层面上的物质沿着这些沟壑被剥离(图 3b).断层崖的顶点从圆润逐渐变的尖锐(图 3b-d),进而沿断层走向形成了三角面状的陡崖(图 3d).
|
图 3 断层三角面的演化过程 实际模型(1500×1500 m)中的一部分(800×800 m)的断层三角面地形和河道.蓝绿色线表示主河道,白色线表示断层崖上游的次级河道,黄色线表示断层崖上的沟壑,红色线表示断层位置. Fig. 3 Evolution of triangular facets Topography and river network of triangular facets. Enlargement (800×800 m) of the numerical box (1500×1500 m) is shown. Cyan lines are the main channel. White lines are secondary channels upstream of the fault scarp. Yellow lines are gullies that cut fault scarp. Red lines indicate the fault trace. |
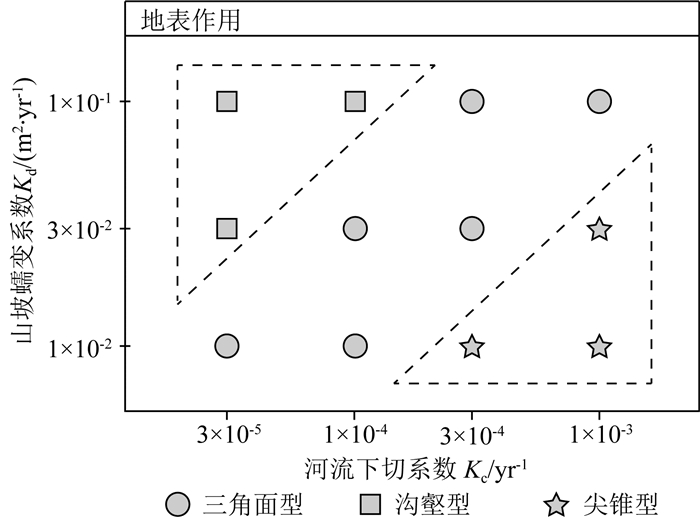
我们通过改变山坡蠕移系数,讨论山坡蠕移作用对正断层陡崖形态的影响.图 4a-b展示了其他参数与算例1相同,山坡蠕移系数减小到Kd=1×10-2m2·yr-1后正断层陡崖的演化结果.结果显示,断层崖上游的山脊山谷的起伏度更大,三角面的顶点也更明显和尖锐.河流在断层崖上切割出的小沟壑难以被减小的山坡蠕移作用填平,形成了带有沟壑的三角面(图 4a-b).
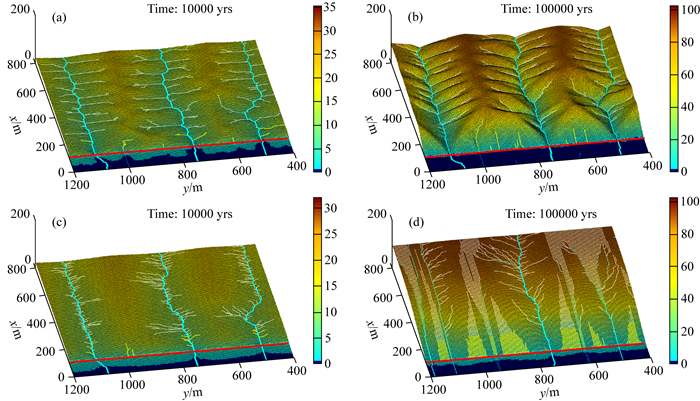
|
图 4 不同山坡蠕移系数条件下的地形和河网特征 Fig. 4 Topography and river network with different hillslope diffusion coefficient |
当山坡蠕移系数增大到Kd=1×10-1m2·yr-1后,由于山坡蠕移作用,主河道逐渐被填充,断层崖上游的山脊山谷的起伏度更低.一开始时,主河道还是沿原先位置侵蚀山谷(图 4c),随着山脊侧翼的山坡蠕移过程逐渐将原先的主河道填平,原先的主河道消失.沿断层崖向上游的溯源侵蚀形成了一组准垂直于断层走向的浅沟壑(图 4d蓝绿色线),成为新的主河道.由于地形起伏度太小,新的次级河道准垂直于断层,平均地分布于上游(图 4d白色线).
2.2.2 河流下切过程对陡崖特征的影响我们通过改变河流下切系数,讨论河流下切过程对正断层陡崖形态的影响.图 5a-b展示了其他参数与算例1相同,河流下切系数增大到Kc=1×10-3yr-1情况下正断层陡崖的演化结果.结果显示,断层崖上游次级河道对山脊侧翼的下切加剧,使山脊更加尖锐,山脊侧翼更明显.主河道对山谷的下切加剧,导致山谷处的高程减小.断层崖上演化出了多条深切的沟壑,将断层崖分割成了多个次级三角面(图 5a),次级三角面上也发育了多条沟壑,进而形成了再次一级的三角面(图 5b).这种全区域加剧的河流下切过程导致区域地形高度下降.
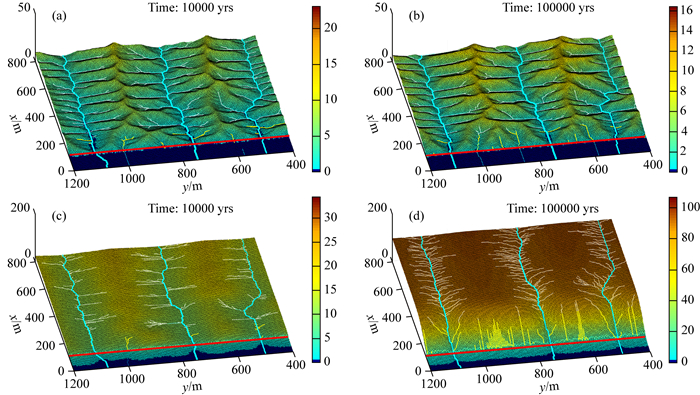
|
图 5 不同河流下切系数条件下的地形和河网特征 Fig. 5 Topography and river network with different river incision coefficient |
图 5c-d展示了其他参数保持不变,河流下切系数减小到Kc=3×10-5yr-1情况下的陡崖形态.结果显示,河流下切作用减弱使得上游山脊山谷非常平缓,在原河道位置形成了一组准垂直于断层走向的浅沟壑(图 5c).随着时间的发展,下盘逐渐抬升,沟壑逐渐加深(图 5d),形成了一组梯形面.另外,因为河流下切作用的降低,上盘的物质没有完全被剥蚀,有所留存(x < 100 m).与图 4c-d所示的例子不同,山坡蠕移作用并没有填平原有河道,因此本例中的浅沟壑仍处于原河道位置.
2.2.3 地表过程参数的敏感性分析我们通过改变河流下切系数和山坡蠕移系数,对地表过程对正断层陡崖形态的影响进行了测试.测试算例的河流下切系数3×10-5yr-1≤Kc≤1×10-3yr-1,扩散系数1×10-2m2·yr-1≤Kd≤1×10-1m2·yr-1,断层平均滑动速率vf=1×10-3m·yr-1,断层倾角dip=60°,断层滑动周期T=1×103yrs,演化时间为10万年(表 1算例1-12).根据演化时间10万年时的构造地貌形态,我们将正断层陡崖分为三种:沟壑型、三角面型和尖锥型.
沟壑型的特征是:断层崖上存在一组垂直于断层走向的沟壑,沟壑将断层崖分割成多个梯形或长方形(图 4d,5d);三角面型的特征是:断层崖上存在一组垂直于断层走向的沟壑,沟壑深切断层崖,将断层崖分割成多个三角形(图 3d,4b);尖锥型的特征是:沟壑深切断层崖,不完全垂直于断层走向,将断层崖切割成多级三角面和尖锥(图 5b).参数敏感性测试结果表明,当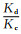
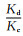
|
图 6 地表过程参数敏感性分析 Fig. 6 Landscape evolution parameter sensitivity tests |
此例中,我们采用了不同的断层滑动速率,图 7展示了断层平均滑动速率为vf=3×10-3m·yr-1和vf=3×10-4m·yr-1情况下正断层陡崖演化结果.结果显示,断层平均滑动速率不改变正断层陡崖的形态类型,演化得到的断层三角面的几何特征与算例1不同.我们引入基底长度BL、高度H、宽度W和坡度角S,对断层三角面的几何特征进行描述(Tsimi et al., 2015).
|
图 7 不同平均断层滑动速率条件下的地形和河网特征 Fig. 7 Topography and river network with different average slip rate |
在模型中,取主河道与断层位置的交点连线为三角面的基底,对应长度为基底长度;将三角面剖面中地形梯度发生变化的位置确定为三角面的顶点;三角面顶点到基底的距离为三角面宽度;宽度在垂直方向的投影为高度;三角面与水平面的夹角为坡度角.
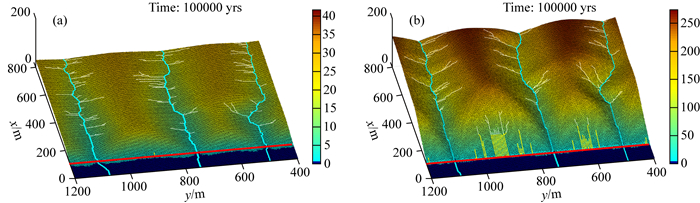
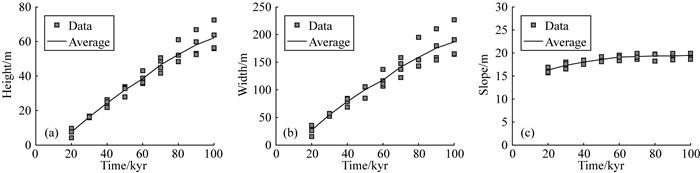
算例1中,基底长度BL不随时间变化,受控于初始河道的分布,共形成4个完整的断层三角面.每万年分别计算4个三角面的高度、宽度和坡度角.结果显示,高度H和宽度W随时间逐渐增大(图 8a-b),坡度角S在演化过程中基本不变(图 8c),由于地表演化对地形的改造,坡度角S远小于断层的倾角.当断层平均滑动速率增大到vf=3×10-3m·yr-1和降低到vf=3×10-4m·yr-1,高度H、宽度W和坡度角S的变化规律与算例1相同.
|
图 8 断层三角面几何特征的演化过程 Fig. 8 Evolution of geometrical characteristics of triangular facet |
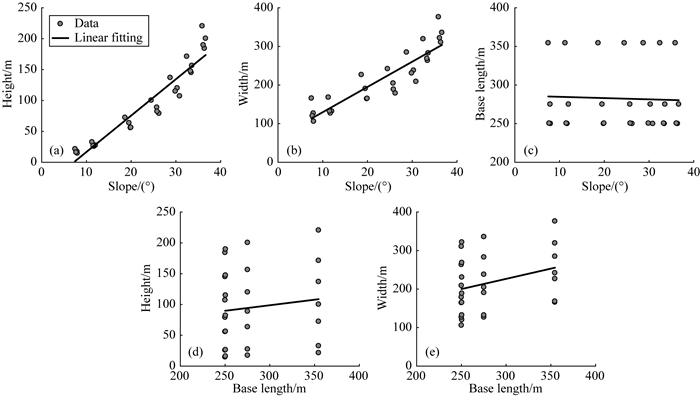
我们取滑动速率3×10-4m·yr-1<vf<3×10-3m·yr-1,不同滑动速率下的结果(表 1算例1, 13, 14,21-25).探讨相同地表演化环境下,三角面几何特征间的关系.结果显示,演化时间为100000年时,三角面高程与坡度角呈现很强的线性相关(图 9a);宽度与坡度角呈现很强的线性相关(图 9b);基底长度与坡度角无关(图 9c);高度与宽度在统计上与基底长度无关,但在给定相同断层滑动速率时,呈正相关(图 9d-e).这与基于DEM数据和统计学方法的地质观测在趋势上相符(Tsimi et al., 2015).差异主要在于实际观测中难以给定相同的地表演化环境.
|
|
表 1 数值模型采用的参数a Table 1 Parameters used in the numerical experimentsa |
|
图 9 断层三角面几何特征间关系 Fig. 9 Relationships between geometrical characteristics |
此例中,我们采用了不同的断层滑动周期,图 10展示了断层滑动周期T=3×102yrs和T=3×103yrs的情况下,正断层陡崖的形态和几何特征.结果表明,在地表演化参数不变的情况下,不同的断层滑动周期演化得到的均是有圆润顶部和平滑陡崖面的断层三角面,且三角面的基底长度、高度、宽度和坡度角的演化过程均相同.因此,正断层陡崖的形态和几何特征在中长时间尺度(104~105yr)下,与正断层的滑动周期无关.当断层平均滑动速率增大到vf=3×10-3m·yr-1和降低到vf=3×10-4m·yr-1,这一规律保持不变(表 1算例1, 13-20).
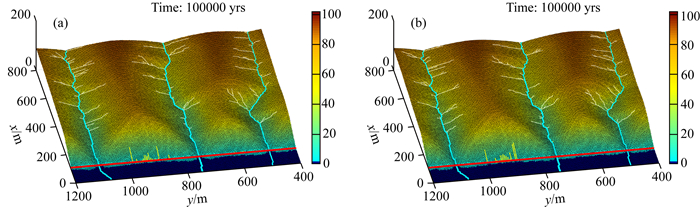
|
图 10 不同平均断层滑动周期条件下的地形和河网特征 Fig. 10 Topography and river network with different recurrence interval |
通过数值模拟,我们系统探讨了正断层陡崖特征的影响因素.这里,我们总结河流下切过程、山坡蠕移过程和断层活动特征影响正断层陡崖特征的动力学方式.
河流下切过程和山坡蠕移过程主要对正断层陡崖的形态特征产生影响.河流下切过程受汇流面积和局部坡度的影响,切割地表.断层活动后,在断层处形成高差,驱动河流沿主河道加剧切割山谷.山谷被切割后,与山脊形成高差,驱动河流沿山脊上的沟壑加剧切割山脊.除此之外,断层处的高差还驱动河流在断层面上溯源侵蚀产生沟壑,切割断层面(图 5).
山坡蠕移作用受重力作用的影响,将高处的物质搬运到低处,在地形上体现的是一种填平磨圆的效果.在断层崖上游,山坡蠕移作用将山脊的物质搬运至山谷,可能会填平山脊侧翼上的沟壑,进而影响山脊侧翼的平滑程度.在断层崖处,通过蠕移填平作用减少断层崖上沟壑的数量,并影响断层崖顶部的圆润程度(图 4).
断层平均滑动速率不改变正断层陡崖的形态特征,但对其几何特征产生影响(图 7).断层活动速率增加后,每次断层活动导致的上下盘之间的高差与断层速率呈正比.河流沿主河道溯源侵蚀山谷,导致的山脊和山谷间的高差与断层速率呈正比.由于山脊和山谷的水平距离与基底长度相关,即受主河道位置控制.主河道位置不变的情况下,山脊与山谷间的梯度与断层速率呈正相关.河流下切过程和山坡蠕移过程均与局部梯度呈正相关,因此其对地形的改造作用也与断层滑动速率呈正相关.因此,改变断层平均滑动速率不对正断层陡崖的形态特征产生影响.断层的活动周期在十万年时间尺度下与断层陡崖的形态和几何特征均无关(图 10).
3.2 地质启示断层活动速率通常是由地质学、地震学和大地测量学方法提供(李煜航等, 2014; 崔笃信等, 2019).然而,对于缺少相关数据或难以获得数据的区域,研究者们也尝试使用断层陡崖的数字高程信息来推算断层的变形信息(Petit et al., 2009a, 2009b; Tsimi et al., 2015).
我们考虑数值计算结果中主河道位置不变的三角面型正断层陡崖,排除河流强烈切割断层崖产生多级三角面后难以对断层陡崖的几何特征进行计算的情况.即基底长度仅受控于初始地形和主河道时,其他3个几何特征与断层滑动速率的关系(表 1算例1, 13, 14,21-25).结果显示,在相同的地表演化环境下,断层滑动速率与三角面高度、宽度和坡度角都呈较强的线性关系(图 11).
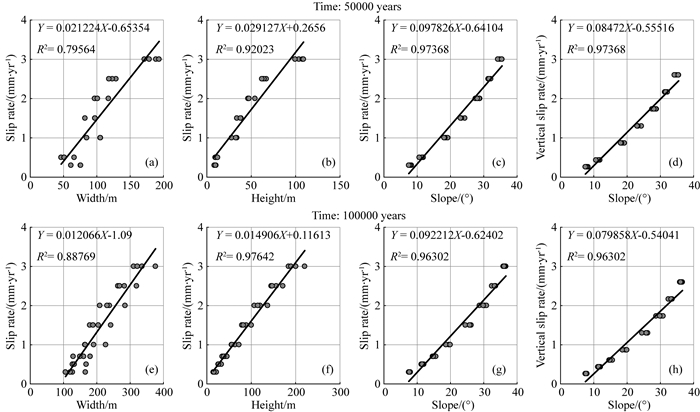
|
图 11 断层滑动速率与三角面型陡崖几何特征关系 Fig. 11 The relationship between the slip rate and the geometric characteristics of triangular faces |
三角面高度和宽度随演化时间增加,因此不同演化时间得到的线性关系不同.由于随着演化时间的增加,初始地形对断层崖的影响逐渐减小,三角面高度和宽度与滑动速率间的相关性增加(图 11a, b, e, f).因为数值实验中所有的断层倾角均为60°,因此三角面几何特征与断层滑动速率或断层垂直方向滑动速率的相关系数相同,线性拟合斜率相除为倾角的正弦值(图 11c, d, g, h).坡度角随演化时间的变化很小(图 8c),更适用于建立与断层滑动速率的关系(图 11c, d, g, h),推演十万年时间尺度下的地表演化环境.
Tsimi等(2015)使用DEM数据并采用统计学方法,分析了希腊和保加利亚的10条正断层的232个断层三角面,结合地质和年代学数据,取每条断层对应三角面参数的平均值,对三角面坡度角和高度与滑动速率进行了线性拟合,提出了三角面高度与滑动速率垂直分量间存在较弱的线性关系:
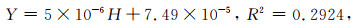
|
(8) |
其中,Y为断层滑动速率(单位为m·yr-1),H为三角面高度(单位为m),R2为最小二乘相关系数.
数值实验结果中,断层滑动速率与三角面高度的相关系数远大于观测拟合值(图 11).数值实验中用于拟合的三角面数据的演化时间相同.三角面高度随演化时间变化,因此观测结果中相关系数较低的原因可能与10条断层的演化时间差异或地表演化过程差异相关.
三角面坡度角与滑动速率间存在线性关系:
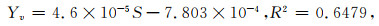
|
(9) |
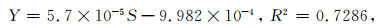
|
(10) |
其中,Y为断层滑动速率(单位为m·yr-1);Yv为竖直方向滑动速率,S为三角面坡度角(单位为°),R2为最小二乘相关系数.
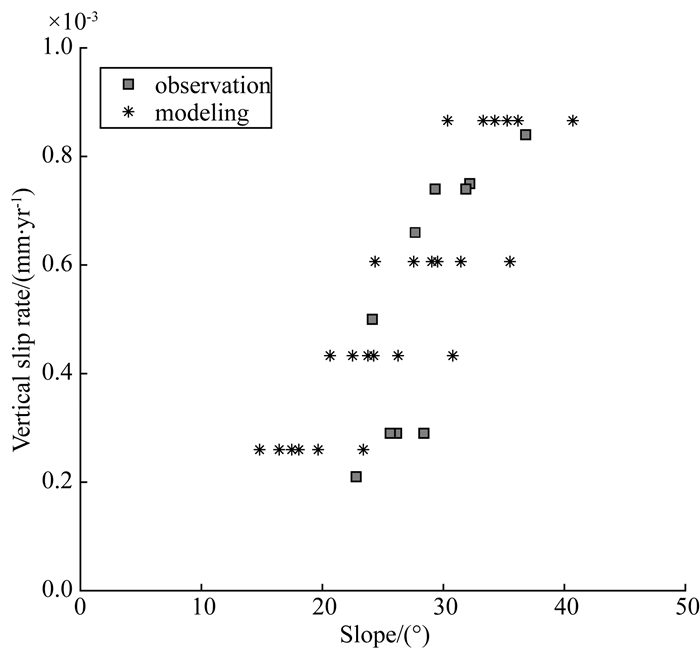
观测结果与通过数值实验得到的坡度角与滑动速率间存在的线性关系相符,但由于气候、岩性对地表演化环境的影响,观测结果与计算得到的线性关系相比更复杂,相关性更弱.观测结果中的10条断层均处在潮湿或半潮湿的环境下,岩性差异较大,包括:火山沉积岩、板状石灰岩、晶体石灰岩、新第三纪沉积岩、变质岩、火成岩、复理石、大理岩和花岗岩等(Tsimi et al., 2015).岩性和降水对河流下切系数和山坡蠕移系数会产生影响.数值实验结果表明,河流下切系数3×10-5yr-1≤Kc≤1×10-4yr-1,扩散系数2×10-3m2·yr-1≤Kd≤1×10-2m2·yr-1,断层平均滑动速率3×10-4m·yr-1<vf<1×10-3m·yr-1,断层倾角dip=60°的情况下(表 1算例26-53),三角面坡度角与滑动竖直方向速率的计算值与观测值的分布相近(图 12,观测数据来自文献:Tsimi et al., 2015).
|
图 12 观测与数值计算结果对比 Fig. 12 Comparison between observed data and modeling result |
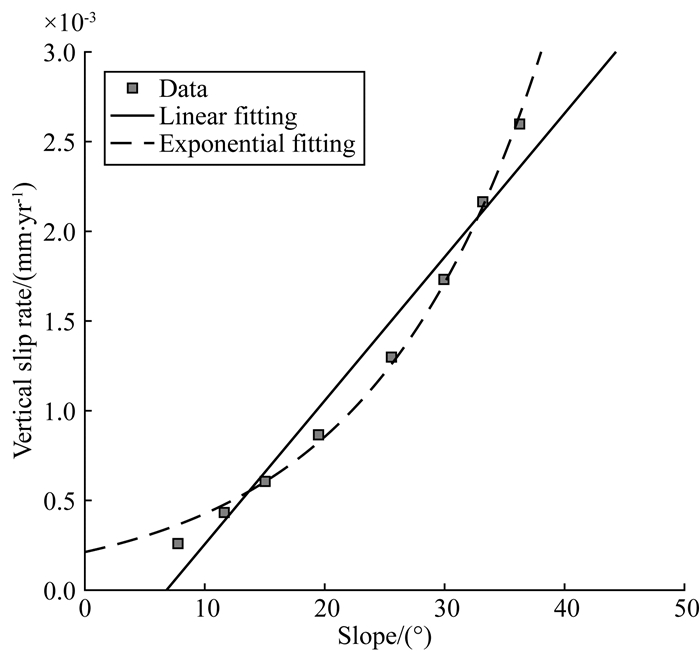
虽然观测值线性拟合的相关性相较指数拟合更好,但考虑断层三角面坡度角与断层滑动速率间的线性关系在扩展到低坡度角时,采用线性拟合时滑动速率可能为负(式9-10).此外,考虑较高断层滑动速率(vf=3×10-3m·yr-1)情况下,线性拟合的效果也远不如指数拟合的情况(图 11g, h).因此,我们认为在相同的地表演化背景下,此处给定的是河流下切系数Kc=1×10-4yr-1,扩散系数Kd=3×10-2m2·yr-1时的例子(表 1算例1, 13, 14,21-25).断层滑动速率较小或较大的情况下,采用指数拟合能更好的描述三角面坡度角与滑动速率间的关系(图 13).
|
图 13 线性拟合与指数拟合 Fig. 13 Linear fitting and exponential fitting |
利用二维有限体积数值模型,我们系统地研究了断层性质及地表过程对正断层陡崖形态和几何特征的影响,其结论包括以下三个方面:
(1) 断层崖是正断层作用与地表演化过程共同作用的结果,其形态特征主要是受地表演化过程即河流下切和山坡蠕移过程的控制.河流下切占主导时,容易形成尖锥型的正断层陡崖;山坡蠕移占主导时,容易形成沟壑型的正断层陡崖;河流下切和山坡蠕移相对平衡时,容易形成三角面型的正断层陡崖.
(2) 三角面型陡崖的高度和宽度随时间逐渐增大,坡度角在演化过程中基本不变.这些几何特征主要受控于断层滑动速率,在地表演化环境相同的情况下,与断层滑动速率呈正相关.十万年时间尺度下,断层滑动周期与三角面的形态和几何特征无关.
(3) 断层滑动速率与三角面坡度角间的正相关关系可用于解释希腊和保加利亚正断层的观测数据.
Aurenhammer F. 1991. Voronoi Diagrams-a Survey of a Fundamental Geometric Data Structure. ACM Computing Surveys, 23(3): 345-405. DOI:10.1145/116873.116880 |
Braun J, Sambridge M. 1997. Modelling landscape evolution on geological time scales:a new method based on irregular spatial discretization. Basin Research, 9(1): 27-52. DOI:10.1046/j.1365-2117.1997.00030.x |
Bucknam R C, Anderson R E. 1979. Estimation of fault-scarp ages from a scarp-height-slope-angle relationship. Geology, 7(1): 11-14. |
Cheng Q G. 1988. An analysis of fault scarps on north Huashan Mountain front and the recurrence intervals of larger earthquakes. Xi'an College of Geology (in Chinese), 10(4): 53-64. |
Cui D X, Hao M, Qin S L, et al. 2019. Inversion of fault dip-slip rate and locking depth in Central-Sourthern Shaanxi of China. Chinese J. Geophys. (in Chinese), 62(12): 4648-4657. |
Culling W E. 1960. Analytical theory of erosion. The Journal of Geology, 68(3): 336-344. |
Culling W E. 1963. Soil Creep and the Development of Hillside Slopes. The Journal of Geology, 71(2): 127-161. |
Deng Q D, You H C. 1985. Fault scarps research and earthquake risk estimation-example in eastern Holanshan fault scarps. Northwestern Seismological Journal. (in Chinese), 7(1): 29-38. |
Fernandes N F, Dietrich W E. 1997. Hillslope evolution by diffusive processes:The timescale for equilibrium adjustments. Water Resources Research, 33(6): 1307-1318. DOI:10.1029/97WR00534 |
Ferrier K L, Huppert K L, Perron J T. 2013. Climatic control of bedrock river incision. Nature, 496: 206-209. DOI:10.1038/nature11982 |
Howard AD. 1994. A detachment-limited model of drainage basin evolution. Water Resources Research, 30(7): 2261-2285. DOI:10.1029/94WR00757 |
Huang X J, Wu Z H, Huang X L, et al. 2018. Tectonic Geomorphology Constrains on Quaternary Activity and Segmentation along Chenghai-Binchuan Fault Zone in Northwest Yunnan, China. Earth Science. (in Chinese), 43(12): 4651-4670. |
Istanbulluoglu E, Tarboton D G, Pack R T, et al. 2003. A sediment transport model for incision of gullies on steep topography. Water Resources Research, 39(4): ESG 6-1-ESG 6-15. |
Kokkalas S, Koukouvelas I K. 2005. Fault-scarp degradation modeling in central Greece:The Kaparelli and Eliki faults (Gulf of Corinth) as a case study. Journal of Geodynamics, 40(2): 200-215. |
Lague D. 2014. The stream power river incision model:evidence, theory and beyond. Earth Surface Processes & Landforms, 39(1): 38-61. |
Li Y H, Hao M, Ji L Y, et al. 2014. Fault slip rate and seismic moment deficit on major active faults in mid and south part of the Eastern margin of Tibet plateau. Chinese J. Geophys (in Chinese), 57(4): 1062-1078. |
Petit C, Gunnell Y, Gonga-Saholiariliva N, et al. 2009a. Faceted spurs at normal fault scarps:Insights from numerical modeling. Journal of Geophysical Research, 114: B05403. |
Petit C, Meyer B, Gunnell Y, et al. 2009b. Height of faceted spurs, a proxy for determining long-term throw rates on normal faults:Evidence from the North Baikal Rift System, Siberia. Tectonics, 28: TC6010. |
Refice A, Giachetta E, Capolongo D. 2012. SIGNUM:A Matlab, TIN-based landscape evolution model. Computers & Geosciences, 45: 293-303. |
Roe G H, Montgomery D R, Hallet B. 2002. Effects of orographic precipitation variations on the concavity of steady-state river profiles. Geology, 30(2): 143-146. |
Stock J D, Montgomery D R. 1999. Geologic constraints on bedrock river incision using the stream power law. Journal of Geophysical Research, 104(B3): 4983-4993. DOI:10.1029/98JB02139 |
Topal S, Keller E, Bufe A, et al. 2016. Tectonic geomorphology of a large normal fault:Aksehir fault, SW Turkey. Geomorphology, 259: 55-69. DOI:10.1016/j.geomorph.2016.01.014 |
Tsimi C, Ganas A. 2015. Using the ASTER global DEM to derive empirical relationships among triangular facet slope, facet height and slip rates along active normal faults. Geomorphology, 234: 171-181. DOI:10.1016/j.geomorph.2015.01.018 |
Wallace R E. 1978. Geometry and rates of change of fault-generated range fronts, north-central Nevada. Journal Research U. S. Geological Survey, 6(5): 637-649. |
Wu Z H, Wu Z H, Hu D G, et al. 2005. Geomorphologic indicators and rates of late Quaternary normal faulting at the west side of the Wenquan graben, central Qinghai-Tibet Plateau. Geological Bulletin of China (in Chinese), 24(1): 48-57. |
程谦恭. 1988. 华山北麓断层崖与大地震重复周期分析. 西安地质学院学报, 10(4): 53-64. |
崔笃信, 郝明, 秦姗兰, 等. 2019. 陕西中南部现今断层滑动速率和闭锁深度反演. 地球物理学报, 62(12): 4648-4657. |
邓起东, 尤惠川. 1985. 断层崖研究与地震危险性估计--以贺兰山东麓断层崖为例. 西北地震学报, 7(1): 29-38. |
黄小巾, 吴中海, 黄小龙, 等. 2018. 滇西北程海-宾川断裂带第四纪分段活动性的构造地貌表现与限定. 地球科学, 43(12): 4651-4670. |
李煜航, 郝明, 季灵运, 等. 2014. 青藏高原东缘中南部主要活动断裂滑动速率及其地震矩亏损. 地球物理学报, 57(4): 1062-1078. |
吴中海, 吴珍汉, 胡道功, 等. 2005. 青藏高原中部温泉盆地西侧晚第四纪正断层作用的地貌标志及断裂活动速率. 地质通报, 24(1): 48-57. DOI:10.3969/j.issn.1671-2552.2005.01.008 |
 2020, Vol. 63
2020, Vol. 63


