2. 中国科学院地球科学研究院, 北京 100029;
3. 中国科学院大学, 北京 100049
2. Innovation Academy for Earth Science, Chinese Academy of Sciences, Beijing 100029, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
地震数据处理的基本目标之一是提高地震数据的信噪比(SNR).对SNR定量和精确地测量, 可以有助于后续地震数据处理工作, 例如带通滤波(Rutten et al., 1972), 加权叠加(Rietsch, 1980), 速度估计(Key and Smithson, 1990)和时间反演成像(Witten and Artman, 2011)等.信噪比的高低是衡量地震资料质量以及评价去噪方法优劣的重要指标之一.准确估计地震信号的信噪比一直是有待解决的难题.
Dash和Obaidullah(1970)描述了用于确定两条地震道的信号和噪声的自相关方法, 获得了低信噪比数据的信号和噪声统计.Rietsch(1980)认为只要信号在三个地震道上具有相同的形状并且任何地震道上的噪声不与信号或其他道上的噪声相关, 就可以估计信号的幅度和至少三条地震道中的每一条上的噪声能量.White(1984)展示频谱相干性在定量地震数据分析中的作用, 多个相干用于估计地震剖面和道集的相干信号和非相干噪声含量, 通过相干分析输出信号和噪声估计.Xu和Gui(2014)在频率域计算地震数据信噪比, 并讨论了计算信噪比和相关关键参数的框架.Zhao等(2014)则提出了一种评估时频域信噪比的方法, 采用短时傅里叶变换来估计信号和噪声的瞬时功率谱, 利用它们的比值来计算地震信号的时频域信噪比. Li等(2016)和刘洋等(2017)提出了一种基于正则化的局部信噪比估计方法, 认为局部信噪比估计能够准确地指示信噪比的变化, 并为地震数据的质量提供可视化判断.上述所有方法都需要估计数据中的有效地震信号和噪声, 相当于进行了一次信噪分离, 导致流程复杂, 不够高效.更重要的是, 其信噪比估计结果的精度依赖于信号估计方法或噪声压制方法的有效性.如果分离出的噪声数据中含有有效信号残差, 则信噪比的估值会偏低;而如果强噪声被拟合成信号, 则信噪比的估值会偏高.提高信噪分离方法的精度难度较大, 若要降低信噪比估计结果的偏差, 更直接的策略是使用不需要信噪分离的方法进行信噪比估计.因此, 我们引入计算机视觉和机器学习领域中的深度学习方法解决这一问题.
自2012年AlexNet (Krizhevsky et al., 2012)获得ImageNet冠军以来, 深度学习尤其是深度卷积神经网络以其优越的性能在计算机视觉领域中的图像分类、图像检测、图像分割、图像处理等方向获得了成功应用.近两三年, 深度学习模型即深层神经网络模型开始被应用在油气勘探领域, 在全波形反演(Lewis and Vigh, 2017)、地震波场分离(Serfaty et al., 2017)、地震数据噪声压制(Li et al., 2018;Yu and Ma, 2018;Liu et al., 2018;王钰清等, 2019)、地震相分类(Dramsch and Lüthje, 2018;Qian et al., 2018)、页岩总有机碳含量的预测(Zhu et al., 2018)、岩石相分类(Liu et al., 2017)、自动断层检测(Araya-Polo et al., 2017;Ma et al., 2018;Zhao and Mukhopadhyay, 2018;Lu et al., 2018)、河道检测(Pham et al., 2018)等方面产生了许多成果.
本文提出了能够估计地震数据局部信噪比的深度卷积神经网络模型, 该模型可以用于评价地震数据的质量.理论模型和实际数据验证的结果表明, 与传统信噪比估计的方法对比, 该深度学习模型可以更准确高效的估计局部地震数据的信噪比, 从而筛选出高质量的局部地震数据.
1 模型架构 1.1 方法原理人工神经网络, 具有强大的拟合能力.万能近似定理(Cybenko, 1989;Hornik, 1991)表明, 如果一个前馈神经网络具有线性输出层和至少一层具有任何一种“挤压”性质的激活函数(例如logistic sigmoid激活函数)的隐藏层, 只要给予网络足够数量的隐藏单元, 它可以以任意的精度来近似任何从一个有限维空间到另一个有限维空间的Borel可测函数.而深度学习模型(LeCun et al., 2015), 又称为深度神经网络, 泛指具有多隐层的人工神经网络, 利用许多自然信号是组合层次结构的特性, 通过构建参数化、层级化的结构体系, 组合低级特征获得高级特征来完成学习任务.
卷积神经网络使用卷积作为线性滤波算子, 这一设计使得其在表征结构化数据(如图像等)时性能优越.因为叠后地震剖面也是一种结构化数据, 所以目前用于地震数据的深度学习方法几乎都采用卷积网络结构.本文将地震数据局部信噪比估计看作是一个针对局部二维数据的回归任务, 需要分析局部的叠后地震剖面, 我们选择使用卷积神经网络完成这一任务.本文构建了用于估计地震数据局部信噪比的深度卷积神经网络模型, 亦称E网络(Estimate Net).
假设地震数据由地震信号与噪声组成, 这里我们对于局部时空窗内的地震数据的信噪比进行估计.局部窗数据用矩阵D表示, 于是有
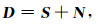
|
(1) |
其中, S是局部窗内的地震信号矩阵, N是相应的噪声矩阵, 这里假设N是高斯白噪声.
为了方便神经网络处理, 需要对局部窗内的地震数据进行高斯归一化.这里我们定义局部窗内的归一化地震数据的信噪比GSNR(Generalized Signal-to-Noise Ratio)如下:

|
(2) |
其中, D和S分别是局部窗内归一化后的地震数据矩阵和其中的地震信号矩阵, ‖·‖F是Frobenius范数, GSNR的单位是分贝(dB).
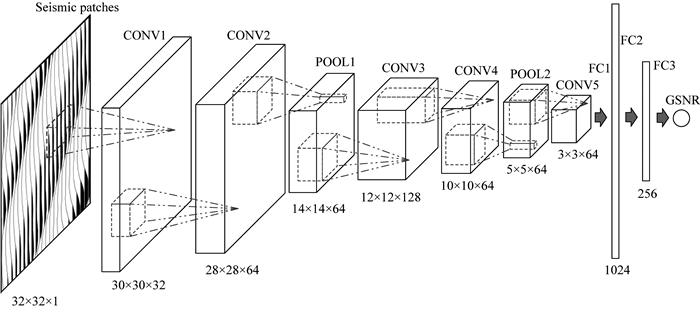
我们以32×32大小的局部地震数据为例, 构建E网络.网络模型的结构如图 1所示, 模型的输入为32×32大小的局部地震数据, 模型的输出则是对局部地震数据的GSNR估计值.这里没有使用已有的深度学习网络结构和预训练模型.网络模型由10层网络构成, 包括卷积层(CONV层)、池化层(POOL层)和全连接层(FC层).网络层级的连接顺序如图 1所示, 各连接上方为相应的网络层的类型和名称, 各特征张量下方为其对应的数据维度.
|
图 1 E网络结构 Fig. 1 The structure of E-Net |
卷积层可以根据任务需求, 自适应地从输入数据中探测和提取有用的信息, 从而达到特征学习的目的.卷积层的输入数据是一个大小为n1×n2×c的张量X, 其中c为输入特征的个数, 也被称为通道数, n1×n2为输入数据的尺寸.卷积层的输出是一个大小为m1×m2×k的张量H, 其中k是特征映射的数目, m1×m2是输出数据的尺寸.每个卷积层都有一套对应的参数, 包括大小为k×l1×l2×c的权重张量W(又称k个卷积核或k个滤波器), 以及大小为k的偏置向量b.H中的每个元素可以通过X中大小为l1×l2×c的局部数据计算得到.相同特征映射中的元素共享同一个权重分量Wh.使用这种架构的原因有两方面(LeCun et al., 2015).首先, 图像、地震信号等结构化数据在局部范围内通常高度相关, 形成易于检测的独特局部特征.其次, 这些信号的局部统计特性具有位置不变性, 不同位置的单元共享相同的权重可以在阵列的不同部分中检测相同的局部特性.卷积层的正向计算过程的数学表达式如下:

|
(3) |
其中, ⊗是二维卷积算子, σ是激活函数, 对应一种非线性映射, i1=1, 2, …, m1, i2=1, 2, …, m2, h=1, 2, …, k.一般, 卷积层的参数W被初始化为较小的随机数, b被初始化为零, 在训练过程中, 通过误差反向传播算法进行优化调整, 直到模型收敛.E网络中的所有卷积算子的大小设定为l1=l2=3, 卷积计算的间隔在每个维度都为1, 计算时不对输入数据进行边缘扩展.我们选择线性整流单元(ReLU)作为所有卷积层的非线性激活函数σ(Glorot et al., 2011).
池化层通过对某个邻域内所有点做统计运算来分析输入数据, 其作用是整合相似的语义特征.在E网络中, 我们统计输入数据在2×2范围内的最大值作为池化输出, 池化运算的间隔在每个维度均为2.
全连接层是传统的神经网络层, 我们将其置于卷积层和池化层之后, 通过匹配标签来学习归一化局部信噪比的回归函数.在E网络中, 标签是E网络输入的训练数据对应的局部归一化信噪比.隐藏全连接层的激活函数也是ReLU函数, 输出层使用线性激活函数, 从而满足GSNR有正有负的数据特性.
关于深度学习以及卷积神经网络的更多细节, 可以参考Bengio等(2016)撰写的图书.
1.3 训练策略使用深度学习模型分为训练和推理两个阶段.在训练阶段, 使用已有的样本和标签, 优化模型参数, 训练一个从样本到标签的近似映射;然后在推理阶段, 将目标数据输入模型, 得到的输出作为推理结果.
我们利用Sigmoid模型(图 2), 拾取了大小为32×32的部分重叠的局部时空窗数据, 形成地震信号数据集进行模型训练与验证, 整个数据集的构建流程如图 3所示.Sigmoid模型中一共包含136161个大小为32×32的局部窗数据, 通过每个方向间隔8个网格点的均匀采样, 选择其中的2209个局部窗数据形成初始地震信号数据集, 用于模型训练.由于Sigmoid模型中只包含单一倾角的倾斜地层、弯曲地层和断层, 其中数据的代表性不足.事实上, 在引言部分已经提到, 地震勘探领域缺少具有广泛代表性的数据集.为了提高E网络的泛化能力, 要使用尽可能多样的数据训练该网络.如果数据有限, 则需要对初始数据集合进行数据增强(Bengio et al., 2016).在这里, 我们通过两种策略扩展地震信号数据集.一是在空间和时间维度分别对Sigmoid模型进行sinc插值, 产生4个类Sigmoid模型数据, 如图 3所示.类Sigmoid模型中基本涵盖了内含大约0.5到5.5个波形、倾斜角范围大约在-80°到80°之间的局部直线状或局部正弦曲线状同相轴的32×32的局部窗数据.然后再从这些类Sigmoid模型中均匀采样出32×32局部窗数据, 具体的采样间隔步长如图 3所示.二是通过对所有已有的数据进行左右翻转变换、上下翻转变换、180°翻转变换的操作, 达到数据增强的效果.翻转变形主要增强了局部窗内信号在波形主频和方向上的变化.最后将所有通过扩展和增强产生的新数据并入地震信号集, 就得到了最终包含超过6万4千个局部窗的地震信号集.使用这些信号进行E网络模型的训练.

|
图 2 Sigmoid模型 Fig. 2 Sigmoid model data |

|
图 3 基于Sigmoid模型的地震信号数据集的构建流程 Fig. 3 Construction process of seismic signal data set based on Sigmoid model data |
我们采用了目前流行的反向传播算法(LeCun et al., 1990)来训练模型, 使用小批量梯度下降法迭代求解网络中的参数, 即在训练过程中, 把整个训练数据集随机分为若干个批次, 每次迭代仅使用其中的一个批次的样本参与参数优化.训练时, 分别给信号样本Sj加上不同强度的零均值高斯随机噪声Nj, 得到含噪数据Dj, 再对Dj做高斯归一化处理得到模型输入Dj, 对应的归一化信噪比作为标签, 其中j=1, 2, …, B, B是单个批次内的样本数量.训练添加的噪声是在迭代时随机产生的, 每次迭代时不同的样本所加的噪声不同, 同一样本在不同次的迭代时所加的噪声也不同.通过控制所加随机噪声N的能量强度保证D的信噪比符合均匀概率分布, 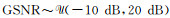

|
(4) |
其中, R是E网络对输入的含噪样本的信噪比的估计值, 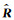
我们使用加入噪声的Sigmoid模型作为验证数据集.为了便于可视化, 后文均是通过全局的模型尺度来显示验证数据的GSNR估计结果.通过增加不同强度的高斯随机噪声, 我们得到3个不同的含噪Sigmoid模型(图 4).噪声的强度在全局保持一致, 使得含噪数据的整体信噪比分别为5.0030 dB, 0.0030 dB, 和-2.9970 dB, 而局部信噪比分别在-4.7316 dB到7.8189 dB之间, -9.7305 dB到2.8193 dB之间, 和-12.7290 dB到-0.1802 dB之间.不同于训练时所用的间隔采样方法, 对于每个模型, 要对所有大小为32×32的局部窗数据进行信噪比预测.如图 3所示, 这相当于将前文提到的Sigmoid模型中析出的全部136161个局部窗信号都用于验证.虽然其中有2209个局部窗信号也出现在训练信号集中, 但是最终参与训练的含噪数据与参与验证的含噪数据所增加的噪声不相同, 则高斯归一化后的模型输入也就不同.因此, 这种数据构建方式可以验证E网络的泛化能力.

|
图 4 含噪Sigmoid模型 数据整体信噪比SNR从左到右依次为5.0030 dB, 0.0030 dB, -2.9970 dB.局部数据归一化信噪比GSNR的范围从左到右依次为[-4.7316 dB, 7.8189 dB], [-9.7305 dB, 2.8193 dB], [-12.7290 dB, -0.1802 dB]. Fig. 4 Noisy Sigmoid modal data From left to right: the global SNR of the data is 5.0030 dB, 0.0030 dB, -2.9970 dB, the GSNR is range from [-4.7316 dB, 7.8189 dB], [-9.7305 dB, 2.8193 dB], [-12.7290 dB, -0.1802 dB]. |
我们将本方法与前人进行信噪比估计的正则化方法(刘洋等, 2017)进行了效果对比, 如图 5所示.将理论有效局部窗信号依次带入公式(2)可以求出理论GSNR值(图 5的左列).从图中可以看出, GSNR很好的刻画了局部窗口信号的信噪比分布.利用基于正则化的局部信噪比估计方法(刘洋等, 2017)估计公式(2), 求得基于正则化的GSNR估计, 如图 5的中列所示.其中对地震信号的估计我们使用了基于深度学习的DnCNN模型(Zhang et al., 2017)和级联信号估计方法(刘洋等, 2017), DnCNN的训练数据集与E网络相同, 训练策略类似.将局部窗数据输入训练好的E网络进行推理, 计算得到基于深度学习的GSNR估计值R, 如图 5的右列所示.对比图 5中的结果, 可以发现, 基于正则化的方法的GSNR估计结果分布更连续, 但准确度稍差, 估计值较理论值偏高, 其结果的准确度受制于有效信号估计方法的准确度.随着噪声强度的提高, 有效信号估计难度增大, 相应的GSNR估计的准确度会降低.而基于深度学习的方法的估计结果, 在三种噪声强度下都更接近于理论值, 准确性都更高, 且受断层、褶皱、薄层等复杂构造的影响较少.模拟数据的计算结果证明了E网络对于GSNR估计的泛化能力.另外, E网络的估计效率更高, 完成单个含噪Sigmoid模型的推理GSNR的时间约为70 s, 而基于正则化的方法需要先进行有效信号估计, 在相同的硬件条件下, 完成单个含噪Sigmoid模型的GSNR估计的时间约为360 s.

|
图 5 含噪Sigmoid模型局部数据归一化信噪比(GSNR) 第一行到第三行对应含不同噪声强度的输入数据(SNR依次为5.0030 dB, 0.0030 dB, -2.9970 dB);第一列到第三列依次为GSNR的理论计算值, 基于正则化的估计结果, 基于E网络的估计结果. Fig. 5 The generalized signal-to-noise ratio (GSNR) of noisy Sigmoid data First-third rows: different input noise level (SNR=5.0030 dB, 0.0030 dB, and -2.9970 dB). First-third columns: GSNRs from theory calculation, regularization methods, and E-Net. |
为了进一步验证本文提出的方法的有效性和模型的泛化能力, 使用如图 6所示的更加真实的二维地震数据进行测试.该数据共有512道, 时间采样间隔为2 ms, 完全没有参与模型的训练.图 6a为不含噪声的干净数据, 图 6b为加入高斯噪声后的数据, 噪声的强度在全局保持一致, 使得含噪数据的整体信噪比为-2.6785 dB, 而局部信噪比在-15.4051~4.3189 dB之间.分别使用正则化方法和E网络对该真实地震数据进行GSNR估计, 结果如图 7所示, 图 7a为根据干净数据计算得到的GSNR的理论值, 7b为正则化方法得到的GSNR估计结果, 7c为E网络得到的GSNR估计结果.通过比较图 7中的三种结果, 可以发现, 与Sigmoid模型的验证结果类似, 基于正则化的方法受制于有效信号估计方法的准确度, 其估计结果与理论值相比整体偏高.相对的, 基于E网络的估计结果与理论值更加接近, 且在GSNR的理论值大于-10 dB的区域具有较好的估计精度, 这验证了E网络的泛化能力.虽然在GSNR的理论值小于-10 dB的区域, E网络的估计结果并不好, 数值偏高, 但仍然优于正则化方法.因为参与E网络模型训练的局部窗数据的GSNR的理论值分布在-10~20 dB之间, 所以E网络对于GSNR小于-10 dB的地震数据, 估计结果将偏高, 接近-10 dB.可以通过拓宽训练数据的GSNR范围, 解决这一问题.值得指出的是, 训练模型时的GSNR范围的选取, 应该与任务匹配, 以避免额外的计算量.由于E网络已经能够筛选出高质量的局部地震数据, 因此这里没有再调整训练数据的GSNR范围.

|
图 6 真实地震数据 (a)干净数据; (b)加噪数据. Fig. 6 Realistic seismic data (a) Clean data; (b) Noisy data. |

|
图 7 真实地震数据的局部数据归一化信噪比(GSNR) (a—c)为GSNR的理论计算值, 基于正则化的估计结果, 基于E网络的估计结果. Fig. 7 The generalized signal-to-noise ratio (GSNR) of realistic seismic data (a—c) GSNRs from theory calculation, regularization methods, and E-Net. |
模拟地震数据和真实地震数据的计算结果均表明, E网络能够高效而准确的完成地震资料的信噪比估计和数据质量定量评价, 为进一步的处理工作提供可靠依据.
3 应用准确高效地估计地震信噪比不仅可用于衡量地震资料质量及评价去噪方法优劣, 而且可用来自动挑选信噪比高的地震数据区域, 提供高质量的训练数据集, 解决将深度学习用于地震数据处理时面临的关键瓶颈.
深度学习模型比传统的有监督机器学习模型的复杂度高很多, 动辄拥有百万级以上的参数.这不仅意味着它们需要大量的计算资源来训练这些模型, 更重要的是, 它们需要大量标记的训练数据来进行学习.例如, 对于基于深度学习的智能去噪模型的训练, 就需要大量的高质量的实际工区地震资料.然而现阶段, 地震勘探领域并没有适用于有监督模型训练的相应标准数据集.目前已有的手段是通过人工挑选低噪的数据(Liu et al., 2018), 这种获取方法人力成本高且耗时, 而且挑选标准很难统一, 无法量化.
可以通过使用本文提出的E网络估计地震数据信噪比来筛选高质量的训练样本.利用E网络的估计结果, 筛选出GSNR高的数据, 其资料质量也相对较高, 可以加入到深度学习模型的训练数据集中.图 8为实际地震资料中GSNR估值较高的局部窗数据, 其GSNR估值为13.2140 dB.实际筛选时, 建议选择GSNR>15 dB的局部窗数据加入训练数据集.

|
图 8 实际资料中GSNR估值较高的局部地震数据 Fig. 8 Local data patch with high GSNR estimate value from field seismic data |
随着深度学习技术的兴起, 数据质量定量评价将起到越来越重要的作用.其中, 不依赖信噪分离进行地震数据的信噪比估计具有重要意义.鉴于此, 本文提出了基于深度卷积网络的局部信噪比估计方法.经过训练以后的模型, 不需要估计有效信号, 就可以估计地震数据的局部归一化信噪比.理论模型数据和真实地震数据的处理结果均表明, 基于深度学习的E网络模型能够更加高效且准确地反映地震数据的局部信噪比特征分布, 为定量分析数据质量提供有力保证.
Araya-Polo M, Dahlke T, Frogner C, et al. 2017. Automated fault detection without seismic processing. The Leading Edge, 36(3): 208-214. DOI:10.1190/tle36030208.1 |
Bengio Y I, Goodfellow I, Courville A. 2016. Deep Learning. Cambridge, MA: MIT Press.
|
Cybenko G. 1989. Approximation by superpositions of a sigmoidal function. Mathematics of Control, Signals and Systems, 2(4): 303-314. DOI:10.1007/BF02551274 |
Dash B P, Obaidullah K A. 1970. Determination of signal and noise statistics using correlation theory. Geophysics, 35(1): 24-32. DOI:10.1190/1.1440077 |
Dramsch J S, Lüthje M. 2018. Deep-learning seismic facies on state-of-the-art CNN architectures.//88th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2036-2040, doi: 10.1190/segam2018-2996783.1.
|
Glorot X, Bordes A, Bengio Y. 2011. Deep sparse rectifier neural networks. Journal of Machine Learning Research, 15: 315-323. |
Hornik K. 1991. Approximation capabilities of multilayer feedforward networks. Neural Networks, 4(2): 251-257. DOI:10.1016/0893-6080(91)90009-T |
Key S C, Smithson S B. 1990. New approach to seismic-reflection event detection and velocity determination. Geophysics, 55(8): 1057-1069. DOI:10.1190/1.1442918 |
Kingma D P, Ba J. 2014. Adam: a method for stochastic optimization. arXiv: 1412.6980.
|
Krizhevsky A, Sutskever I, Hinton G E. 2012. ImageNet classification with deep convolutional neural networks. Communications of the ACM, 60(6): 84-90. DOI:10.1145/3065386 |
Le Cun Y, Boser B E, Denker J S, et al. 1990. Handwritten digit recognition with a back-propagation network.//Advances in Neural Information Processing Systems. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 2: 396-404.
|
LeCun Y, Bengio Y, Hinton G. 2015. Deep learning. Nature, 521(7553): 436-444. DOI:10.1038/nature14539 |
Lewis W, Vigh D. 2017. Deep learning prior models from seismic images for full-waveform inversion.//87th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1512-1517, doi: 10.1190/segam2017-17627643.1.
|
Li B X, Wang D A, Liu Y, et al. 2016. Local SNR estimation method for seismic data.//86th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 4720-4724, doi: 10.1190/segam2016-13853984.1.
|
Li H S, Yang W Y, Yong X S. 2018. Deep learning for ground-roll noise attenuation.//88th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1981-1985, doi: 10.1190/segam2018-2981295.1.
|
Liu D W, Wang W, Chen W C, et al. 2018. Random-noise suppression in seismic data: What can deep learning do?//88th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts 2016-2020, doi: 10.1190/segam2018-2998114.1.
|
Liu L H, Lu R, Li J H, et al. 2017. Seismic lithofacies computation method based on deep learning.//87th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 649-652, doi: 10.1190/IGC2017-165.
|
Liu Y, Li B X, Wang D, et al. 2017. Local SNR estimation method based on regularization for seismic data. Chinese Journal of Geophysics (in Chinese), 60(5): 1979-1987. DOI:10.6038/cjg20170529 |
Lu P, Morris M, Brazell S, et al. 2018. Using generative adversarial networks to improve deep-learning fault interpretation networks. The Leading Edge, 37(8): 578-583. DOI:10.1190/tle37080578.1 |
Ma Y, Ji X, BenHassan N M, et al. 2018. A deep learning method for automatic fault detection.//88th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1941-1945, doi: 10.1190/segam2018-2984932.1.
|
Pham N, Fomel S, Dunlap D. 2018. Automatic channel detection using deep learning.//88th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2026-2030, doi: 10.1190/segam2018-2991756.1.
|
Qian F, Yin M, Liu X Y, et al. 2018. Unsupervised seismic facies analysis via deep convolutional autoencoders. Geophysics, 83(3): A39-A43. DOI:10.1190/geo2017-0524.1 |
Rietsch E. 1980. Estimation of the signal-to-noise ratio of seismic data with an application to stacking. Geophysical Prospecting, 28(4): 531-550. DOI:10.1111/j.1365-2478.1980.tb01241.x |
Rutten K, Valeton M, Van Grunsven T. 1972. Measurement of the signal to noise ratio in seismic profiling. Marine Geophysical Researches, 1(4): 445-450. DOI:10.1007/BF00286746 |
Serfaty Y, Itan L, Chase D, et al. 2017. Wavefield separation via principle component analysis and deep learning in the local angledomain.//87th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts 991-995, doi: 10.1190/segam2017-17676855.1.
|
Wang Y Q, Lu W K, Liu J L, et al. 2019. Random seismic noise attenuation based on data augmentation and CNN. Chinese Journal of Geophysics (in Chinese), 62(1): 421-433. DOI:10.6038/cjg2019M0385 |
White R E. 1984. Signal and noise estimation from seismic reflection data using spectral coherence methods. Proceedings of the IEEE, 72(10): 1340-1356. DOI:10.1109/PROC.1984.13022 |
Witten B, Artman B. 2011. Signal-to-noise estimates of time-reverse images. Geophysics, 76(2): MA1-MA10. DOI:10.1190/1.3543570 |
Xu H Q, Gui Z X. 2014. Signal-to-noise ratio application to seismic marker analysis and fracture detection. Applied Geophysics, 11(1): 73-79. DOI:10.1007/s11770-014-0411-y |
Yu S W, Ma J W. 2018. Deep learning for denoising.//88th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 461-464, doi: 10.1190/IGC2018-113.
|
Zhang K, Zuo W M, Chen Y J, et al. 2017. Beyond a Gaussian denoiser:residual learning of deep CNN for image denoising. IEEE Transactions on Image Processing, 26(7): 3142-3155. DOI:10.1109/TIP.2017.2662206 |
Zhao T, Mukhopadhyay P. 2018. A fault-detection workflow using deep learning and image processing.//88th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1966-1970, doi: 10.1190/segam2018-2997005.1.
|
Zhao Y, Liu Y, Li X X, et al. 2014. Time-frequency domain SNR estimation and its application in seismic data processing. Journal of Applied Geophysics, 107: 25-35. DOI:10.1016/j.jappgeo.2014.05.002 |
Zhu L Q, Zhang C, Zhang C M, et al. 2018. Prediction of total organic carbon content in shale reservoir based on a new integrated hybrid neural network and conventional well logging curves. Journal of Geophysics and Engineering, 15(3): 1050-1061. DOI:10.1088/1742-2140/aaa7af |
刘洋, 李炳秀, 王典, 等. 2017. 基于正则化条件的地震数据局部信噪比估计方法. 地球物理学报, 60(5): 1979-1987. DOI:10.6038/cjg20170529 |
王钰清, 陆文凯, 刘金林, 等. 2019. 基于数据增广和CNN的地震随机噪声压制. 地球物理学报, 62(1): 421-433. DOI:10.6038/cjg2019M0385 |
 2020, Vol. 63
2020, Vol. 63


