2. 同济大学海洋地质国家重点实验室, 上海 200092
2. State Key Laboratory of Marine Geology, Tongji University, Shanghai 200092, China
射线束(Beam-Ray)类成像方法是目前国际上引人注目的一大类成像方法,无论高斯射线束、控制射线束、胖射线束或共反射面元射线束均可归为此类成像方法(王华忠等, 2015).虽然逆时偏移在强横向速度变化的复杂构造区有更好的表现,但是前者由于具有使用灵活以及计算效率高的优点,在快速成像以及偏移速度分析中发挥着重要的作用.典型的射线束成像方法包括射线束偏移(Sun et al., 2000;Liu et al., 2018)、共反射面元叠加(Hubral et al., 1999)、共反射面元射线束偏移(Garabito et al., 2012)和高斯射线束偏移(Hill,1990).本文的基本观点是强调射线束类成像方法可以在克希霍夫统一成像理论框架下进行解读.这种解读除了可以帮助我们获得更为深入的认识,同时可以总结出关于射线束成像方法的一种基于输出道成像观点的“两步弥散“实现方式.归因于作者的前期研究基础,本文的研究以共反射面元射线束偏移成像(CRS-BEAM-PSDM)和共反射面元叠加成像(CRS-STACK)为例.
如我们所知,CRS叠加成像和多次聚焦成像(Multi-focusing)是最早将局部运动学属性引入射线束成像方法的两种算法.这两种方法都使用了相同的局部特征波属性参数即NORMAL波与NIP波的运动学属性参数(HUBRAL,1983).在过去20年中这两种方法被证明是处理低信噪比数据的强有力工具,国内外学者在这方面已经有大量工作(Mann et al., 1999;Landa et al., 1999;Zhang et al., 2001;杨锴等, 2001, 2004;杨锴, 2002; 李振春等,2003;韩立国等,2003;王华忠等,2004;李振春和孙小东,2006;童思友等,2010;Yang et al., 2006;杨锴和马在田, 2006; Yang and Jiang, 2010;倪瑶和杨锴,2013;汪小将等,2014;王征等,2015).除了能够产生高质量的零偏移距成像剖面或共偏移距剖面外,这些局部运动学属性还可用于计算菲涅耳区(Mann et al., 1999)或反演宏观速度模型(Duveneck,2004). Garabito等(2012)将常规克希霍夫PSDM和CRS叠加方法相结合,提出了所谓的共反射面元射线束叠前深度偏移(CRS-BEAM-PSDM).CRS-BEAM-PSDM的本质是利用叠前地震数据中两种特征波的运动学属性参数实现射线束PSDM.这些运动学属性参数是基于叠前数据体应用数据驱动的方式估算得到的(Jäger et al., 2001; 孙小东等,2008).值得注意的是,根据克希霍夫统一成像理论,CRS-BEAM-PSDM属于典型的Hugens曲线叠加方式(或输入道成像方式),因此理论上必然存在一个等价的等走时面弥散方式(或输出道成像方式).本文借助统一成像理论,对CRS-BEAM-PSDM进行了深入研究后,提出了一种等价的、输出道成像方式的两步弥散算子实现CRS-BEAM-PSDM.在实践中这种新算法继承了克希霍夫输出道成像方式的固有的如计算成本相对经济的优势.
在以下章节,我们首先梳理CRS叠加的核心思想,并用一种新的观点来解读CRS-BEAM-PSDM.然后在统一成像理论理论框架内提出了等时面弥散方式的CRS-BEAM-PSDM算法.稍后我们会发现如果将公式中的一重积分分解为两重积分来实现,即得到一种全新的、两步弥散的实现方式.最后通过典型的理论数据和实际数据例子验证本文提出的基于两步弥散算子的CRS-BEAM-PSDM的有效性和鲁棒性.
1 结合克希霍夫叠前深度偏移和CRS叠加特点的CRS射线束叠前深度偏移CRS射线束叠前深度偏移(以下简称CRS-BEAM-PSDM)是Garabito等(2012)提出的一种基于射线束的叠前深度成像方法.该算法的核心思想是将克希霍夫叠前深度偏移(以下简称克希霍夫PSDM)与CRS叠加算子进行了有机结合.图 1a显示了关于地下反射点R的克希霍夫PSDM叠加面(红色)绘制在共中心点(X)-半偏移距(H)-时间(T)域内的情形.共偏移距反射数据面(蓝色线)是基于图 1a下半部分的深度域穹隆状反射界面通过射线正演模拟生成的.从图 1a中可见常规克希霍夫叠前深度偏移的实现过程很容易理解,只需沿着(X, H, T)域内的PSDM叠加面进行叠加并将叠加结果放在深度域对应的反射点R即可.注意图 1a中的粗绿色线代表R点在时间域内的共反射点(Common Reflection Point, 以下简称CRP)轨迹,PSDM叠加面与共反射数据面沿着CRP轨迹相切.
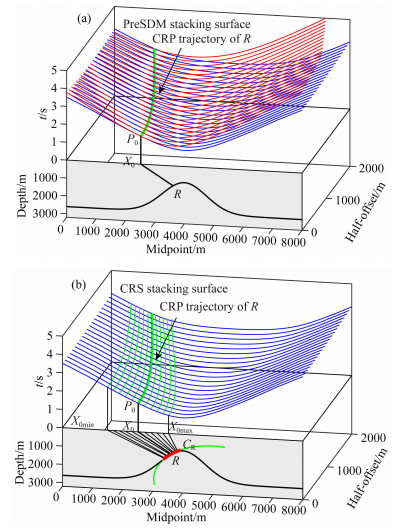
|
图 1 (a) 叠前深度叠加面(红色)与共反射点(CRP) (绿色)轨迹;(b) CRS叠加面(红色)与共反射点(CRP) (绿色)轨迹 Fig. 1 (a) The PreSDM stacking surface and the CRP trajectory; (b) The CRS stacking surface and the CRP trajectory |
图 1b上半部分将共偏移距反射数据面(蓝色线)、CRS叠加面(绿色细线)、CRP轨迹(粗绿色)进行了联合显示.该图下半部分为深度域的一个盐丘状反射界面,上半部分为基于该反射界面模拟得到的共偏移距剖面内的分布情况(用细黑色线表示).对于R点实现零偏成像意味着要沿着R点的CRP轨迹进行叠加,并将叠加结果置于P0处,这种叠加方式也称为CRP叠加.CRS叠加的范围则不限于CRP轨迹,理论上认为应该考察与R点局部形状拟合最好的一个反射弧段CR在(时间-中心点-半偏移距)域(以下简称(t-xm-h)域)内的反射响应(Hubral et al., 1999).该反射响应即为(t-xm-h)域内的多条细绿线组成,称其为CRS叠加面(或CRS算子),显然它覆盖了CRP轨迹.沿这个面进行叠加并将叠加结果置于P0处可得到关于R点的最优零偏成像剖面.
Hoecht等在1999年从共反射点(CRP)叠加公式入手,在傍轴近似意义下导出CRS算子表达式.最常用的双曲型二维CRS叠加算子表达式为

|
(1) |
其中循环变量有4个:x0、t0为零偏移距剖面上的某一点, h为半偏移距, xm为x0附近某一点,xm-x0的差即为叠加孔径.未知参数有四个:近地表速度V0,零偏移距射线的出射角α,两种特征波的波前曲率半径RN和RNIP.Hubral(1983)给出了两种特征波的具体物理含义.由于V0相对容易获得,可视为已知量.所以真正的未知参数为α、RN和RNIP.注意通过三重循环搜索三个属性参数的计算量是不可承受的,因此传统方法采用了“数据驱动”的搜索策略, 将三参数寻优拆解为针对三个单参数的分步自动相关分析,随后再对其进行优化处理,合成能够对构造局部形态产生最佳照明的叠加算子,实现最优叠加得到高质量的零偏移距成像剖面(Jäger et al., 2001).
从图 1b可看出,CRS叠加面不仅覆盖了R点的共反射点(CRP)轨迹,同时也覆盖了R点邻近的一些反射点的CRP轨迹,由于它集中了远多于CRP叠加的有效能量参与叠加,因此在实践中CRS零偏成像剖面的信噪比和同相轴连续性相比常规叠加均有大幅提高,在低信噪比地震数据成像处理中具有不错的实用价值.国内外学者中绝大部分采取上述方式实现二维CRS零偏成像,他们之间的差别仅在于搜索参数的顺序和采取的优化算法有所不同,没有本质区别(Jäger et al., 2001;Mann et al., 1999;杨锴等, 2001, 2004;李振春等, 2003; 韩立国等,2003; 谭未一等,2007; 孙小东等,2008;吴小羊等,2008).
Garabito等(2012)结合CRS叠加与克希霍夫叠前深度偏移提出了所谓的共反射面元射线束叠前深度偏移(CRS-BEAM-PSDM),其计算公式为

|
(2) |
这里ICRS-beam-mig(R)代表关于地下任一反射点R的CRS-Beam-PSDM像.U(ξ, τ(ξ, R))代表共偏移距剖面内由CRS叠加曲线所定义的输入数据(对于共偏移距剖面内定义的某一个样点,很明显这时CRS叠加面已经退化为CRS叠加曲线).积分变量ξh代表共偏移距剖面内CRS叠加轨迹内的一个横向位置.积分变量ξ代表克希霍夫偏移孔径内的一个横向位置.
对公式(2)可以用地球物理语言进行如下解读:首先输入数据被分选为共偏移距道集逐一输入,对于深度域中的任何反射点R,我们都可以在某个共偏移域剖面中计算出它的CRS叠加轨迹(可以理解为:在一个单偏移距剖面内,CRS叠加面退化为CRS叠加轨迹).然后,对于CRS叠加轨迹上的每一个样点都可以执行一个局部叠加并将叠加结果赋值给自己.注意这个局部叠加非常关键,这个局部叠加事实上可以认为是一个束形成(BEAM-FORMING)的过程,在物理上等价于Baykulov和Gajewski(2009)提出的部分CRS叠加算法.在完成这个基于CRS叠加曲线的局部叠加后,第二步依然采用传统的惠更斯曲线叠加方式完成克希霍夫叠前深度偏移.这两个过程综合在一起就是一个完整的CRS-BEAM-PSDM实现过程.因此CRS-BEAM-PSDM可以分解为一个连续的两步操作,这个两步操作确实可用公式(2)所示的两重积分来表达.
2 关于(X, H, T)域中CRS-BEAM-PSDM叠加面的一个新的解读本文对于CRS-BEAM-PSDM给出一个新的解读.如第1节所述,CRS-BEAM-PSDM算子可以被理解为如图 1a所示的常规克希霍夫PSDM叠加算子与如图 1b所示的CRS叠加面的线性组合.为了更清楚的说明CRS-BEAM-PSDM是如何工作的,我们特意绘制了图 2.在图 2a中可以看到,反射线段CR是由若干相邻的反射点组成的.就本图而言,反射线段CR是由11个相邻的反射点组成的,从中我们可以算出由11个相邻的克希霍夫叠前深度偏移叠加面组成的“克希霍夫射线束叠前深度偏移算子”,该算子绘制在图 2a的上半部,用红色表示.关于地下每一个反射点的叠前深度偏移叠加面与共反射叠加面都相切于其对应的CRP叠加轨迹(注意图 2a上部中的绿色曲线是传统的CRS叠加面,它由11个相邻的CRP叠加轨迹组成).图 2a上部中的所有红色曲线这里不妨定义为CRS-BEAM-PSDM叠加面,CRS-BEAM-PSDM所做的就是沿着(X, H, T)域中的克希霍夫射线束叠前深度偏移叠加面(图 2a中所示红线)进行叠加,并将叠加结果置于R点处.换言之,图 2a中所示克希霍夫射线束叠前深度偏移叠加算子即等价于Garabito等(2012)提出的CRS-BEAM-PSDM算子.
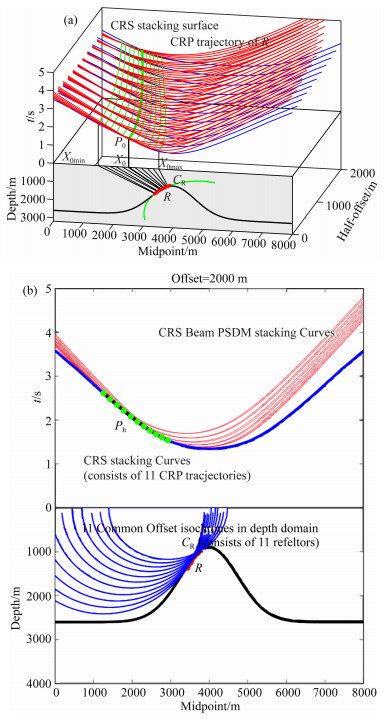
|
图 2 (a) CRS-BEAM-PSDM叠加面;(b) 2 km偏移距剖面内的CRS-BEAM-PSDM叠加轨迹以及对应的深度域内的共偏移距等时面 Fig. 2 (a) The CRS-BEAM-PSDM stacking surface; (b) The CRS-beam-PSDM stacking curves in one common-offset section and their common-offset isochrones in depth section |
注意在单偏移距域中最容易理解Garabito等(2012)提出的传统的、输入道成像方式的CRS-BEAM-PSDM以及本文将要提出的输出道成像方式的CRS-BEAM-PSDM.不妨先考察单偏移距的情形.在单偏移距域中,CRS-BEAM-PSDM叠加面降维退化为CRS-BEAM-PSDM叠加轨迹,CRS叠加面降维退化为CRS叠加轨迹.图 2b显示了2 km偏移距剖面内的CRS-BEAM-PSDM叠加轨迹和CRS叠加轨迹.其中CRS-BEAM-PSDM叠加轨迹由11个相邻的克希霍夫PSDM叠加轨迹组成(如图 2b上半部分所示).请注意在深度域中也有一个由11个相邻的共偏移距等时面组成的算子(如图 2b下半部分所示).
从图 2可以看出,“沿着CRS-BEAM-PSDM叠加轨迹实施叠加并将叠加能量放在R处”这个操作可以用形如公式(3)所示的一重积分公式来表达,即:
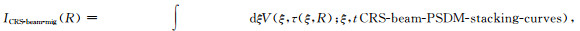
|
(3) |
这里V(ξ, τ(ξ, R))代表CRS-BEAM-PSDM的输入数据,ξ为积分变量,代表偏移孔径内由CRS-BEAM-PSDM轨迹内所定义的某个位置.注意公式(3)与公式(2)完全等价.公式(3)可以自然分解为如公式(2)所示的一个二重积分,物理上这个二重积分的物理意义是先沿着CRS叠加轨迹做一个局部叠加,然后在共偏移距剖面内再做一个惠更斯曲线叠加方式的克希霍夫PSDM.下一节将基于图 2b回顾克希霍夫统一成像理论中的相关概念和术语,并仔细分析输出道成像方式(或等走时面弥散方式)的CRS-BEAM-PSDM如何实现.
3 基于克希霍夫统一成像理论分析CRS-BEAM-PSDM“克希霍夫型成像方法”是地震成像领域所有积分叠加型成像方法的总称.从CRS-BEAM-PSDM的实现方式来看,CRS-BEAM-PSDM无疑属于克希霍夫型成像方法.关于克希霍夫型积分成像方法最为重要的工作当属Hubral等(1996)提出的克希霍夫统一成像理论.克希霍夫统一成像理论是根据克希霍夫型成像方法中惠更斯面叠加方式和等走时面叠加方式的内在同一性提出的,它是一种可以概括所有积分叠加型成像方法的框架性理论,该理论认为各种成像方法、数据集变换与分选甚至包括基准面变换都可以归结为克希霍夫积分叠加意义下的某种数据映射过程.
统一成像理论有一个重要结论:克希霍夫型成像方法总有两种实现方式—惠更斯面叠加方式(或称为输入道成像方式)和等走时面叠加方式(或称为输出道成像方式).如果对于目标成像空间的一个点,在输入数据空间内构造出对应的一个数据面(这个输入数据空间内的数据面被称为惠更斯面或数据输入面), 沿着该面进行叠加并将叠加结果放到目标成像空间的这个点时,这种成像方式被称为惠更斯面叠加方式(或输入道成像方式);如果基于输入数据空间的一个点能构造出目标成像空间内的一个面(这个数据面被称为等走时面或数据输出面),根据输入数据空间内的所有点所构造出的所有等走时面在目标成像空间内相互叠加之后将得到成像结果.这种成像方式被称为等走时面叠加方式(或输出道成像方式).统一成像理论表明这两种实现方式在数学意义上是互为转置的两个算子,物理上则完全等价,无论用哪一种方式实现将得到相同的成像结果(Tygel et al., 1996).
对于CRS-BEAM-PSDM而言,无论根据公式(2)或公式(3),都可以判定传统的CRS-BEAM-PSDM属于惠更斯曲线叠加方式(或输入道成像方式).那么基于统一克希霍夫成像理论可以立即总结出关于CRS-BEAM-PSDM的四个要点:(1)CRS-BEAM-PSDM的输入空间为共偏移距时间剖面,输出空间为深度域;(2)CRS-BEAM-PSDM的数据输入面为CRS-BEAM-PSDM叠加曲线(如图 2b上半部分所示),输入空间为共偏移距时间域;(3)实现CRS-BEAM-PSDM的另一个等效实现方式(即等时面弥散方式或输出道成像方式)必定存在;(4)Garabito等(2012)提出的传统CRS-BEAM-PSDM算法的脉冲响应就是其对应的等时面弥散方式的数据输出面.
基于图 2b继续分析CRS-BEAM-PSDM的各种特点,仔细审视图 2b下半部分可以看到在深度域中有一个由11个共偏移距等时线组成的算子(用蓝色绘出).注意这11个共偏移距等时线都是从图 2b上半部分同相轴中的对应样点(即11个绿色的Ph)中弥散产生的.而且每个共偏移距等时线都在各自对应的反射点位置与反射面界面相切,因为反射段CR(红色)就是由11个相邻的反射点R′组成的.
图 3显示了CRS-BEAM-PSDM在2 km共偏移距剖面上的脉冲响应(该共偏移距剖面内有7个子波,这里未显示).注意在计算脉冲响应之前,同相轴的局部斜率和局部曲率都必须固定,这里的局部斜率为24°,局部曲率为4.5×10-8s·m-2.需要强调一下,这些局部运动学属性值就是在图 2b上半部分所示的2 km共偏移剖面的Ph位置测量得到的.

|
图 3 CRS-BEAM-PSDM在2 km偏移距剖面内的脉冲响应 Fig. 3 The impulse responses of the CRS beam PSDM operator according to the local slope and local curvature of the events around Ph in Fig. 2b |
从脉冲响应的形状上不难观察出CRS-BEAM-PSDM算子具有明确的波束方向特性.刚才已经提到,这个局部方向特性对应于Ph样点所在的局部同相轴.换言之,图 3所示的这些具有特定方向的BEAM成像算子对那些具有与Ph相同运动学信息的局部同相轴具有最佳的成像分辨率.基于克希霍夫统一成像理论,我们知道图 3所示的脉冲响应曲线正是CRS-BEAM-PSDM的等时面弥散算子.也就是说,CRS-BEAM-PSDM的最终成像结果也可以通过所有非零样点的CRS-BEAM-PSDM等时面弥散算子的累加来得到.如果用一个积分公式来表达,显然该公式可以写为
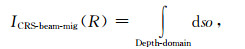
|
(4) |
(4)公式(4)即为CRS-BEAM-PSDM的一重积分算子表达形式.注意公式(4)中有一个特殊的积分变量SO,这里SO是弥散算子(Smearing Operator)的缩写.根据克希霍夫统一成像理论中关于等时线弥散方式的定义,所有弥散算子的叠加就构成了最终的成像结果.这就是为什么我们在方程(4)中直接使用弥散算子本身作为积分变量的原因.公式(4)中的弥散算子就是如图 3所示的CRS-BEAM-PSDM脉冲响应.
4 基于克希霍夫统一成像理论进一步推出两步弥散算子的CRS-BEAM-PSDM在第2节中我们已经做了分析,CRS-BEAM-PSDM叠加可分解为两个步骤:(1)在共偏移距剖面内沿CRS叠加曲线进行叠加,并将叠加结果放置在Ph处;(2)沿共偏移距剖面内的克希霍夫惠更斯叠加曲线进行叠加,并将最后的叠加结果放置在深度域的R处.显然这两步计算均属于惠更斯曲线叠加型运算.在克希霍夫统一成像理论框架下,这两种操作都可以找到对应的等时线弥散算子.注意对应于波束形成的局部叠加完全可以用一个沿着CRS叠加曲线的局部弥散来替代.而对应于克希霍夫PSDM的惠更斯曲线叠加完全可以被一个深度域的共偏移距等时线弥散所替代.如此CRS-BEAM-PSDM的两步弥散实现方式就可以得到建立.
事实上,图 2b上半部分CRS叠加曲线中的11个Ph与图 2b下半部分深度域内11个共偏移等时线的严格对应关系已经揭示了CRS-BEAM-PSDM的两步弥散机制,基于公式(4)的一步弥散确实可以自然的分解为两步弥散.仔细观察图 2b即可发现,两步弥散可以这样操作:(1)对于共偏移距剖面中的任何非零样点Ph, 沿着其CRS叠加曲线在一定孔径内进行第一次弥散;(2)对于从Ph中弥散出来的每一个新样点,沿着其共偏移距等时线在深度域中进行第二次弥散.注意第一步弥散中的数据输出面就是在共偏移距剖面中搜索到的局部CRS叠加轨迹(图 2b上半部分,绿色线绘制);而第二步弥散中的数据输出面则是这些新样点在深度域上的共偏移距等时线(图 2b下半部分,蓝色线绘制).显然上述实现过程也可以表达为一个两重积分,即:

|
(5) |
公式(5)即为CRS-BEAM-PSDM的双重弥散算子.注意公式(5)中有两个特殊的积分变量:SO1和SO2.这里SO1、SO2分别是弥散算子1,弥散算子2的缩写.
如前所述,第一重积分中的弥散算子1位于共偏移距时间域,它表示在共偏移域中的任何非零样点Ph,在给定孔径下沿着其局部CRS叠加曲线进行弥散得到的结果.关于弥散算子1的积分意味着所有非零样点对应的弥散算子1在共偏移域剖面中实施叠加.第二重积分中的弥散算子2位于深度域.注意这个操作是对于在第一次弥散生成的共偏移域时间剖面中的所有非零样点,沿着各自在深度域中的共偏移距等时线再次实施弥散.从图 2b下半部分蓝色线画出的深度域PSDM等时线完全可以看出,关于弥散算子2的积分就是所有非零样点对应的PSDM等时线在深度域中的叠加.因此由公式(5)定义的、基于共偏移剖面的所有非零样本的二重弥散积分可以获得最终的CRS-BEAM-PSDM像.公式(5)在数学上与公式(4)完全等价,在物理上与Garabito等(2012)提出的公式(2)也完全等价.需要强调,在实际应用中,公式(5)的价值在于当只实施第一步弥散时,可以得到一个信噪比大幅提高、更为规则化的叠前数据体,在这个数据体上再做其他处理都将是非常有益的.不难看出当局部CRS叠加曲线退化到一个样点的时候,CRS-BEAM-PSDM算法将精确的退回到常规克希霍夫叠前深度偏移,也就是说常规克希霍夫叠前深度偏移其实可以认为是一种特殊的、CRS叠加曲线长度为1的CRS-BEAM-PSDM.
基于两步弥散算子的CRS-BEAM-PSDM的实现方式可以概括为图 4所示的工作流程.注意深度偏移速度模型以及有关的CRS属性参数必须在运行此流程之前准备好.

|
图 4 基于双弥散算子的共偏移截面CRS-BEAM-PSDM的工作流程 Fig. 4 A work-flow of double-smearing operator based CRS beam PSDM for a common-offset section |
为了验证上述CRS-BEAM-PSDM两步弥散算子的性能,基于一个简单的模型对理论数据进行测试.图 5a显示了一个穹窿状反射界面,它被一个速度为2 km·s-1的常速介质覆盖.基于图 5a所示的模型实施射线正演模拟生成了41个从0~4 km的共偏移距剖面,其增量为100 m.图 5b、c分别显示了模拟得到的零偏移距剖面和4 km共偏移距剖面.在搜索所有局部运动学属性之前,我们在所有共偏移距剖面中加入很强的随机噪声来测试算法的性能.本文基于每一个偏移距剖面都提取了对应的CRS属性参数,保证了CRS属性参数在近、中、远偏移处的提取精度.图 5d、e、f分别显示了零偏移距剖面的出射角α剖面、NORMAL波半径Rn剖面和NIP波半径RNIP剖面.非零偏移距的运动学属性参数可以类似的算法搜索得到(Zhang et al., 2001).

|
图 5 基于简单理论模型的正演与属性提取过程 (a)真实速度模型;(b)加入随机噪声后的0 km共偏移距剖面; (c)加入随机噪声后的4 km共偏移距剖面; (d)出射角α剖面; (e) NORMAL波半径RN剖面; (f) NIP波半径RNIP剖面. Fig. 5 The ray-based forward modeling and the determination of attributes (a) The ture velocity model; (b) 0 km common-offset section with noise; (c) 4 km common-offset section with noise; (d) Emergence angle α section; (e) The radii of Normal wave RN section; (f) The radii of NIP wave RNIP section. |
图 6显示了基于两步弥散算子的CRS-BEAM-PSDM是如何在一个共偏移距剖面中工作的.图 6a显示了在图 5c所示4 km共偏移距剖面中的三个样点(选定了三个Ph用棕色点高亮显示).对于这些样点,我们可以用公式(4)中的第一重弥散积分构造三个数据输出面(即公式(4)中的三个弥散算子1).如前所述,这意味着沿着它们各自的CRS叠加曲线进行第一次弥散(如图 6b所示).在完成第一次弥散后,我们可以用公式(4)中的第二次弥散积分再构造出三个数据输出面(即公式(4)中的三个弥散算子2).这意味着,对于从三个原始样点Ph实施第一次弥散后产生的每一个新样点,都将沿着其相关的共偏移距PSDM等时线再次弥散.图 6c显示了源于图 6a所示的三个样点Ph的、在经历了两步弥散之后的CRS-BEAM-PSDM像.图 6d显示了最终的CRS-BEAM-PSDM像,该图像基于图 6a所示的输入4 km共偏移段中的所有非零样点.它是由所有来自4 km共偏移剖面中所有非零样本的所有双重弥散算子的叠加来定义的.图 6e显示了最终的常规克希霍夫PSDM像,该成像结果是基于图 6a所示的4 km共偏移剖面中所有非零样点得到的.它是由来自4 km共偏移剖面中所有非零样本的所有常规等距弥散算子的叠加来定义的.可以看出,图 6d中的信噪比比和同相轴连续性要远好于图 6e.它证明了CRS-BEAM-PSDM的鲁棒性.
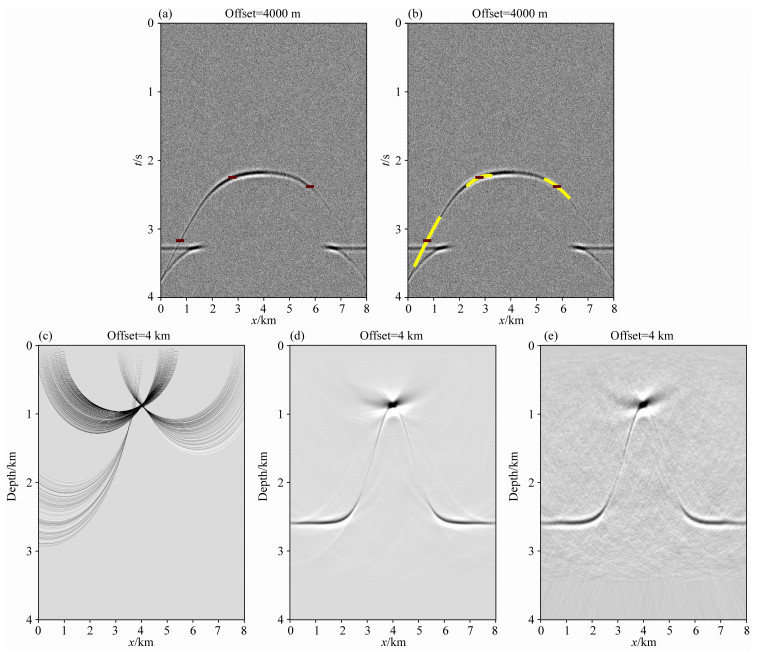
|
图 6 基于两步弥散算子的CRS-BEAM-PSDM在单偏移距剖面上的实现过程 (a)在4 km共偏移距剖面中选定的三个样点Ph; (b)关于这三个Ph,基于共偏移距剖面内各自的CRS叠加轨迹实现第一次弥散; (c)关于所有新弥散出的P′h基于深度域内各自的PSDM等时线完成第二次弥散; (d)通过所有的两步弥散CRS-BEAM-PSDM算子的累加获得的最终CRS-BEAM-PSDM像; (e)通过所有的常规克希霍夫PSDM算子累加获得的最终PSDM像. Fig. 6 The double smearing CRS beam PSDM based on a single common-offset section (a) Three samples Ph being highlighted in 4 km common-offset section; (b) Smearing Ph along their CRS stacking curves in the common-offset section; (c) Smearing each P′ h in depth section along its common-offset PSDM isochrone; (d) The final depth image is defined by superposition of all double-smearing operators; (e) The final depth image is defined by conventional Kirchhoff isochrones-smearing operatos. |
图 7显示了常规克希霍夫PSDM和基于双弥散算子的CRS-BEAM-PSDM的最终成像以及不同CDP位置处成像点道集(CIG)的比较.图 7a、b、c、d分别显示了CDP201、301、501、601处,常规克希霍夫PSDM与基于双弥散算子的CRS-BEAM-PSDM的成像点道集比较.常规克希霍夫PSDM深度域成像、基于双弥散算子CRS-BEAM-PSDM深度域成像、基于传统CRS-BEAM-PSDM深度域成像比较如图 7e、f、g所示.显然,无论传统CRS-BEAM-PSDM成像还是本文双弥散CRS-BEAM-PSDM成像都能提供在深度成像域中,同相轴连续性和信噪比明显优于传统克希霍夫PSDM成像的处理结果.但是注意传统CRS-BEAM-PSDM的成像结果中有更强的成像噪声,这是由于克希霍夫成像算法的两种实现方式即输入道成像方式与输出道成像方式的固有差别造成的.证实了本文提出的基于双弥散算子的CRS-BEAM-PSDM完全实现了传统CRS-BEAM-PSDM算法所声称的目标.但是注意其中的实现方式是完全不同的.

|
图 7 常规克希霍夫PSDM和基于双弥散算子的CRS-BEAM-PSDM的最终成像以及不同CDP位置处成像点道集的比较 (a) CDP 201;(b) CDP 301;(c) CDP 501;(d) CDP 601的成像点道集比较,图中左半边为常规克希霍夫成像结果,右边一半为CRS-BEAM-PSDM成像结果;(e)常规克希霍夫PSDM深度域成像结果; (f)基于双弥散算子的CRS-BEAM- PSDM成像结果;(g)基于传统的CRS-BEAM-PSDM成像结果. Fig. 7 The comparisons of depth image in Common-Image Gathers (CIG) and the final images of conventional Kirchhoff PSDM and the double-smearing operator based CRS beam PSDM The CIG comparison at the location of (a) CDP 201; (b) CDP 301; (c) CDP 501; (d) CDP 601; (e) The depth image of conventional Kirchhoff PSDM; (f) The depth image of the double-smearing operator based CRS beam PSDM; (g) The depth image of the traditional CRS beam PSDM. |
本文所使用的实际二维数据采集于2011年,其采集参数如下:50 m炮间距,25 m道间距,最大偏移距8 km,平均覆盖次数150次.在实施CRS-BEAM-PSDM之前的常规处理流程包括多次波压制、线性噪声衰减、叠加速度分析和剩余静校正.在将图 4所示工作流程应用于真实数据之后,图 8显示了常规克希霍夫PSDM获得的成像点道集和两步弥散CRS-BEAM-PSDM获得的成像点道集之间的比较.图 9显示出了常规克希霍夫PSDM成像和两步弥散CRS-BEAM-PSDM成像之间的比较.和理论数据上的测试结果一样,CRS-BEAM-PSDM的成像极大改善了叠前数据的信噪比和最终成像剖面中同相轴的连续性.

|
图 8 常规克希霍夫PSDM(a)和基于双弥散算子的CRS-BEAM-PSDM(b)在三个位置处的成像点道集比较 Fig. 8 The comparison between conventional PSDM (a) and the presented double smearing CRS beam PSDM (b) on CIGs |

|
图 9 常规克希霍夫PSDM(a)和基于双弥散算子的CRS-BEAM-PSDM(b)的最终成像 Fig. 9 The comparison between conventional PSDM (a) and presented double smearing CRS beam PSDM (b) on final image section |
本节简要介绍下CRS-BEAM-PSDM的三维应用,重点介绍实施第一步弥散之后的效果.因为从实际应用的角度,实施第一步弥散后的效果至关重要,如果在第一步弥散之后获得了信噪比大幅提高的叠前道集,那么基于该道集无论实施叠后还是叠前成像都会获得成像品质大幅提高的结果.
7.1 算例1——三维CRS-BEAM-PSDM的第一步弥散后信噪比加强效果首先设计一个三维常速速度模型中的单个散射体合成理论数据.常速设为2000 m·s-1,散射体的坐标是x=500 m,y=500 m,z=500 m.模型的x、y、z方向延伸长度均为1000 m(图 10a).在地表z=0 m处总共部署了10201炮和10201个检波器.检波器间距和炮点间距均为10 m.基于上述观测系统进行了一次偏移距为1000 m的观测.这个非零偏移距的正演过程如下:对于10201炮的每一炮而言,都仅有一个检波点接收.比如对于第1炮而言,其炮点位置为(x=0 m, y=-500 m),其对应的检波点位置为(x=0 m,y=500 m),因此保证了其共中点(CMP)坐标为(x=0 m,y=0 m).对于第10201炮而言,其炮点位置为(x=1000 m, y=500 m),其对应的检波点位置为(x=1000 m,y=1500 m),因此保证了其共中点(CMP)坐标为(x=1000 m,y=1000 m).所有10201炮的炮检点坐标都在y方向上差1000 m.
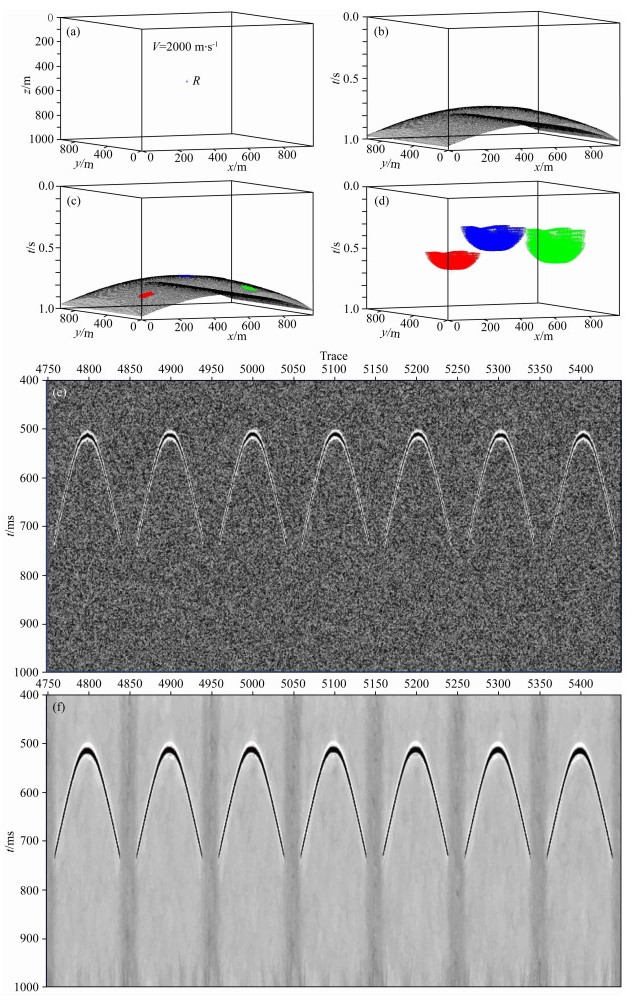
|
图 10 实施3D CRS-BEAM-PSDM的第一步弥散后的噪声压制效果 (a)一个散射体D放在一个常速2000 m·s-1的常速介质中x=500 m, y=500 m, z=500 m;(b)正演得到的1000 m 3D共偏移距剖面;(c)三块3D局部同相面,分别用红、蓝、绿色绘制;(d)基于图(d)中三块局部同相面弥散得到的三个CRS-BEAM-PSDM算子;(e)初始的三维共偏移距数据切片显示(加噪声后);(f)实施3D CRS-BEAM-PSDM的第一步弥散后的噪声压制效果. Fig. 10 The implementation of first-smearing of 3D CRS-BEAM-PSDM on synthetic data (a) The diffractor D is overlain with a constant velocity of 2000 m·s-1, which is located at the x-coordinate of 500 m, y-coordinate of 500 m, depth of 500 m; (b) A 1000 m common offset diffraction hyperbola simulated from a single diffractor; (c) Three 3D local coherent events highlighted in red, blue and green in the common offset diffraction hyperbola shown in (b); (d) Three 3D CRS-BEAM-PSDM operators; (e) 3D raw data with random noise being added; (f) The same 3D common offset section after the first-smearing of 3D CRS-BEAM-PSDM. |
我们使用一个运动学两点射线追踪程序计算了这10201个走时,并在(x,y,t)域相应的位置放置了10201个Ricker子波.图 10b显示了模拟得到的1000 m 3D共偏移距剖面;图 10c显示了在该3D共偏移距剖面上随机选定的三个3D局部同相面,分别用红、蓝、绿色绘制.图 10e显示了基于图 10d中三个局部同相面弥散得到的三个CRS-BEAM-PSDM算子;图 10f显示了初始三维共偏移距数据切片显示(加噪声后的五条检波线);图 10g显示了实施3D CRS-BEAM-PSDM的第一步弥散后的噪声压制效果,可以看到这5条检波线剖面在处理之后信噪比大幅提高,在这样的叠前道集上再进行速度分析与成像无疑将获得更为理想的处理结果.
7.2 算例2——三维CRS-BEAM-PSDM第一步弥散后数据插值效果基于二维CRS-BEAM-PSDM的数据插值实例已经在童思友等(2008)利用输出道方式CRS叠加算法(CRS-OIS)实现插值和规则化一文中有过详细介绍,这里就不再赘述.本文第二个算例重点介绍基于三维CRS-BEAM-PSDM的第一步弥散实施三维插值的理论与实际数据算例.图 11a显示了一个三维理论数据的炮点、检波点位置的平面分布图.其中炮点用白色点表示,检波点位置用黑色点表示.总共部署了900个炮点和15000个检波点.炮点在x、y方向上的间距均为20 m,检波点在x、y方向上的间距均为10 m,x方向为0~1300 m,y方向为0~1500 m.无论是x方向还是y方向,炮点分布范围都是在500~1100 m之间,每炮101条检波线,每条检波线101个检波点.地下真实模型是一个三维楔形模型.图 11b显示了该模型在x=650 m中心位置处的一个切片.然后随机删除900炮中的77炮以验证第一步弥散之后的正规化效果.图 11c显示了被删除后的炮点位置平面图(蓝色点表示删除炮的位置).图 11d显示了第99炮被整体删除后的炮道集;图 11e显示了应用三维CRS-BEAM-PSDM的第一步弥散之后的结果,可以看到第99炮已经得到了很好的重建.其实现过程完全类似于算例1中的流程:先将数据分选为三维共偏移距数据体,然后在三维共偏移距数据体内实施CRS-BEAM-PSDM的第一步弥散.这里需要强调,之所以第一步弥散能够得到很好的插值效果的根本原因在于虽然在炮域里这些炮数据都整体缺失了,但是在三维共偏移距数据体上,900道仅仅随机缺失了77道,基于三维共偏移距数据体的属性搜索依然可以获取准确的CRS运动学属性参数,这是实施三维CRS-BEAM-PSDM的第一步弥散能够获得理想插值效果的根本原因.如果在三维共偏移距数据体上有很多道连续缺失,那就很难用上述算法获得满意的插值效果了.图 11f、g显示了将三维CRS-BEAM-PSDM的第一步弥散用于中国西部某三维区块的插值效果,可以看到数据缺失的三维数据体在应用之后插值效果非常明显(为对比方便,仅应用于3 s以下).
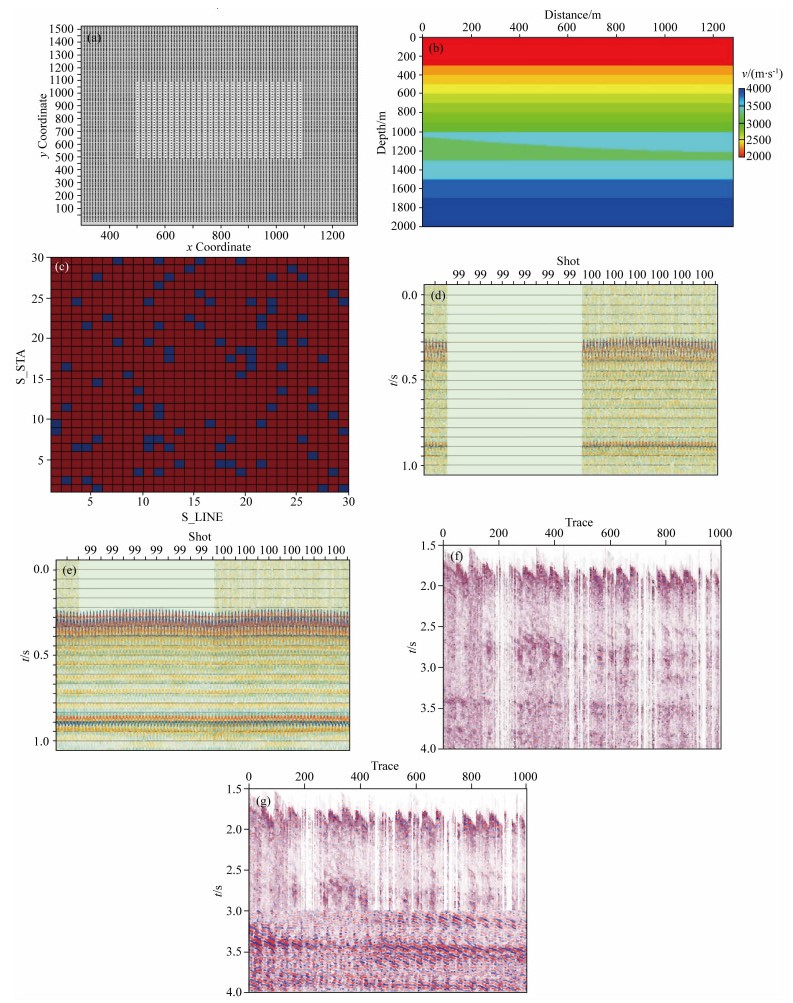
|
图 11 三维CRS-BEAM-PSDM的第一步弥散在理论与实际数据上体现出的插值效果 (a)三维理论数据的炮点、检波点位置的平面分布图.其中炮点用白色点表示,检波点位置用黑色点表示;(b)该模型在x=650 m位置处的一个切片;(c)被随机删除的77炮位置(蓝色点表示删除炮的位置);(d)第99炮被整体删除后的炮道集;(e)应用三维CRS-BEAM-PSDM第一步弥散之后第99炮得到重建后的结果;(f)中国西部某三维实际数据炮记录; (g)三维CRS-BEAM-PSDM的第一步弥散用于(f)后的插值效果(为对比方便,算法仅应用到3 s以下). Fig. 11 The interpolation performance of the first smearing of 3D CRS beam PSDM on the synthetic and real data (a) A base-map of model. It consist of 900 shot locations (in white dot) and 15000 receiver locations (in black dot); (b) a slice of the model; (c) The positions of randomly killed shot gathers (in blue color); (d) The original shot gathers of No. 99 and No. 100, note that shot No. 99 is killed; (e) The shot gathers of No. 99 after the first-smearing of 3D-CRS-BEAM; (f) a real 3D shot gather acquired in western China; (g) The same 3D shot gather after the first-smearing of 3D-CRS-BEAM. |
最后一个算例是在南海采集的某三维实际数据.所研究的三维数据集是从整个采集工区中提取的某一束.该束三维数据采集于2010年,共获得1176炮、每炮6条电缆接收、每条电缆的道间距为25 m、最大偏移距10 km、平均覆盖次数60次.注意本测线的处理是三维共反射面元射线束时间偏移(CRS-BEAM-PSTM)而不是三维CRS-BEAM-PSDM.也就是说第一步弥散时完全相同的,区别仅仅在于第二步弥散是沿着时间域的等时线进行弥散而不是深度域的等时线进行弥散,这对于算法而言是一个非常小的改动,同时完全不影响我们讨论第一步弥散的处理效果.再次之前的处理流程包括表面相关多次波消除(SRME)、几何扩展补偿、预测反褶积和叠加速度分析.在实施SRME后,数据连续性和信噪比都有所降低(如图 12a所示).图 12b显示了三维CRS-BEAM-PSTM第一次弥散之后的第551炮道集.图 12c、d显示了原始数据的成像剖面和第一次弥散后的成像剖面之间的对比,可以清楚看到在信噪比和同相轴连续性一如既往的得到了有效加强的同时也增加了很多构造细节.基于CRS-BEAM-PSTM后的成像剖面进行解释能够揭示更多的地质规律.
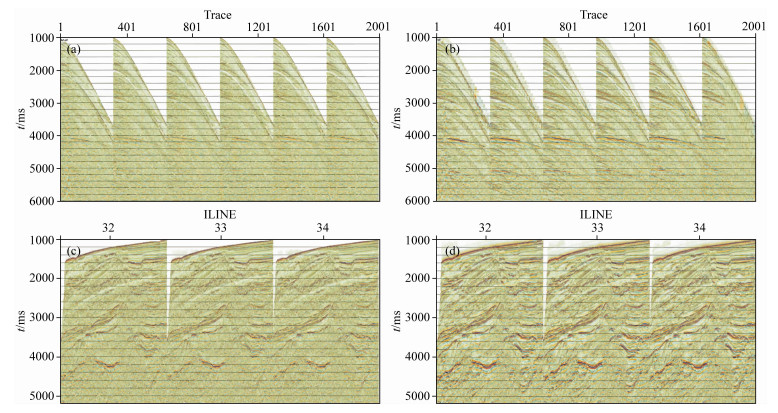
|
图 12 三维CRS-BEAM-PSTM在南海三维实际数据上的应用 (a)弥散处理之前的第551炮记录;(b) 3D CRS-BEAM-PSTM第一步弥散处理之后的第551炮记录; (c)常规三维PSTM像来自INLINE 32-34; (d)三维CRS-BEAM-PSTM像来自INLINE 32~34. Fig. 12 Application of 3D CRS-BEAM-PSTM on real data acquired in the South China Sea (a) The shot No. 551 before CRS-BEAM-PSTM processing; (b) The shot No. 551 after CRS-BEAM-PSTM rocessing; (c) The conventional 3D PSTM image of inline 32~34 sorted from marine data example; (d) The 3D PSTM image of inline 32~34 sorted from marine data example calculated with 3D CRS-BEAM-PSTM. |
基于克希霍夫统一成像理论,对前人提出的CRS-BEAM-PSDM给出了更为深入的理解,同时提出了一种等价的、等时面弥散方式的CRS-BEAM-PSDM算法.在对等时面弥散方式再进行深入分析之后可以将其分解为两步操作:第一步是对于共偏移距剖面中的任何非零样点Ph, 沿着其CRS叠加曲线在一定孔径内进行第一次弥散;第二步是对于从Ph中弥散出来的每一个新样点,沿着其共偏移距等时线在深度域中进行第二次弥散.显然上述实现过程也可以表达为一个两重积分.于是一个基于两步弥散算子的CRS-BEAM-PSDM算法就得到了.可以直观看出,当局部CRS叠加曲线退化到一个样点的时候,CRS-BEAM-PSDM算法将精确的退回到常规克希霍夫叠前深度偏移,也就是说常规克希霍夫叠前深度偏移其实可以认为是一种当CRS叠加曲线长度为1时CRS-BEAM-PSDM算法的特例.
需要强调,基于两步弥散算子的CRS-BEAM-PSDM算法与传统的基于两步叠加的CRS-BEAM-PSDM算法在理论上完全等价.但是在实际应用效果上二者略有差别,基于两步弥散算子的CRS-BEAM-PSDM将会继承传统的输出道方式克希霍夫成像方法固有的计算成本更为经济、同时成像噪声略低的优势.同时,当只实施第一步弥散时,即可得到一个信噪比大幅提高、更为规则化的叠前数据体,基于这个数据体实施PSDM就得到本文阐述的CRS-BEAM-PSDM像;如果基于该数据体实施PSTM就得到本文最后一个三维实例中展示的CRS-BEAM-PSTM像;如果基于该数据体实施常规CMP叠加就等价于杨锴(2003)和杨锴等(2005)提出的输出道方式的CRS叠加成像算法(CRS-OIS).因此将算法分解为两步弥散确有很好的应用价值,无论在二维、三维理论或实际数据上的测试均证实了该算法的鲁棒性.
致谢 感谢中海油研究总院有限责任公司允许发布有关处理实例.
Baykulov M, Gajewski D. 2009. Prestack seismic data enhancement with partial common-reflection-surface (CRS) stack. Geophysics, 74(3): V49-V58. DOI:10.1190/1.3106182 |
Duveneck E. 2004. Velocity model estimation with data-derived wavefront attributes. Geophysics, 69(1): 265-274. DOI:10.1190/1.1649394 |
Garabito G, Stoffa P L, Ferreira C A S, et al. 2012. CRS-beam PSDM:Kirchhoff-beam prestack depth migration using the 2D CRS stacking operator. Journal of Applied Geophysics, 85: 102-110. DOI:10.1016/j.jappgeo.2012.07.004 |
Han L G, Sun J G, He Q D, et al. 2003. Imaging by joint CRS and CMP stacking. Geophysical Prospecting For Petroleum, 42(1): 25-28. |
Hill N R. 1990. Gaussian beam migration. Geophysics, 55(11): 1416-1428. DOI:10.1190/1.1442788 |
Hubral P. 1983. Computing true amplitude reflections in a laterally inhomogeneous earth. Geophysics, 48(8): 1051-1062. DOI:10.1190/1.1441528 |
Hubral P, Hocht G, Jaeger R. 1999. Seismic illumination. The Leading Edge, 18(11): 1268-1271. DOI:10.1190/1.1438196 |
Hubral P, Schleicher J, Tygel M. 1996. A unified approach to 3-D seismic reflection imaging, PART I:basic concepts. Geophysics, 61(3): 742-758. DOI:10.1190/1.1444001 |
Jäger R, Mann J, H cht G, et al. 2001. Common-Reflection-Surface stack:image and attributes. Geophysics, 66(1): 97-109. DOI:10.1190/1.1444927 |
Landa E, Gurevich B, Keydar S, et al. 1999. Application of multifocusing method for subsurface imaging. Journal of Applied Geophysics, 42(3-4): 283-300. DOI:10.1016/S0926-9851(99)00041-5 |
Li Z C, Sun X D, Liu H. 2006. Common reflection surface stack for rugged surface topography. Chinese Journal of Geophysics (in Chinese), 49(6): 1794-1801. |
Li Z C, Yao Y X, Ma Z T, et al. 2003. Common reflection surface stack method based on multi-level optimization of parameters and its application. Oil Geophysical Prospecting, 38(2): 156-161. |
Liu S Y, Gu H M, Tang Y J, et al. 2018. Angle-domain common imaging gather extraction via Kirchhoff prestack depth migration based on a traveltime table in transversely isotropic media. Journal of Geophysics and Engineering, 15(2): 568-575. DOI:10.1088/1742-2140/aaa149 |
Mann J, Jäger R, Müller T, et al. 1999. Common-reflection-surface stack-A real data example. Journal of Applied Geophysics, 42(3-4): 301-318. DOI:10.1016/S0926-9851(99)00042-7 |
Ni Yao, Yang Kai. 2013. A GPU Based 3D Common Reflection Surface Stack Algorithm with the Output Imaging Scheme (3D-CRS-OIS). Oil Geophysical Prospecting, 48(1): 49-57. |
Sun J G. 2002. On 3D demigration with isochrones stack. Journal of Jilin University (Earth Science), 32(2): 273-278. |
Sun X D, Li Z C, Teng H H. 2008. CRS technology and its applications in seismic imaging. Geophysical Prospecting For Petroleum, 47(5): 465-469. |
Sun Y H, Qin F H, Checkles S, et al. 2000. 3-D prestack Kirchhoff beam migration for depth imaging. Geophysics, 65(5): 1592-1603. DOI:10.1190/1.1444847 |
Tan W Y, Zhao B, Yang C C. 2007. Calculation of travel-time curved face of common reflection surface. Progress in Geophysics (in Chinese), 22(3): 843-849. |
Tong S Y, Yang K, Kong J B. 2010. Noise Suppresion and Data Interpolation by Using CRS-OIS. Journal of Tongji University (Earth Science), 38(5): 753-757. |
Tygel M, Schleicher J, Hubral P. 1996. A unified approach to 3D seismic reflection imaging PART II:Theory. Geophysics, 61(3): 759-775. DOI:10.1190/1.1444002 |
Wang H Z, Feng B, Liu S Y. 2015. Characteristic wavefield decomposition, imaging and inversion with prestack seismic data. Chinese Journal of Geophysics (in Chinese), 58(6): 2024-2034. DOI:10.6038/cjg20150617 |
Wang H Z, Yang K, Ma Z T. 2004. An applied theory on common reflection surface stack-From common reflection point to common reflection surface. Chinese Journal of Geophysics (in Chinese), 47(1): 137-142. |
Wang X J, Chen B S, Zhang J M, et al. 2014. Multifocusing CRS stack and its applications to the imaging of middle and deep reflectors. China Offshore Oil and Gas, 26(1): 44-48. |
Wang Z, Yang K, Dong S L, et al. 2015. Attenuating the dip discrimination phenomenon in CRS stack by combining CRS-OIS and prestack time migration/demigration. Oil Geophysical Prospecting, 50(5): 839-847. |
Wu X Y, Liu T Y, Wei W, et al. 2008. Two dimensional common reflection surface stack based on the Fresnel zone. Chinese Journal of Geophysics (in Chinese), 51(6): 1892-1898. |
Yang K, 2003. Common Reflection Surface Stack: from input imaging scheme to output imaging scheme[Ph.D. thesis]. Shanghai: TongJi University.
|
Yang K, Jiang X G. 2010. Application of an output imaging scheme of 3D common reflection surface stack (3D CRSOIS) to 3D real data acquired in Chinese mountainous area.//80th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 3614-3617.
|
Yang K, Ma Z T. 2006. Common reflection surface stack by an output imaging scheme. Chinese Journal of Geophysics (in Chinese), 49(2): 546-553. |
Yang K, Ma Z T, Luo W D. 2006. Common reflection surface stack by the outplanat Ⅱ:Practice. Chinese Journal of Geophysics (in Chinese), 49(3): 895-902. |
Yang K, Wang H Z, Dong L G, et al. 2006. An output imaging scheme of the common reflection surface stack: applications to real data.//76th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 131-154.
|
Yang K, Wang H Z, Ma Z T. 2001. The preliminary practice of common reflection surface stack.//Annual of the 2001 Chinese Geophysical Society-Proceedings of the 17th annual meeting of the Chinese Geophysical Society. Kunming: Yunnan Science and Technology Press, 363.
|
Yang K, Wang H Z, Ma Z T. 2004. The practice on common reflection surface stack. Chinese Journal of Geophysics (in Chinese), 47(2): 327-331. |
Yang K, Xu S Y, Wang H Z, et al. 2005. A method of dip decomposition common reflection surface stack. Chinese Journal of Geophysics (in Chinese), 48(5): 1148-1155. DOI:10.1002/cjg2.758 |
Zhang Y H, Bergler S, Hubral P. 2001. Common-reflection-surface (CRS) stack for common offset. Geophysical Prospecting, 49(6): 709-718. DOI:10.1046/j.1365-2478.2001.00292.x |
韩立国, 孙建国, 何樵登, 等. 2003. 共反射面与共中心点联合叠加成像. 石油物探, 42(1): 25-28. DOI:10.3969/j.issn.1000-1441.2003.01.006 |
李振春, 孙晓东, 刘洪. 2006. 复杂地表条件下共反射面元(CRS)叠加方法研究. 地球物理学报, 49(6): 1794-1801. DOI:10.3321/j.issn:0001-5733.2006.06.027 |
李振春, 姚云霞, 马在田, 等. 2003. 基于参数多级优化的共反射面叠加方法及其应用. 石油地球物理勘探, 38(2): 156-161. DOI:10.3321/j.issn:1000-7210.2003.02.011 |
倪瑶, 杨锴. 2013. 基于GPU计算平台实现三维输出道方式的共反射面元(3D-CRS-OIS)叠加. 石油地球物理勘探, 48(1): 49-57. |
孙小东, 李振春, 滕厚华. 2008. 共反射面元叠加技术及其在偏移成像中的应用. 石油物探, 47(5): 465-469, 504. DOI:10.3969/j.issn.1000-1441.2008.05.007 |
谭未一, 赵兵, 杨长春. 2007. 共反射面元走时曲面计算方法. 地球物理学进展, 22(3): 843-849. DOI:10.3969/j.issn.1004-2903.2007.03.028 |
童思友, 杨锴, 孔剑冰, 等. 2010. 利用CRS-OIS实现噪声压制与数据插值. 同济大学学报(自然科学版), 38(5): 753-757. DOI:10.3969/j.issn.0253-374x.2010.05.022 |
王华忠, 冯波, 刘少勇, 等. 2015. 叠前地震数据特征波场分解、偏移成像与层析反演. 地球物理学报, 58(6): 2014-2034. DOI:10.6038/cjg20150617 |
王华忠, 杨锴, 马在田. 2004. 共反射面元叠加的应用理论-从共反射点到共反射面元. 地球物理学报, 47(1): 137-142. DOI:10.3321/j.issn:0001-5733.2004.01.021 |
汪小将, 陈宝书, 张金淼, 等. 2014. 中深层成像多次聚焦共反射面元叠加技术研究及应用. 中国海上油气, 26(1): 44-48. |
王征, 杨锴, 董水利, 等. 2015. 应用叠前时间偏移/反偏移与CRS-OIS叠加削弱倾角歧视影响. 石油地球物理勘探, 50(5): 839-847. |
吴小羊, 刘天佑, 魏伟, 等. 2008. 二维菲涅耳带共反射面元叠加方法研究. 地球物理学报, 51(6): 1892-1898. DOI:10.3321/j.issn:0001-5733.2008.06.032 |
杨锴. 2003.共反射面元叠加-从输入道观点到输出道观点[博士论文].上海: 同济大学.
|
杨锴, 马在田. 2006. 输出道成像方式的共反射面元叠加方法I-理论. 地球物理学报, 49(2): 546-553. DOI:10.3321/j.issn:0001-5733.2006.02.030 |
杨锴, 王华忠, 马在田. 2001.共反射面元(CRS)叠加之初步实践.//2001中国地球物理学会年刊——中国地球物理学会第十七届年会论文集.昆明: 云南科技出版社, 363.
|
杨锴, 王华忠, 马在田. 2004. 共反射面元叠加的应用实践. 地球物理学报, 47(2): 327-331. DOI:10.3321/j.issn:0001-5733.2004.02.021 |
杨锴, 许士勇, 王华忠, 等. 2005. 倾角分解共反射面元叠加方法研究. 地球物理学报, 48(5): 1148-1155. DOI:10.3321/j.issn:0001-5733.2005.05.024 |
 2020, Vol. 63
2020, Vol. 63


