0 引言

高精度GNSS速度场是研究区域地壳运动的基础，能够为GIA建模提供外部检核和新的约束，进而对板块运动、地壳垂向运动、大地水准面变化、海平面变化(姜卫平等, 2009, King et al., 2010; Khan et al., 2010; Argus et al., 2011; Thomas et al., 2011; Serpelloni et al., 2013; 柯灏等, 2016, 高春春等，2016)等提供重要改正.南极地区当前地壳运动特征的研究对全球板块构造格局的形成与演化机制、地球参考框架的构建与维持、极地冰雪环境动态变化监测等具有重要参考价值(Larson et al., 1997; Kreemer and Holt, 2000; Morelli and Danesie, 2004; Capra and Dietrich, 2008; Hampel et al., 2009).但一直以来，南极地区由于环境恶劣，测站稀疏，导致数据质量较差.随着GNSS数据的不断积累以及精度不断提高，用高精度GNSS数据分析南极地区构造形变特征日趋成熟.GNSS坐标时间序列具有时间相关性和空间相关性, 时间相关性一般采用最大似然估计法进行计算，而空间相关误差(CME)则采用数据后处理方法予以削弱，一般称为区域时空滤波.GNSS时间序列的空间相关性与GNSS网的尺度有关，对于全球尺度而言，主要的误差源是参考框架，而对于区域GNSS网，空间相关噪声是最大的误差源，通常称为共性误差CME(Wdowinski et al., 1997)，前者可以用7参数或者14参数转化移除(Ji and Herring, 2011; Blewitt et al., 2013)，后者需要使用区域滤波进行改正.使用空间滤波方法移除CME得到精准的速度场，一方面可以对移除的CME物理成分进行科学解释，另一方面用于研究区域垂向形变的机理，为GNSS数据在极地的应用提供参考.

Wdowinski等(1997)在南加州地区首次使用堆栈法(Stacking)对兰德斯地震前后GNSS垂向时间序列进行分析，但堆栈法假设CME在区域内平均分布，无法处理大尺度GNSS网.Márquez-Azú和DeMets(2003)采用GNSS时间序列和基线长度作为权重，使用改进的堆栈法探究了墨西哥地区的大尺度地壳运动.田云锋和沈正康(2011), Tian和Shen(2016)，谢树明等(2014)则使用站点之间的相关性作为权重，对陆地大尺度GNSS网进行区域滤波处理.为了克服堆栈法存在的不足，并探究CME产生的物理机制，Dong等(2006)使用PCA和Karhunen-Loeve展开(KLE)方法对南加利福尼亚州5年的GNSS时间序列进行了滤波分析.马超等(2016)使用PCA、KLE和堆栈法对南极半岛地区11个GNSS站时间序列进行区域滤波，并对三种滤波方法的结果进行了对比.

相较于堆栈法，PCA在理论上更加严密，但PCA基于方差和协方差二阶统计量，没用充分利用CME的高阶统计信息，CME中包含有色噪声，并不满足正态分布，因此使用PCA方法可能导致某一主成分包含不同的物理模式，进而导致虚假特征.Ming等(2017)使用ICA方法对中国259个GNSS站进行区域滤波分析，并根据空间响应的正负用一种绘制多边形的方法对异常测站进行了剔除.相对于PCA法，ICA引入高阶统计量，能够分离出统计独立的非高斯信号.马超等(2016)使用堆栈法、PCA、KLE方法只分析了南极半岛地区11个GNSS站2010—2014年的U方向时间序列，且对有较大空间响应的ROTH、OHI2、OHI3站没有单独分析，直接作为异常站进行剔除.考虑到堆栈法、PCA方法的不足，本文引入了ICA方法对南极半岛地区的GNSS网进行区域滤波，首先采用因子分析法探讨了南极半岛地区的GNSS站数据PCA、ICA方法的适用性，然后用ICA和PCA法对比分析了GNSS时间序列的区域滤波效果.

1 原理 1.1 主分量分析(PCA)

假设某一区域共n个GNSS站点，时间跨度为m, X(m×n)矩阵每一列为一个站的残差序列，假设m>n, 则可计算得到X的协方差阵B：

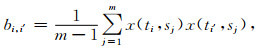
(1)

B为n维对称阵，对B进行正交分解：

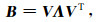
(2)

其中，Λ是具有r个非零特征值的对角矩阵(n≥r)，V^T是一个行向量正交的n×n特征向量矩阵，用正交基V来扩充矩阵X可得：

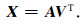
(3)

根据正交矩阵的性质，公式(3)可以转变为：

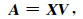
(4)

即

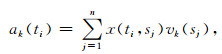
(5)

(5) 式中a_k(t)称为矩阵X的第j个主分量，代表时间变化；v_k(s)代表对主分量a_k(t)的空间响应.将特征向量按照特征值大小进行降序排列，排在前面的方差较大的主分量代表残差时间序列X中的CME信号.假设前p个主分量代表CME，那么PCA方法的共性误差可以定义为：

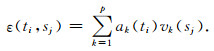
(6)

1.2 独立成分分析(ICA)

假设矩阵A由不同的时间序列X组成，X为相互独立的未知信号的叠加，在某一历元瞬时数学形式为：

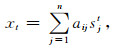
(7)

其中x_t为t时刻m×1维观测向量，s_j^t为t时刻第j个信号源，a_ij为t时刻第j个信号源对应的贡献系数，满足1≪i≪m, 1≪j≪n.考虑所有的观测时刻T，写成矩阵形式：

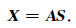
(8)

为求A的逆矩阵恢复原始信号，需要解混合矩阵W：

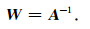
(9)

由于CME在空间域具有相关性，本文采用各信号源在时间域相互独立的tICA来提取CME：

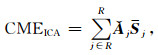
(10)

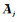
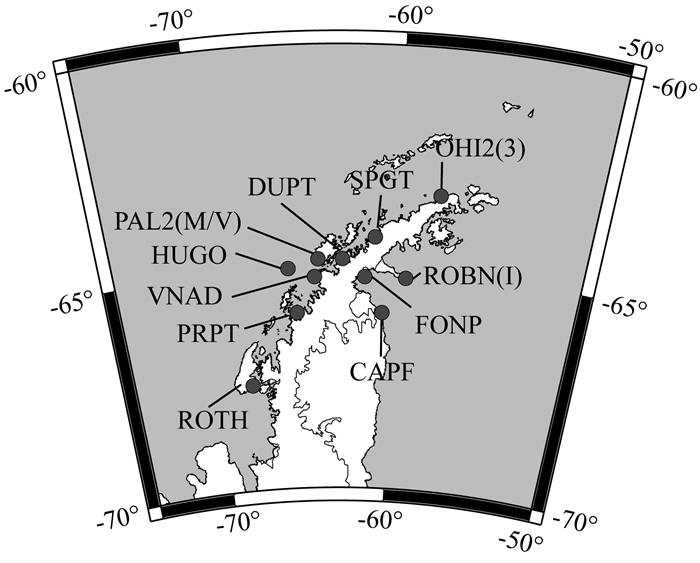
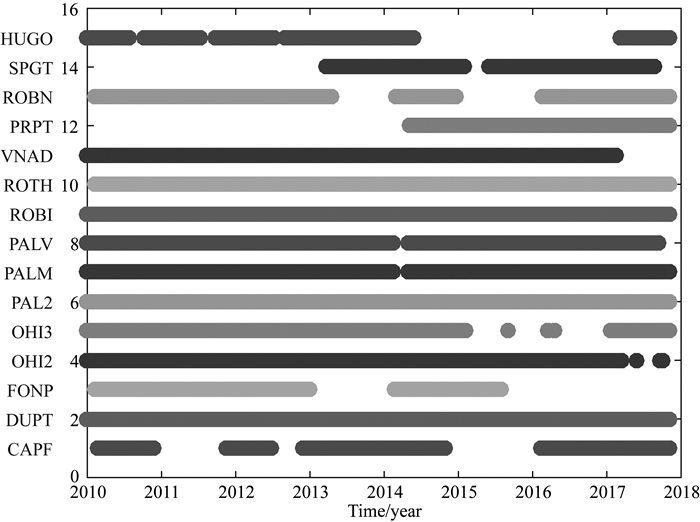
其中S是R中具有“共同空间特征的”IC子集，为S_j对应的空间响应SR(spatial response).

2 数据处理 2.1 数据插值

原始GNSS时间序列来自Nevada Geodetic Laboratory http://geodesy.unr.edu/NGL Station Pages/Global Station List，根据GNSS站点的分布和数据完整性，最终选取了南极半岛地区CAPF、DUPT、FONP、HUGO、OHI2、OHI3、PAL2、PALV、PALM、ROBI、ROTH、VNAD、PRPT、ROBN、SPGT等15个站点，其中PAL2, PALV和PALM以及ROBI和ROBN位置相同，时间跨度为2010-02-08—2017-11-03，GNSS站点分布见图 1，GNSS站点数据信息见图 2.

原始的时间序列通过三倍四分位法进行异常值剔除，然后移除线性项和周期项得到GNSS残差时间序列.若缺失数据比例过大，则在时间域上对坐标序列建模时必然影响参数估计的精度，特别是速度的不确定度(Blewitt and Lavalliée，2002)；而在频率域上对其进行谱分析时，则会导致混频现象(Kirchner，2005; 明锋等，2016)，主分量分析和独立分量分析提取共性误差前，要求坐标时间序列不能包含缺失数据.本文选用Schneider(2001)提出的RegEM数据插值法，RegEM法考虑站点坐标时间序列的物理背景以及各站之间的相关性，不依赖数据模型，也不引入先验信息，只依据数据自身特性进行插值，其原理如下：

假设观测矩阵X由p个测站，n个观测历元组成, 对于X中的每一历元的观测值，缺失坐标向量与非缺失坐标向量可以用一个线性回归模型描述，即：

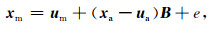
(11)

其中，非缺失的测站坐标构成的向量为x_a，均值为u_a，剩余缺失的测站坐标构成的向量为x_m，均值为u_m，B∈R^P_a×P_m为回归系数，残差e为一均值为0，协方差阵C∈R^P_m×P_m未知的随机变量，给定的观测矩阵的均值μ和协方差阵ε通过条件最大似然估计计算X中每一行包含数据缺失的观测值的回归系数B和残差协方差阵C.之后，通过(12)式对缺失数据进行填补，即：

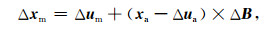
(12)

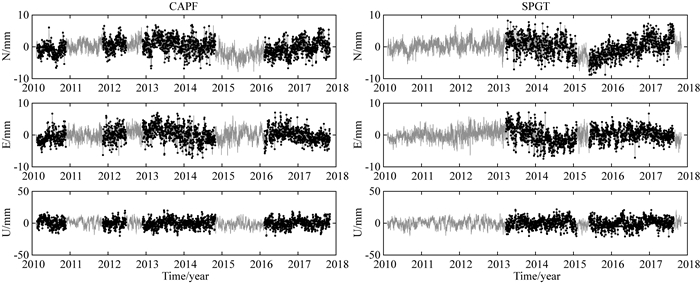
Δu_m，Δu_a分别为非缺失和缺失数据均值的估计值，ΔB为估计得到的回归系数.对缺失数据进行填补后，再计算新的均值μ和协方差阵ε.直至迭代达到指定的终止水平，B为回归系数通过岭估计得到.图 3为CAPF和SPGT站的RegEM插值效果图，黑点为原始残差序列，灰线为RegEM插值结果.

2.2 因子分析

为验证数据是否适用于进行主分量和独立分量分析，首先对数据进行KMO(Kaiser-Meyer-Olkin)因子分析(Kaiser, 1974; Cerny and Kaiser, 1977)，KMO通过检验原始变量间的简单相关系数和偏相关系数来确定数据是否适合做因子分析，若变量间的简单相关系数平方和比偏相关系数平方和越大，则KMO值越接近1，相关性越强，适合做因子分析；反之，则不适合做因子分析.通过分析，GNSS数据的E、N、U三个分量的KMO测度值分别为0.910、0.947、0.949，表明数据适合做因子分析.巴特利特检验统计值的显著性概率小于0.01，即数据具有相关性，E、N、U巴特利特检验值均为0.00，可用做主成分分析.

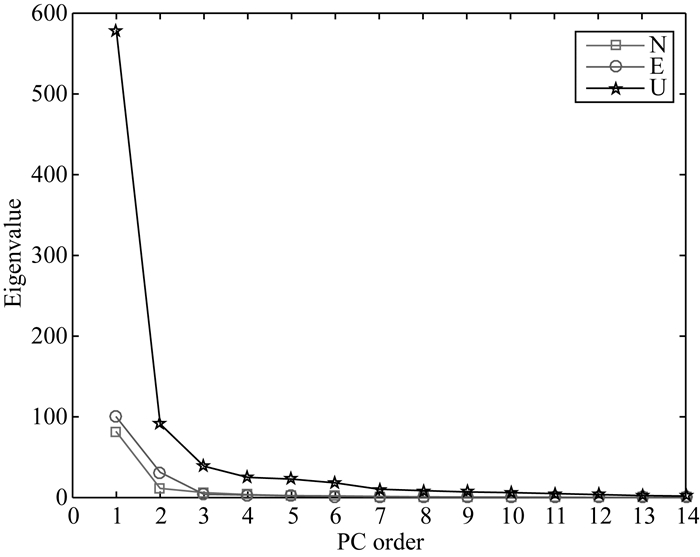
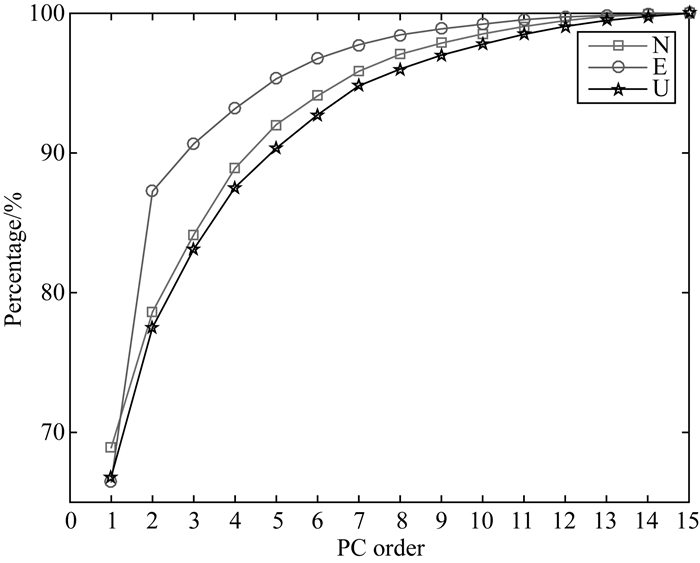
对E、N、U分量残差序列的协方差阵进行奇异值分解，得到特征值谱和累计方差如图 4、图 5所示，可以看出E、N、U分量前3个PC的方差之和分别占总方差的90.66%、84.14%、83.11%，其中PC1的方差对总方差的贡献分别为66.46%、68.91%、66.83%，表明各分量信号主要集中在PC1上.为进一步评估E、N、U分量前多少个PC具有统计显著性，我们采用PA(parallel analysis)进行检验(Peres-Neto et al., 2005)，通过随机模拟大量服从正态分布的观测数据，求得各特征值在一定显著性水平下的边界值.若观测值矩阵第i个特征值大于对应的边界值，就认为该特征值是显著的.

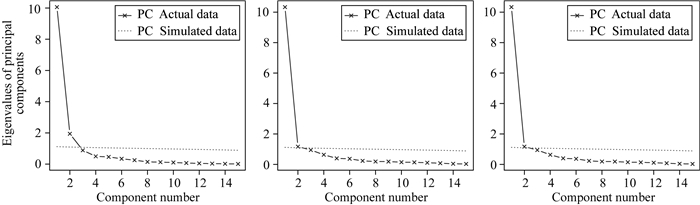
图 6为E、N、U PA检验结果，实线为坐标残差序列矩阵的特征值，虚线为随机模拟1000次得到的平均特征值，从图 6可以看出E、N、U三个分量前2个PC是统计显著的，为更加详细的分析因子情况，我们取前3分量进行分析.图 7为因子分析结果，表示观测变量与主成分的相关系数，结果统计在表 1中(V1—V15分别对应15个测站).从图 7可以看出ROBI(V10)站始终与其他站有较大差异，同位置的ROBN站则与其他站有较好的一致性，表明ROBI站的数据可能存在问题，同时OHI2、OHI3站在E方向均存在异常的情况，在进行PCA，ICA滤波分析时，会进一步讨论.

3 结果分析 3.1 PCA滤波

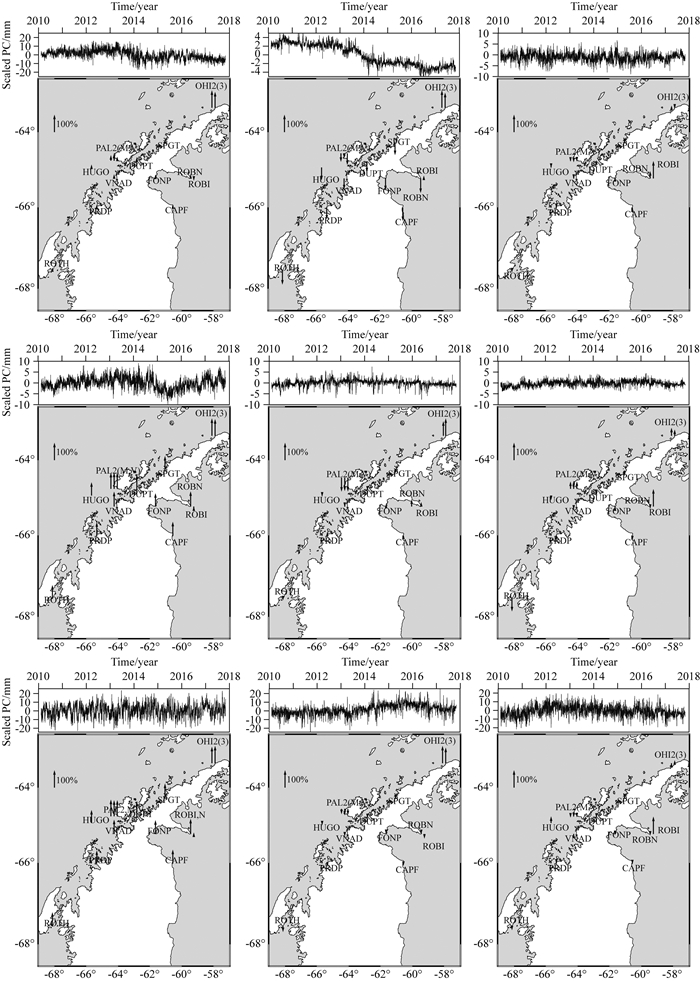
基于上述方法对E、N、U分量进行PCA滤波，如图 8所示(空间响应SR是归一化后的结果，即绝对值最大的响应为±100%，下同).

从图 8可以看出，在E、N、U前3主分量中，ROBI站始终与其他各站有不一致的空间响应，ROBI站的第三主分量空间响应远大于其他站，但同位置的ROBN站显示出与其他站较一致的空间响应，我们认为ROBI站的数据的确存在问题，说明使用因子分析法能够检测出异常测站，为进一步分析首先剔除ROBI站.

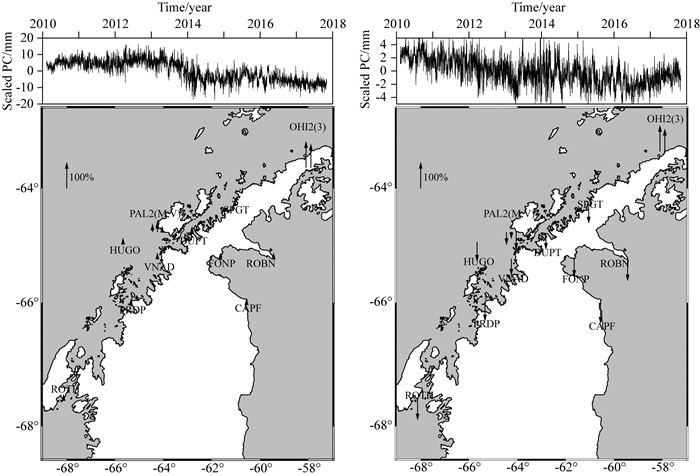
图 9为PCA E方向前2个主分量响应图，从图 9可以看出，剔除ROBI站后，E方向第一主分量OHI2、OHI3站的空间响应远大于其他站，对N、U方向进行分析发现没有出现异常.从最终的空间响应可以看出，SR1的空间响应方向一致，根据某一主分量模式中大多数测站(50%)具有明显(＞25%)的标准化空间响应(Dong et al., 2006)，且该模式的特征值超过了所有特征值总和的1%，可认为是共有模式，据此我们尝试用14个站的PCA第一主分量进行CME剔除，结果显示在OHI2、OHI3站E方向滤波效果较差.

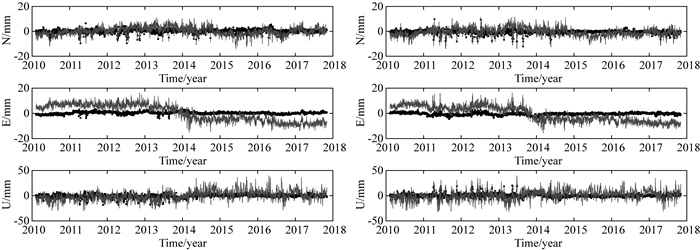
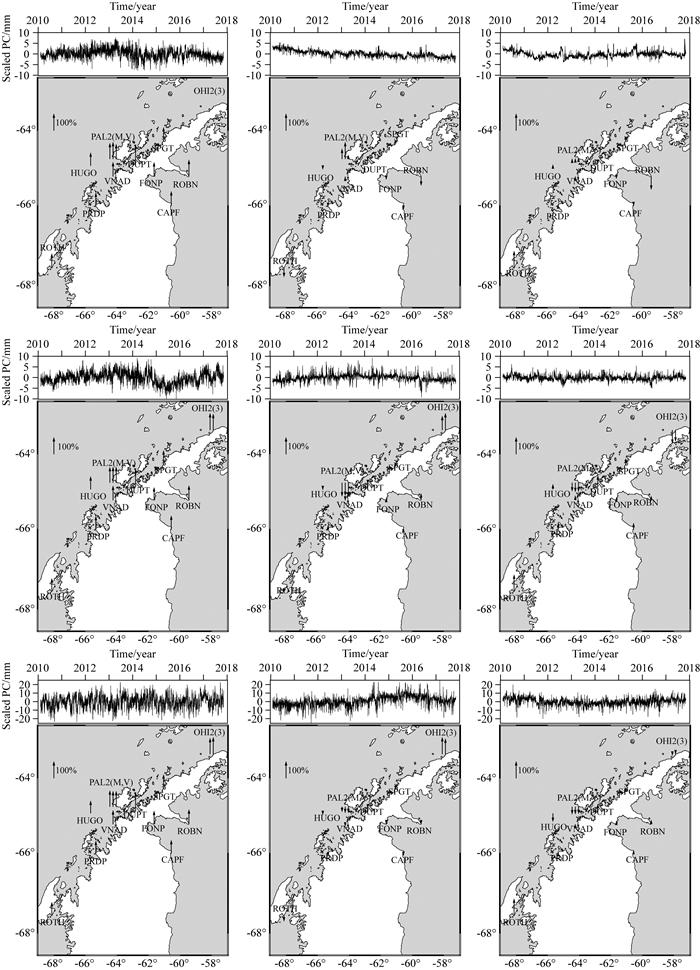
图 10为PCA滤波前后OHI2、OHI3残差对比，灰线为原始GNSS残差序列，黑线为经过PCA滤波后残差时间序列.如图 10所示，OHI2、OHI3两个测站E方向时间序列，在2014年有一个明显的转折，经过PCA滤波后，残差时间序列变成了一条趋近于0的直线，原始残差序列的变化趋势发生了改变，我们认为是由于OHI2、OHI3时间序列E方向存在较强烈的局部效应，导致PCA滤波剔除了测站的某些原始信息，所以单独对E方向移除OHI2、OHI3站后重新进行PCA分析，选择第一主分量计算CME，使用其他站的平均主分量作为OHI2、OHI3主分量，主分量分析结果见图 11.

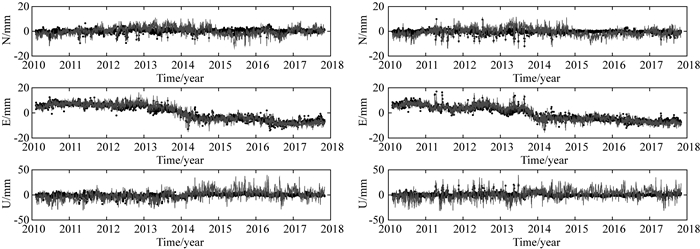
图 12为残差序列PCA滤波前后对比图，灰色线为原始残差序列，黑点为滤波后残差序列.从图 12可知，经过上述处理OHI2、OHI3站E分量残差序列的发散性得到明显的降低.

3.2 ICA滤波

由于PCA滤波中ROBI站的异常，进行ICA时仍然剔除掉此站.从实验结果分析可得，E、N、U分量的IC14、IC14、IC11对应的测站具有几乎一致的SR，而其他IC对应的SR则无明显空间分布特征.据此分析，IC14、IC14、IC11对应的SR分别代表了CME在E、N、U分量的“共同空间”特征.因此，本文分别采用IC14、IC14、IC11分量计算E、N、U方向的CME.

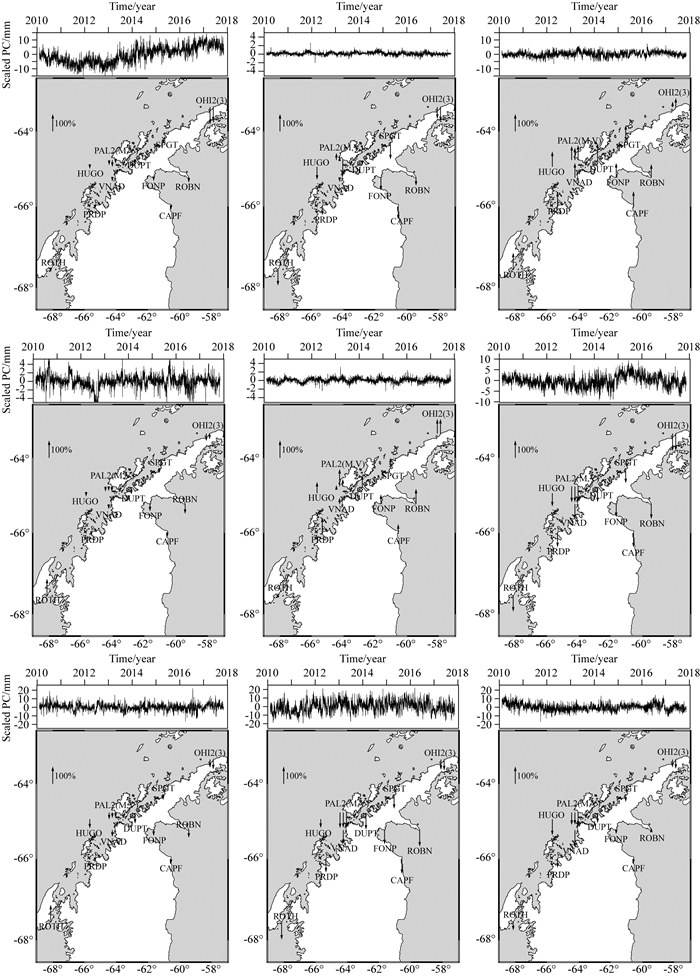
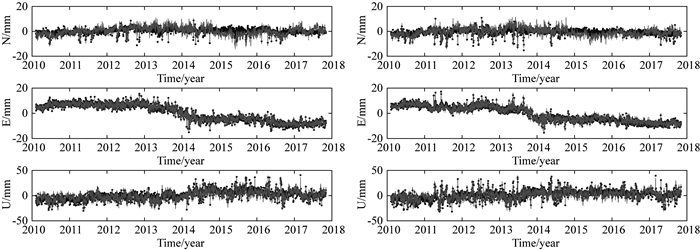
图 13为ICA E、N方向IC11、IC12、IC14分量及U方向IC10、IC11、IC12分量结果，箭头向上表示空间响应为正，向下为负.在进行ICA分析时，对E方向没有移除OHI2、OHI3站，得到了与PCA相同的结果，图 14列出了ICA滤波前后残差序列结果，基于上述可知，ICA因为能够最大化非高斯分量，把异常信号当成独立的分量分离出来，观测网中的异常测站能够和共同信号分离，而PCA基于二阶统计量，异常信号对其影响很大，所以当有异常测站时效果较差.

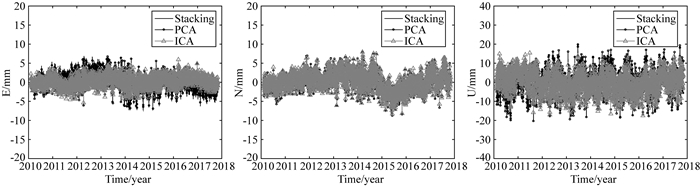
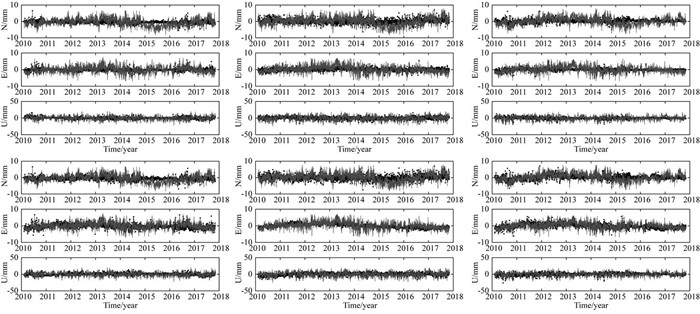
为得到与堆栈法一致的结果，利用PCA和ICA计算CME时，用平均空间响应替代最大空间响应.由于南极半岛站点数较少，除ROBI站外，使用剩余14个测站进行堆栈法计算.图 15为堆栈法、PCA、ICA得到的一维共性误差，PCA与ICA一维共性误差在E、N、U三个方向之间最大差异2.80 mm、3.77 mm、15.66 mm；平均相差0.14 mm、0.09 mm、0.30 mm.相对于PCA，ICA在E、U方向上的发散性较低.图 16为CAPF、DUPT、FONP站PCA(上)和ICA(下)滤波前后E、N、U三个方向残差序列对比图.

表 2和表 3分别统计了PCA、ICA滤波前后残差序列的RMS变化，从表 2可以看出经过PCA滤波后原始残差序列的E、N、U方向RMS平均降低了59.09%、51.86%、57.42%，从表 3可以看出经过ICA滤波后原始残差序列的RMS值平均降低了44.69%、26.94%、34.87%.由前文所述，由于PCA是取残差序列方差最大的PC计算CME，因而滤波后的残差序列二阶统计量(RMS)要小于ICA法，PCA滤波后在HUGO站E方向，PAL2、PALM、PALV站的N方向RMS降低过大，我们认为PCA可能会剔除测站的原始信息，或者残差时间序列中存在某些未建模误差PCA没有剔除，因此在南极半岛地区ICA方法要优于PCA方法.

表 4和表 5分别统计了原始序列PCA、ICA滤波前后速度和不确定度, 从表 4和表 5可知，经过PCA滤波后，78%(3个站)的水平速度变化在±0.2 mm·a^-1，78%的垂直速度变化在±0.4 mm·a^-1，E、N、U三个分量的速度不确定度分别平均降低65.1%，56.9%，55.9%；经过ICA滤波后78%(3个站)的水平速度变化在±0.2 mm·a^-1，93%(1个站)的垂直速度变化在±0.4 mm·a^-1，E、N、U三个分量的速度不确定度分别平均降低44.6%，37.4%，55.9%.差异比较大出现在时间序列较短的站，因为短期的速度很容易被系统性误差影响.

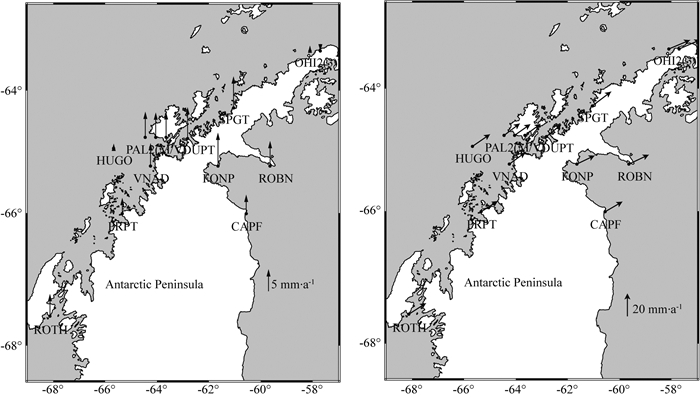
图 17为利用ICA滤波后得到的垂直和水平方向的速度场，从图中可知，南极半岛地区在垂直方向基本呈现上升趋势，最大速度为FONP站可达14.12 mm·a^-1, 平均量级为5.89 mm·a^-1，该地区由于拉森B冰架的崩塌，导致附近几个站近几年地壳垂直抬升速率较快.水平方向上呈现向东北方向运动的趋势，最大速度为SPGT站可达20.6 mm·a^-1，平均量级可达18.13 mm·a^-1.

4 结论

高精度GNSS速度场是研究地壳垂向运动及板块运动的基础，南极地区当前地壳运动特征的研究对全球板块构造格局的形成与演化机制、地球参考框架的构建与维持、极地冰雪环境动态变化监测等具有重要参考价值，由于南极地区特殊的地理环境，本文首次在南极半岛地区采用因子分析法识别了GNSS数据中异常测站，然后使用PCA和ICA方法对南极半岛地区15个GNSS站时间序列进行区域滤波分析，结果表明：

(1) 因子分析法可用于检测具有局部强烈响应的异常测站，在南极半岛地区，ROBI站为异常测站，OHI2、OHI3站在E方向存在强烈的局部效应.

(2) PCA滤波前后残差序列的RMS值在E、N、U三个方向平均降低51.86%、59.09%、57.42%，速度不确定度分别降低65.10%，56.91%，55.86%；ICA滤波前后RMS平均降低26.94%、44.69%、34.87%，ICA滤波后速度的不确定度分别降低44.58%，37.43%，55.86%. PCA滤波后在HUGO站E方向，PAL2、PALM、PALV三个站的N方向RMS降低过大，我们认为PCA可能剔除了测站的原始信息，当测站存在局部效应时，ICA滤波方法优于PCA.

(3) 南极半岛地区在垂直方向基本呈现上升趋势，最大速度为FONP站可达14.12 mm·a^-1, 平均量级为5.89 mm·a^-1，该地区由于拉森B冰架的崩塌，导致附近几个站近几年地壳垂直抬升速率较快.水平方向上呈现向东北方向运动的趋势，最大速度为SPGT站可达20.6 mm·a^-1，平均量级可达18.13 mm·a^-1.