地球物理学报  2019, Vol. 62 Issue (9): 3269-3278   PDF    
引用本文
李钊伟, 郑伟, 房静, 等. 2019. 基于新型主成分加权平均归一化法优选水下重力匹配导航适配区. 地球物理学报, 62(9): 3269-3278, doi: 10.6038/cjg2019M0346.  
Li Z W, Zheng W, Fang J, et al. 2019. Optimizing suitability area of underwater gravity matching navigation based on a new principal component weighted average normalization method. Chinese J. Geophys. (in Chinese), 62(9): 3269-3278, doi: 10.6038/cjg2019M0346.  
基于新型主成分加权平均归一化法优选水下重力匹配导航适配区
李钊伟1, 郑伟1,2,3,4,5, 房静6, 吴凡1     
1. 中国空间技术研究院钱学森空间技术实验室, 北京 100094;
2. 辽宁工程技术大学测绘与地理科学学院, 辽宁阜新 123000;
3. 河南理工大学测绘与国土信息工程学院, 河南焦作 454000;
4. 江苏海洋大学测绘与海洋信息学院, 江苏连云港 222005;
5. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 武汉 430077;
6. 中国电子科技集团公司第三十九研究所, 西安 710065
收稿日期 2018-06-05, 2019-04-09 收修定稿
基金项目: 国家自然科学基金面上项目（41574014，41774014）、国防科技创新特区创新工作站项目、中央军委科技委前沿科技创新项目（085015）、中国空间技术研究院杰出青年人才基金、中国航天科技集团航天系统发展中心基金、中国航天科技集团钱学森空间技术实验室自主创新基金联合资助
第一作者简介: 李钊伟, 男, 1986年生, 助理研究员, 主要从事水下重力导航研究.E-mail:lizhaowei@qxslab.cn
通讯作者: 郑伟, 男, 1977年生, 首席研究员, 主要从事卫星重力反演和天空海一体化导航与探测等方面研究.E-mail:zhengwei1@qxslab.cn
摘要：本文开展了水下潜器重力匹配导航的匹配区适配性评价研究.第一，本文综合考虑了重力异常标准差、坡度标准差、粗糙度、重力异常差异熵、分形维数等重力场主要特征参数，联合主成分分析准则和加权平均原理，提出了新型主成分加权平均归一化法；第二，基于新型主成分加权平均归一化法，计算可评价重力异常基准图各区域匹配效果的总体特征参数指标，依据总体特征参数指标进行优良适配区、一般适配区和非适配区划分；第三，在相同条件下，在划分的优良适配区、一般适配区和非适配区内，分别进行重力匹配数值模拟验证比较，结果表明，优良适配区的重力匹配效果显著，匹配概率约为98%，匹配稳定性高，位置误差小于1个重力异常基准图格网.
关键词: 主成分加权平均归一化法      水下重力匹配导航      重力适配性      海洋重力异常总体特征参数指标     
Optimizing suitability area of underwater gravity matching navigation based on a new principal component weighted average normalization method
LI ZhaoWei1, ZHENG Wei1,2,3,4,5, FANG Jing6, WU Fan1     
1. Qian Xuesen Laboratory of Technology, China Academy of Space Technology, Beijing 100094, China;
2. School of Geomatics, Liaoning Technical University, Liaoning Fuxin 123000, China;
3. School of Surveying and Landing Information Engineering, Henan Polytechnic University, Henan Jiaozuo 454000, China;
4. School of Geomatics and Marine Information, Jiangsu Ocean University, Jiangsu Lianyungang 222005, China;
5. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China;
6. The 39 th Research Institute of China Electronics Technology Group Corporation, Xi'an 710065, China
Abstract: The suitability evaluation study of the matching area of underwater gravity matching navigation is carried out in this paper. Firstly, we comprehensively consider the main characteristic parameters of the gravity field such as standard deviation of gravity anomaly, standard deviation of slope, roughness, differential entropy of gravity anomaly and fractal dimension. And a new Principal Component Weighted Average Normalization (PCWAN) method is proposed based on principal component analysis guideline and weighted average principle. Secondly, according to the new PCWAN method, we obtain the overall characteristic parameter index that can evaluate the matching results of each area of the gravity anomaly reference map, in order to divide excellent suitability area, general suitability area and non-suitability area. Finally, in the same condition, we compare the numerical simulation results of gravity matching in three different matching areas. It is shown by the results that the gravity matching effect is significant in excellent suitability area. For example, the matching probability is about 98% as well as high matching stability, and the matching accuracy is less than 1 gravity anomaly grid.
Keywords: PCWAN method    Underwater gravity matching navigation    Gravity suitability    Overall characteristic parameter index of marine gravity anomaly    
0 引言

目前，水下潜器导航系统主要为惯性导航系统(Inertial Navigation System，INS)，具有不依赖外界信息、不向外界辐射能量、不受地点(气候)等外界条件限制、隐蔽性好等特点，可为水下潜器航行和武器系统精准打击提供有利条件，但INS系统存在误差随时间积累的缺点，因此需要外部导航设备校正(王可东和杨勇, 2008; 朱海, 2009; 赵建虎等, 2011; 赵建虎, 2013; 秦宇杰和王可东, 2016).由于地球形状的不规则性和介质密度的不均匀性导致地球上各点的重力值不同，并表现为空间位置(经度、纬度、高度)的函数，因此载体在航行过程中经过重力特征比较明显的区域时利用重力仪实时采集周围重力场信息，通过和预先得到的重力异常基准图匹配，构建成水下重力匹配导航系统，其不需要水下潜器浮出或接近水面，测量时不向外辐射能量，且地球重力场在长时间内保持稳定，因此有望实现水下潜器精确、自主、连续和长航时的定位(许大欣, 2005; 童余德等, 2011, 2012).

重力匹配导航实现的核心问题不仅是解决高精度和高分辨率重力异常基准图(郑伟等, 2010, 2015)、高精度重力测量系统(黄谟涛等, 2002; 于波等, 2007)、重力匹配定位算法(李珊珊等, 2011; 吴太旗等, 2011; 蒋东方等, 2012)等关键技术，而且重力适配区的选择亦是其主要影响因素，相同的匹配算法在具有不同重力特征的区域进行匹配时，其匹配效果各不相同，重力特征丰富的区域能够明显提高匹配精度.因而，为了评价重力匹配导航在重力异常基准图不同区域的匹配效果，为优选适配区提供有效支撑.程力等(2007)通过在重力场区域中移动局部计算窗口的方法，计算了实测重力场各个局部的多种统计特征并使用填色等值线图进行了对比和分析，以局部重力场的标准差和经纬度方向相关系数作为匹配区域选择的数量指标，给出了重力匹配区经验选择准则；夏冰和蔡体菁(2010)提出一种基于SPSS回归分析和量纲分析基本原理，通过在重力有效数据和重力场特征参数之间建立定量关系，以此作为重力匹配判断准则对重力匹配区域进行选择；张凯等(2013)提出了一种基于支持向量机的背景场适配/误配区自动识别和划分的方法，该方法通过借助支持向量机来构建输入特征参量与匹配性能的映射关系，最终实现适配/误配区的自动识别和划分；蔡体菁和陈鑫巍(2013)运用层次分析法，基于反演重力图的多项统计特征及匹配仿真结果，给出一种新的重力匹配区域选择准则；马越原等(2016)利用信息熵具有能够整合多种统计参数且算法计算量小的特点，提出了一种基于特征参数信息熵的重力辅助导航适配区的选择方法.

不同于前人已有研究，本文综合统计分析重力异常标准差、坡度标准差、粗糙度、重力异常差异熵、分形维数等重力场主要特征参数，联合主成分分析准则和加权平均原理，提出主成分加权平均归一化法，得出重力异常基准图各区域的总体特征参数指标，进而依据总体特征参数指标进行优良适配区、一般适配区和非适配区的划分，并通过仿真验证了该划分指标的合理性.

1 重力场特征参数

本文依据现有概念对重力异常标准差、坡度标准差、粗糙度、重力异常差异熵、分形维数等重力场主要特征参数进行了分析及部分推导(王文晶, 2009; 蔡体菁和陈鑫巍, 2013).

(1) 重力异常标准差，公式为

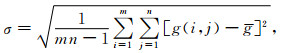
(1)

其中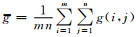，，σ表示重力异常标准差；g表示所选区域的重力异常值；g表示计算窗口(10 km×10 km)内重力异常平均值；m、n分别为经纬度跨越网格数.

(2) 坡度标准差，公式为

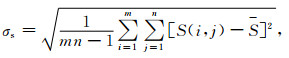
(2)

其中：

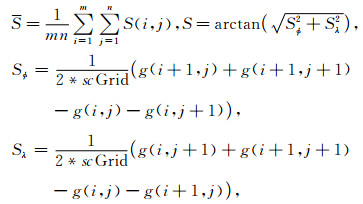
σs表示坡度标准差；S表示重力场坡度；Sϕ为纬度方向的坡度；Sλ为经度方向的坡度；scGrid为格网边长；S表示计算窗口(10 km×10 km)内坡度平均值.

(3) 粗糙度，公式为

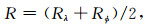
(3)

其中：

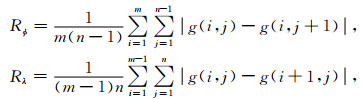
R表示粗糙度；Rϕ为纬度方向的粗糙度；Rλ为经度方向的粗糙度.

(4) 重力异常差异熵，公式为

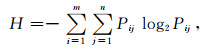
(4)

其中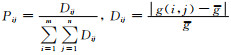，，H表示重力异常差异熵；Pij局部差异概率；Dij表示重力异常差异值.

(5) 分形维数，公式为

(5)

其中，A(s)表示分形曲面的表面积；s表示度量时所使用的面积尺度；D表示曲面的分形维数；C表示常数.

2 重力匹配区域选择准则

重力场各特征参数都不同程度的反映了重力场的变化特点，运用主成分分析准则(PCA: Principal Component Analysis)与加权平均原理(秦寿康, 2003; 李春林和陈旭红, 2013)，综合考虑各特征参数的影响，来确定重力匹配区域选择准则.

主成分分析，是一种将多个有相关性的变量F1、F2、…Fk重新组合，生成少数几个彼此不相关的变量Z1、Z2、…Zp，使其尽可能多地表示原有变量的信息，从而实现对数据的降维，分析多特征变量内在关系的方法.其中Z1、Z2、…Zp叫做主成分，依次是第一主成分、第二主成分、…第p主成分.

本文为了便于比较分析重力场各特征参数之间的取值大小与特点，消除数据单位和量纲的影响，采用正规化方法(z-score)进行数据标准化处理，这种方法基于原始数据的均值和标准差进行计算，经过处理的数据符合标准正态分布，即均值为0，标准差为1，且无量纲.其转化函数为

表 1 重力场主要特征参数 Table 1 The main characteristic parameters of the gravity field

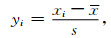
(6)

其中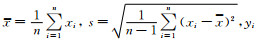，表示处理后新序列，其均值为0，标准差为1；xi表示原始数据序列；x表示原始数据的均值；s表示原始数据的标准差.

假设有k个重力场特征参数F1、F2、…Fk，每个特征参数中有n个数据信息，利用公式(6)对原始数据进行标准化处理后，则组成的标准化矩阵表示为

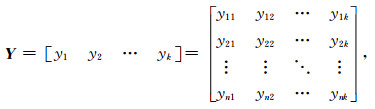
(7)

其中，yij表示第j个特征参数中第i个数据信息标准化值.

标准化矩阵Y的样本相关系数矩阵公式为

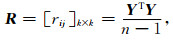
(8)

解相关矩阵R的特征方程|R－λIk|=0，求得k个依次递减的特征根λi，i=1、2、…p、…k，则特征根λi的信息贡献率为

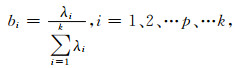
(9)

一般取p(p≤k)个主成分，使主成分累计贡献率大于85%，即：

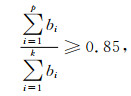
(10)

即通过线性组合，将原有k个标准化重力场特征参数重新组合，生成p个彼此不相关的新参数Z1、Z2、…Zp，表示为

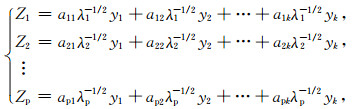
(11)

其中，aij表示第i个主成分在第j个特征参数上的载荷数；λi表示第i个主成分的特征根.

由于贡献率越大则表示该主成分越重要，因而主成分的贡献率可以表示不同主成分的权重，所以指标系数可以看作是对该指标在各主成分线性组合中的系数的加权平均，即：

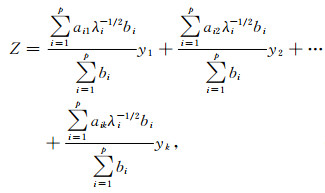
(12)

经过归一化处理，最终可得指标权重表达式为

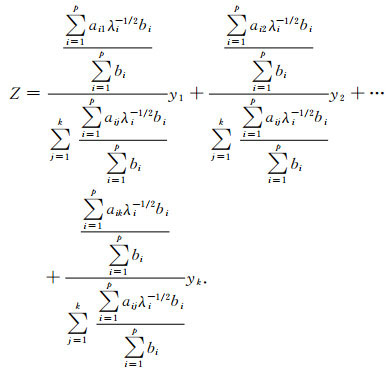
(13)

3 数值模拟及验证

计算数据源于加利福尼亚大学圣迭戈分校网站(http://topex.ucsd.edu/)，其为分辨率1′×1′的海洋重力异常数据.如图 1所示，本研究选取南海地区重力异常数据进行研究.数据经纬度取值范围为(经度113°E—115°E，纬度10°N—12°N)，其中重力异常最大值为129.9 mGal，最小值为-33.3 mGal，平均值为15.34 mGal.本文通过Matlab插值计算将数据转换成格网分辨率100 m×100 m进行模拟分析，如图 2所示.

图 1 研究区域卫星遥感图像及局部放大图(GEBCO web) Fig. 1 Satellite images of the study area and local amplification(GEBCO web)

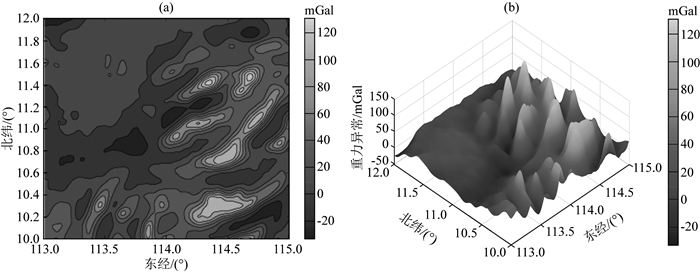
图 2表示经插值加密后研究区域的100 m×100 m分辨率的二维/三维海洋重力异常基准图.据图 2可知，东部及东南部重力场起伏剧烈，而西北部重力场变化较平缓，与该区域卫星遥感图像1基本相符，但亦存在部分差异，这是由于地球并非密度均衡球体，介质密度的不均衡性导致地形与重力值并非一一对应.

图 2 海洋重力异常基准图(分辨率100 m×100 m) (a)二维；(b)三维. Fig. 2 Marine gravity anomaly map with 100 m×100 m resolutions (a) 2D; (b) 3D.

在图 2研究区域中，以100×100个格网的区域作为一个样本区块，则图 2可分割成441个样本区块(每个样本大小约为10 km×10 km)，分别利用重力场各特征参数公式(1)—(5)对研究区域的适配性进行分析，可得结果如图 3.其中，为了便于比较分析各特征参数之间的取值大小与特点，采用公式(6)正规化方法对矩阵数据进行标准化处理, 可消除不同数据单位和量纲产生的影响.

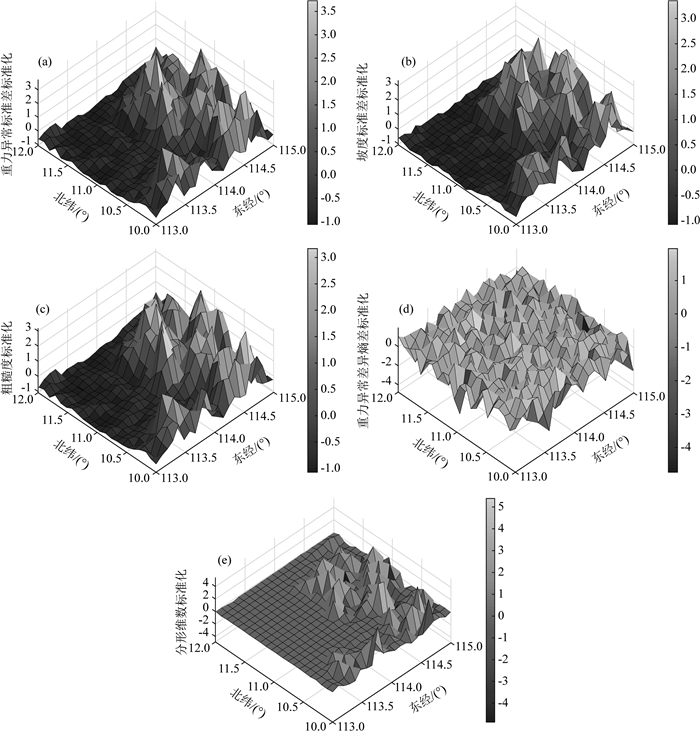
图 3 海洋重力场各特征参数标准化三维图 (a)重力异常标准差; (b)坡度标准差; (c)粗糙度; (d)重力异常差异熵; (e)分形维数. Fig. 3 Standardized 3D characteristic parameters of marine gravitational field (a) Standard deviation of gravity anomaly; (b) Standard deviation of slope; (c) Roughness; (d) Differential entropy of gravity anomaly; (e) Fractal dimension.

图 3表示研究区域441个样本区块(样本大小约为10 km×10 km)的重力场各特征参数标准化三维图.图 3a、b、c、d、e分别表示重力异常标准差图、坡度标准差图、粗糙度图、重力异常差异熵图和分形维数图.由于重力异常标准差越大、坡度标准差越大、粗糙度越大、分形维数越大、重力异常差异熵越小，则信息越丰富，越有利于匹配(郑彤等, 2009).据图 3d可知，重力异常差异熵值较小的样本区块比较均匀的分布在整个研究区域中，表明若单一以重力差异熵特征值为评价指标，则这几个区域适配性较好；据图 3a、b、c、e比较可知，重力异常标准差、坡度标准差、粗糙度和分形维数特征值较大的样本区块大都分布在研究区域东部及东南部，表明这些区域更不平坦，重力特征起伏剧烈且重力场变化速率更快，适配性较好.但图 3a、b、c、e在东部及东南部中的局部起伏亦存在差异，并不完全相同.

综上所述，基于单一重力场特征参数无法有效的评价适配性，这是由于单一的特征参数包含的重力信息量有限，以此为依据得到的结果可信度不高.因而需要综合多种重力场特征参数的信息量来作为判断适配性的依据.综合上述5个重力场特征参数，按照主成分分析准则进行计算，经公式(7)—(11)，分别求出特征根、方差贡献率、累计贡献率、载荷数等，如表 2和表 3所示.其中由于重力异常标准差、坡度标准差、粗糙度和分形维数越大越好，而重力异常差异熵越小越好，因此为了方便解算，重力异常差异熵可取负值.

表 2 特征根、方差贡献率、累计贡献率 Table 2 Characteristic root, variance contribution rate, cumulative contribution rate
表 3 各主成分载荷数 Table 3 Load number of each principal component

据表 2可知，前2个主成分的累计贡献率小于85%，而前3个主成分的累计贡献率达到了96.819%，超过了85%，即前3个主成分包含了原始特征参数中96.819%的有效信息，因而选取前3个主成分已足够对研究区域的适配性进行综合评估.

表 3表示了表 2前3个主成分中重力场各特征参数的载荷数大小.结果表明，第一主成分对重力异常标准差、坡度标准差、粗糙度有绝对值较大的载荷数；第二主成分和第三主成分均对重力异常差异熵、分形维数有绝对值较大的载荷数.

利用表 3中的载荷数除以表 2中特征根的开方，可得3个主成分线性组合矩阵为

(14)

利用公式(12)—(13)进行加权平均归一化处理，可得5个重力场特征参数的综合权重系数Q为

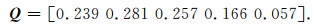
(15)

基于综合权重系数Q及重力场各特征参数标准化矩阵Y，可得一种可评价重力异常基准图各区域匹配效果的总体特征参数指标为

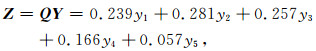
(16)

则海洋重力异常总体特征参数指标如图 4所示.

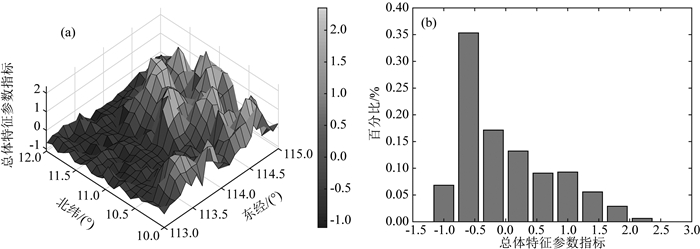
图 4 海洋重力异常总体特征参数指标 (a)三维图; (b)统计直方图. Fig. 4 Overall characteristic parameter index of marine gravity anomaly map (a) 3D map; (b) Statistical histogram.

图 4a表示研究区域441个样本区块(样本大小约为10 km×10 km)的海洋重力异常总体特征参数指标三维图.图 4b表示海洋重力异常总体特征参数指标统计直方图.总体特征参数指标越大，适配性越好.据图 4可知，东部及东南部局部区域适配性较好.

在此我们将总体特征参数指标Z的大小作为划分优良适配区、一般适配区和非适配区的判断依据，则匹配区划分准则为

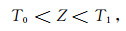
(17)

其中，T0为划分非适配区和一般适配区的阈值，T1为划分一般适配区和优良适配区的阈值，则小于T0的区域为非适配区，介于T0和T1之间的为一般匹配区，大于T1的为优良适配区，综合大量仿真实验和经验确定阈值T0=0.5和T1=1.2较为准确.因此依据准则对海洋重力异常总体特征参数指标图 4a进行匹配区划分，可得到理论上的重力匹配适配性分布图，如图 5所示.

图 5 重力匹配适配性分布图(理论) Fig. 5 Suitability division of gravity matching area (theory)

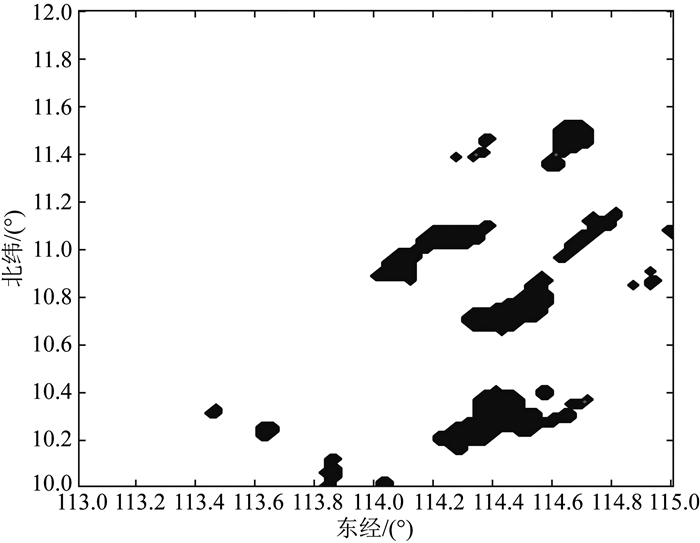
但考虑到水下航行器航行时的安全问题，航线应避免浅滩、礁盘分布密集的区域.在此假设水深100 m以上为安全水深，适合航行，因此提取同区域(数据经纬度取值范围为：经度113°E—115°E，纬度10°N—12°N)的海底地形数据进行分析比较，如图 6深灰色区域表示危险区域(水深小于100 m).在图 5中剔除图 6的危险航行区域，可得图 7.

图 6 危险区域分布图 Fig. 6 Distribution of unsafety area
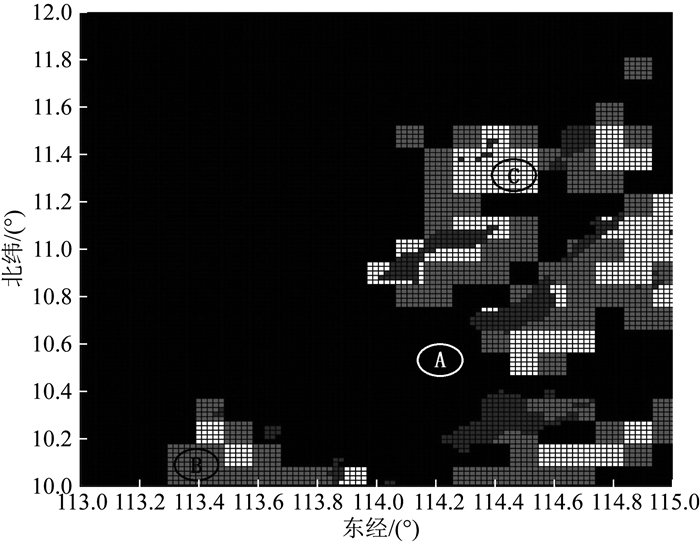
图 7 重力匹配适配性分布图 Fig. 7 Suitability division of gravity matching area

图 7表示研究区域重力匹配适配性分布图.其中，白色区域为优良匹配区，匹配定位精度高，匹配效果好；浅灰色区域为一般匹配区，匹配效果一般，在无优良匹配区情况下，可作为备用；黑色区域为非匹配区，匹配效果差，不适于进行匹配；深灰色区域为危险区域，分布浅滩、礁盘，不适合航行.

在图 7中分别选出三个区域A(非适配区)、B(一般适配区)和C(优良适配区)利用Tercom算法进行100次重力匹配数值模拟验证.样本区块内重力异常格网分辨率为100 m×100 m，陀螺仪常值漂移0.01°/h、加速度计常值零偏10-3 m·s-2(惯导均方根误差服从正态分布)、航速10 m·s-1、航向北偏东70°、初始位置误差0 m、速度误差0.04 m·s-1、航向误差0.05°、重力仪实时测量数据是真实航迹在重力异常数据库中的采样值叠加标准差为1 mGal的随机噪声、采样点数110个、采样周期20 s.其中，本文定义定位精度(匹配位置与真实位置之差)在一个格网对角线长(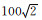 m)之内是为有效匹配，则匹配概率=(有效匹配数/实验次数)×100%.

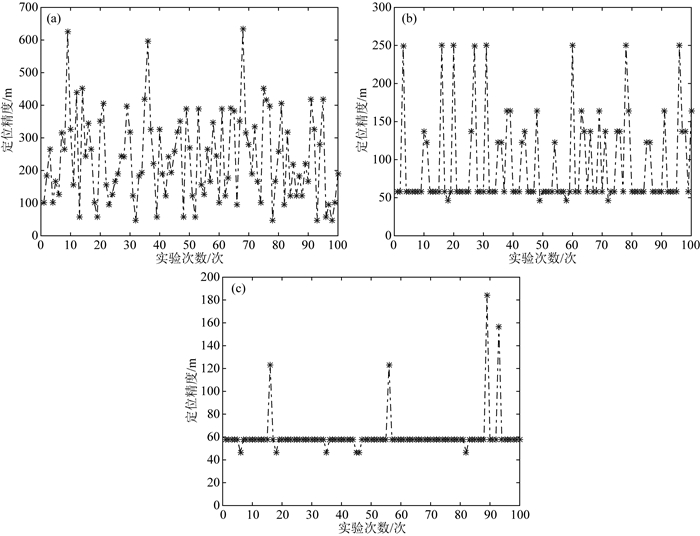
为了验证图 7所示划分区域的适配性效果，本文在相同条件下分别在A(非适配区)、B(一般适配区)和C(优良适配区)三个区域进行了100次模拟匹配，其结果如图 8所示.表 4是图 8的统计结果.据表 4可知，在C区域内，重力匹配效果明显，匹配概率约为98%，匹配稳定性高，且平均定位精度可达60.8 m，定位精度标准差为18.2 m，即位置误差小于1个重力异常基准图格网；在B区域内，重力匹配效果一般，匹配概率为84%，匹配稳定性较好，平均定位精度为107.5 m，定位精度标准差为55.7 m，且位置误差均小于3个重力异常基准图格网；在A区域内，重力匹配效果差，匹配概率仅为30%，且匹配稳定性差，平均定位精度仅为257.6 m，定位精度标准差为143.3 m，位置误差可达7个重力异常基准图格网，不适于进行重力匹配.

图 8 三个区域的重力匹配效果 (a) A(非适配区); (b) B(一般适配区); (c) C(优良适配区). Fig. 8 Gravity matching results in three areas (a) Non-suitability; (b) General-suitability; (c) Excellent-suitability.
表 4 不同区域重力匹配统计结果 Table 4 Statistical results of gravity matching in different areas
4 结语

本文提出了主成分加权平均归一化法，旨在进行水下潜器重力匹配导航的匹配区适配性评价研究，为适配区的优选提供有效依据.

(1) 构建新型主成分加权平均归一化法.由于单一的重力场特征参数包含的重力信息量有限，单一特征参数无法有效的评价适配性，以此为依据得到的结果可信度不高.因而本文综合考虑了重力异常标准差、坡度标准差、粗糙度、重力异常差异熵、分形维数等重力场主要特征参数，联合主成分分析准则和加权平均原理，提出了新型主成分加权平均归一化法，以此作为判断匹配区适配性的依据.

(2) 基于新型主成分加权平均归一化法获得匹配区适配性分布图.基于新型主成分加权平均归一化法，求得5个重力场特征参数的综合权重系数，并结合重力场各特征参数标准化矩阵，计算可评价重力异常基准图各区域匹配效果的总体特征参数指标，依据总体特征参数指标(并综合考虑水下航行安全情况)进行优良适配区、一般适配区和非适配区划分，从而有利于提升水下重力匹配效果.

(3) 验证新型主成分加权平均归一化法的合理性.在优良适配区、一般适配区和非适配区内，以本文参数设置分别进行100次模拟验证，结果表明：优良适配区的重力匹配效果显著，匹配概率约为98%，匹配稳定性高，位置误差小于1个重力异常基准图格网.因此，新型主成分加权平均归一化法有利于优选水下潜器重力匹配导航的匹配区，进而有利于提高水下潜器导航匹配精度和稳定性.

致谢  感谢加利福尼亚大学圣迭戈分校网站提供重力异常数据.
References
Cai T J, Chen X W. 2013. Selection criterion based on analytic hierarchy process for matching region in gravity aided INS. Journal of Chinese Inertial Technology (in Chinese), 21(1): 93-96.
Cheng L, Zhang Y J, Cai T J. 2007. Selection criterion for matching area in gravity aided navigation. Journal of Chinese Inertial Technology (in Chinese), 15(5): 559-563.
Huang M T, Cui G J, OU Y Y Z, et al. 2002. Two-step processing for compensating the systematic errors in marine gravity measurements. Geomatics and information Science of Wuhan University (in Chinese), 27(3): 251-255.
Jiang D F, Tong Y D, Bian S F, et al. 2012. The study on ICCP algorithm for gravity matching based on local continuous field. Geomatics and Information Science of Wuhan University (in Chinese), 37(10): 1203-1206.
Li S S, Wu X P, Ma B. 2011. Correlative extremum matching algorithm using underwater gravity anomalies. Acta Geodaetica et Cartographica Sinica (in Chinese), 40(4): 464-469.
Ma Y Y, Ouyang Y Z, Huang M T, et al. 2016. Selection method for gravity-field matchable area based on information entropy of characteristic parameters. Journal of Chinese Inertial Technology (in Chinese), 24(6): 763-768.
Qin Y J, Wang K D. 2016. Research on the gravity gradient aided navigation system based on gravity satellite. GNSS World of China (in Chinese), 41(1): 19-23.
Tong Y D, Bian S F, Jiang D F, et al. 2011. Gravity matching simulation of real-time ICCP algorithm. Journal of Chinese Inertial Technology (in Chinese), 19(3): 340-343.
Tong Y D, Bian S F, Jiang D F, et al. 2012. A new integrated gravity matching algorithm based on approximated local gravity map. Chinese Journal of Geophysics (in Chinese), 55(9): 2917-2924. DOI:10.6038/j.issn.0001-5733.2012.09.011
Wang K D, Yang Y. 2008. Research on matching error of Terrain-aided navigation. Journal of Astronautics (in Chinese), 29(6): 1809-1813.
Wang W J. 2009. Underwater navigation methods based on gravity and environmental features[Ph. D. thesis] (in Chinese). Harbin: Harbin Engineering University.
Wu T Q, Ouyang Y Z, Lu X P, et al. 2011. Analysis on effecting mode of several essential factors to gravity aided navigation. Journal of Chinese Inertial Technology (in Chinese), 19(5): 559-564.
Xia B, Cai T J. 2010. Gravity matching regions selection by statistical product and service solutions. Journal of Chinese Inertial Technology (in Chinese), 18(1): 81-84.
Xu D X. 2005. Using gravity anomaly matching techniques to implement submarine navigation. Chinese Journal of Geophysics (in Chinese), 48(4): 812-816.
Yu B, Liu Y C, Bao J Y, et al. 2007. Study on Eätväs effect correction in marine gravimetry. Science of Surveying and Mapping (in Chinese), 32(3): 80-82.
Zhang K, Zhao J H, Wang Q. 2013. Study on recognition and classification of appropriate matching area for underwater navigation based on SVM. Journal of Geodesy and Geodynamics (in Chinese), 33(6): 72-77.
Zhao J H, Wang S P, Wang A X. 2011. Study on the selection of the geomagnetic adaptable matching area based on the geomagnetic co-occurrence matrix. Geomatics and Information Science of Wuhan University (in Chinese), 36(4): 446-449.
Zheng T, Cai L F, Wang Z G, et al. 2009. Selection of matching area in terrain match aided navigation. Journal of Chinese Inertial Technology (in Chinese), 17(2): 191-196.
Zheng W, Xu H Z, Zhong M, et al. 2010. Efficient and rapid estimation of the accuracy of future GRACE Follow-On Earth's gravitational field using the analytic method. Chinese Journal of Geophysics (in Chinese), 53(4): 796-806. DOI:10.3969/j.issn.0001-5733.2010.04.004
Zheng W, Xu H Z, Zhong M, et al. 2015. A study on the improvement in spatial resolution of the Earth's gravitational field by the next-generation ACR-Cartwheel-A/B twin-satellite formation. Chinese Journal of Geophysics (in Chinese), 58(3): 767-779. DOI:10.6038/cjg20150307
Zhu H, Wang S J, Cai P. 2009. Straight-line geomagnetic matching for underwater base on ICCP. Journal of Chinese Inertial Technology (in Chinese), 17(2): 153-155.
蔡体菁, 陈鑫巍. 2013. 基于层次分析法的重力匹配区域选择准则. 中国惯性技术学报, 21(1): 93-96. DOI:10.3969/j.issn.1005-6734.2013.01.022
程力, 张雅杰, 蔡体菁. 2007. 重力辅助导航匹配区域选择准则. 中国惯性技术学报, 15(5): 559-563. DOI:10.3969/j.issn.1005-6734.2007.05.012
黄谟涛, 翟国君, 欧阳永忠, 等. 2002. 海洋重力测量误差补偿两步处理法. 武汉大学学报·信息科学版, 27(3): 251-255.
蒋东方, 童余德, 边少锋, 等. 2012. ICCP重力匹配算法在局部连续背景场中的实现. 武汉大学学报·信息科学版, 37(10): 1203-1206.
李春林, 陈旭红. 2013. 应用多元统计分析. 北京: 清华大学出版社.
李姗姗, 吴晓平, 马彪. 2011. 水下重力异常相关极值匹配算法. 测绘学报, 40(4): 464-469.
马越原, 欧阳永忠, 黄谟涛, 等. 2016. 基于重力场特征参数信息熵的适配区选择方法. 中国惯性技术学报, 24(6): 763-768.
秦寿康. 2003. 综合评价原理与应用. 北京: 电子工业出版社.
秦宇杰, 王可东. 2016. 基于重力测量卫星的重力梯度辅助导航研究. 全球定位系统, 41(1): 19-23.
童余德, 边少锋, 蒋东方, 等. 2011. 实时ICCP算法重力匹配仿真. 中国惯性技术学报, 19(3): 340-343.
童余德, 边少锋, 蒋东方, 等. 2012. 一种新的基于局部重力图逼近的组合匹配算法. 地球物理学报, 55(9): 2917-2924. DOI:10.6038/j.issn.0001-5733.2012.09.011
王可东, 杨勇. 2008. 地形辅助导航匹配误差研究. 宇航学报, 29(6): 1809-1813.
王文晶. 2009.基于重力和环境特征的水下导航定位方法研究[博士论文].哈尔滨: 哈尔滨工程大学. http: //cdmd.cnki.com.cn/Article/CDMD-10217-2010075273.htm
吴太旗, 欧阳永忠, 陆秀平, 等. 2011. 重力匹配导航的影响模式分析. 中国惯性技术学报, 19(5): 559-564.
夏冰, 蔡体菁. 2010. 基于SPSS的重力匹配区域选择算法. 中国惯性技术学报, 18(1): 81-84.
许大欣. 2005. 利用重力异常匹配技术实现潜艇导航. 地球物理学报, 48(4): 812-816. DOI:10.3321/j.issn:0001-5733.2005.04.012
于波, 刘雁春, 暴景阳, 等. 2007. Eätväs效应改正中航速、航向角计算方法研究. 测绘科学, 32(3): 80-82. DOI:10.3771/j.issn.1009-2307.2007.03.031
张凯, 赵建虎, 王锲. 2013. 基于支持向量机的水下地形匹配导航中适配区划分方法研究. 大地测量与地球动力学, 33(6): 72-77.
赵建虎, 王胜平, 王爱学. 2011. 基于地磁共生矩阵的水下地磁导航适配区选择. 武汉大学学报·信息科学版, 36(4): 446-449.
赵建虎. 2013. 地磁与惯性水下组合导航定位关键技术研究. 中国科技成果, (14): 33-34. DOI:10.3772/j.issn.1009-5659.2013.14.015
郑彤, 蔡龙飞, 王志刚, 等. 2009. 地形匹配辅助导航中匹配区域的选择. 中国惯性技术学报, 17(2): 191-196.
郑伟, 许厚泽, 钟敏, 等. 2010. 利用解析法有效快速估计将来GRACE Follow-On地球重力场的精度. 地球物理学报, 53(4): 796-806. DOI:10.3969/j.issn.0001-5733.2010.04.004
郑伟, 许厚泽, 钟敏, 等. 2015. 基于下一代三向车轮双星编队改善地球重力场空间分辨率研究. 地球物理学报, 58(3): 767-779. DOI:10.6038/cjg20150307
朱海, 王顺杰, 蔡鹏. 2009. 基于ICCP的水下直线段地磁匹配. 中国惯性技术学报, 17(2): 153-155.
基于新型主成分加权平均归一化法优选水下重力匹配导航适配区
李钊伟, 郑伟, 房静, 吴凡