2. 新疆维吾尔自治区地震局, 乌鲁木齐 830011
2. Earthquake Agency of Xinjiang Uygur Autonomous Region, Vrümqi 830011, China
在地震波动正反问题数值模拟中计入实际介质阻尼可有效提升实测波形记录的幅值、相位(到时)的模拟精度(Savage et al., 2010);提升基于实测记录反演地下波速结构的精度及可靠性(Kurzmann et al., 2013; Groos et al., 2014).地震学常基于线性滞弹性阻尼理论(Aki and Richards, 2002)建立阻尼介质本构,其频域本构与弹性介质频域本构形式上完全一致,区别在于前者中弹性模量为与频率相关的复数,后者弹性模量为常实数.计入复弹性模量在频域波动数值模拟中易于实现(Stekl and Pratt, 1998),但在时域数值模拟中却十分困难.因复弹性模量与频域应变乘积的傅里叶反变换由卷积给出,且就一般形式的复弹性模量而言,离散卷积计算需存储以往所有时刻的应变值.基于广义标准线性体模型建立阻尼介质本构可规避这一问题(Blanc et al., 2016).广义标准线性体频域本构中复弹性模量M(ω)为若干单极点有理分式之和:M(ω)= 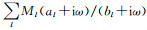
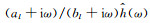
利用时域波动数值模拟方法:有限差分、有限体积、(间断)有限元,求解近场波动问题需引入人工边界(Artificial boundary)截断无限域以获取有限计算区,并在截断处设置无反射边界条件(Non-reflecting Boundary Condition: NRBC)使得从有限计算区向无限域行进的外行波能无反射地穿过人工边界并不再返回至计算区(廖振鹏,2002).由于滞弹性近场波动数值模拟研究起步较晚,NRBC的研究多局限于完全弹性介质(Givoli, 1991, 2004).对弱阻尼介质或对NRBC精度要求不高的情形,可直接采用弹性NRBC(王振宇和刘晶波,2004;Askan et al., 2007; Bielak et al., 2011),但对强阻尼介质或对NRBC精度要求较高情形,将高精度弹性NRBC未加修正地应用于滞弹性情形会导致数值失稳或模拟精度降低等问题.
应用高精度NRBC可有效提升计算效率.Liu最早开展了滞弹性近场波动问题高精度NRBC—PML的研究,分别就导电媒介电磁波方程以及黏性介质声波方程(阻尼介质本构基于单个开尔文体建立)构建了对应的PML(Liu, 1997; Liu and Tao, 1997),其研究工作表明PML能高效衰减从有限计算区辐射出来的外行波动且数值稳定性较好,清晰揭示了PML的应用前景.
PML是当前时域滞弹性近场波动数值模拟中应用最广泛的高精度NRBC,其等价于无限域波动方程的解析延拓(Chew et al., 1997; Collino and Monk, 1998),可通过对无限域波动方程进行复坐标延拓得到.对速度-应力形式波动方程,滞弹性PML的相关研究工作包括:有限差分(Liu and Tao, 1997; Ely et al., 2008; Martin and Komatitsch, 2009); 有限元(Groby and Tsogka, 2006;Ma and Liu, 2006);对位移-应力(应变)形式波动方程,其中应力(应变)作为独立存储变量,相关研究包括:有限元(Basu and Chopra 2004;Assimaki et al., 2012);对位移形式波动方程,相关研究包括:有限差分(Moczo et al., 2014);有限元(Ping et al., 2016).直接基于位移形式波动方程建立PML及相应的数值离散格式,能显著降低计算存储,提高计算效率,避免额外引入变量的边界条件难于设置等问题(Kreiss et al., 2002;Moczo et al., 2014),但相比前两类PML而言,第三类PML中多极点有理分式与频域函数乘积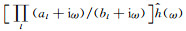
针对上述问题,考虑位移形式波动方程及其高阶集中质量有限元离散,本文构建了适用于滞弹性近场波动勒让德谱元模拟的完美匹配层.首先,采用作者提出的基于复坐标延拓技术变换弱形式无限域波动方程以构建PML的方法(谢志南和章旭斌,2017),建立了弱形式时域滞弹性PML,规避以往基于复坐标延拓技术独立延拓无限域内波动方程及界面条件可能导致的:延拓后所得场方程和界面条件匹配不合理而引发数值失稳、计算精度低下等问题(Duru and Kreiss, 2014).其次,结合PML计算精度对微调复坐标延拓函数中的参数不敏感的特点,给出了明确的参数微调准则,并建立了一种普适、简便的多极点有理分式与频域函数乘积傅里叶反变换的计算方法,极大简化了PML计算.基于该方法可实现任意高阶PML(Feng et al., 2017)以及多轴PML(Meza-Fajardo and Papageorgiou, 2008).最后,基于新构建滞弹性完美匹配层,结合高阶勒让德谱元建立了滞弹性近场波动问题离散方案.
文中第一节给出了无限域内滞弹性波动方程及基于广义标准线性体建立的阻尼介质时域本构.第二节详细阐述了弱形式滞弹性PML的构建.第三节给出了一种PML参数的微调方案及多极点卷积简便计算方法.在此基础上,将弱形式滞弹性PML与勒让德谱元结合建立滞弹性近场波动谱元模拟方案.第四节基于数值算例阐明滞弹性PML的精度、计算效率及新建方案的稳定性.最后给出本文工作小结.
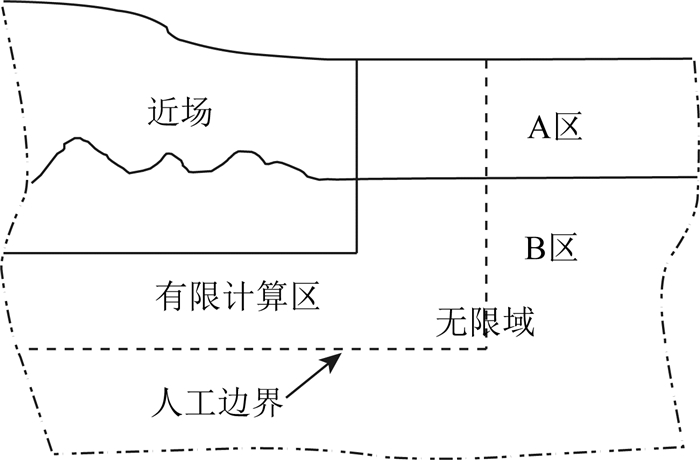
1 无限域滞弹性波动方程就近场波动问题而言,常假定无限域为层状构造(图 1),在小应变前提假定下,无限域内滞弹性介质波动满足平衡方程,即:
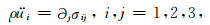
|
(1) |
|
图 1 滞弹性近场波动问题示意图 Fig. 1 Sketch of the viscoelastic wave problem in the near field |
ρ为介质密度,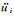
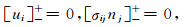
|
(2) |
自由地表处应力为零,即:
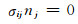
|
(3) |
nj为界面外法线单位矢量分量.无穷远处位移、应力为零且满足无穷远辐射条件(廖振鹏,2002).
与弹性介质不同,滞弹性介质应力(应变)与应变(应力)历史相关,应力-应变关系满足Boltzmann叠加原理.就各向同性滞弹性介质而言,其频域本构可表示为
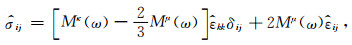
|
(4) |
时域本构为
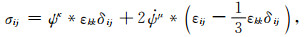
|
(5) |
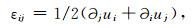
|
(6) |
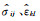
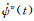
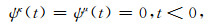
|
(7) |
与松弛函数满足因果律对应,复模量Mv(ω)的实部与虚部满足Kramers-Krönig关系(Waters et al., 2000).将(5)、(6)式代入(1)式得到位移形式波动方程,即方程中只有位移为独立变量.
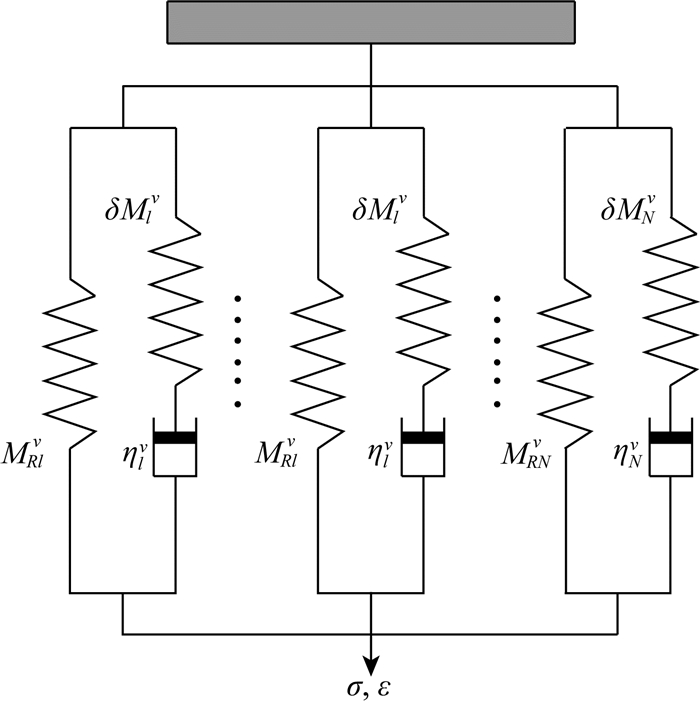
基于广义标准线性体模型(图 2)建立阻尼介质本构,可得:
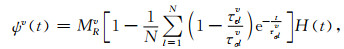
|
(8) |
|
图 2 由N个标准线性体并联得到广义标准线性体 Fig. 2 Schematic diagram showing generalized standard linear body composed of N standard linear solids parallel connected |
N为标准线性体个数,下标l为标准线性体的编号,l=1, …, N.τσlv、τεlv为第l个SLS对应的应力松弛时间和应变蠕变时间.τσlv=ηlv/δMlv,τεlv=τσlv(MRlv+δMlv)/MRlv,MRlv、δMlv为第l个标准线性体中的弹簧元件的弹性系数,ηlv为第l个标准线性体中黏性阻尼元件的阻尼系数.Mv(ω)为
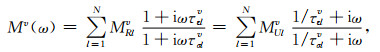
|
(9) |
Mv(0)=MRv为广义标准线性体的松弛弹性模量,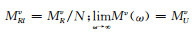
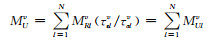
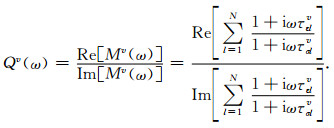
|
(10) |
结合(10)式, 利用最小误差的非线性优化方法拟合广义标准线性体模型Q值与实际介质的Q值可获取τεlv、τσlv取值.MR取值通过令广义标准线性体与目标介质在某一选定参考频率ωref点处的波传播的相速度值(参考波速)相等得到(Blanc et al., 2016).图 3给出了在地震波动数值模拟常用频带[0.1 Hz, 10 Hz]内,基于广义标准线性体模型对两类阻尼介质(介质Q值为常数以及Q值随频率变化)的Q值及相速度拟合结果.这里令阻尼介质在参考频率ωref=1 Hz处的相速度为1.由图 3可知,增加标准线性体的个数,在给定频带范围内,可准确拟合介质Q值及波传播的相速度.另外,由于广义标准线性体在选定频率点处的相速度计算较为繁琐(谢志南等,2018),且广义标准线性体在ωref=0 Hz及ωref=∞ Hz退化为弹性体,为此常将介质弹性波速作为参考频率ωref=0 Hz(Carcione et al., 1988; Martin and Komatitsch, 2009)或ωref=∞ Hz处的参考波速(Carcione,2010).值得注意的是,若采用介质弹性波速作为0 Hz或∞Hz处的参考波速,在人为选取模拟频率范围不同的情形,将导致不同频带范围内拟合得到的相速度频散曲线存在较大差异,这一差异可通过给定滞弹性介质在某一频率点处的参考波速加以消除(Emmerich and Korn, 1987;Kristek and Moczo, 2003;袁士川等,2018).但这一差异并不影响PML的精度和稳定性,本文不做深入讨论.

|
图 3 基于由N=2,4,6标准线性体并联得到的广义标准线性体拟合 (a) Q(ω)=10ω-0.1介质;(b) Q(ω)=10介质的Q-1值及相速度频散曲线.模拟频带为[0.1 Hz, 10 Hz].目标介质在参考频率ωref=1 Hz的相速度为1. Fig. 3 Reciprocal of the quality factor, when using a generalized Zener body with N=2, N=4 to N=6 relaxation mechanisms based nonlinear optimization in viscoelastic media (a) Q(ω)=10 ω-0.1; (b) Q(ω)=10. The simulated frequency band is 0.1~10 Hz. The phase velocity of the medium at the reference frequency ωref=1 Hz is 1. |
弱形式时域滞弹性PML可通过对无限域内弱形式滞弹性波动方程进行复坐标延拓得到(谢志南和章旭斌,2017).这一过程可分解为:(1)利用虚功(虚位移)原理建立弱形式无限域波动方程;(2)将这一方程变换至频域,并对其做复坐标延拓得到弱形式频域PML;(3)对弱形式频域PML进行坐标变换将其转换为实坐标系下弱形式频域PML;进而基于傅里叶反变换得到弱形式时域PML.下面以外部无限域A区PML构建为例阐述这一过程.
2.1 利用虚位移原理建立弱形式无限域波动方程与波动问题的强形式表达(1)—(3)式不同,基于虚位移原理可建立有限区域的弱形式平衡方程即:弱形式波动方程.这一方程耦合了波动方程(1)以及相应的边界条件:(2)、(3)式和无穷远辐射条件.下面阐明图 4中A区弱形式波动方程的建立过程.引入边界条件允许的xi方向虚位移wi,将其与波动方程(1)点乘,然后做区域积分,利用高斯定理得到:
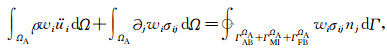
|
(11) |
|
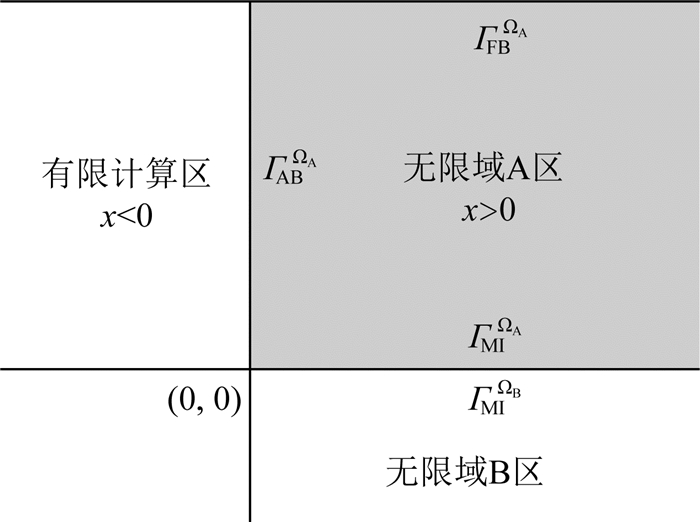
图 4 无限域A区弱形式时域PML构建示意图 Fig. 4 Sketch of the weak-form time-domain PML in infinite domain part A |
ΩA表征A区域面积或体积,ΓMIΩA为介质A、B的分界面,ΓFBΩA为A区自由地表,ΓABΩA为A区人工边界.nj为外法线矢量分量,njdΓ=dΩ/dxj.二维的dΩ为面积微元,三维的dΩ为体积微元.式(11)隐含假定了A区右侧无穷远处位移、应力为零的无穷远辐射条件.因自由表面处应力为0,即:
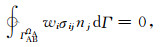
|
(12) |
由于ΓMIΩA、ΓMIΩB外法线单位向量方向相反且介质分界面处应力连续,即:
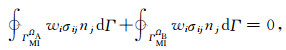
|
(13) |
由此得到A区弱形式波动方程为
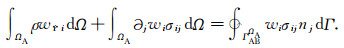
|
(14) |
基于傅里叶变换将(14)式变换至频域,即:
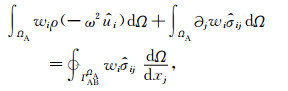
|
(15) |
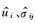
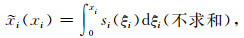
|
(16) |
si为解析的复坐标延拓函数.常用的复坐标延拓函数为单极点复频移坐标延拓函数,即:
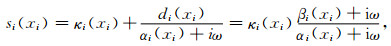
|
(17) |
其中di(xi)为ni外法线方向行波衰减因子,κi(xi)为坐标缩放系数,αi为频移参数.当κi(xi)=1, αi(xi)=0时,复频移延拓函数(17)式退化为传统延拓函数,即:
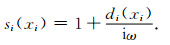
|
(18) |
基于复频移延拓函数构建PML能提高PML对快衰波以及大角度入射平面波的吸收精度,但与基于传统延拓函数构建PML相比,在一定程度上降低了对低频(ω≤αi(xi))波动的吸收能力(Festa and Vilotte, 2005).为此,研究人员提出采用多极点复坐标延拓函数构建高阶PML以解决这一问题(Correia and Jin, 2005).公式为
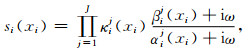
|
(19) |
Feng等(2017)将高阶PML应用于宽频带地震波动数值模拟,结果表明高阶PML精度优于基于单极点复坐标延拓函数构建所得PML.
将(15)式中实坐标替换为复坐标(16)式得到:
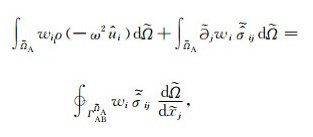
|
(20) |
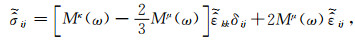
|
(21) |
|
(22) |
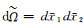
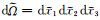
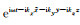
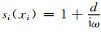
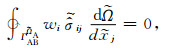
|
(23) |
进而得到A区弱形式频域PML的表达式为
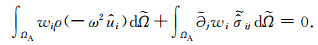
|
(24) |
由于坐标变换不会改变方程的解,因此在这一过程中我们无须考虑方程中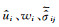
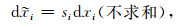
|
(25) |
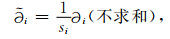
|
(26) |
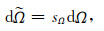
|
(27) |
二维情形: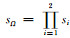
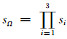
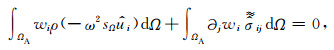
|
(28) |
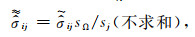
|
(29) |
利用傅里叶逆反变换将(28)式转换至时域,即:
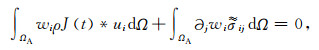
|
(30) |
式中,J(t)=F-1[-ω2sΩ],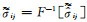
由(30)式可知,即便基于单极点复坐标延拓函数构建PML,亦需处理多极点有理分式与频域函数乘积的傅里叶反变换计算问题.下面以式(31)为例,即:
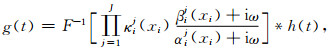
|
(31) |
其中h(t)为任意函数,阐述这一傅里叶反变换普适、简化计算方法.该方法的关键是找出重复极点,通过微调将多重极点转化为单重极点,然后对单重极点有理分式乘积进行依次分解.我们仅调整PML的参数,保持1/τσlv不变.PML参数微调的依据在于ki(xi)及αi(xi)的变动不会改变PML的完美匹配特性(Collino and Tsogka, 2001; Feng et al., 2017),且PML精度对较大范围的ki(xi)及αi(xi)取值并不敏感(Zhang and Shen, 2010; Feng et al., 2017).
考虑到常用延拓函数参数取值方案,即:
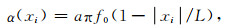
|
(32) |
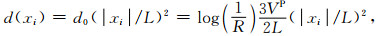
|
(33) |
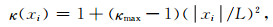
|
(34) |
其中f0为模拟频带主频,VP为PML相邻计算区的P波波速,|xi|/L为PML层内点距人工边界距离与PML层厚的比值,反射系数R一般取为0.001.依据Zhang和Shen(2010)以及Collino和Tsogka(2001),a的取值可在1.0~2.0之间,对不同模型κmax的优化取值区间分布在1.0~13.0之间.但上述区间范围内PML吸收精度变化不大.这里将调整系数取为aπf0Δx0/(8L),其中Δx0为PML延拓方向相邻节点之间最小间距.这一调整系数为PML中α(xi)参数最小取值的八分之一.通过微调参数,我们保证每个极点之间的差值大于这一调整系数,且保证调整后的极点仍为大于0的正实数,以κ1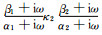
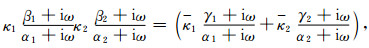
|
(35) |
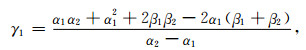
|
(36) |
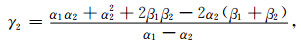
|
(37) |
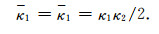
|
(38) |
按照上述方法可依次将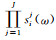
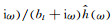
(1) 对多极点函数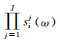
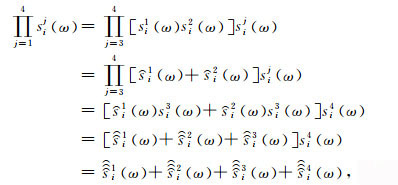
|
(39) |
两个单极点有理因式乘积的分解由(35)—(38)式给出.
(2) 将分离得到的单极点函数与h(t)分别作卷积,然后逐个叠加得到g(t),即:
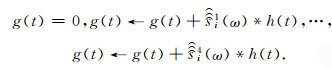
|
(40) |
在此基础上,采用固定边界截断PML(Duru and Kreiss, 2014),与建立弹性PML及有限计算区内弹性波动方程的勒让德时空离散一致(Komatitsch and Tromp, 1999; Savage et al., 2010; 谢志南和章旭斌, 2017),可建立滞弹性PML以有限计算区内的滞弹性波动方程勒让德谱元时空离散方案.详细表达式参看附录1.
4 数值算例本节基于算例检验滞弹性PML的精度、计算效率及滞弹性近场谱元模拟方案的长持时稳定性.首先,基于全空间均匀介质波动问题论证滞弹性PML对体波的吸收精度.进一步,阐明即便对于介质阻尼较大情形,PML的计算效率优于“完美匹配”物理阻尼吸收层(吸收层内介质与相接计算区阻尼介质完全一致).其次,基于半空间均匀介质波动问题论证滞弹性PML对瑞利面波的吸收精度.最后,基于层状半空间波动问题论证滞弹性PML对复杂波动的吸收精度及新构建滞弹性近场谱元模拟方案的长持时稳定性,同时揭示不加修正地将“弹性介质”PML应用于滞弹性近场波动数值模拟可导致数值失稳.
4.1 全空间均匀介质波动模拟给定介质参数:密度ρ=2000 kg·m-3,考虑强衰减阻尼介质Qκ=12,Qμ=5,基于一级近似得到的介质弹性P波,S波波速分别为VP=900 m·s-1,VS=500 m·s-1.
在坐标原点(0 m, 0 m)y方向上施加垂直向下集中力荷载,荷载时间函数为主频f0=1 Hz的Ricker子波,即:
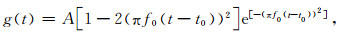
|
(41) |
其中A为无量纲化幅值系数.通过调整这一系数使得接收点处竖向位移幅值为1.在x、y=±3000 m处设置人工边界截断无限域.
在0.1~10 Hz频带范围基于标准线性体建立阻尼介质时域本构,由于模型尺寸与模拟主波长的比值较小,依据谢志南等(2018)可知,仅需采用包含2个标准线性体的广义标准线性体即可满足模拟精度要求.将弹性波速作为ω=∞ Hz处参考波速,采用最小误差的非线性优化方法可拟合得到广义标准线性体系数.
基于单位插值函数为4阶,单元节点数为25的正方形勒让德谱元对有限计算区进行空间离散.依据谱元模拟精度要求,考虑阻尼介质本构拟合频带最高频率10 Hz,将单元长度设为50 m,大致为一个波长范围内包含一个单元.时间离散采用Newmark-Beta预估校正法(β=0, γ=1/2),时间离散步长取为8×10-4s.
在人工边界外设置两类高精度吸收层形式人工边界条件.(1)滞弹性PML,PML层厚为600 m(三层单元),令a=1, κmax=1, R=0.001,VP=900 m·s-1,复坐标延拓函数中参数取值由(32)—(34)式给出.(2)“完美匹配”物理阻尼吸收层.利用滞弹性介质自身的衰减特性,直接在人工边界外设置同一阻尼介质的吸收层亦能保证计算区域辐射的波动能无反射地穿过人工边界且在吸收层内逐渐衰减.阻尼吸收层厚取为4500 m、9000 m以及13500 m,分别对应为5λP、10λP、15λP,其中λP为主频f0=1 Hz处P波波长,λP=VP/f0=900 m.
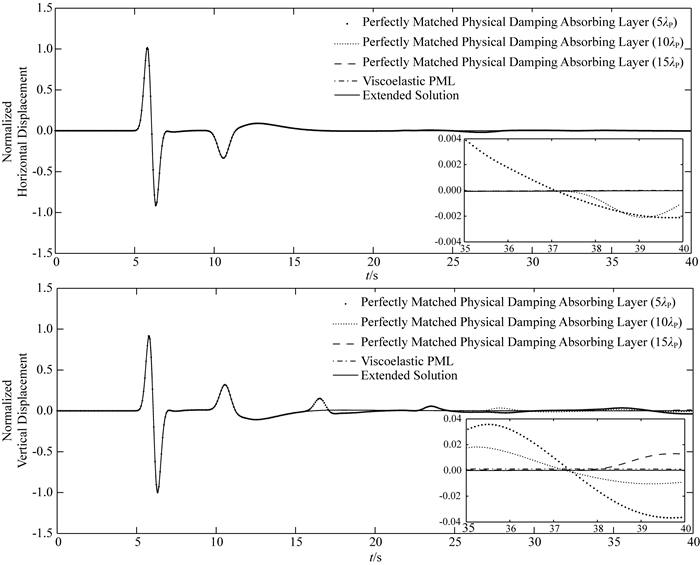
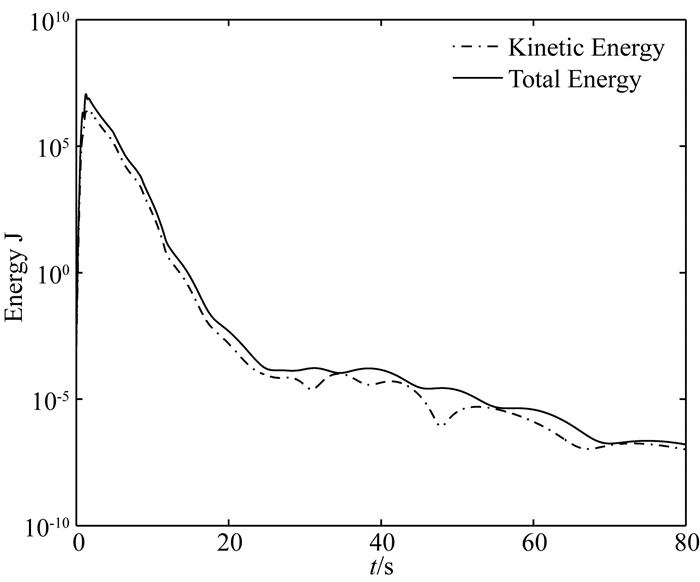
图 5给出了采用滞弹性PML与不同层厚“完美匹配”物理阻尼吸收层情形下,(2800 m, 2800 m)处观测点的水平和竖向位移模拟波形及对应的大区域解.由图 5可知,3层单元滞弹性PML能有效吸收从计算区域向外辐射的体波,模拟波形与大区域解基本完全吻合,且优于“完美匹配”物理阻尼吸收层.考虑到标准线性体个数为2情形,单个滞弹性PML单元的计算量为单个“完美匹配”物理阻尼吸收层内单元计算量的6倍,本算例中PML层内单元个数为396.5λP、10λP、15λP厚,阻尼吸收层内单元个数分别为4725、13500、26325,由此可知即便对强衰减阻尼介质,滞弹性PML的计算效率亦远优于“完美匹配”物理阻尼吸收层.对弱衰减介质,由于介质对波的衰减速度变慢,滞弹性PML的计算效率更为突出.图 6给出了采用滞弹性PML情形,计算区内总能量E随时间的衰减曲线,公式为
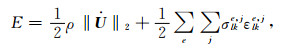
|
(42) |
|
图 5 观测点(2800 m, 2800 m)处水平向及竖直向位移时程 震源位于(0 m, 0 m)处,人工边界条件分别采用采用150 m厚滞弹性PML,以及4500 m、9000 m、13500 m厚“完美匹配”物理阻尼吸收层(分别对应于5λP,10λP,15λP,其中λP为主频处P波波长900 m).为对比分析,实线给出该点大区域解,并且基于大区域解最大竖向位移值对水平向以及竖向位移做归一化处理. Fig. 5 Comparison of synthetic normalized horizontal and vertical displacement at station located at (2800 m, 2800 m) The source is located at (0 m, 0 m). Different artificial boundary conditions are: viscoelastic PML with 150 m thickness, perfectly matched physical damping absorbing layer with 4500 m (5λP), 9000 m (10λP), 13500 m (15λP) thickness, where λP is the wavelength of P-wave at the dominating frequency. The solid line represents extended solutions obtained by extending the artificial boundary far away to ensure the reflected waves do not reenter into the computational domain. The displacement time-histories are normalized by the maximum vertical displacement of extended solution in vertical direction. |
|
图 6 除去PML区外,计算区内所有节点能量随时间衰减曲线(虚线为计算区域内动能,实线为总能量) Fig. 6 Decay curves of total energy (solid line) and the kinetical energy (dashed line) with time in the main domain (the medium without the PML layers) |
其中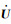
考虑半空间均匀介质波动模拟,介质参数同上一算例.自由面设置在y=0 m处.在(500 m, 0 m)y方向上施加垂直向下方向集中力荷载,荷载时间函数为主频f0=1 Hz的Ricker子波.在x=0 m、5000 m以及y=-2500 m处设置人工边界截断无限域.
在0.1~10 Hz频带范围基于标准线性体建立阻尼介质时域本构,由于模型尺寸与模拟主波长的比值较小,采用包含3个标准线性体的广义标准线性体即可满足精度要求.将弹性波速作为ω=∞ Hz处参考波速,采用最小误差的非线性优化方法可拟合得到广义标准线性体系数.
基于单位插值函数为4阶,单元节点数为25的正方形勒让德谱元对有限计算区进行空间离散.单元长度设为50 m.时间离散采用Newmark-Beta预估校正法(β=0, γ=1/2),时间离散步长取为8×10-4s.
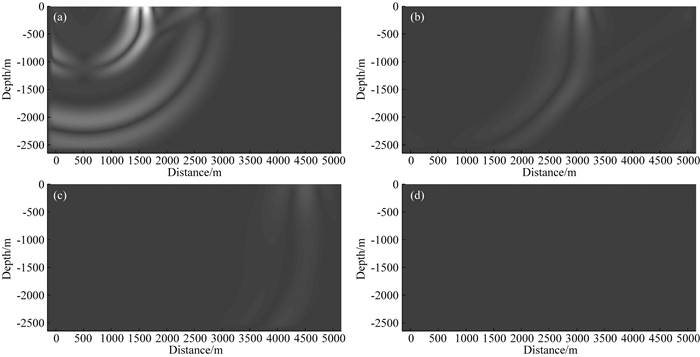
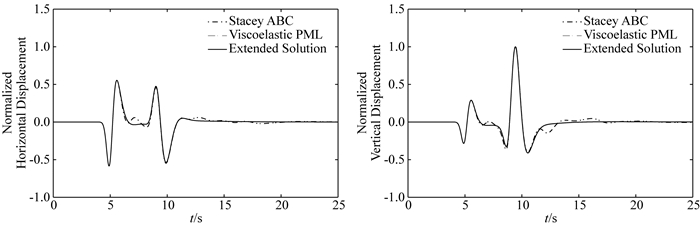
在人工边界外层厚为150 m的滞弹性PML,复坐标延拓函数内参数取值同算例1.图 7给出不同时刻位移波场快照图.图 8给出(3500 m, 0 m)处接收点水平及竖向位移时程,且为对比分析,图 8亦给出了人工边界条件设为黏性边界情形下接收点处位移时程(Komatitsch and Tromp, 1999).由图 7、8可知,滞弹性PML对强衰减的瑞利面波同样具有极高的吸收精度.同时图 8表明,在滞弹性介质中,瑞利面波幅值并不一定总是远大于P波振幅,在本算例中瑞利面波对应的位移幅值与P波位移振幅相接近.
|
图 7 自由面竖直向下集中力作用下半空间模型不同时刻的波场快照(位移矢量的模) (a) t=4 s; (b) t=8 s; (c) t=12 s; (d) t=16 s. Fig. 7 Wavefield snapshots of the norm of displacement times with a point force source at the free surface in the downward direction (a) t=4 s; (b) t=8 s; (c) t=12 s; (d) t=16 s. |
|
图 8 观测点(3500 m, 0 m)处位移时程 震源位于(500 m, 0 m)处, 人工边界条件分别采用采用150m厚滞弹性PML,以及黏性边界即Stacey ABC.为对比分析,实线给出该点大区域解,并且基于大区域解最大竖向位移值对水平向以及数值向位移统一做归一化处理. Fig. 8 Comparison of synthetic normalized horizontal and vertical displacement at station located at (3500 m, 0 m) The source is located at (500 m, 0 m). Computed with different artificial boundary condition: viscoelastic PML with 150 m thickness, Stacey ABC. The solid line represents extended solutions. All the displacement time-histories in the figure are normalized by the maximum vertical displacement of extended solution in vertical orientation. |
给定两层介质参数,上覆软基岩介质参数:密度ρ1=2000 kg·m-3,P波波速V1P=1800 m·s-1,S波波速V1S=1040 m·s-1,Q1κ=120,Q1μ=50,覆盖层厚度为500 m.下卧基岩半空间介质参数为:ρ2=2550 kg·m-3,P波波速V2P=4500 m·s-1,S波波速V2S=2630 m·s-1,介质品质因子Q2κ=680,Q2μ=263.自由表面位于y=0 m处.在(5000 m, -6000 m)处施加位错震源,矩震级MW=3.3,地震矩张量为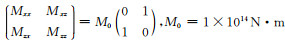
在x=0 m、20000 m、y=-10500 m处设置人工边界截断无限域.采用包含2个标准线性体的广义标准线性体在[0.1 Hz~10 Hz]频带范围近似滞弹性介质本构.在采用最小误差的非线性优化方法拟合广义标准线性体系数过程中,将弹性波速作为ω=∞ Hz处参考波速.基于单位插值函数为4阶,单元节点数为25的正方形勒让德谱元对有限计算区进行空间离散.单元长度设为100 m,时间离散采用Newmark-Beta预估校正法(β=0, γ=1/2),时间离散步长取为8×10-4s.
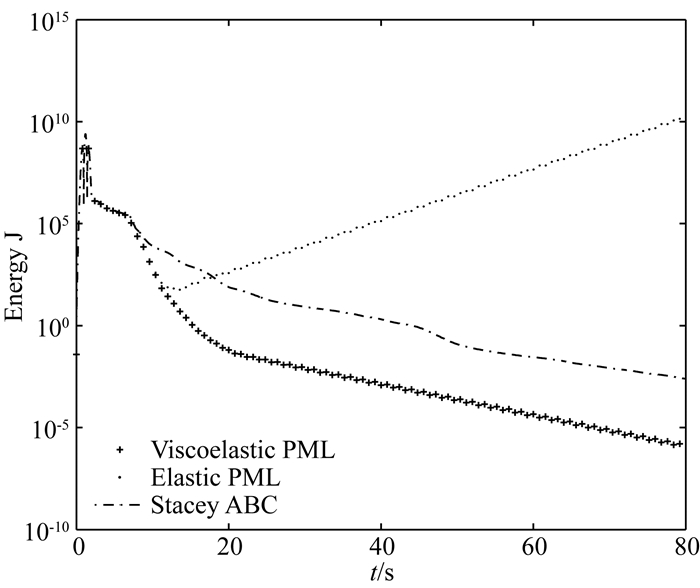
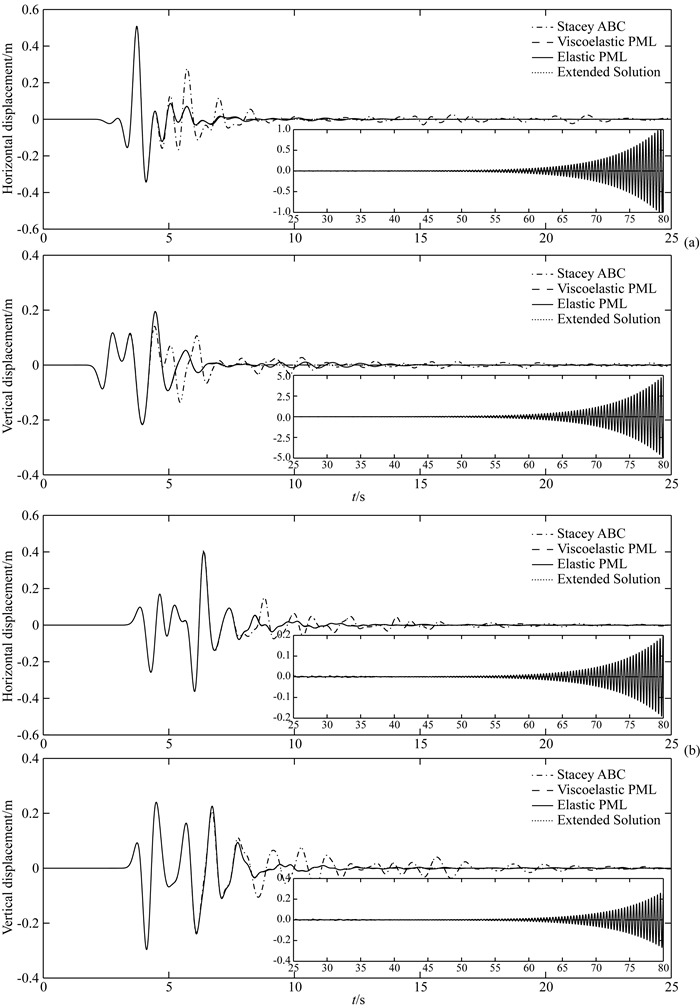
在人工边界处设置三类人工边界条件:(1)弹性PML,层厚为300 m(三层单元),令a=1, κmax=1, R=0.001复坐标延拓函数中参数值由(32)至(34)给出,VP=max(V1P, V2P)=4500 m·s-1;(2)滞弹性PML,层厚为300 m(三层单元),其中延拓函数参数取值同与弹性PML;(3)黏性边界.总计算时长为80 s,即迭代步数100000步.图 9中分别采用不同人工边界条件计算区域内的能量衰减曲线.由图 9可知,将弹性PML直接应用于滞弹性波动数值模拟将导致数值失稳.基于滞弹性PML和黏性边界建立的滞弹性近场波动数值模拟方案长持时稳定.进一步,图 10给出接收点处(3700 m, 0 m)和(15700 m, 0 m)处位移时程,如图 10所示,滞弹性PML能有效吸收由于介质分界面存在而导致的复杂外行波动,吸收精度远优于黏性边界.计算所得接收点位移时程与大区域解几乎完全一致.本文算例所采用的均为四边形单元,但文中结果可直接推广至Meng和Fu(2017)建立的三角形有限元单元波动模拟优化方案中.
|
图 9 除PML层内节点外,计算区内所有节点总能量时间衰减曲线 “+”代表人工边界条件采用滞弹性PML对应的计算结果,“.”蓝线代表弹性PML,虚线代表黏性边界,即Stacey ABC. Fig. 9 Decay curves of total energy with time in the main domain (the medium without the PML layers) '+' line represents viscoelastic PML, '.' line represents elastic PML, dashed line represents Stacey ABC. |
|
图 10 (a) 和(b)为基于不同人工边界条件建立滞弹性近场波动数值模拟方案计算所得观测点(3700 m, 0 m)和(15700 m, 0 m)处水平以及竖直分量的位移时程 “-·-.”、“--”、实线为人工边界条件采用黏性边界、滞弹性PML的位移时程,弹性PML对应的位移时程,“.”代表大区域解. Fig. 10 Comparison of synthetic normalized horizontal and vertical displacement at stations located at (a) (3700 m, 0 m) and (b) (15700 m, 0 m) Computed with different artificial boundary conditions: Stacey ABC('-·-.' line), viscoelastic PML('--' line) and elastic PML(solid line), extended ABC('.' line). |
本文基于复坐标延拓技术变换弱形式无限域滞弹性波动方程建立了弱形式时域滞弹性PML.给出了明确的PML参数微调准则,建立了多极点有理分式与频域函数乘积傅里叶反变换的普适、简便计算方法,极大地简化了PML计算.基于该方法可实现任意高阶PML.在此基础结合谱元建立了滞弹性近场波动谱元模拟方案.基于算例检验了PML的精度、计算效率.结果表明:PML对体波,面波均有极好的吸收精度.新构建滞弹性近场谱元模拟方案长持时稳定.同时阐明了不加修正地将“弹性介质”PML应用于滞弹性近场波动数值模拟可能导致数值失稳这一问题.新方案可直接推广应用至基于任意高阶滞弹性PML的宽频带地震波动正反问题研究(Komatitsch et al., 2016; Feng et al., 2017).
附录A 二维弱形式频域PML的详尽表达式基于分量形式表述弱形式频域滞弹性PML(28)式得到:
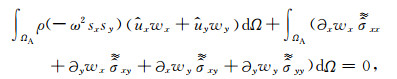
|
(A1) |
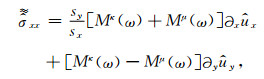
|
(A2) |
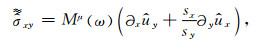
|
(A3) |
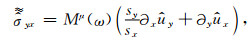
|
(A4) |
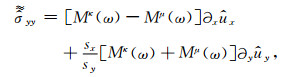
|
(A5) |
利用多极点的分离方法,并作傅里叶逆变换可得:
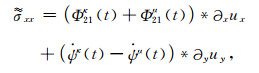
|
(A6) |
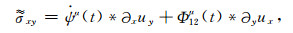
|
(A7) |
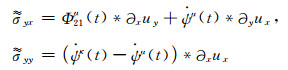
|
(A8) |
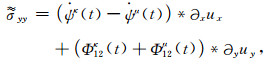
|
(A9) |
其中:
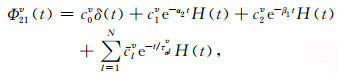
|
(A10) |
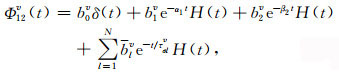
|
(A11) |
式中各系数为
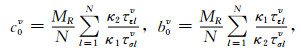
|
(A12) |
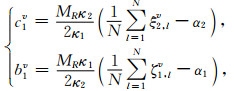
|
(A13) |
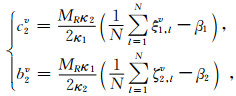
|
(A14) |
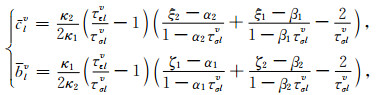
|
(A15) |
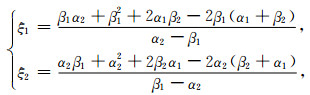
|
(A16) |
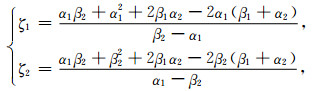
|
(A17) |
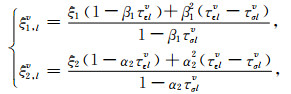
|
(A18) |
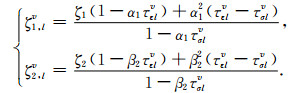
|
(A19) |
等式(A1)左侧第一项的时域表达式涉及卷积积分项,可通过两极点的分离得到,即:
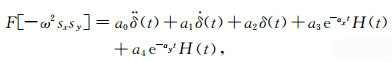
|
(A20) |
式中各系数为
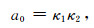
|
(A21) |
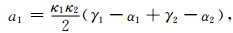
|
(A22) |
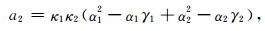
|
(A23) |
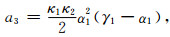
|
(A24) |
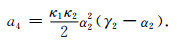
|
(A25) |
将(A20)式及(A6)—(A7)式代入(30)式整理得到:
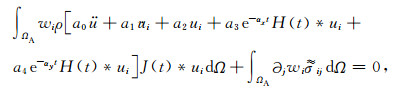
|
(A26) |
采用勒让德谱元离散(A26)可得局部节点系运动方程为
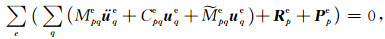
|
(A27) |
其中:
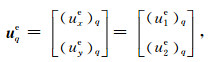
|
(A28) |
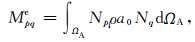
|
(A29) |
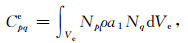
|
(A30) |
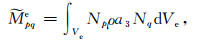
|
(A31) |
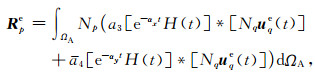
|
(A32) |
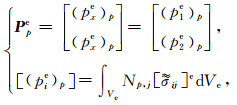
|
(A33) |
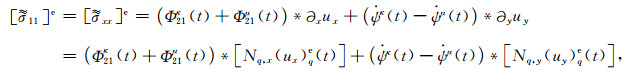
|
(A34) |
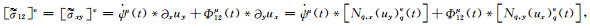
|
(A35) |
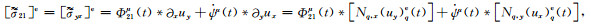
|
(A36) |
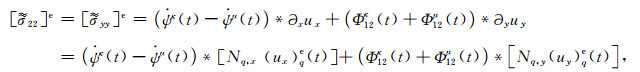
|
(A37) |
uqe为单元q节点上的位移矢量,Nq表示单元q节点上插值函数,Nq, x、Nq, y单元q节点上插值函数对x、y的偏导数.经组装可得到近场波动勒让德谱元模拟所需全部节点上的运动方程组为
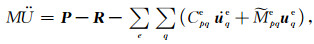
|
(A38) |
全局矢量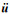
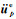
Aki K, Richards P G. 2002. Quantitative Seismology. 2nd ed. California: University Science Books.
|
Askan A, Akcelik V, Bielak J, et al. 2007. Full waveform inversion for seismic velocity and anelastic losses in heterogeneous structures. Bulletin of the Seismological Society of America, 97(6): 1990-2008. DOI:10.1785/0120070079 |
Assimaki D, Kallivokas L F, Kang J W, et al. 2012. Time-domain forward and inverse modeling of lossy soils with frequency-independent Q for near-surface applications. Soil Dynamics and Earthquake Engineering, 43: 139-159. DOI:10.1016/j.soildyn.2012.07.001 |
Basu U, Chopra A K. 2004. Perfectly matched layers for transient elastodynamics of unbounded domains. International Journal for Numerical Methods in Engineering, 59(8): 1039-1074. DOI:10.1002/nme.896 |
Bielak J, Karaoglu H, Taborda R. 2011. Memory-efficient displacement-based internal friction for wave propagation simulation. Geophysics, 76(6): T131-T145. DOI:10.1190/geo2011-0019.1 |
Blanc E, Komatitsch D, Chaljub E, et al. 2016. Highly accurate stability-preserving optimization of the Zener viscoelastic model, with application to wave propagation in the presence of strong attenuation. Geophysical Journal International, 205(1): 427-439. |
Carcione J M, Gei D, Treitel S. 2010. The velocity of energy through a dissipative medium. Geophysics, 75(2): T37-T47. DOI:10.1190/1.3346064 |
Carcione J M, Kosloff D, Kosloff R. 1988. Wave propagation simulation in a linear viscoelastic medium. Geophysical Journal International, 95(3): 597-611. DOI:10.1111/j.1365-246X.1988.tb06706.x |
Chew W C, Jin J M, Michielssen E. 1997. Complex coordinate stretching as a generalized absorbing boundary condition. Microwave and Optical Technology Letters, 15(6): 363-369. DOI:10.1002/(SICI)1098-2760(19970820)15:6<363::AID-MOP8>3.0.CO;2-C |
Collino F, Monk P. 1998. The perfectly matched layer in curvilinear coordinates. SIAM Journal on Scientific Computing, 19(6): 2061-2090. |
Collino F, Tsogka C. 2001. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media. Geophysics, 66(1): 294-307. DOI:10.1190/1.1444908 |
Connolly D P, Giannopoulos A, Forde M C. 2014. A higher order perfectly matched layer formulation for finite-difference time-domain seismic wave modeling. Geophysics, 80(1): T1-T16. |
Correia D, Jin J M. 2005. On the development of a higher-order PML. IEEE Transactions on Antennas and Propagation, 53(12): 4157-4163. DOI:10.1109/TAP.2005.859901 |
Duru K, Kreiss G. 2014. Numerical interaction of boundary waves with perfectly matched layers in two space dimensional elastic waveguides. Wave Motion, 51(3): 445-465. DOI:10.1016/j.wavemoti.2013.11.002 |
Ely G P, Day S M, Minster J B. 2008. A support-operator method for viscoelastic wave modelling in 3-D heterogeneous media. Geophysical Journal International, 172(1): 331-344. DOI:10.1111/j.1365-246X.2007.03633.x |
Emmerich H, Korn M. 1987. Incorporation of attenuation into time-domain computations of seismic wave fields. Geophysics, 52(9): 1252-1264. DOI:10.1190/1.1442386 |
Feng H K, Zhang W, Zhang J, et al. 2017. Importance of double-pole CFS-PML for broad-band seismic wave simulation and optimal parameters selection. Geophysical Journal International, 209(2): 1148-1167. |
Festa G, Vilotte J P. 2005. The Newmark scheme as velocity-stress time-staggering:An efficient PML implementation for spectral element simulations of elastodynamics. Geophysical Journal International, 161(3): 789-812. DOI:10.1111/j.1365-246X.2005.02601.x |
Fichtner A. 2011. Full Seismic Waveform Modelling and Inversion. Berlin, Heidelberg: Springer Science & Business Media.
|
Givoli D. 1991. Non-reflecting boundary conditions. Journal of Computational Physics, 94(1): 1-29. |
Givoli D. 2004. High-order local non-reflecting boundary conditions:A review. Wave Motion, 39(4): 319-326. DOI:10.1016/j.wavemoti.2003.12.004 |
Groby J P, Tsogka C. 2006. A time domain method for modeling viscoacoustic wave propagation. Journal of Computational Acoustics, 14(2): 201-236. DOI:10.1142/S0218396X06003001 |
Groos L, Schäfer M, Forbriger T, et al. 2014. The role of attenuation in 2D full-waveform inversion of shallow-seismic body and Rayleigh waves. Geophysics, 79(6): R247-R261. DOI:10.1190/geo2013-0462.1 |
Komatitsch D, Tromp J. 1999. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophysical Journal International, 139(3): 806-822. DOI:10.1046/j.1365-246x.1999.00967.x |
Komatitsch D, Xie Z N, Bozdağ E, et al. 2016. Anelastic sensitivity kernels with parsimonious storage for adjoint tomography and full waveform inversion. Geophysical Journal International, 206(3): 1467-1478. DOI:10.1093/gji/ggw224 |
Kreiss H O, Petersson N A, Yström J. 2002. Difference approximations for the second order wave equation. SIAM Journal on Numerical Analysis, 40(5): 1940-1967. DOI:10.1137/S0036142901397435 |
Kristek J, Moczo P. 2003. Seismic-wave propagation in viscoelastic media with material discontinuities:A 3D fourth-order staggered-grid finite-difference modeling. Bulletin of the Seismological Society of America, 93(5): 2273-2280. DOI:10.1785/0120030023 |
Kurzmann A, Przebindowska A, Köhn D, et al. 2013. Acoustic full waveform tomography in the presence of attenuation:A sensitivity analysis. Geophysical Journal International, 195(2): 985-1000. DOI:10.1093/gji/ggt305 |
Liao Z P. 2002. Introduction to Wave Motion Theories in Engineering (in Chinese). 2nd ed. Beijing: Science Press.
|
Liu Q H. 1997. An FDTD algorithm with perfectly matched layers for conductive media. Microwave and Optical Technology Letters, 14(2): 134-137. DOI:10.1002/(SICI)1098-2760(19970205)14:2<134::AID-MOP17>3.0.CO;2-B |
Liu Q H, Tao J P. 1997. The perfectly matched layer for acoustic waves in absorptive media. The Journal of the Acoustical Society of America, 102(4): 2072-2082. DOI:10.1121/1.419657 |
Luebbers R J, Hunsberger F. 1992. FDTD for Nth-order dispersive media. IEEE Transactions on Antennas and Propagation, 40(11): 1297-1301. DOI:10.1109/8.202707 |
Ma S, Liu P C. 2006. Modeling of the perfectly matched layer absorbing boundaries and intrinsic attenuation in explicit finite-element methods. Bulletin of the Seismological Society of America, 96(5): 1779-1794. DOI:10.1785/0120050219 |
Martin R, Komatitsch D. 2009. An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation. Geophysical Journal International, 179(1): 333-344. DOI:10.1111/j.1365-246X.2009.04278.x |
Meng W J, Fu L Y. 2017. Seismic wavefield simulation by a modified finite element method with a perfectly matched layer absorbing boundary. Journal of Geophysics and Engineering, 14(4): 852-864. DOI:10.1088/1742-2140/aa6b31 |
Meza-Fajardo K C, Papageorgiou A S. 2008. A nonconvolutional, split-field, perfectly matched layer for wave propagation in isotropic and anisotropic elastic media:Stability analysis. Bulletin of the Seismological Society of America, 98(4): 1811-1836. DOI:10.1785/0120070223 |
Moczo P, Kristek J, Gális M. 2014. The Finite-Difference Modelling of Earthquake Motions:Waves and Ruptures. Cambridge: Cambridge University Press.
|
O'Connell R J, Budiansky B. 1978. Measures of dissipation in viscoelastic media. Geophysical Research Letters, 5(1): 5-8. DOI:10.1029/GL005i001p00005 |
Ping P, Zhang Y, Xu Y X, et al. 2016. Efficiency of perfectly matched layers for seismic wave modeling in second-order viscoelastic equations. Geophysical Journal International, 207(3): 1367-1386. DOI:10.1093/gji/ggw337 |
Ramadan O. 2003. Auxiliary differential equation formulation:An efficient implementation of the perfectly matched layer. IEEE Microwave and Wireless Components Letters, 13(2): 69-71. DOI:10.1109/LMWC.2003.808706 |
Savage B, Komatitsch D, Tromp J. 2010. Effects of 3D attenuation on seismic wave amplitude and phase measurements. Bulletin of the Seismological Society of America, 100(3): 1241-1251. DOI:10.1785/0120090263 |
Štekl I, Pratt R G. 1998. Accurate viscoelastic modeling by frequency-domain finite differences using rotated operators. Geophysics, 63(5): 1779-1794. DOI:10.1190/1.1444472 |
Teixeira F L, Chew W C. 2000. Complex space approach to perfectly matched layers:A review and some new developments. International Journal of Numerical Modelling:Electronic Networks, Devices and Fields, 13(5): 441-455. DOI:10.1002/1099-1204(200009/10)13:5<441::AID-JNM376>3.0.CO;2-J |
Wang Z Y, Liu J B. 2004. Study on wave motion input and artificial boundary for problem of nonlinear wave motion in layered soil. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 23(7): 1169-1173. |
Waters K R, Hughes M S, Brandenburger G H, et al. 2000. On a time-domain representation of the Kramers-Krönig dispersion relations. The Journal of the Acoustical Society of America, 108(5): 2114-2119. DOI:10.1121/1.1315294 |
Xie Z N, Matzen R, Cristini P, et al. 2016. A perfectly matched layer for fluid-solid problems:Application to ocean-acoustics simulations with solid ocean bottoms. The Journal of the Acoustical Society of America, 140(1): 165-175. DOI:10.1121/1.4954736 |
Xie Z N, Zhang X B. 2017. Weak-form time-domain perfectly matched layer. Chinese Journal of Geophysics (in Chinese), 60(10): 3823-3831. DOI:10.6038/cjg20171012 |
Xie Z N, Zheng Y L, Zhang X B. 2018. Optimized approximation for constitution of constant Q viscoelastic media in time domain seismic wave simulation. Chinese Journal of Geophysics (in Chinese), 61(10): 4007-4020. DOI:10.6038/cjg2018L0704 |
Yuan S C, Song X H, Zhang X Q, et al. 2018. Finite-difference modeling and characteristics analysis of Rayleigh waves in viscoelastic media. Chinese Journal of Geophysics (in Chinese), 61(4): 1496-1507. DOI:10.6038/cjg2018L0532 |
Zhang W, Shen Y. 2010. Unsplit complex frequency-shifted PML implementation using auxiliary differential equations for seismic wave modeling. Geophysics, 75(4): T141-T154. DOI:10.1190/1.3463431 |
廖振鹏. 2002. 工程波动理论导论. 2版. 北京: 科学出版社.
|
王振宇, 刘晶波. 2004. 成层地基非线性波动问题人工边界与波动输入研究. 岩石力学与工程学报, 23(7): 1169-1173. DOI:10.3321/j.issn:1000-6915.2004.07.023 |
谢志南, 章旭斌. 2017. 弱形式时域完美匹配层. 地球物理学报, 60(10): 3823-3831. DOI:10.6038/cjg20171012 |
谢志南, 郑永路, 章旭斌. 2018. 常Q滞弹性介质地震波动数值模拟-时域本构优化逼近. 地球物理学报, 61(10): 4007-4020. DOI:10.6038/cjg2018L0704 |
袁士川, 宋先海, 张学强, 等. 2018. 黏弹性介质瑞雷波有限差分模拟与特性分析. 地球物理学报, 61(4): 1496-1507. DOI:10.6038/cjg2018L0532 |
 2019, Vol. 62
2019, Vol. 62

