2. 中国石油大学(华东)地球科学与技术学院, 山东青岛, 266580
2. School of Geosciences, China University of Petroleum(East China), Shandong Qingdao 266580, China
最小二乘反演成像方法早已成为油气勘探领域的一种高分辨率探测工具,但由于基于各向同性假设的声波最小二乘偏移方法忽略了介质的各向异性,可能导致强各向异性地层及其下覆构造出现成像误差拉大、分辨率降低、偏移噪声严重、甚至迭代发散等问题,严重损坏反演结果的质量(李振春等,2017).此外,在“声学近似”理论下,各向异性介质拟声波方程偏移及反偏移算子始终存在纵横波耦合及不稳定现象,因此,常规的各向异性拟声波最小二乘偏移也面临诸多缺陷.鉴于此,要开展各向异性储层油气勘探与开发,关键在于实现针对纯qP波信息的快速且精确成像.
Tarantola(1984)建立了比较完备的最小二乘反演基础理论,其基本思想是利用模拟数据与观测数据的最佳匹配程度来设计目标泛函,进而达到更新并改善成像结果直至最佳成像的目的,这种从偏移成像过渡到反演成像的理论突破引起了国内外专家学者的深入探讨.由于当时计算机技术的限制,早期的最小二乘偏移实现主要依托于Kirchhoff积分算子(Nemeth et al., 1999;Duquet et al., 2000),因其计算成本低,被广泛应用于商业软件中;随后,伴随着相移法等单程波算子的不断运用,出现了实现方式灵活多样的最小二乘单程波偏移(Kuehl and Sacchi, 2002;Clapp et al., 2005;Kaplan et al., 2010;Huang and Schuster, 2012);近年来,Dai和Schuster(2009)率先提出并实现了最小二乘逆时偏移及多震源优化策略,在双程波方程的约束下实现反演成像,理论严谨、成像优势显著,迅速成为工业界与学术界探讨的前沿热点(Tang,2009;Dai et al., 2011, 2012;Wong et al., 2010, 2011;Dong et al., 2012).为了适用于不同类型的地球介质,国内外学者先后提出了弹性波最小二乘逆时偏移(Gu et al., 2017;Feng and Schuster, 2017;Stanton and Sacchi, 2017;Duan et al., 2017;Chen and Sacchi, 2017)、黏介质最小二乘逆时偏移(李振春等,2014;Dutta and Schuster, 2014;Guitton et al., 2007;Sun et al., 2016;Guo and McMechan, 2018)与各向异性介质最小二乘逆时偏移(李振春等,2017)等反演成像方法;紧接着,针对反演成像中的不足,又相继发展了不依赖于地震子波(李庆洋等,2017)、缓解速度模型依赖性(Dai and Schuster, 2013)、利用多次波信息进行反演成像(刘伊克等,2018;刘学建和刘伊克,2016;Li et al., 2017;Wong et al., 2015)等的一系列优化措施,用以弥补最小二乘逆时偏移的不足,并进一步改善反演成像质量;在迭代算法方面,先后实现了最速下降法、共轭梯度法、抛物拟合法及L-BFGS方法等迭代优化方案(Nocedal,1980;Hou and Symes, 2015;Vigh and Starr, 2008);在目标泛函构建上,通过修改成本函数设计了基于l2模、基于l1模、基于混合l1/l2模与基于互相关等方式的目标泛函构建方式(Gu et al., 2017;李庆洋等,2016;敖瑞德等,2015).但调研发现,各向异性介质最小二乘逆时偏移成像方法研究较少,且依然存在如下两方面的不足:
首先,拟声波最小二乘逆时偏移仍然存在计算效率低、收敛速度慢、对速度等模型参数依赖性高等问题.各向异性介质最小二乘偏移只在速度模型与各向异性参数都较为准确的情况下,才能保证反演结果有效地收敛,若模型参数存在较大的系统误差,则很可能出现迭代收敛慢甚至发散(李振春等,2017).从已出版的文献中可见,针对上述问题已有大量的解决方案,Dai和Schuster(2013)提出采用平面波最小二乘逆时偏移来提升计算速率,并发展了叠前平面波最小二乘逆时偏移进一步改善方法对速度误差的依赖性;李振春等(2017)将平面波编码策略应用到VTI介质最小二乘逆时偏移成像中,实现了基于平面波加速的VTI介质最小二乘逆时偏移,在一定程度上加快了反演成像效率,但该方法对模型参数误差的敏感性依然较高;Liu等(2013)通过引入空移成像条件,提出了扩展最小二乘逆时偏移,有效地降低了最小二乘逆时偏移对速度模型的依赖性;在此基础上,Hou和Symes(2016)进一步采用加权共轭梯度法来加快收敛速度,缓解了收敛速度慢的问题.为了改善各向异性介质最小二乘逆时偏移对各向异性参数的依赖性,本文欲将叠前平面波优化策略应用于各向异性介质最小二乘逆时偏移中.
其次,常规的拟声波方程反偏移记录存在伪横波二次扰动,并伴有低速伪横波引入的数值频散假象,当该方法拓展到TTI介质时,在对称轴倾角急剧变化的强各向异性区域极易出现模拟不稳定现象,导致地震波异常振幅掩盖真实的有效波信息,这是各向异性声学近似理论的固有缺陷,在最小二乘反演成像中表现更为剧烈(黄金强等,2017).从传统的拟声波方程出发,根据扰动理论与VTI介质Born近似假设,所推导的线性化正演算子也即反偏移算子遭受伪横波影响,在各向异性区域将出现伪横波二次扰动,不利于迭代的进行.为了准确模拟复杂介质中纯qP波的传播特征,Zhan等(2012, 2013)提出在声学近似的基础上进一步简化相速度公式,进而导出完全不含伪横波干扰的TTI介质纯qP波控制方程,但是该类方程在时空域表现为拟微分形式,求解困难,且难以运用Born近似求取纯qP波线性化正演算子;伪横波在声学近似下之所以表现为菱形干扰,是因为令沿对称轴方向的横波速度为零时,横波群速度曲线正好为菱形形态,伪横波产生的本质原因在于对qP波相速度公式中的根式项进行了平方处理,进而引入了增根(Chu et al., 2013;Sheng and Zhou, 2014;黄建平等,2016;程玖兵等,2013).基于此,Song等(2016)提出采用函数拟合的方法来近似相速度的根式项,进而消除伪横波干扰,从而实现纯qP波数值模拟,但该方法在某些相角区间内误差较大,且难以扩展到TTI介质中.
为了克服各向异性声学近似理论的固有缺陷,黄金强和李振春(2017)将Fomel等(2010)提出的Low-rank分解策略运用于各向异性介质正演模拟中,由于Low-rank分解无需对频散关系进行近似,因而保证了地震波运动学特征的准确性且消除了伪横波假象及由此产生的一系列问题,随后将该方法成功应用于逆时偏移成像中,成像效果显著,但计算成本较高;为了继承有限差分的效率优势,Song等(2011, 2013)将Low-rank分解与有限差分结合,提出了效率更高的Low-rank有限差分法,并推广到TTI介质高精度正演模拟中,准确且高效地模拟出了TTI介质纯qP波信息,编程方式简单灵活,有很好的推广价值.对此,本文选用Low-rank有限差分法来设计各向异性介质纯qP波线性化正演算子,进而避免传统拟声波最小二乘逆时偏移的缺陷.
为了消除伪横波干扰等对反演成像的影响,本文在前人研究基础上,将Low-rank有限差分算法应用到各向异性TTI介质正、反向波场延拓中,首次推导出TTI介质纯qP波线性化正演算子,进而在反演框架下实现TTI介质纯qP波最小二乘逆时偏移;为了提升反演成像的计算效率,同时改善本方法对模型参数误差的依赖性,及对地震数据噪声的适应性,通过引入叠前平面波优化策略,最终形成一种优化的各向异性纯qP波叠前平面波最小二乘逆时偏移成像方法;在编程实现方法的基础上,通过开展模型成像测试,展示了本方法的优势和潜力:一方面加快了反演成像的效率,另一方面提升了方法的抗噪性,同时还降低了方法对模型参数的依赖性.
1 方法原理 1.1 Low-rank有限差分法波场延拓准确高效的纯qP波正、反向延拓算子是实现各向异性介质正演模拟、逆时偏移、最小二乘逆时偏移以及多参数全波形反演的第一步.近年来,基于Low-rank有限差分法的波场延拓算法因其计算效率高、无伪横波干扰等优势,正被广泛应用于各向异性介质地震波正演模拟、逆时偏移处理实践中(Song and Alkhalifah, 2013;黄金强和李振春,2017;黄金强等,2018).根据前人研究,记在空间位置为x、t时刻的地震波场为p(x, t),在相同空间位置、上一时刻(t-Δt)的地震波场为p(x, t-Δt),则在下一时刻的地震波场p(x, t+Δt)满足如下关系:
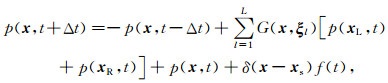
|
(1) |
其中,f(t)代表震源子波函数,xs为震源坐标位置,δ(x)为狄拉克函数,xL=(x-ξlxΔx, y-ξlyΔy, z-ξlzΔz),xR=(x+ξlxΔx, y+ξlyΔy, z+ξlzΔz);矩阵G代表空间x处的Low-rank有限差分权系数,与模型参数有关,并构成一一对应关系,具体的计算步骤可参见(黄金强等,2018);ξl=(ξlx, ξly, ξlz)为三维整数矢量,代表Low-rank有限差分加权所需的第l个网格点对应位置坐标,L代表差分模板长度(即所用的邻近网格点数),决定差分阶数.
分析公式(1)可见:①该差分系数与Taylor差分系数不同,从频散关系来看,方刚等(2014)证实它是一种全局优化的差分系数,而Taylor差分系数仅对低波数成分有效,只是局部优化的差分系数,因此该差分系数在频散压制方面具有一定的优势;②从公式特点来看,通过对邻近两个时刻的地震波场进行加权求和即可实现地震波场的前向延拓,无需计算复杂的空间偏导数算子及混合偏导数算子,易于计算机编程;③同时,该种延拓方式具有Low-rank分解无伪横波干扰等优势:能够准确计算出纯qP波信息、适应较大时间空间步长、适应高频震源,还兼具有限差分法快速高效的优点,计算效率较高,节省成本;④对于不同类型的地球介质拥有完全相同的延拓模式和计算量,因为没有波动方程的概念,所以不会因为介质复杂度增加而增加计算量,方法及程序都易于直接拓展到其他介质中,唯一不同之处在于差分系数G的值不尽相同,需预先计算并存储.
如果说函数是数集到数集的映射,泛函是空间到数集的映射,那么算子可以理解为是空间到空间的映射,即正演算子可定义为模型空间到数据空间的映射,当然实现该类映射的地球物理数值计算方法有很多,如双程波类有限差分正演、伪谱法正演、谱元法正演、单程波类正演、射线类正演等,这里的Low-rank有限差分法也是一种双程波类正演算子,但是没有显式的波动方程,而是一个离散的半解析的递推公式.因此,类似于矩阵表示方法,公式(1)也可以表示为矩阵算子的形式:
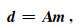
|
(2) |
其中,m表示模型空间,这里代表网格化的速度及各向异性参数;A表示由Low-rank有限差分法所设计的双程波正演算子,它由模型参数决定;d表示数据空间,也即通过数值模拟得到的地震数据.
1.2 Low-rank有限差分法线性正演与伴随Low-rank有限差分是消除各向异性介质中存在伪横波干扰,实现纯qP波场延拓的有效工具.若已知沿着对称轴方向的qP波背景相慢度sp0及背景各向异性参数,并选定差分系数模板,可以确定Low-rank有限差分系数矩阵G0,同时给定震源坐标xs及震源函数f(t),可依据公式(1)构建背景波场或入射波场p0(x, t+Δt):
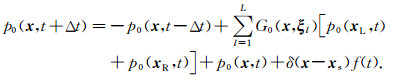
|
(3) |
反偏移是利用成像结果或者说近似反射系数通过两次正演模拟来获取线性正演记录,这也是最小二乘逆时偏移成像的核心步骤.由于基于拟声波方程的反偏移算子存在伪横波噪声,造成两次正演所得到的反偏移记录面临伪横波二次扰动、严重的数值频散和不稳定现象.为此,下文将借助Low-rank有限差分工具,推导TTI介质纯qP波线性化正演模拟算子,即纯qP波反偏移算子,这是本文的创新所在.定义慢度扰动m=Δsp2,sp2=sp02+Δsp2,这里sp表示地下真实相慢度,Δsp表示扰动慢度.根据地震波摄动理论与Born近似理论,背景慢度sp0与背景波场p0存在线性关系,并采用背景波场p0代替总场p,可导出基于Low-rank有限差分法的线性化地震散射波场延拓公式:
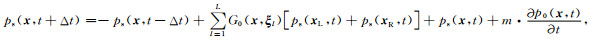
|
(4) |
这里,ps为扰动波场,也即地震散射波场.公式(4)清楚地反映了反射系数模型与扰动波场之间的定量关系.实际上,计算散射波场仍需进行两步正演模拟,第一步是基于公式(3)通过背景模型参数与震源函数来计算背景波场p0,当然,Low-rank有限差分系数矩阵根据背景模型参数及选定的差分模板确定;第二步是基于公式(4)采用相同的差分系数矩阵,通过加载入射波场的一阶偏导数与反射系数的乘积作为二次震源激发来获得散射波场ps.为了便于表示,上述两步正演可用矩阵算子表示为:
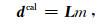
|
(5) |
其中,m表示反射系数模型,L表示线性化正演算子,dcal表示散射正演计算所得的地震数据.
同理,假设在炮点xs处激发,在检波点坐标xg处接收的观测炮记录为d(xg, t; xs),则通过伴随状态法可以重构伴随波场p*,基于Low-rank有限差分法的伴随方程可表示为如下形式:
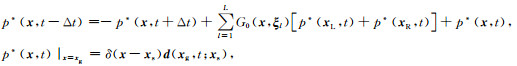
|
(6) |
其中,p*(x, t)表示t时刻的检波点波场或伴随波场,也即反传波场.观察可见:在时间上,重构反传波场是逆时传播,而计算震源波场是正向传播,重构检波点波场p*与计算震源波场p0所采用的差分系数矩阵G0完全相同.
通过应用震源波场的二阶偏导数与检波点波场的零延迟互相关,可得炮点坐标为xs所对应的单炮成像结果:
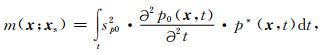
|
(7) |
式中,m(x; xs)表示炮点坐标为xs所对应的单炮成像结果.为了简化上述成像公式,用矩阵算子符号代替公式(6)和公式(7),进而将其改写为:
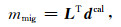
|
(8) |
其中,与线性正演算子L类似,LT表示偏移成像算子,mmig表示单炮成像结果.值得一提的是,本文给出的线性正演算子、偏移成像算子既源于波动方程线性化之后的结果,但又不同于波动方程的线性化形式,因为Low-rank有限差分法地震波场延拓公式并不是显式的解析解形式,只是伪解析解,所以只能通过数值试验来验证其共轭特征.幸运的是,有限差分与Low-rank有限差分等数值计算方法并不影响算子的性质特征,因此上述两算子完全互为共轭,这也是进行最小二乘逆时偏移的基本要求.
1.3 Lrfd-LSRTM与Lrfd-Pre-PLSRTM对于经典的炮域最小二乘逆时偏移,在理论上,反射系数模型m与观测系统类型无关,对于Ns炮地震数据集,其目标泛函可表示为:
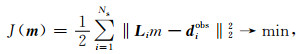
|
(9) |
这里,m表示待求反射系数模型.每次迭代的最终成像结果是通过叠加所有的独立单炮成像结果所得.从公式可以看出,在编程实现迭代更新的过程中,①第一步是对观测数据做一次双程波RTM获得初始反射系数模型;随后,②输入初始模型与各向异性参数模型,利用公式(5)计算出预测炮数据,并与观测数据做差获得数据残差;③根据公式(8),对炮数据残差做偏移进而计算出当前炮的反射系数模型修正量;④在迭代中,对每一炮数据是逐炮分别进行计算,最后叠加所有的修正量获得总的模型更新量,最终更新模型得到叠加后的成像结果,循环往复直至残差数据与预定阈值相吻合为止.从步骤来看,这与标准的声波最小二乘逆时偏移(LSRTM)基本一致,唯一的不同点在于采纳的线性正演算子为基于Low-rank有限差分的适用于各向异性介质的线性正演算子,偏移成像算子也是基于Low-rank有限差分的适用于各向异性介质的偏移成像算子,因此本文将该方法简称为Lrfd-LSRTM.
在实现Lrfd-LSRTM成像中,需慎重选择如下关键参数:①首先是差分模板L,L越大,波场延拓精度越高,但计算效率变低,因此在选择中应权衡精度和效率;②其次是Low-rank分解中秩的选择,本文采用预设误差与最大秩相结合的办法,即秩的选择优先满足Low-rank分解中的误差值小于预设误差,但秩的容许值不能超过给定的最大秩;③再就是迭代次数,在理论上,稳健的最小二乘偏移方法随着迭代次数的增加,成像精度逐步升高,但对成像质量的改善力度将明显减缓,本文测试中设置最大迭代次数为30次.炮域LSRTM虽然缓解了诸如低频噪声强、深部能量弱、振幅不均衡等系列问题,但是当速度及各向异性参数模型的误差较大时,来自不同炮的单炮成像结果在相同成像位置处并不一定完全相同,这就很可能导致叠加后的成像结果出现成像模糊、甚至收敛变慢或发散,即炮域LSRTM对速度误差敏感性较高.此外,炮域LSRTM对数据噪声的适应能力较差,且计算成本高、内存消耗大.
为了进一步提升反演成像效率,同时改善反演成像方法对模型参数误差的依赖性及对地震数据噪声的适应性,本文将叠前平面波编码策略引入到各向异性介质Low-rank有限差分法最小二乘逆时偏移成像中.其中,平面波编码提升了反演成像效率、减小了计算机内存消耗,而叠前平面波编程实现方式进一步改善了算法的稳健性,在迭代中自动优化方法的抗噪性并降低方法对模型误差的敏感性.所谓叠前平面波编码,主要是优化了平面波最小二乘逆时偏移的实现方式,其第一步仍然是对炮域地震数据按照线性时移的方式合成平面波域地震数据,在平面波域或射线参数p域,合成地震记录可表示为
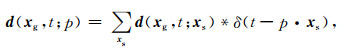
|
(10) |
d(xg, t; xs)表示炮域的地震数据;d(xg, t; p)表示平面波域地震数据,即平面波记录;δ(t-p·xs)是时移函数,*表示卷积运算,xs是每一炮震源坐标,xg是接收点坐标,时移量为p·xs,它随震源坐标线性变化.因此,平面波编码过程可以表述为:首先将炮域的地震数据进行逐炮时移,然后进行线性叠加,最终将多炮地震数据压缩成1个平面波记录.当然选择不同的射线参数,其时移量就不同,也就合成了不同的平面波道集.
第二步是对合成的Np(≪Ns)个平面波道集进行逐个偏移成像,获得Np个独立的成像结果.具体方式为采用相同的编码方式合成对应的平面波震源,随后激发产生平面波震源波场,将合成的平面波道集作为边界条件反传获得平面波反传波场,最后将两者进行零延迟互相关即可获得不同平面波道集对应的成像结果mi(i=1, …, Np).
与平面波偏移不同的是,需对上述Np个平面波成像结果进行分别存储,而不是叠加成一个剖面.Low-rank有限差分法叠前平面波LSRTM的处理流程与Lrfd-LSRTM类似,只是在每次迭代中,观测记录为平面波记录,需按照公式(10)对激发震源进行平面波编码处理.此外,每个平面波道集所对应的成像结果都不进行叠加成像处理,而是对其进行分别存储,且在迭代中独自地进行更新,相互之间互不影响,即在进行下一次迭代时,输入的反射系数模型为叠加之前对应的前一次成像结果.这种做法的优势在于,有利于减弱LSRTM对偏移速度与各向异性参数模型误差的依赖性、抑制数据噪声、且方便提取平面波域共成像点道集用于质量监控等;缺点是略微增加了额外内存,内存大小与平面波道集的个数成正比,将上述成像方法简记为Lrfd-Pre-PLSRTM.
对于规则观测系统,LSRTM、PLSRTM、Pre-PLSRTM方法的计算时间及I/O成本如表 1所示,表中可见:①PLSRTM与Pre-PLSRTM的计算时间小于LSRTM,主要是由于Np≪Ns;②Pre-PLSRTM的I/O成本明显高于LSRTM与PLSRTM,这是因为各个叠前平面波成像结果需分别存储、独立更新.值得一提的是,最速下降法LSRTM需要两次基于散射波方程的线性正演,其中一次是求取反偏移数据,用来匹配观测数据,另一次是对梯度进行线性正演,用于计算更新步长,加上一次基于伴随方程的逆时偏移,用以计算梯度更新量.
|
|
表 1 LSRTM、PLSRTM、Pre-PLSRTM的计算时间及I/O成本对比 Table 1 Comparison of computation time and I/O costs of LSRTM, PLSRTM and Pre-PLSRTM |
本文首先选用简单Salt模型进行Low-rank有限差分法纯qP波线性正演模拟、纯qP波最小二乘逆时偏移成像以及纯qP波叠前平面波最小二乘逆时偏移成像测试,并与拟声波线性正演模拟及相应的反演成像结果进行对比来验证本方法的正确性;随后,将本方法应用于含有不同强度噪声的地震数据成像试验中,进一步测试本方法的抗噪性;在验证了方法正确性及对噪声地震数据有效性的基础上,开展复杂MarII模型成像试处理,以测验方法对复杂地质模型的正、反演适应性,同时,测试了本方法对速度及各向异性参数模型误差的敏感性,突出本方法的优势所在;最后,将本方法应用于实际资料试处理中.下列测试统一采用Cerjan衰减边界条件处理人工边界反射,在成像处理中,使用震源归一化互相关成像条件来补偿中深部成像能量.
2.1 简单Salt模型验证 2.1.1 模型参数图 1a—d分别展示了Salt模型对应的真实纵波速度、偏移纵波速度以及各向异性参数.真实纵波速度用来合成观测记录,偏移纵波速度是通过对真实纵波速度的平滑获得,用以表征背景速度.根据定义,通过背景速度与真实速度能够求出反射系数模型(如图 1e所示),这是反演成像试图通过迭代来逼近的理论值,也是成像试验中用以比较成像质量优劣的重要参考.需要说明的是,在常规的有限差分法波场计算中,通常需要对各向异性参数进行平滑处理,以提高算法的稳定性,但对于Low-rank有限差分算法,无需平滑各向异性参数,这是因为Low-rank分解更偏向于处理线性相关的传播矩阵,平滑处理只会增加传播矩阵的秩.
|
图 1 简单Salt模型 (a)真实纵波速度;(b)偏移纵波速度;(c) Epsilon模型;(d) Delta模型;(e)慢度扰动模型. Fig. 1 Simple Salt models (a) True P-wave velocity model; (b) Migration P-wave velocity model; (c) Epsilon model; (d) Delta model; (e) Slowness perturbation model. |
此外,从图中可见,模型总体上表现为在速度缓慢变化的背景模型之上穿插了几组高速反射体,该模型中心位置处含有一个横向约3.2 km、垂向约1 km跨度的高速盐丘,盐顶上部及盐下地层的断裂构造发育,是检验各向异性成像算法的经典模型.模型网格大小为676×201,空间网格间距Δx=Δz=10 m,因此模型尺寸总计为6750 m×2000 m,模型速度变化范围处于1500~4482 m·s-1之间,权衡稳定性条件与计算效率,时间步长Δt设计为1.0 ms.依据上述计算参数并根据Low-rank有限差分计算步骤可以求出Salt模型的Low-rank有限差分权系数矩阵.
根据数值频散条件,代入Salt模型的网格间距及最小传播速度,选定主频为20 Hz的雷克子波作为激发震源,观测系统设计如下:激发总炮数338炮,激发井深20 m,炮点间距20 m,首炮位置位于模型左端第一个网格点处,采用676道接收,接收点间距10 m,总的记录长度为5.0 s,因此每道采样点数为5001.首先按照上述参数选用真实纵波速度模型及各向异性参数,并采用Low-rank有限差分纯qP波线性正演算法(即公式(4))合成散射波地震记录.
2.1.2 炮记录对比分析计算所得的VTI介质散射波地震响应如图 2a所示,分析可见:线性化的反偏移记录,也即散射波记录中不含有直达波,这是由于直达波属于入射波场;散射波记录中蕴含着更加丰富的反射波信息,这是因为散射波的激发震源为地下介质中所有的反射源,且无直达波等强能量干扰;反射同相轴清晰、不存在严重的数值频散假象、反射波刻画准确,这些现象初步证实了方法的正确性.为了对比,按照同样的计算参数和模型参数,选用VTI介质二阶拟声波方程对应的线性化波场计算公式合成散射波记录,如图 2b所示,从主要反射波同相轴的到达时间可以判断出图 2b与图 2a具有很好的相似性,也从侧面佐证了本文方法的有效性.进一步,分别将上述两种方法用于各向同性介质的散射波正演计算中,Low-rank有限差分法及拟声波方法计算结果分别如图 2c与d所示,观察反射波走时可知:①不同方法所计算的同一类介质的散射波记录走时一致;②在远偏移距位置,可以明显看出各向异性介质的走时略小于各向同性介质,这是由各向异性参数大于零,地震波传播速度高于各向同性介质地震波速度所致,这也是各向异性成像通过校正走时畸变,能够改善成像质量,减小井震闭合差的原因所在;③此外,②中所看到的走时畸变在远偏移距比近偏移距更为明显,这说明随着传播距离增加,各向异性走时畸变造成的时间误差及距离误差将逐步积累.因此在深层和超深层资源探查中,考虑各向异性是降低风险的一种重要手段之一.
|
图 2 线性化的散射波正演记录 (a) VTI介质纯qP波记录;(b) VTI介质拟声波记录;(c)各向同性介质Low-rank FD计算结果;(d)各向同性介质波动方程正演结果. Fig. 2 Comparison of linearized scattered-wave records (a) Pure qP-wave gathers for VTI medium; (b) Pseudo acoustic wave gathers for VTI medium; (c) P-wave records computed by Low-rank FD and (d) P-wave records acquired by Conventional FD for isotropic medium. |
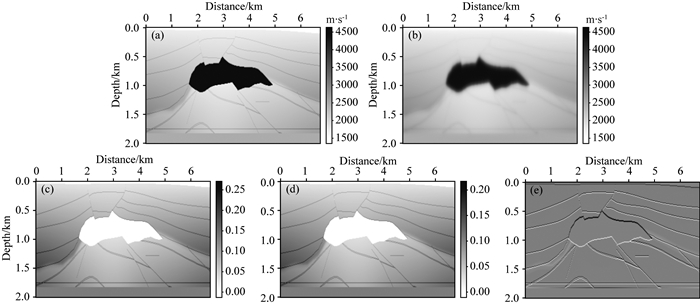
为了更直观地说明本文线性化正演算子的正确性,并清晰地展示上述记录的相似性,依次抽取了图 2中CDP号等于320(如图 2a实线箭头所指,代表近偏移距)和CDP号等于30(如图 2a虚线箭头所指,代表远偏移距)处的地震单道记录进行对比.图 3a展示了CDP号等于320时的各向异性VTI介质纯qP波单道记录(如图 3a红线标示)与拟声波单道记录(如图 3a蓝线标示),对比可见:两条曲线基本重合,这说明本文Low-rank有限差分法线性化正演算子(即公式(4)与公式(5))在近偏移距位置处的计算结果是基本正确的.图 3b对应CDP号等于30时的纯qP波单道记录(如图 3b红线标示)与拟声波单道记录(如图 3b蓝线标示),对比可知:在远偏移距位置,Low-rank有限差分法线性化正演算子也能够准确地计算出散射波场,进一步说明了本文方法的合理性.图 3c表示与图 3a相对应的各向同性介质P波记录,图 3d表示与图 3b相对应的各向同性介质P波记录,仔细观察可得:本文推导的Low-rank有限差分法线性化正演算子完全适应各向同性介质;在各向同性介质中,近偏移距的地震波走时与各向异性介质基本吻合,而远偏移距的地震波走时略慢于各向异性介质.图 3e还给出了前文四类地震记录(图 2a—d)对应的频谱,图中可见:通过不同方法计算的同一介质中的地震波频谱更趋向于一致,证明了本方法的正确性.
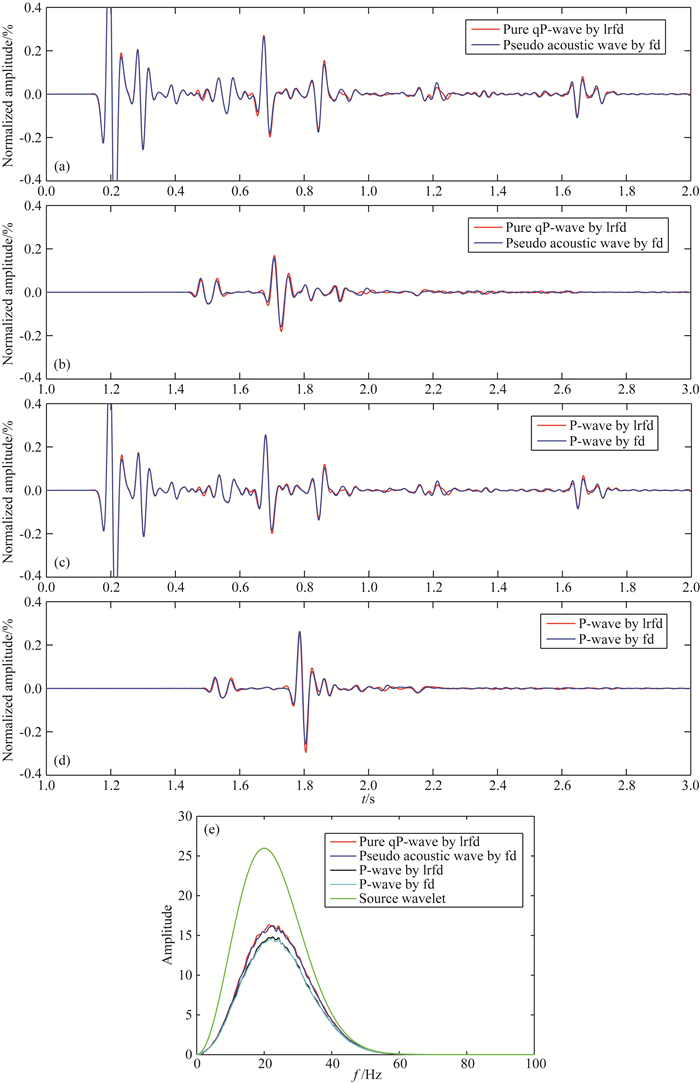
|
图 3 时频域单道记录对比 (a)近偏移距(CDP=320)处VTI介质单道记录;(b)远偏移距(CDP=30)处VTI介质单道记录;(c)近偏移距(CDP=320)处各向同性介质单道记录;(d)远偏移距(CDP=30)处各向同性介质单道记录;(e)散射波记录频谱. Fig. 3 Comparison of single trace records in time domain and frequency domain Single trace record of VTI media which is located at (a) CDP=320 and (b) CDP=30; Single trace record of isotropic media which is located at (c) CDP=320 and (d) CDP=30;(e) Spectrum of scattered-waves. |
为了测试平面波偏移成像方法的优势,首先按照公式(10)将上述Salt模型的炮记录合成31个含不同射线参数p的平面波域地震记录,其中p的取值范围是-0.27~0.27 s·km-1(对应的地表激发倾角范围是-23°~23°),其取值按照31个平面波等间距分布.图 4a—c分别展示了射线参数p依次为-0.27 s·km-1、0 s·km-1及0.27 s·km-1值时的三种平面波记录,观察分析可知:①由于采用了平面波线性时移编码策略,将338炮炮域地震记录压缩成31个平面波记录,数据量减少为原来的十分之一,释放了大量存储空间,计算中也明显降低了I/O成本与计算时间;②合成的平面波记录在地震波形形态上更接近于叠加剖面,特别是射线参数为零时,能够从平面波记录中粗略地判断出浅表层的地层分布情况(如图 4b所示);③至于深部地层及复杂地质体所对应的反射波由于相互干涉叠加,很难从记录中直接辨识,需要通过进一步的偏移成像处理来使反射波归位、绕射波收敛.
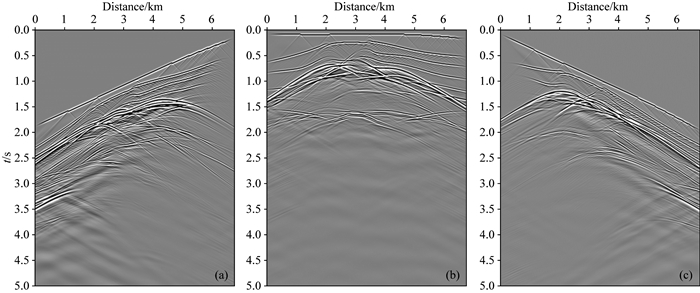
|
图 4 平面波记录.射线参数分别是(a)p=-0.27 s·km-1;(b) p=0.0 s·km-1;(c) p=0.27 s·km-1 Fig. 4 Plane-wave gathers with (a) p=-0.27 s·km-1; (b) p=0.0 s·km-1; and (c) p=0.27 s·km-1 |
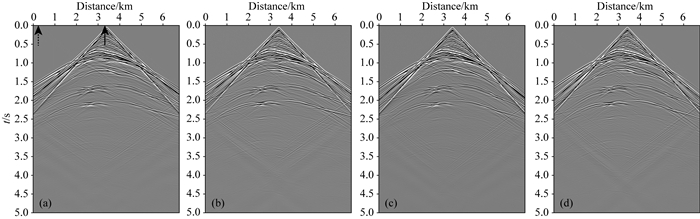
图 5展示了Salt模型最小二乘逆时偏移成像结果,其中,图 5a与b分别对应Low-rank有限差分法纯qP波LSRTM迭代1次及30次的成像剖面,图中可见:①在类似于各向异性常规逆时偏移成像的第1次迭代结果中,剖面遭受低频噪声干扰,尤其是浅层与高速盐丘周围及其顶、底部地层最为严重,震源位置出现很强的能量团,深部同相轴连续性差、成像能量相对较弱;②通过30次迭代反演之后,低频噪声基本消除,震源效应得到很好的抑制,中深部能量得到加强,整个剖面的成像振幅更为均衡、同相轴的连续性更为清晰,这体现出反演成像的质量明显优于偏移成像;③上述现象也表明本文提出的纯qP波LSRTM基本达到了反演成像的预期效果.为了进一步验证成像方法的正确性,图 5c还给出了较为成熟的各向异性拟声波LSRTM迭代30次的成像结果,对比可见:图 5b与该成像结果十分吻合,这也恰好说明本方法是合理的.图 7a给出了上述纯qP波LSRTM(如图 7红点虚线所示)与拟声波LSRTM(如图 7圆圈实线所指)的数据残差收敛曲线,其变化趋势反映出:随着迭代次数的增加,两种方法的数据残差都逐渐收敛到5%以下,且两条收敛曲线几乎完全重合,这种一致性正好体现了本文反演成像方法的正确性.
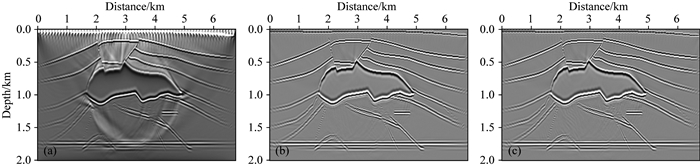
|
图 5 炮域最小二乘逆时偏移成像剖面 (a)纯qP波Lrfd-LSRTM迭代1次;(b)纯qP波Lrfd-LSRTM迭代30次;(c)拟声波LSRTM迭代30次. Fig. 5 Profiles of shot-domain LSRTM images by using (a) pure qP-wave Lrfd-LSRTM with one iteration; (b) pure qP-wave Lrfd-LSRTM with 30 iterations; and (c) pseudo acoustic wave LSRTM with 30 iterations |
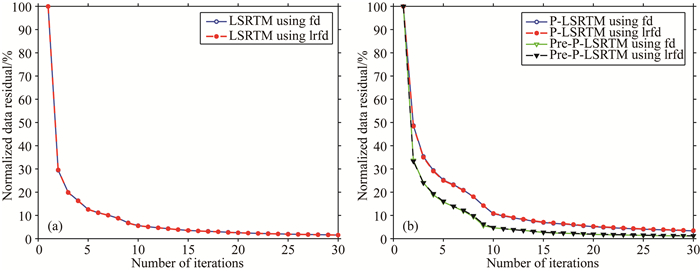
|
图 7 归一化数据残差收敛曲线 (a) LSRTM;(b) PLSRTM. Fig. 7 Normalized convergence curves of data residuals |
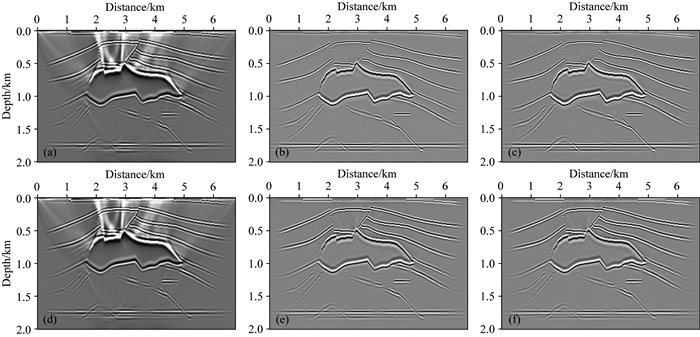
图 6a—f分别展示了各种平面波最小二乘逆时偏移的成像结果.其中,图 6a和b分别对应纯qP波Lrfd-PLSRTM迭代1次及30次的成像剖面,图 6c为拟声波PLSRTM迭代30次的结果,图 6d和e分别对应纯qP波Lrfd-Pre-PLSRTM迭代1次及30次的成像剖面,图 6f为拟声波Pre-PLSRTM迭代30次的结果.由图可见:①通过对比图 6a与b或对比图 6d与e可以看出,无论是平面波LSRTM还是叠前平面波LSRTM,都能够在迭代过程中显著地补偿中深部成像质量、均衡成像振幅、改善同相轴的连续性、增强信噪比、提升成像剖面的反演质量,其结果接近于图 5b所展示的成像效果,但计算成本缩小为炮域LSRTM的近十分之一,这是平面波LSRTM的最大优势;②通过对比图 6b与c或对比图 6e与f可以得出,对于相同的(叠前)平面波LSRTM成像方法,选用Low-rank有限差分法波场延拓策略与选用拟声波波场延拓方案进行成像处理,所得结果基本相同,这种一致性证实了本文Low-rank有限差分法线性化正演算子、Low-rank有限差分偏移成像算子以及成像方法流程的正确性;③在纵向上,通过对比图 6b与e或对比图 6c与f可以得知,相同条件下,叠前平面波LSRTM的成像质量高于平面波LSRTM,反射波同性轴的子波旁瓣更少,分辨率更高.这种优越性可以通过图 7b所示的数据残差收敛曲线清晰地反映出来,从图 7b可知:利用叠前平面波编程方式来实现LSRTM具有更快的收敛速度,在相同迭代次数时,成像质量更高.
|
图 6 平面波域最小二乘逆时偏移成像剖面 (a)纯qP波Lrfd-PLSRTM迭代1次;(b)纯qP波Lrfd-PLSRTM迭代30次;(c)拟声波PLSRTM迭代30次;(d) Lrfd-Pre-PLSRTM迭代1次;(e) Lrfd-Pre-PLSRTM迭代30次;(f)拟声波Pre-PLSRTM迭代30次. Fig. 6 Profiles of plane-wave LSRTM images by using pure qP-wave Lrfd-PLSRTM with (a) one iteration and (b) 30 iterations; (c) pseudo acoustic wave PLSRTM with 30 iterations, and pure qP-wave Lrfd-Pre-PLSRTM with (d) one iteration and (e) 30 iterations; and (f) pseudo acoustic wave Pre-PLSRTM with 30 iterations |
此外,本文还给出了在同一台工作站上,采用单个节点时不同方法的CPU计算时间与I/O成本:①纯qP波LSRTM和拟声波LSRTM迭代一次所需的计算时间分别为15.773 h、48.446 h,而I/O成本分别为2.549 GB、2.785 GB;②纯qP波PLSRTM和纯qP波Pre-PLSRTM迭代一次所需的计算时间分别为1.533 h、1.495 h,而I/O成本分别为2.527 GB、2.695 GB;此外,③拟声波PLSRTM和拟声波Pre-PLSRTM迭代一次所需的计算时间分别为4.725 h、4.677 h,而I/O成本分别为2.802 GB、2.965 GB,从统计结果可知:PLSRTM与Pre-PLSRTM的CPU计算时间远小于LSRTM;无论在炮域、平面波域、还是在叠前平面波域,纯qP波类成像方法在计算时间上都明显优于拟声波类成像方法;在I/O成本方面,叠前平面波域成像算法与炮域成像方法相当,但略高于平面波域成像方法,同时,由于拟声波类成像方法较纯qP波类方法需耗费多个波场变量,因此占用内存偏高.
2.1.4 成像方法抗噪性试验在验证了Low-rank有限差分法纯qP波LSRTM及叠前平面波LSRTM成像方法正确性的基础上,下面对成像效率较高Low-rank有限差分法叠前平面波LSRTM进行抗噪性试验,并与Low-rank有限差分法平面波LSRTM进行对比,进一步突出其在噪声地震数据成像方面的良好适应性.
首先将上述31个平面波道集分别加载三种强度不一的随机噪声,三种信噪比(SNR)分别等于2:1、1:1及1:2的平面波域地震数据依次如图 8a—c所示,从图中可见:伴随地震数据信噪比降低,噪声能量逐步增强,在信噪比为2:1时,能量较强的同相轴还能较为清楚地辨识,而当信噪比为1:2时,有效能量几乎完全被噪声所掩盖,噪声能量较为强烈,能够达到测试本方法在迭代中能否压制噪声干扰的目的.

|
图 8 不同信噪比的平面波域地震数据 (a) SNR=2:1;(b) SNR=1:1;(c) SNR=1:2. Fig. 8 Plane-wave gathers with (a) SNR=2:1;(b) SNR=1:1;and (c) SNR=1:2 |
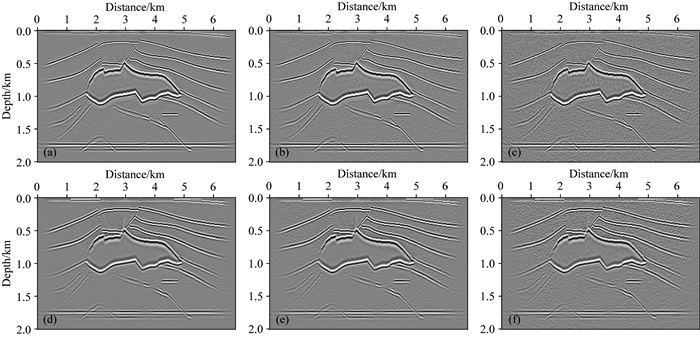
针对上述三类噪声地震数据,分别采用Low-rank有限差分法平面波LSRTM及叠前平面波LSRTM进行成像处理,迭代次数为30次,其结果如图 9a—f所示.从左往右看,每一列分别对应SNR为2:1、1:1及1:2时的反演成像结果,上边采用的是Low-rank有限差分法PLSRTM,下边采用的是Low-rank有限差分法Pre-PLSRTM.从中可见:①尽管地震数据噪声较为强烈,但总体上看反演质量还是可观的,盐丘、断裂等复杂地质体边界都得到很好的刻画,主要的反射界面也得到充分的展现,这说明本方法对随机噪声具备一定的适应性;②随着信噪比的逐步减小,地震数据的噪声能量逐渐加强,两种方法的成像质量随之变差,主要是剖面中弥散着一些随机干扰,降低了成像剖面的信噪比,影响了同相轴的分辨率;③对比上、下两行可知,相比于Lrfd-PLSRTM,Lrfd-Pre-PLSRTM的成像质量更佳,噪声压制更加彻底,剖面信噪比更高,这正好体现了叠前平面波实现方式的优越性.当地震数据含有噪声、单个平面波成像结果存在偏差时,各平面波成像结果不进行叠加,而是分别存储,且独自迭代更新,这种误差不会累积,也不会扩散到其他道集,在最终的成像剖面中还会得到进一步削弱.因此,可以得出Lrfd-Pre-PLSRTM成像方法成像效果好、收敛速度快、计算成本低、且具备良好的抗噪性优势.
|
图 9 平面波域最小二乘逆时偏移成像剖面. 从左到右:SNR分别为2:1、1:1、1:2;从上到下:分别为Lrfd-PLSRTM和Lrfd-Pre-PLSRTM成像结果 Fig. 9 Profiles of plane-wave LSRTM images. From left to right:SNR=2:1, 1:1, 1:2. Upper: Lrfd-PLSRTM; Lower:Lrfd-Pre-PLSRTM |
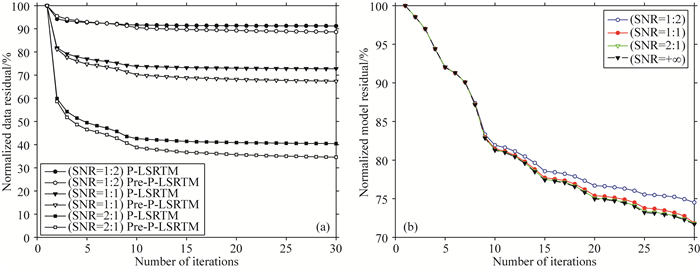
图 10a展示了不同信噪比情况下Lrfd-PLSRTM和Lrfd-Pre-PLSRTM的数据残差收敛曲线,对比可知:①当地震数据存在噪声时,数据残差的收敛速度会变得十分缓慢,且残差下降阈值会显著减小,对于同一种反演成像方法,随着地震数据信噪比增强,数据残差收敛效果会更好;②对于同一信噪比地震数据,Lrfd-Pre-PLSRTM成像方法的收敛特性优于Lrfd-PLSRTM,主要表现为残差下降范围更大、残差下降速度更快,这进一步说明Lrfd-Pre-PLSRTM能够更好地适应噪声地震数据,具有一定的抗噪性能.图 10b还给出了Low-rank有限差分法Pre-P-LSRTM方法的模型残差收敛曲线,从中可见:①总体来看,随着地震数据信噪比的增加,模型残差收敛得更好,随着迭代次数的增加,模型残差逐渐减小,直至逼近于真实模型;②当信噪比大于1:1,也即有效信号能量大于或等于随机噪声能量时,模型残差的收敛曲线变化不大,与理想收敛曲线相当,这表明当SNR≥1时,该方法基本能够适应;③当信噪比SNR减小到1:2时,模型残差收敛效果明显变差.
|
图 10 归一化收敛曲线 (a)数据残差;(b)模型残差. Fig. 10 Normalized convergence curves of (a) data residuals and (b) model residuals |
在验证本文方法正确性的基础上,将其应用于改造的复杂MarII模型成像试算,以测验方法对复杂地质模型的正、反演适应性.
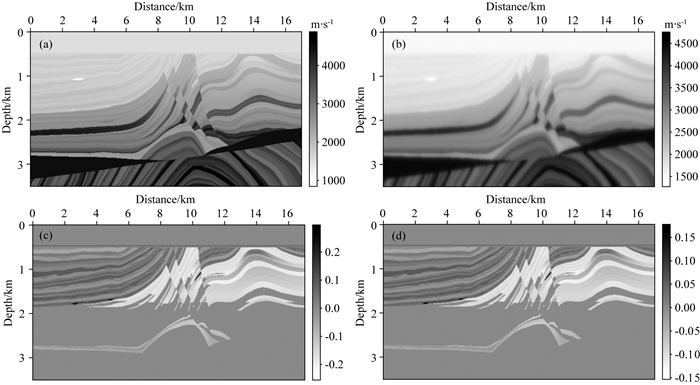
2.2.1 模型参数改造后的标准MarII模型如图 11所示,其中,图 11a为真实的纵波速度模型,从速度结构可见:模型中深部含有一个高速不整合面,不整合下覆地层倾斜角度大,不整合之上背斜构造及断裂系统发育,在位置(3 km,1.1 km)处存在一个低速异常体,极易造成数值频散假象;模型中部的三组大断裂造成反射结构紊乱、绕射波发育,是检验反演成像方法的典型模型.图 11b为偏移速度模型,通过平滑真实速度模型得到,主要用于构建线性正演算子与偏移成像算子,图 11c与d分别为各向异性Epsilon和Delta模型参数,是表征速度各向异性的必要参数.本文主要基于两点假设:①各向异性强度随着速度增加而减小,②qP波横向传播速度随着深度线性增加,来构建各向异性参数模型.显然,到目前为止并没有足够的证据证实上述假设的真实性,然而本文并不需要去建立一个真实的地质模型,而是为了建立一个相对合理的各向异性参数模型,以达到测试本文各向异性反演成像算法的目的.
|
图 11 改造的MarII模型 (a)真实速度;(b)偏移速度;(c) Epsilon模型;(d) Delta模型. Fig. 11 Modified MarII models (a) True P-wave velocity model; (b) Migration P-wave velocity model; (c) Epsilon model; (d) Delta model. |
模型网格大小为1361×351,横向网格间距Δx=12.5 m,纵向网格间距Δz=10 m,因此该模型横向变化范围是0~17 km,模型深度为3.5 km,水深约500 m,传播速度的取值范围是1028 ~4700 m·s-1.为了满足稳定性条件,同时兼顾反演成像的计算效率,取时间步长Δt为1.0 ms.同理,依据上述计算参数,并选取8阶紧致差分模板,即可求出MarII模型的Low-rank有限差分权系数矩阵.
观测系统设计如下:激发总炮数为681炮,激发井深20 m,炮点间距25 m,首炮位置位于模型左端第一个网格点处,采用1361道全接收,接收点间距12.5 m,总的记录长度为7.0 s,因此每道地震数据的采样点数为7001.
2.2.2 炮记录选定主频为18 Hz的雷克子波作为激发震源,采用Low-rank有限差分法线性正演算子形成炮域地震记录如图 12a所示,图 12b为拟声波正演记录,对比可见:两者基本一致,说明Low-rank有限差分法线性正演算子能够很好地适应复杂地质模型.进一步,抽取了CDP号为51时的散射波记录进行对比,如图 13所示,图中可见:两条曲线基本重合,体现了反射波形的一致性,也充分展示了本文线性化正演算子对复杂地质模型的适应能力.
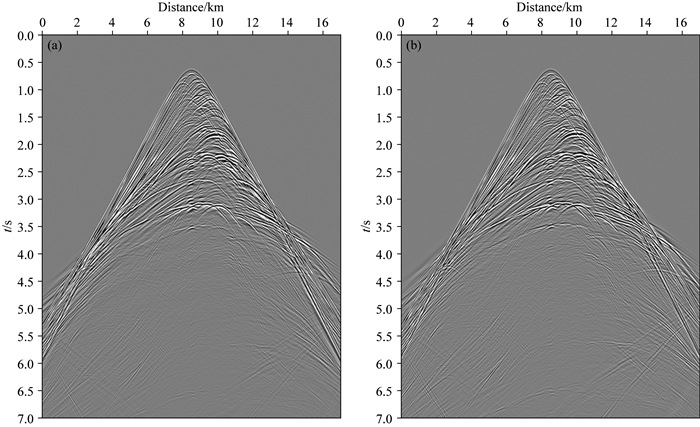
|
图 12 线性化的地震散射波炮记录 (a) VTI介质纯qP波记录;(b) VTI介质拟声波记录. Fig. 12 Linearized scattered-wave records (a) Pure qP-wave gathers for VTI medium; (b) Pseudo acoustic wave gathers for VTI medium. |
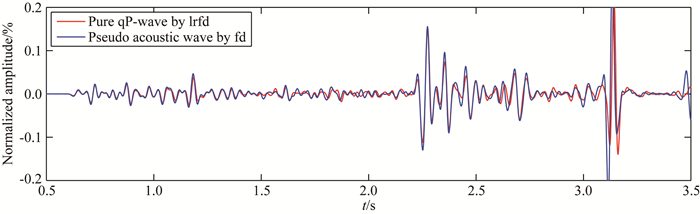
|
图 13 单道记录 Fig. 13 Single trace record in receiver |
为了进行复杂模型平面波域成像算法适应性测试,将炮域地震记录合成35个平面波域地震记录,射线参数取值为-0.2~0.2 s·km-1,并按照平面波个数呈等间距分布.射线参数p依次为-0.2 s·km-1、0 s·km-1及0.2 s·km-1时的三种平面波记录分别如图 14a—c所示,由图可见:①在平面波记录中,仍然可以粗略地观察到地下构造形态,特别是浅表层以及受构造运动破坏较小,保存较完好的沉积地层等;②但是对于低速异常体周围、断裂构造附近以及深部反射能量难以识别,因为绕射波发育、且受多次波影响.
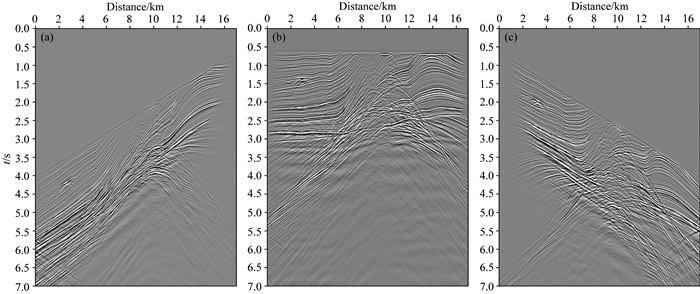
|
图 14 平面波记录.射线参数分别是(a)p=-0.2 s·km-1; (b) p=0.0 s·km-1; (c) p=0.2 s·km-1. Fig. 14 Plane-wave gathers with (a) p=-0.2 s·km-1; (b) p=0.0 s·km-1; and (c) p=0.2 s·km-1 |
复杂模型平面波域最小二乘逆时偏移成像结果分别如图 15a—f所示,其中,图 15a和b分别为拟声波PLSRTM与Pre-PLSRTM迭代30次的成像结果,而图 15c和d分别对应纯qP波Lrfd-PLSRTM与Lrfd-Pre-PLSRTM迭代30次的成像结果,分析对比可以得出如下结论:总体看来,①对于复杂地质模型,在速度及各向异性参数都相对准确、且地震数据不含噪声干扰的情况下,上述几类方法都能获得相对合理的反演成像结果,这也证实了方法的正确性及对复杂模型的适应性;从成像细节来看,②对比图 15a与b(或对比图 15c与d),无论是拟声波还是纯qP波类方法,叠前平面波LSRTM比平面波LSRTM有更好的成像效果,这一点从下文的收敛曲线可以清晰地展示出来;③对比图 15a与c(或对比图 15b与d),成像结果基本一致,这表明本文方法能够适应复杂模型成像.图 15e与f分别展示了地震数据信噪比为1:1时,采用纯qP波Lrfd-PLSRTM及Lrfd-Pre-PLSRTM迭代30次的成像结果,观察可见:当地震数据存在噪声时,会降低成像剖面的信噪比,但主要的地质目标如断裂系统、背斜构造、不整合面以及倾斜构造都准确归位,且Lrfd-Pre-PLSRTM方法对应的成像剖面更为清晰,分辨率也更高.
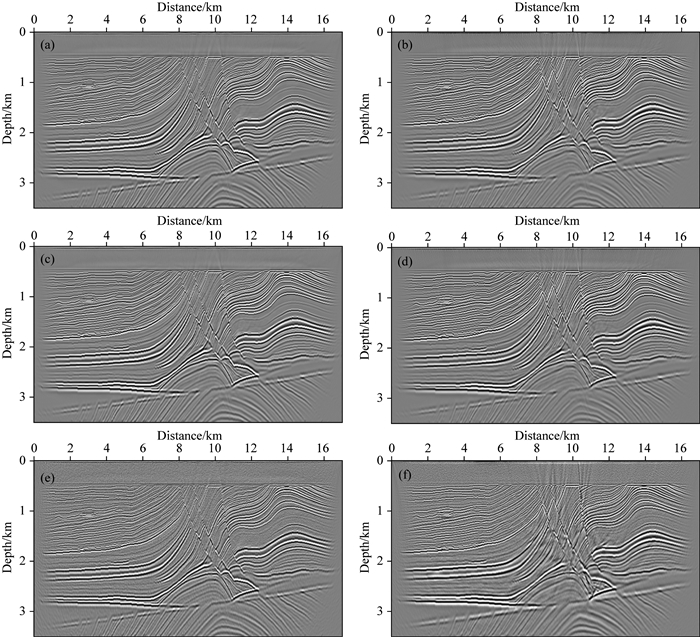
|
图 15 不同方法成像结果对比 (a)、(b)分别为拟声波PLSRTM与Pre-PLSRTM迭代30次;(c)、(d)分别为纯qP波Lrfd-PLSRTM及Lrfd-Pre-PLSRTM迭代30次;(e)、(f)分别为SNR=1:1时,纯qP波Lrfd-PLSRTM及Lrfd-Pre-PLSRTM迭代30次. Fig. 15 Comparison of images using different methods (a) Pseudo acoustic wave PLSRTM with 30 iterations; (b) Pseudo acoustic wave Pre-PLSRTM with 30 iterations; (c) Pure qP-wave Lrfd-PLSRTM with 30 iterations; (d) Pure qP-wave Lrfd-Pre-PLSRTM with 30 iterations; (e) Same as (c) but adding SNR=1:1; (f) Same as (d) but adding SNR=1:1. |
图 16展示了上述几类反演成像处理的收敛曲线,对比可知:①在存在数据噪声的情况下,收敛效果明显变差,但叠前平面波LSRTM比平面波LSRTM方法具有更好的收敛效果,这体现了叠前平面波LSRTM对于复杂模型仍然具备良好的抗噪性,该方法能够在迭代成像中自动压制数据噪声、提高剖面信噪比、改善成像质量;②从收敛曲线可以清晰地反映叠前平面波LSRTM明显优于平面波LSRTM,而纯qP波类偏移方法与拟声波类偏移方法相比,在MarII模型成像中,对效果的改善并不十分明显.
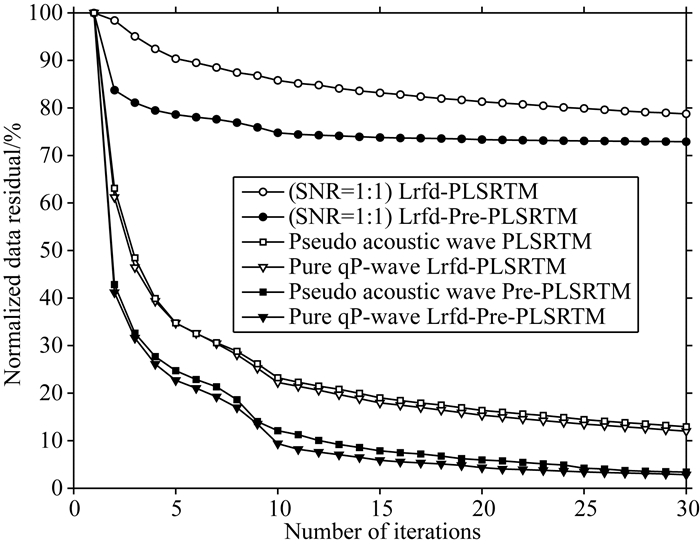
|
图 16 不同方法的归一化数据残差收敛曲线对比 Fig. 16 Comparison of normalized convergence curves of data residuals of different methods |
考查成像方法对速度及各向异性参数误差的敏感性,并试图减弱成像方法对模型参数误差的依赖性是勘探地球物理学领域永恒的研究课题.基于控制变量法,下面分别测试了当存在速度误差、Epsilon误差、Delta误差以及倾角误差时Lrfd-Pre-PLSRTM的成像特点,并与Lrfd-PLSRTM进行对比,展示了Lrfd-Pre-PLSRTM的优势,最后总结出一套关于反演成像方法对模型参数误差的容错性规律,用以指导生产实践,并推广本方法更好地为实际生产服务.
2.3.1 速度模型误差图 17a—b分别展示了速度误差为0%(真实值)、2%、5%及8%时的Lrfd-Pre-PLSRTM迭代30次的成像结果,这里专指系统误差.从图中可见:①随着速度误差的增大,成像质量逐渐变差;②当速度误差增加至8%时,断层边界已经难以识别,构造形态也已模糊,成像位置也出现了巨大偏差,深度方向偏离实际位置达250 m左右,且随着深度增加,这种成像偏差越大,成像剖面出现整体上拉现象.总之,速度误差对成像的影响极大,是成像处理中最为敏感的模型参数,为此,在实际生产中,速度分析成为事关地震勘探成败的重要原因.
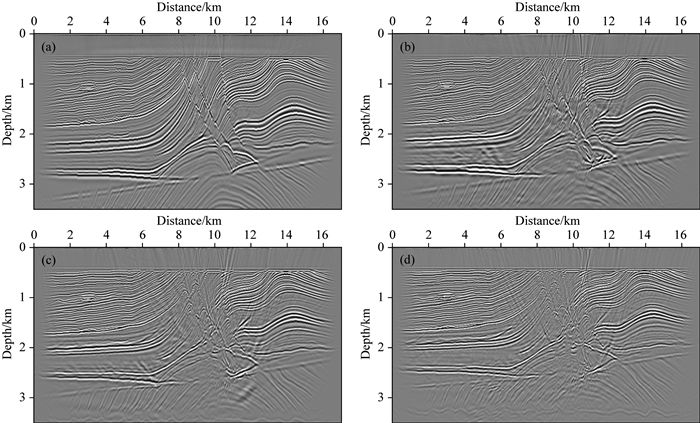
|
图 17 不同速度误差的Lrfd-Pre-PLSRTM成像结果 (a) 0% (真实值); (b) 2%; (c) 5%; (d) 8%. Fig. 17 Images using Lrfd-Pre-PLSRTM method when the velocity error equals (a) 0%(true), (b) 2%, (c) 5%, and (d) 8%, respectively |
图 18a展示了上述四组成像试验的数据残差收敛曲线,为了对比,图 18b给出了Lrfd-PLSRTM的数据残差收敛曲线,从收敛曲线也反映出:①当存在速度误差时,收敛效果明显变差,表现为收敛速度变慢、收敛范围减小;②对比图 18a与b可以发现,对于Lrfd-Pre-PLSRTM方法,尽管速度误差变化范围较大,但经过30次迭代后,数据残差仍能稳定地收敛到45%~50%之间,而对于Lrfd-PLSRTM方法,当存在不同速度误差时,其收敛曲线波动范围较大,且收敛效果明显不如Lrfd-Pre-PLSRTM方法.这表明Lrfd-Pre-PLSRTM方法的收敛效果更佳,收敛速度更稳定,收敛阈值更低,也从侧面表明Lrfd-Pre-PLSRTM方法在缓和速度误差依赖性方面具有一定的优势.
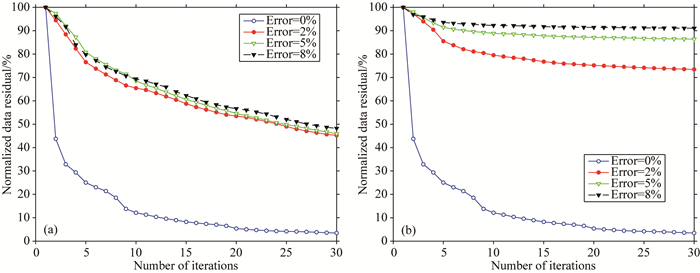
|
图 18 存在速度误差时的归一化数据残差收敛曲线 (a) Lrfd-Pre-PLSRTM; (b) Lrfd-PLSRTM. Fig. 18 Normalized convergence curves of data residuals when velocity error exists |
此外,本文还测验了各向异性Epsilon参数误差为0%(真实值)、8%、18%及28%和Delta参数误差为0%(真实值)、8%、28%及48%时的Lrfd-Pre-PLSRTM成像情况.由于在理论上Epsilon和Delta都是影响地震波传播速度的参数(Epsilon参数间接影响横向速度的变化量,Delta参数间接影响动校正速度的变化量),对成像方法的影响规律大同小异(主要是敏感性有所不同),在这里,其成像结果就不再一一展示.通过测试可以得出:①Epsilon参数误差对成像有一定的影响,但敏感性远不如速度误差大,随着Epsilon误差增大,成像剖面在整体上保持清晰、稳定、且无偏差,仅在断层边界及附近出现同相轴扭曲、倾斜地层发生错动等现象,这是由于Epsilon参数在本质上决定着地震波横向传播速度的大小,且Epsilon参数的影响范围远远小于速度误差所带来的影响;②Delta误差对成像的影响最小,当Delta误差为28%时,反演成像结果仍然接近于零误差时的最佳成像结果,仅在高陡断层区域出现部分偏移噪声,而断层轮廓依然较为清晰;当Delta误差为48%时,Delta值已经严重偏离真实模型,但成像依然稳定,除倾斜构造变得模糊之外,其他地质构造仍然准确成像.
图 19a和b分别给出了存在Epsilon误差和存在Delta误差时Lrfd-Pre-PLSRTM方法的归一化数据残差收敛曲线,从图中可以更直观地反映出:①Epsilon参数误差对成像有一定的敏感性,这体现在随着参数误差增加,收敛速度稍有减缓,但依赖性并不是很强,当Epsilon误差增至28%时,经过30次迭代之后,数据残差仍能收敛至25%左右,这种低敏感性也说明在多参数全波形反演中,Epsilon参数很难直接反演;②Delta参数误差影响很小,且小于Epsilon参数误差对成像的影响,对比可见,Delta误差增加至48%时,数据残差依然收敛,收敛阈值为22%左右,与Epsilon误差为28%时的收敛情况相当(对比图 19a),这是由于Delta参数决定地震波动校正速度,对成像影响较小.
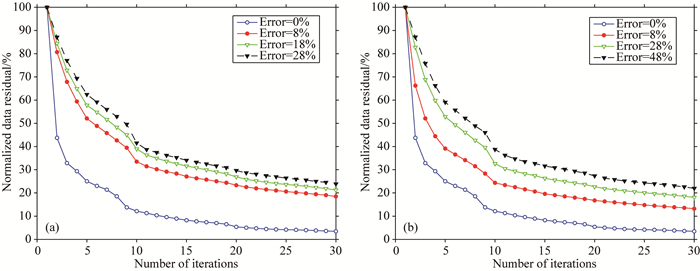
|
图 19 存在各向异性参数误差时的归一化数据残差收敛曲线 (a) Epsilon误差; (b) Delta误差. Fig. 19 Normalized convergence curves of data residuals when error of anisotropic parameter exists (a) Epsilon error; (b) Delta error. |
同理,图 20a—d分别展示了极化倾角为80°(真实值)、60°、30°及0°时的Lrfd-Pre-PLSRTM迭代30次的成像结果,从中可见:当存在倾角误差时,会造成成像剖面出现整体扭曲,特别是陡倾构造的极度扭曲、表层噪声严重、成像位置紊乱等问题,且随着误差的加剧,这些现象愈加明显.这表明成像方法对倾角误差十分敏感,虽然不同于速度误差造成成像位置出现严重偏移,但会造成成像位置错乱、构造形态、断层边界等难以分辨.
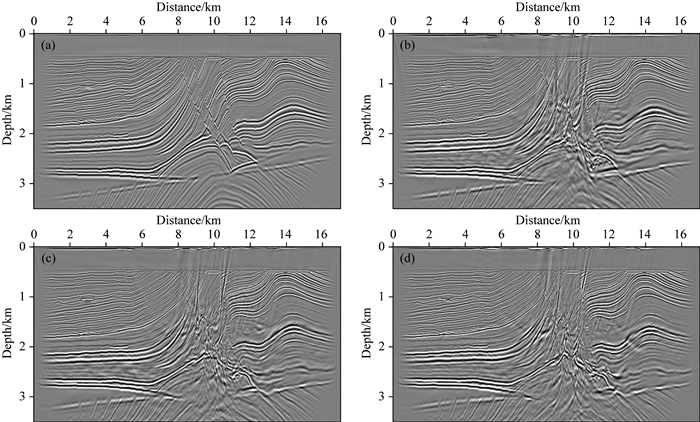
|
图 20 不同倾角值的Lrfd-Pre-PLSRTM成像结果 (a) 80°(真实值); (b) 60°; (c) 30°; (d) 0°. Fig. 20 Images using Lrfd-Pre-PLSRTM method when the theta error equals (a) 80°(true), (b) 60°, (c) 30°, and (d) 0°, respectively |
图 21a与b也给出了Lrfd-Pre-PLSRTM及Lrfd-PLSRTM方法的归一化数据残差收敛曲线,从图中可以证实:在存在倾角误差的情况下,虽然Lrfd-Pre-PLSRTM成像结果不甚理想,但数据残差仍能保持收敛,而Lrfd-PLSRTM成像方法完全发散.这表明本文提出的Lrfd-Pre-PLSRTM能够很好地适应倾角误差剧变的情形,这在实际生产中,倾角参数缺失或者反演不准确时,采用该方法来保持计算稳定是十分有效的.
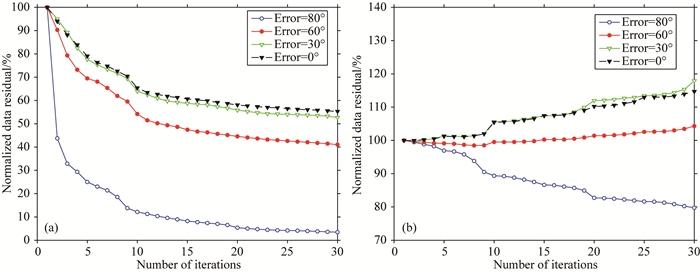
|
图 21 存在倾角误差时的归一化数据残差收敛曲线 (a) Lrfd-Pre-PLSRTM; (b) Lrfd-PLSRTM. Fig. 21 Normalized convergence curves of data residuals when error of dip angle exists |
在验证算法正确性及适应性的基础上,将本文方法应用于某探区实际资料试处理中,该探区成像区域的横向范围约0~29 km,纵向深度10.25 km,纵、横向网格间距分别为Δx=12.5 m、Δz=10 m,因此网格点数为2901×821,该数据炮检点坐标分布极不均匀,且炮点密度低(共157炮),覆盖次数严重不足.此外,炮点与检波点并不严格分布在同一条二维测线上,而是存在-0.5~0.5 km的横向距离误差.
图 22a与b分别为各向异性介质最小二乘逆时偏移成像迭代1次和5次的结果,观察可见:①采用各向异性成像之后,地下地质构造基本展现出来,断层构造较为清晰;②通过各向异性最小二乘逆时偏移迭代5次之后,深部能量得到补偿,但成像噪声也被明显放大,总体而言,成像剖面更加清晰,浅层同相轴更加连续,分辨率更高;③但是,由于从三维采集资料中抽取的二维测线存在炮检点坐标分布不均,覆盖次数少等缺陷,成像效果不甚显著.
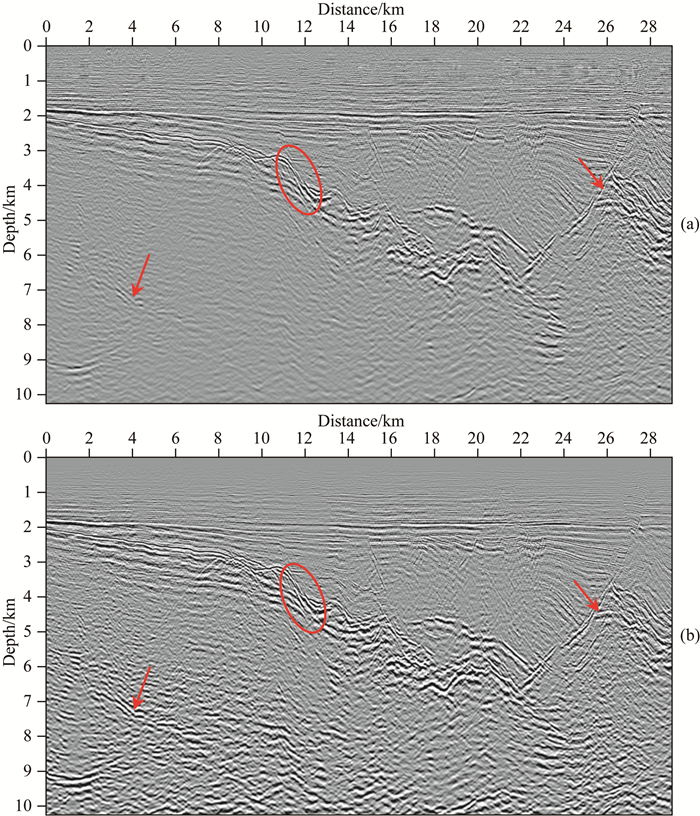
|
图 22 实际资料反演成像结果 (a)各向异性纯qP波LSRTM迭代1次; (b)各向异性纯qP波LSRTM迭代5次. Fig. 22 Inversion images of field data (a) Pure-qP-wave LSRTM with one iteration; (b) Same as (a) but five iterations. |
本文借助Low-rank有限差分法在各向异性纯qP波正演模拟中的优势,在最小二乘反演框架下,首次提出并实现了各向异性介质纯qP波最小二乘逆时偏移,该方案消除了各向异性介质中伪横波噪声对反演成像的影响,并在保证计算稳定的情况下,将其拓展到各向异性TTI介质中;进一步,为了提升反演成像效率,同时改善反演成像方法对模型参数误差的依赖性及对地震数据噪声的适应性,通过引入叠前平面波优化策略,发展了TTI介质纯qP波叠前平面波最小二乘逆时偏移优化方法;最后通过Salt模型及MarII模型成像测试,得出以下认识:
(1) 本文推导的Low-rank有限差分法纯qP波线性化正演算子,能够彻底消除伪横波干扰在反演成像中的影响,且较为精确地计算纯qP波散射波场并扩展到各向异性TTI介质,而将纯qP波偏移算子作用于数据残差可以构建出较为准确的误差泛函梯度方向矢量;
(2) 本文提出的各向异性介质Low-rank有限差分法纯qP波LSRTM的成像质量与拟声波LSRTM具有相似性,都能很好地解决各向异性走时畸变带来的成像误差,但其优势在于波场延拓效率更高、无模型参数限制及伪横波干扰;
(3) 从模型参数误差敏感性试验得知,各向异性介质LSRTM成像方法对速度模型误差与倾角模型误差最为敏感、对Epsilon模型误差敏感性较大、而对Delta模型误差不敏感,因此多参数反演中,在不考虑多参数相互干扰的情况下,Delta参数反演最为困难;
(4) 优化之后的Low-rank有限差分法纯qP波叠前平面波LSRTM,在计算效率方面,通过压缩炮域地震记录,极大地减少了I/O成本,提高了计算效率.此外,通过采用叠前平面波编程方式,与常规的平面波LSRTM相比,该方法对地震数据噪声具有更好的适应性,也在很大程度上,缓和了方法对速度及各向异性模型参数误差的依赖性.
综上所述,本文研发的Low-rank有限差分法纯qP波LSRTM及叠前平面波LSRTM,能够实现对复杂各向异性区域(包括存在模型参数限制η < 0的区域)的准确成像,同时在各向异性参数缺失或者参数反演不大准确,以及地震数据存在严重随机干扰的情况下,通过选取本文迭代反演算法能够获得相对更加合理的成像结果,数据残差能够更好地保持稳定收敛,而不至于发散.此外,文中选用Cerjan边界条件来衰减人工边界反射、采用雷克子波进行反演迭代以及基于l2模来构建目标泛函等处理方式都有待于进一步改善.在今后的研究中,构建基于Low-rank复矩阵分解的PML(Perfectly Matched Layer)边界条件、不依赖于子波的反演方式、互相关目标泛函等是下一步的研究重点.
附录A 伪横波产生的本质原因伪横波干扰是一种由于采用了两次平方运算与声学近似而引入的数值假象,在实际采集中是不存在的.为了阐明伪横波干扰产生的本质原因进而消除其对成像造成的影响,下面从推导拟声波方程的核心步骤来进行说明.qP波与qSV波的频散关系分别如公式(A1)与(A2)所示:
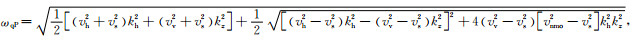
|
(A1) |
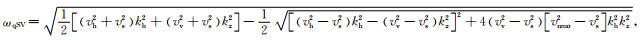
|
(A2) |
若直接模拟公式(A1)所描述的走时特征,并不会产生伪横波干扰,直接模拟公式(A2)所包含的走时关系,也不会出现qP波成分.然而,在实际推导拟声波方程的过程中,为了简化波动方程的形式,避免出现拟微分算子,需对上述频散方程进行两次平方运算用以消除频散公式所包含的根式项,对qP波频散关系式(A1)两边取平方得:
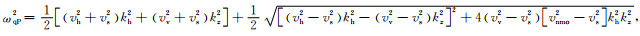
|
(A3) |
对(A3)式移项,并重写为:
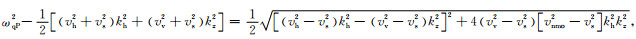
|
(A4) |
再对(A4)式进行平方运算得到:
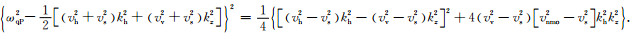
|
(A5) |
最后再通过引入辅助函数、辅助变量以及必要的数学近似(对模型参数有限制),可以得到不同类型的qP波拟声波方程.观察可见,若对qSV波频散关系(A2)进行同样的处理,会得到跟公式(A5)完全一样的形式,因此得出一个结论:对频散关系进行两次平方处理所得到的波动方程产生了增根,且这个解正好符合qSV波的走时关系,导致最终的模拟结果中既包含qP波成分,也蕴含qSV波成分.
如何解释伪横波波前形态表现为菱形呢?事实上,菱形形态只是一种特例,菱形干扰只是在公式(A5)的基础上,进一步应用声学近似,即令vs=0,得到
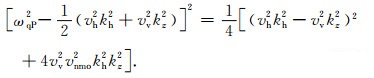
|
(A6) |
当vs≠0时,其波前形态视具体的各向异性参数大小而定.如带非零横波速度项的拟声波方程模拟结果会出现椭圆、菱形、方形等形态的伪横波干扰.而采用Low-rank分解,则始终未对频散关系进行平方运算,也不必推导显式的波动方程,因此不会产生增根,也就避免了伪横波干扰的产生以及对模型参数的限制.
致谢 作者感谢两位匿名审稿专家提出宝贵意见.
Ao R D, Dong L G, Chi B X. 2015. Source-independent envelope-based FWI to build an initial model. Chinese J. Geophys. (in Chinese), 58(6): 1998-2010. DOI:10.6038/cjg20150615 |
Chen K, Sacchi M D. 2017. Elastic least-squares reverse time migration via linearized elastic full-waveform inversion with pseudo-Hessian preconditioning. Geophysics, 82(5): S341-S358. DOI:10.1190/geo2016-0613.1 |
Cheng J B, Kang W, Wang T F. 2013. Description of qP-wave propagation in anisotropic media, Part Ⅰ:Pseudo-pure-mode wave equations. Chinese J. Geophys. (in Chinese), 56(10): 3474-3486. DOI:10.6038/cjg20131022 |
Chu C L, Macy B K, Anno P D. 2013. Pure acoustic wave propagation in transversely isotropic media by the pseudospectral method. Geophysical Prospecting, 61(3): 556-567. DOI:10.1111/j.1365-2478.2012.01077.x |
Clapp M L, Clapp R G, Biondi B L. 2005. Regularized least-squares inversion for 3-D subsalt imaging.//75th Annual International Meeting. SEG, Expanded Abstracts, 1814-1817.
|
Dai W, Schuster J. 2009. Least-squares migration of simultaneous sources data with a deblurring filter.//79th Annual International Meeting. Houston, Texas: SEG, Expanded Abstracts, 2990-2994.
|
Dai W, Wang X, Schuster G T. 2011. Least-squares migration of multisource data with a deblurring filter. Geophysics, 76(5): R135-R146. DOI:10.1190/geo2010-0159.1 |
Dai W, Fowler P, Schuster G T. 2012. Multi-source least-squares reverse time migration. Geophysical Prospecting, 60(4): 681-695. DOI:10.1111/j.1365-2478.2012.01092.x |
Dai W, Schuster G T. 2013. Plane-wave least-squares reverse-time migration. Geophysics, 78(4): S165-S177. DOI:10.1190/geo2012-0377.1 |
Dong S, Cai J, Guo M, et al. 2012. Least-squares reverse time migration: Towards true amplitude imaging and improving the resolution.//82nd Annual International Meeting. Las Vegas, Nevada: SEG, Expanded Abstracts, 1190-1194.
|
Duan Y T, Guitton A, Sava P. 2017. Elastic least-squares reverse time migration. Geophysics, 82(4): S315-S325. DOI:10.1190/geo2016-0564.1 |
Duquet B, Marfurt K J, Dellinger J A. 2000. Kirchhoff modeling, inversion for reflectivity, and subsurface illumination. Geophysics, 65(4): 1195-1209. DOI:10.1190/1.1444812 |
Dutta G, Schuster G T. 2014. Attenuation compensation for least-squares reverse time migration using the viscoacoustic-wave equation. Geophysics, 79(6): S251-S262. DOI:10.1190/geo2013-0414.1 |
Fang G, Fomel S, Du Q Z. 2014. Lowrank finite difference on a staggered grid and its application on reverse time migration. Journal of China University of Petroleum (in Chinese), 38(2): 44-51. |
Feng Z C, Schuster G T. 2017. Elastic least-squares reverse time migration. Geophysics, 82(2): S143-S157. DOI:10.1190/geo2016-0254.1 |
Fomel S, Ying L X, Song X L. 2010. Seismic wave extrapolation using lowrank symbol approximation.//80th Annual International Meeting. Denver, Colorado: SEG, Expanded Abstracts, 3092-3096.
|
Gu B L, Li Z C, Yang P, et al. 2017. Elastic least-squares reverse time migration with hybrid l1/l2 misfit function. Geophysics, 82(3): S271-S291. DOI:10.1190/geo2016-0235.1 |
Guitton A, Kaelin B, Biondi B. 2007. Least-squares attenuation of reverse-time-migration artifacts. Geophysics, 72(1): S19-S23. DOI:10.1190/1.2399367 |
Guo P, McMechan G A. 2018. Compensating Q effects in viscoelastic media by adjoint-based least-squares reverse time migration. Geophysics, 83(2): S151-S172. DOI:10.1190/geo2017-0235.1 |
Hou J, Symes W W. 2015. An approximate inverse to the extended born modeling operator. Geophysics, 80(6): R331-R349. DOI:10.1190/geo2014-0592.1 |
Hou J, Symes W W. 2016. Accelerating extended least-squares migration with weighted conjugate gradient iteration. Geophysics, 81(4): S165-S179. DOI:10.1190/geo2015-0499.1 |
Huang J P, Huang J Q, Li Z C, et al. 2016. Staggered grid pseudo-spectral numerical simulation of first-order quasi P-wave equation for TTI media. Oil Geophysical Prospecting (in Chinese), 51(3): 487-496. |
Huang J Q, Li Z C. 2017. Modeling and reverse time migration of pure quasi-P-waves in complex TI media with a low-rank decomposition. Chinese J. Geophys. (in Chinese), 60(2): 704-721. DOI:10.6038/cjg20170223 |
Huang J Q, Li Z C, Huang J P, et al. 2017. Lebedev grid high-order finite-difference modeling and elastic-wave-mode separation for TTI media. Oil Geophysical Prospecting (in Chinese), 52(5): 915-927. |
Huang J Q, Li Z C, Jiang W. 2018. An efficient forward modeling with the Low-rank finite-difference algorithm for complex TTI media and its application in reverse time migration. Oil Geophysical Prospecting (in Chinese), 53(2): 1198-1209. |
Huang Y S, Schuster G T. 2012. Multisource least-squares migration of marine streamer and land data with frequency-division encoding. Geophysical Prospecting, 60(4): 663-680. DOI:10.1111/j.1365-2478.2012.01086.x |
Kaplan S T, Routh P S, Sacchi M D. 2010. Derivation of forward and adjoint operators for least-squares shot-profile split-step migration. Geophysics, 75(6): S225-S235. DOI:10.1190/1.3506146 |
Kuehl H, Sacchi M. 2002. Robust AVP estimation using least-squares wave-equation migration.//72nd Annual International Meeting. SEG, Expanded Abstracts, 281-284.
|
Li Q Y, Huang J P, Li Z C, et al. 2016. Mean-residual normalized cross-correlation least-squares reverse time migration and its application. Chinese J. Geophys. (in Chinese), 59(8): 3006-3015. DOI:10.6038/cjg20160823 |
Li Q Y, Huang J P, Li Z C. 2017. Source-independent least-squares reverse time migration using student's t distribution. Chinese J. Geophys. (in Chinese), 60(12): 4790-4800. DOI:10.6038/cjg20171220 |
Li Z C, Guo Z B, Tian K. 2014. Least-squares reverse time migration in visco-acoustic medium. Chinese J. Geophys. (in Chinese), 57(1): 214-228. DOI:10.6038/cjg20140118 |
Li Z C, Huang J Q, Huang J P, et al. 2017. Fast least-squares reverse time migration based on plane-wave encoding for VTI media. Chinese J. Geophys. (in Chinese), 60(1): 240-257. DOI:10.6038/cjg20170120 |
Li Z N, Li Z C, Wang P, et al. 2017. Reverse time migration of multiples based on different-order multiple separation. Geophysics, 82(1): S19-S29. DOI:10.1190/geo2015-0710.1 |
Liu X J, Liu Y K. 2016. Least-squares reverse-time migration of surface-related multiples. Chinese J. Geophys. (in Chinese), 59(9): 3354-3365. DOI:10.6038/cjg20160919 |
Liu Y J, Symes W W, Li Z C. 2013. Multisource least-squares extended reverse-time migration with preconditioning guided gradient method.//83rd Annual International Meeting. Houston, Texas: SEG, Expanded Abstracts, 3709-3715.
|
Liu Y K, Liu X J, Zhang Y B. 2018. Migration of seismic multiple reflections. Chinese J. Geophys. (in Chinese), 61(3): 1025-1037. DOI:10.6038/cjg2018L0368 |
Nemeth T, Wu C J, Schuster G T. 1999. Least-squares migration of incomplete reflection data. Geophysics, 64(1): 208-221. DOI:10.1190/1.1444517 |
Nocedal J. 1980. Updating quasi-Newton matrices with limited storage. Mathematics of Computation, 35(151): 773-782. DOI:10.1090/S0025-5718-1980-0572855-7 |
Sheng X, Zhou H B. 2014. Accurate simulations of pure quasi-P-waves in complex anisotropic media. Geophysics, 79(6): T341-T348. DOI:10.1190/geo2014-0242.1 |
Song G J, Huang R, Tian J D, et al. 2016. A new QP-wave equation for 2D VTI media.//86th Annual International Meeting. Dallas, Texas: SEG, Expanded Abstracts, 3977-3981.
|
Song X L, Fomel S, Ying L X, et al. 2011. Lowrank finite-differences for wave extrapolation.//81st Annual International Meeting. SEG, Expanded Abstracts, 3372-3376.
|
Song X L, Alkhalifah T. 2013. Modeling of pseudoacoustic P-waves in orthorhombic media with a low-rank approximation. Geophysics, 78(4): C33-C40. DOI:10.1190/geo2012-0144.1 |
Song X L, Fomel S, Ying L X. 2013. Lowrank finite-differences and lowrank Fourier finite-differences for seismic wave extrapolation in the acoustic approximation. Geophysical Journal International, 193(2): 960-969. DOI:10.1093/gji/ggt017 |
Stanton A, Sacchi M D. 2017. Elastic least-squares one-way wave-equation migration. Geophysics, 82(4): S293-S305. DOI:10.1190/geo2016-0391.1 |
Sun J Z, Fomel S, Zhu T Y, et al. 2016. Q-compensated least-squares reverse time migration using low-rank one-step wave extrapolation. Geophysics, 81(4): S271-S279. DOI:10.1190/geo2015-0520.1 |
Tang Y X. 2009. Target-oriented wave-equation least-squares migration/inversion with phase-encoded Hessian. Geophysics, 74(6): WCA95-WCA107. DOI:10.1190/1.3204768 |
Tarantola A. 1984. Linearized inversion of seismic reflection data. Geophysical Prospecting, 32(6): 998-1015. DOI:10.1111/j.1365-2478.1984.tb00751.x |
Vigh D, Starr E W. 2008. 3D prestack plane-wave, full-waveform inversion. Geophysics, 73(5): VE135-VE144. DOI:10.1190/1.2952623 |
Wong M, Biondi B L, Ronen S. 2010. Joint least-squares inversion of up-and down-going signal for ocean bottom data sets.//80th Annual International Meeting. SEG, Expanded Abstracts, 2752-2756.
|
Wong M, Ronen S, Biondi B L. 2011. Least-squares reverse time migration/inversion for ocean bottom data: A case study.//81st Annual International Meeting. San Antonio, Texas: SEG, Expanded Abstracts, 2369-2373.
|
Wong M, Biondi B L, Ronen S. 2015. Imaging with primaries and free-surface multiples by joint least-squares reverse time migration. Geophysics, 80(6): S223-S235. DOI:10.1190/geo2015-0093.1 |
Zhan G, Pestana R C, Stoffa P L. 2012. Decoupled equations for reverse time migration in tilted transversely isotropic media. Geophysics, 77(2): T37-T45. DOI:10.1190/geo2011-0175.1 |
Zhan G, Pestana R C, Stoffa P L. 2013. An efficient hybrid pseudospectral/finite-difference scheme for solving the TTI pure P-wave equation. Journal of Geophysics and Engineering, 10(2): 025004. DOI:10.1088/1742-2132/10/2/025004 |
敖瑞德, 董良国, 迟本鑫. 2015. 不依赖子波、基于包络的FWI初始模型建立方法研究. 地球物理学报, 58(6): 1998-2010. DOI:10.6038/cjg20150615 |
程玖兵, 康玮, 王腾飞. 2013. 各向异性介质qP波传播描述Ⅰ:伪纯模式波动方程. 地球物理学报, 56(10): 3474-3486. DOI:10.6038/cjg20131022 |
方刚, Fomel S, 杜启振. 2014. 交错网格Lowrank有限差分及其在逆时偏移中的应用. 中国石油大学学报(自然科学版), 38(2): 44-51. DOI:10.3969/j.issn.1673-5005.2014.02.007 |
黄建平, 黄金强, 李振春, 等. 2016. TTI介质一阶qP波方程交错网格伪谱法正演模拟. 石油地球物理勘探, 51(3): 487-496. |
黄金强, 李振春. 2017. 基于Low-rank分解的复杂TI介质纯qP波正演模拟与逆时偏移. 地球物理学报, 60(2): 704-721. DOI:10.6038/cjg20170223 |
黄金强, 李振春, 黄建平, 等. 2017. TTI介质Lebedev网格高阶有限差分正演模拟及波型分离. 石油地球物理勘探, 52(5): 915-927. |
黄金强, 李振春, 江文. 2018. TTI介质Low-rank有限差分法高效正演模拟及逆时偏移. 石油地球物理勘探, 53(6): 1198-1209. |
李庆洋, 黄建平, 李振春, 等. 2016. 去均值归一化互相关最小二乘逆时偏移及其应用. 地球物理学报, 59(8): 3006-3015. DOI:10.6038/cjg20160823 |
李庆洋, 黄建平, 李振春. 2017. 基于Student's t分布的不依赖子波最小二乘逆时偏移. 地球物理学报, 60(12): 4790-4800. DOI:10.6038/cjg20171220 |
李振春, 郭振波, 田坤. 2014. 黏声介质最小平方逆时偏移. 地球物理学报, 57(1): 214-228. DOI:10.6038/cjg20140118 |
李振春, 黄金强, 黄建平, 等. 2017. 基于平面波加速的VTI介质最小二乘逆时偏移. 地球物理学报, 60(1): 240-257. DOI:10.6038/cjg20170120 |
刘学建, 刘伊克. 2016. 表面多次波最小二乘逆时偏移成像. 地球物理学报, 59(9): 3354-3365. DOI:10.6038/cjg20160919 |
刘伊克, 刘学建, 张延保. 2018. 地震多次波成像. 地球物理学报, 61(3): 1025-1037. DOI:10.6038/cjg2018L0368 |
 2019, Vol. 62
2019, Vol. 62


