2. 莱斯大学地球科学学院, 美国休斯顿 77005
2. Department of Earth, Environmental and Planetary Sciences, Rice University, Houston, TX 77005, USA
地震波穿过地球内部介质,在不同传播与偏振方向上表现出的不同传播速度,称为地震各向异性.在地震波的尺度下,地震各向异性包含了随方向变化的晶体总体弹性特征,反映了地球内部的构造变形和应力应变特征.在没有定向的外界过程作用时,组成介质的晶体随机排列,从宏观上看,各向异性特征相互抵消,在地震波上表现为各向同性;当介质受到外在应力作用时会产生形变,晶体定向排列,在地震波上表现为各向异性(Christensen,1984).当地震波穿过均匀各向异性介质时,出现三种体波:准纵波(qP)和两个准横波(qS).准纵波的速度随着传播方向不同发生变化,准横波的速度随着裂隙或者晶格的优势排列不同发生变化,分裂成两个传播速度不同且质点振动方向与传播方向垂直的两个波,这个现象称为“横波分裂”(Mainprice,2007).通常用两个波的到时差δt,以及快波与N方向的夹角θ作为衡量各向异性特征的两个参数,当计算出地震波在地层中传播的距离和有限应变方向后,根据应变和地层形变的关系,可以进一步推测出岩石圈的形变特征和动力学机制(Nur and Simmons, 1969;Crampin,1981;Mainprice and Silver, 1993;Russo and Silver, 1994;Granet et al., 1998;Conrad et al., 2007).
相比地球深部各向异性对地震波的影响,近地表构造活动频繁,局部形变剧烈,产生较强的各向异性,所以远震数据记录到的分裂通常被认为来自岩石圈及其下方的软流圈(Silver,1996).当用远震震相对岩石圈的各向异性进行研究时,通常需要对介质做一些假设,即接收台站下方的各向异性介质是均匀的,并具有水平对称轴和六角对称结构.当地震波近垂直入射到这种各向异性介质时,得到的两各向异性参数,只与介质本身性质和入射角有关,与波的初始极化方向无关.当介质的对称轴与反方位角方向相近时,测量参数偏离实际地层的各向异性,除此之外,快波与对称轴方向一致或垂直.通常将不同方位的远震数据进行叠加,平均的测量结果作为台站下方各向异性特征.叠加不仅提高了数据的信噪比,而且又较好的反映真实地层的各向异性特征(Wolfe and Silver, 1998).
但是实际岩石圈的结构十分复杂,当各向异性地层不满足上述简化的介质时,测量结果与方位角有关(Ansel and Nataf, 1989;Kuo and Forsyth, 1992).当地层倾斜或者不具有六角对称结构时,测量结果随着波的初始极化方向呈现周期变化(Hirn et al., 1998;Plomerová and Babuka,2010).即便实际各向异性地层与简化介质相似,但在大入射角情况下,测量结果随方位角会呈π周期变化(Crampin et al., 1985).当不止一层各向异性介质时,例如介质为两水平层时,测量结果随方位角呈π/2周期变化.通常对具有这种周期变化规律的数据,用两层各向异性模型来进行分析(Rümpker and Silver, 1998;Silver and Long, 2011;Romanowicz and Yuan, 2011).
一般情况下,上地壳主要以脆性形变为主,下地壳主要以塑性形变为主,而岩石圈上地幔的强度比下地壳稍大,但主要的形变仍和下地壳相似,以流变为主(Zhang and Karato, 1995;Meissner et al., 2002;Crampin and Peacock, 2005).一般远震数据记录的岩石圈各向异性,主要反映了上地幔的特征,地壳的贡献较小.即便浅层的形变复杂,也因为层厚较薄,可以忽略分裂对远震数据的影响.但是在地壳较厚的地区,例如经过了漫长造山运动的青藏高原,内部地壳厚度可达70 km,不能忽略其各向异性强度,这时远震数据记录的分裂结果就综合了地壳和上地幔两部分的各向异性特征(Royden et al., 2008).
本文利用理论地震波近垂直入射两层简化各向异性介质,生成两次分裂后的波形数据,测试两种计算双层各向异性方法(剥去法和反演法)的有效性.然后建立不同的两层各向异性理论模型,讨论测量结果是否与模型参数一致;比较经过不同方法校正后的切向能量大小,探讨这些方法在什么条件下能更好地消除分裂的影响;比较它们之间的优缺点.针对青藏高原东南缘台站接收的远震SKS数据,用测试的方法计算地壳和岩石圈地幔的各向异性特征,讨论该地区岩石圈的内部是否存在两层各向异性,从而揭示台站下方垂直形变的特征.
1 方法 1.1 等效一层各向异性
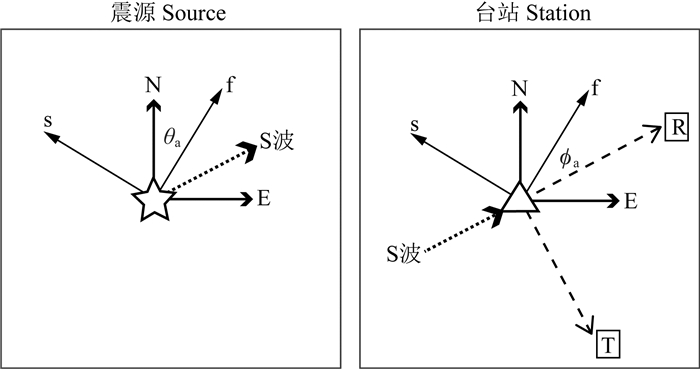
横波穿过各向异性介质产生分裂现象,对其进行测量的结果反映了地震波经过所有分裂后的综合响应(Long and Silver, 2009).理论上可将路径上的所有分裂影响视为一层各向异性介质,横波穿过后发生一次综合分裂(图 1),生成了快波

|
图 1 横波穿过一层各向异性介质时,分裂产生快波和慢波.定义快波与北方向的夹角为θa,与径向方向的夹角为ϕa Fig. 1 A shear wave splits into fast and slow waves once it propagates through an anisotropic medium. The angle between fast and north directions is θa, and the angle between fast and radial directions is ϕa |

|
(1) |
分裂后的位移公式可以写为:
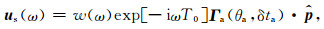
|
(2) |
其中w(ω)表示一个偏振方向为
分裂后的快慢波在时间域的表达式为:

|
(3) |
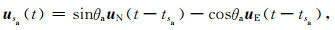
|
(4) |
其中
将快慢波旋转到径向和切向方向后,表达式为:
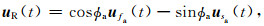
|
(5) |
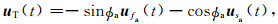
|
(6) |
其中ϕa为快波方向θa与径向方向的夹角.利用最小能量法和最小特征值法(Silver and Chan, 1991),通过网格搜索得到目标函数极小值,对应的(θa, δta)为最终结果.最小能量法和最小特征值法的目标函数分别为切向分量的能量ET(θa, δta)=

当不把路径上的所有各向异性影响视为一次分裂时,例如横波穿过两层各向异性地层,会依次发生两次分裂(Yardley and Crampin, 1991).先经过下层后的快慢波为



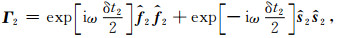
|
(7) |

|
(8) |
经过两层各向异性介质后的位移公式写成一层各向异性模型的形式(2):
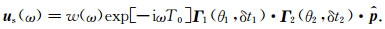
|
(9) |
下层分裂后的快慢波表达式与公式(3)和(4)类似:
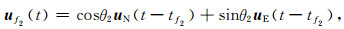
|
(10) |
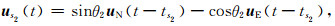
|
(11) |
其中
然后经过上层分裂后的波形表达式为:
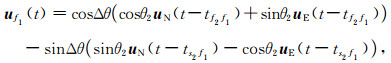
|
(12) |

|
(13) |
其中Δθ=θ1-θ2,且今


如果一个完整波形的周期小于分裂的时差,那么经过两次分裂后,会观测到四个独立分开的波.但由于实际上地层是弱各向异性的,且对于远震数据来说,产生的延迟时间远远小于地震波的周期,所以四个分裂波形最终混叠在一起,在地震记录上显示为一个复杂的波形.仅通过观察波形的特征,无法确定是否经过多次分裂,对比公式(2)和(9)可以得到下面的等式(Savage and Silver, 1993):
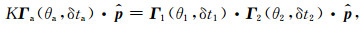
|
(14) |
因为分裂算子是一个正交矩阵,所以引入复标量K,使得当延迟时间为任何值时,都满足|K|=1.可见Γa(θa, δta)是Γ1(θ1, δt1)和Γ2(θ2, δt2)的函数,令αi=2ϕi和

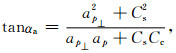
|
(15) |

|
(16) |
其中

|
(17) |

|
(18) |

|
(19) |
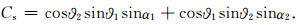
|
(20) |
通过网格搜索(θ1, δt1, θ2, δt2),计算理论(θa, δta),该测量结果是方位角的函数,当将实际的两次分裂视为一次时,测量结果随方位角成π/2周期变化(Silver and Savage, 1994).
1.2.1 剥去法在两次分裂情况中,当去掉上层各向异性影响后,剩余的分裂特征反映了下层的各向异性(Kaneshima and Silver, 1992).所以已知上层各向异性特征的基础上,确定其分裂算子的逆为Γ1-1(θ1, δt1),在公式(9)的基础上进行角度旋转和时间延迟校正,经过下层分裂后的波形表达式为:

|
(21) |
并通过公式(10)和(11)旋转到径向和切向方向,在时间域为:
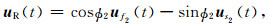
|
(22) |
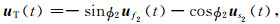
|
(23) |
其中ϕ2为下层快波方向θ2与径向方向的夹角.构建最小切向能量法和最小特征值法的目标函数,当取极小值时的参数(θ2, δt2)为最佳的下层各向异性测量结果.
1.2.2 反演法反演法是在等效单层测量法基础上的一种扩展,即同时对四个分裂参数(θ1, δt1)和(θ2, δt2)进行网格搜索,使目标函数取极小值(Özalaybey and Savage, 1994).将分裂后的波形旋转到径向和切向方向,时间域的表达式为:

|
(24) |

|
(25) |
其中ϕ1为上层快波方向θ1与径向方向的夹角,通过公式(12)和(13)可知,uf1(t)和us1(t)也是(ϕ2, δt2)的函数.当目标函数取极小值时,对应的参数(θ1, δt1, θ2, δt2)为最佳的两层各向异性测量结果.
2 理论测试 2.1 建立理论模型
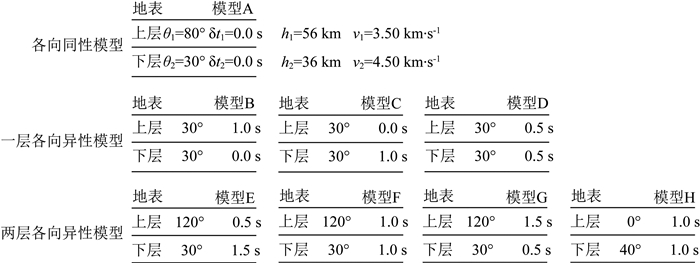
针对各向异性特征随深度变化的介质,可以通过建立两种理论模型测试不同计算方法的有效性.第一种模型的顶、底层分裂特征不一样,层中的各向异性特征缓慢变化;第二种模型存在独立的多层各向异性特征.对满足射线定理的长周期波形(本文观测的SKS震相)来说,第一种模型可以看成具有若干分层的第二种模型,其中整体的延迟时间δta与层数n存在倒数关系:δta≈
|
图 2 一共建立了74844个理论模型,可分成三大类:各向同性、一层各向异性和两层各向异性模型 Fig. 2 A total of 74844 synthetic models, including three classes: isotropic, one-layer and two-layer models, are used in the numerical modeling |
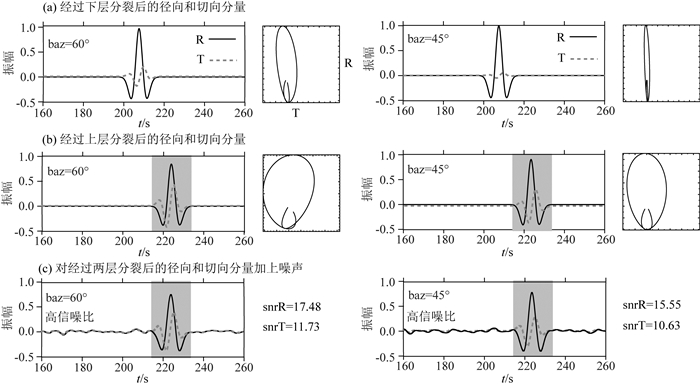
为了模拟远震SKS波在地球内部的传播路径,首先生成一个周期为10 s的雷克子波,时间采样间隔为0.005 s.让其垂直从下往上穿过理论模型,在上层顶部被接收.由于SKS波经过了地核,所以初始极化方向可以近似为方位角方向,于是把讨论初始极化方向对分裂结果的影响,转成研究入射方位角对各向异性的影响.文中设定了不同的入射方位角,范围为0°~175°,以5°为间隔,每个理论模型能记录到36个不同方向入射的三分量数据.以两层各向异性模型H为例,理论雷克子波分别以60°和45°方位角依次通过下层和上层分裂后的波形如图 3a和图 3b.为了更加真实的模拟实际观测数据,在两次分裂后的水平分量上加入随机噪声.本文采用两种噪声水平,经过0.02~0.2 Hz频带范围滤波后,分别生成了低信噪比和高信噪比数据(图 3c).在低信噪比数据中,径向和切向分量的信噪比大约在7~13和2~4之间;在高信噪比数据中,径向和切向分量的信噪比大约在13~20和7~13之间.
|
图 3 (a) 当一个周期为10 s的雷克子波,从方位角分别为60°或45°方向穿过模型H的下层,发生分裂生成径向(实线)和切向(点线)波形,以及两水平分量的质点振动图; (b)产生分裂的S波经过上层再次分裂,以及质点振动图; (c)对理论数据加入随机噪声,生成高信噪比数据 Fig. 3 (a) When a Ricker wavelet with a period of 10 s, coming from 60° or 45° clockwise from north, travels through the lower layer of model H, it splits into radial (solid) and transverse (dotted) components. The particle motion of the arrival is shown in the right; (b) The split S waves are then undergone another splitting as they propagate the upper anisotropic layer. Its particle motion is also evolving; (c) Random noise has been added to the synthetic data to generate a dataset characterizing with high signal-to-noise ratio (SNR) |
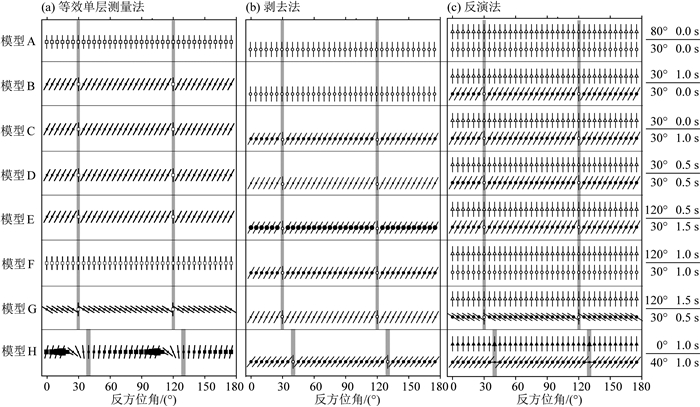
网格搜索的快波方向在0°~179°之间,间距为1°;延迟时间的搜索范围,一层和剥去法在0.00~4.00 s之间,而反演法的上层和下层分别在0.00~1.50 s和0.00~2.50 s之间,间距都为2倍数据采样间隔(0.01 s).先在无噪声情况下对单方位角数据进行测量,由于通过各向同性介质后没有产生分裂或者两次分裂相互抵消,原始切向能量的大小已经在极小值范围内,所以无法通过搜索极小值方法得到与理论模型一致的分裂参数.在等效一层各向异性介质的假设条件下(图 4a),除了当入射方位角靠近下层快波方向和其垂直方向时计算结果不稳定外,各向同性和一层模型的测量结果与模型参数一致,不随方位角变化.两层模型中,只有模型H的分裂参数随方位角呈现π/2周期变化,这与两层各向异性被当成一层进行测量的特征一致(Silver and Savage, 1994).特殊两层模型E、G和F的测量结果,也分别与一层和各向同性模型一样.在两层各向异性的假设下,剥去上层分裂特征后,对剩余波形的测量结果与模型的下层分裂参数一致(图 4b).但是模型A和模型B属于各向同性介质,所以无法确定快波的方向.同时反演4个分裂参数时,一层模型B、C和D的结果一样,都认为上层为各向同性,分裂强度都集中在下层,无法准确测量每一层的分裂特征,因为这种情况下无法区分各向异性在两层中的分布(图 4c).当两层模型的理论分裂参数存在明显差别时(模型H),测量结果与理论模型一致性较好,特殊的两层模型E、G和F同一层各向异性和各向同性模型的测量结果一样.
|
图 4 无噪声时,不同测量方法得到的单个反方位角数据结果.空心表示无分裂特征,两垂直灰色轴表示当反方位角靠近下层快波或慢波方向的范围 (a)等效单层测量法的结果用正方形表示;(b)剥去法计算的下层结果,用圆圈表示;(c)反演法计算的下、上层结果分别用圆圈和三角形表示. Fig. 4 Under noise free condition, the single backazimuth splitting results are calculated by different methods. Open symbols mean no measurable anisotropy. The two vertical grey bars refer to the backazimuths close to the fast or slow directions of the lower layer (a) Squares denote the equivalent one-layer results; (b) Circles are the results of the lower layer calculated by top-layer stripping-off method; (c) Circles and triangles refer to the results of the lower and upper layer calculated by the inversion method. |
综合所有方位角数据,计算结果如表 1所示,综合测量的结果与单方位角相同,与模型一致性好.总的来说,当准确估计上层分裂参数时,剥去法适用于任何模型;而反演法只适用于两层各向异性不一样的模型,对两层分裂特征差别不明显的模型,无法约束各向异性特征在两层中的分布.
|
|
表 1 综合所有方位角数据,三种测量方法对8个理论模型的各向异性计算结果(无噪声) Table 1 Combining the data from all backazimuths, the splitting results are calculated from three different measurements for eight synthetic models (free-noise) |
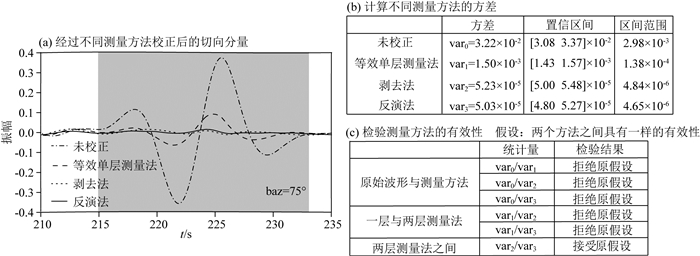
加入随机噪声后对单方位角数据的计算,等效单层测量法和剥去法的结果与无噪声时大致相同.而反演法的结果受噪声影响较大,以75°单方位角高信噪比切向波形为例,比较经过不同各向异性校正后剩余能量的大小,评价不同方法之间的有效性.相比原始切向分量,这三种测量方法都在一定程度上消去了部分因分裂导致的能量(图 5a).通过方差分析,首先估计的方差值都落在了95%的置信区间内(图 5b).然后不管是经过等效单层还是两层测量法的校正,方差都比原始波形的小,且估计值的波动范围更窄.而两层测量法对应的方差比一层法的小,说明当实际存在两层各向异性介质时,在两层假设条件下的测量结果更有效.最后通过假设检验,发现用反演法和已知上层各向异性后的剥去法,对模型的分裂参数进行计算,结果的可靠程度一样.
|
图 5 (a) 对高信噪比的理论雷克横波,比较校正前(点划线)和利用等效单层测量法(虚线)、剥去法(点线)和反演法(实线)校正后的切向波形; (b)估算校正后的剩余波形方差及其置信区间(置信度为95%); (c)假设检验的结果 Fig. 5 (a) An example showing a comparison of uncorrected transverse recording of a Ricker shear wave with a high SNR (dash-dot line) and the corrected ones using the equivalent one-layer (dashed line), top-layer stripping-off (dotted line) and inversion method (solid line); (b) Estimating the variance of each residual waveform within 95% confident region; (c) Null hypothesis testing results |
综合所有入射方位角数据,剥去法的结果综合已知的上层各向异性,用公式(Savage and Silver, 1993)分别换算成随方位角变化的一对分裂参数(θa, δta),取周期为10 s,由于均匀分布的方位角,所以在不同信噪比水平下,下层分裂参数都与理论模型较一致(图 6a).同样反演法测量的结果用公式换算,当数据的信噪比较高时,分裂参数能较准确的反映模型的两层分裂特征,但是当信噪比较低时,随方位角变化的曲线偏离理论模型分裂特征(图 6b),这说明反演法的抗噪性没有剥去法好(Zhang et al., 2013;张建利等,2017).所以只针对高信噪比数据,三种测量方法的计算结果如表 2所示,剥去法和反演法的结果能较好的反映理论模型的各向异性参数.虽然存在噪声影响,但是若数据的信噪比较高,且方位角覆盖范围广泛,计算的结果能有效的反映实际地层的各向异性特征.

|
图 6 比较所有反方位角数据在高信噪比(实线)和低信噪比(点线)的测量结果 (a)剥去法测量得到的下层和已知的上层各向异性,并用一对分裂参数表示随反方位角的变化趋势; (b)同样反演法测量的岩石圈各向异性结果,换算成一对分裂参数 Fig. 6 A comparison of measurement results with high (solid line) and low (dotted line) SNR data (a) The variation is estimated with the lower layer anisotropy calculated by top-layer stripping-off method and known upper layer anisotropy, re-written as an equivalent pair parameters; (b) The variation is estimated with the lithospheric anisotropy calculated by inversion method. |
|
|
表 2 综合所有方位角数据,三种测量方法对8个理论模型的各向异性计算结果(噪声) Table 2 Combining the data from all backazimuths, the splitting results are calculated from three different measurements for eight synthetic models (noise) |
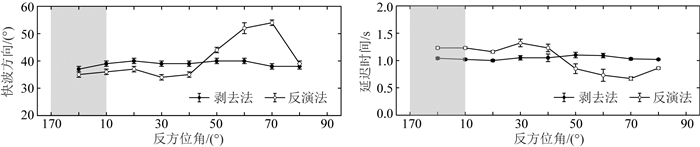
在实际工作中,由于事件和台站的位置,以及噪声等等因素,使数据的方位角分布不可能如理论波形一样广泛.同时为了提高信噪比,增加测量结果的可靠程度,常常会综合多个方位角数据来进行测量.由以上的讨论可知,单方位角数据的反演结果受噪声影响较大,而全方位角数据的测量结果又比较可靠,所以分析不同方位角范围内的反演结果是否稳定可靠尤为重要.以模型H为例,由于等效单层测量法的结果随方位角呈π/2周期变化,所以只需考虑一半的方位角范围.把临近的5个方位角波形看成一组部分方位角数据(170°~10°),利用剥去法和反演法分别计算分裂参数.然后以顺时针10°为间隔进行移动,对下一组部分方位角数据(0°~20°)做同样的计算,这样一共有9组部分方位角数据.图 7显示了剥去法和反演法计算的下层各向异性结果,把每个区间的中间位置当成入射方位角.在不同的方位角范围内,剥去法测量的各向异性结果变化小,与模型H的下层参数40°/1.00 s较一致.而反演法的计算结果变化较大,说明该方法的适应能力十分依赖于方位角的分布(Zhang et al., 2013;张建利等,2017).当方位角的范围在170°~40°内时,剥去法和反演法的计算结果较一致;当方位角的方向在等效单层测量结果趋近于平稳的范围内时(50°~75°),反演的结果与剥去法的偏离较大.综上可知,当数据的入射方位角在两层快波分裂参数之间时,反演结果比较可靠.而等效单层测量法的结果变化剧烈,这主要与切向分量随方位角变化剧烈有关(图 8),有时会显示弱各向异性特征(如图 8中baz=15°).
|
图 7 在窄方位角的分布(20°)情况下,比较剥去法(实心点)和反演法(空心点)对下层的测量结果.以灰色区域为例,把临近方位角(170°、175°、0°、5°和10°)的数据看成第一组,将计算结果显示在中心方位角(0°)上.同样地,第二组数据的方位角整体以10°为间隔顺时针移动(0°、5°、10°、15°和20°).于是从170°~90°一共有9组部分方位角数据 Fig. 7 A comparison of the splitting results of the lower layer using the top-layer stripping-off (solid dots) and inversion (open dots) methods with narrow backazimuthal data (20° in width). Take the grey region for an example, the five data showing adjacent backazimuth (170°, 175°, 0°, 5° and 10°) can be seen as the first group. The results are displayed on the middle backazimuth (0°). Similarly, the second group includes data showing backazimuth (0°, 5°, 10°, 15° and 20°) with 10° clockwise shift from the first one. There are total 9 different groups within 170°~90° backazimuth range |

|
图 8 以径向(实线)和切向(虚线)波形为例 Fig. 8 Examples of the radial (solid line) and transverse (dashed line) recordings |
通过理论测试,发现一层和两层测量法,在不同的条件下都能有效的计算模型分裂参数.特别针对两层各向异性不同的模型,详细讨论了方位角分布对反演结果的影响,现将这些方法应用到实际各向异性地层中.印度板块和欧亚板块碰撞,青藏高原岩石圈内物质向东挤出,由于受到稳定的扬子板块阻挡,一部分物质向东南方向流动.青藏高原东南缘地区的构造运动非常活跃和复杂,地表高程变化大,例如云南中部地区平缓的地势,以及龙门山断裂带区域强烈的高程差.对高原东南缘形变特征的研究,主要的争论点是物质向东逃逸的方式,目前主要分为两大端元,即“下地壳流模型” (Royden et al., 1997)和“块体挤出模型”(Molnar and Tapponnier, 1978).“下地壳流模型”认为地壳增厚的原因是下地壳物质的堆积,造成了地表隆起(Clark and Royden, 2000;Kirby et al., 2002;Clark et al., 2004, 2005);“块体挤出模型”认为这种构造变形的原因是地块之间的相互作用,形成了大型断裂带,且形变主要集中在块体边界附近.哪一个模型更适合用来解释青藏高原东南缘岩石圈内的形变呢?根据前人对红河断裂运动的研究,发现两种模型同时存在的证据(Tapponnier et al., 1990;Schoenbohm et al., 2006),所以目前对该区域岩石圈内的形变特征及形成过程仍存在很大的争议.一些地球物理学家的研究表明,该地区地壳横向厚度变化较大,中下地壳广泛分布低速层,且下地壳相对较软(Bai et al., 2010;Yang et al., 2012);但是也有一些学者认为低速层分布不均匀,可能受大型断裂带分布的影响,局部存在低速层,但无法连通(Wang et al., 2010).所以证明“下地壳流”是否存在,就成为解决岩石圈内部动力学问题的关键.
Sun等(2012)收集了东南缘地区Moho面的转换Ps波,并利用接收函数法对12个台站下方的地壳各向异性进行了约束,发现若干台站的地壳各向异性强度较大(平均为~0.53 s).说明当利用远震SKS波对这些台站下方岩石圈的各向异性进行测量时,若按照通常的假设,忽略地壳对远震结果的影响,认为其结果就代表了上地幔的各向异性,这显然不符合实际地层的特征.于是本文考虑了东南缘岩石圈内,可能存在地壳和上地幔两层各向异性的情况,类比上述的理论模型,将上层视为地壳,下层视为上地幔.对台站不同方位角的波形,先用等效单层测量法和剥去法进行计算,然后对可能存在两层各向异性的台站,用反演法再进行测量.由于剥去法须已知台站下方地壳的各向异性特征,所以在Sun研究结果的基础上,文中只对这12个地壳各向异性约束好的台站进行测量.
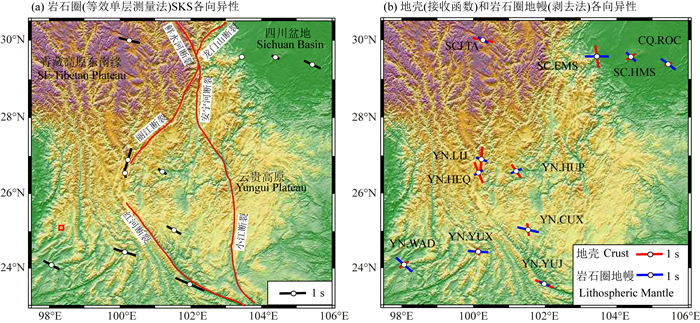
收集的事件从2007年7月到2010年7月之间,震级大于5.8,震中距在85°~120°之间.通过0.05~0.5 Hz的滤波后,选取的波形清晰,具有一个完整周期的SKS震相,没有受到后续SKKS波到时的影响,且径向分量的信噪比大于3. 11个台站叠加平均的等效单层测量法和剥去法的结果如图 9,具体的值见表 3(台站SC.YJI的测量结果不稳定,未显示在图中).等效单层测量结果的平均延迟时间为0.58 s,这与前人计算的平均延时(~0.58 s)一样(Lev et al., 2006).对比地壳各向异性的特征和剥去后的分裂参数,发现区域内的两层各向异性特征并不明显,大部分台站显示为一层分裂结果.四川盆地边缘各向异性较弱,地壳和上地幔各向异性强度变化较大,三个相邻台站的横向间距小于150 km,这说明局部形变强烈.靠近龙门山断裂带(SC.EMS),地表地形复杂,高程横向变化大,地壳各向异性明显,而盆地中部(SC.HMS和CQ.ROC)由于地形简单,没有经历大的地质构造作用,各向异性强度较小.上地幔的各向异性特征较一致,快波方向大致为西北-东南向,说明四川盆地经历了稳定的形变.高原东南缘地壳的各向异性较强(~0.70 s),上地幔延迟时间(~0.34 s)对远震分裂的影响较小,这时观察到的复合波形依次由上地幔分裂的快、慢波产生的地壳分裂快波,以及上地幔分裂的快、慢波产生的地壳分裂慢波组成.位于红河断裂附近的台站YN.YUJ,地壳各向异性较强,快波方向与断裂走向基本一致,说明地壳各向异性主要受断裂的影响.位于云贵高原的台站YN.CUX,接收函数计算的地壳各向异性为南北向,剥去法计算的上地幔分裂为东南向,相差近67°,延迟时间相近,岩石圈的各向异性呈现为两层特征.于是针对这个台站的数据,再用反演法进行两层各向异性的测量.
|
图 9 图中显示青藏高原东南缘区域11个台站的各向异性测量结果,轴的长度表示延迟时间的大小,方向表示快波的极化方向 (a)每个台站叠加平均后的等效单层测量结果,用黑色表示; (b)利用接收函数法测量得到的地壳各向异性,用红色表示;剥去法计算的岩石圈地幔各向异性,用蓝色表示. Fig. 9 Maps showing the estimated splitting parameters of 11 stations located on the southeastern margin of Tibetan plateau. The direction and length of bars refer to the fast direction and delay time, respectively (a) Black bars mean averaged equivalent one-layer anisotropy for each station; (b) Red bars mean crustal anisotropy calculated by receiver function; blue bars mean lithospheric mantle anisotropy calculated by top-layer stripping-off method. |
|
|
表 3 12个台站的各向异性测量结果 Table 3 Splitting measurements at 12 stations |
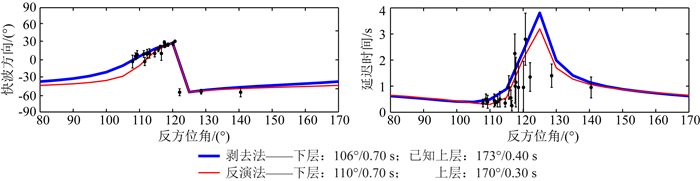
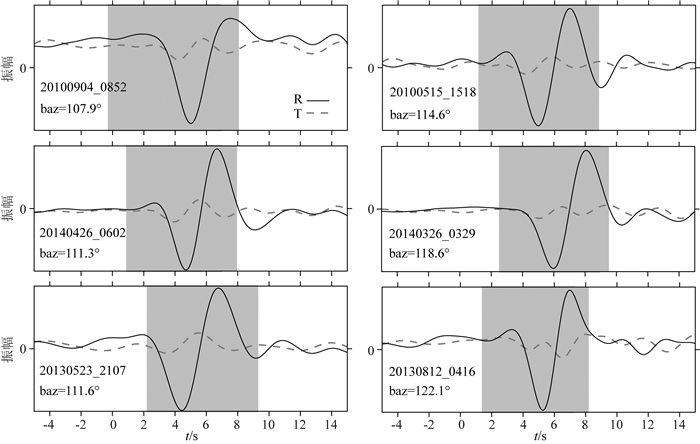
经过上述的数据挑选后,台站YN.CUX一共有31个事件,主要来自于Tonga地区,方位角的分布较窄,且与剥去法测量的上地幔快波方向接近.因为反演法对数据的信噪比和方位角的分布范围较敏感,所以为了增加方位角的分布范围,又添加了从2010年7月到2015年9月的事件,经过同样的数据处理.然后选取径向分量信噪比大于8的数据,以提高反演结果的可靠性.最后一共得到28个新老事件,方位角的分布范围为107°~140°.图 10显示了高信噪比数据的一层和两层各向异性测量结果随方位角变化的趋势,数据的方位角分布在两层快波方向之间,说明这些数据可以用反演法来估计台站下方地壳和地幔的各向异性特征,任意取6个方位角的高信噪比波形如图 11所示.反演的结果认为地壳的各向异性为170°/0.30 s,与接收函数计算的结果(173°/0.40 s)接近;岩石圈地幔的各向异性为110°/0.70 s,这与剥去法得到的结果(106°/0.70 s)接近.同样将两层测量法计算的结果用公式(Savage and Silver, 1993)分别换算成一对分裂参数(θa, δta),剥去和反演法随方位角变化的曲线与单方位角等效单层的测量结果拟合得较好.说明利用剥去法和反演法计算的地壳和岩石圈地幔分裂参数符合实际地层的各向异性特征.
|
图 10 对台站YN.CUX计算的快波方向和延迟时间 比较等效单层(黑色点)和两层测量法的各向异性结果随方位角变化的趋势.蓝色曲线表示综合剥去法计算的岩石圈地幔各向异性和已知的地壳各向异性,换算得到的一对等效单层各向异性参数.红色曲线表示利用反演法计算的岩石圈各向异性,换算得到的一对分裂参数. Fig. 10 Measured fast polarization direction and delay time at station YN.CUX A comparison of the splitting results varying with backazimuth calculated by equivalent one-layer (black dots) and two-layer method. Blue curve means a pair splitting parameters estimated by lithospheric mantle anisotropy, calculated by top-layer stripping-off method, and known crustal anisotropy.Red curve means a pair splitting parameters estimated by lithospheric anisotropy calculated by inversion method. |
|
图 11 以台站YN.CUX观测的6个方位角SKS波形为例,径向和切向分量分别用实线和虚线表示 Fig. 11 Examples of recorded SKS waveforms at station YN.CUX from 6 backazimuth. The radial and transverse components are shown in solid and dashed lines, respectively |
青藏高原东南缘是物质流动的通道,而且该地区的构造运动极其活跃和复杂.从岩石圈的各向异性测量结果可以看出:26°N以北区域,岩石圈的形变特征主要由地壳的各向异性贡献,快波方向主要为南北向;以南区域,岩石圈地幔的各向异性特征增强,快波方向主要呈东南偏东方向,地壳分裂影响可以忽略不计.由北往南,地壳各向异性强度逐渐减小,而岩石圈地幔的分裂强度逐渐增大.这可能与地壳厚度横向变化大有关,在北部大约为50~70 km,而在南部大约为20~40 km;同时岩石圈地幔厚度也从北往南由薄变厚.
通常地壳的各向异性主要来自于上地壳,由于定向排列的裂缝或者变质岩常常分布在大型断裂带附近,并且其各向异性的强度对SKS分裂的影响不可忽略(姚陈等,2016).同时根据前人利用接收函数对26°N以北的地壳,计算得到了较高的VP/VS比值,说明下地壳可能存在铁镁物质.而且定向排列的斜长石可以产生6%的各向异性,所以认为高原东南缘较强的地壳各向异性主要来自中下地壳,且测量的快波方向指示了物质流通方向(Sun et al., 2012).岩石圈上地幔呈现弱各向异性特征,原因除了厚度较薄之外,还可能与垂直形变有关(Yao et al., 2010).由于俯冲角度较小的印度板块在欧亚板块下引起的东南向拐角流,受到冷却且稳定的四川盆地阻挡后,形成向下的垂直形变.此时利用SKS震相观测不到明显的分裂特征.同时一部分原有的岩石圈地幔物质被转移,然后被部分增厚的下地壳物质所取代,使地壳在增厚的过程中,岩石圈地幔厚度逐渐减薄.下地壳可能存在强各向异性的软弱物质,说明地壳内和上地幔的应力应变不能很好进行传递,并且岩石圈内动力学特征的差异也能说明该地区具有“下地壳流模型”的特点.
云南南部没有像四川盆地一样的阻挡,地壳内部形变减小,同时地表高程变化缓慢,厚度逐渐减薄,此时不能完全排除软流圈对地幔各向异性的贡献.上地幔受到了稳定的且近东西向的拉张应力作用,可能与远场的俯冲系统有关,即西边的印度—缅甸俯冲系统的向西板块回撤作用,东边的菲律宾—印度尼西亚俯冲系统的向东板块回撤作用.特别是缅甸俯冲板片在靠近缅甸弧区域以大角度向东俯冲(Li et al., 2008),穿过了410 km间断面,在过渡带内继续向东延伸可至小江断裂附近(Lei and Zhao, 2016).根据前人对26°N以南地区的层析成像反演研究,可知地表至大约200 km深度广泛存在连通的低速异常区,被认为是俯冲板片在地幔楔中引起的拐角流,以及深部板片的变质脱水作用的共同结果.例如腾冲火山的主要形成原因是上涌的地幔过渡带热物质,以及发生于2003年震级为6.2的大姚地震也与印度俯冲板片的变质脱水作用有关(Lei et al., 2009).
5 结论在Silver和Chan(1991)的等效单层测量法基础上,推导了剥去法和反演法的各向异性测量公式,并对它们进行了理论测试.针对不同的模型,剥去和反演法都能较可靠的计算理论模型的分裂参数.对单方位角数据来说,相比剥去法的结果,反演法受噪声影响较大;当方位角数据分布广泛时,这两种方法的计算结果都比较可靠.为了更好的模拟实际观测情况,讨论了不同方位角范围对反演结果的影响.发现反演法只有当入射方位角在两层快波方向之间时,估算的结果与理论模型参数较一致,说明在很大程度上也受方位角分布范围的影响.
将等效单层和两层测量方法对实际SKS波记录的各向异性进行计算,我们的结果对青藏高原东南缘岩石圈内的垂向形变特征进行了更详细的研究.大部分台站的结果呈现一层各向异性特征,但是位于云贵高原的台站YN.CUX,一层分裂参数随方位角的变化趋势显示为两层各向异性特征.然后用反演法计算该台站下方岩石圈的各向异性,结果与剥去法的较一致,支持了该区域内岩石圈的“下地壳流”动力学模型的观点.
总的来说从北往南,岩石圈地幔的各向异性变化不一样.东南缘的形变主要来自增厚的下地壳,受垂直形变的影响,岩石圈地幔厚度减薄,且SKS观测为弱各向异性特征.云南南部逐渐减薄的地壳对SKS分裂的贡献小,强烈的上地幔形变受东西向拉张应力的作用,可能包括了受缅甸俯冲板片影响的软流圈形变特征.
致谢 中国地震局地球物理研究所地震科学探测台阵数据中心为本研究提供地震波形数据.
Ansel V, Nataf H C. 1989. Anisotropy beneath 9 stations of the GEOSCOPE broadband network as deduced from shear-wave splitting. Geophysical Research Letters, 16(5): 409-412. DOI:10.1029/GL016i005p00409 |
Bai D H, Unsworth M J, Meju M A, et al. 2010. Crustal deformation of the eastern Tibetan plateau revealed by magnetotelluric imaging. Nature Geoscience, 3(5): 358-362. DOI:10.1038/ngeo830 |
Christensen N I. 1984. The magnitude, symmetry and origin of upper mantle anisotropy based on fabric analyses of ultramafic tectonites. Geophysical Journal International, 76(1): 89-111. DOI:10.1111/j.1365-246X.1984.tb05025.x |
Clark M K, Royden L H. 2000. Topographic ooze:Building the eastern margin of Tibet by lower crustal flow. Geology, 28(8): 703-706. DOI:10.1130/0091-7613(2000)28<703:TOBTEM>2.0.CO;2 |
Clark M K, Schoenbohm L M, Royden L H, et al. 2004. Surface uplift, tectonics, and erosion of eastern Tibet from large-scale drainage patterns. Tectonics, 23(1): TC1006. DOI:10.1029/2002TC001402 |
Clark M K, House M A, Royden L H, et al. 2005. Late Cenozoic uplift of southeastern Tibet. Geology, 33(6): 525-528. DOI:10.1130/G21265.1 |
Conrad C P, Behn M D, Silver P G. 2007. Global mantle flow and the development of seismic anisotropy:differences between the oceanic and continental upper mantle. Journal of Geophysical Research:Solid Earth, 112(B7): B07317. DOI:10.1029/2006JB004608 |
Crampin S. 1981. A review of wave motion in anisotropic and cracked elastic-media. Wave Motion, 3(4): 343-391. DOI:10.1016/0165-2125(81)90026-3 |
Crampin S, Evans R, Ucer S B. 1985. Analysis of records of local earthquakes:The Turkish Dilatancy Projects (TDP1 and TDP2). Geophysical Journal International, 83: 1-16. DOI:10.1111/j.1365-246X.1985.tb05152.x |
Crampin S, Peacock S. 2005. A review of shear-wave splitting in the compliant crack-critical anisotropic Earth. Wave Motion, 41(1): 59-77. DOI:10.1016/j.wavemoti.2004.05.006 |
Granet M, Glahn A, Achauer U. 1998. Anisotropic measurements in the Rhinegraben area and the French Massif Central:Geodynamic implications. Pure and Applied Geophysics, 151(2-4): 333-364. DOI:10.1007/s000240050117 |
Hirn A, Diaz J, Sapin M, et al. 1998. Variation of shear-wave residuals and splitting parameters from array observations in southern Tibet. Pure and Applied Geophysics, 151(2-4): 407-431. DOI:10.1007/s000240050120 |
Kaneshima S, Silver P G. 1992. A search for source side mantle anisotropy. Geophysical Research Letters, 19(10): 1049-1052. DOI:10.1029/92GL00899 |
Kirby E, Reiners P W, Krol M A, et al. 2002. Late Cenozoic evolution of the eastern margin of the Tibetan Plateau:Inferences from 40Ar/39Ar and (U-Th)/He thermochronology. Tectonics, 21(1): 1001. DOI:10.1029/2000TC001246 |
Kuo B Y, Forsyth D W. 1992. A search for split SKS waveforms in the North Atlantic. Geophysical Journal International, 108(2): 557-574. DOI:10.1111/j.1365-246X.1992.tb04636.x |
Lei J S, Zhao D P, Su Y J. 2009. Insight into the origin of the Tengchong intraplate volcano and seismotectonics in southwest China from local and teleseismic data. Journal of Geophysical Research:Solid Earth, 114(B5): B05302. DOI:10.1029/2008JB005881 |
Lei J S, Zhao D P. 2016. Teleseismic P-wave tomography and mantle dynamics beneath Eastern Tibet. Geochemistry, Geophysics, Geosystems, 17(5): 1861-1884. DOI:10.1002/2016GC006262 |
Lev E, Long M D, Van Der Hilst R D. 2006. Seismic anisotropy in Eastern Tibet from shear wave splitting reveals changes in lithospheric deformation. Earth and Planetary Science Letters, 251(3-4): 293-304. DOI:10.1016/j.epsl.2006.09.018 |
Li C, Van Der Hilst R D, Meltzer A S, et al. 2008. Subduction of the Indian lithosphere beneath the Tibetan Plateau and Burma. Earth and Planetary Science Letters, 274(1-2): 157-168. DOI:10.1016/j.epsl.2008.07.016 |
Long M D, Silver P G. 2009. Shear wave splitting and mantle anisotropy:measurements, interpretations, and new directions. Surveys in Geophysics, 30(4-5): 407-461. DOI:10.1007/s10712-009-9075-1 |
Mainprice D, Silver P G. 1993. Interpretation of SKS-waves using samples from the subcontinental lithosphere. Physics of the Earth and Planetary Interiors, 78(3-4): 257-280. DOI:10.1016/0031-9201(93)90160-B |
Mainprice D. 2007. Seismic anisotropy of the deep earth from a mineral and rock physics perspective.//Schubert G ed. Treatise on Geophysics. 2nd ed. Amsterdam: Elsevier, 2: 487-538.
|
Meissner R, Mooney W D, Artemieva I. 2002. Seismic anisotropy and mantle creep in young orogens. Geophysical Journal International, 149(1): 1-14. DOI:10.1046/j.1365-246X.2002.01628.x |
Molnar P, Tapponnier P. 1978. Active tectonics of Tibet. Journal of Geophysical Research:Solid Earth, 83(B11): 5361-5375. DOI:10.1029/JB083iB11p05361 |
Nur A, Simmons G. 1969. Stress-induced velocity anisotropy in rock:an experimental study. Journal of Geophysical Research, 74(27): 6667-6674. DOI:10.1029/JB074i027p06667 |
Özalaybey S, Savage M K. 1994. Double-layer anisotropy resolved from S phases. Geophysical Journal International, 117(3): 653-664. DOI:10.1111/j.1365-246X.1994.tb02460.x |
Plomerová J, Babuška V. 2010. Long memory of mantle lithosphere fabric-European LAB constrained from seismic anisotropy. Lithos, 120(1-2): 131-143. DOI:10.1016/j.lithos.2010.01.008 |
Rümpker G, Silver P G. 1998. Apparent shear-wave splitting parameters in the presence of vertically varying anisotropy. Geophysical Journal International, 135(3): 790-800. DOI:10.1046/j.1365-246X.1998.00660.x |
Romanowicz B, Yuan H Y. 2011. On the interpretation of SKS splitting measurements in the presence of several layers of anisotropy. Geophysical Journal International, 188(3): 1129-1140. |
Royden L H, Burchfiel B C, King R W, et al. 1997. Surface deformation and lower crustal flow in eastern Tibet. Science, 276(5313): 788-790. DOI:10.1126/science.276.5313.788 |
Royden L H, Burchfiel B C, Van Der Hilst R D. 2008. The geological evolution of the Tibetan Plateau. Science, 321(5892): 1054-1058. DOI:10.1126/science.1155371 |
Russo R M, Silver P G. 1994. Trench-parallel flow beneath the Nazca Plate from seismic anisotropy. Science, 263(5150): 1105-1111. DOI:10.1126/science.263.5150.1105 |
Savage M, Silver P G. 1993. Mantle deformation and tectonics:constraints from seismic anisotropy in the western United States. Physics of the Earth and Planetary Interiors, 78(3-4): 207-227. DOI:10.1016/0031-9201(93)90156-4 |
Schoenbohm L M, Burchfiel B C, Chen L Z, et al. 2006. Miocene to present activity along the Red River fault, China, in the context of continental extrusion, upper-crustal rotation, and lower-crustal flow. GSA Bulletin, 118(5-6): 672-688. DOI:10.1130/B25816.1 |
Silver P G, Chan W W. 1991. Shear wave splitting and subcontinental mantle deformation. Journal of Geophysical Research:Solid Earth, 96(B10): 16429-16454. DOI:10.1029/91JB00899 |
Silver P G, Savage M K. 1994. The interpretation of shear-wave splitting parameters in the presence of two anisotropic layers. Geophysical Journal International, 119(3): 949-963. DOI:10.1111/j.1365-246X.1994.tb04027.x |
Silver P G. 1996. Seismic anisotropy beneath the continents:probing the depths of geology. Annual Review of Earth and Planetary Sciences, 24: 385-432. DOI:10.1146/annurev.earth.24.1.385 |
Silver P G, Long M D. 2011. The non-commutivity of shear wave splitting operators at low frequencies and implications for anisotropy tomography. Geophysical Journal International, 184(3): 1415-1427. DOI:10.1111/j.1365-246X.2010.04927.x |
Sun Y, Niu F L, Liu H F, et al. 2012. Crustal structure and deformation of the SE Tibetan plateau revealed by receiver function data. Earth and Planetary Science Letters, 349-350: 186-197. DOI:10.1016/j.epsl.2012.07.007 |
Tapponnier P, Meyer B, Avouac J P, et al. 1990. Active thrusting and folding in the Qilian Shan, and decoupling between upper crust and mantle in northeastern Tibet. Earth and Planetary Science Letters, 97(3-4): 382-403. DOI:10.1016/0012-821X(90)90053-Z |
Wang C Y, Chan W W, Mooney W D. 2003. Three-dimensional velocity structure of crust and upper mantle in southwestern China and its tectonic implications. Journal of Geophysical Research, 108(B9): 2442. DOI:10.1029/2002JB001973 |
Wang C Y, Lou H, Silver P G, et al. 2010. Crustal structure variation along 30°N in the eastern Tibetan Plateau and its tectonic implication. Earth and Planetary Science Letters, 289(3-4): 367-376. DOI:10.1016/j.epsl.2009.11.026 |
Wolfe C J, Silver P G. 1998. Seismic anisotropy of oceanic upper mantle:shear wave splitting methodologies and observations. Journal of Geophysical Research:Solid Earth, 103(B1): 749-771. DOI:10.1029/97JB02023 |
Yang Y J, Ritzwoller M H, Zheng Y, et al. 2012. A synoptic view of the distribution and connectivity of the mid-crustal low velocity zone beneath Tibet. Journal of Geophysical Research:Solid Earth, 117(B4): B04303. DOI:10.1029/2011JB008810 |
Yao C, Hao C T, Zhang G L. 2016. A study of synthetic seismograms for SKS-wave response to crustal fractured-induce anisotropy. Chinese Journal of Geophysics (in Chinese), 59(7): 2498-2509. DOI:10.6038/cjg20160715 |
Yao H J, Van Der Hilst R D, Montagner J P. 2010. Heterogeneity and anisotropy of the lithosphere of SE Tibet from surface wave array tomography. Journal of Geophysical Research:Solid Earth, 115(B12): B12307. DOI:10.1029/2009JB007142 |
Yardley G S, Crampin S. 1991. Extensive-dilatancy anisotropy:relative information in VSPs and reflection surveys. Geophysical Prospecting, 39(3): 337-355. DOI:10.1111/j.1365-2478.1991.tb00316.x |
Zhang J L, Wang Y, Lu J. 2013. A new algorithm for frequency-dependent shear-wave splitting parameters extraction. Journal of Geophysics and Engineering, 10(5): 055005. DOI:10.1088/1742-2132/10/5/055005 |
Zhang J L, Wang Y, Liu Z B, et al. 2017. Fracture detection with three dual-scanning shear-wave splitting methods. Oil Geophysical Prospecting (in Chinese), 52(1): 105-113. |
Zhang S Q, Karato S. 1995. Lattice preferred orientation of olivine aggregates deformed in simple shear. Nature, 375(6534): 774-777. DOI:10.1038/375774a0 |
姚陈, 郝重涛, 张广利. 2016. SKS波对地壳裂隙各向异性的响应——理论地震图研究. 地球物理学报, 59(7): 2498-2509. DOI:10.6038/cjg20160715 |
张建利, 王赟, 刘志斌, 等. 2017. 三种双扫描横波分裂算法在裂缝探测中的应用研究. 石油地球物理勘探, 52(1): 105-113. |
 2019, Vol. 62
2019, Vol. 62


