2. 中国石油化工股份有限公司石油物探技术研究院, 南京 211103
2. Sinopec Geophysical Research Institute, Nanjing 211103, China
随着油气地震勘探的不断深入,地震数据处理面临的复杂地表和复杂地下介质问题越来越严重,针对复杂探区的叠前深度偏移成像技术已成为工业生产的主流, 然而叠前深度偏移算法高度依赖于深度域浅中深层速度模型的精度(王华忠等, 2012; 崔岩和王彦飞, 2015).高精度的地震波成像是储层描述的重要基础数据, 精确的浅中深层速度模型决定了地震成像的质量.在强调保真成像的情况下, 浅层速度模型的精度有至关重要的作用.近地表非均匀介质层的厚度、速度扰动的幅度以及非均匀体的尺度等都对地震数据成像品质有明显的影响(陈波等, 2016).常规静校正处理通过整道时移来消除道间时差, 没有考虑横向速度变化引起的修正量, 浅表层速度模型误差会引起中深层偏移构造假象(王华忠等, 2012).通过近地表精细速度建模来替代静校正, 进而建立高精度的深度域浅中深层速度模型对于改善复杂探区成像精度具有重要意义.
传统的浅中深层速度建模方法往往把近地表建模和中深层建模分开进行, 并通过插值、融合等主观性较大的方法融合初至走时层析近地表模型和常规中深层速度模型(杨勤勇和方伍宝, 2008; 费建博和杨子川, 2016), 然后通过成像域反射走时层析迭代提高速度模型精度(刘小民等,2017).常规的浅中深层速度建模方法, 没有考虑浅表层速度变化对中深层反射波层析走时的影响, 同时也没考虑反射层析对浅层速度的影响, 从而导致后续的成像域反射走时层析更新速度时会不可控地改变近地表速度.从方法原理上讲, 波动方程走时层析方法就可以自动地将折射波、反射波的到达时进行联合反演(Luo and Schuster, 1991;Zhou et al., 2014), 不过其缺点是难以对不同的波场分别进行灵活处理.在近地表建模中, 通过将P波与S波、面波与折射波、以及初至波与浅层反射波等多种地震波场进行联合层析可以提高近地表速度模型的精度和稳定性(Li et al., 2009; Giustiniani et al., 2010; Orlando and Pelliccioni, 2010; Mendes et al., 2014; 刘江平等, 2015).此外, 折射波与反射波联合走时层析方法已广泛应用于研究壳幔几何构造和速度参数, 可以提供大尺度的速度模型(Zhang et al., 1998), 国内外众多学者对该技术的稳定性、速度与界面等多参数同时反演权系数等问题展开了大量的研究(Hobro et al., 2003; Zelt et al., 1999, 2006; 左建军等, 2011; 俞贵平等, 2017), 黄国娇等将多次反射波走时信息纳入多震相走时加权联合反演成像中, 降低了速度模型重建失真度(黄国娇和白超英, 2010; 白超英等, 2011), 李庆春等采用多尺度渐进联合层析有效地解决了层析正反演网格剖分大小的矛盾, 提高了成像空间分辨率(李庆春和叶佩, 2013).实践表明, 多种特征波场的联合层析能够有效地克服单一波场层析的局限性, 提高浅中深层速度模型的反演精度.然而, 上述联合层析方法都是基于单一的数据域波场走时信息, 而勘探地震中主流的深度域速度建模方法是成像域反射走时层析.
本文建立了包含数据域初至走时层析和成像域反射走时层析的统一目标函数, 推导了数据域初至走时和成像域反射走时联合层析方程, 构建了基于构造特征的正则化算子与模型预条件正则化方法, 给出了基于非线性共轭梯度法的求解方法和联合层析反演实现策略, 实现了勘探地震复杂地表条件下深度域浅中深层速度模型的同时迭代更新, 理论和实际数据试验证明了本文提出方法的有效性.
1 数据域初至波走时与成像域反射波走时联合层析反演方法原理数据域初至波走时与成像域反射波走时联合层析速度反演的目标是:把前者对浅表层速度估计的优势和后者对中深层速度估计的优势相结合, 并通过引入合适的正则化方法, 逐步迭代更新浅中深层速度场, 得到满足高精度地震成像要求的统一速度模型.
1.1 数据域初至波走时层析反演方法基于初至波到达时信息的初至走时层析反演属于数据域的速度估计方法, 在表层速度估计、井间层析、全球地震层析等领域中得到了广泛的应用(Nolet, 2008; Taillandier et al., 2009).初至走时层析反演一般地归于广义Radon变换与反变换,可以通过引入Fredholm第一类积分方程来统一表示(崔岩和王彦飞, 2015; 李勇德等, 2017),
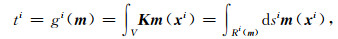
|
(1) |
其中K为Fredholm积分核, 其元素由射线在每个网格内的长度决定, ti是第i根射线走时, m(xi)、dsi分别代表第i根射线上每个网格点对应的慢度值和射线长度, Ri(m)表示第i根射线的传播路径.一般的, 我们希望解一个线性问题,即假设慢度扰动不影响射线的传播路径, 从而可以基于背景慢度计算射线路径和到达时, 进而利用走时残差估计慢度扰动值.为此, 基于背景慢度m0可得到线性化后的走时扰动与慢度扰动之间的线性关系式:
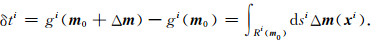
|
(2) |
上式用矩阵的形式表示为
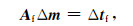
|
(3) |
其中Af通常称为初至走时敏感度核函数矩阵, 由射线在每个网格内的长度决定, Δtf表示初至走时残差, Δm代表慢度扰动量.(3)式建立了走时扰动与慢度扰动之间的线性关系.
根据(3)式可建立起反问题对应的正则化误差泛函:
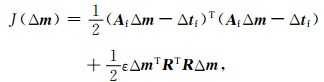
|
(4) |
其中R表示模型正则化算子.一般来说, 数据域初至波层析反演需要对初至数据进行拾取和筛选, 实际工作中在叠前数据上拾取走时的工作量巨大, 且易受叠前数据信噪比低的影响, 尤其是陆上复杂山前带探区, 地形起伏剧烈对复杂走时敏感度核函数的构建有很大影响.虽然射线层析是基于高频近似的假设, 速度建模精度有所限制, 但是由于初至波走时射线层析速度建模计算效率高、存储量小、实现方式灵活, 因此仍是石油工业界中浅地表速度建模的主流技术.尤其是随着高密度地震观测方式的普及, 为初至波射线层析提供了更高密度和更均匀覆盖的数据体, 近地表速度建模的精度不断提高.本文采用基于Fermat原理以及图论的最小走时射线路径追踪方法(Moser, 1991)构建初至波走时层析敏感度核函数.
1.2 成像域反射波走时层析反演方法相对于数据域反射波,成像域反射波同相轴具有更好的连续性和信噪比, 因此反射波走时层析在成像域共成像点道集上进行具有一定优势.目前利用成像域反射波走时层析建立中深层速度模型仍是石油工业界广泛使用的方法技术, 它通过最小化共成像点道集的剩余深度差来更新深度域速度模型.根据道集拉平准则, 共成像点道集拉平时道间剩余深度差为零, 表示偏移速度模型准确(Stork, 1992; Woodward et al., 2008).基于道集拉平准则的成像域反射波走时层析目标泛函可以表示为
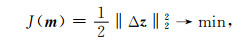
|
(5) |
其中Δz表示所有成像点处不同偏移距或角度道集对应的深度差.当偏移速度模型不准确时,来自地下同一反射点不同偏移距或角度的反射波偏移成像后不能出现在同一深度上, 道集间出现剩余深度差.假设偏移速度与正确的速度偏离不大, 可以认为速度扰动和成像深度扰动之间存在线性关系, 对应地剩余走时差可沿射线追踪的路径对慢度扰动进行积分得到(图 1), 对于一条射线(一个方程)满足如下关系:
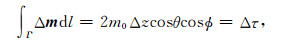
|
(6) |
|
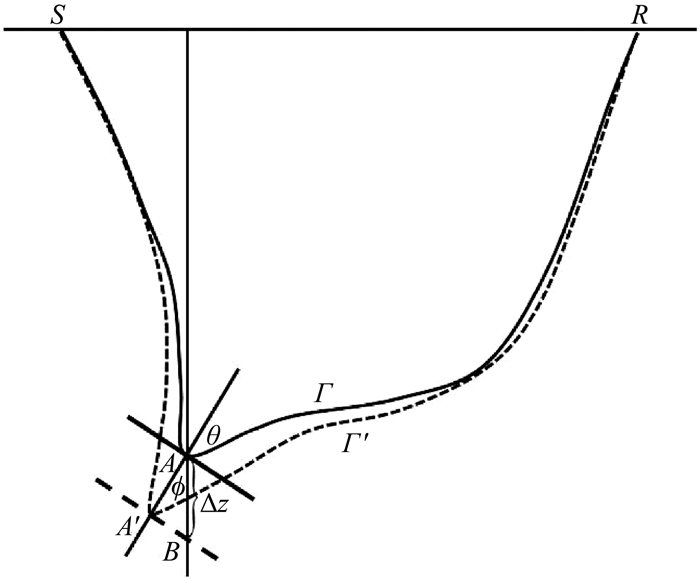
图 1 真实速度和偏移速度中传播的射线路径示意图(张兵等,2012) Fig. 1 Schematic diagram of ray paths propagating in real velocity and migration velocity (Zhang et al., 2012) |
其中θ和ϕ分别是入射角和地层倾角, m0是成像点处的偏移慢度, Δz是共成像点道集对应的成像点与真实位置的深度差.每拾取一个剩余深度差Δz, 就可以得到一个剩余时差Δτ, 再跟对应的射线路径Γ相匹配,即可建立一个层析射线方程(张兵等, 2012; 秦宁等, 2013; 蔡杰雄等, 2017).地层倾角ϕ可在偏移剖面上通过倾角扫描进行自动拾取,剩余深度差Δz需要首先拾取共成像点道集上每道的偏移深度, 然后通过剩余曲率公式估算成像点的真实深度位置,再将其与每道拾取的偏移深度做差来求取.
对偏移剖面上所有拾取的反射点, 按照不同偏移距或角度建立对应的炮点、检波点射线路径, 并与相应的走时扰动联立, 形成规模巨大的反射层析矩阵方程:
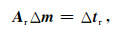
|
(7) |
其中Ar通常称为反射走时敏感度核函数矩阵, 由射线在每个网格内的长度决定; Δtr是由Δτ=2m0Δzcosθcosϕ构成的反射波走时残差向量.根据(7)式可建立反问题对应的成像域反射波层析正则化目标泛函:
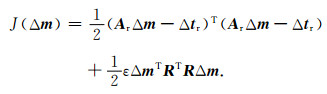
|
(8) |
从地震波传播的物理过程分析, 不论是反射波还是初至波, 都是基于同一介质按照同一波动方程进行传播, 其传播特征基本相同, 具备建立联合层析的物理可行性.因此, 基于式(4)和式(8)可以建立数据域初至走时与成像域反射走时的联合目标泛函, 其带有模型正则化的表达式如下:
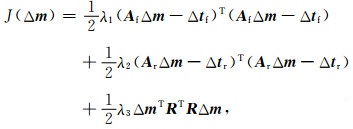
|
(9) |
其中R表示模型正则化算子, 可选为拉普拉斯算子或具有构造特征的预条件算子, 合理构建正则化算子能够有效地提高层析反演的稳定性和收敛性.λ1, λ2, λ3是权重函数, λ1, λ2用来平衡初至走时残差和反射走时残差,其选择原则是让初至走时残差和反射走时残差得到相同程度的收敛,从而保证反演模型的浅中深层都得到有效更新.为了便于分析一般选λ2=1, λ1取值1.0附近, 当λ1>λ2时, 初至走时对近地表附近速度模型反演贡献更大, 浅层反演结果趋向于初至层析反演结果, λ1<λ2时, 成像域反射走时对近地表附近速度模型反演贡献更大, 浅层反演结果趋向于成像域反射层析反演结果.通过测试我们发现λ1取值0.8至1.2之间时反演相对残差稳定收敛、反演结果较好,本文选择λ1=λ2=1.0.λ3为平滑权重参数,是一正值小数,本文选择λ3=0.0008.
复杂地表油气探区需要首先构建一个接近地表的浮动基准面, 后续的速度建模和深度偏移成像都要基于这个基准面, 主要原因是基于当前的地震观测数据无法建立包含精确的近地表小尺度速度异常体的速度模型, 这是当前山前带油气勘探必须遵循的成像处理路线.基于初始速度模型, 开展数据域初至波走时和成像域反射波走时联合层析同时更新浅中深层速度模型, 提高复杂油气探区的建模精度.
1.4 联合层析反演正则化方法地震勘探中观测方式的限制及介质变化特征决定了地震层析成像解的非唯一性很强, 射线层析由于射线的高频近似特征以及不均匀覆盖决定了射线走时层析方程病态性较明显(崔岩和王彦飞, 2015).正则化是使不适定(或非线性较强或凸性差)的地球物理反问题的解更稳定、更有地质意义的一类方法, 可以根据地下构造特征构建光滑算子对反演模型直接进行正则化约束(Zhou et al., 2009, Zhou, 2013; Zdraveva et al., 2013)或利用预条件思想实现对反演模型的预条件约束(Clapp et al., 2004).基于射线理论的线性化走时层析反演, 一般来说目标泛函可以定义为(Tarantola, 2004)
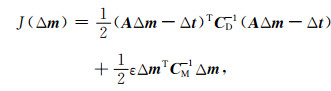
|
(10) |
式中:Δm是模型参数扰动量,Δt是模拟走时与观测走时的残差, CD-1是数据协方差矩阵的逆矩阵,CM-1是模型协方差矩阵的逆矩阵, ε是阻尼因子(引入协方差阵后, 一般地令ε=1).若只考虑模型的正则化, 可令数据协方差矩阵的逆矩阵CD-1为单位阵I, 则式(10)的泛函梯度为
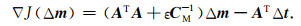
|
(11) |
但是模型协方差矩阵的逆矩阵CM-1不能直接构造, 一般从模型协方差矩阵的特点来构造模型正则化算子.协方差算子是一个光滑算子, 可以用(各向异性)高斯函数来构建,协方差算子的逆算子自然是粗糙算子, 合适地应取为Laplace算子.Laplace算子作用到模型上去除模型中的结构信息,使式(10)中第二项更符合高斯分布的假设, 约束了模型的突变成分(Zhou, 2013), 此即构建模型正则化的基本思想.据此可以得到:
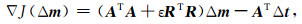
|
(12) |
方程(12)即为层析反演中加入模型正则化后的泛函梯度, 其对应的解为光滑解.事实上方程(12)所表达的模型正则化即为Tikhonov正则化, R为Laplace算子.式(12)对应的法方程为
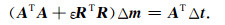
|
(13) |
模型正则化的关键是在方程(12)或(13)中如何引入构造信息.粗糙化算子R的逆是一个光滑算子S, 相对于粗糙化算子, 光滑算子更加容易构造, 且物理意义更为明确.光滑算子S中的地质构造特征体现为沿构造界面方向的平滑范围较大, 垂直构造界面方向的平滑范围较小, 一般地光滑算子S选为各向异性高斯算子(李辉等, 2015).令方程(13)两端左乘矩阵SST得到:
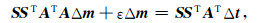
|
(14) |
此时方程式(14)的解即为引入地质构造方向信息后的模型正则化法方程.
在此基础上还可以进一步实施模型预条件方法, 模型预条件可以表示为(Clapp et al., 2004)
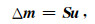
|
(15a) |
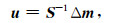
|
(15b) |
此时正则化方程(14)变为
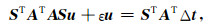
|
(16) |
其对应的层析泛函为
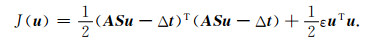
|
(17) |
方程(15)本质上是对要估计的参数Δm进行稀疏特征表达, 光滑矩阵S实现对参数的稀疏特征表达(使得参数Δm是光滑的), 这可以大大降低模型空间的参数自由度.如果从基函数表达的角度来进一步认识光滑矩阵S, 实际上是用不同尺度的基函数对参数向量Δm进行表达, 会出现多个尺度的参数向量Δm, 从而实现多尺度的层析反演.
将(9)式代入(17)式,得到最终的正则化联合层析反演泛函, 具体如下:
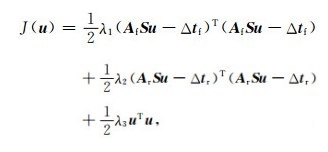
|
(18) |
(18) 式对应的梯度方程为
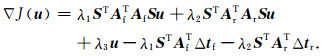
|
(19) |
据此,通过选取合适的正则化算子S, 可以同时实现基于构造的正则化约束与多尺度反演.根据式(19)利用非线性共轭梯度法即可求得中间结果u, 然后根据式(15a)得到从浅层到中深层的深度域慢度更新量, 实现深度域浅中深层速度模型同时进行迭代更新.
1.5 非线性共轭梯度法联合层析反演步骤与策略针对式(19)定义的泛函梯度, 采用FR(Fletcher-Reeves)型非线性共轭梯度法进行求解, 流程步骤归纳如下:
(1) 令i=0,给定初始值u0, 计算目标函数的梯度g0和初始搜索方向p0其中
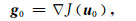
|
(20) |
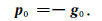
|
(21) |
(2) 计算步长αi, 使得目标函数J(ui+αipi)取局部极小,
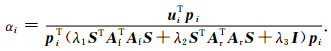
|
(22) |
(3) 利用步长更新中间参数,
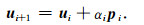
|
(23) |
(4) 将中间结果ui+1代入目标函数计算新的梯度向量gi+1, 并判断是否满足‖gi+1‖<ε, 满足则退出循环,
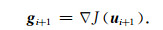
|
(24) |
(5) 更新共轭方向参数βi
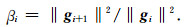
|
(25) |
(6) 更新搜索方向pi+1
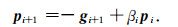
|
(26) |
(7) 重复步骤(2)至(6)直到满足截止条件或最大迭代次数.
(8) 根据公式(15a)计算慢度更新量.
本文提出的数据域初至波走时与成像域反射波走时联合层析反演具体的步骤与策略为:
(1) 拾取初至波到达时;
(2) 利用输入速度模型计算初至波走时射线路径和走时, 构建初至射线敏感度矩阵Af, 计算走时差Δtf;
(3) 利用输入速度模型进行叠前深度偏移, 产生偏移剖面和共成像点道集;
(4) 在偏移剖面上拾取反射点和反射倾角, 在共成像点道集上拾取成像道集深度差, 利用公式(6)构建Δtr;
(5) 在拾取的反射点处按照反射定律进行入射和反射射线追踪,匹配成像道集偏移距或角度,构建反射波射线敏感度矩阵Ar;
(6) 根据剖面构造特征构建正则化算子S, 选取权重函数λ1, λ2, λ3;
(7) 利用上述FR型非线性共轭梯度法进行迭代求解, 计算模型更新量Δm,获得更新后的速度模型;
(8) 根据初至走时残差和偏移成像质量, 判断是否满足终止条件, 如不满足, 重复步骤(2)至(7).
在上述步骤中, 射线敏感度矩阵的高效压缩存储是整个流程能够实现的关键, 本文采用动态数据结构仅存储射线坐标及长度.
一般来说,传统的成像域反射波走时层析(传统方法)是将近地表速度建模和中深层速度建模分开进行, 其步骤主要包括首先将初至层析速度模型与初始速度模型进行融合, 然后按照联合层析步骤与策略中的(3)、(4)、(5)、(6)根据剖面构造特征构建正则化算子S、(7)以及(8)根据偏移成像质量,判断是否满足终止条件, 如不满足重复步骤(3)至(7).从上述传统方法和本文联合层析的步骤对比可以看出, 传统方法不考虑中深层反射波层析对浅层速度变化的影响, 而数据域初至走时与成像域反射走时联合层析方法, 可以将初至走时射线和反射走时射线同时联合求解, 将近地表初至层析对浅层速度模型的更新自动融合到整个深度域速度模型的反演迭代中, 实现浅层速度建模与中深层速度建模的同时联合迭代更新.
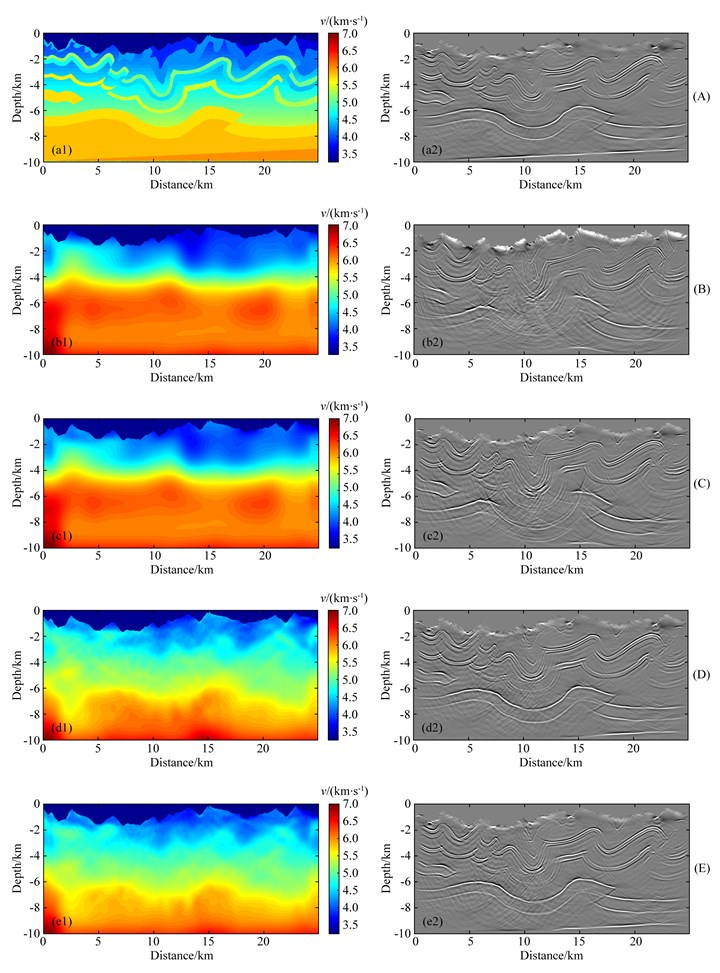
2 数值实验选取加拿大起伏地表模型进行数值测试, 模型观测系统为277炮, 炮间距90 m, 每炮480道, 道间距15 m, 偏移距-3600 m到3600 m.该模型(图 2a1)的横向大小为25 km, 纵向为10 km, 横向网格大小为7.5 m, 纵向网格大小为10 m, 模型地表起伏明显, 起伏落差达到1500 m, 横向速度变化剧烈.对其进行高斯束叠前深度偏移得到偏移剖面(图 2a2)和角度道集(图 3a).
|
图 2 不同的速度模型(a1—e1)及其高斯束叠前深度偏移剖面(a2—e2) (a1)真实速度模型; (b1)联合层析初始速度模型; (c1)初至层析速度模型; (d1)传统反射层析速度模型; (e1)本文联合层析速度模型. Fig. 2 Different veolcity models (a1—e1) and PSDM profile by GBM (a2—e2) (a1) True velocity model; (b1) Initial velocity model for joint tomography; (c1) Velocity model by first-arrival traveltime tomography; (d1)Velocity model by traditional imaging domain reflection tomography; (e1) Velocity model by this paper joint tomography. |
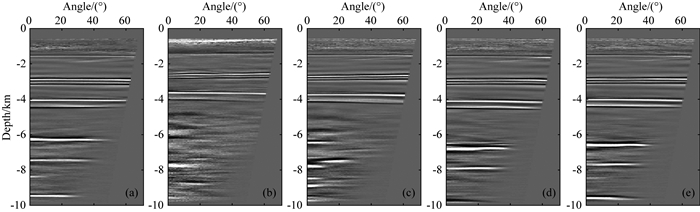
|
图 3 CDP 1821角度道集 (a)真实模型角度道集;(b)初始模型角度道集;(c)初至层析模型角度道集;(d)传统方法层析模型角度道集;(e)本文方法层析模型角度道集. Fig. 3 Angle CIGs at CDP=1821 (a) Angle gather of true velocity model; (b) Angle gather of initial velocity model; (c) Angle gather of first-arrival traveltime tomography velocity model; (d) Angle gather of traditional tomography velocity model; (e) Angle gather of this paper joint tomography velocity model. |
测试首先利用常规速度分析方法建立深度域初始速度模型(图 2b1), 然后分别进行初至波层析、成像域反射波层析迭代(传统方法)建立最终速度模型(图 2d1), 以及初至波与成像域反射波联合层析迭代(本文方法)建立最终速度模型(图 2e1).对初始速度模型(图 2b1)进行高斯束叠前深度偏移得到偏移剖面(图 2b2)及角度道集(图 3b), 可以看出初始模型对应的偏移剖面上的各层位成像深度并不准确, 绕射波也没有完全收敛.对于传统方法建模流程,基于初始速度模型(图 2b1)首先进行初至波层析得到近地表速度模型(图 2c1), 经高斯束叠前深度偏移得到偏移剖面(图 2c2)及角度道集(图 3c), 可以看出初至波层析建模后模型近地表速度得到明显改善, 偏移剖面和角度道集质量得到一定提升, 尤其是浅层成像质量提升明显, 但中深层成像深度并不准确, 绕射波依然没有有效收敛; 然后, 以初至波层析更新速度模型(图 2c1)作为成像域反射层析的输入模型进行迭代更新, 得到传统方法层析速度模型(图 2d1), 经高斯束叠前深度偏移得到剖面(图 2d2)和角度道集(图 3d).对于本文方法建模流程,直接以初始速度模型(图 2b1)作为联合层析方法的输入模型进行迭代更新, 得到本文方法层析速度模型(图 2e1),经高斯束叠前深度偏移得到剖面(图 2e2)和角度道集(图 3e).通过对比传统方法与本文方法的最终速度模型、偏移剖面和角度道集可以看出,相对于初始速度模型, 整体上本文方法与传统方法反演结果都得到明显改善, 偏移剖面和角度道集质量得到明显提升, 不过在近地表处本文方法得到的速度模型与真实速度模型更加接近, 从而导致浅中深层各层的偏移成像深度更加准确, 断层聚焦更好, 浅中深层成像道集整体拉平程度更高, 与标准速度模型角度道集的一致性更好.
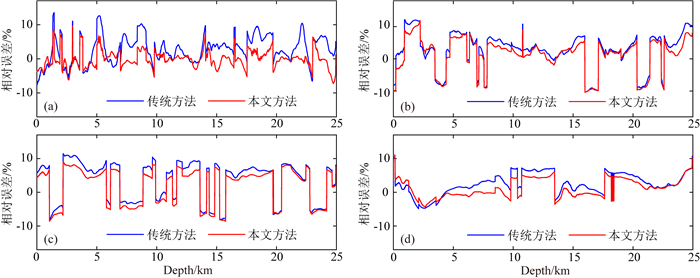
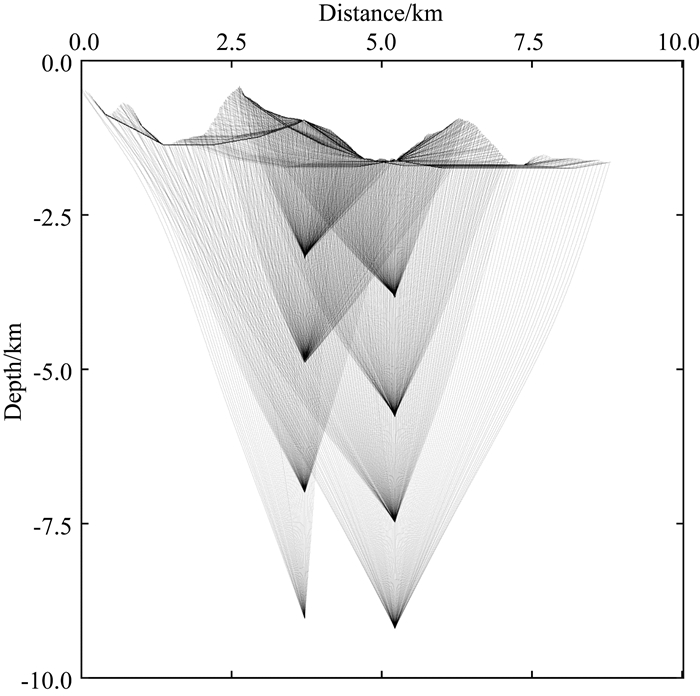
图 4是起伏地表下100 m、1500 m、3500 m、6000 m处传统方法和本文方法最终速度模型相对于真实速度模型的误差对比, 整体来看本文层析方法速度相对误差较传统方法明显偏小, 尤其是近地表 100 m处(图 4a), 传统方法相对速度误差的绝对值平均为3.88%, 本文方法速度相对误差的绝对值平均为1.81%, 速度误差对比验证了传统反射层析对近地表速度的不可控更新, 同时验证了本文方法对浅层速度的精确建模能力.不过, 在中深层速度横向变化比较剧烈的区域(图 4b、图 4c), 无论是传统方法还是本文方法都难于准确反演出速度的剧烈变化, 而只能反演出比较平缓的背景速度变化.通过分析联合层析射线路径示意图(图 5)可以看出, 初至射线主要集中在近地表附近, 近乎平行于近地表分布, 且照明角度大, 而反射射线则在浅层则近乎垂直于地表分布.近地表处初至射线与反射射线路径的大角度交叉, 为速度模型的高精度联合层析迭代更新提供了数据保证.至于模型的中深层部分, 受偏移距和穿透深度的影响, 经过的射线主要是反射射线, 并且相互间夹角比较小, 照明角度也比较小, 从而导致了中深层速度模型的建模精度比较低, 剧烈的横向速度变化难以有效反演.
|
图 4 地表下(a) 100 m、(b) 1500 m、(c) 3500 m、(d) 6000 m深度处的传统方法与本文方法反演速度相对误差对比 Fig. 4 Relative error comparison of traditional tomography velocity with this paper joint tomography velocity at depths of (a) 100 m, (b) 1500 m, (c) 3500 m, (d) 6000 m |
|
图 5 数据域初至走时与成像域反射走时联合层析射线路径示意图 Fig. 5 Schematic diagram of data domain first-arrival traveltime and imaging domain reflection traveltime joint tomography ray path |
模型测试表明, 传统方法层析会对近地表速度进行不可控的更新,而本文方法则能对浅中深层速度模型进行整体迭代更新, 保证在近地表附近处具有更高的建模精度,同时不需要将浅层和中深层速度进行人为的拼接, 不存在速度拼接界面, 展现了联合层析速度建模的优势.因此, 浅中深层速度模型应该通过联合层析同时进行迭代更新, 而不应该分开进行.
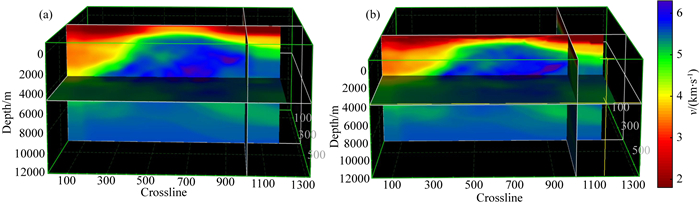
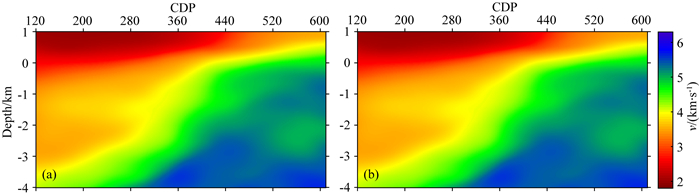
3 实际应用采用某山前带资料进行实际数据测试, 该工区地形起伏海拔范围400~750 m, 数据信噪比低, 地表、地下构造复杂, 是典型的山前带探区, 观测系统为24条检波线接收, 检波线距150 m, 检波点距50 m, 总共18条炮线, 1236炮, 最大偏移距6672 m.受近地表复杂地震地质条件的影响, 山前带高陡构造偏移剖面同相轴聚焦不准, 成像精度不够高.基于前期处理人员结合该工区的地质构造特点建立的深度域初始建模, 本文分别进行了传统方法层析速度建模和联合层析速度建模.图 6是传统方法层析速度模型(图 6a)和本文方法层析速度模型(图 6b)的整体对比显示, 图 7是局部山前带区域传统方法层析速度模型(图 7a)和本文方法层析速度模型(图 7b)的对比显示, 可以看出两者中深层比较接近,本文方法反演的浅层速度变化细节更多, 建模精度进一步提高.
|
图 6 传统方法层析速度模型(a)和本文方法层析速度模型(b) Fig. 6 (a) Velocity model with traditional tomography and (b) velocity model with joint tomography |
|
图 7 传统方法层析速度模型局部(a)和本文方法层析速度局部(b) Fig. 7 (a) Part of velocity model with traditional tomography and (b) part of velocity model with joint tomography |
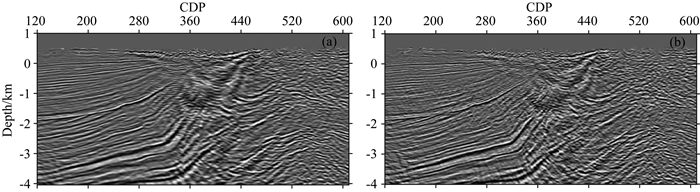
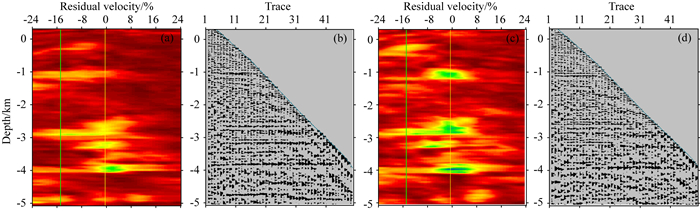
图 8a是传统方法层析速度模型偏移剖面, 图 8b是本文方法层析速度模型偏移剖面, 对比可以看出本文方法得到的偏移剖面在复杂山前带中浅层高陡构造部分具有更好的聚焦, 同相轴分辨率更高.从共成像点道集(CIG)及其剩余曲率谱(图 9)的对比中看出, 本文方法层析速度模型得到的共成像点道集浅层信息更丰富, 同相轴更平, 剩余曲率谱能量团更聚焦, 说明联合层析速度模型更加准确.山前带实际数据测试表明, 本文提出的数据域初至走时与成像域反射走时联合层析浅中深层速度建模技术方法能够更好地适应复杂山前带探区, 提高深度域速度建模质量, 表明本文方法对复杂地表、复杂构造速度模型具有有效性和适用性.
|
图 8 传统方法层析速度模型偏移剖面(a)和本文方法层析速度模型偏移剖面(b) Fig. 8 (a) PSDM profile of traditional tomography velocity model and (b) PSDM profile of joint tomography velocity model |
|
图 9 传统方法层析速度模型剩余曲率谱(a)与共成像点道集(b)和本文方法层析速度模型剩余曲率谱(c)与共成像点道集(d) Fig. 9 Semblance (a) and CIG (b) of traditional tomography velocity model and semblance (c) and CIG (d) of joint tomography velocity model |
盆山过渡区是油气勘探的重点探区, 复杂地表与复杂地下地质结构严重限制了该区域油气勘探的成功率, 建立高精度的浅中深层速度模型是获得该区域高精度成像结果进而提高勘探效益的中心问题.本文提出了一种数据域初至走时和成像域反射走时联合层析正则化反演速度建模方法.该方法结合了数据域初至走时层析对近地表速度的高分辨率特点和成像域反射走时层析对中深层速度有效更新的优势, 实现了复杂深度域速度模型的浅层和中深层同时稳定更新, 克服了反射层析对浅层速度模型的不可控修正.复杂山地理论模型测试表明, 联合层析反演建立的速度模型具有更高的精度, 反演结果更可信, 实际资料测试验证了该方法的适用性和有效性.
此外, 通过测试发现, 浅层及中上层速度更新受初至射线的影响比较大, 因此增加初至波的偏移距范围对于提高浅层及中上层速度模型精度, 进而提高浅中深层整体速度模型精度具有重要的意义.对于提高中深层层析速度建模的横向分辨率, 可以考虑从偏移剖面上提取层位、断裂的构造特征并建立正则化算子, 提高层析反演的精度, 这也是推进联合层析反演实用化的重要内容.
致谢 感谢中国石油化工股份有限公司科技部和石油物探技术研究院对本项研究的大力支持, 感谢石油物探潘宏勋主编对本文提出的宝贵意见.
Bai C Y, Huang G J, Li Z S. 2011. Simultaneous inversion combining multiple-phase travel times within 3D complex layered media. Chinese Journal of Geophysics (in Chinese), 54(1): 182-192. DOI:10.3969/j.issn.0001-5733.2011.01.019 |
Cai J X, Wang H Z, Chen J, et al. 2017. Traveltime tomography in the image domain based on the Gaussian-beam-propagator. Chinese Journal of Geophysics (in Chinese), 60(9): 3539-3554. DOI:10.6038/cjg20170921 |
Chen B, Ning H X, Xie X B. 2016. Investigating the effect of shallow scatterings from small-scale near-surface heterogeneities on seismic imaging:A resolution analysis based method. Chinese Journal of Geophysics (in Chinese), 59(5): 1762-1775. DOI:10.6038/cjg20160520 |
Clapp R G, Biondi B L, Claerbout J F. 2004. Incorporating geologic information into reflection tomography. Geophysics, 69(2): 533-546. DOI:10.1190/1.1707073 |
Cui Y, Wang Y F. 2015. Tikhonov regularization and gradient descent algorithms for tomography using first-arrival seismic traveltimes. Chinese Journal of Geophysics (in Chinese), 58(4): 1367-1377. DOI:10.6038/cjg20150423 |
Fei J B, Yang Z C. 2016. Double interfaces matching integrated velocity model building and its application to Yangxia area at the piedmont zone in the South of Tianshan Mountain. Geophysical Prospecting for Petroleum (in Chinese), 55(4): 533-539. |
Giustiniani M, Tinivella U, Accaino F. 2010. P and S reflection and P refraction:an integration for characterising shallow subsurface. Journal of applied Geophysics, 71(4): 149-156. DOI:10.1016/j.jappgeo.2010.06.004 |
Hobro J W D, Singh S C, Minshull T O. 2003. Three-dimensional tomographic inversion of combined reflection and refraction seismic traveltime data. Geophysical Journal International, 152(1): 79-93. DOI:10.1046/j.1365-246X.2003.01822.x |
Huang G J, Bai C Y. 2010. Simultaneous inversion with multiple traveltimes within 2-D complex layered media. Chinese Journal of Geophysics (in Chinese), 53(12): 2972-2981. DOI:10.3969/j.issn.0001-5733.2010.12.021 |
Li H, Wang H Z, Zhang B. 2015. The study of regularization in tomography. Geophysical Prospecting for Petroleum (in Chinese), 54(5): 569-581. |
Li P M, Yan Z H, Guo M J, et al. 2009.2-D deformable-layer tomostatics with the joint use of first breaks and shallow reflections.//89th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 28: 1335-1339.
|
Li Q C, Ye P. 2013. Joint tomography of first break and reflection traveltime with multi-scale netsize method. Oil Geophysical Prospecting (in Chinese), 48(4): 536-544. |
Li Y D, Dong L G, Liu Y Z. 2017. First-arrival traveltime tomography based on a new preconditioned adjoint-state method. Chinese Journal of Geophysics (in Chinese), 60(10): 3934-3941. DOI:10.6038/cjg20171021 |
Liu J P, Wang Y Y, Liu Z, et al. 2015. Progress and application of near-surface reflection and refraction method. Chinese Journal of Geophysics (in Chinese), 58(9): 3286-3305. DOI:10.6038/cjg20150923 |
Liu X M, Wu D L, Liang S B, et al. 2017. Diving wave tomography velocity inversion using fat ray in prestack depth migration. Geophysical Prospecting for Petroleum (in Chinese), 56(5): 718-726. |
Luo Y, Schuster G T. 1991. Wave-equation traveltime inversion. Geophysics, 56(5): 645-653. DOI:10.1190/1.1443081 |
Mendes M, Mari J L, Hayet M. 2014. Imaging geological structures up to the acquisition surface using a hybrid refraction-reflection seismic method. Oil & Gas Science and Technology-Rev. IFP Energies Nouvelles, 69(2): 351-361. |
Moser T J. 1991. Shortest path calculation of seismic rays. Geophysics, 56(1): 59-67. DOI:10.1190/1.1442958 |
Nolet G. 2008. A Breviary of Seismic Tomography:Imaging the Interior of the Earth and Sun. New York: Cambridge University Press.
|
Orlando L. Pelliccioni G. 2010. P and PS data to reduce the uncertainty in the reconstruction of near-surface alluvial deposits (Case study-central Italy). Journal of Applied Geophysics, 72(1): 57-69. |
Qin N, Li Z C, Zhang K, et al. 2013. Joint tomography inversion of image domain for elastic vector wavefield. Chinese Journal of Geophysics (in Chinese), 56(9): 3109-3117. DOI:10.6038/cjg20130923 |
Stork C. 1992. Reflection tomography in the postmigrated domain. Geophysics, 57(5): 680-692. DOI:10.1190/1.1443282 |
Taillandier C, Noble M, Chauris H, et al. 2009. First-arrival traveltime tomography based on the adjoint-state method. Geophysics, 74(6): 57-66. |
Tarantola A. 2004. Inverse Problem Theory and Methods for Model Parameter Estimation. Philadelphia:Society for Industrial and Applied Mathematics: 1-352. |
Wang H Z, Zhang B, Liu S Y, et al. 2012. Discussion on the imaging processing workflow for foothill seismic data. Geophysical Prospecting for Petroleum (in Chinese), 51(6): 574-583, 597. |
Woodward M J, Nichols D, Zdraveva O, et al. 2008. A decade of tomography. Geophysics, 73(5): VE5-VE11. DOI:10.1190/1.2969907 |
Yang Q Y, Fang W B. 2008. A study on seismic imaging techniques in complex surface and subsurface areas. Oil & Gas Geology (in Chinese), 29(5): 676-682, 689. |
Yu G P, Xu T, Zhang M H, et al. 2017. Nonlinear travel-time inversion for 3-D complex crustal velocity structure. Chinese Journal of Geophysics (in Chinese), 60(4): 1398-1410. DOI:10.6038/cjg20170414 |
Zdraveva O, Hydal S, Woodward M. 2013. Tomography with geological constraints: an alternative solution for resolving of carbonates.//73rd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Zelt C A, Hojka A M, Flueh E E, et al. 1999. 3D simultaneous seismic refraction and reflection tomography of wide-angle data from the central Chilean margin. Geophysical Research Letters, 26(16): 2577-2580. DOI:10.1029/1999GL900545 |
Zelt C A, Ellis R M, Zelt B C. 2006. Three-dimensional structure across the Tintina strike-slip fault, northern Canadian Cordillera, from seismic refraction and reflection tomography. Geophysical Journal International, 167(3): 1292-1308. DOI:10.1111/gji.2006.167.issue-3 |
Zhang B, Xu Z T, Wang H Z, et al. 2012. Common imaging gathers tomography velocity inversion and model building in foothill area. Geophysical Prospecting for Petroleum (in Chinese), 51(6): 590-597. |
Zhang J H, ten Brink U S, Toksoz M N. 1998. Nonlinear refraction and reflection travel time tomography. Journal of Geophysical Research:Solid Earth, 103(B12): 29743-29757. DOI:10.1029/98JB01981 |
Zhou C, Brandsberg D S, Jiao J. 2009. A continuation approach to regularize the reflection tomography with a 3D gaussian filter.//71st EAGE Conference & Exhibition, Amsterdam, The Netherlands, Expanded Abstracts, U031.
|
Zhou C 2013. Incorporating geologic information into reflection tomography with a dip oriented Gaussian filter.//75th EAGE Conference & Exhibition incorporating SPE EUROPEC 2013, London, UK. Expanded Abstracts, Th-04-02.
|
Zhou W, Brossier R, Operto S, et al. 2014. Combining diving and reflected waves for velocity model building by waveform inversion.//84th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Zuo J J, Lin S H, Kong Q F, et al. 2011. Imaging by a joint tomography of direct wave traveltime and reflection wave traveltime in crosswell seismic and its application. Oil Geophysical Prospecting (in Chinese), 46(2): 226-231. |
白超英, 黄国娇, 李忠生. 2011. 三维复杂层状介质中多震相走时联合反演成像. 地球物理学报, 54(1): 182-192. DOI:10.3969/j.issn.0001-5733.2011.01.019 |
蔡杰雄, 王华忠, 陈进, 等. 2017. 基于高斯束传播算子的成像域走时层析成像方法. 地球物理学报, 60(9): 3539-3554. DOI:10.6038/cjg20170921 |
陈波, 宁宏晓, 谢小碧. 2016. 通过地震成像分辨率研究近地表复杂介质散射对成像质量的影响. 地球物理学报, 59(5): 1762-1775. DOI:10.6038/cjg20160520 |
崔岩, 王彦飞. 2015. 基于初至波走时层析成像的Tikhonov正则化与梯度优化算法. 地球物理学报, 58(4): 1367-1377. DOI:10.6038/cjg20150423 |
费建博, 杨子川. 2016. 双界面匹配一体化速度建模技术研究与应用——以天山南山前带阳霞区块为例. 石油物探, 55(4): 533-539. DOI:10.3969/j.issn.1000-1441.2016.04.008 |
黄国娇, 白超英. 2010. 二维复杂层状介质中地震多波走时联合反演成像. 地球物理学报, 53(12): 2972-2981. DOI:10.3969/j.issn.0001-5733.2010.12.021 |
李辉, 王华忠, 张兵. 2015. 层析反演中的正则化方法研究. 石油物探, 54(5): 569-581. DOI:10.3969/j.issn.1000-1441.2015.05.010 |
李庆春, 叶佩. 2013. 初至波与反射波旅行时多尺度渐进联合层析成像. 石油地球物理勘探, 48(4): 536-544. |
李勇德, 董良国, 刘玉柱. 2017. 一种新的预条件伴随状态法初至波走时层析. 地球物理学报, 60(10): 3934-3941. DOI:10.6038/cjg20171021 |
刘江平, 王莹莹, 刘震, 等. 2015. 近地表反射和折射法的进展及应用. 地球物理学报, 58(9): 3286-3305. DOI:10.6038/cjg20150923 |
刘小民, 邬达理, 梁硕博, 等. 2017. 潜水波胖射线走时层析速度反演及其在深度偏移速度建模中的应用. 石油物探, 56(5): 718-726. DOI:10.3969/j.issn.1000-1441.2017.05.012 |
秦宁, 李振春, 张凯, 等. 2013. 弹性矢量波成像域联合层析反演. 地球物理学报, 56(9): 3109-3117. DOI:10.6038/cjg20130923 |
王华忠, 张兵, 刘少勇, 等. 2012. 山前带地震数据成像处理流程探讨. 石油物探, 51(6): 574-583, 597. DOI:10.3969/j.issn.1000-1441.2012.06.005 |
杨勤勇, 方伍宝. 2008. 复杂地表复杂地下地区地震成像技术研究. 石油与天然气地质, 29(5): 676-682, 689. DOI:10.3321/j.issn:0253-9985.2008.05.017 |
俞贵平, 徐涛, 张明辉, 等. 2017. 三维复杂地壳结构非线性走时反演. 地球物理学报, 60(4): 1398-1410. DOI:10.6038/cjg20170414 |
张兵, 徐兆涛, 王华忠, 等. 2012. 山前带地震数据共成像点道集层析速度反演建模方法研究. 石油物探, 51(6): 590-597. DOI:10.3969/j.issn.1000-1441.2012.06.007 |
左建军, 林松辉, 孔庆丰, 等. 2011. 井间地震直达波和反射波联合层析成像及应用. 石油地球物理勘探, 46(2): 226-231. |
 2019, Vol. 62
2019, Vol. 62


