2. 东北大学资源与土木工程学院, 沈阳 110819
2. School of Resources and Civil Engineering, Northeastern University, Shenyang 110819, China
21世纪以来,全球气温上升已是不争的事实,其中受影响最大的就是北极地区.最近几十年来的监测数据表明,北极圈气温上升的速度几乎是同时期北半球平均升温速度的两倍(Bekryaev et al., 2010),格陵兰冰盖消融的速度也逐渐加速.因此,对格陵兰冰盖的研究和保护刻不容缓.
ICESat(Ice, Cloud, and land Elevation Satellite)是世界上首颗绕地球飞行的激光测高卫星,其主要任务是确定两极冰盖质量的季节性和长期变化趋势.凭借激光地面光斑小、数据分辨率高等特点,ICESat测高任务在格陵兰冰盖变化的研究中取得了众多令人瞩目的成果.Slobbe等(2008)通过对ICESat重叠点的分析,得到2003至2007年格陵兰冰盖体积变化速度约为-149 km3·a-1,其中高程2000 m以下区域冰盖表面正以-24 cm·a-1的速度下降;Pritchard等(2009)采用三角内插的方法对ICESat数据进行处理,并分析了两极冰盖变化,结果表明格陵兰岛冰川高程下降速度与冰川流速有关;Sørensen等(2011)系统地研究了利用ICESat数据确定格陵兰冰盖质量变化的方法,得到格陵兰冰盖在2003至2008年间质量变化在-191~-240 Gt/a之间,但不同算法的结果存在一定差异;Schenk和Csathó(2012)则融合了ICESat及机载激光测高数据,并提出了一种称为交叉区域的新算法,得到格陵兰冰盖的体积变化速度为-259 km3·a-1.国内也有不少学者利用ICESat数据对两极冰盖进行过相关研究,例如黄海兰(2011)对格陵兰冰盖的质量损失进行了估计,并与GRACE卫星重力观测结果进行了对比;史红岭等(2011)对南极冰盖的质量变化进行了计算,并分析了各冰川流域物质平衡变化尺度及空间分布特征;马跃等(2015)对ICESat重复点和交叉点数据确定冰盖变化的方法进行了讨论,并估计了格陵兰冰盖2000m以上区域的高程变化;李斐等(2016)在引入坡度改正后,利用ICESat重复轨道数据对南极冰盖的质量变化进行了分析.
在这些研究的基础上,本文针对坡度拟合函数的选择、平差法方程病态等问题,对ICESat重复轨道数据确定冰盖表面高程的算法进行了改进,并对2003年9月至2009年10月间格陵兰冰盖的高程和体积变化进行了估计.结果表明,改进后的算法可以有效地提高格陵兰冰盖边缘地区表面高程变化估值的空间分布率,从而更好地反映冰盖高程和体积变化.
1 数据介绍及粗差编辑 1.1 ICESat/GLAS(R34)数据介绍ICESat卫星由美国国家航天局(NASA)于2003年1月在戈达德航天中心发射升空,轨道倾角为94°,纬度覆盖范围为±86°,飞行高度约600 km,搭载的主要观测仪器为地学激光测高系统GLAS(Geoscience Laser Altimeter System),采样率40 Hz.ICESat/GLAS每年观测2~3次,每次连续观测约33天,轨道重复周期为91天,在6年半的工作时间内共传回18期观测数据.为使用方便,对其按观测顺序和使用的激光器号进行了编号,如表 1所示.其数据由美国冰雪数据中心(NSIDC)处理并分为15种产品进行发布,其中GLA12为Level 2两极冰盖测高数据,采用了专门针对冰盖表面的算法对脉冲波形进行处理,是本文的主要数据源.使用的数据版本为Release 34(R34),是目前ICESat数据的最新版.与以往版本的ICESat数据相比,R34的最大变化是G-C(Gaussian-minus-centroid)误差的改正,更正了过去ICESat数据处理过程中波形拟合参考点错误的问题(Borsa et al., 2014).
|
|
表 1 格陵兰冰盖观测值数量 Table 1 Number of observations on Greenland Ice Sheet |
尽管NSIDC已经对GLA12数据进行了精密而富有针对性的处理,但由于观测条件复杂多变,数据集仍然存在一定数量的粗差观测值,因此,需要通过有效的数据编辑,剔除受系统误差或粗差影响的观测值.数据编辑的准则除了GLA12数据中提供的质量标记以外,主要通过对激光回波波形参数的筛选来实现,通过实验验证(陈国栋,2015),本文所选的波形参数主要包括接收机增益、波形拟合标准差、回波反射率以及波形饱和改正,具体阈值如表 2所示.由于执行最后三个任务期时ICESat的激光器发射能量过低,接收机增益一直保持在较高的水平,导致其回波波形特征与前15个任务期有明显差别,因此,L2d—L2f三个任务期的编辑准则与其他任务期有显著区别.其他编辑准则包括:为避免普通陆地、海洋等无冰覆盖区域数据的干扰,根据格陵兰地区1 km分辨率地表类型格网数据(Bamber et al., 2013)进行筛选,仅保留冰盖及冰川表面的测高数据;为尽量避免地形坡度对计算的影响,剔除偏离ICESat设计轨迹500 m以上的观测值.经过筛选,每个任务期的格陵兰冰盖测高数据数量如表 1所示.其中,L1任务期的轨道为试运行轨道,与其余任务期所采用的正式轨道不重复,无法形成重复轨迹,故本文针对格陵兰冰盖变化的计算只采用L2a至L2f的17个任务期数据,时间跨度为6年.
|
|
表 2 ICESat冰盖数据编辑准则 Table 2 Thresholds for ICESat data filtering |
交叉点和重复轨迹是利用测高数据确定冰盖表面高程变化的两种常用方法,但在格陵兰地区,ICESat轨迹交叉点数量仅不到6000个,空间分辨率较低,特别是在轨迹分布较稀疏的南部地区,临近交叉点的间隔长达数十公里,难以体现冰盖变化细节.因此,本文采用重复轨迹的方法进行冰盖高程变化的估计.
由于卫星轨道具有周期性,因此,测高卫星在地球表面上的轨迹经过一段时间后会出现重复,称为重复轨迹,利用重复轨迹数据之间的高差和时间差,即可对地表高程变化进行估计.但由于卫星运行轨道、星下点指向等的变化,所谓的重复轨迹之间存在一定的偏差,并不能完全重合,因此,当地表存在坡度时,重复轨迹数据之间的高差除了地表随时间的变化外,还包含了由于重复轨迹位置差异所引起的高差.显然,为得到正确的高程变化速度,必须先将上述两种因素引起的高差进行有效的分离.然而,格陵兰地区现有的DEM分辨率和精度不足以对ICESat数据进行直接的坡度改正,因此,本文通过内插和参数估计的方法消除地面坡度的影响,具体做法如下:以ICESat设计轨迹为基准,将相邻的ICESat观测数据在沿轨方向上内插到与设计轨道垂直且通过最近的设计轨迹点的直线上,如图 1所示,其中黑点表示设计轨道的星下点位置,“+”表示卫星轨迹沿轨内插后的位置.对于每一排内插点(+号位置),设内插点的高程为H1,…,Hi,…,Hn,每个Hi可表示为
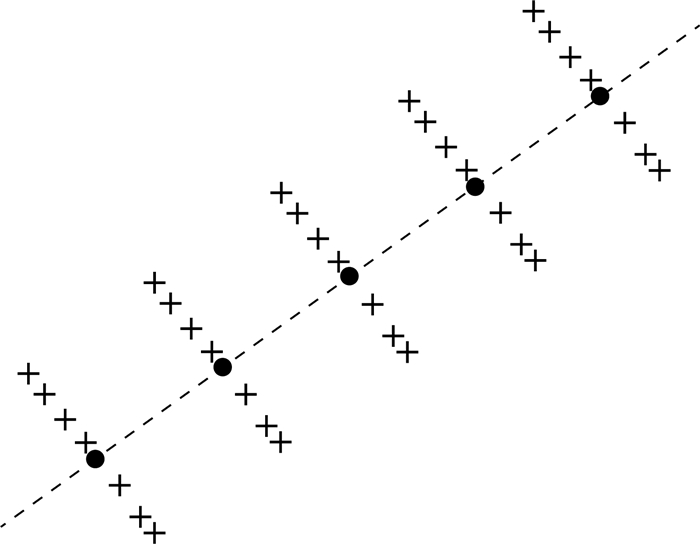
|
图 1 重复轨迹沿轨内插示意图 Fig. 1 Illustration of along-track interpolation |
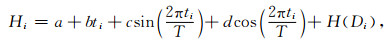
|
(1) |
式中等号右侧第一项a为高程常数项,第二项为高程随时间的线性变化项,b和ti分别表示高程年变化率及时间,三、四项是用三角函数表示的周年变化项,c、d为系数,H(Di)则是用于拟合地面坡度的函数,自变量Di表示内插点至设计轨迹的距离(规定位于设计轨迹东侧的距离为正,西侧为负).
2.2 坡度拟合函数选择根据地表起伏的复杂程度,H(Di)可以选择不同阶数的多项式进行拟合,显然,地面坡度变化越复杂,拟合函数的阶次就应更高.国外研究表明,格陵兰沿海地区高程起伏较大,因此,许多学者使用了较为复杂的曲面模型对格陵兰冰盖地面坡度进行拟合(Schenk and Csathó,2012;Ewert et al., 2012).然而,复杂的拟合模型会增加参数的数量,而激光难以穿透云雾的特点导致ICESat重复轨迹数据时常产生缺失,造成观测值数量不足而无法求解,从而使得局部区域数据分辨率下降,并引起对整个冰盖的高程和体积变化估计发生偏差.本文分别用一阶常数坡度和三次多项式(后文分别用d1和d3表示)对H(Di)进行拟合,两者的差异如图 2所示.两种方法获得的冰盖体积变化约相差19 km3·a-1(d1为-295.33 km3·a-1,d3为-276.30 km3·a-1),差异主要集中在沿海区域.统计结果表明两者在高程2000 m以上的冰盖内陆仅相差1.06 km3·a-1(d1—d3),2000 m以下区域的差别则高达-20.09 km3·a-1.进一步的分析发现,存在明显差异的区域都集中在三阶多项式拟合时由于参数过多而无法求解,造成数据空缺的区域,相比之下,采用一阶常数进行拟合时的结果则具有更好的空间分布.由上述结果可知,高阶的坡度拟合函数并没有对结果带来明显的改善,反而由于空间数据分布的缺失,在格网化时引起误差,得不偿失.因此,本文采用一阶函数对H(Di)进行拟合,即认为图 1所示的同一排内插点之间的坡度变化一致,若以e表示坡度,则(1)式可表示为
|
图 2 不同坡度拟合函数引起的高程变化结果差异(a)及三阶坡度拟合函数造成的数据缺失空间分布(b) Fig. 2 Differences of elevation changes due to different slope fitting function (a) and distribution of data missing when using third order polynomial function for slope fitting (b) |
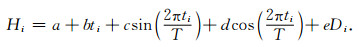
|
(2) |
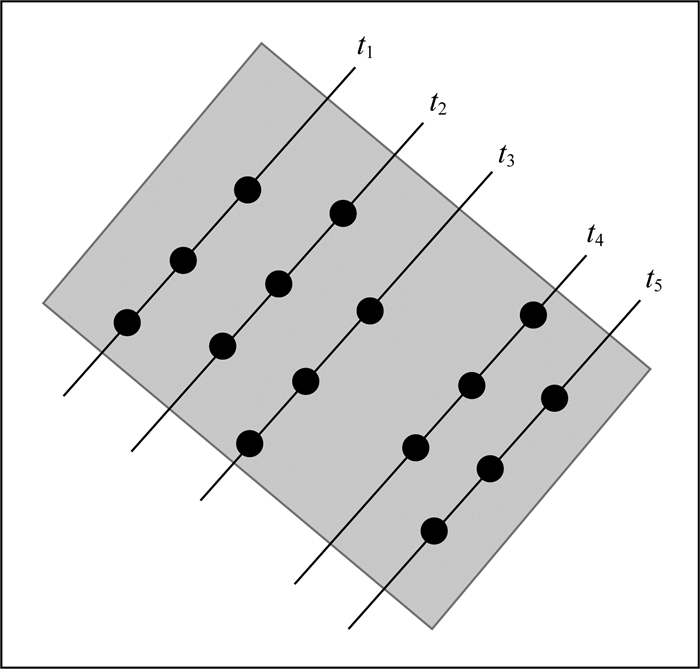
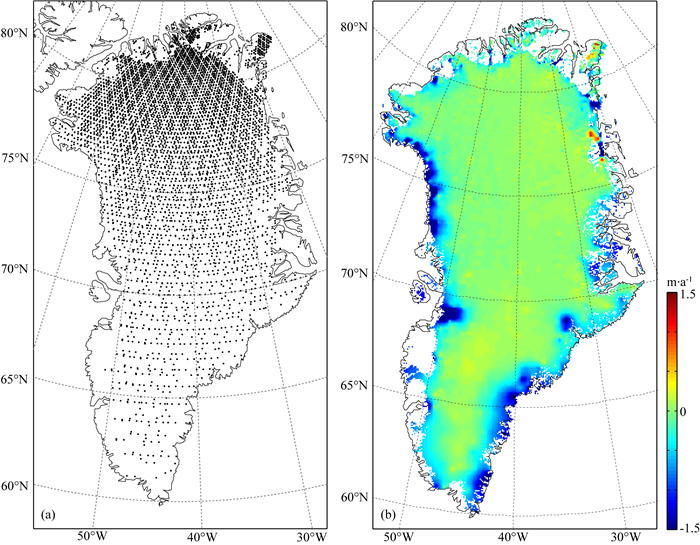
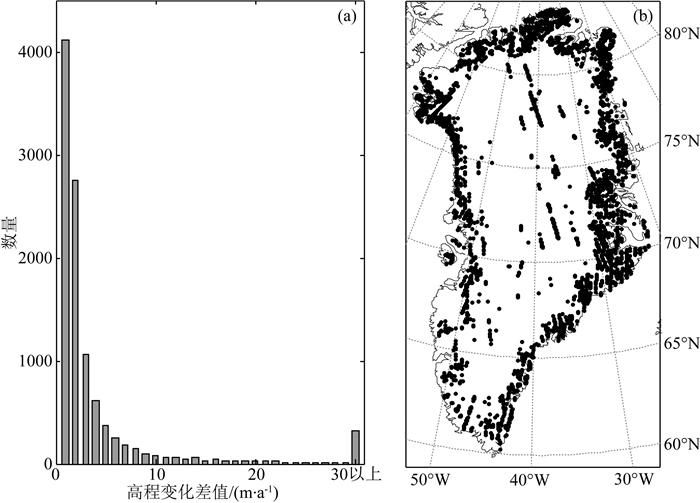
当重复轨迹在空间上的排列顺序恰好与观测时间顺序相同(或逆序)时(如图 3所示),(2)式中的系数b和e有较强的相关性,从而造成方程中高程的时间变化趋势项bti和坡度变化项eDi难以分离,甚至可能引起平差模型法方程病态而无法求解(Schenk and Csathó,2012).为解决这一问题,本文对算法进行了改进,加入虚拟观测值以改善平差模型结构,并通过权值调整尽量减小虚拟观测值对计算的影响.为此,首先利用ICESat交叉点数据获得了格陵兰冰盖高程变化格网(如图 4),并将该格网结果作为虚拟观测值,即
|
图 3 较差的轨道排列顺序示意图(引自Ewert et al., 2012),圆点表示重复轨迹点位置,ti表示观测时间 Fig. 3 Bad time and space distribution of repeat tracks (cited from Ewert et al., 2012). Dots represent footprints of repeat tracks, ti represents observation time |
|
图 4 ICESat交叉点分布(a)及利用交叉点获得的格陵兰冰盖高程变化(b) Fig. 4 Distribution of ICESat crossovers (a) and corresponding elevation changes of Greenland Ice Sheet (b) |
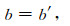
|
(3) |
其中b与(1)式相同,表示冰盖表面某点的高程年变化率,b′表示该处对应的虚拟观测值,即交叉点数据获得的高程变化格网值.联合上式与(2)式组成观测方程组.由于(3)式中参数b和e的系数分别为1和0,与(2)式组成系数阵后一定不相关,因此可以有效地改善法方程的病态性.同时,为了避免交叉点格网过多的影响解算结果,必须对虚拟观测值的权加以限制,通过实验(陈国栋,2015),给出经验定权公式:
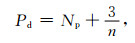
|
(4) |
其中Pd表示虚拟观测值的权(其余观测值的权为1),n为重复轨迹数量,Np是本文定义的用于描述重复轨迹与观测时间之间相关程度的参数:对于观测时间为ti的轨迹,判断所有在ti时刻之后观测的重复轨迹与该轨迹的相对位置,规定在东侧为正、西侧为负,则对所有的n条轨迹共有N=n(n-1)/2次判断,其中N+个为正,N-个为负,则Np为
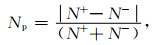
|
(5) |
显然,Np的取值范围为[0, 1],并且Np越接近1表示bti与eDi相关程度越高.考虑到重复轨迹数量最多为17(ICESat正式轨道只有17个重复周期),式(2)求解所需的最少观测量为5个,因此Pd的取值范围为[3/17, 1.6].当重复轨迹观测值数量较多或排列顺序较好时,Pd的取值都较小,因而可以保证在观测条件有利的情况下,虚拟观测值不会过多地影响平差结果.
用V1、V2分别表示加入虚拟观测值前后获得的高程变化,图 5所示为位于71.0°N,41.4°W的一段重复轨迹计算结果.从图中可以看到,V1与Np存在明显的相关性,在V1发生跳变时,排列指数Np的数值都明显偏高,而在加入虚拟观测值后,V2的结果则比较平滑,没有明显的突变.由于该轨迹位于冰盖内陆地区,高程变化量级小且变化稳定(Zwally et al., 2012),不可能出现V1所显示的这种剧烈变化,因此可以判断加入虚拟观测值显著改善了估算结果.而对于较小的Np值,V1、V2的差值则非常小,表明本文提出的经验定权方法也是有效的.
|
图 5 虚拟观测值作用示例 Fig. 5 An example of the effect after the application of virtual observations |
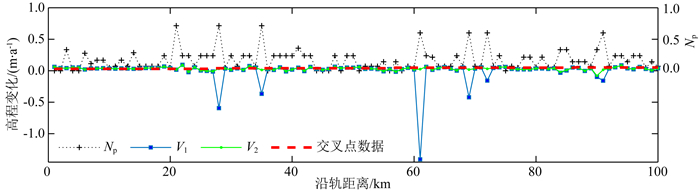
通过上述方法解决法方程病态问题后,可以有效地增加高程变化估值的数量,从而能够更好地反映格陵兰冰盖体积变化的情况.图 6所示为加入虚拟观测前后高程变化估值差异在1 m·a-1以上数据的统计图及位置分布.尽管这些数据只占数据总量的1.2%,但从图 6的结果可以看出,其分布主要集中在冰盖边缘,这些区域由于坡度较大导致ICESat观测值数量较少,而冰盖边缘的冰川流失又是格陵兰冰盖体积变化的重要因素,因此,在加入虚拟观测值后得到改善的这些数据对于提高冰盖边缘数据密度、正确反应冰盖高程和体积变化具有重要意义.
|
图 6 加入虚拟观测值后改正值1 m·a-1以上的数据统计直方图(a)及空间分布(b) Fig. 6 Histogram (a) and distribution (b) of data adjusted over 1 m/a after the application of virtual observations |
实际计算冰盖高程变化时,只在Np>0.2时采用虚拟观测值参与计算,以尽量减少虚拟观测值对最终结果的影响.
3 结果 3.1 ICB改正的探讨由于模型误差、卫星轨道变化、测高仪工作状态等众多已知和未知的因素,卫星测高数据本身可能存在一定的时变误差,ICESat各任务期的数据间也存在这种系统性的差异,称为任务期偏差(Inter-Campaign Bias,ICB)(Siegfried et al., 2011),在对冰盖变化进行研究时必须予以考虑(Hofton et al., 2013;李斐等,2016).本文采用纬度±66°之间Release34的GLA15数据(ICESat海洋观测数据)对ICB进行了分析,首先以3.0 mm·a-1的速率对观测数据中包含的海平面变化进行改正,然后通过交叉点不符值确定各任务期测高值之间的偏差.所得结果与国外相关研究获得的ICB变化进行对比,如图 7所示,其中,Shepherd等(2012)是根据±66°纬度之间ICESat测高数据与海平面模型的差值确定ICB的变化(Shepherd et al., 2012),Ewert等(2012)是对南极沃斯托克湖表面测高数据分析获得的结果(Ewert et al., 2012),Hofton等(2013)则通过对东南极地区数据的分析获得(Hofton et al., 2013).由于现有研究成果使用的均是未加入G-C误差改正的旧版ICESat数据,为增加与本文结果的可比性,对上述国外研究成果均进行了G-C误差变化趋势的改正(Borsa et al., 2014).由图 7可知,Shepherd等(2012)与本文所采用的数据分布范围一致,ICB分析结果也非常接近,而采用的数据分布区域不同时,Ewert等(2012)、Hofton等(2013)与前两组结果都有明显的差异,因此,本文认为,ICB分析结果与数据分布有关,上述几组结果并不能直接用于格陵兰地区的数据改正.另外,根据本文的分析结果拟合的ICB线性变化趋势不到0.1 mm·a-1,表明R34版本数据中,由ICB造成的长期性变化趋势已基本消除,对高程时变计算的影响较小,这与Borsa等(2014)的结论一致.因此,本文没有对ICB进行改正.
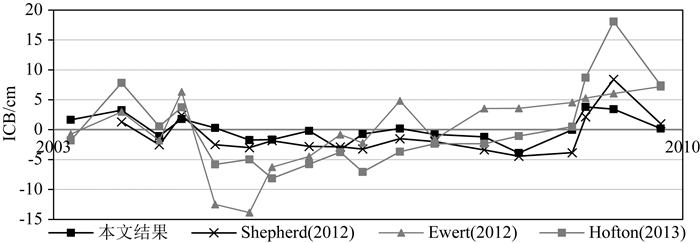
|
图 7 不同研究获得的ICB变化 Fig. 7 ICB variation trends obtained by different researches |
根据作用原理的不同,地壳形变可以分为两类,弹性回弹(Elastic Rebound,ER)和冰后回弹(Postglacial Rebound,PGR)(Spada et al., 2012),两者都不会引起冰盖体积的变化,需要在ICESat获得的冰盖表面高程变化中进行剔除.本文利用ICE-6G冰川均衡模型(Peltier et al., 2015)对PGR进行了改正,并利用Khan等(2010)提供的格陵兰岛弹性回弹模型进行ER改正.加入两项改正后,对格陵兰冰盖体积变化估值的影响合计约-6.04 km3·a-1.
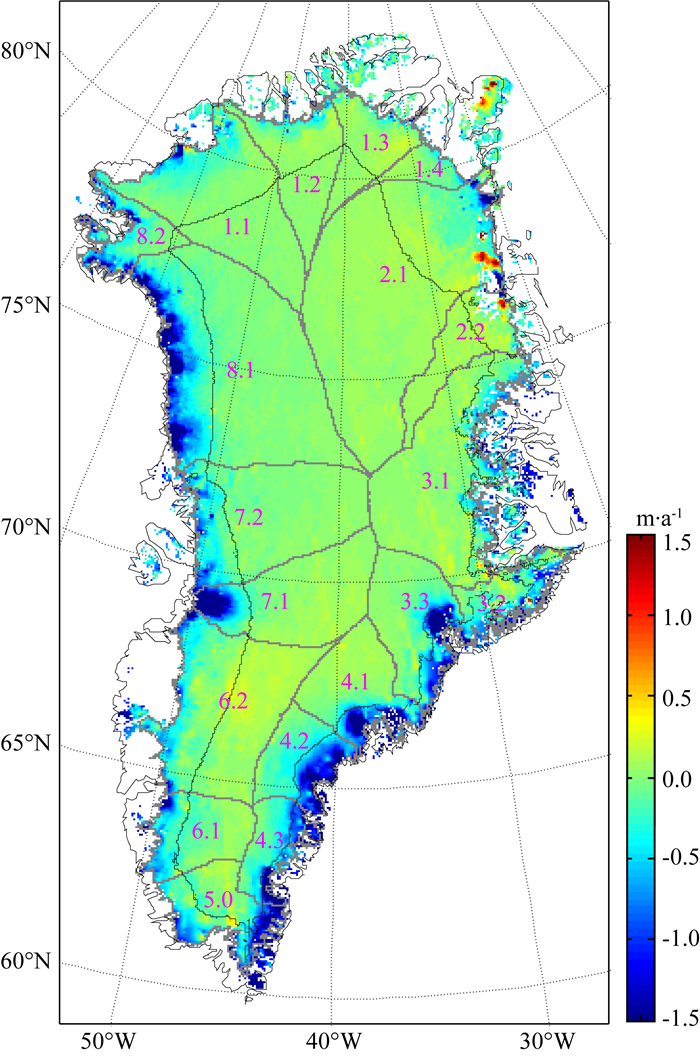
3.3 格陵兰冰盖体积变化利用ICESat重复轨迹数据,采用第3节所述方法计算2003年10月至2009年10月间格陵兰冰盖表面高程变化,并按照5 km×5 km分辨率进行格网化,结果如图 8所示.参考国外相关研究(Sørensen et al., 2011),采用自助抽样法对精度进行估计后,得到整个格陵兰地区冰盖、冰川的平均高程变化约为-16.79±0.84 cm·a-1.将每个格网的高程变化乘以格网面积后得到整个冰盖的体积变化为-301.37±15.16 km3·a-1,其中呈现高程上升趋势的面积约为866×103 km2,占总面积的48.2%,主要集中在海拔较高的冰盖内陆地区;而体积损失则主要发生在冰盖边缘,特别是东北沿海、西南沿海以及雅各布港等冰川密集区域.
|
图 8 格陵兰冰盖高程变化及流域系统划分,黑色虚线表示2000 m高程等高线 Fig. 8 Elevation change and drainage system of Greenland Ice Sheet. Black dashed line represents the 2000-meter elevation contour line |
表 3所示为近年来不同学者利用ICESat数据获得的格陵兰冰盖体积变化与本文结果的对比(为与国外研究统一,表 3中结果均未进行PGR和ER改正),尽管这些研究所采用的ICESat数据版本中尚不包含G-C误差改正,但Ewert等(2012)和Schenk & Csathó(2012)已对结果进行了ICB偏差的改正,可以在很大程度上消除G-C误差的影响(Borsa et al., 2014),而未进行任何改正的Slobbe等(2008)和Sørensen等(2011)的结果则通过Borsa等(2014)提供的G-C误差变化趋势进行相应改正,以增强与本文结果的可比性.
|
|
表 3 不同研究获得的格陵兰冰盖体积变化 Table 3 Estimates of volume change of Greenland Ice Sheet from different researches |
表 3的结果表明,在以ICESat单一数据源进行的研究中,本文获得的格陵兰冰盖整体消融速度明显高于既往研究成果.虽然本文采用的观测数据时间跨度与其他研究略有不同,但当采用2003年10月至2008年3月间的数据并按照本文算法进行计算时,其结果与表 3所给出的本文结果之间的差异不到10 km3·a-1,与Schenk和Csathó(2012)的研究结论一致,因此,时间差异并不是本文结果与国外结果产生差异的主要原因.
除ICESat数据以外,Schenk和Csathó(2012)的研究还采用了ATM机载测高数据,局部地区的数据空间分辨率更高,比表 3中的其他结果更具可靠性,而该结果与本文结果较为接近,说明本文的结果是准确的.对于冰盖局部区域结果的对比则表明本文并没有过高地估计格陵兰消融速度.例如,在高程2200 m以上的冰盖内陆区域(占格陵兰冰盖总面50%以上),本文获得高程变化速度为+0.8 cm·a-1,而Zwally等(2011)的结果(ICESat单一数据源)为+1.0 cm·a-1,对应的体积变化差异仅为-2 km3·a-1左右.在冰盖边缘区域,本文结果则与融合了多源数据的观测结果较为接近,例如Howat等(2005)联合ICESat测高和ASTER遥感影像数据得到的格陵兰冰盖东南沿海2000 m高程以下区域冰川体积变化为-80.4 km3·a-1,Hurkmans等(2012)联合ICESat卫星测高数据、ATM机载测高数据对雅各布港冰川的研究表明该区域冰川流失速度为-20.5 km3·a-1,Kjeldsen等(2013)同样利用ICESat和ATM数据对西北沿海冰川进行了研究,得到的体积变化为-55.8 km3·a-1,而本文在这些地区的结果分别为-75.6、-20.3以及-51.9 km3·a-1.
上述对比表明本文对格陵兰冰盖体积变化的估计是可靠的,而造成表 3中结果差异的原因主要是计算方法的不同,本文对算法的改进以及低阶坡度拟合函数的应用都提高了数据的空间分布率,特别是在冰盖边缘地区,数据量的增加能够更好地反映冰川流失情况,从而更准确地估计冰盖整体的体积变化速度.
4 冰川流域体积和高程变化分析为更好地对格陵兰冰盖进行研究和分析,Zwally等(2012)根据冰川流向将格陵兰冰盖划分为8个冰川流域系统,每个流域又分割为若干个子流域(如图 8中灰色实线所示).在流域划分的基础上,本文以2000 m等高线(图 8中黑色虚线)为界进一步细分,分别计算了每个区域内冰盖的体积变化情况,如表 4所示.需要注意的是,表 4中结果只含格陵兰冰盖主体,与冰盖不相连的独立冰川、冰帽等都未统计在内,因此表 4中总和与3.3节的结果相差了约60 km3·a-1,这几乎是格陵兰冰盖体积流失总量的四分之一,可见格陵兰岛周边独立冰盖和冰帽的流失情况也非常严重,甚至有研究认为这些独立冰川与冰帽的消融速度达到了格陵兰冰盖本体的2.5倍(Bolch et al., 2013).
|
|
表 4 格陵兰冰盖体积变化分区统计 Table 4 Summary of volume change rates in different regions in Greenland Ice Sheet |
根据表 4结果可知,从各流域系统来看,仅有DS2流域有体积增长的趋势,而DS3、DS4、DS7和DS8都呈现较严重的下降趋势.冰盖体积流失主要发生在2000 m以下的沿海区域,其中DS1.2-1.4以及DS2.2处在大体平衡的状况,其余区域由于冰川流失严重,则都呈现明显的体积减少趋势.国外早期研究表明,由于雪层的堆积,格陵兰冰盖2000 m以上的区域处于明显的体积积聚状态,在2007年之前的高程上升速度约为2~6 cm·a-1(Johannessen et al., 2005;Zwally et al., 2005;Thomas et al., 2006;Slobbe et al., 2008).但表 4结果则显示该区域在2003—2009年间的体积变化仅为+1.90 km3·a-1(平均高程变化约为+0.2 cm·a-1),相较于此前的结果,其增长趋势明显下降.
为更好地分析格陵兰冰盖高程/体积变化情况,以表 4中的每块小区域为单位,用三次函数拟合其平均高程变化情况,即
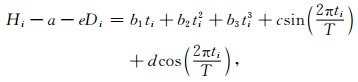
|
(6) |
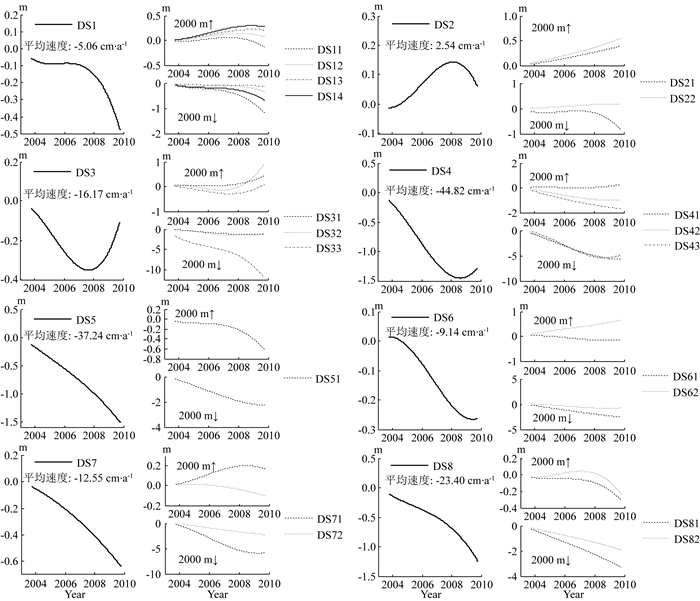
式中的a和e由(2)式的平差结果获得,bi为高程随时间变化的各阶系数.根据(6)式得到各区域高程变化趋势及平均速度如图 9所示.
|
图 9 格陵兰冰盖各流域高程变化,横轴表示时间,纵轴表示各流域高程变化数值 Fig. 9 Elevation change in different drainage system in Greenland Ice Sheet, where the horizontal axis stands for time and the vertical axis stands for elevation changes of each drainage system |
图 9结果表明,冰雪体积损失最严重的流域是DS4、DS5以及DS8,速度均超过-20 cm·a-1,这些区域冰川流失严重,因此,即使是2000 m高程以上的区域也出现了不同程度的下降趋势,特别是DS5和DS8的各个子流域,从2007年开始,其高程下降速度(2000 m以下)有明显加速趋势.DS3流域平均高程下降速度虽不如上述几个流域严重,但其中的子流域DS33却是所有子流域中累积高程下降最多的,其2000 m以下的区域在6年间下降了近10 m,且下降速度仍在加剧,其中的重要原因是位于该子流域的Kangerd冰川的流失(Howat et al., 2005).类似的情况还有DS7流域中的子流域DS71,全球流速最快的雅各布港冰川位于此处(Hurkmans et al., 2012),但不同与DS33的是,该区域的速度变化较为稳定,没有明显的加速趋势.
由于距离海岸较远,DS1、DS2、DS6流域以及DS3的DS31、DS32两个子流域体积损失并不严重甚至略有增加,多数区域2000 m以上都处在高程增长的状态,特别是位于气候更寒冷的格陵兰北部的DS22子流域,2000 m以下也处在高程增长的状态,这在格陵兰非常少见.但这些流域的变化情况并不能令人安心,其中的大部分区域在2007年之后都逐渐显现出下降趋势,例如DS1流域2000 m以上区域以及DS22子流域2000 m以下区域都由高程增加转为高程下降,DS12、DS13、DS14子流域2000 m以下区域下降速度明显加速,而DS21、DS32子流域以及DS6流域2000 m以下区域则是一直保持着下降趋势,速度较为稳定.
5 总结本文基于ICESat卫星激光测高数据,在对算法进行改进的基础上,采用重复轨迹法对格陵兰冰盖在2003年9月至2009年10月间的高程和体积变化进行了分析.通过与国外研究结果的对比发现,由于在坡度拟合和平差模型方面的改进,本文的算法可以提供更多的高程变化估值,从而提高结果的空间分辨率,减小格网化时的内插误差,更好地体现冰盖边缘体积变化.根据本文的结果,2003—2009年间格陵兰冰盖年平均体积变化约为-301.37±15.16 km3·a-1,体积损失主要发生在冰盖边缘,特别是西北沿海、东南沿海以及雅各布港等区域.而对格陵兰冰盖各流域高程变化的分析则表明,冰盖内陆地区高程2000 m以上的区域高程积聚的速度已经明显减缓,而且许多区域的高程变化趋势在2007年之后都发生了改变,表明格陵兰冰盖消融的情况仍在加剧.
致谢 感谢NSIDC提供ICESat数据产品、布里斯托大学Bamber教授提供格陵兰地区1 km分辨率地表类型格网数据、多伦多大学Peltier教授提供的ICE-6G冰后回弹模型、丹麦技术大学Khan教授提供的格陵兰岛弹性回弹模型以及美国国家航空航天局Zwally教授提供格陵兰冰盖冰川流域系统划分.感谢各位评审专家和编辑对本文的肯定以及提出的宝贵建议,为研究内容的完善提供了许多有益的帮助.
Bamber J L, Griggs J A, Hurkmans R T W L, et al. 2013. A new bed elevation dataset for Greenland. The Cryosphere, 7(2): 499-510. DOI:10.5194/tc-7-499-2013 |
Bekryaev R V, Polyakov I V, Alexeev V A. 2010. Role of polar amplification in long-term surface air temperature variations and modern Arctic warming. Journal of Climate, 23(14): 3888-3906. DOI:10.1175/2010JCLI3297.1 |
Bolch T, Sandberg Sørensen L, Simonsen S B, et al. 2013. Mass loss of Greenland's glaciers and ice caps 2003-2008 revealed from ICESat laser altimetry data. Geophysical Research Letters, 40(5): 875-881. DOI:10.1002/grl.50270 |
Borsa A A, Moholdt G, Fricker H A, et al. 2014. A range correction for ICESat and its potential impact on ice-sheet mass balance studies. The Cryosphere, 8(2): 345-357. DOI:10.5194/tc-8-345-2014 |
Chen G D. 2015. Study on the methodology of determining ice and snow melting in arctic using ICESat data[Ph.D.thesis] (in Chinese). Wuhan: Wuhan University.
|
Ewert H, Groh A, Dietrich R. 2012. Volume and mass changes of the Greenland ice sheet inferred from ICESat and GRACE. Journal of Geodynamics, 59-60: 111-123. DOI:10.1016/j.jog.2011.06.003 |
Hofton M A, Luthcke S B, Blair J B. 2013. Estimation of ICESat intercampaign elevation biases from comparison of lidar data in East Antarctica. Geophysical Research Letters, 40(21): 5698-5703. DOI:10.1002/2013GL057652 |
Howat I M, Joughin I, Tulaczyk S, et al. 2005. Rapid retreat and acceleration of Helheim Glacier, east Greenland. Geophysical Research Letters, 32(22): L22502. DOI:10.1029/2005GL024737 |
Huang H L. 2011. Determination of polar ice sheet change from ICESat and GRACE satellite observations[Ph.D.thesis] (in Chinese). Wuhan: Wuhan University.
|
Hurkmans R T W L, Bamber J L, Sørensen L S, et al. 2012. Spatiotemporal interpolation of elevation changes derived from satellite altimetry for Jakobshavn Isbræ, Greenland. Journal of Geophysical Research, 117(F3): F03001. DOI:10.1029/2011JF002072 |
Johannessen O M, Khvorostovsky K, Miles M W, et al. 2005. Recent ice-sheet growth in the interior of Greenland. Science, 310(5750): 1013-1016. DOI:10.1126/science.1115356 |
Khan S A, Liu L, Wahr J, et al. 2010. GPS measurements of crustal uplift near Jakobshavn Isbræ due to glacial ice mass loss. Journal of Geophysical Research, 115(B9): B09405. DOI:10.1029/2010JB007490 |
Kjeldsen K K, Khan S A, Wahr J, et al. 2013. Improved ice loss estimate of the northwestern Greenland ice sheet. Journal of Geophysical Research, 118(2): 698-708. |
Li F, Yuan L X, Zhang S K, et al. 2016. Mass change of the Antarctic ice sheet derived from ICESat laser altimetry. Chinese Journal of Geophysics (in Chinese), 59(1): 93-100. DOI:10.6038/cjg20160108 |
Ma Y, Yang F L, Wang M W, et al. 2015. Calculation of elevation changing of Greenland's ice sheet using GLAS laser altimeter. Infrared and Laser Engineering (in Chinese), 44(12): 3565-3569. |
Peltier W R, Argus D F, Drummond R. 2015. Space geodesy constrains ice age terminal deglaciation:the global ICE-6G_C (VM5a) model. Journal of Geophysical Research, 120(1): 450-487. |
Pritchard H D, Arthern R J, Vaughan D G, et al. 2009. Extensive dynamic thinning on the margins of the Greenland and Antarctic ice sheets. Nature, 461(7266): 971-975. DOI:10.1038/nature08471 |
Schenk T, Csathó B. 2012. A new methodology for detecting ice sheet surface elevation changes from laser altimetry data. IEEE Transactions on Geoscience and Remote Sensing, 50(9): 3302-3316. DOI:10.1109/TGRS.2011.2182357 |
Shepherd A, Ivins E R, A G, et al. 2012. A reconciled estimate of ice-sheet mass balance. Science, 338(6111): 1183-1189. DOI:10.1126/science.1228102 |
Shi H L, Lu Y, Du Z L, et al. 2011. Mass change detection in Antarctic ice sheet using ICESat block analysis techniques from 2003-2008. Chinese Journal of Geophysics (in Chinese), 54(4): 958-965. DOI:10.3969/j.issn.0001-5733.2011.04.010 |
Siegfried M R, Hawley R L, Burkhart J F. 2011. High-resolution ground-based GPS measurements show intercampaign bias in ICESat elevation data near summit, Greenland. IEEE Transactions on Geoscience and Remote Sensing, 49(6): 3393-3400. DOI:10.1109/TGRS.2011.2127483 |
Slobbe D C, Lindenbergh R C, Ditmar P. 2008. Estimation of volume change rates of Greenland's ice sheet from ICESat data using overlapping footprints. Remote Sensing of Environment, 112(12): 4204-4213. DOI:10.1016/j.rse.2008.07.004 |
Sørensen L S, Simonsen S B, Nielsen K, et al. 2011. Mass balance of the Greenland ice sheet (2003-2008) from ICESat data-the impact of interpolation, sampling and firn density. The Cryosphere, 5(1): 173-186. DOI:10.5194/tc-5-173-2011 |
Spada G, Ruggieri G, Sørensen L S, et al. 2012. Greenland uplift and regional sea level changes from ICESat observations and GIA modelling. Geophysical Journal International, 189(3): 1457-1474. DOI:10.1111/gji.2012.189.issue-3 |
Thomas R, Frederick E, Krabill W, et al. 2006. Progressive increase in ice loss from Greenland. Geophysical Research Letters, 33(10): L10503. DOI:10.1029/2006GL026075 |
Zwally H J, Giovinetto M B, Li J, et al. 2005. Mass changes of the Greenland and Antarctic ice sheets and shelves and contributions to sea-level rise:1992-2002. Journal of Glaciology, 51(175): 509-527. DOI:10.3189/172756505781829007 |
Zwally H J, Li J, Brenner A C, et al. 2011. Greenland ice sheet mass balance:distribution of increased mass loss with climate warming; 2003-07 versus 1992-2002. Journal of Glaciology, 57(201): 88-102. DOI:10.3189/002214311795306682 |
Zwally H J, Giovinetto M B, Beckley M A, et al. 2012. Antarctic and Greenland drainage systems. GSFC Cryospheric Sciences Laboratory. http://icesat4.gsfc.nasa.gov/cryo_data/ant_grn_drainage_systems.php.
|
陈国栋. 2015.利用ICESat数据确定北极冰雪消融方法的研究[博士论文].武汉: 武汉大学.
|
黄海兰. 2011.利用ICESat和GRACE卫星观测数据确定极地冰盖变化[博士论文].武汉: 武汉大学.
|
李斐, 袁乐先, 张胜凯, 等. 2016. 利用ICESat数据解算南极冰盖冰雪质量变化. 地球物理学报, 59(1): 93-100. DOI:10.6038/cjg20160108 |
马跃, 阳凡林, 王明伟, 等. 2015. 利用GLAS激光测高仪计算格陵兰冰盖高程变化. 红外与激光工程, 44(12): 3565-3569. DOI:10.3969/j.issn.1007-2276.2015.12.011 |
史红岭, 陆洋, 杜宗亮, 等. 2011. 基于ICESat块域分析法探测2003-2008年南极冰盖质量变化. 地球物理学报, 54(4): 958-965. DOI:10.3969/j.issn.0001-5733.2011.04.010 |
 2019, Vol. 62
2019, Vol. 62

